Иные способы выведения прямого угла
Если нет желания заниматься выведением углов самостоятельно, а финансы позволяют обратиться за помощью к специалистам, можно вообще не думать об этом вопросе. Один звонок − и на участке уже находится геодезист с теоделитом, который в сжатые сроки сделает разметку. Однако в этом случае необходимо быть готовым к внушительным затратам на оплату его труда.
ФОТО: omegagalvanoplastia.com.brТеоделит – высокоточная техника, однако стоимость подобной разметки может влететь «в копеечку»
Если говорить о минимальных затратах, то, основываясь на прайс-листах фирм, оказывающих подобные услуги, вызов и работа геодезиста с инструментом обойдётся в 1 000 руб./час при минимальной оплате 7 000 руб. Дальше − больше. Разметка осей (2 точки) – ещё 3 000 рублей. Если же потребуется определить точные координаты по GPS, то здесь каждые три точки обойдутся владельцу в 5 000 руб. Можно посчитать, какова будет общая сумма (все цены указаны с учётом на конец сентября 2020 года). Не проще ли самому произвести все необходимые разметки? Ведь сэкономленные средства всегда можно потратить на что-то полезное в дальнейшем строительстве.
ФОТО: thelundreport.orgСтоит приготовиться к тому, что карман значительно облегчится
Основные величины и их формулы
Все геометрические фигуры имеют свои характеристики и собственную величину. Самыми распространёнными являются такие величины как площадь и периметр. Они используются в повседневной жизни, в строительстве и в других областях. Например, во время ремонта или нового строительства, количество необходимых материалов и объём работ не определить, не вычислив заранее площадь и периметр.
Периметр
Периметром называется замкнутая граница плоской геометрической фигуры, которая отделяет её внутреннюю область от внешней. Периметр есть у любой замкнутой геометрической фигуры:
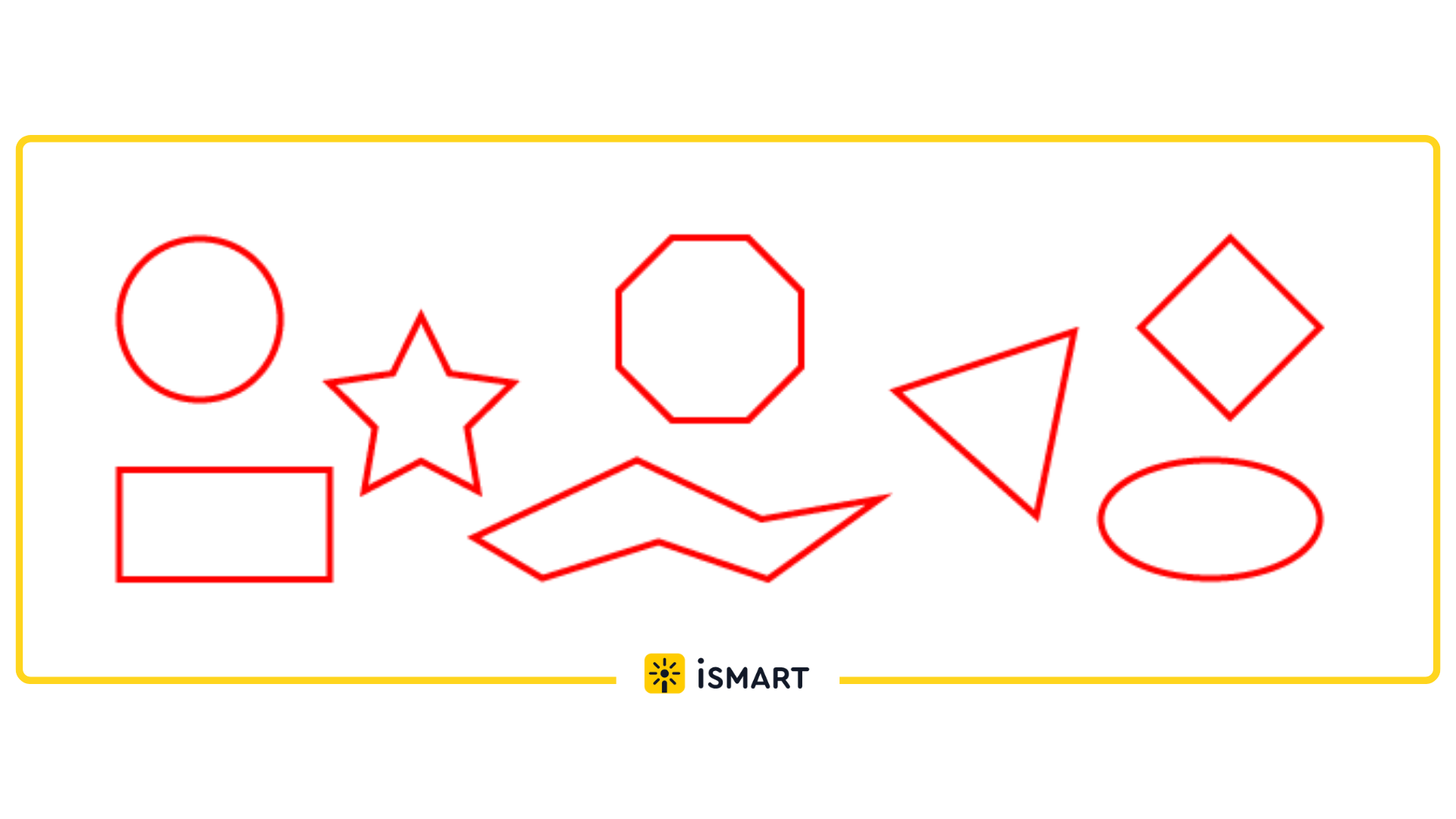
На рисунке периметры выделены красной линией. Периметр окружности часто называют длиной.
Периметр измеряется в единицах измерения длины: мм, см, дм, м, км.
Обозначается заглавной латинской P.
Площадь
Площадь — это часть плоскости, занимаемая замкнутой плоской геометрической фигурой, то есть та часть плоскости, которая находится внутри периметра. Именно она даёт нам основную информацию о её размере. Любая плоская замкнутая геометрическая фигура имеет определённую площадь.
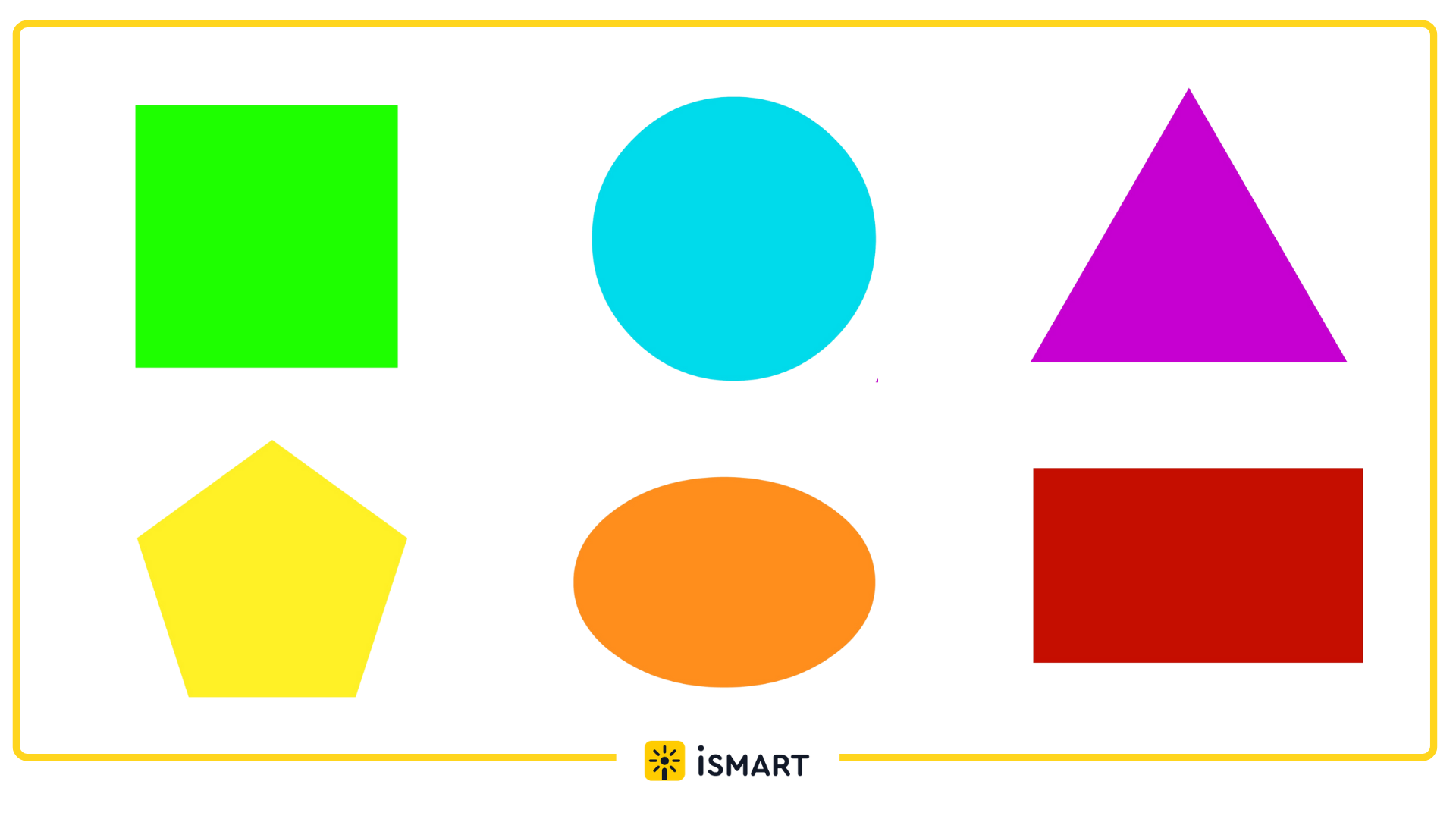
На рисунке площади фигур окрашены различными цветами.
Измерить площадь фигуры — значит найти, сколько раз в данной фигуре помещается другая фигура, принятая за единицу измерения. Площадь измеряется в квадратных единицах измерения длины. К единицам измерения площади относятся: мм2, см2, м2, км2 и т. д. S (square) — знак площади.
Вычисление периметра и площади
Периметр — это длина замкнутого контура геометрической фигуры. Можно, конечно, измерить линейкой длины всех сторон и сложить их. Но лучше воспользоваться специальными формулами для вычисления периметра, это значительно упростит задачу.
- Квадрат: периметр = 4 * сторона.
- Треугольник: периметр = сторона 1 + сторона 2 + сторона 3.
- Неправильный многоугольник: периметр = сумме всех сторон многоугольника.
- Круг: длина окружности = 2 * π * радиус = π * диаметр (где π – это число пи (константа, примерно равная 3,14), радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности, диаметр – это длина отрезка, проходящего через центр окружности и соединяющего любые две точки, лежащие на этой окружности).
Для вычисления площади фигуры также потребуется соответствующая формула. К разным фигурам применяются разные формулы. Для вычисления площади стандартных геометрических фигур можно воспользоваться следующими формулами:
- Параллелограмм: площадь = основание * высота
- Квадрат: площадь = сторона 1 * сторона 2
- Треугольник: площадь = ½ * основание * высота
- Круг: площадь = π * радиус² (где радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности. Квадрат радиуса – это значение радиуса, умноженное само на себя).
Итак, мы перечислили основные и самые распространённые геометрические фигуры и их свойства. Образовательная платформа iSmart поможет вашему ребёнок изучить основные геометрические фигуры, их виды, названия и свойства с помощью увлекательных заданий. Преимущества занятий на умных тренажёрах iSmart:
- интерактивные задания больше похожи на игру;
- их можно отрабатывать многократно и они не будут повторяться;
- платформа сформирует индивидуальную траекторию обучения на основе диагностики знаний;
- достаточно всего 20 минут занятий в день, чтобы в короткий срок увидеть прогресс в обучении.
Кроме того, занятия помогут вам освободить своё время, ведь ребёнок сможет заниматься самостоятельно, а родитель — получать отчёты и наблюдать за динамикой обучения. Метод обучения iSmart основан на последних научных практиках: микрообучение и поведенческий анализ.
Образовательная платформа iSmart предлагает подготовку к контрольным работам, тестам, ВПР, олимпиадам, а также изучение дополнительных предметов, не вошедших в школьную программу.
Элементы остроугольного треугольника:
Кроме сторон и углов у одностороннего треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. остроугольного, 6 внешних углов, по 2 на каждый внутренний. Любой внешний угол остроугольного треугольника всегда будет тупым углом.
Рис. 4. Остроугольный треугольник и внешний угол
∠ ВСD – внешний угол
Медиана остроугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.
Рис. 5. Остроугольный треугольник и медиана остроугольного треугольника
MС – медиана остроугольного треугольника
Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Рис. 6. Остроугольный треугольник и высота остроугольного треугольника
MС – высота остроугольного треугольника
Высота остроугольного треугольника находится внутри треугольника. Все 3 высоты остроугольного треугольника (как и любого треугольника) пересекаются в одной точке, называемой ортоцентром.
Биссектриса в остроугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы пересекаются в точке, которая является центром вписанной окружности.
Рис. 7. Остроугольный треугольник и биссектриса угла остроугольного треугольника
MС – биссектриса угла остроугольного треугольника
Кроме того, биссектриса остроугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Кому подойдет
Татуировка с ромбом подходит чувственным и эмоциональным людям с неординарным мышлением и специфическим восприятием мира. Обладатели тату с таким символом имеют свой взгляд на обычные вещи, интересуются философией и стремятся познать сущность бытия.
Поскольку ромб с древних времен ассоциировался с женским началом, он очень актуален для женщин, мечтающих познать радость материнства. При выборе эскиза нужно отдавать предпочтение лаконичной фигуре с точками или узорами внутри. Заполненный ромб ассоциируется с плодородием, женственностью и материнством.
У тату ромб значение во многом зависит от того, где располагается рисунок. Наличие символа внутри другой геометрической фигуры, квадрата, на безымянном пальце выдает бывшего заключенного, принадлежавшего к низшей касте в криминальном мире. Заштрихованный в том же месте ромб свидетельствует о том, что человека наказали по преступным законам, и он исправился. Оба варианта относятся к тюремным наколкам, поэтому людям, не имеющим отношения к криминальной среде, рекомендуется воздержаться от нанесения подобных тату, чтобы избежать возможных неприятных ситуаций.
Слайд 11Папирус Ахмеса Папирус Ахмеса был обнаружен в
1858 году. В 1870 он был расшифрован, переведён и издан.
Ныне большая часть рукописи находится в Британском музее в Лондоне, а вторая часть — в Нью-Йорке. Он представляет собой собрание решений 84 задач, имеющих прикладной характер; эти задачи относятся к действиям с дробями, определению площади прямоугольника, треугольника, трапеции и круга, объёма прямоугольного параллелепипеда и цилиндра; имеются также арифметические задачи на пропорциональное деление, определение соотношений между количеством зерна и получающегося из него хлеба или пива; решение одной задачи приводится к вычислению суммы геометрической прогрессии. Однако для решения этих задач не даётся никаких общих правил, не говоря уже о попытках каких-нибудь теоретических обобщений.

Толстость окружностей, эллипсов и их частей
Тонкость круга по шарику, конечно же, равна 1 — наименьшее возможное значение.
Для кругового сегмента с центральным углом θ диаметр описанной окружности — это длина хорды, а диаметр вписанной окружности — это высота сегмента, поэтому тонкость двух шариков (и ее приближение когда θ мало ):
- длина хорды высота сегмента = 2 R sin θ 2 R (1 — cos θ 2) = 2 sin θ 2 (1 — cos θ 2) ≈ θ θ 2/8 = 8 θ {\ displaystyle {\ frac {\ text {длина хорды}} {\ text {высота сегмента}}} = {\ frac {2R \ sin {\ frac {\ theta} { 2}}} {R \ left (1- \ cos {\ frac {\ theta} {2}} \ right)}} = {\ frac {2 \ sin {\ frac {\ theta} {2}}} { \ left (1- \ cos {\ frac {\ theta} {2}} \ right)}} \ приблизительно {\ frac {\ theta} {\ theta ^ {2} / 8}} = {\ frac {8} {\ theta}}}
Для кругового сектора с центральным углом θ (когда θ мало) диаметр описанной окружности — это радиус окружности, а диаметр вписанной окружности — это длина хорды, поэтому тонкость двух шаров составляет:
- радиус окружности длина хорды = R 2 R sin θ 2 = 1 2 sin θ 2 ≈ 1 2 θ / 2 = 1 θ {\ displaystyle {\ frac {\ text {radiu s круга}} {\ text {длина хорды}}} = {\ frac {R} {2R \ sin {\ frac {\ theta} {2}}}} = {\ frac {1} {2 \ sin {\ frac {\ theta} {2}}}} \ приблизительно {\ frac {1} {2 \ theta / 2}} = {\ frac {1} {\ theta}}}
Для эллипса коэффициенты тонкости в разных местах различаются. Например, рассмотрим эллипс с короткой осью a и длинной осью b. длина хорды находится в диапазоне от 2 a sin θ 2 {\ displaystyle 2a \ sin {\ frac {\ theta} {2}}}на узкой стороне эллипса до 2 b sin θ 2 {\ displaystyle 2b \ sin {\ frac {\ theta} {2}}}на его широкой стороне; аналогично, высота сегмента находится в диапазоне b (1 — cos θ 2) {\ displaystyle b \ left (1- \ cos {\ frac {\ theta} {2}} \ right)}на узкой стороне и a (1 — cos θ 2) {\ displaystyle a \ left (1- \ cos {\ frac {\ theta} {2}} \ right)}на широкой стороне. Таким образом, толщина двух шаров составляет:
- 2 a sin θ 2 b (1 — cos θ 2) ≈ 8 ab θ {\ displaystyle {\ frac {2a \ sin {\ frac {\ theta} {2 }}} {b \ left (1- \ cos {\ frac {\ theta} {2}} \ right)}} \ приблизительно {\ frac {8a} {b \ theta}}}
и:
- 2 б грех θ 2 a (1 — соз θ 2) ≈ 8 ba θ {\ displaystyle {\ frac {2b \ sin {\ frac {\ theta} {2}}} {a \ left (1- \ cos {\ frac {\ theta} {2}} \ right)}} \ приблизительно {\ frac {8b} {a \ theta}}}
В общем, когда секущая начинается под углом, коэффициент тонкости может быть приблизительно:
- 2 грех θ 2 (1 — соз θ 2) {\ displaystyle {\ frac {2 \ sin {\ frac {\ theta} {2}}} {\ left (1- \ cos { \ гидроразрыва {\ theta} {2}} \ right)}}}(ba cos 2 (Θ + θ 2) + ab sin 2 (Θ + θ 2)) {\ displaystyle \ left ({\ frac {b} {a}} \ cos ^ {2} (\ Theta + {\ frac {\ theta} {2}}) + {\ frac {a} {b}} \ sin ^ {2} (\ Theta + {\ frac {\ theta} {2}}) \ right)}
Подсчет толстых объектов
Если объект o имеет диаметр 2a, то каждый шар, охватывающий o, должен иметь радиус не менее a и объемом не менее V d a. Следовательно, по определению толщины охватывающего шара объем объекта с R-жиром диаметром 2a должен быть не менее: V d a / R. Следовательно:
- Лемма 1 : Пусть R≥1 и C≥0 — две константы. Рассмотрим набор неперекрывающихся d-мерных объектов, которые в глобальном масштабе являются R-толстыми (т.е. с тонкостью охватывающего шара ≤ R). Количество таких объектов диаметром не менее 2a, содержащихся в шаре радиуса C⋅a, не превосходит:
- V d ⋅ (C a) d / (V d ⋅ ad / R d) = (RC) d {\ displaystyle V_ {d} \ cdot (Ca) ^ {d} / (V_ {d} \ cdot a ^ {d} / R ^ {d}) = (RC) ^ {d}}
Для пример (принимая d = 2, R = 1 и C = 3): количество неперекрывающихся дисков с радиусом не менее 1, содержащихся в окружности радиуса 3, не превышает 3 = 9. (На самом деле это максимум 7).
Если мы рассматриваем локальную жирность вместо глобальной, мы можем получить более сильную лемму:
- Лемма 2 : Пусть R≥1 и C≥0 — две константы. Рассмотрим набор неперекрывающихся d-мерных объектов, которые все являются локально R-толстыми (то есть с локальной тонкостью охватывающего шара ≤ R). Пусть o будет единственным объектом в этой коллекции с диаметром 2a. Тогда количество объектов в коллекции диаметром больше 2a, находящихся на расстоянии 2C⋅a от объекта o, не превышает:
- (4 R ⋅ (C + 1)) d {\ displaystyle (4R \ cdot (C +1)) ^ {d}}
Например (принимая d = 2, R = 1 и C = 0): количество неперекрывающихся дисков с радиусом больше 1, которые касаются данного единичного диска, не превышает 4 = 16 (это не точная оценка, поскольку в этом случае легко доказать верхнюю оценку 5).
Признаки равенства прямоугольных треугольников
Для прямоугольных треугольников, кроме перечисленных трёх признаков равенства, имеются ещё дополнительные признаки, так как у них у всех есть прямой угол, а все прямые углы равны между собой.
Два прямоугольных треугольника будут равны в следующих четырёх случаях:
- Если катеты одного треугольника равны катетам другого.
- Если катет и прилежащий к нему острый угол одного треугольника равны катету и прилежащему к нему острому углу другого.
- Если гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого.
- Если гипотенуза и катет одного треугольника равны гипотенузе и катету другого.
Древнее происхождение
Некоторые знаки появились задолго до нашей эры, и точно определить их первоначальное значение теперь практически невозможно. Древнейшим символом триединства стало изображение треугольника, которое можно наблюдать в виде вырезов на кости и рисунков на первой керамике каменного века.
Со временем появлялись круги, точки, спирали, другие фигуры, составлявшие окружность или треугольник. Не всегда подобные рисунки имели какое-либо значение, чаще всего они были просто орнаментом. Порой такие изображения отмечали места культов и погребений.
С развитием богатой мифологии и организованной религии древних египтян, шумеров, греков, кельтов, иранских и других народов некоторые знаки стали священными. Они символизировали триады богов или ипостаси одного божества, трех его качеств и проявлений, обозначали мир высший, человеческий, подземный, процесс от рождения до смерти, а также другие представления о мироздании.
В период формирования античной философии, астрономии, геометрии знаки триад обрели дополнительное значение.
Целое, состоящее из трех частей, означало человеческие качества, состояния, действия, природные явления, стихии, небесные объекты, временные соотношения, виды искусства, математические функции, другие понятия. Появились визуальные варианты пересекающихся элементов треугольных форм и сочетания их с другими геометрическими фигурами.
Вариации символа были найдены в ходе многочисленных археологический раскопок. Мистический символ часто встречался с тремя головами, завязанным ртом или глазами. Эти разновидности талисмана можно отнести к символизму. Данные обереги напоминают о том, что нельзя полагаться и оценивать происходящее лишь по внешнему облику, необходимо понять суть, и только после этого делать выводы.
Также призывают осознать единство Тела и человеческой Души. Огромное значение для каждого человека имеют его собственные мысли и поступки. Необходимо стремиться к правильному образу жизни, включающему добрые помыслы и искреннее отношение к окружающим, только тогда может наступить мир и гармония.
Внимание также нужно уделять саморазвитию, оно поможет постичь много нового и является достижением мудрости
Чье это место?
Заготовьте коробку с прорезанными в ней разного размера отверстиями геометрических форм — круга, квадрата, а также предметы соответствующей формы для этих отверстий. Ребенок должен неоднократно практически «примерить» геометрическую форму к отверстию в коробке, чтобы убедиться, что круг и квадрат проходят только в соответствующие вырезы и любой стороной.
Найди форму своего предмета
Подберите картинки с изображением предметов различной формы.
Круглые: мяч, колечко, глобус, шарик, печенье, яблоко, апельсин, помидор.
Овальные: яйцо, огурец, лимон, слива, батон.
Четырехугольные: конверт, портфель, окно, книга, аквариум, шкаф.
Треугольные: крыша, колпак, сачок, флажок.
Лучше наклеить подобранные картинки на карточки соответствующего размера — ими удобнее пользоваться и в таком виде они дольше сохраняют опрятный вид.
В игру можно подключить и других детей. Раздайте всем карточки с изображением предметов. На стулья положите карточки с изображением геометрической формы: круг, квадрат, треугольник, овал, прямоугольник. По сигналу «В свой домик» ребенок должен подбежать к стулу с карточкой соответствующего предмета, изображенного на его карточке. Карточками дети потом меняются.
Устаревший эллипс: какой геометрической фигурой его можно заменить?
Эллипс — это геометрическая фигура, которая представляет собой замкнутую кривую линию, образованную точками, для которых сумма расстояний от двух фокусов эллипса постоянна. Однако, в современной геометрии эллипс можно считать немного устаревшей фигурой, поскольку в большинстве случаев его функции могут быть заменены другими геометрическими фигурами, которые обладают аналогичными свойствами.
Одной из самых простых и практичных замен эллипса может быть окружность. Окружность, как и эллипс, является замкнутой кривой линией, но в отличие от эллипса, у нее все точки находятся на одинаковом расстоянии от центра окружности. Окружность имеет множество применений и хорошо изучена в геометрии. Поэтому, если нет особой необходимости использовать именно эллипс, окружность можно рассматривать как альтернативу.
Еще одним возможным вариантом замены эллипса может быть прямоугольник. Прямоугольник также является замкнутой кривой линией и обладает свойством, что все его углы равны 90 градусов. Хотя прямоугольник не обладает теми же свойствами, что и эллипс, он может быть использован во многих ситуациях, например, для представления объектов с прямыми углами в плоскости. Кроме того, прямоугольник также легко можно рассматривать как более общий случай эллипса.
Таким образом, если вам необходимо заменить эллипс в геометрической задаче, двумя основными альтернативами могут быть окружность или прямоугольник. Выбор конкретной фигуры зависит от контекста и специфических требований задачи, но в большинстве случаев эти альтернативы позволяют достаточно точно заменить функционал эллипса.
Как поэтапно рисовать 3D треугольник
Сейчас 3D рисунки очень популярны. Люди восхищаются нарисованными от руки реалистичными изображениями, которые, кажется, могут в любую секунду ожить.
Создавать изображение в трехмерном пространстве только кажется трудно. Предлагаем освоить основы 3D искусства с нашей пошаговой инструкцией.
1
Нарисуйте квадрат средней величины. Если хотите, чтобы рисунок был больше, увеличьте основу.

2
Внутри квадрата изобразите треугольник в плоском измерении. Нижняя сторона является частью квадрата.
3
Аккуратно стираем квадрат и оставляем только треугольник.
4
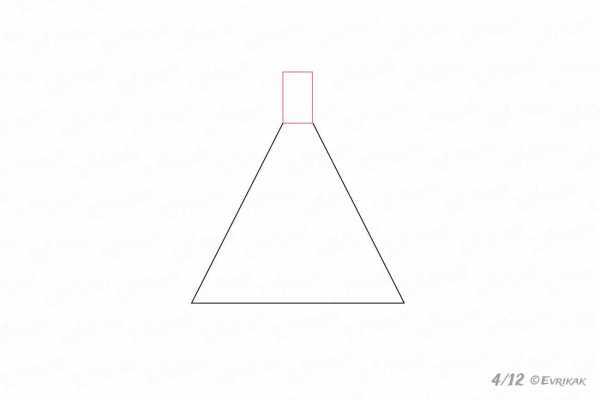
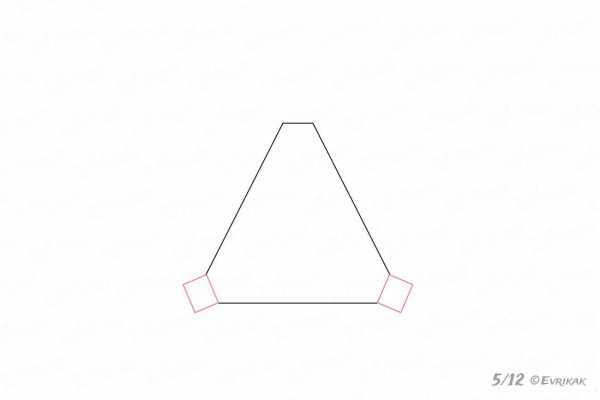
5
Прямоугольники аккуратно стираем, оставляя треугольник со срезанными углами.
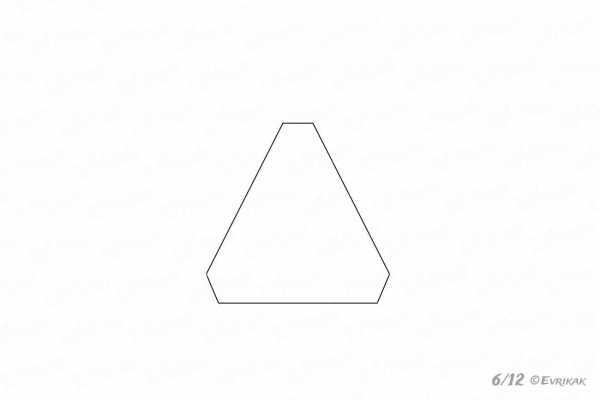
7
Третье измерение
От верхней левой линии проводим еще одну вниз, будто изображая маленький треугольник. Еще одну горизонтальную часть изображаем справа.

Соединяем все последней линией, которая начинается от первой горизонтальной.

8
Раскрашиваем
Чтобы 3D треугольник выглядел более реалистично, нужно его правильно раскрасить. Можете использовать один цвет, как показано на рисунке, но внутренние детали сделать более темными.

Выберите как хотите закрашивать.
9
Тату-треугольник на локтях: трактовка, фото, идеи
Объединение растительного мотива в треугольник указывает на то, что человек может возродиться в любой из своих циклов. То есть в юность, зрелость и в старость. В любом этом периоде жизни хозяин тату в состоянии найти себя.
Татуировка в виде треугольника на локтях
Множество треугольников в одном треугольнике – многократное усиление значения фигуры. То есть красоты, силы, мудрости. Человек стремится получить в виде татуировки мощный оберег, который поможет обрести гармонию.
Черный треугольник – эта тату-треугольник может быть отнесена к популярному сейчас стилю блэк-ворк. Подобные изображения отлично перекрывают неудачные тату или шрамы, а также стильно смотрятся. Особенно рекомендованы людям с жестким характером – блэк-ворк треугольник отлично подчеркнет внутреннюю силу своего хозяина.
Еще два варианта тату в виде треугольников
Развитие геометрии в Древней Греции
Древняя Греция считается одним из кульминационных пунктов в развитии геометрии. Большой вклад в развитие этой науки внесли древнегреческие математики, такие как Пифагор, Евклид и Архимед.
Пифагор известен как основатель теоремы, названной в его честь. Он установил, что в прямоугольном треугольнике сумма квадратов двух катетов равна квадрату гипотенузы. Эта теорема стала одной из основных основ геометрии и находит широкое применение в различных областях науки и техники.
Евклид, в свою очередь, создал знаменитые «Элементы» — сборник, включающий в себя аксиомы, определения и доказательства геометрических теорем. Содержание «Элементов» стало непреходящим классическим наследием и является основой современной геометрии.
Архимед также внес весомый вклад в развитие геометрии. Он изучал площади кривых, обьемы ицентры различных фигур, подняв геометрию на новый уровень. Он также известен своими многочисленными открытиями в области механики и физики.
Развитие геометрии в Древней Греции имело огромное значение для последующих научных исследований. Великие греческие ученые продолжили свое наследие, и их открытия стали фундаментом для развития современной геометрии.
Слайд 5Измерения. В строительстве очень важно было
знать площадь участка, отведенного под застройку. Для этого древние египтяне
использовали особый треугольник, у которого были фиксированные длины сторон. Занимались измерениями особые специалисты, их называли «натягивателями веревки» — гарпетонаптами. Они брали длинную веревку, делили ее узелками (расстояние между ними равно одному локтю фараона) на двенадцать частей, а концы ее связывали. В направлении север-юг строители устанавливали два колышка на расстоянии четырех частей, отмеченных на веревке. Затем при помощи третьего колышка натягивали ее так, чтобы образовался треугольник, у которого одна сторона имела 3 части, другая 4, а третья — 5. Получался прямоугольный треугольник, площадь которого принимали за эталон, если пользовались одной и той же веревкой. При этом сторона, имеющая три части, указывала восточно-западное направление.

Свойства остроугольного треугольника:
Свойства остроугольного треугольника аналогичны свойствам обычного треугольника:
1. Против большей стороны лежит больший угол, и наоборот.
Рис. 8. Остроугольный треугольник
2. Против равных сторон лежат равные углы, и наоборот.
Рис. 9. Остроугольный треугольник с равными боковыми сторонами
АВ = ВС
3. Сумма углов остроугольного треугольника равна 180°.
4. Любая сторона остроугольного треугольника меньше суммы двух других сторон и больше их разности:
-
- a < b + c;
- a > b – c;
- b < a + c,
- b > a – c;
- c < a + b;
- c > a – b.
Примечание: Фото https://www.pexels.com, https://pixabay.com
карта сайта
Коэффициент востребованности
1 792
Пифагор Пифагор Самосский. (ок. 580 – ок. 500 г. до н.э.)
(Пифагор VI век до н.э., основал свою школу).
Пифагор известен как великий ученый – философ, математик, выдающийся оратор и тонкий психолог.
Пифагор сделал много важных открытий, но наибольшую славу учёному принесла доказанная им теорема, которая сейчас носит его имя. Интересна история теоремы Пифагора. Хотя эта теорема и связывается с именем Пифагора, она была известна задолго до него. В вавилонских текстах она встречается за 1200 лет до Пифагора. По-видимому, он первым нашёл её доказательство. Сохранилось древнее предание, что в честь своего открытия Пифагор принёс в жертву богам быка, по другим свидетельствам – даже сто быков. Это, однако, противоречит сведениям о моральных и религиозных воззрениях Пифагора. В литературных источниках можно прочитать, что он «запрещал даже убивать животных, а тем более ими кормиться, ибо животные имеют душу, как и мы». В связи с этим более правдоподобной можно считать следующую запись: «… когда он открыл, что в прямоугольном треугольнике гипотенуза имеет соответствие с катетами, он принес в жертву быка, сделанного из пшеничного теста».
Пифагор организовал тайный союз молодёжи из представителей аристократии. В этот союз принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками. В школе существовал декрет, по которому авторство всех математических работ приписывалось учителю.
Пифагорейцами было сделано много важных открытий в арифметике и геометрии, в том числе:
теорема о сумме внутренних углов треугольника;
построение правильных многоугольников и деление плоскости на некоторые из них;
геометрические способы решения квадратных уравнений;
деление чисел на чётные и нечётные, простые и составные; введение фигурных, совершенных и дружественных чисел;
доказательство того, что не является рациональным числом;
создание математической теории музыки и учения об арифметических, геометрических и гармонических пропорциях и многое другое. (Слайд 16).
Черновые материалы[править]
Фигура, существующая в отрыве от «почвы» в угловатой и жесткой самодостаточности. Устойчивость ромба в его внутренней площади, а ударная сила — в остроте и прочности углов. Ромб — жесткая и «упрямая» фигура, сугубо автономная в своем существовании и обеспечивающая свою «живучесть» своеобразной, только ему присущей адаптационностью. Она заключается в способности изменять остроту углов и поперечное сечение. Иными словами, ромб способен предельно обострять свои углы, «вытягиваясь» в длину или, наоборот, превращаться в некое подобие квадрата, «поставленного» на угол. В первом случае острие, как жало, резко повышает разящую проникаемость, а во втором — образуется укрепленный со всех сторон форт. Знак ромба — символ «жесткой идеи», некой парадигмы, он, как и треугольник, олицетворяет ударную силу и могущество, при этом последнее качество у «ромбов» представлено весьма агрессивно. Ромб — это диктат единого властного центра, поэтому ромб как нельзя лучше олицетворяет персонализацию власти. Они предельно жестки и догматичны (жесткость и прочность ромбов обеспечивается изнутри крестовиной!), и для изменения конфигурации ромба должны быть очень веские причины, да и сам процесс подобной модификации для ромба отнюдь не безболезнен.
Пример задачи на использование 4 замечательных точек треугольника
Пример 1
Серединные перпендикуляры к сторонам $AB$ и $AC$ треугольника $ABC$ пересекаются в точке $D$ стороны $BC$. Докажите, что
а) точка $D$ — середина стороны $BC$.
б) $\angle A=\angle B+\angle C$
Решение.
Изобразим рисунок.
Рисунок 5.
а) По теореме 4, все серединные перпендикуляры пересекаются в точке $D$. Следовательно, $D$ — основание серединного перпендикуляра к стороне $BC$. Значит точка $D$ — середина стороны $BC$.
б) Так как $X$ и $D$ — середины сторон, то $XD$ — средняя линия треугольника. Тогда, по теореме о средней линии треугольника $XD||AC$. Значит,$\angle A=\angle DXB$, как соответственные углы. Значит, $\angle A={90}^0$. Тогда$\angle B+\angle C={180}^0-\angle A={180}^0-{90}^0={90}^0=\angle A$
ч. т. д.
Свойства тупоугольного треугольника:
Свойства тупоугольного треугольника аналогичны свойствам обычного треугольника:
1. Против большей стороны лежит больший угол, и наоборот.
Рис. 9. Тупоугольный треугольник
2. Против равных сторон лежат равные углы, и наоборот.
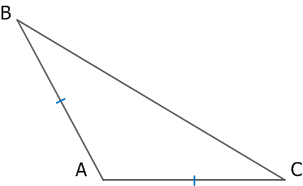
Рис. 10. Тупоугольный треугольник с равными боковыми сторонами
АВ = АС
3. Сумма углов тупоугольного треугольника равна 180°.
4. Любая сторона тупоугольного треугольника меньше суммы двух других сторон и больше их разности:
-
- a < b + c;
- a > b – c;
- b < a + c,
- b > a – c;
- c < a + b;
- c > a – b.
Примечание: Фото https://www.pexels.com, https://pixabay.com
карта сайта
Коэффициент востребованности
4 223


























