Что такое спектр сигнала для чайников?

Спектральная плотность мощности и автокорреляция

Расчет с использованием автокорреляции дает точную оценку ее, несмотря на то, что расчет автокорреляции требует больших ресурсов. Определение усредненной по времени автокорреляционной функции непрерывного сигнала x :

γ(τ)знак равноLimТ→∞12Т∫-Т+ТИкс*(т)Икс(т+τ)dт{\ displaystyle \ gamma (\ tau) = \ lim _ {T \ to \ infty} {\ frac {1} {2T}} \ int _ {- T} ^ {+ T} x ^ {*} (т) х (т + \ тау) \, дт}

где * — комплексное сопряжение .

В фокусе эта функция измеряет способ, которым структуры, которые можно увидеть в сигнале, повторяются во временных масштабах порядка .
τ{\ Displaystyle \ тау}τ{\ Displaystyle \ тау}

Свойства преобразования Фурье подразумевают, что спектральная плотность является преобразованием Фурье автокорреляции. Это теорема Винера — Хинчина :

Fγзнак равноFИкс×FИкс*(-)знак равноИкс⋅Икс*знак равноΓ{\ Displaystyle {\ mathcal {F}} = {\ mathcal {F}} \ times {\ mathcal {F}} = X \ cdot X ^ {*} = \ Gamma}

Согласно гипотезе эргодичности мы уподобляем автоковариантность сигнала (статистическое свойство) его автокорреляции (временное свойство). Это предположение не обязательно проверяется на практике, в частности, когда исследуемый процесс не является стационарным (для некоторых деталей см. Непрерывный процесс и Стационарный процесс ).

Детальный расчет

Подсчитаем преобразование Фурье автокорреляционной:
Γ(ω){\ displaystyle \ Gamma (\ omega)}

Γ(ω)знак равно∫-∞+∞∫-∞+∞Икс*(т)Икс(т+τ)е-ȷωτdтdτ{\ displaystyle \ Gamma (\ omega) = \ int _ {- \ infty} ^ {+ \ infty} \ int _ {- \ infty} ^ {+ \ infty} x ^ {*} (t) x (t + \ tau) e ^ {- \ jmath \ omega \ tau} \, dt \, d \ tau}, обозначающий мнимую единицу .ȷ{\ displaystyle \ jmath}

Это выражение можно записать в виде:

Γ(ω)знак равно∫-∞+∞(∫-∞+∞Икс(т+τ)е-ȷω(т+τ)dτ)Икс*(т)е+ȷωтdт{\ displaystyle \ Gamma (\ omega) = \ int _ {- \ infty} ^ {+ \ infty} \ left (\ int _ {- \ infty} ^ {+ \ infty} x (t + \ tau) e ^ {- \ jmath \ omega (t + \ tau)} d \ tau \ right) x ^ {*} (t) e ^ {+ \ jmath \ omega t} \, dt}

Произведем в центральном интеграле замену переменной u = t + τ и получим:

Γ(ω)знак равно∫-∞+∞(∫-∞+∞Икс(ты)е-ȷωтыdты)Икс*(т)е+ȷωтdт{\ displaystyle \ Gamma (\ omega) = \ int _ {- \ infty} ^ {+ \ infty} \ left (\ int _ {- \ infty} ^ {+ \ infty} x (u) e ^ {- \ jmath \ omega u} du \ right) x ^ {*} (t) e ^ {+ \ jmath \ omega t} \, dt}

Или еще раз:

Γ(ω)знак равноИкс(ω)∫-∞+∞Икс*(т)е+ȷωтdт{\ displaystyle \ Gamma (\ omega) = X (\ omega) \ int _ {- \ infty} ^ {+ \ infty} x ^ {*} (t) e ^ {+ \ jmath \ omega t} \, dt }

Произведем замену переменной u = — t и получим:

Γ(ω)знак равноИкс(ω)∫-∞+∞Икс*(-ты)е-ȷωтыdты{\ displaystyle \ Gamma (\ omega) = X (\ omega) \ int _ {- \ infty} ^ {+ \ infty} x ^ {*} (- u) e ^ {- \ jmath \ omega u} \, из}

Мы узнаем во втором члене преобразование Фурье от . Теперь преобразование Фурье имеет ценность , а преобразование Фурье , следовательно, стоит преобразования Фурье is . Таким образом, получаем:
Икс*(-ты){\ Displaystyle х ^ {*} (- и)}Икс*(ты){\ Displaystyle х ^ {*} (и)}Икс*(-ν){\ Displaystyle X ^ {*} (- \ ню)}Икс(-ты){\ Displaystyle х (-u)}Икс(-ν){\ Displaystyle Х (- \ ню)}Икс*(-ты){\ Displaystyle х ^ {*} (- и)}Икс*(ν){\ Displaystyle X ^ {*} (\ ню)}

Γ(ω)знак равноИкс(ω)Икс*(ω){\ Displaystyle \ Гамма (\ omega) = Икс (\ omega) X ^ {*} (\ omega)}

И наконец :

Γ(ω)знак равно|Икс(ω)|2{\ Displaystyle \ Гамма (\ омега) = | Икс (\ омега) | ^ {2}}

Спектральная плотность мощности сигнала также является преобразованием Фурье автокорреляции.
|Икс(ω)|2{\ Displaystyle | Икс (\ омега) | ^ {2}}

См. Основные соображения в разделе « Спектральный анализ» .

Для чего обрабатывается сигнал?

Сигнал обрабатывается с целью передачи и получения информации, которая в нем зашифрована. Как только она будет извлечена, ее можно использовать различными способами. В отдельных ситуациях ее переформатируют.

Существует и другая причина обработки всех сигналов. Она заключается в небольшом сжатии частот (чтобы не повредить информацию). После этого ее форматируют и передают на медленных скоростях.

В аналоговом и цифровом сигналах используются особенные методы. В частности, фильтрация, свертка, корреляция. Они необходимы для восстановления сигнала, если он поврежден или имеет шум.

Сигнал

Сигнал представляет собой специальный код, который передается в пространство одной или несколькими системами. Эта формулировка является общей.

В сфере информации и связи сигналом назван специальный носитель каких-либо данных, который используется для передачи сообщений. Он может быть создан, но не принят, последнее условие не обязательно. Если же сигнал является сообщением, то его «ловля» считается необходимой.

Описываемый код передачи данных задается математической функцией. Она характеризует все возможные изменения параметров. В радиотехнической теории эта модель считается базовой. В ней же аналогом сигнала был назван шум. Он представляет собой функцию времени, которая свободно взаимодействует с переданным кодом и искажает его.

В статье охарактеризованы виды сигналов: дискретный, аналоговый и цифровой. Также коротко дана основная теория по описываемой теме.

Типы сигналов

Детерминированный, или регулярный – это сигнал, закон изменения которого известен и известны все его параметры.

Такой сигнал передает информацию? Информация уменьшает неопределенность. В детерминированном сигнале мы знаем все, мы знаем какой он будет через минуту, через год. Детерминированный сигнал информацию в себе никакую не несет. Например, сигнал с гетеродина, мы сами его сформировали, задали частоту, амплитуду, фазу.

Квазидетерминированный — это сигнал, закон изменения которого известен, но один или несколько параметров является случайной величиной.

Пример: x(t)=Asin(wt+j), где амплитуда А и j — случайная величина.

Например, мы знаем его частоту, но не знаем амплитуду и фазу — это квазидетерминированный сигнал, “квази”-почти, почти определенный сигнал. Информация вносит некоторую случайность. Если мы знаем амплитуду, частоту и фазу, значит информации там нет. Квазидетерминированный сигнал передает информацию, передача информации идет в тех параметрах, которые случайны, в нашем примере амплитуда и фаза случайные величины. Именно в этих величинах передается информация. Информация всегда несет в себе хаос, случайность. Все модулированные сигналы, ЧМ, ФМ это квазидетерминированные сигналы.

Случайным называют сигнал, мгновенные значения которого не известны, а могут быть лишь предсказаны с некоторой вероятностью.

Кроме этого все сигналы могут быть непрерывными (аналоговыми) и дискретными (цифровыми или импульсными).

О случайном сигнале мы можем судить о его вероятностных характеристиках. Мы можем знать его плотность вероятности, но какое значение примет сигнал через секунду, минуту мы не знаем. Когда мы работаем со случайным сигналом, мы всегда работаем с вероятностью.

Параметры сигналов

Какие параметры мы будем использовать? Это энергия за некоторый интервал времени T. X(t) это сам сигнал, чтобы определить энергию мы должны взять по модулю, возвести в квадрат, проинтегрировать на некотором промежутке времени и получим энергию.

Средняя мощность за некоторое время t. Это энергия деленная на время.

Мгновенная мощность, если средняя мощность измеряется на некотором участке времени, то мгновенная измеряется в один, конкретный момент времени.

Средняя мощность измеряется на промежутке времени, а мгновенная в точке.

Спектральная плотность энергии и мощности

Спектральная плотность сигнала характеризует распределение энергии или мощности сигнала по диапазону частот. Спектральная плотность энергии, это как у нас энергия распределяется по частотному диапазону. Вычисляется через преобразование Фурье.

И соответственно, СПМ это, как у нас распределяется мощность по частотному диапазону.

В формуле, модуль в квадрате это спектральная плотность энергии, поделили ее на время T и по определению, время T должно стремиться к бесконечности. Но на практике, никто не ждет бесконечности, все оценивают СПМ на некотором интервале времени.

СПМ это некоторая функция зависящая от частоты. По шкале СПМ возьмем 10 Вт/Гц, и окрестности в 1 Гц по частоте. То в полосе 1 Гц будет заключено 10 Вт мощности.

Есть два сигнал и представлены их спектральные плотности мощности. ВОПРОС. Мощность какого сигнала больше?

Мы должны определить площадь под кривой, проинтегрировать. S1=2*10=20 Вт, S2=1*30=30 Вт. В первом случае S1 имеет мощность 20 Вт, а во втором 30 Вт.

СПМ реального сигнала, отображаемая на спектральном анализаторе.

Современные анализаторы спектра могут считать автоматически площадь, вы включаете определение мощности, задаете частотный интервал в котором он должен измерить эту мощность и он сам вычисляет канальную мощность сигнала.

Что такое усилитель?

В электрических схемах очень часто встречаются сигналы малой мощности. Например, это может быть звуковой сигнал с динамического микрофона слабый радиосигнал, который ловит из эфира ваш китайский радиоприемник

Либо отраженный сигнал от ракеты противника, который уже потом ловит, усиливает и отслеживает радиолокационная установка.

Как вы видите, в электронике абсолютно везде требуется усиление слабых сигналов. Для того, чтобы их усиливать, как раз нужны усилители сигналов. Усилители широко применяются в радиолокации, телевидении, радиовещании, телеметрии, в вычислительной технике, авторегулировании, в системах автоматики и тд.

Что происходит с сигналом в канале связи

С ним происходят ослабления, задержка, доплеровский сдвиг, шумы и тому подобное.

Ослабление

Сигнал ослабевает за счет рассеивания в пространстве. Например, у нас есть источник радиосигнала, всенаправленный и изотропный, т.е. он во все стороны излучает одинаково. Получается сферический фронт волны. На одном расстоянии r1 и на другом r2.

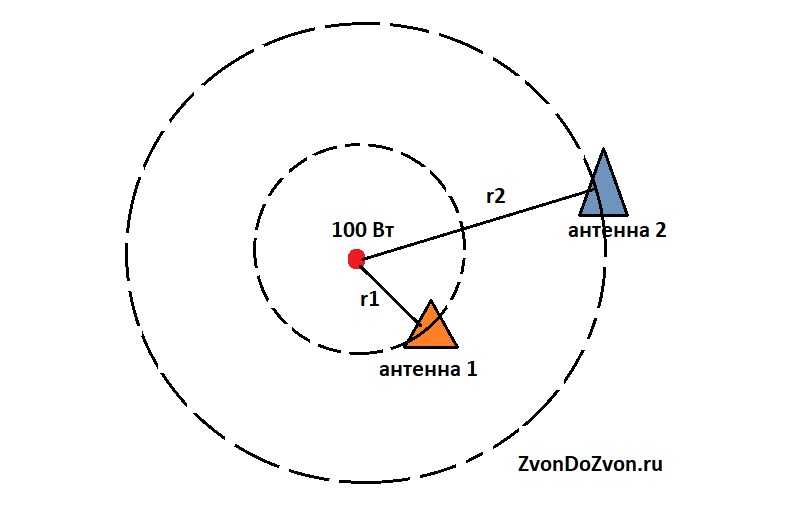
Пусть излучаемая мощность 100 Вт, все эти 100 ватт распределяются по всей сфере. Приемные антенны не большие, они охватывают только небольшой участок пространства. И количество мощности, проходящее через небольшой участок пространства, будет разный на расстоянии r1 и r2. Потому что плотность мощности на расстоянии r1 будет выше, чем на расстоянии r2.

Площадь сферы равна S=4pi*R^2. И эта формула фигурирует во всех формулах оценки дальности радиосвязи. Потому что радиоволна равномерно рассеивается в пространстве. И помимо того, что сигнал сам ослабевает по мере распространения в пространстве, электромагнитная волна проходит через некую среду, которую пытается нагреть и за счет этого теряет свою энергию.

Задержка распространения сигнала

Не смотря на то, что электромагнитная волна, это самое быстрое, что есть у нас во вселенной, тем не менее скорость распространения этой волны конечна. И поддается измерениям. Например, на 1 км задержка распространения ~3.3 мкс.

На что влияет задержка распространения? Обычно, мы точно не знаем расстояние между передатчиком и приемником с точность до микрон. И задержка распространения, которая нам неизвестна, мы не знаем расстояние и не знаем за какое время примем этот сигнал. И соответственно мы не знаем начальную фазу сигнала.

Доплеровский сдвиг частоты

Приняли сигнал с частотой, который отличается от той, которую мы передали. Это дало информацию о скорости объекта. Доплеровский сдвиг частоты появляется, когда у нас либо приемник, или передатчик, двигаются относительно друг друга. Либо двигается отражающая среда, передатчик излучил, радиосигнал отразился от какого-то объекта, если этот объект тоже двигается, то возникает доплеровский сдвиг частоты. Более подробно читайте полную статью “Доплеровский сдвиг частоты”.

Замирания сигнала

Замирания сигнала это процесс, когда у сигнала, случайным образом скачет амплитуда и фаза. То больше амплитуда, то меньше. Выделяют:

Быстрые замирания (интерференционное замирание) — накладывание собственных копий сигнала от переотражений с разными фазами. Вызываются многолучевым распространением сигнала.

Когда есть источник, есть приемник, есть множество путей распространения радиоволны, одна волна может прийти прямой, другая переотраженной.

Например, одна волна прошла 100 км, другая 101 км, к чему это приводит? Если две электромагнитные волны проделали разный путь, то фазы у этих сигналов тоже будут разные. Соответственно, если сигналы сложились в противофазе, то сигналы друг друга подавили, если сложились в фазе, то друг друга усилили.

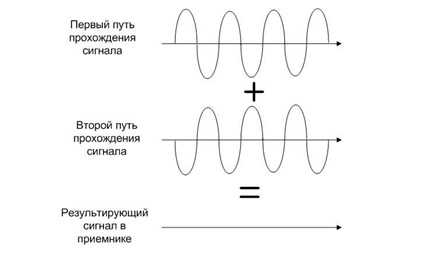
Из-за многолучевого распространения, каждый луч проделывает разное расстояние, это приводит к тому, что начальная фаза каждого луча отличается. И когда в приемнике эти сигналы складываются, они могут друг друга усиливать либо ослаблять. Это приводит к тому, что амплитуда результирующего сигнала постоянно изменяется, это и есть быстрые замирания.

Медленные замирания (затенение) – возникновение препятствий на пути следования радиоволны. Если радиоволна распространяется в пространстве и встречает препятствия, причем эти препятствия то появляются, то исчезают.

На рисунке ниже представлен характер изменения амплитуды сигнала от времени. Сплошной линией показаны быстрые замирания, пунктирной медленные. Медленные замирания происходят из за затенения, быстрые из-за многолучевого распространения. Получается, что амплитуда постоянно скачет на десятки дБ.

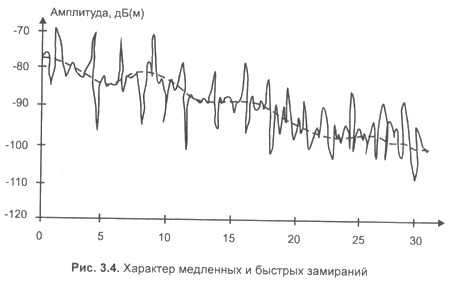
Линейные искажения

Канал связи всегда имеет АЧХ и ФЧХ. Какие-то частоты он усиливает, какие-то ослабляет, фаза где-то поворачивается в одну сторону, где-то в другую это и есть линейные искажения.

Если мы хотим сделать модель канала связи, то чем больше этих параметров мы учтем, тем точнее будет эта модель.

Ссылки [ править ]

^ Р Стоик & R Моисей (2005). «Спектральный анализ сигналов» .
^ Р Стоик & R Моисей (2005). «Спектральный анализ сигналов» .
^ Р Стоик & R Моисей (2005). «Спектральный анализ сигналов» .
^ Жерар Мараль (2003). Сети VSAT . Джон Уайли и сыновья. ISBN 978-0-470-86684-9.
^ Майкл Питер Нортон и Денис Г. Карчуб (2003). Основы анализа шума и вибрации для инженеров . Издательство Кембриджского университета . ISBN 978-0-521-49913-2.
^ Майкл Серна и Одри Ф. Харви (2000). «Основы анализа и измерения сигналов на основе БПФ» .
^ Алессандро Биролини (2007). Техника надежности . Springer. п. 83. ISBN 978-3-540-49388-4.
^ Оппенгейм; Verghese. Сигналы, системы и выводы . С. 32–4.
^ a b Стейн, Джонатан Ю. (2000). Цифровая обработка сигналов: перспектива компьютерных наук . Вайли. п. 115.
^ Ханнес Рискен (1996). Уравнение Фоккера – Планка: методы решения и приложения (2-е изд.). Springer. п. 30. ISBN 9783540615309.
^ Фред Рике; Уильям Биалек и Дэвид Варланд (1999). Шипы: изучение нейронного кода (вычислительная нейробиология) . MIT Press . ISBN 978-0262681087.
^ Скотт Миллерс и Дональд Чайлдерс (2012). Вероятностные и случайные процессы . Академическая пресса . С. 370–5.
^ Теорема Винера – Хинчина дает смысл этой формуле для любого стационарного процесса в широком смысле при более слабых гипотезах: он не должен быть абсолютно интегрируемым, он просто должен существовать. Но интеграл уже нельзя интерпретировать как обычно. Формула также имеет смысл, если ее интерпретировать как включающую распределения (в смысле Лорана Шварца , а не в смысле статистической кумулятивной функции распределения ) вместо функций. Еслион непрерывен, теорема Бохнера может использоваться, чтобы доказать, что его преобразование Фурье существует как положительная мераRxx{\displaystyle R_{xx}}Rxx{\displaystyle R_{xx}}, функция распределения которого равна F (но не обязательно как функция и не обязательно имеет плотность вероятности).
^ Деннис Уорд Рикер (2003). Обработка эхо-сигнала . Springer. ISBN 978-1-4020-7395-3.
^ Роберт Гровер Браун и Патрик YC Hwang (1997). Введение в случайные сигналы и прикладную фильтрацию Калмана . Джон Вили и сыновья . ISBN 978-0-471-12839-7.
^ Сторч, Х. Фон; Ф. В. Цвиерс (2001). Статистический анализ в исследованиях климата . Издательство Кембриджского университета. ISBN 978-0-521-01230-0.
^ Введение в теорию случайных сигналов и шума, Уилбур Б. Давенпорт и Виллиан Л. Рут, IEEE Press, Нью-Йорк, 1987, ISBN 0-87942-235-1
^ Уильям Д. Пенни (2009). «Курс обработки сигналов, глава 7» .

Преимущества и недостатки сигналов разных видов

Со времени изобретения аналоговая передача сигнала была значительно усовершенствована. И прослужила долгое время передавая информацию, звук и изображение. Несмотря на множество улучшений сохранила все свои недостатки – шумы при воспроизведении и искажения при передаче информации. Но главным аргументом для перехода на другую систему обмена данными стал потолок качества передаваемого сигнала. Аналоговый не может вместить объём современных данных.

Совершенствование методов записи и хранения, прежде всего видео контента, оставили аналоговый сигнал в прошлом. Единственным преимуществом аналоговой обработки данных пока ещё является широкое распространение и дешевизна устройств. Во всём остальном аналоговый уступает цифровому сигналу.

Что такое черный ящик в электронике

В общем виде усилитель можно рассматривать как черный ящик. Что представляет из себя этот черный ящик? Это ящик. Он черный). А так как он черный, то абсолютно никто не знает, что находится в нем. Остается только предполагать. Но возможен и такой вариант, что мы можем предпринять какие-либо действия и ждать ответной реакции. После ответной реакции этого черного бокса, можно предположить, что находится у него внутри.

То есть по сути черный ящик должен иметь какие-либо «сенсоры» для восприятия информации извне, некий «вход», а также некий «выход» для ответной реакции. То есть подавая на вход какое-либо воздействие, мы ждем ответной реакции черного ящика на выходе.

Пусть в черном ящике будет кот или кошка, но пока никто не знает, что он(а) там есть. Что мы сделаем в первую очередь? Потрясем ящик или пнем по нему, так ведь? Если там кто-то мяукнет, значит однозначно или кошка, или кот). То есть последовала ответная реакция. Как определить дальше кошка или кот? Открываем ящик, и из него вылазит лохматое чудо. Если побежала — значит кошка. Если побежал — значит кот).

Но также в черном ящике может быть абсолютно любое тело или вещество. Для таких ситуаций мы должны провести как можно больше опытов, то есть произвести как можно больше входных воздействий для более точного определения содержимого черного ящика.

Список лекций

Сигналы: аналоговые, дискретные, цифровые. Z-преобразование,
Преобразование Фурье: амплитудный и фазовый сигнала, ДПФ и БПФ,
Свертка и корреляция. Линейная и циклическая свертка. Быстрая свёртка,
Случайные процессы. Белый шум. Функция плотности вероятностей,
Детерминированные сигналы. Модуляция: АМ, ЧМ, ФМ, ЛЧМ. Манипуляция,
Фильтрация сигналов: БИХ, КИХ фильтры,
Оконные функции в задачах фильтрации. Детектирование слабых сигналов,
Ресемплинг: децимация и интерполяция. CIC-фильтры, фильтры скользящего среднего,
Непараметрические методы спектрального анализа,
Усреднение по частоте и по времени. Полифазный БПФ.

~~но, разумеется, неполный~~

Сигналы. Z-преобразование

аналоговые — описываются непрерывными во времени функциями,
дискретные — прерываются во времени с шагом заданным дискретизации,
квантованные — имеют набор конечных уровней (как правило, по амплитуде),
цифровые — комбинация свойств дискретных и квантованных сигналов.

Теорема Котельникова (Найквиста-Шеннона)Любой непрерывный сигнал с ограниченным спектром может быть восстановлен однозначно и без потерь по своим дискретным отсчетам, взятым с частотой строго больше удвоенной верхней частоты спектра непрерывного сигнала.
Z-преобразование

-1-2-4-5-6

Преобразование Фурье. Свойства. ДПФ и БПФ

вещественнаячетнаянечетная

Сравнение эффективности ДПФ и БПФ

N	ДПФ	БПФ	Отношение числа комплексных сложений	Отношение числа комплексных умножений
Число операций умножения	Число операций сложения	Число операций умножения	Число операций сложения
2	4	2	1	2	4	1
4	16	12	4	8	4	1.5
8	64	56	12	24	5.3	2.3
16	256	240	32	64	8	3.75
32	1024	992	80	160	12.8	6.2
64	4096	4032	192	384	21.3	10.5
128	16384	16256	448	896	36.6	18.1
…	…	…	…	…	…	…
4096	16777216	16773120	24576	49152	683	341
8192	67108864	67100672	53248	106496	1260	630

Свертка и корреляция

корреляциюСверткаАвтокорреляционная функцияпроигрывает

N	Свертка	Быстрая свертка	Отношение
8	64	448	0.14
16	256	1088	0.24
32	1024	2560	0.4
64	4096	5888	0.7
128	16K	13312	1.23
…	…	..	…
2048	4M	311296	13.5

Случайные сигналы и шум

белого шумаСлучайным сигналомвероятностью

закон распределения (относительное время пребывания значения сигнала в определенном интервале),
спектральное распределение мощности сигнала.

шумы — беспорядочные колебания, состоящие из набора разных частот и амплитуд,
сигналы, несущие информацию, для обработки которых требуется прибегать к вероятностным методам.

ДецимацияИнтерполяцияCicFilter
Python CicFilter Class for Digital Signal Processing

Непараметрические методы спектрального анализа (Владимир Фадеев)
Усреднение по частоте и по времени. Полифазный БПФ.

Отличие дискретного сигнала от цифрового

Про Азбуку Морзе наверное слышали все. Придумал художник Самуэль Морзе, другие новаторы усовершенствовали, а использовали все. Это способ передачи текста, где точками и тире закодированы буквы. Упрощенно, кодировка называется морзянкой. Её долго использовали на телеграфе и для передачи информации по радио. Кроме того, сигналить можно с помощью прожектора или фонарика.

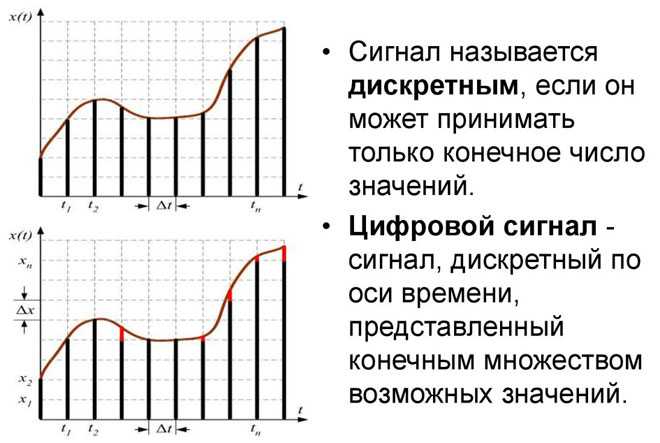
Код морзянки зависит только от самого знака. А не от его продолжительности или громкости (силы). Как ни ударь ключом (моргни фонариком), воспринимаются только два варианта– точка и тире. Можно только увеличить скорость передачи. Ни громкость, ни продолжительность в расчёт ни принимаются. Главное, что бы сигнал дошёл.

Так же и цифровой сигнал

Важно закодировать данные с помощью 0 и 1. Получатель должен только разобрать, комбинацию нолей и единиц

Неважно с какой громкостью и какой продолжительностью будет каждый сигнал. Важно получить нолики и единички. Это суть цифровой технологии.

Дискретный сигнал получится если закодировать ещё громкость (яркость) и продолжительность каждой точки и тире, или 0 и 1. В этом случае вариантов кодировки больше, но и путаницы тоже. Громкость и продолжительность можно не разобрать. В этом и разница между цифровым и дискретным сигналами. Цифровой генерируется и воспринимается однозначно, дискретный с вариациями.

Оценка [ править ]

Целью оценки спектральной плотности является оценка спектральной плотности случайного сигнала из последовательности временных отсчетов. В зависимости от того, что известно о сигнале, методы оценки могут включать параметрические или непараметрические подходы и могут быть основаны на анализе во временной или частотной области. Например, общий параметрический метод включает подгонку наблюдений к авторегрессионной модели . Распространенным непараметрическим методом является периодограмма .

Спектральная плотность обычно оценивается с использованием методов преобразования Фурье (таких как метод Велча ), но также могут использоваться другие методы, такие как метод максимальной энтропии .

Классификация усилителей

Все усилители можно классифицировать по следующим признакам:

По частоте усиливаемого сигнала:

усилители низкой частоты (УНЧ) для усиления сигналов от десятков герц до десятков или сотен килогерц;
широкополосные усилители, усиливающие сигналы в единицы и десятки мегагерц;
избирательные усилители, усиливающие сигналы узкой полосы частот;

По роду усиливаемого сигнала

усилители постоянного тока (УПТ), усиливающие электрические сигналы с частотой от нуля герц и выше;
усилители переменного тока, усиливающие электрические сигналы с частотой, отличной от нуля;

По функциональному назначению

усилители напряжения, усилители тока и усилители мощности в зависимости от того, какой из параметров усилитель усиливает. Основным количественным параметром усилителя является коэффициент усиления.

КU = Uвх / Uвых

КI= Iвх/ Iвых

КP= Pвх / Pвых

где Uвх, Iвх — амплитудные значения переменных составляющих соответственно напряжения и тока на входе;

Uвых , Iвых — амплитудные значения переменных составляющих соответственно напряжения и тока на выходе;

Рвх, Рвых— мощности сигналов соответственно на входе и выходе. Коэффициенты усиления часто выражают в логарифмических единицах — децибелах:

КU (дБ) = 20LgKu

КI(дБ) = 20LgKi

КР (дБ) = 10LgKp

Усилитель может состоять из одного или нескольких каскадов. Для многокаскадных усилителей его коэффициент усиления равен произведению коэффициентов усиления отдельных его каскадов: К = К1 · К2 · … · Кn

К (дБ) = К1 (дБ) + К2 (дБ) +… + Кn(дБ).

Обычно в усилителе содержатся реактивные элементы, в том числе и «паразитные», а используемые усилительные элементы обладают инерционностью. В силу этого коэффициент усиления является комплексной величиной:

ЌU = КU · ejφ

КU = Uвых / Uвх

где КU— модуль коэффициента усиления; φ — сдвиг фаз между входным и выходным напряжениями с амплитудами Uвх и Uвых.

Помимо коэффициента усиления важным количественным показателем является коэффициент полезного действия:

η = Pвых / Pист

где Рист — мощность, потребляемая усилителем от источника питания.

К количественным показателям усилителя относятся также входное Rвх и выходное Rвых сопротивления усилителя:

Rвх = Uвх / Iвх

Rвых = |∆ Uвых | / |∆ Iвых |

где Uвх и Iвх — амплитудные значения напряжения и тока на входе усилителя;

∆Uвых и ∆Iвых — приращения аплитудных значений напряжения и тока на выходе усилителя, вызванные изменением сопротивления нагрузки. Рассмотрим теперь основные характеристики усилителей.

Интересное видео о параметрах усилителя смотрите ниже:

Предыдущая
РазноеЭлектромагнитное излучение – невидимый убийца.
Следующая
РазноеКак правильно соединить провода между собой

Время и электрический сигнал

Как я уже сказал, сигнал передается во времени и в пространстве. То есть время — важный параметр для электрического сигнала. Сейчас нам придется немного попотеть и вспомнить курс математики и физики за среднюю школу. Вспоминаем декартову систему координат. Как вы помните, по вертикали мы откладывали ось Y, по горизонтали Х:

В электронике и электротехнике по Х мы откладываем время, назовем его буквой t, а по вертикали мы отложим напряжение, обозначим его буквой U. В результате наша система координат будет выглядеть вот таким образом:

Прибор, который показывает нам изменение напряжения во времени называется осциллографом , а график этого напряжения называется осциллограммой. Осциллограф может быть цифровым

или аналоговым

Обобщенная схема усилителя

Она выглядит примерно вот так:

Как мы можем видеть на схеме, ко входу усилительного каскада через клеммы 1 и 2 подсоединяется какой-либо источник слабого сигнала с ЭДС EИ и внутренним сопротивлением RИ . Именно этот слабый сигнал с этого источника мы будем усиливать. Далее, как и полагается, каждый усилитель обладает своим каким-либо входным сопротивлением Rвх . Сила тока Iвх в цепи EИ —>RИ—>Rвх , как ни трудно догадаться, будет зависеть от входного сопротивления усилительного каскада Rвх .

Как вы уже знаете, источник питания играет главную роль в усилительном каскаде. Маломощный слабый сигнал управляет расходом энергии источника питания. В результате на выходе мы получаем умощненную копию входного слабого сигнала. Усиление произошло благодаря тому, что источник питания давал свою мощность для усиления входного сигнала. Ну как-то вот так).

В выходной цепи усилителя мы получаем усиленный сигнал с ЭДС (Что такое ЭДС) Eвых и выходным сопротивлением Rвых . Через клеммники 3 и 4 мы цепляем нагрузку Rн , которая уже будет потреблять энергию усиленного сигнала. Сила тока в цепи Eвых —> Rвых —> Rн будет зависеть от сопротивления нагрузки Rн .

Какие системы связи используют цифровой сигнал а какие аналоговый

Несмотря на архаичность аналоговая технология ещё используется для телефонной и радио связи. Многие проводные сети до сих пор остаются аналоговыми. В основном это традиционные телефонные линии местных операторов. Но, для магистральной передачи данных связи уже повсеместно используют цифровые каналы. Так же аналоговая технология применяется в простых и дешёвых переносных радиостанциях.

Во всех вновь создаваемых системах используют цифровую технологию обработки сигнала. Это оптоволоконные и проводные линии, сигнализация и телеметрия, военная и гражданская промышленная связь. И конечно же на цифровое вещание переходит телевидение. Аналоговый способ передачи данных исчерпал себя. На смену пришла новая высококачественная и защищенная связь.

Сравнение цифрового и аналогового сигналов

Сигнал радиостанции телецентра или мобильной связи может передаваться в цифровой и аналоговой форме. Например звук и изображение, это аналоговые сигналы. Микрофон и камера воспринимают окружающую действительность и преобразуют в электромагнитные колебания. Частота колебаний на выходе зависит от частоты звука и света, а амплитуда передачи от громкости и яркости.

Изображение и звук, преобразованные в электромагнитные колебания распространяются в пространство передаточной антенной. В приемнике идёт обратный процесс — электромагнитных колебаний в звук и видео.

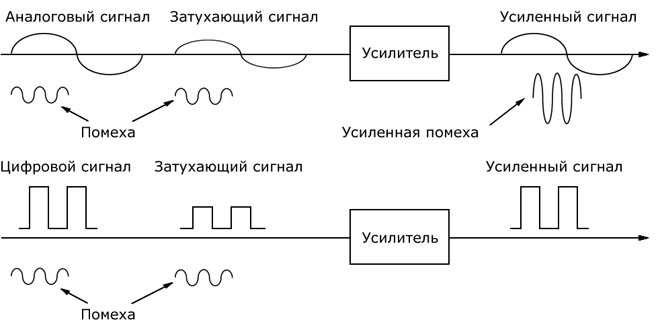
Распространению электромагнитных колебаний в эфире препятствуют облака, грозы, рельеф местности, промышленные электронаводки, солнечный ветер и прочие помехи. Частота и амплитуда нередко искажаются и сигнал от передатчика к приемнику приходит с изменениями.

Голос и изображение аналогового сигнала воспроизводятся с искажениями, вызванными помехами, а фоном воспроизводится шипение, хрипы и цветовое искажение. Чем хуже прием, тем отчетливее эти посторонние эффекты. Но если сигнал дошёл, его хоть как то видно и слышно.

При цифровой передаче изображение и звук перед трансляцией в эфир оцифровываются и до приёмника доходят без искажений. Влияние посторонних факторов минимально. Звук и цвет хорошего качества либо их нет вовсе. Сигнал гарантированно поступает на определенное расстояние. Но для дальней передачи необходим ряд ретрансляторов. Поэтому для передачи сотового сигнала антенны ставят как можно ближе друг к другу.

Наглядным примером отличия двух типов сигналов может служить сравнение старой проводной телефонной и современной сотовой связи.

Проводная телефония не всегда хорошо работает даже в пределах одного населённого пункта. Звонок на другой конец страны это испытание голосовых связок и слуха. Нужно докричаться и прислушаться к ответу. Шумы и помехи отфильтровываем ушами, недостающие и искаженные слова додумываем сами. Хоть и плохой звук, но есть.

Звук в сотовой связи отлично слышно даже с другого полушария. Оцифрованный сигнал передаётся и принимается без искажений. Но и он не без изъянов. Если случаются сбои, то звук не слышен вовсе. Выпадают буквы, слова и целые фразы. Хорошо, что это бывает редко.

Примерно то же самое с аналоговым и цифровым телевидением. Аналоговое использует сигнал подверженный помехам, ограниченного качества и уже исчерпало возможности развития. Цифровое не искажается, обеспечивает звук и видео отличного качества, постоянно совершенствуется.