Таблица кубов натуральных чисел

Таблица кубов

Определение
Калькулятор — куб числа
Таблица кубов

Определение.Куб числа — есть данное число, возведенное в третью степень.

a3 = a · a · a

«Кубом» оно называется, потому что такая операция аналогична вычислению объема куба.

3 = 827 ≈ 0.2962962962962963

Ниже приведены две удобные таблицы кубов натуральных чисел от 1 до 100.

Таблица кубов чисел от 1 до 100

13 = 1 23 = 8 33 = 27 43 = 64 53 = 125 63 = 216 73 = 343 83 = 512 93 = 729 103 = 1000	113 = 1331 123 = 1728 133 = 2197 143 = 2744 153 = 3375 163 = 4096 173 = 4913 183 = 5832 193 = 6859 203 = 8000	213 = 9261 223 = 10648 233 = 12167 243 = 13824 253 = 15625 263 = 17576 273 = 19683 283 = 21952 293 = 24389 303 = 27000	313 = 29791 323 = 32768 333 = 35937 343 = 39304 353 = 42875 363 = 46656 373 = 50653 383 = 54872 393 = 59319 403 = 64000	413 = 68921 423 = 74088 433 = 79507 443 = 85184 453 = 91125 463 = 97336 473 = 103823 483 = 110592 493 = 117649 503 = 125000
513 = 132651 523 = 140608 533 = 148877 543 = 157464 553 = 166375 563 = 175616 573 = 185193 583 = 195112 593 = 205379 603 = 216000	613 = 226981 623 = 238328 633 = 250047 643 = 262144 653 = 274625 663 = 287496 673 = 300763 683 = 314432 693 = 328509 703 = 343000	713 = 357911 723 = 373248 733 = 389017 743 = 405224 753 = 421875 763 = 438976 773 = 456533 783 = 474552 793 = 493039 803 = 512000	813 = 531441 823 = 551368 833 = 571787 843 = 592704 853 = 614125 863 = 636056 873 = 658503 883 = 681472 893 = 704969 903 = 729000	913 = 753571 923 = 778688 933 = 804357 943 = 830584 953 = 857375 963 = 884736 973 = 912673 983 = 941192 993 = 970299 1003 = 1000000

 Распечатать таблицу кубов

Таблица кубов

	1	2	3	4	5	6	7	8	9
1	8	27	64	125	216	343	512	729
1	1000	1331	1728	2197	2744	3375	4096	4913	5832	6859
2	8000	9261	10648	12167	13824	15625	17576	19683	21952	24389
3	27000	29791	32768	35937	39304	42875	46656	50653	54872	59319
4	64000	68921	74088	79507	85184	91125	97336	103823	110592	117649
5	125000	132651	140608	148877	157464	166375	175616	185193	195112	205379
6	216000	226981	238328	250047	262144	274625	287496	300763	314432	328509
7	343000	357911	373248	389017	405224	421875	438976	456533	474552	493039
8	512000	531441	551368	571787	592704	614125	636056	658503	681472	704969
9	729000	753571	778688	804357	830584	857375	884736	912673	941192	970299

 Распечатать таблицу кубов

2011-2022 Довжик МихаилКопирование материалов запрещено.

Добро пожаловать на OnlineMSchool.Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Таблица степеней чисел до 100 в кубе

Часто в примерах требуется возвести двузначное число в куб. Сделать это будет проще со следующей таблицей:

_{*Для лучшего понимания примеры подсвечены голубым.}

Пример 4. Работаем с таблицей натуральных степеней чисел в кубе.

Задача. Найти 453.

Решение. Делим число на десятки и единицы. Находим 4 десятка (левый столбец) и 5 единиц (верхняя полоса) и ищем значение их пересечения.

Ответ. 157464.

Пример 5. Вычисляем квадрат по таблице.

Задача. Найти 403.

Решение. Найти значение можно двумя способами. Первый — руководствуясь таблицей. 4 — десятки, 0 — единицы. Ищем пересечение этих цифр. Результат — 6400. Второй способ: возводим 4 в куб и прибавляем два нуля (т.к. 10 в кубе = 100). 43=64. Прибавляем «00» и получаем идентичный ответ: 6400.

Ответ. 6400.

Пользоваться таблицами степеней по математике несложно. Но только в том случае, если речь идет о небольших цифрах. В длинных примерах, состоящих из множества чисел в степенях, можно использовать онлайн калькуляторы. Это позволит избежать ошибок, которые могут быть вызваны просмотром не той ячейки.

Таблица кубов чисел от 1 до 100

13 = 1 23 = 8 33 = 27 43 = 64 53 = 125 63 = 216 73 = 343 83 = 512 93 = 729 103 = 1000	113 = 1331 123 = 1728 133 = 2197 143 = 2744 153 = 3375 163 = 4096 173 = 4913 183 = 5832 193 = 6859 203 = 8000	213 = 9261 223 = 10648 233 = 12167 243 = 13824 253 = 15625 263 = 17576 273 = 19683 283 = 21952 293 = 24389 303 = 27000	313 = 29791 323 = 32768 333 = 35937 343 = 39304 353 = 42875 363 = 46656 373 = 50653 383 = 54872 393 = 59319 403 = 64000	413 = 68921 423 = 74088 433 = 79507 443 = 85184 453 = 91125 463 = 97336 473 = 103823 483 = 110592 493 = 117649 503 = 125 000
513 = 132651 523 = 140608 533 = 148877 543 = 157464 553 = 166375 563 = 175616 573 = 185193 583 = 195112 593 = 205379 603 = 216000	613 = 226981 623 = 238328 633 = 250047 643 = 262144 653 = 274625 663 = 287496 673 = 300763 683 = 314432 693 = 328509 703 = 343000	713 = 357911 723 = 373248 733 = 389017 743 = 405224 753 = 421875 763 = 438976 773 = 456533 783 = 474552 793 = 493039 803 = 512000	813 = 531441 823 = 551368 833 = 571787 843 = 592704 853 = 614125 863 = 636056 873 = 658503 883 = 681472 893 = 704969 903 = 729000	913 = 753571 923 = 778688 933 = 804357 943 = 830584 953 = 857375 963 = 884736 973 = 912673 983 = 941192 993 = 970299 1003 = 1000000

Кубы чисел от 10 до 99

РАЗ	ЕДИНИЦЫ
	1	2	3	4	5	6	7	8	9
1	1000	1331	1728	2197	2774	3375	4096	4913	5832	8659
2	8000	9261	10648	12167	13824	15625	17576	19683	21952	24389
3	27000	29791	32768	35937	39304	42875	46656	50653	54872	59319
4	64000	68921	74088	79507	85184	91125	97336	103823	110592	117649
5	125 000	132651	140608	148877	157464	166375	175616	185193	195112	205379
6	216000	226981	238328	250047	262144	274625	287496	300763	314432	328509
7	343 000	357911	373248	389017	405224	421875	438976	456533	474552	493039
8	512 000	531441	551368	571787	592704	614125	636056	658503	681472	704969
9	729 000	753571	778688	804357	830584	857375	884736	912673	941192	970299

Как пользоваться таблицей:

Уровень в первом столбце, один в верхнем ряду. Кость определенного числа ставится на пересечение нужных десятков и единиц.

Допустим, что нам нужно найти куб числа 64. В столбце десятков ищем число 6, в ряду единиц — число 4. Их пересечение соответствует числу 262144 — ответ, который мы хотели найти.

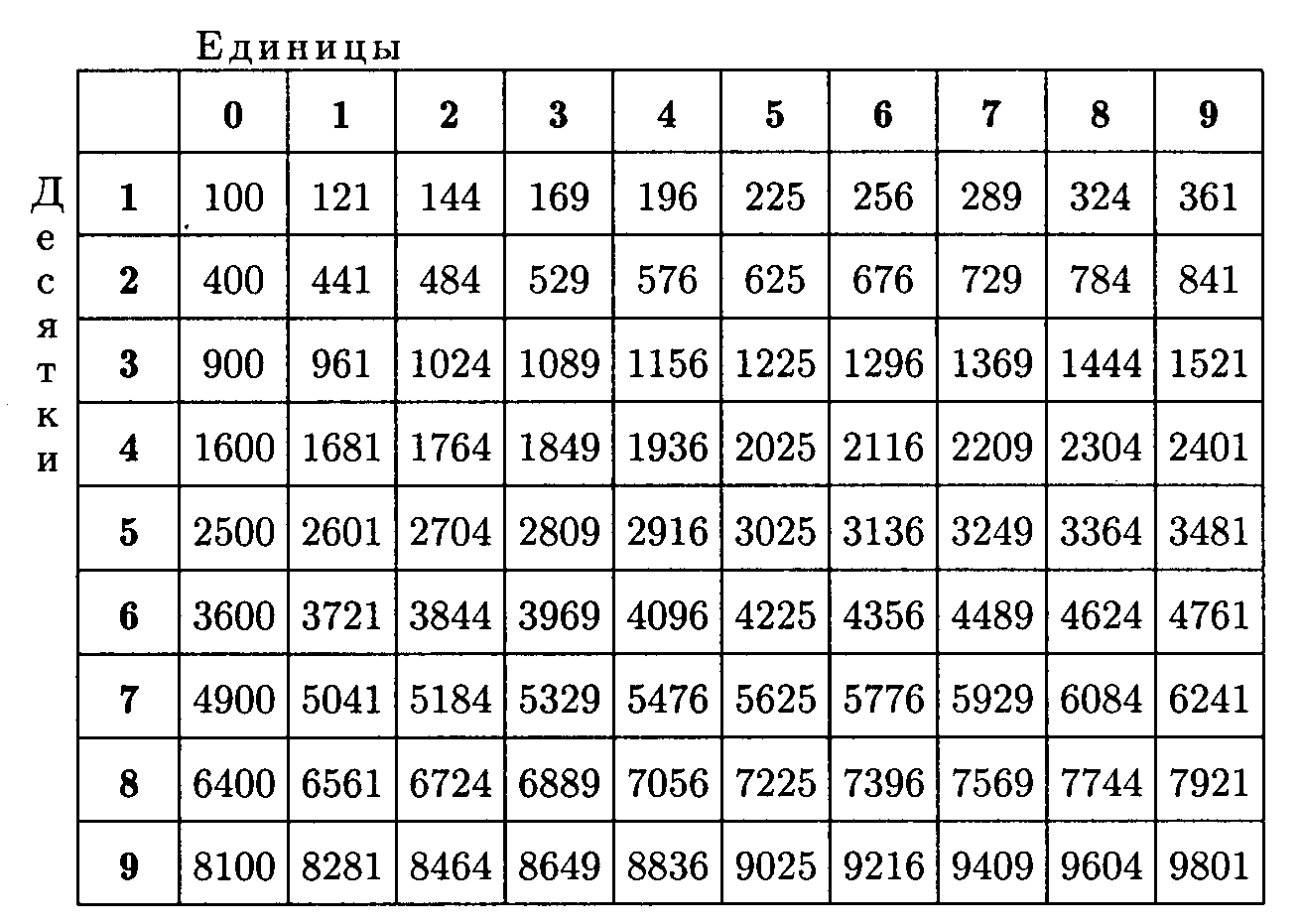
Таблица степеней по алгебре: числа в квадрате

Расписать абсолютно каждое число и найти его значение во всех степенях — невозможно. В сложных примерах рекомендуется использовать онлайн калькуляторы. Мы же рассматриваем наиболее примитивные и распространенные случаи. В основном, в средней школе (вплоть до 11 класса) рассматриваются примеры с перемножением незначительное количество раз. Часто используется квадрат (a2). Некоторые числа мы уже возводили в него (от 1 до 25). Значения больших чисел же можно искать тут:

_{*Для лучшего понимания примеры подсвечены голубым.}

С левой стороны указаны десятки, а сверху — единицы. Т.е., для возведения в квадрат числа 24 ищем пересечение его десятка и единицы (2 — десяток, 4 — единица). Получаем показатель 576. Таким образом данная таблица степеней натуральных чисел может использоваться для возведения в квадрат цифр до 99.

Пример 3. Возводим большие значения в квадрат.

Задача. Найти 632.

Решение. В числе «63» 6 десятков и 3 единицы. Десятки у нас находятся с левой стороны, а единицы — в верхней строчке. Ищем нужные значения в таблице степеней по алгебре и находим число, находящееся на их пересечении.

Ответ. 3969.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Таблица кубов

1	8	27	64	125	216	343	512	729
1	1000	1331	1728	2197	2744	3375	4096	4913	5832	6859
2	8000	9261	10648	12167	13824	15625	17576	19683	21952	24389
3	27000	29791	32768	35937	39304	42875	46656	50653	54872	59319
4	64000	68921	74088	79507	85184	91125	97336	103823	110592	117649
5	125 000	132651	140608	148877	157464	166375	175616	185193	195112	205379
6	216000	226981	238328	250047	262144	274625	287496	300763	314432	328509
7	343 000	357911	373248	389017	405224	421875	438976	456533	474552	493039
8	512 000	531441	551368	571787	592704	614125	636056	658503	681472	704969
9	729 000	753571	778688	804357	830584	857375	884736	912673	941192	970299

Свойства степеней

a, b — любое рациональное число, n, m — любое натуральное

Произведение степеней

Данное действие подразумевает то, что одинаковое основание остается без изменений, а показатели складываются.

\(a^n\cdot a^m=a^{n+m}\)

Частное степеней

Под выполнением данной операции понимается то, что одинаковое основание остается без изменений, а из показателя делимого вычитают показатель делителя.

\(\frac{a^m}{a^n}=a^{m-n}\)

Возведение степени в степень

Для вычисления результата этой операции основание остается без изменения, а показатели перемножаются.

\(\left(a^m\right)^n=a^{m\cdot n}\)

Степень произведения

Для выполнения этого арифметического действия каждый из множителей возводится в степень, после чего полученные результаты перемножаются.

\(\left(a\cdot b\right)^n=a^n\cdot b^n\)

Степень частного

Чтобы выполнить данную арифметическую операцию, следует возвести в степень делимое и делитель, а затем первый результат разделить на второй.

\(\left(\frac{a}{b}\right)^n=\frac{a^n}{b^n}\)

Традиционная таблица степеней натуральных чисел: от 1 до 10

Проще всего находить значение многократного перемножения небольших натуральных чисел. Для поиска решения можно использовать следующую подсказку:

По методу вычисления эта таблица натуральных степеней схожа с таблицей умножения. Чтобы найти результат произведения числа нужное количество раз, достаточно найти соответствующую формулу в столбике.

Пример 1. Используем простую таблицу степеней по алгебре.

Задача. Найти 79.

Решение. Находим 79. Расположено значение во втором столбике нижней строки.

Ответ. 40353607.

Пример 2. Используем простую таблицу по алгебре.

Задача. Найти 17.

Решение. В данном случае найти значение выражения можем без использования вспомогательных инструментов. Достаточно вспомнить одно из свойств степеней: единица всегда остается единицей.

Ответ. 1.

Возведение в степень: определение

Возведение числа в натуральную степень — это умножение его на само себя определенное количество раз. Это такая же операция в алгебре, как сложение, вычитание, умножение или деление.

Если определенное число нужно умножить на себя несколько раз, это значит, что его необходимо возвести в соответствующую степень. Например, если четыре нужно умножить само на себя три раза, это равно тому, что четыре следует возвести в третью степень. Закодировать это выражение можно следующей арифметической записью:

43, где 4 — это основание, а 3 — показатель. Также 43 = 4·4·4 = 64

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Основные правила выполнения данных вычислений:

• итог возведения отрицательного основания в четную степень — положительный;
• итог возведения отрицательного основания в нечетную — отрицательный;
• итог возведения положительного основания в любую — положительный;
• любое основание с показателем один равно себе;
• ноль при любом возведении в результате дает ноль;
• единица с любым показателем равна единице;
• любое основание с показателем ноль равно единице.

Таблица представляет собой ряд чисел, возведенных в определенные степени.

Куб от 1 до 10 | Значения кубиков от 1 до 10 [Скачать PDF]

LearnPracticeDownload

Кубик от 1 до 10 — это список кубиков всех чисел от 1 до 10. Значение кубиков от 1 до 10 находится в диапазоне от 1 до 1000. Запоминание этих значений поможет учащимся быстро решать трудоемкие математические уравнения. Куб от 1 до 10 в экспоненциальной форме выражается как (x) 3 .

Куб от 1 до 10:

• Экспоненциальная форма: (x) 3
• Наибольшее значение: 10 3 = 1000
• Наименьшее значение: 1 3 = 1

1.	Куб от 1 до 10
2.	Куб от 1 до 10 PDF
3.	Как рассчитать кубики от 1 до 10?
4.	Часто задаваемые вопросы

Кубы от 1 до 10 Таблица

Кубики от 1 до 10

Изучение кубов от 1 до 10 может помочь учащимся распознавать все совершенные кубы до 4 цифр и аппроксимировать кубический корень путем интерполяции между известными кубами. Значения кубов от 1 до 10 перечислены в таблице ниже.

Список всех кубов от 1 до 10
1 3 = 1	2 3 = 8
3 3 = 27	4 3 = 64
5 3 = 125	6 3 = 216
7 3 = 343	8 3 = 512
9 3 = 729	10 3 = 1000

☛ Кубики от 1 до 10 PDF

Ученикам рекомендуется тщательно запомнить эти значения кубов от 1 до 10 для более быстрого выполнения математических вычислений.

Как рассчитать значения куба от 1 до 10?

Чтобы вычислить значение кубов от 1 до 10, мы можем использовать следующий метод:

Умножение само на себя: Например, куб 9 = 9 × 9 × 9 = 729. Здесь результирующее произведение «729 » дает нам куб числа «9». Этот метод хорошо работает для небольших чисел.

Решенные примеры на кубе с 1 по 10

1. Пример 1: Если длина стороны куба 10 дюймов. Найдите объем куба в кубических дюймах.

   Решение:

   Объем куба = a 3 = 10 3

   Используя значения куба с 1 по 10 диаграммы;

   т.е. V = 1000

   Следовательно, объем куба = 1000 дюймов 3 .

2. Пример 2: Вычислить 3 раза 2 куб плюс 4.

   Решение:

   3 × 2 3 + 4 = 3 × 8 + 4 = 28

   Таким образом, значение 3 умножить на 2 куб плюс 4 равно 28.

3. Пример 3: Найдите объем сферы радиусом 2 дюйма.

   Решение:

   Объем сферы = 4/3 π R

   2 3

   8 3

   3

   ⇒ V = 4/3 π R 3 = 4/3 × 3,14 × 2 3

   ⇒ V = 4 × 3,14 × 8 = 100,48 дюйма 3

   Следовательно, объем сферы равен 100,48 дюйма 3

перейти к слайдуперейти к слайдуперейти к слайду

Готовы увидеть мир глазами математика?

Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.

Запись на бесплатный пробный урок

Часто задаваемые вопросы по Cube 1–10

Сколько стоит кубик от 1 до 10?

Значение кубов от 1 до 10 находится в диапазоне от 1 до 1000. Эти числа получаются путем трехкратного умножения целого числа (y × y × y). От 1 до 10 значение кубиков чисел 2, 4, 6, 8, 10 будет четным, а значение кубиков чисел 1, 3, 5, 7, 9 будет нечетным.

Сколько чисел в кубах от 1 до 10 нечетные?

Нечетные числа от 1 до 10 — это 1, 3, 5, 7, 9. Так как куб нечетных чисел всегда нечетен. Следовательно, значение кубиков чисел 1, 3, 5, 7, 9будет странно.

Какие существуют методы вычисления кубов от 1 до 10?

Мы можем вычислить число в кубе, используя многократное умножение. Например, куб 6 можно вычислить, умножив 6 три раза, т.

Возведение чисел в куб

Возведение чисел в куб – это операция, при которой число умножается само на себя, а затем еще раз на себя. Таким образом, получается число, в котором каждая цифра повторяется три раза.

Например, если возвести число 7 в куб, то получится число 343. Число 2 в кубе равно 8, число 5 в кубе равно 125, число 4 в кубе равно 64, число 1 в кубе равно 1, число 6 в кубе равно 216, число 0 в кубе равно 0, а число 8 в кубе равно 512.

Возведение чисел в куб широко используется в математике, естественных и технических науках, а также в программировании. Например, при решении задач в физике или при создании компьютерных алгоритмов.

Для удобства, можно составить таблицу, в которой будут перечислены числа и их значения в кубе:

Число	Значение в кубе
7	343
2	8
5	125
4	64
1	1
6	216
8	512

Таким образом, возведение чисел в куб является важной математической операцией, которая имеет множество практических применений и способствует решению различных задач

Числа от 4 до 6

Возведение чисел в куб — это процесс умножения числа на само себя три раза. Рассмотрим числа от 4 до 6 и их кубы.

Число 4 в кубе равно 64. Это означает, что число 4 нужно умножить на само себя три раза: 4*4*4 = 64. Куб числа 4 равен 64.

Число 5 в кубе равно 125. Умножив число 5 на само себя три раза, получим: 5*5*5 = 125. Куб числа 5 равен 125.

Число 6 в кубе равно 216. Умножив число 6 на само себя три раза, получим: 6*6*6 = 216. Куб числа 6 равен 216.

Таким образом, числа 4, 5 и 6 в кубе равны соответственно 64, 125 и 216.

Число 4 в кубе

Число 4 в кубе равно 64. Чтобы получить куб числа 4, нужно перемножить его само на себя два раза. Таким образом, 4 в кубе = 4 * 4 * 4 = 64.

Видно, что результатом умножения 4 на 4 будет 16, а умножение 16 на 4 даст нам 64. Таким образом, для получения куба числа 4 мы умножаем его само на себя дважды.

Куб числа 4 имеет форму куба со стороной 4. Все его грани, ребра и углы равны между собой. Такой куб можно представить в виде трехмерной фигуры.

Если возвести в куб число 4, то получится число 64. Обратный процесс называется извлечением кубического корня. В данном случае, кубический корень из 64 равен 4. То есть, ∛64 = 4.

Число 5 в кубе

Число 5 в кубе равно 125. Для того чтобы получить куб числа 5, нужно число умножить само на себя дважды. Таким образом, 5 * 5 * 5 = 125.

5 в кубе представляет собой объем куба со стороной 5 единиц. Куб с ребром длиной 5 единиц будет иметь объем 125 кубических единиц.

Для удобства расчетов можно использовать таблицу степеней числа 5. Например, 5 в первой степени равно 5, 5 во второй степени равно 25, 5 в третьей степени равно 125.

Следующие числа после 5 в кубе в таблице степеней: 8, 0, 3, 4, 2, 6, 7. Для каждого из этих чисел можно посчитать его куб, перемножив число само на себя дважды.

Таким образом, 8 в кубе равно 512, 0 в кубе равно 0, 3 в кубе равно 27, 4 в кубе равно 64, 2 в кубе равно 8, 6 в кубе равно 216, 7 в кубе равно 343.

Число 6 в кубе

Число 6 в кубе равно 216. Для получения куба числа 6 нужно умножить его само на себя два раза. Таким образом, 6 * 6 * 6 = 216. Куб числа 6 можно представить в виде кубического массива, состоящего из шести граней.

Куб числа 6 имеет три оси, каждая из которых содержит по 6 элементов. Из каждой вершины куба выходит по 3 ребра, образуя в итоге 12 ребер.

Примером чисел, которые можно получить в кубе числа 6, могут быть:

• Число 1 в кубе равно 1
• Число 2 в кубе равно 8
• Число 3 в кубе равно 27
• Число 4 в кубе равно 64
• Число 5 в кубе равно 125
• Число 6 в кубе равно 216
• Число 7 в кубе равно 343
• Число 8 в кубе равно 512
• Число 9 в кубе равно 729
• Число 10 в кубе равно 1000

Куб числа 6 является одним из чисел, которые часто используются в математике и физике. Его значение может быть использовано для моделирования объема кубических тел, расчета объема жидкости или газа, и в других приложениях.

Практическое применение куба числа

Куб числа является полезным понятием в математике и имеет множество практических применений. Например, куб числа может быть использован для определения объема трехмерной фигуры.

Также, куб числа является важным понятием в физике. Например, скорость куба числа будет равна ускорению в квадрате, умноженному на время.

Куб числа также может быть использован для вычисления площади поверхности трехмерной фигуры. Например, если мы имеем куб со стороной длиной 2, то его площадь поверхности будет равна 24.

• Применение куба числа в программировании:
  • Куб числа может использоваться в математических алгоритмах, таких как алгоритмы шифрования.
  • Куб числа может использоваться для вычисления сложных математических функций, таких как квадратный корень.

Таким образом, куб числа является важным математическим понятием, имеющим широкий спектр практических применений в различных областях жизни и производства.

Вопрос-ответ:

Как вычислить куб числа?

Чтобы вычислить куб числа, нужно число умножить само на себя три раза. То есть, если нужно найти куб числа 4, нужно умножить 4 на 4 на 4, получив результат 64.

Зачем нужен куб числа?

Куб числа может использоваться в различных математических формулах, а также в физике и других науках. Например, скорость света в вакууме равна кубу числа 10, или 1000.

Какие есть способы вычисления куба числа?

Существует несколько способов вычисления куба числа, например, умножение числа самого на себя три раза, использование формулы куба суммы двух чисел или куба разности двух чисел, или использование тождества (a+b)³=a³+3a²b+3ab²+b³, где a и b — любые числа.

Какие числа можно возводить в куб?

В куб можно возводить все действительные и комплексные числа, в том числе и отрицательные. Например, куб числа -2 равен -8, а куб комплексного числа 2+3i равен -46+9i.

Как связаны куб числа и квадрат числа?

Куб числа может быть выражен через квадрат числа, так как куб числа равен квадрату числа, умноженному на само число. Например, куб числа 5 равен 25 умножить на 5, то есть 125.

Как использовать куб числа в алгебре?

Куб числа может использоваться в алгебре для решения различных задач, например, вычисления корней кубического уравнения или поиска объема куба со стороной заданной длины. Кроме того, куб числа может использоваться в формулах сумм и разностей кубов чисел.

Таблица Брадиса — КУБЫ ЧИСЕЛ

Кубы чисел (Таблица Брадиса 5)

Таблица Брадиса 5 содержит кубы чисел от 1,000 до 2,159 через 0,001 и от 2.16 до 9,99 через 0,01, округлённые до 4 значащих цифр. Поправки, помещённые справа (курсив), облегчают применение интерполяции на следующую цифру возводимого в куб числа, если такая цифра имеется. Поправки выражены в единицах последнего разряда табличных кубов, находящихся на той же строке. Поправка прибавляется к ближайшему меньшему табличному кубу, если следующая цифра есть 1, 2, 3, 4, 5, и отнимается от ближайшего большего табличного куба в остальных случаях. Например, 8,044 3 =520,5 (берётся 519,7 и прибавляется 0,8), 8,047 8 =521,1 (берётся 521,7 и отнимается 0,6). Для возведения в куб числа, меньшего 1 или большего 10, его предварительно преобразуют, вводя множитель 10 с положительным или отрицательным показателем, подобно тому, как это делалось при возведении в квадрат.

Эта же таблица Брадиса служит для получения кубического корня из любого числа. Если оно заключено между 1 и 1000, по таблице подбирается число, заключённое между 1 и 10, куб которого ему равен. Если оно меньше 1 или больше 1000, его предварительно преобразуют, вводя множитель 10 с целым показателем, положительным или отрицательным, кратным 3.

При перенесении запятой в числе N на одно место запятая в числе N 3 переносится на три места.

N	1	2	3	4	5	6	7	8	9	1	2	3	4	5
1,00	1,000	1,003	1,006	1,009	1,012	1,015	1,018	1,021	1,024	1,027	1	1	1	2
1,01	1,030	1,033	1,036	1,040	1,043	1,046	1,049	1,052	1,055	1,058	1	1	1	2
1,02	1,061	1,064	1,067	1,071	1,074	1,077	1,080	1,083	1,086	1,090	1	1	1	2
1,03	1,093	1,096	1,099	1,102	1,106	1,109	1,112	1,115	1,118	1,122	1	1	1	2
1,04	1,125	1,128	1,131	1,135	1,138	1,141	1,144	1,148	1,151	1,154	1	1	1	2
1,05	1,158	1,161	1,164	1,168	1,171	1,174	1,178	1,181	1,184	1,188	1	1	1	2
1,06	1,191	1,194	1,198	1,201	1,205	1,208	1,211	1,215	1,218	1,222	1	1	1	2
1,07	1,225	1,228	1,232	1,235	1,239	1,242	1,246	1,249	1,253	1,256	1	1	1	2
1,08	1,260	1,263	1,267	1,270	1,274	1,277	1,281	1,284	1,288	1,291	1	1	1	2
1,09	1,295	1,299	1,302	1,306	1,309	1,313	1,317	1,320	1,324	1,327	1	1	1	2
1,10	1,331	1,335	1,338	1,342	1,346	1,349	1,353	1,357	1,360	1,364	1	1	1	2
1.11	1,368	1,371	1,375	1,379	1,382	1,386	1,390	1,394	1,397	1,401	1	1	1	2
1,12	1,405	1,409	1,412	1,416	1,420	1,424	1,428	1,431	1,435	1,439	1	1	2	2
1,13	1,443	1,447	1,451	1,454	1,458	1,462	1,466	1,470	1,474	1,478	1	1	2	2
1,14	1,482	1,485	1,489	1,493	1,497	1,501	1,505	1,509	1,513	1,517	1	1	2	2
1,15	1,521	1,525	1,529	1,533	1,537	1,541	1,545	1,549	1,553	1,557	1	1	2	2
1,16	1,561	1,565	1,569	1,573	1,577	1,581	1.585	1,589	1,593	1,598	1	1	2	2
1,17	1,602	1,606	1,610	1,614	1,618	1,622	1,626	1,631	1,635	1,639	1	1	2	2
1,18	1,643	1,647	1,651	1,656	1,660	1,664	1,668	1,672	1,677	1,681	1	1	2	2
1,19	1,685	1,689	1,694	1,698	1,702	1,706	1,711	1.715	1.719	1,724	1	1	2	2
1,20	1,728	1,732	1,737	1,741	1,745	1,750	1.754	1,758	1,763	1,767	1	1	2	2
1,21	1,772	1.776	1,780	1,785	1,789	1,794	1,798	1,802	1,807	1,811	1	1	2	2
1,22	1,816	1,820	1,825	1,829	1,834	1,838	1,843	1,847	1,852	1,856	1	1	2	2
1,23	1,861	1,865	1,870	1,875	1,879	1,884	1,888	1,893	1,897	1,902	1	1	2	2
1,24	1,907	1,911	1,916	1,920	1,925	1,930	1,934	1,939	1,944	1,948	1	1	2	2
1,25	1,953	1,958	1,963	1,967	1,972	1,977	1,981	1,986	1,991	1,996	1	1	2	2
1,26	2,000	2,005	2,010	2,015	2,019	2,024	2,029	2,034	2,039	2,044	1	1	2	2
1,27	2,048	2,053	2,058	2,063	2,068	2,073	2,078	2,082	2,087	2,092	1	1	2	2
1,28	2,097	2,102	2,107	2,112	2,117	2,122	2,127	2,132	2,137	2,142	1	1	2	2
1,29	2,147	2,152	2,157	2,162	2,167	2,172	2,177	2,182	2,187	2,192	1	1	2	2	3
1,30	2,197	2,202	2,207	2,212	2,217	2,222	2,228	2,233	2,238	2,243	1	1	2	2	3
1,31	2,248	2,253	2,258	2,264	2,269	2,274	2,279	2,284	2,290	2,295	1	1	2	2	3
1,32	2,300	2,305	2,310	2,316	2,321′	2,326	2,331	2,337	2,342	2,347	1	1	2	2	3
1,33	2,353	2,358	2,363	2,369	2,374	2,379	2,385	2,390	2,395	2,401	1	1	2	2	3
1,34	2,406	2,411	2,417	2,422	2,428	2,433	2,439	2,444	2,449	2,455	1	1	2	2	3
N	1	2	3	4	5	6	7	8	9	1	2	3	4	5

При перенесении запятой в числе N на одно место запятая в числе N 3 переносится на три места.

Виды таблиц

Таблица степеней натуральных чисел

Натуральными являются те числа, которые получаются при счете предметов. Наименьшее — один, наибольшего не существует.

Чтобы вычислить результат возведения, нужно основание умножить само на себя столько раз, сколько указано в показателе. То есть основание а с показателем n значит, что а нужно умножить на себя n раз.

аn = а·а·…·а

Таблица для чисел от одного до десяти:

Таблица отрицательных степеней

Деление является обратной операцией умножению. Отрицательный показатель указывает на то, сколько раз необходимо разделить число. Легче всего представить в виде десятичной дроби:

\(а^{-n} = \frac{1}{а*а*\dots*а}\)

Для вычисления \(а^{-n}\) нужно:

1. Возвести а в степень n.
2. Затем разделить единицу на полученный результат, то есть \(\frac{1}{a^n}\).

Пример таблицы для двойки:

Что такое степень числа в математике — основные понятия

Степень в алгебре и информатике — это выражение, которое записано в виде:

\({{a}^{b}}\),

где a обозначает основание степени, а b играет роль ее показателя, который может быть квадратом, в том числе.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Записанную информацию следует читать, как: «а в степени b».

Таким образом, показатель степени b обозначает количество раз, в течение которых число а умножают само на себя.

Пример 1

Требуется возвести число 2 в третью степень. Тогда запишем 2 в степени 3:

\(2^{3} = 2\cdot 2 \cdot 2\)

В данном случае 2 является основанием степени, число 3 обозначает показатель степени.

Перечислим несколько принципов, которые следует учитывать при решении задач со степенями:

1. Если отрицательное число возвести в четную степень, то получится положительное число.
2. Если отрицательное число возвести в нечетную степень, то получится число со знаком минус.
3. При возведении положительного число в какую-либо степень результатом является положительное число.
4. Ноль при возведении в какую-либо степень дает ноль.
5. При возведении какого-либо числа в нулевую степень получается единица.

Степень с целым показателем является такой степенью, показатель которой записан в виде натурального числа, то есть целого или положительного числа.

Степень с рациональным показателем представляет собой степень с показателем, имеющим знак минус или записанным в виде дробного числа.

Степень с иррациональным показателем — это такая степень, которая имеет на месте показателя бесконечную десятичную дробь или корень.

Как найти корень кубический в калькуляторе

Корень кубический — это число, которое умноженное на себя два раза дает исходное число. Корень кубический можно найти в калькуляторе, используя функцию встроенную в большинство научных калькуляторов.

Для поиска корня кубического в калькуляторе необходимо ввести исходное число, затем нажать кнопку «3 √x». Результат будет выведен на экран. Если результатом окажется дробное число, то следует округлить его до нужного числа знаков после запятой.

При работе с калькулятором следует учитывать, что значение корня кубического может быть как положительным, так и отрицательным. Калькулятор может выдавать только положительный результат, поэтому в таких случаях следует использовать формулу для нахождения корня кубического вручную.

Для поиска корня кубического вручную необходимо использовать формулу:

Где х — исходное число, y — корень кубический. Чтобы избежать ошибок в вычислениях, следует использовать калькулятор для выполнения промежуточных операций.

Вопрос-ответ

Вопрос: Как найти корень кубический из отрицательного числа?

Ответ: Для нахождения корня кубического из отрицательного числа необходимо возвести его в куб и затем извлечь из него корень. Полученный результат нужно домножить на (-1), чтобы получить корень из исходного отрицательного числа. Например, корень кубический из -27 равен -3, так как (-3) * (-3) * (-3) = -27.

Вопрос: Можно ли найти корень кубический из комплексного числа?

Ответ: Да, корень кубический из комплексного числа можно найти. Для этого необходимо использовать формулу Муавра и найти все три корня, как для обычных действительных чисел. Однако результат будет также комплексным числом, а не только действительным.

Вопрос: Можно ли найти корень кубический из нецелого числа?

Ответ: Да, из нецелого числа также можно найти корень кубический. Для этого достаточно возвести его в степень 1/3. Если число нецелое, то ответ также будет нецелым, но это не мешает найти корень.

Вопрос: Можно ли найти корень кубический без использования калькулятора?

Ответ: Да, корень кубический можно найти без использования калькулятора, если известны таблицы степеней чисел или если известны формулы для нахождения корней кубических. Однако в большинстве случаев использование калькулятора упрощает задачу и экономит время.

Вопрос: Как найти корень кубический по методу Герона?

Ответ: Метод Герона, также известный как метод брахистохроны, является одним из методов нахождения корней уравнения. Для нахождения корня кубического методом Герона нужно выбрать начальное приближение, затем подставить его в формулу и повторять вычисления с новыми значениями, пока ответ не станет достаточно близким к искомому. Этот метод может потребоваться, когда другие способы нахождения корня кубического не применимы.

Главная — Полезно — Простые шаги для поиска корня кубического: полезные советы и методы

Комментарии

Дмитрий

5.0 out of 5.0 stars5.0

Nikita88
5.0 out of 5.0 stars5.0

Честно говоря, я всегда считал, что поиск корня кубического сложный процесс, но благодаря этой статье все оказалось намного проще. Все шаги описаны детально и понятно, а примеры помогли на практике закрепить материал. Рекомендую всем, кто сталкивается с этой задачей!

Александр
5.0 out of 5.0 stars5.0

Я инженер-механик и нередко сталкиваюсь с задачами, связанными с вычислением корней, в том числе и кубического. До этой статьи я часто использовал специальные программы или калькуляторы. Однако, после прочтения, я убедился, что все это можно сделать вручную и достаточно просто.

В целом, статья очень полезна и информативна. Я уверен, что она будет полезна не только инженерам, но и студентам и школьникам, изучающим математику на более продвинутом уровне.

Иван Петров
5.0 out of 5.0 stars5.0

Поначалу казалось, что материал немного сложный для меня, но благодаря ясному изложению и примерам, я смог разобраться. Очень пригодится в учебе, я буду рекомендовать эту статью своим друзьям.

Сергей Иванов
5.0 out of 5.0 stars5.0

Статья помогла мне быстро разобраться в поиске корня кубического. Спасибо автору!

Maximus24
5.0 out of 5.0 stars5.0

Статья очень полезная, я нашел то, что искал, спасибо!