Основные и неосновные носители заряда

Полупроводники

Само название “полупроводник” произошло от различия электропроводности полупроводников от электропроводности металлов и диэлектриков.

Действительно, . Но этот признак не является решающим в классификации.

Основными свойствами, отличающими полупроводники от других твердых тел, являются следующие:

1. Характер и величина зависимости электропроводности от температуры. Проводимость полупроводников возрастает с увеличением температуры по экспоненциальному закону ( на 1° Кельвин). У металлов увеличение температуры приводит к уменьшению проводимости.
2. Сильное влияние примеси на проводимость. Что значит сильнее? Концентрация примеси , % уже существенно увеличивает проводимость. У металлов же введение примеси уменьшает проводимость. Почему?
3. Высокая чувствительность электрических свойств полупроводников ко всякого рода внешним воздействиям (механическая деформация, облучение светом, рентгеновскими лучами или быстрыми частицами и др.).

В электронике находят применение ограниченное число полупроводников. Это германий, кремний, арсенид галия, антимонид индия и др.

1. Кристаллическая структура полупроводников и зонная теория

1. Применяемые в технике полупроводники имеют весьма совершенную кристаллическую структуру – атомы размещены в пространстве на постоянных расстояниях, образуя кристаллическую решетку. Такие полупроводники, как германий и кремний имеют структуру типа алмаза, в которой каждый атом окружен такими же атомами, находящимися в вершинах правильного тетраэдра. Плотность размещения атомов для германия 4,45·1022 1/см3, для кремния – 5·1022 см -3.

Каждый атом в кристаллической решетке или электрически нейтрален и связан ковалентными (парно–электронными) связями с четырьмя равно–отстоящими от него соседними атомами. В полупроводниках типа ионно–ковалентная связь. Валентные электроны распределяются между соседними атомами. В результате каждый атом окружен стабильной группой из восьми электронов связи.

2. Если не нужно выделять кристаллографического направления, такую решетку изображают на плоскости (рисунок 1.1).

Рисунок 1.1- Кристаллическая решетка , изображенная на плоскости

Это идеальная решетка. При все узлы заняты, все связи заполнены. Свободных носителей заряда нет.

3. С точки зрения зонной теории твердого тела, такой кристалл изображается энергетической диаграммой, представленной на рисунке 1.2.

Рисунок 1.2 — Энергетическая диаграмма полупроводников	Рисунок 1.3 – Зависимость функции распределения электронов от энергии при Т=0 К.

Заполнение энергетических уровней электронами подчиняется статистике Ферми–Дирака, в основе которой лежат следующие положения:

1. все электроны тождественны;
2. выполняется принцип Паули;
3. функция распределения , т. е. вероятность заполнения уровня с энергией W имеет следующий вид: где – энергия Ферми, смысл–уровень энергии, вероятность заполнения которого равна .

По определению функция распределения есть отношение числа частиц с энергией в интервале от W до W+dW к числу возможных состояний в этом же интервале энергий N(W), т. е.

При (обычный случай для полупроводников, используемых для приборов) единицей в знаменателе функции распределения Ферми–Дирака можно пренебречь, и функция принимает вид

Зная функцию распределения и можно определить число частиц с определенной энергией :

где k – постоянная Больцмана.

При T=0 (рисунок 1.3) валентная зона полностью заполнена f(W)=1 (это электроны, участвующие в ковалентных связях); зона проводимости пустая f(W)=0 (свободных носителей заряда нет), ΔW– ширина запрещенной зоны. Уровень Ферми расположен строго посередине запрещенной зоны.

Ток в полупроводниках

3.1. Дрейфовый ток

Когда отсутствует внешнее поле, электроны и дырки находятся в хаотическом движении. При наличии электрического поля на хаотическое движение накладывается компонента направленного движения, т. е. дырки направленно движутся вдоль электрического поля, электроны против, создавая ток одного направления (рисунок 3.1).

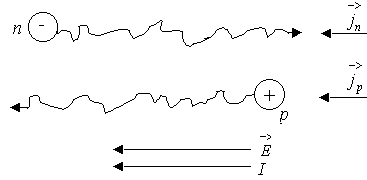
Рисунок 3.1 – Схема движения электронов и дырок под действием внешнего поля.

Ток обусловленный внешним полем напряженностью называют дрейфовым. Электронная и дырочная составляющие плотности дрейфового тока равны следующим выражениям:

,

где – заряд электрона, и – концентрация дырок и электронов:

,

т. е. это выражение закона Ома в дифференциальной форме, где и подвижности электронов и дырок, т. е. скорости электронов и дырок , возникающие при напряженности поля равном единице:

;.

Например, при К

, в

, в

3.2. Диффузионный ток

Электрический ток, обусловленный градиентом концентрации носителей называют диффузионным током.

В одномерном случае плотность диффузионного тока электронов и дырок равна следующим выражениям:

где и – градиент концентрации электронов и дырок, и – коэффициенты диффузии электронов и дырок, численно равные количеству электронов (или дырок), проходящему через единицу площади в единицу времени при градиенте концентрации носителей равном единице.

Движение носителей заряда происходит в сторону убывания их концентрации (знак минус у дырочной составляющей). Электронная составляющая тока имеет знак (+), т. к. за направление тока принято направление положительного заряда. В общем случае в полупроводниках может быть и электрическое поле и градиент концентрации носителей. Полная плотность тока пи этом равна:

— электронная составляющая тока;

— дырочная составляющая.

Физические процессы в p-n переходах

Выполнил:

студент гр. РЭ-100

Проверил:

Владимир, 2002

1. Вопрос №7

Физический смысл понятия “Эффективная плотность
состояний”

Физический смысл понятия
“Эффективная плотность состояний” определяется в зоне проводимости и в
валентной зоне. В зоне проводимости эффективная плотность состояний
определяется формулой:

(1)

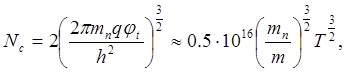
где N_C
– эффективная плотность состояний в зоне проводимости;

m_n
– эффективная масса электрона;

q –
элементарный заряд;

φ_t– температурный потенциал;

h – постоянная
Планка;

m – масса
свободного электрона;

T –
термодинамическая температура.

Из формулы (1) следует,
что эффективная плотность состояний в зоне проводимости представляет собой
максимально возможную концентрацию электронов в невырожденном полупроводнике.
Понятие “эффективная плотность состояний” применимо в тех случаях, когда
выполняется условие: энергия уровня Ферми стремиться быть равной энергии дна
зоны проводимости. По физическому смыслу величина N_Cблизка к плотности энергитических уровней в зоне
проводимости в полосе энергий от φ_с до φ_с+φ_t (где φ_с — энергия дна зоны проводимости, φ_t — температурный потенциал).

В валентной зоне эффективная плотность состояний
определяется формулой:

(2)

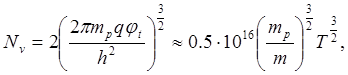
где N_V
– эффективная плотность состояний в валентной зоне;

m_p
– эффективная масса “дырки”;

q –
элементарный заряд;

φ_t– температурный потенциал;

h –
постоянная Планка;

m – масса
свободного электрона;

T
– термодинамическая температура.

Из формулы (2) следует,
что эффективная плотность состояний в валентной зоне представляет собой
максимально возможную концентрацию “дырок” в невырожденном полупроводнике.
Понятие “эффективная плотность состояний” применимо в тех случаях, когда
выполняется условие: энергия уровня Ферми стремиться быть равной энергии
потолка валентной зоны. По физическому смыслу величина N_Vблизка к плотности энергитических уровней в валентной
зоне в полосе энергий от φ_v до φ_v-φ_t (где φ_v — энергия потолка валентной зоны,
φ_t — температурный потенциал).

2.
Задача № 7

Условие:

Используя распределение
Ферми-Дирака для примесного полупроводника

(3)

где N_dn – концентрация нейтральных атомов донорной
примеси; E_d–
энергия донорного уровня, определить относительную долю ионизированных атомов
фосфора с энергией активации E_c-E_d=0.044 эВ при температурах 50, 100, 300 К.

Решение:

Относительная доля
ионизированных атомов фосфора определяется распределением Ферми-Дирака:

(4)

где N_dn–
концентрация нейтральных атомов донорной примеси;

N_d– концентрация
ионизированных атомов донорной примеси;

E_c-E_d –
энергиея активации;

k – коэффициент Больцмана;

T – термодинамическая температура.

При температуре, равной
300 К, уровень Ферми размещается в середине примесной зоны, поэтому разность
между энергией донорного уровня и энергией уровня Ферми равна половине энергии
активации:

(5)

Относительная доля
ионизированных атомов фосфора при температуре — 300 К, равна:

При более низких
температурах (T=50 К; T=100 К)
уровень Ферми располагается несколько ближе к дну зоны проводимости и дальше 
от донорного уровня, т.к. энергия электронов прямо пропорциональна kT, и им необходимо затратить большую энергию для достижения
энергии уровня Ферми. Разность  между энергией донорного уровня и энергией
уровня Ферми изменяется не значительно, поэтому берётся такое же значение
энергии активации как при температуре 300 К для 100 К:

, для 50 К:

Ответ: для значений
температур T=300 К, T=100 К и T=50 К полученны соответственно следующие результаты
относительной доли ионизированных атомов фосфора: 0.459, 0.13, 0.1.

Зонная теория проводников

В случае если зоны соседних энергетических уровней перекрываются или верхняя зона не полностью заполнена электронами,
то им легко переходить на более высокие уровни и достаточно даже небольшого напряжения, чтобы возник электрический ток.
Такие материалы называются металлами. Их проводимость обычно составляет ρ = 10-5 ÷
10-6 Ом/см. График пересечения валентной зоны и зоны проводимости в металлах показан на рисунке 3.

На примере металлов легко ввести понятие электронного газа и распределения электронов по энергетическим уровням. В
металлах электроны принадлежат не отдельным атомам, а всему материалу в целом и могут свободно перемещаться по всему
объему металла. Совокупность электронов в твердом теле в статистической физике принято рассматривать как «электронный
газ» — систему, состоящую из большого числа частиц. Эта система описывается функцией плотности заполнения
энергетических состояний частицами F(W). Если число частиц в системе равно N, а число возможных
состояний Z, то функция плотности заполнения энергетических состояний определяется следующим образом:

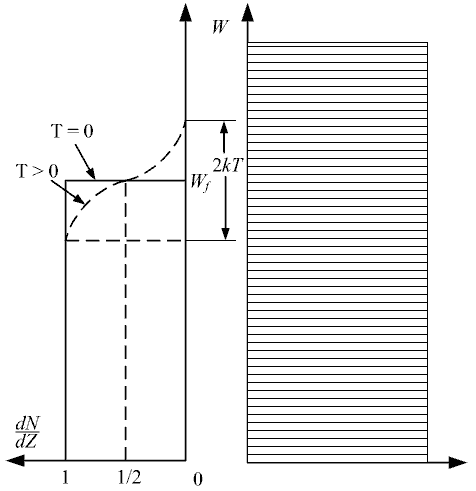
Плотность заполнения энергетических уровней электронами зависит от температуры вещества. При T=0°K заполнены
будут уровни с самой низкой энергией. При повышении температуры часть электронов займет более высокий энергетический
уровень (начнет подобно молекулам газа хаотически перемещаться по металлу). Плотность заполнения энергетических уровней
электронами описывается функцией Ферми-Дирака

При температуре абсолютного нуля все электроны постараются занять наименьший возможный энергетический уровень. Поэтому
функция будет выглядеть подобно прямоугольнику, а максимальный энергетический уровень, занятый электронами получил название
уровня Ферми. На рисунке 4 приведены кривые Ферми-Дирака при двух разных температурах: температуре абсолютного нуля и
комнатной температуре.

Плотность заполнения энергетических уровней электронами и энергетические уровни в слившихся валентной зоне и зоне
проводимости металла на одном графике приведены на рисунке 5

Приложения

6.1. Универсальные физические постоянные

Электрический заряд электрона, квант заряда Кл

Удельный заряд электрона Кл/кг

Масса покоя электрона кг

Масса покоя протона кг

Масса покоя нейтрона кг

Скорость света в вакууме м

Магнетон Бора

Магнетон ядерный

Постоянная Планка

Постоянная Авогадро

Постоянная Больцмана Дж/К

Постоянная Стефана–Больцмана

Постоянные Ридберга

Боровский радиус м

Комптоновская длина волны электрона м

Энергия ионизации атома водорода Дж

Энергия покоя электрона МэВ

Энергия покоя протона МэВ

Энергия покоя нейтрона МэВ

Электрическая постоянная Ф/м

Магнитная постоянная Гн/м

6.2. Приставки и множители для образования кратных и дольных единиц

Наименование (обозначение)	Множитель
Гита (Г)
Мега (М)
Кило (К)
Деци (д)
Санти (с)
Милли (м)
Микро (мк)
Нано (н)
Пико (п)
Фемто (ф)

6.3. Соотношение между некоторыми несистемными единицами и единицами СИ

Наименование	Множитель
Длина	(ангстрем) м
Масса	кг
Энергия, работа	1эВ Дж
Количество теплоты	1 кал = 4,19 Дж
Давление	1 атм = 760 мм.рт.ст. = 101,3 кПа
Время	1 год = с

Вырожденный полупроводник

F>E_>C>+5KT

она не зависит от температуры.

Уровень Ферми находится в зоне
проводимости выше ее дна не менее чем
на 5 КТ.

В невырожденном полупроводнике
концентрация дырок определяется
статистикой Больцмана при условии F
> E_>v>
+ KT
т.е. уровень Ферми лежит выше
потолка валентной зоны на величину КТ.

В полностью вырожденном
полупроводнике

или F<E_>v>-KT

т.е.
в валентной зоне ниже ее потолка на
величину не менее 5КТ. N_>v>
– число состояний в валентной зоне.

Невырожденный полупроводник

Вырожденный полцпроводник

В невырожденном:

не зависит от уровня Ферми

В вырожденном

где V_>F>
– объем зоны Бриллюэна. Для сферических
поверхностей
,

где радиус сферы Ферми

Функция распределения электронов:

где g_>i>
– степень вырождения, если E_>i>=E_>d>
принадлежит донорной примеси, то g_>i>=2.
Если E_>i>=E_>a>
принадлежит акцепторной примеси, то
g_>i>=1/2

Распределение электронов по
донорным уровням

по акцепторным

Для дырок:

;

Число электронов:

Число дырок:

N_>D>
= N_>a>
= 0 собственный полупроводник.

Уравнение электронейтральности
n =
P.
Если N_>v>
= N_>c>
т.е.
,
тогда

откуда

положение уровня Ферми от температуры
не зависит и лежит посередине запрещенной
зоны. Собственный полупроводник является
невырожденным.

Генерация электронов и дырок
проводимости в собственном полупроводнике:

Переход
каждого электрона из валентной зоны
порождает в ней дырку.

Если N_>V>

N_>C>,
то

Уровень Ферми при Т = 0, лежит в
середине запрещенной зоны, он линейно
зависит от температуры.

Температурная зависимость уровня
Ферми в собственном полупроводнике. С
ростом температуры уровень Ферми
приближается к той зоне, которая имеет
меньшую плотность состояний и поэтому
заполняется быстрее.

или

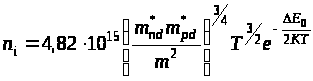
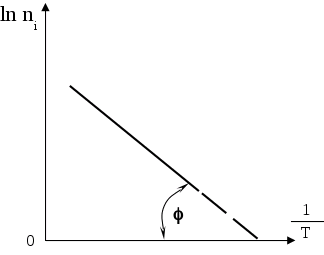
На рисунке график ln
n_>i>
от обратной температуры представляет
прямую линию:

Зависимостью ln1/T
по сравнению с линейным членом можно
пренебречь. Угол наклона прямой
определяется шириной запретной зоны:

откуда

tg

измеряется по графику (ln
n_>i>,
1/T)

Оценим собственную концентрацию
носителей заряда в германии и кремнии

равны 0,299 и 0,719, и при Т300К,

и

Концентрация
носителей заряда при Т 
0 обращается в нуль, и сопротивление
собственного полупроводника должно
расти до бесконечности. Однако, в реальных
полупроводниках всегда остается примесь,
которая обеспечивает проводимость при
любых температурах.

Тепловая генерация на рисунке
носителей заряда в полупроводнике с
донорной примесью.

Низкие температуры: электроны
проводимости определяются концентрацией
примеси, которая возникает за счет
ионизации донорной примеси.

При повышении температуры уровень
Ферми повышается, проходит при некоторой
температуре через максимум, затем
опускается. При K_>d>=N_>2>_>C>
он снова находится в середине между Е_>С>
и Е_>D>.

При достаточно высокой температуре
N_>C>
>> N_>D>,
то

концентрация электронов не
зависит от температуры и равна концентрации
примеси. (Область истощения примеси).
Носители заряда называют основными,
если их концентрация больше концентрации
собственных носителей заряда n_>i>
при данной температуре, если же
концентрация меньше n_>i>,
то их называют неосновными носителями
заряда. В области истощения примеси
концентрация неосновных носителей
заряда должна резко возрастать с
температурой

Последнее справедливо до тех
пор, пока концентрация дырок остается
много меньше концентрации электронов.

P<<n=N_>D>

Высокие
температуры

С ростом температуры число дырок
возрастает и может стать сравнимой с
концентрацией электронов

вся примесь ионизирована и
необходимо учитывать ионизацию вещества.

Из уравнения

P=N_>D>
или n=2N_>D>_>
>Температура перехода к
собственной концентрации, тем выше, чем
больше

и чем больше концентрация примесей.

Акцепторный полупроводник.

Температурная зависимость на
рисунке уровня Ферми в полупроводнике
с акцепторной примесью.

Оценим температуру, при которой
наступает истощение примеси.

Когда вся примесь ионизирована:

Когда вся примесь ионизирована
и происходит ионизация основного
вещества: n=N_>D>+P

Чем шире запрещенная зона и чем
больше концентрация примеси, тем при
большей температуре происходит переход
к собственной проводимости.