Сколько будет число в кубе

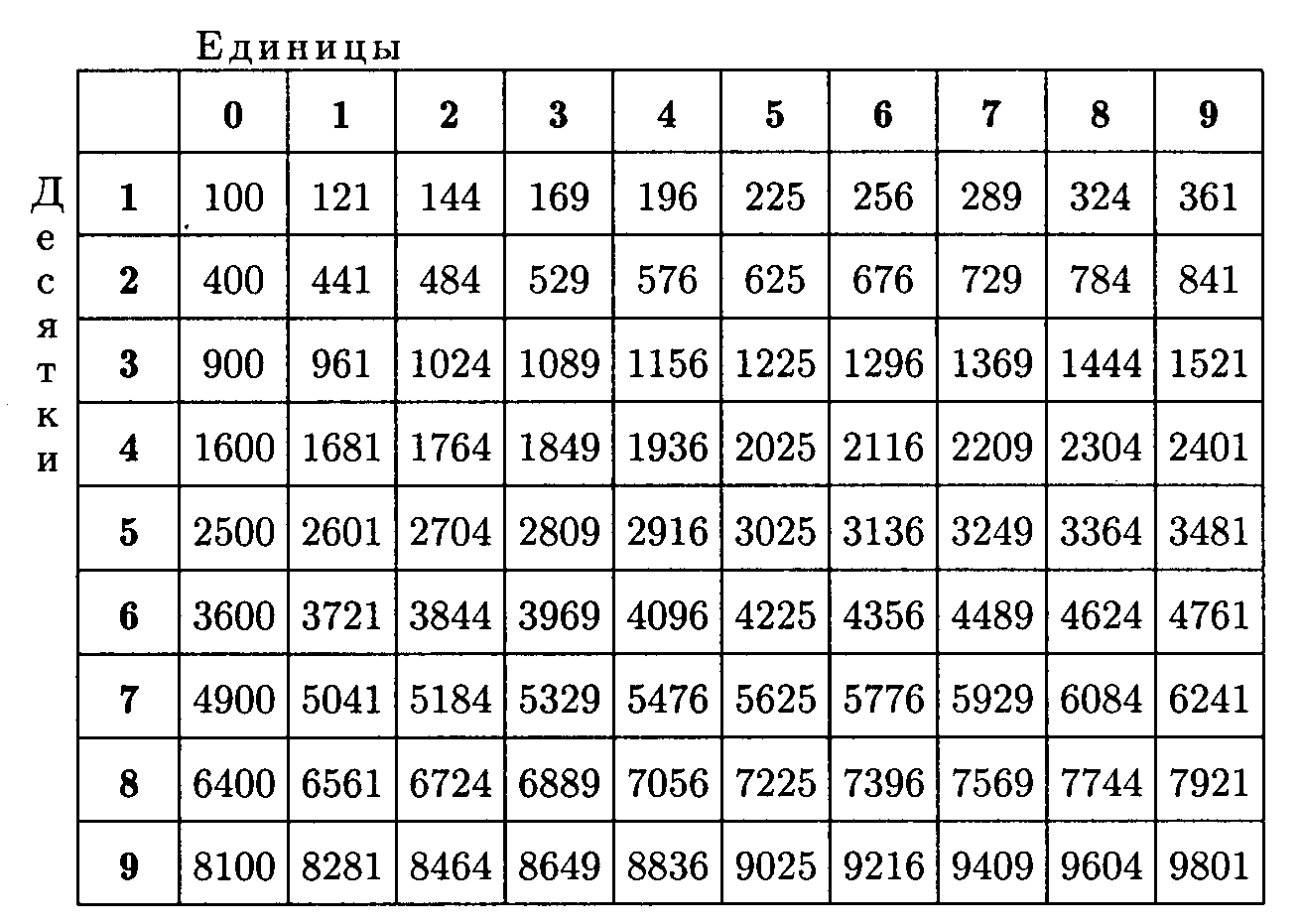
Свойства степеней

a, b — любое рациональное число, n, m — любое натуральное

Произведение степеней

Данное действие подразумевает то, что одинаковое основание остается без изменений, а показатели складываются.

\(a^n\cdot a^m=a^{n+m}\)

Частное степеней

Под выполнением данной операции понимается то, что одинаковое основание остается без изменений, а из показателя делимого вычитают показатель делителя.

\(\frac{a^m}{a^n}=a^{m-n}\)

Возведение степени в степень

Для вычисления результата этой операции основание остается без изменения, а показатели перемножаются.

\(\left(a^m\right)^n=a^{m\cdot n}\)

Степень произведения

Для выполнения этого арифметического действия каждый из множителей возводится в степень, после чего полученные результаты перемножаются.

\(\left(a\cdot b\right)^n=a^n\cdot b^n\)

Степень частного

Чтобы выполнить данную арифметическую операцию, следует возвести в степень делимое и делитель, а затем первый результат разделить на второй.

\(\left(\frac{a}{b}\right)^n=\frac{a^n}{b^n}\)

Квадрат числа

На изготовление одного килограмма творога уходит три литра молока. Сколько молока потребуется для изготовления трех килограммов творога?

Чтобы ответить на главный вопрос, мы должны молоко необходимое для изготовления одного килограмма творога, взять три раза, чтобы в результате должно получиться три килограмма творога.

Получим: 3+3+3.

Слагаемое три, взяли три раза, полученную сумму заменим произведением. Для этого числовое значение слагаемых (3) умножаем на количество таких слагаемых (3) – 3×3.

Пользуясь изученным определением, зная, что в произведении множитель три использован два раза, полученное выражение запишем иначе: 32

Выражение 32, произносится «три в квадрате». 

3×3=32 =9.

Для изготовления трех килограммов творога потребуется девять литров молока.

Если показатель степени числа равен 2, то говорят « число в квадрате».

42 – четыре в квадрате;

72 – семь в квадрате;

152 – пятнадцать в квадрате.

Важно!

Чтобы возвести число в квадрат, умножаем его само на себя два раза.

Примеры решения задач

Задача 1

Дано выражение, значение которого требуется определить:

\({{3}^{7}}+{{5}^{6}}-{{9}^{4}}\)

Решение

С помощью таблицы вычислим значения всех компонентов выражения:

\({{3}^{7}}=2187\)

\({{5}^{6}}=15625\)

\({{9}^{4}}=6561\)

Путем подстановки преобразуем начальное выражение:

\({{3}^{7}}+{{5}^{6}}-{{9}^{4}}=2187+15625-6561=11251\)

Ответ: \({{3}^{7}}+{{5}^{6}}-{{9}^{4}}=11251.\)

Задача 2

Необходимо определить степень, в которую следует возвести число 8 для получения в результате числа 32768.

Решение

По таблице степеней определим:

\({{8}^{5}}=32768\)

Таким образом, нужная степень равна 5.

Ответ: 5.

Задача 3

Дано выражение, значение которого требуется вычислить:

\(\frac{(4^3)^{-4}}{4^{-11}}\)

Решение

Зная, что возведение степени в степень заключается в необходимости умножения показателей этих степеней, преобразуем числитель:

\( (4^3)^{-4} = 4^{-12}\)

В результате:

\(\frac{(4^3)^{-4}}{4^{-11}}=\frac{4^{-12}}{4^{-11}}=4^{-12-(-11)}=4^{-1}=\frac{1}{4}=0,25\)

Ответ: 0,25.

Задача 4

Требуется вычислить значение выражения:

\(6^{-8} \cdot (6^2)^3\)

Решение

В процессе возведения степени в степень необходимо найти произведение показателей этих степеней. Заметим так же, что при умножении степеней, которые имеют идентичные основания, показатели суммируют. Выполним соответствующие преобразования:

\(6^{-8} \cdot (6^2)^3 = 6^{-8} \cdot 6^6 = 6^{-8+6}=6^{-2} = \frac{1}{36}\)

Ответ: \(\frac{1}{36}.\)

Задача 5

Дано выражение, значение которого необходимо вычислить:

\(5^{12} \cdot (5^5)^{-3}\)

Решение

Воспользуемся свойствами степени и выполним соответствующие преобразования:

\(5^{12} \cdot (5^5)^{-3} = 5^{15} \cdot 5^{-15} = 5^{12-15}=5^{-3} = \frac{1}{5^3} = \frac{1}{125}\)

Ответ: \( \frac{1}{125}.\)

Задача 6

Необходимо рассчитать значение следующего выражения:

\(\frac{2^{2} \cdot 8^{-2}}{2^{-5}}\)

Решение

Каждую из степеней требуется привести к основанию в виде числа 2:

\(8^{-2} = {(2^3)}^{-2} = 2^{-6}\)

В результате:

\(\frac{2^{2} \cdot 8^{-2}}{2^{-5}} = \frac{2^{2} \cdot 2^{-6}}{2^{-5}} = 2^{2-6-(-5)} = 2^{1} = 2\)

Ответ: 2.

Задача 7

Нужно найти значение следующего выражения:

\(\frac{5^{6} }{25^{3}\cdot 5^{-2}}\)

Решение

Следует привести каждую из представленных степеней к основанию 5:

\(25^{3} = {(5^2)}^{3} = 5^{6}\)

Таким образом:

\(\frac{5^{6} }{25^{3}\cdot 5^{-2}} = \frac{5^{6} }{5^{6}\cdot 5^{-2}} = 5^{6-6-(-2)}=5^2=25\)

Ответ: 25.

Задача 8

Дано выражение, значение которого нужно вычислить:

\(\frac{l^{6} \cdot {(l^{2})}^{-2}}{l^{-3}}\)

Решение

Заметим, что в процессе возведения степени в степень требуется найти произведение показателей этих степеней:

\({(l^{2})}^{-2} = l^{-4}\)

В результате:

\(\frac{l^{6} \cdot {(l^{2})}^{-2}}{l^{-3}} = \frac{l^{6} \cdot l^{-4}}{l^{-3}} = l^{6-4-(-3)}=l^{5}\)

Ответ: \( l^{5}.\)

Задача 9

Необходимо определить значение такого выражения:

\(\frac{p^{4} \cdot {(p^{2})}^{-3}}{p^{-5} \cdot p^{3}}\)

Решение

Возвести степень в степень можно путем умножения их показателей:

\({(p^{2})}^{-3} = p^{-6}\)

В результате:

\(\frac{p^{4} \cdot {(p^{2})}^{-3}}{p^{-5} \cdot p^{3}} = \frac{p^{4} \cdot p^{-6}}{p^{-5} \cdot p^{3}} = p^{4-6-(-5)-3}=p^{0}=1\)

Ответ: 1.

Задача 10

Дано несколько чисел, среди которых требуется выбрать самое большое:

\(2,5 \cdot 10^{-5}\)

\(1,05 \cdot 10^{-3}\)

\(0,1 \cdot 10^{-3}\)

Решение

Преобразуем перечисленные выражения так, чтобы привести их к виду:

\(a \cdot 10^{-6}\)

В результате:

\(2,5 \cdot 10^{-5} = 2, 5 \cdot 10 \cdot 10^{-6} = 25 \cdot 10^{-6},\)

\(0,1 \cdot 10^{-3}= 0,1 \cdot 10^3 \cdot 10^{-6} = 100 \cdot 10^{-6},\)

\(1,05 \cdot 10^{-3} = 1,05 \cdot 10^3 \cdot 10^{-6} =1050 \cdot 10^{-6}.\)

При сравнении чисел со знаком плюс справедливо, что:

\(a < b\)

\(ac < bc\)

В таком случае целесообразно сравнить множители перед \(\cdot 10^{-6}\). Тогда наибольшим является число \(1,05 \cdot 10^{-3}\).

Ответ: \(1,05 \cdot 10^{-3}.\)

Таблица кубов

1	8	27	64	125	216	343	512	729
1	1000	1331	1728	2197	2744	3375	4096	4913	5832	6859
2	8000	9261	10648	12167	13824	15625	17576	19683	21952	24389
3	27000	29791	32768	35937	39304	42875	46656	50653	54872	59319
4	64000	68921	74088	79507	85184	91125	97336	103823	110592	117649
5	125 000	132651	140608	148877	157464	166375	175616	185193	195112	205379
6	216000	226981	238328	250047	262144	274625	287496	300763	314432	328509
7	343 000	357911	373248	389017	405224	421875	438976	456533	474552	493039
8	512 000	531441	551368	571787	592704	614125	636056	658503	681472	704969
9	729 000	753571	778688	804357	830584	857375	884736	912673	941192	970299

Калькулятор куба x³

Базовый калькулятор

Поделись этим калькулятором и страницей

Калькулятор Использование

Найдите значение числа n в кубе. Введите положительные или отрицательные целые числа или десятичные числа или научную нотацию E.

Кубирование отрицательных чисел

При кубировании отрицательных чисел ответ всегда будет отрицательным. В этом калькуляторе вам не нужно использовать круглые скобки при вводе, потому что вы все равно получите правильный ответ, хотя вы должны знать, что ниже показано, как ваши вводы на самом деле интерпретируются калькулятором.

• -2³ означает -(2 × 2 × 2) = -8
• -(2)³ означает -(2 × 2 × 2) = -8
• (-2)³ означает (-2 × -2 × -2) = -8

Когда выражение степени записывается с положительным значением, таким как 4³, большинству легко понять, что это означает 4 × 4 × 4 = 64

отрицательное значение без круглых скобок означает неоднозначность. Для разных людей это имеет разное значение.

Различные возможные интерпретации -4³:

1. минус (4 в кубе) или -(4)³ = -(4 × 4 × 4) = -64

2. (минус 4) в кубе или (-4 )³ = (-4 × -4 × -4) = -64

Используйте круглые скобки, чтобы четко указать, какое вычисление вы действительно хотите выполнить. Скобки не изменяют ваши результаты, когда показатель степени нечетен, например, 3, но они имеют явное значение, когда показатель степени четен, например, 2. Калькулятор площади для -4²

Куб

Число n в кубе записывается как n³ и n³ = n × n × n. Если n — целое число, то n³ — совершенный куб.

Например, 3 в кубе записывается как 3³ и 3³ = 3 × 3 × 3 = 27. 27 — совершенный куб.

Числа от 0 до 10 в кубе и полученные в результате идеальные кубы

• 0 в кубе равно 0³ = 0 × 0 × 0 = 0
• 1 куб равен 1³ = 1 × 1 × 1 = 1
• 2 в кубе равно 2³ = 2 × 2 × 2 = 8
• 3 в кубе равно 3³ = 3 × 3 × 3 = 27
• 4 в кубе равно 4³ = 4 × 4 × 4 = 64
• 5 в кубе равно 5³ = 5 × 5 × 5 = 125
• 6 в кубе равно 6³ = 6 × 6 × 6 = 216
• 7 в кубе равно 7³ = 7 × 7 × 7 = 343
• 8 в кубе равно 8³ = 8 × 8 × 8 = 512
• 9 в кубе равно 9³ = 9 × 9 × 9 = 729
• 10 в кубе равно 10³ = 10 × 10 × 10 = 1000

Дополнительные показания

Википедия «Куб (алгебра)» по адресу https://en. wikipedia.org/wiki/Куб_(алгебра)

Википедия «Куб» по адресу https://en.wikipedia.org/wiki/Куб

Подписаться на калькуляторSoup:

Числа от 0 до 3

• 0 в кубе равно 0, так как куб любого числа равен нулю.
• 1 в кубе равно 1, так как куб единицы равен самой единице.
• 2 в кубе равно 8, так как два в кубе равно двум умножить на два умножить на два.
• 3 в кубе равно 27, так как три в кубе равно трем умножить на три умножить на три.

Число 0 в кубе

Число 0 в кубе равно 0, так как куб нуля равен нулю. В математике куб числа получается путем умножения числа на себя три раза. В данном случае, когда число равно 0, все множители также равны 0, и результатом будет 0.

Более формально, 0 в кубе можно представить как: 0 * 0 * 0 = 0.

Куб нуля — это крайний случай, когда основное число равно нулю. В этом случае все множители в равенстве равны нулю и, следовательно, произведение равно нулю.

Еще одним способом рассмотреть число 0 в кубе — это представить его в виде таблицы, где в первом столбце будут числа от 0 до 1, во втором столбце числа от 0 до 2, в третьем — от 0 до 3 и т.д., с последующим умножением чисел от 0 до 10 в каждом столбце. Такая таблица поможет наглядно увидеть, что куб нуля равен 0.

Итак, число 0 в кубе равно 0, так как куб нуля равен нулю.

Число 1 в кубе

1 в кубе равно самому себе. Когда число возводится в куб, оно умножается на себя три раза. Для числа 1 это будет:

1. 1*1*1 = 1

Итак, число 1 в кубе равно 1. Это означает, что если мы возведем число 1 в куб, то получим результат 1.

Чтобы лучше понять процесс возведения чисел в куб, посмотрим, что получится, если возвести в куб несколько других чисел:

• Число 2: 2 в кубе равно 2*2*2 = 8
• Число 3: 3 в кубе равно 3*3*3 = 27
• Число 4: 4 в кубе равно 4*4*4 = 64
• Число 5: 5 в кубе равно 5*5*5 = 125
• Число 6: 6 в кубе равно 6*6*6 = 216
• Число 7: 7 в кубе равно 7*7*7 = 343
• Число 8: 8 в кубе равно 8*8*8 = 512

И так далее. Возведение чисел в куб – это важная математическая операция, которая широко применяется в науке и технике. Оно позволяет быстро и точно вычислять результаты и решать различные задачи.

Число 2 в кубе

2 в кубе равно 2 * 2 * 2 = 8. Возведение числа 2 в куб является процессом умножения числа на само себя три раза. Таким образом, результатом является число 8.

Возведение числа 2 в куб может быть представлено следующей формулой: 23 = 8. Здесь символ «^» означает возведение числа в степень. В данном случае, число 2 возводится в степень 3, что равносильно умножению числа 2 на само себя три раза.

Кроме того, можно представить вычисление 2 в кубе в виде таблицы с помощью тегов

Что такое степень числа в математике — основные понятия

Степень в алгебре и информатике — это выражение, которое записано в виде:

\({{a}^{b}}\),

где a обозначает основание степени, а b играет роль ее показателя, который может быть квадратом, в том числе.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Записанную информацию следует читать, как: «а в степени b».

Таким образом, показатель степени b обозначает количество раз, в течение которых число а умножают само на себя.

Пример 1

Требуется возвести число 2 в третью степень. Тогда запишем 2 в степени 3:

\(2^{3} = 2\cdot 2 \cdot 2\)

В данном случае 2 является основанием степени, число 3 обозначает показатель степени.

Перечислим несколько принципов, которые следует учитывать при решении задач со степенями:

1. Если отрицательное число возвести в четную степень, то получится положительное число.
2. Если отрицательное число возвести в нечетную степень, то получится число со знаком минус.
3. При возведении положительного число в какую-либо степень результатом является положительное число.
4. Ноль при возведении в какую-либо степень дает ноль.
5. При возведении какого-либо числа в нулевую степень получается единица.

Степень с целым показателем является такой степенью, показатель которой записан в виде натурального числа, то есть целого или положительного числа.

Степень с рациональным показателем представляет собой степень с показателем, имеющим знак минус или записанным в виде дробного числа.

Степень с иррациональным показателем — это такая степень, которая имеет на месте показателя бесконечную десятичную дробь или корень.

Числа от 4 до 6

Возведение чисел в куб — это процесс умножения числа на само себя три раза. Рассмотрим числа от 4 до 6 и их кубы.

Число 4 в кубе равно 64. Это означает, что число 4 нужно умножить на само себя три раза: 4*4*4 = 64. Куб числа 4 равен 64.

Число 5 в кубе равно 125. Умножив число 5 на само себя три раза, получим: 5*5*5 = 125. Куб числа 5 равен 125.

Число 6 в кубе равно 216. Умножив число 6 на само себя три раза, получим: 6*6*6 = 216. Куб числа 6 равен 216.

Таким образом, числа 4, 5 и 6 в кубе равны соответственно 64, 125 и 216.

Число 4 в кубе

Число 4 в кубе равно 64. Чтобы получить куб числа 4, нужно перемножить его само на себя два раза. Таким образом, 4 в кубе = 4 * 4 * 4 = 64.

Видно, что результатом умножения 4 на 4 будет 16, а умножение 16 на 4 даст нам 64. Таким образом, для получения куба числа 4 мы умножаем его само на себя дважды.

Куб числа 4 имеет форму куба со стороной 4. Все его грани, ребра и углы равны между собой. Такой куб можно представить в виде трехмерной фигуры.

Если возвести в куб число 4, то получится число 64. Обратный процесс называется извлечением кубического корня. В данном случае, кубический корень из 64 равен 4. То есть, ∛64 = 4.

Число 5 в кубе

Число 5 в кубе равно 125. Для того чтобы получить куб числа 5, нужно число умножить само на себя дважды. Таким образом, 5 * 5 * 5 = 125.

5 в кубе представляет собой объем куба со стороной 5 единиц. Куб с ребром длиной 5 единиц будет иметь объем 125 кубических единиц.

Для удобства расчетов можно использовать таблицу степеней числа 5. Например, 5 в первой степени равно 5, 5 во второй степени равно 25, 5 в третьей степени равно 125.

Следующие числа после 5 в кубе в таблице степеней: 8, 0, 3, 4, 2, 6, 7. Для каждого из этих чисел можно посчитать его куб, перемножив число само на себя дважды.

Таким образом, 8 в кубе равно 512, 0 в кубе равно 0, 3 в кубе равно 27, 4 в кубе равно 64, 2 в кубе равно 8, 6 в кубе равно 216, 7 в кубе равно 343.

Число 6 в кубе

Число 6 в кубе равно 216. Для получения куба числа 6 нужно умножить его само на себя два раза. Таким образом, 6 * 6 * 6 = 216. Куб числа 6 можно представить в виде кубического массива, состоящего из шести граней.

Куб числа 6 имеет три оси, каждая из которых содержит по 6 элементов. Из каждой вершины куба выходит по 3 ребра, образуя в итоге 12 ребер.

Примером чисел, которые можно получить в кубе числа 6, могут быть:

• Число 1 в кубе равно 1
• Число 2 в кубе равно 8
• Число 3 в кубе равно 27
• Число 4 в кубе равно 64
• Число 5 в кубе равно 125
• Число 6 в кубе равно 216
• Число 7 в кубе равно 343
• Число 8 в кубе равно 512
• Число 9 в кубе равно 729
• Число 10 в кубе равно 1000

Куб числа 6 является одним из чисел, которые часто используются в математике и физике. Его значение может быть использовано для моделирования объема кубических тел, расчета объема жидкости или газа, и в других приложениях.

Возведение в степень: определение

Возведение числа в натуральную степень — это умножение его на само себя определенное количество раз. Это такая же операция в алгебре, как сложение, вычитание, умножение или деление.

Если определенное число нужно умножить на себя несколько раз, это значит, что его необходимо возвести в соответствующую степень. Например, если четыре нужно умножить само на себя три раза, это равно тому, что четыре следует возвести в третью степень. Закодировать это выражение можно следующей арифметической записью:

43, где 4 — это основание, а 3 — показатель. Также 43 = 4·4·4 = 64

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Основные правила выполнения данных вычислений:

• итог возведения отрицательного основания в четную степень — положительный;
• итог возведения отрицательного основания в нечетную — отрицательный;
• итог возведения положительного основания в любую — положительный;
• любое основание с показателем один равно себе;
• ноль при любом возведении в результате дает ноль;
• единица с любым показателем равна единице;
• любое основание с показателем ноль равно единице.

Таблица представляет собой ряд чисел, возведенных в определенные степени.

Возведение в степень, основные свойства

Возведение в степень представляет собой арифметическое действие в виде итога множественного умножения числа самого на себя.

Обозначают степень, основание которой равно а, и натуральный показатель составляет b, таким образом:

\(a^{b}=\underbrace {a\cdot a\cdot \ldots \cdot a} _{b}\),

где b — число множителей, то есть умножаемых чисел.

Пример 2

Запишем несколько степеней для примера:

\(3^{2}=3\cdot 3=9\)

\(2^{4}=2\cdot 2\cdot 2\cdot 2=16\)

Существуют ключевые свойства, которые распространяют свое действие на операции возведения в степень чисел из множества натуральных, целых, рациональных и вещественных. При этом если требуется возвести в степень комплексное число, то показатель должен быть натуральным. Перечислим эти свойства:

1. \(a^{1}=a\)
2. \(\left(ab\right)^{n}=a^{n}b^{n}\)
3. \(\left({a \over b}\right)^{n}={{a^{n}} \over {b^{n}}}\)
4. \(a^{n}a^{m}=a^{n+m}\)
5. \(\left.{a^{n} \over {a^{m}}}\right.=a^{n-m}\)
6. \(\left(a^{n}\right)^{m}=a^{nm}.\)

Следует отметить, что выражение \(a^{n^{m}}\) лишено свойства ассоциативности (сочетательности). Таким образом, в общем случае:

\( (a^{n})^{m}\neq a^{\left({n^{m}}\right)}\)

Пример 3

\((2^{2})^{3}=4^{3}=64\)

\(2^{\left({2^{3}}\right)}=2^{8}=256\)

В процессе решения математических задач данные записи можно считать равнозначными:

\(a^{n^{m}}\)

\(a^{\left({n^{m}}\right)}\)

Руководствуясь записанным свойством, допустимо упростить запись:

\((a^{n})^{m}\)

\(a^{nm}.\)

Операция возведения в степень не характеризуется свойством коммутативности (переместительности):

\(a^{b}\neq b^{a}\)

Пример 4

\(2^{5}=32\)

\(5^{2}=25.\)

Таблица степеней чисел до 100 в кубе

Часто в примерах требуется возвести двузначное число в куб. Сделать это будет проще со следующей таблицей:

_{*Для лучшего понимания примеры подсвечены голубым.}

Пример 4. Работаем с таблицей натуральных степеней чисел в кубе.

Задача. Найти 453.

Решение. Делим число на десятки и единицы. Находим 4 десятка (левый столбец) и 5 единиц (верхняя полоса) и ищем значение их пересечения.

Ответ. 157464.

Пример 5. Вычисляем квадрат по таблице.

Задача. Найти 403.

Решение. Найти значение можно двумя способами. Первый — руководствуясь таблицей. 4 — десятки, 0 — единицы. Ищем пересечение этих цифр. Результат — 6400. Второй способ: возводим 4 в куб и прибавляем два нуля (т.к. 10 в кубе = 100). 43=64. Прибавляем «00» и получаем идентичный ответ: 6400.

Ответ. 6400.

Пользоваться таблицами степеней по математике несложно. Но только в том случае, если речь идет о небольших цифрах. В длинных примерах, состоящих из множества чисел в степенях, можно использовать онлайн калькуляторы. Это позволит избежать ошибок, которые могут быть вызваны просмотром не той ячейки.

Таблица кубов

Определение
Калькулятор — куб числа
Таблица кубов

Определение.Куб числа — есть данное число, возведенное в третью степень.

a3 = a · a · a

«Кубом» оно называется, потому что такая операция аналогична вычислению объема куба.

3 = 827 ≈ 0.2962962962962963

Ниже приведены две удобные таблицы кубов натуральных чисел от 1 до 100.

Таблица кубов чисел от 1 до 100

13 = 1 23 = 8 33 = 27 43 = 64 53 = 125 63 = 216 73 = 343 83 = 512 93 = 729 103 = 1000	113 = 1331 123 = 1728 133 = 2197 143 = 2744 153 = 3375 163 = 4096 173 = 4913 183 = 5832 193 = 6859 203 = 8000	213 = 9261 223 = 10648 233 = 12167 243 = 13824 253 = 15625 263 = 17576 273 = 19683 283 = 21952 293 = 24389 303 = 27000	313 = 29791 323 = 32768 333 = 35937 343 = 39304 353 = 42875 363 = 46656 373 = 50653 383 = 54872 393 = 59319 403 = 64000	413 = 68921 423 = 74088 433 = 79507 443 = 85184 453 = 91125 463 = 97336 473 = 103823 483 = 110592 493 = 117649 503 = 125000
513 = 132651 523 = 140608 533 = 148877 543 = 157464 553 = 166375 563 = 175616 573 = 185193 583 = 195112 593 = 205379 603 = 216000	613 = 226981 623 = 238328 633 = 250047 643 = 262144 653 = 274625 663 = 287496 673 = 300763 683 = 314432 693 = 328509 703 = 343000	713 = 357911 723 = 373248 733 = 389017 743 = 405224 753 = 421875 763 = 438976 773 = 456533 783 = 474552 793 = 493039 803 = 512000	813 = 531441 823 = 551368 833 = 571787 843 = 592704 853 = 614125 863 = 636056 873 = 658503 883 = 681472 893 = 704969 903 = 729000	913 = 753571 923 = 778688 933 = 804357 943 = 830584 953 = 857375 963 = 884736 973 = 912673 983 = 941192 993 = 970299 1003 = 1000000

 Распечатать таблицу кубов

Таблица кубов

	1	2	3	4	5	6	7	8	9
1	8	27	64	125	216	343	512	729
1	1000	1331	1728	2197	2744	3375	4096	4913	5832	6859
2	8000	9261	10648	12167	13824	15625	17576	19683	21952	24389
3	27000	29791	32768	35937	39304	42875	46656	50653	54872	59319
4	64000	68921	74088	79507	85184	91125	97336	103823	110592	117649
5	125000	132651	140608	148877	157464	166375	175616	185193	195112	205379
6	216000	226981	238328	250047	262144	274625	287496	300763	314432	328509
7	343000	357911	373248	389017	405224	421875	438976	456533	474552	493039
8	512000	531441	551368	571787	592704	614125	636056	658503	681472	704969
9	729000	753571	778688	804357	830584	857375	884736	912673	941192	970299

 Распечатать таблицу кубов

2011-2022 Довжик МихаилКопирование материалов запрещено.

Добро пожаловать на OnlineMSchool.Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Применение корня третьей степени в реальной жизни

Корень третьей степени – это математическая операция, которая позволяет извлекать кубический корень числа. В реальной жизни корень третьей степени широко применяется в различных областях, включая науку, инженерию, экономику и финансы. Вот несколько примеров применения корня третьей степени:

1. Физика и наука

   В физике корень третьей степени используется для решения задач, связанных с объемом, плотностью и массой тел. Например, в задачах о нахождении объема куба со сферическим вырезом требуется извлечь кубический корень из объема вырезанной фигуры, чтобы найти длину ребра куба.

2. Инженерия и архитектура

   В инженерных и архитектурных расчетах часто требуется извлечь кубический корень из объема или площади. Например, при проектировании водопроводной трубы необходимо определить диаметр трубы, зная общий объем воды, скорость потока и давление.

3. Экономика и финансы

   Корень третьей степени может быть использован для вычисления среднего показателя или индекса. Например, при анализе доходности инвестиций или финансовых показателей компании может потребоваться извлечь кубический корень из общей прибыли или общего объема продаж для определения среднего значения.

4. Медицина и биология

   В медицине и биологии корень третьей степени может использоваться для анализа роста организмов или для расчетов объемов жидкости, необходимой для введения в организм. Например, при определении дозы лекарства для пациента требуется извлечь кубический корень из общего объема лекарственного препарата, чтобы определить количество, которое необходимо ввести.

Это лишь некоторые из примеров применения корня третьей степени. В реальной жизни корень третьей степени находит множество применений в различных областях, и его использование справедливо и интересно для людей, связанных с наукой, техникой, финансами и другими областями знания.

Объём куба: как его вычислить

Формула	Описание
V = a³	Объём куба равен длине ребра в третьей степени

Где «V» – объём куба, а «a» – длина ребра.

Например, если длина ребра куба равна 5 сантиметрам, то его объём можно вычислить по формуле: V = 5³ = 5 * 5 * 5 = 125 сантиметров кубических.

Зная формулу вычисления объёма куба, можно легко определить объём кубического объекта в повседневной жизни. Например, при рассмотрении объёма коробки, можно измерить длину одной стороны и применить формулу a³. Это позволит определить, сколько предметов можно поместить в коробку или какой объём он займет.

Формула вычисления объёма куба

Чтобы вычислить объём куба, необходимо знать длину его стороны. Формула для вычисления объёма куба проста:

V = a3

где V – объём куба, а a – длина стороны.

Таким образом, чтобы найти объём куба, нужно возвести длину его стороны в куб. Полученное число будет являться объёмом куба. Например, если длина стороны куба равна 3 см, то объём куба будет равен 33 = 27 см3.

Объём куба измеряется в кубических единицах длины, таких как кубический сантиметр (см3), кубический метр (м3) и т.д. Это показывает, сколько пространства занимает куб.

Формула вычисления объёма куба является базовой для изучения объёма других геометрических объектов, таких как параллелепипеды, призмы и т.д. Знание этой формулы позволяет решать задачи связанные с определением объёма различных фигур в геометрии и применять её в повседневной жизни, например, при расчёте объёма коробки или емкости сосуда.

Наблюдаемый объём куба в повседневной жизни

В повседневной жизни мы часто сталкиваемся с кубами и используем их без особого задумываясь. Так, многие предметы, с которыми мы взаимодействуем ежедневно, имеют кубическую форму.

Например, мы можем наблюдать куб в виде игрального кубика. Он имеет шесть граней, каждая из которых имеет форму квадрата. Когда мы бросаем такой кубик, на его верхней грани может выпасть любое число от 1 до 6. Игра с использованием кубика позволяет нам принимать решения случайным образом, что делает ее интересной и увлекательной.

Кроме того, кубическую форму можно увидеть в различных предметах быта. Многие книги, коробки, телевизоры, мониторы имеют форму куба или приближенную к нему. Это объясняется тем, что куб имеет простую и устойчивую форму, которая позволяет удобно размещать и хранить предметы.

Также кубическая форма используется в архитектуре. Многие здания и сооружения имеют кубическую форму или элементы, напоминающие куб. Например, многие дома имеют форму прямоугольного параллелепипеда, который является производным от куба.

Кубическая форма может быть встречена и в природе. Некоторые кристаллы и минералы образуют кубические структуры. Такие структуры обладают определенной геометрической регулярностью и симметрией.

В целом, куб имеет множество практических применений в повседневной жизни. Его форма и свойства делают его удобным и функциональным для использования в различных сферах, начиная от игр и развлечений до архитектуры и науки.

Практическое применение куба числа

Куб числа является полезным понятием в математике и имеет множество практических применений. Например, куб числа может быть использован для определения объема трехмерной фигуры.

Также, куб числа является важным понятием в физике. Например, скорость куба числа будет равна ускорению в квадрате, умноженному на время.

Куб числа также может быть использован для вычисления площади поверхности трехмерной фигуры. Например, если мы имеем куб со стороной длиной 2, то его площадь поверхности будет равна 24.

• Применение куба числа в программировании:
  • Куб числа может использоваться в математических алгоритмах, таких как алгоритмы шифрования.
  • Куб числа может использоваться для вычисления сложных математических функций, таких как квадратный корень.

Таким образом, куб числа является важным математическим понятием, имеющим широкий спектр практических применений в различных областях жизни и производства.

Вопрос-ответ:

Как вычислить куб числа?

Чтобы вычислить куб числа, нужно число умножить само на себя три раза. То есть, если нужно найти куб числа 4, нужно умножить 4 на 4 на 4, получив результат 64.

Зачем нужен куб числа?

Куб числа может использоваться в различных математических формулах, а также в физике и других науках. Например, скорость света в вакууме равна кубу числа 10, или 1000.

Какие есть способы вычисления куба числа?

Существует несколько способов вычисления куба числа, например, умножение числа самого на себя три раза, использование формулы куба суммы двух чисел или куба разности двух чисел, или использование тождества (a+b)³=a³+3a²b+3ab²+b³, где a и b — любые числа.

Какие числа можно возводить в куб?

В куб можно возводить все действительные и комплексные числа, в том числе и отрицательные. Например, куб числа -2 равен -8, а куб комплексного числа 2+3i равен -46+9i.

Как связаны куб числа и квадрат числа?

Куб числа может быть выражен через квадрат числа, так как куб числа равен квадрату числа, умноженному на само число. Например, куб числа 5 равен 25 умножить на 5, то есть 125.

Как использовать куб числа в алгебре?

Куб числа может использоваться в алгебре для решения различных задач, например, вычисления корней кубического уравнения или поиска объема куба со стороной заданной длины. Кроме того, куб числа может использоваться в формулах сумм и разностей кубов чисел.

Возведение чисел в куб

Возведение чисел в куб – это операция, при которой число умножается само на себя, а затем еще раз на себя. Таким образом, получается число, в котором каждая цифра повторяется три раза.

Например, если возвести число 7 в куб, то получится число 343. Число 2 в кубе равно 8, число 5 в кубе равно 125, число 4 в кубе равно 64, число 1 в кубе равно 1, число 6 в кубе равно 216, число 0 в кубе равно 0, а число 8 в кубе равно 512.

Возведение чисел в куб широко используется в математике, естественных и технических науках, а также в программировании. Например, при решении задач в физике или при создании компьютерных алгоритмов.

Для удобства, можно составить таблицу, в которой будут перечислены числа и их значения в кубе:

Число	Значение в кубе
7	343
2	8
5	125
4	64
1	1
6	216
8	512

Таким образом, возведение чисел в куб является важной математической операцией, которая имеет множество практических применений и способствует решению различных задач