Скалярное произведение векторов презентация, доклад

Физический смысл скалярного произведения

Механика рассматривает приложение скалярного произведения.

При работе А с постоянной силой F→ перемещаемое тело из точки M в N можно найти произведение длин векторов F→ и MN→ с косинусом угла между ними, значит работа равна произведению векторов силы и перемещения:

A=(F→,MN→).

Пример 8

Перемещение материальной точки на 3 метра под действием силы равной 5 ньтонов направлено под углом 45 градусов относительно оси. Найти A.

Решение

Так как работа – это произведение вектора силы на перемещение, значит, исходя из условия F→=5, S→=3, (F→,S→^)=45°, получим A=(F→,S→)=F→·S→·cos(F→,S→^)=5·3·cos(45°)=1522.

Ответ: A=1522.

Пример 9

Материальная точка, перемещаясь из M(2,-1,-3) в N(5,3λ-2,4) под силой F→=(3,1,2), совершила работа равную 13 Дж. Вычислить длину перемещения.

Решение

При заданных координатах вектора MN→ имеем MN→=(5-2, 3λ-2-(-1), 4-(-3))=(3, 3λ-1,7).

По формуле нахождения работы с векторами F→=(3,1,2) и MN→=(3, 3λ-1,7) получим A=(F⇒, MN→)=3·3+1·(3λ-1)+2·7=22+3λ.

По условию дано, что A=13Дж, значит 22+3λ=13. Отсюда следует λ=-3, значит и MN→=(3,3λ-1,7)=(3,-10,7).

Чтобы найти длину перемещения MN→ , применим формулу и подставим значения:

MN→=32+(-10)2+72=158.

Ответ: 158.

Применение в физике

Впервые скалярное произведение ввёл У. Гамильтон в 1846 году. Одновременно учёные начали использовать в своих работах векторное произведение, сумму скаляров. Понятие получило широкое применение и в физике. На его основе сформулированы главные законы электродинамики и механики.

Скаляр является физической величиной. Чтобы его задать, используется одно число. Примеры скаляров в физике:

• масса тела, равная 4 кг;
• температура воздуха на уровне +10 градусов.

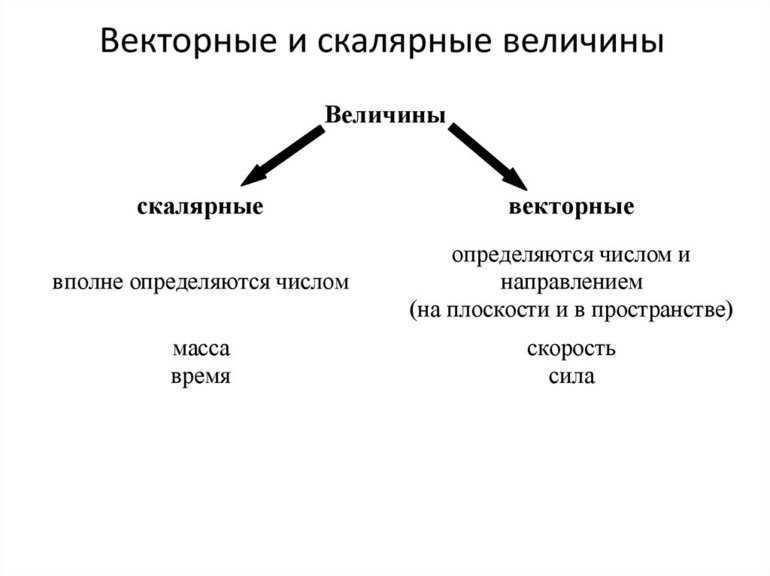
В каждом предложенном варианте величина задаётся с помощью одного числа, поэтому масса тела и температура относятся к скалярам. Но это понятие в физике не считается простым числом. Для него характерна размерность.

Если в условиях задачи известно, что масса тела равна 3, необходимо указывать единицу измерения (килограммы, граммы). В математике можно сложить числа 3 и 10, а в физике суммируются только скаляры с одинаковой размерностью: массы с массой, градусы с градусами.

Если рассматривать векторную физическую величину, она характеризуется следующим образом:

1. Неотрицательность.
2. Направленность в пространстве.

Понятие скаляр — модуль вектора либо абсолютная величина. Если предположить, что транспортное средство двигается со скоростью 60 км/ч, такая информация считается неполной

В физике важно знать направление движения. Кроме модуля скорости как абсолютной величины, потребуется знать направление в пространстве, поэтому скорость считается векторной величиной.

Если сила идёт вдоль горизонта, тогда объект поедет горизонтально. При вертикальном воздействии силы вниз кирпич останется на прежнем месте. Он будет вжиматься в землю. Подобные явления указывают на то, что сила является вектором, поэтому для неё характерна размерность, модуль.

Для обозначения вектора в физике используются латинские буквы и стрелка:

• вектор скорости: →v;
• вектор силы: →F.

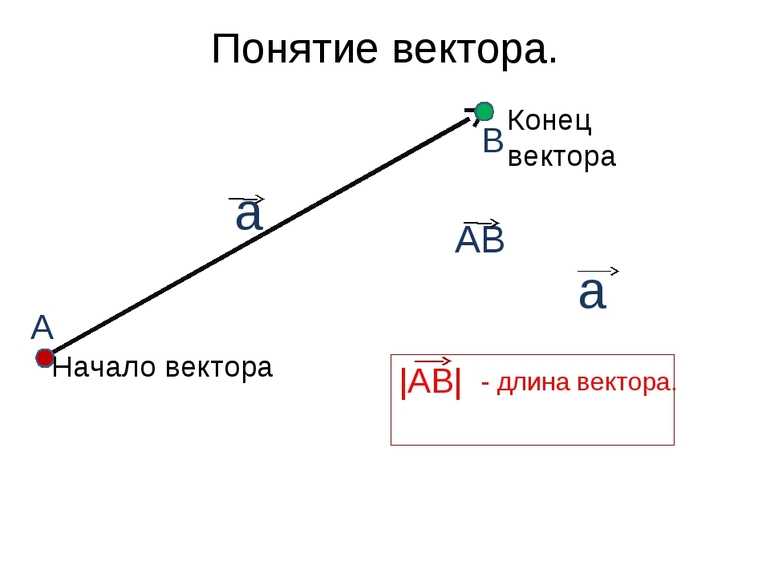
Стрелка является направленным отрезком. Её начальная точка — начало вектора, а конечная или остриё — конец вектора. В математике величина с начальной точкой А и концом В обозначается →АВ. Если начало и конец направленного отрезка совпадают, тогда получается нулевой вектор. Он обозначается →0.

Такой отрезок считается точкой. У него нет конкретного направления, а длина равняется нулю. К безразмерным скалярам относятся коэффициенты трения и полезного действия, показатель преломления света.

Линии второго порядка

3.1. Алгебраическая линия и её порядок3.2. Классификация линий второго порядка3.3. Эллипс3.3.1. Каноническое уравнение эллипса. Как построить эллипс?3.3.2. Определение эллипса. Фокусы эллипса3.3.3. Эксцентриситет эллипса и его геометрический смысл3.3.4. Поворот и параллельный перенос эллипса3.4. Гипербола3.4.1. Каноническое уравнение и построение гиперболы3.4.2. Определение гиперболы3.4.3. Фокусы и эксцентриситет гиперболы3.4.4. Равносторонняя гипербола3.4.5. Поворот и параллельный перенос гиперболы3.5. Парабола3.5.1. Построение, уравнение, определение, фокусы, директриса, эксцентриситет3.5.2. Поворот и параллельный перенос параболы3.6. Неравенства с линиями второго порядка3.7. Задачи с линиями второго порядка3.7.1. Директрисы эллипса3.7.2. Директрисы гиперболы3.8. Приведение уравнения к каноническому виду3.8.1. Приведение уравнения центральной линии. Метод инвариантов3.8.2. Приведение уравнения нецентральной линии3.8.3. Универсальный метод приведения

Свойства скалярного произведения

1. $\vec{a}\cdot \vec{b}=\vec{b}\cdot \vec{a}$;
2. $(k\vec{a})\cdot \vec{b}=k(\vec{a}\cdot \vec{b})$;
3. $(\vec{a}+\vec{b})\cdot \vec{c}=\vec{a}\cdot \vec{c}+\vec{b}\cdot \vec{c}$.

Доказательство

Первое свойство очевидно в силу определения скалярного произведения.

Действительно, $\vec{a}\cdot \vec{b}=|\vec{a}||\vec{b}|\cos{\angle (\vec{a};\vec{b})}=|\vec{b}||\vec{a}|\cos{\angle (\vec{b};\vec{a})}=\vec{b}\cdot \vec{a}$.

Докажем второе свойство, используя теорему \ref{149}.

Пусть $\vec{a}$ имеет координаты $(x_1;y_1)$, а вектор $\vec{b}$ имеет координаты $(x_2;y_2)$.

Тогда вектор $(k\vec{a})\cdot\vec{b}=kx_1;ky_1)\cdot(x_2;y_2)=kx_1x_2+ky_1y_2=k(x_1x_2+y_1y_2)=k\vec{a}\cdot\vec{b}$.

Докажем третье свойство, используя теорему \ref{149}.

Пусть вектор $a$ имеет координаты $(x_a;y_a)$, вектор $b$ имеет координаты $(x_b;y_b)$, вектор $c$ имеет координаты $(x_c;y_c)$.

Тогда $(\vec{a}+\vec{b})\cdot \vec{c}=(x_a+x_b;y_a+y_b)\cdot(x_c;y_c)=(x_a+x_b)x_c+(y_a+y_b)y_c=\\=x_ax_c+x_bx_c+y_ay_c+y_by_c=(x_ax_c+y_ay_c)+(x_bx_c+y_by_c)=\vec{a}\cdot\vec{c}+\vec{b}\cdot \vec{c}$.

Плоскость и прямая в пространстве

5.1. Плоскость и её уравнение5.1.1. Понятие плоскости5.1.2. Общее уравнение плоскости5.1.3. Линейные неравенства в пространстве5.1.4. Как построить плоскость?5.1.5. Уравнение плоскости в отрезках5.2. Как составить уравнение плоскости?5.2.1. Уравнение плоскости по точке и двум неколлинеарным векторам5.2.2. Как составить уравнение плоскости по трём точкам?5.2.3. Вектор нормали плоскости (нормальный вектор)5.2.4. Как составить уравнение плоскости по точке и вектору нормали?5.3. Простейшие задачи с плоскостью5.3.1. Как найти плоскость, параллельную данной?5.3.2. Как найти расстояние от точки до плоскости?5.3.3. Как найти расстояние между плоскостями?5.3.4. Взаимное расположение двух плоскостей5.3.5. Как найти угол между плоскостями?5.3.6. Как найти плоскость, перпендикулярную данной?5.3.7. Взаимное расположение трёх плоскостей5.4. УравнениЯ прямой в пространстве5.4.1. Канонические уравнения прямой5.4.2. Как составить уравнения прямой по двум точкам?5.4.3. Параметрические уравнения прямой5.4.4. Прямая, заданная пересечением двух плоскостей5.5. Задачи с прямой в пространстве5.5.1. Взаимное расположение прямых5.5.2. Скрещивающиеся прямые5.5.3. Как найти прямую, содержащую общий перпендикуляр?5.5.4. Как найти расстояние между скрещивающимися прямыми?5.5.5. Пересекающиеся прямые в пространстве5.5.6. Как найти прямую, перпендикулярную данной?5.5.7. Как найти расстояние от точки до прямой?5.5.8. Как найти точку, симметричную относительно прямой?5.5.9. Как найти угол между прямыми?5.5.10. Параллельные прямые в пространстве5.6. Основные задачи с прямой и плоскостью5.6.1. Взаимное расположение прямой и плоскости5.6.2. Как найти точку пересечения прямой и плоскости?5.6.3. Как найти проекцию прямой на плоскость?5.6.4. Как найти угол между прямой и плоскостью?5.6.5. Прямая перпендикулярна плоскости5.6.6. Прямая параллельна плоскости5.6.7. Добро пожаловать в «реальные боевые условия»!5.7. Задача с треугольной пирамидой

21 Условие перпендикулярности векторов

Если
ненулевые векторы

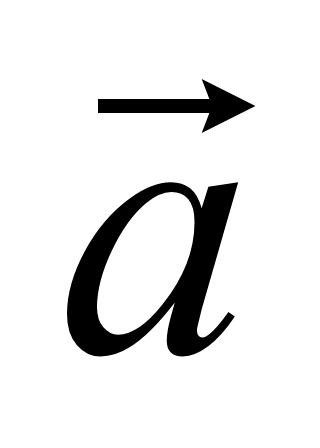
= (x₁; y₁;
z₁) и

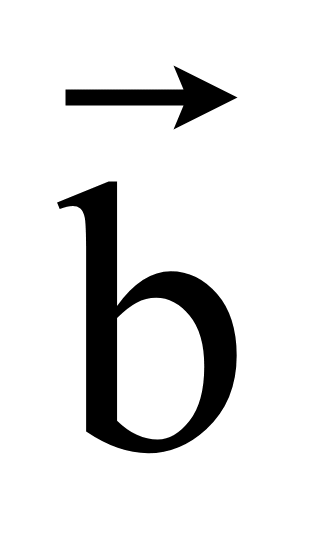
= (x₂; y₂;
z₂) перпендикулярны, то их
скалярное произведение равно нулю

=
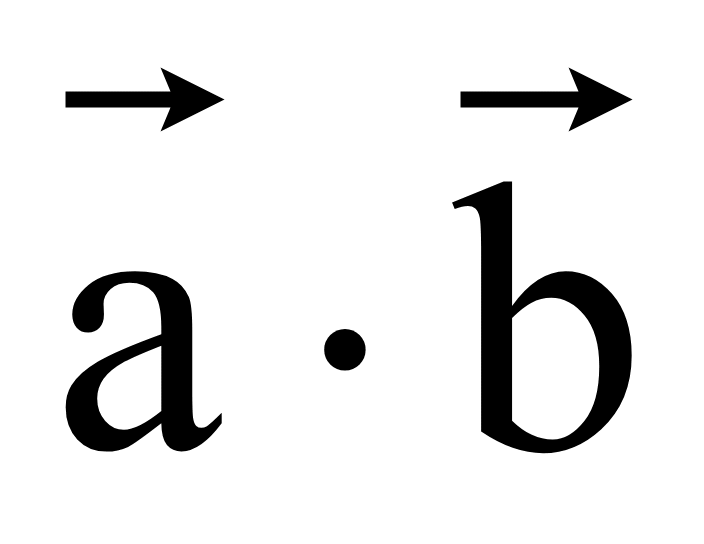0,

=
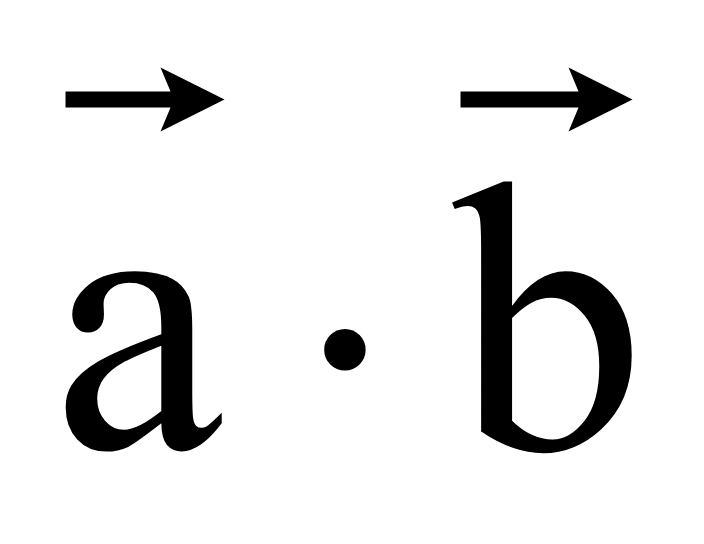x₁x₂
+ y₁y₂
+ z₁z₂
= 0.

Если
задан один ненулевой вектор

= (x₁; y₁;
z₁), то координаты
перпендикулярного (нормального) ему ненулевого
вектора

= (x₂; y₂;
z₂) должны удовлетворять
равенству

x₁x₂
+ y₁y₂
+ z₁z₂
= 0.

Таких
векторов

бесконечное множество.

Если
на плоскости задан один ненулевой вектор

= (x₁; y₁),
то координаты перпендикулярного (нормального) ему вектора

= (x₂; y₂)
должны удовлетворять равенству

x₁x₂
+ y₁y₂
= 0.

Отсюда
можно выразить произведение координат y

y₁y₂
= — x₁x₂.

Если
на плоскости задан ненулевой вектор

= (x₁; y₁),
то достаточно задать произвольно одну из координат перпендикулярного
(нормального) ему вектора

= (x₂; y₂)
и из условия перпендикулярности векторов

x₁x₂
+ y₁y₂
= 0

выразить
вторую координату вектора

.

Например,
если подставить произвольную координату x₂,то из равенства

y₁y₂
= — x₁x₂

выражается
вторая координата вектора

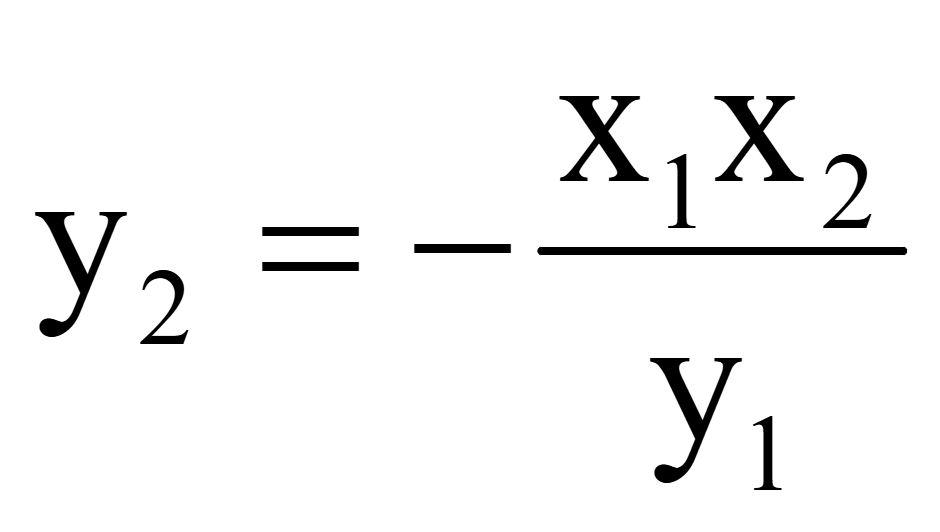
Если
произвольно придать x₂ = y₁,
то вторая координата вектора

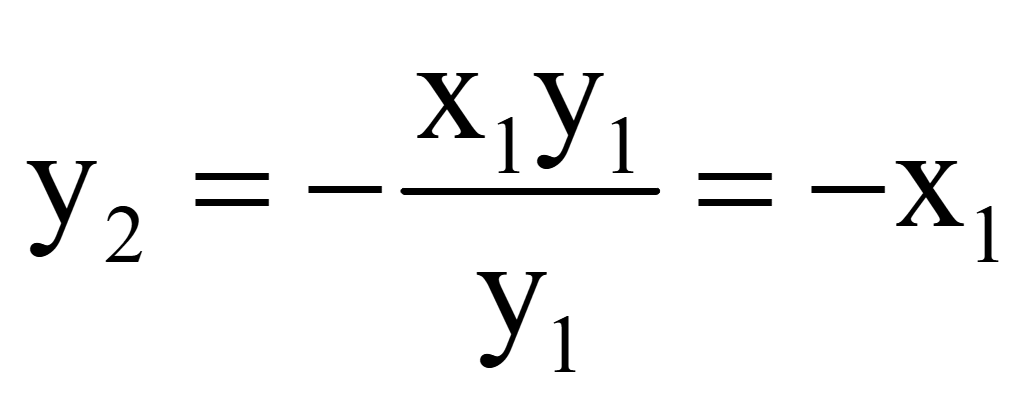
Если
на плоскости задан ненулевой вектор

= (x₁; y₁),
то перпендикулярный (нормальный) ему вектор

= (y₁; -x₁).

Если
одна из координат ненулевого вектора

равна нулю, то у перпендикулярного ему ненулевого вектора

такая же координата не равна нулю, а вторая координата равна нулю.
Такие векторы лежат на осях координат, поэтому перпендикулярны.
Например, если

= (; y₁),
то этот вектор лежит на оси Oy, тогда
перпендикулярный ему ненулевой вектор

= (x₂;
0) лежит на оси Ox.

Определим
второй вектор, перпендикулярный вектору

= (x₁; y₁),
но противоположный вектору

= (y₁; -x₁),
то есть вектор —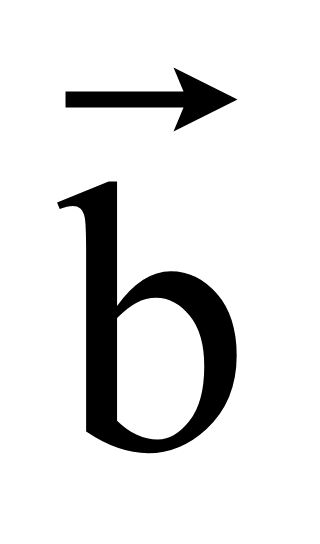
.
Тогда достаточно поменять знаки координат вектора

—

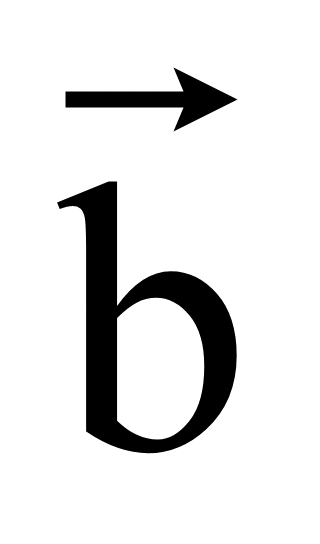
= -1·

= (-1·y₁;
-1·(-x₁))=
(-y₁; x₁).

Координаты
двух векторов, перпендикулярных вектору

= (x₁; y₁)
на плоскости

₁
= (y₁; -x₁),

₂
= (-y₁; x₁).

Для
получения координат ненулевых векторов, перпендикулярных заданному
ненулевому вектору на плоскости, достаточно поменять местами
координаты заданного вектора и поменять знак одной из координат.

Задача.
Задан вектор

= (3; -5). Найти два нормальных вектора с различной ориентацией.

Решение

Координаты
двух векторов, перпендикулярных вектору

= (x₁; y₁)
на плоскости

₁
= (y₁; -x₁),

₂
= (-y₁; x₁).

Подставляем
координаты вектора

= (3; -5)

₁
= (-5; -3),

₂
= (-(-5); 3) = (5; 3).

Для
проверки перпендикулярности векторов подставим их координаты в
условие перпендикулярности векторов

x₁x₂
+ y₁y₂
= 0

3·(-5)
+ (-5)·(-3) = -15 + 15 = 0

верно!

3·5
+ (-5)·3 = 15 — 15 = 0

верно!

Ответ:
₁
= (-5; -3),
₂
= (5; 3).

Если
присвоить x₂ = 1, подставить

x₁
+ y₁y₂
= 0.

y₁y₂
= -x₁

Получим
координату y₂ вектора,
перпендикулярного вектору

= (x₁; y₁)

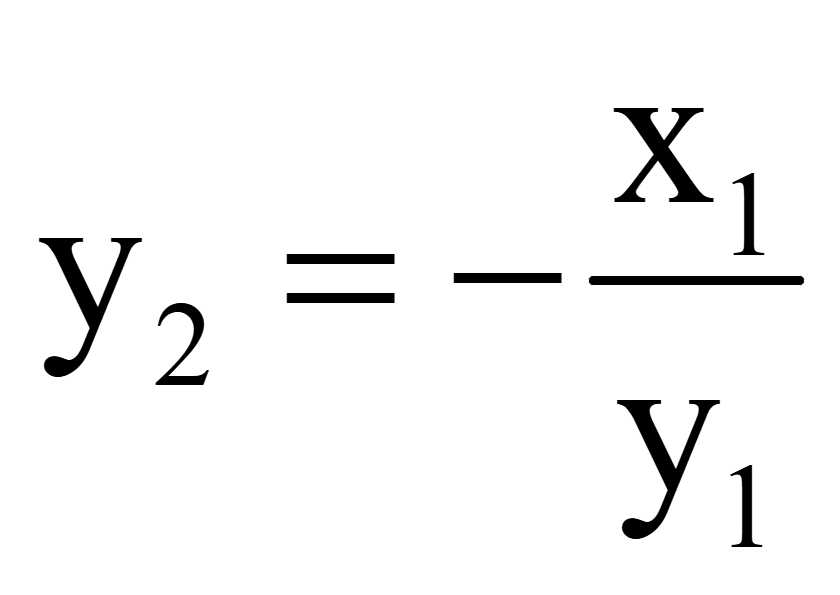
Координаты
одного вектора, перпендикулярного на плоскости ненулевому вектору

= (x₁; y₁)

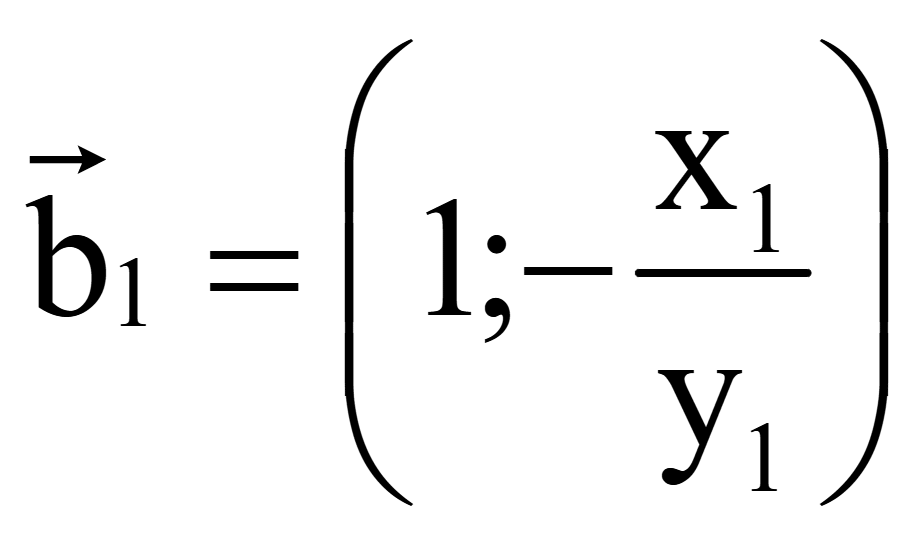
Для
получения второго вектора, перпендикулярного вектору

= (x₁; y₁),
но противоположно направленного вектору

.
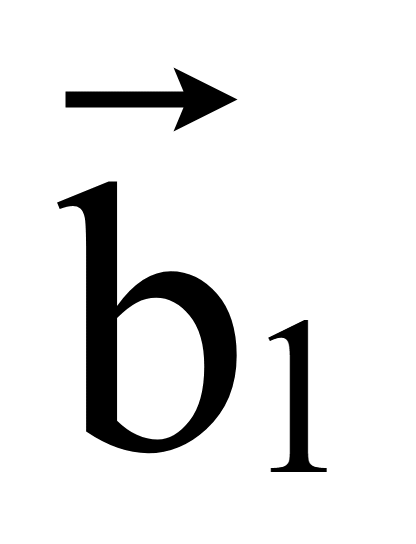
Пусть

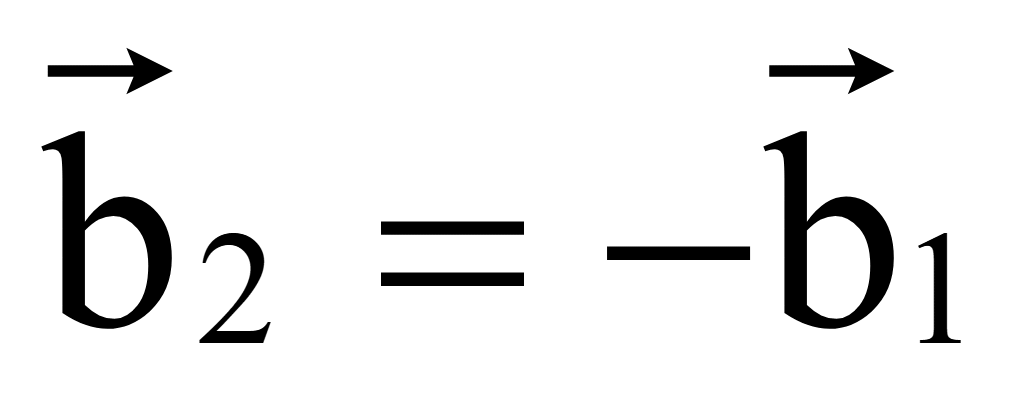
Тогда
достаточно поменять знаки координат вектора

.

Координаты
второго вектора, перпендикулярного на плоскости вектору

= (x₁; y₁)

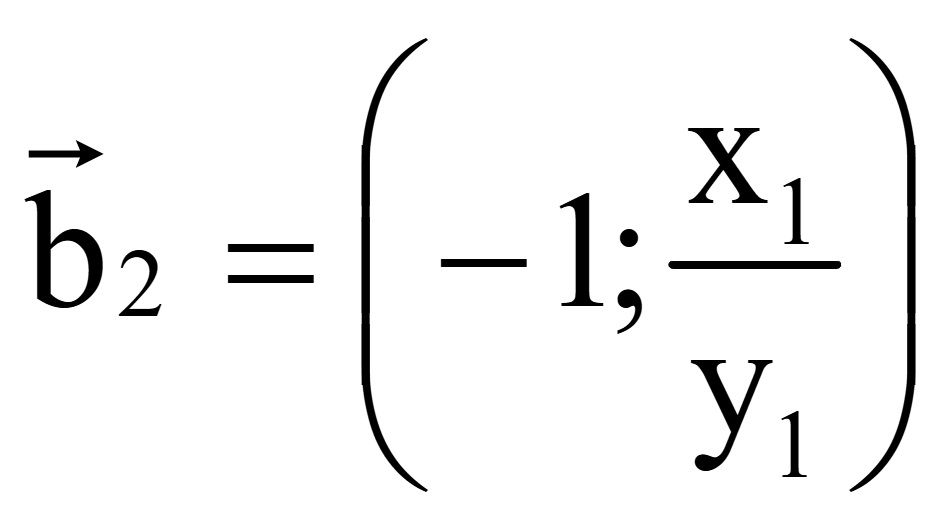
Координаты
двух векторов, перпендикулярных вектору

= (x₁; y₁)
на плоскости

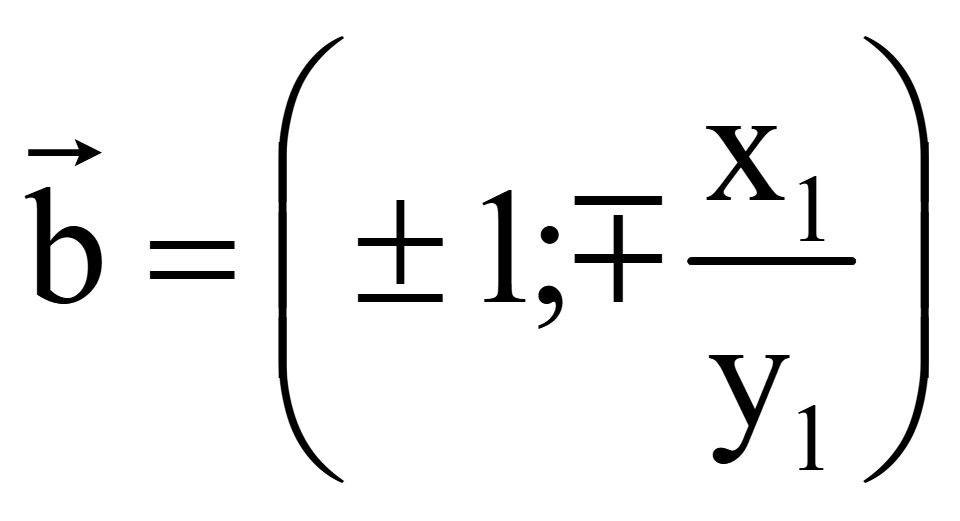
Задача.
Задан вектор

= (3; -5). Найти два нормальных вектора с различной ориентацией.

Решение

Координаты
двух векторов, перпендикулярных вектору

= (x₁; y₁)
на плоскости

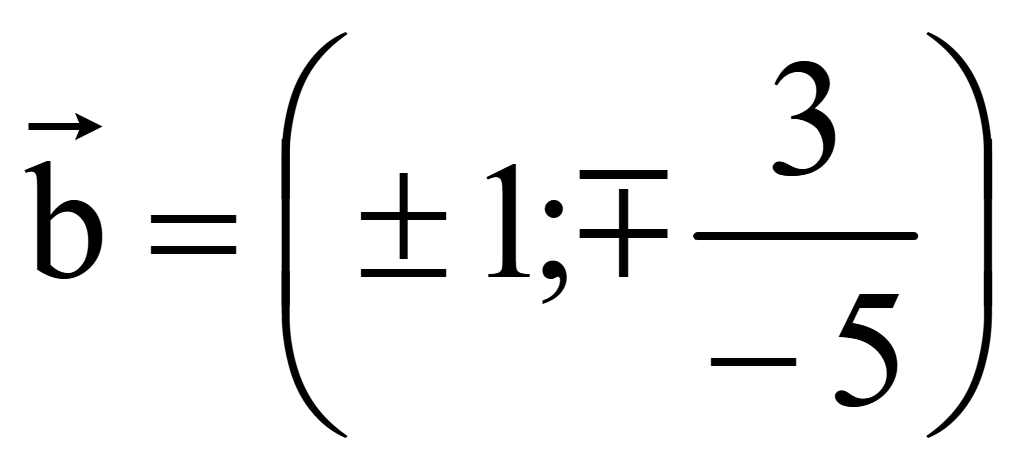
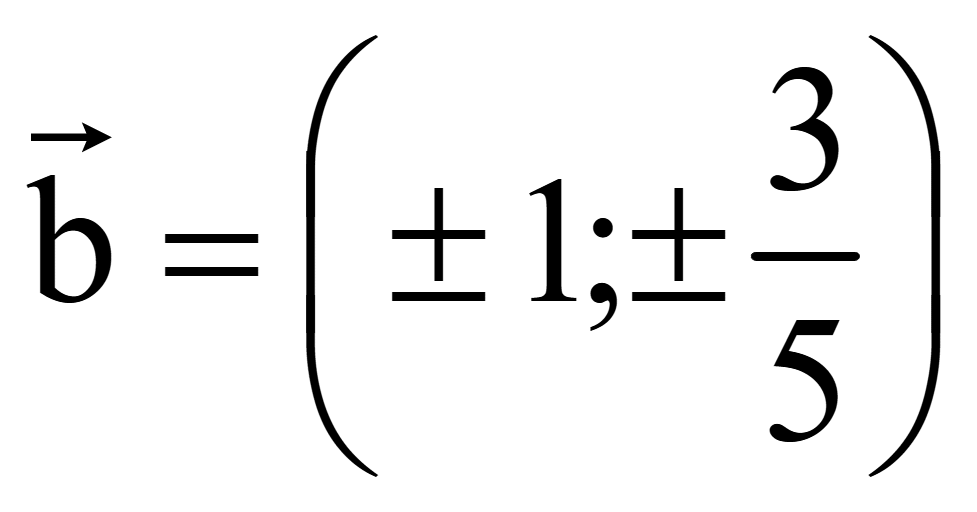
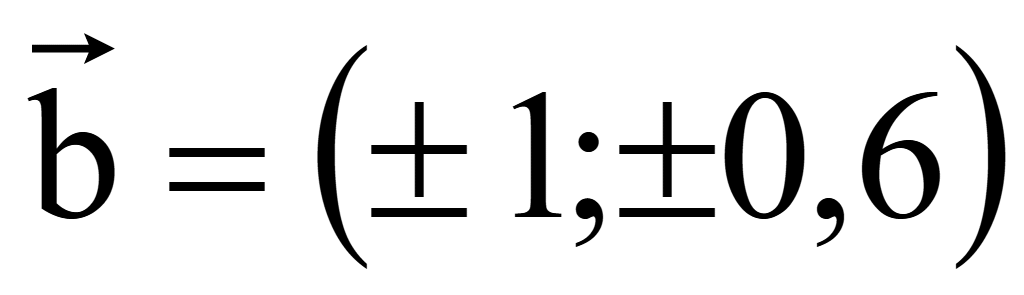
Координаты
одного вектора

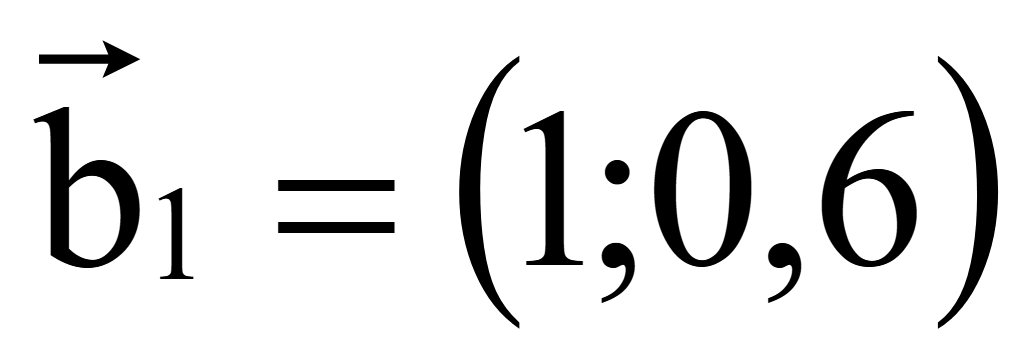
Координаты
второго вектора

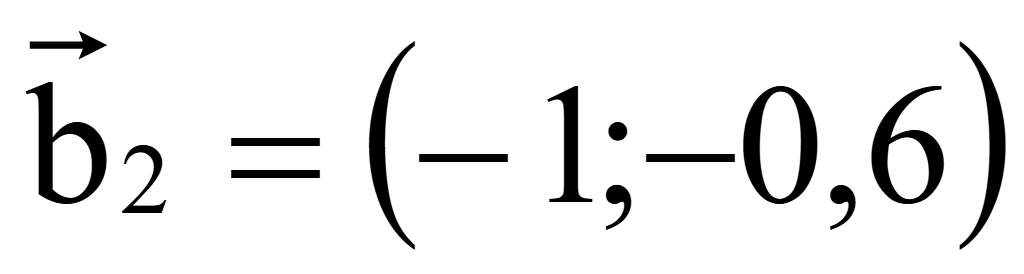
Для
проверки перпендикулярности векторов подставим их координаты в
условие перпендикулярности векторов

x₁x₂
+ y₁y₂
= 0

3·1
+ (-5)·0,6 = 3 — 3 = 0

верно!

3·(-1)
+ (-5)·(-0,6) = -3 + 3 = 0

верно!

Ответ:

и

.

Если
присвоить x₂ = — x₁,
подставить

x₁(-x₁)
+ y₁y₂
= 0.

-x₁2
+ y₁y₂
= 0.

y₁y₂
= x₁2

Получим
координату вектора, перпендикулярного вектору

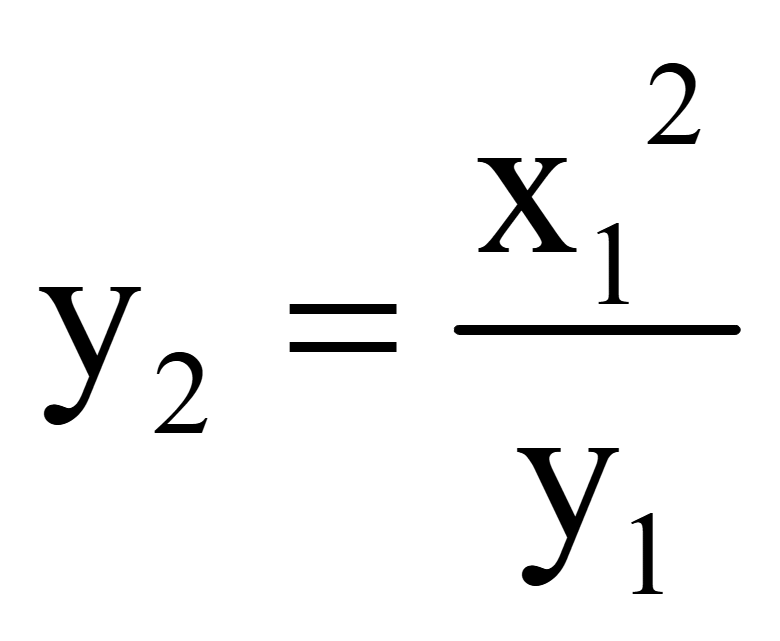
Если
присвоить x₂ = x₁,
подставить

x₁x₁
+ y₁y₂
= 0.

x₁2
+ y₁y₂
= 0.

y₁y₂
= -x₁2

Получим
координату y второго вектора,
перпендикулярного вектору

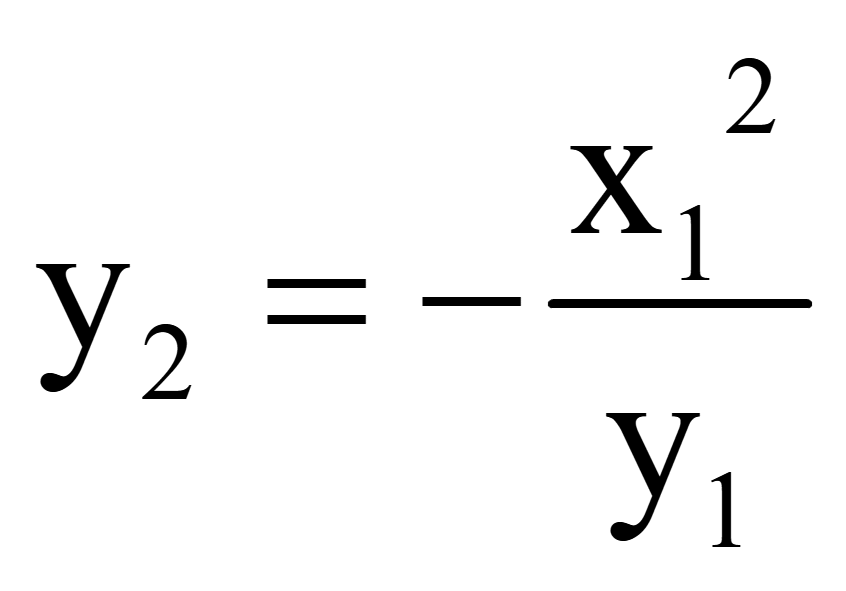
Координаты
одного вектора, перпендикулярного на плоскости вектору

= (x₁; y₁)

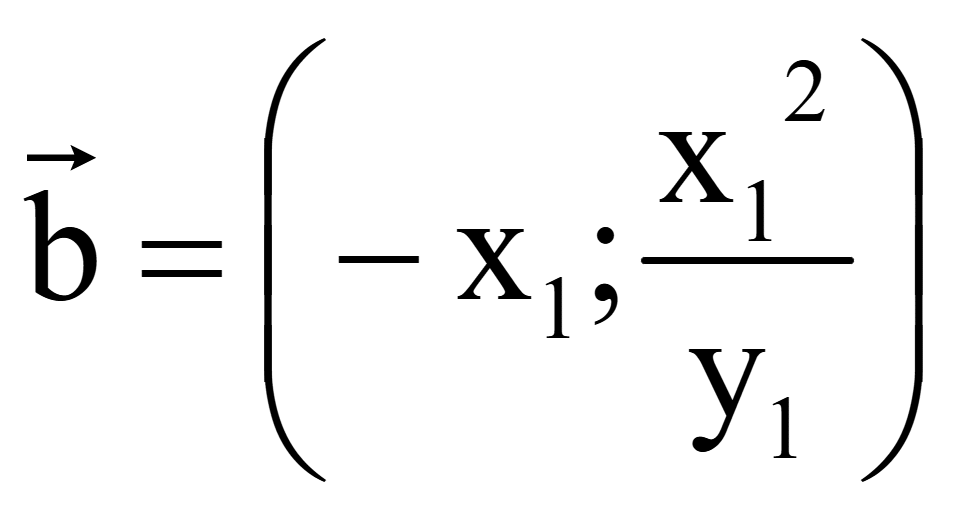
Координаты
второго вектора, перпендикулярного на плоскости вектору

= (x₁; y₁)

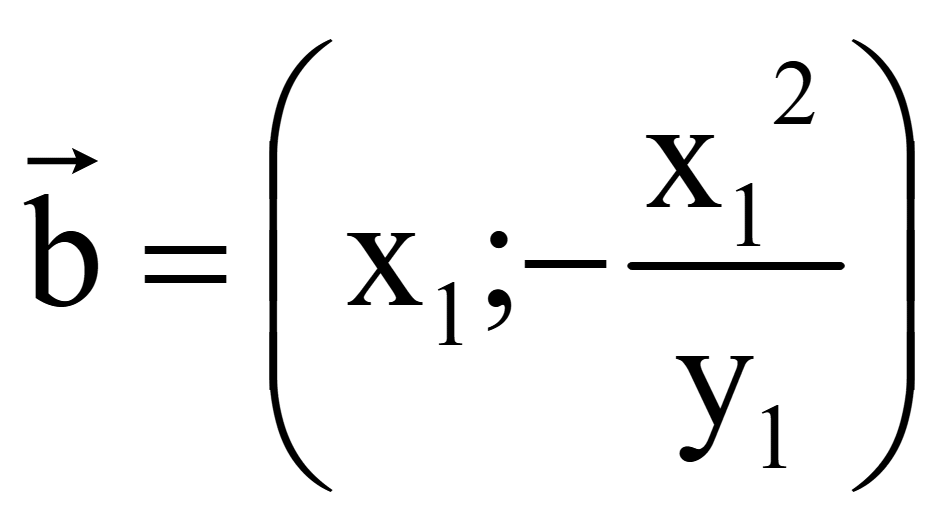
Координаты
двух векторов, перпендикулярных вектору

= (x₁; y₁)
на плоскости

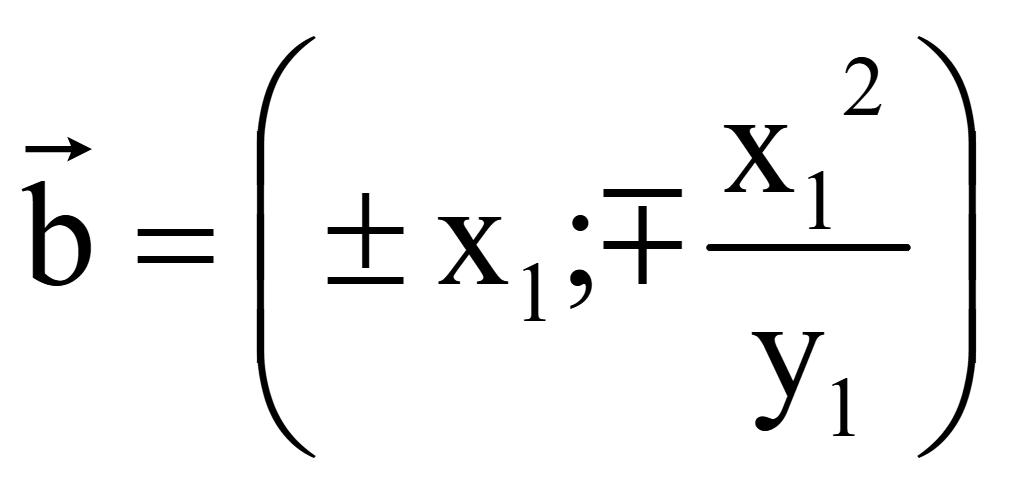
Скалярное произведение в координатах

Скалярное произведение двух векторов равно сумме произведений их соответствующих координат.

Доказательство

Если хотя бы один из векторов $\vec{a}$ или $\vec{b}$ нулевой, то справедливость теоремы очевидна.

Рассмотрим случай, когда векторы $\vec{a}$ и $\vec{b}$ ненулевые.

Отложим от произвольной точки $O$ векторы $\overrightarrow{OA}=\vec{a}$ и $\overrightarrow{OB}=\vec{b}$.

Пусть $\alpha=\angle (\vec{a};\vec{b})$.

Если векторы $\vec{a}$ и $\vec{b}$ не коллинеарны, то по теореме косинусов $AB^2=OA^2+OB^2-2OA\cdot OB\cos{\alpha}$.

Это равенство верно и в том случае, если векторы $\vec{a}$ и $\vec{b}$ коллинеарны.

Действительно, если $\vec{a}\upuparrows \vec{b}$, то $AB^2=(OA-OB)^2=OA^2+OB^2-2OA\cdot OB=OA^2+OB^2-2OA\cdot OB\cos{0^\circ}=OA^2+OB^2-2OA\cdot OB\cos{\alpha}$.

Если же $a\updownarrows b$, то $AB^2=(OA+OB)^2=OA^2+OB^2+2OA\cdot OB=OA^2+OB^2-2OA\cdot OB\cos{180^\circ}=OA^2+OB^2-2OA\cdot OB\cos{\alpha}$.

Так как $\overrightarrow{AB}=\vec{b}-\vec{a}, \overrightarrow{OA}=\vec{a}, \overrightarrow{OB}=\vec{b}$, то равенство \eqref{eq008} можно записать так: $|\vec{a}-\vec{b}|^2=|\vec{a}|^2+|\vec{b}^2|-2\vec{a}\cdot \vec{b}$.

Откуда $\vec{a}\cdot\vec{b}=\frac{1}{2}(|\vec{a}|^2+|\vec{b}|^2-|\vec{a}-\vec{b}|^2)$.

Векторы $\vec{a}, \vec{b}$ и $\vec{b}-\vec{a}$ имеют координаты $(x_1; y_1), (x_2; y_2)$ и
$(x_2-x_1; y_2-y_1)$.

Поэтому $|\vec{a}|^2=x_1^2+y_1^2, |\vec{b}|^2=x_2^2+y_2^2, |\vec{b}-\vec{a}|^2=(x_2-x_1)^2+(y_2-y_1)^2$.

Подставив эти выражения в правую часть равенства \eqref{eq009}, получим
$\vec{a}\cdot \vec{b}=\frac{1}{2}\left(x_1^2+y_1^2+x_2^2+y_2^2-x_1^2-x_2^2+2x_1x_2-y_1^2-y_2^2+2y_1y_2\right)=x_1x_2+y_1y_2$.

Угол между векторами

Любую пару векторов можно отложить от одной точки. Если при этом вектора не сонаправлены друг с другом, то они образуют некоторый угол. Его и именуют углом между векторами.

Если же пара векторов сонаправлена, то принято считать, что угол между такими векторами составляет 0°.

На рисунке показаны два вектора, a и b. Чтобы определить угол между a и b, надо отложить их от одной и той же точки:

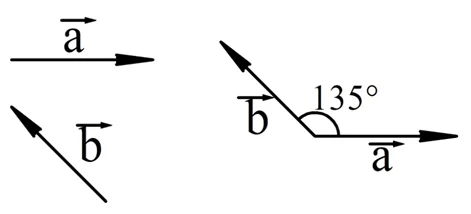
В приведенном примере угол составил 135°. Для обозначения этого угла может быть использована такая запись:

Задание. В квадрате АВСD проведены диагонали, они пересекаются в точке О. Определите, какой угол образуют вектора:

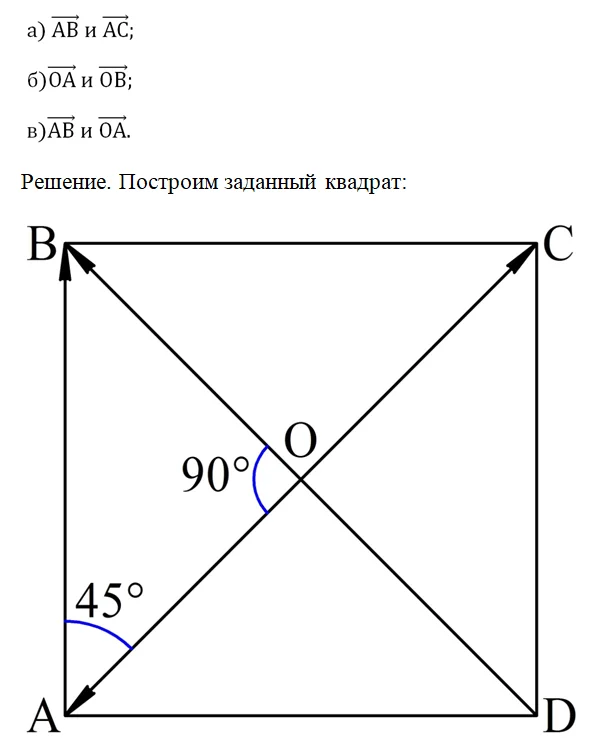
Так как в квадрате диагонали пересекаются под углом 90°, а со сторонами образуют угол 45°, то мы легко определим, что

Здесь нам помог тот факт, что вектора из пунктов а) и б) изначально отложены из одной точки. С пунктом в) ситуация сложнее. Надо отложить от точки А вектор ОА и определить угол, образующийся при этом:

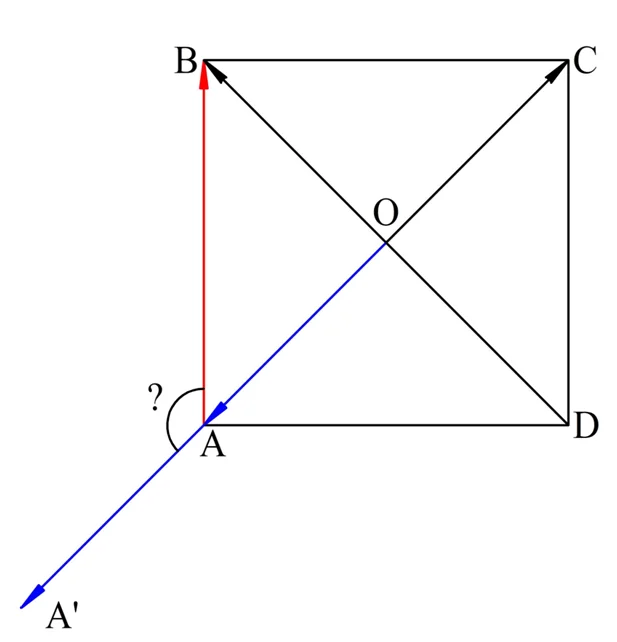
Пусть после откладывания вектора ОА от А получился вектора АА’. Нам надо найти ∠ВАА’. Нам уже известен ∠ОАВ, который является смежным с ∠ВАА’, поэтому можно записать равенство:

Ответ: а) 45°; б) 90°; в) 135°.

7 Компланарные векторы

Компланарными
называются векторы, лежащие в одной плоскости или в параллельных
плоскостях. Если провести векторы, равные данным компланарным
векторам из одной точки, то они будут лежать в одной плоскости.
Поэтому можно сказать, что компланарными называются векторы, если
имеются равные им векторы, лежащие в одной плоскости.

Два
произвольных вектора всегда компланарны потому что всегда можно
подобрать две параллельные плоскости, в которых будут лежать эти
векторы. Три вектора могут быть компланарными или не компланарными.
Три вектора, из которых хотя бы два коллинеарные, всегда компланарны.
Коллинеарные векторы всегда компланарны.

Аксиоматический подход[править]

При аксиоматическом подходе скалярное произведение определяется как некоторая функция, аргументы которой — два вектора, результат — число, не зависящее от системы координат, обладающее свойствами:

• Коммутативность
• Линейность по первому аргументу
• Положительная определенность

Тогда производными понятиями становятся

• Длина вектора — число, вычисляемое по правилу |a|=a⋅a{\displaystyle |\mathbf {a} |={\sqrt {\mathbf {a} \cdot \mathbf {a} }}}
• Угол между ненулевыми векторами — число, косинус которого cos⁡(a,b^)=a⋅b|a||b|{\displaystyle \cos({\widehat {\mathbf {a} ,\mathbf {b} }})={\frac {\mathbf {a} \cdot \mathbf {b} }{|\mathbf {a} ||\mathbf {b} |}}}
• Ортогональные (перпендикулярные) векторы — векторы, скалярное произведение которых равно 0.

Угол между векторами

Угол между векторами ∠(→a, →b) может принимать значения от 0° до 180° градусов включительно. Аналитически это можно записать в виде двойного неравенства: 0°=<∠(→a; →b)=<180° либо 0°=<∠(→a; →b)=<>

Значок угла ∠ можно опустить и писать просто: (→a;→b).

Пусть даны два вектора →a, →b.

Отложим их от некоторой точки О пространства: →OA = →a; →OB = →b. Тогда угол между векторами — это угол ∠AOB = (→a, →b).

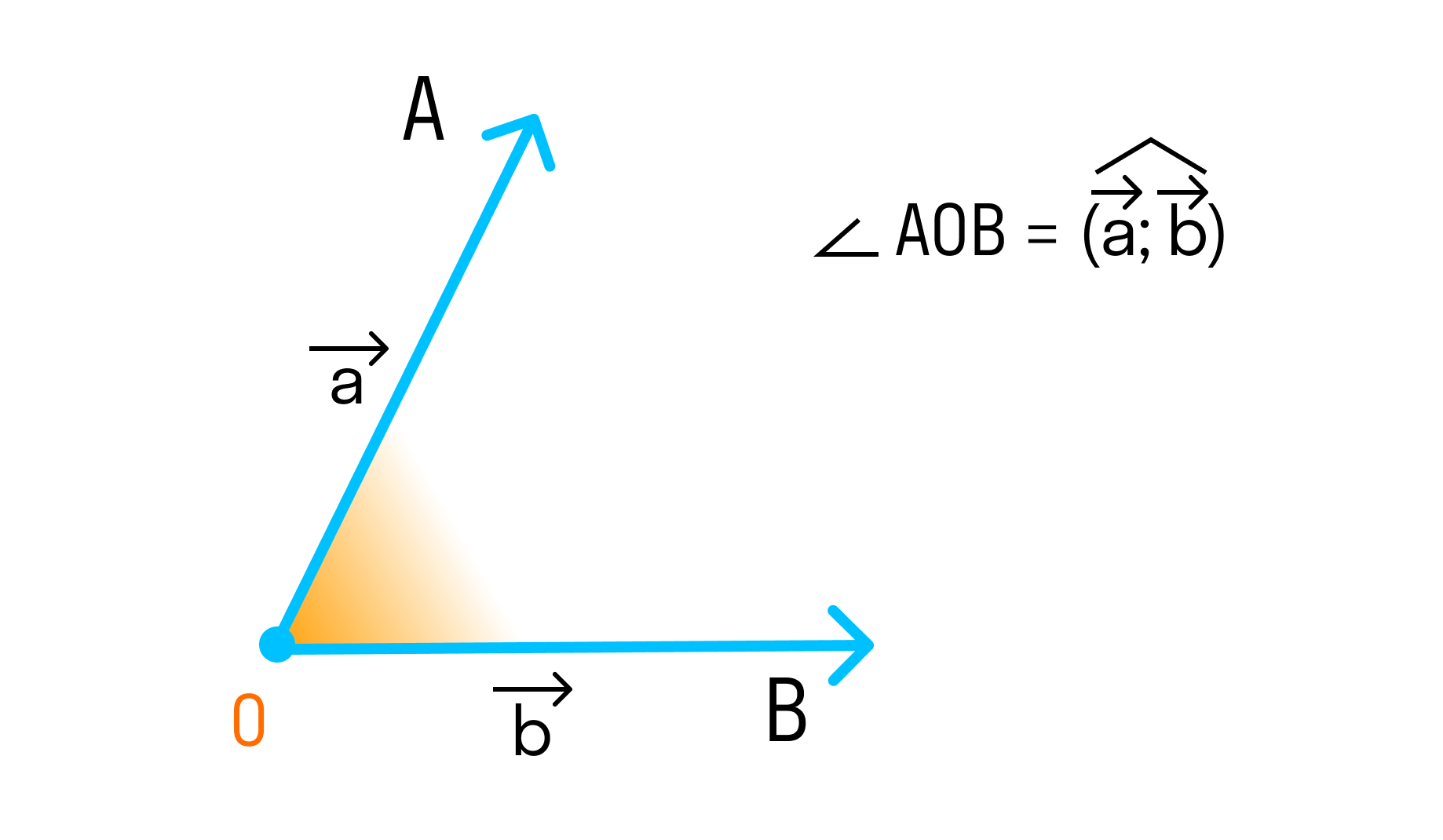
Угол между векторами может быть прямым, тупым или острым. Рассмотрим каждый случай:

Если векторы сонаправлены, то угол между ними равен 0°.

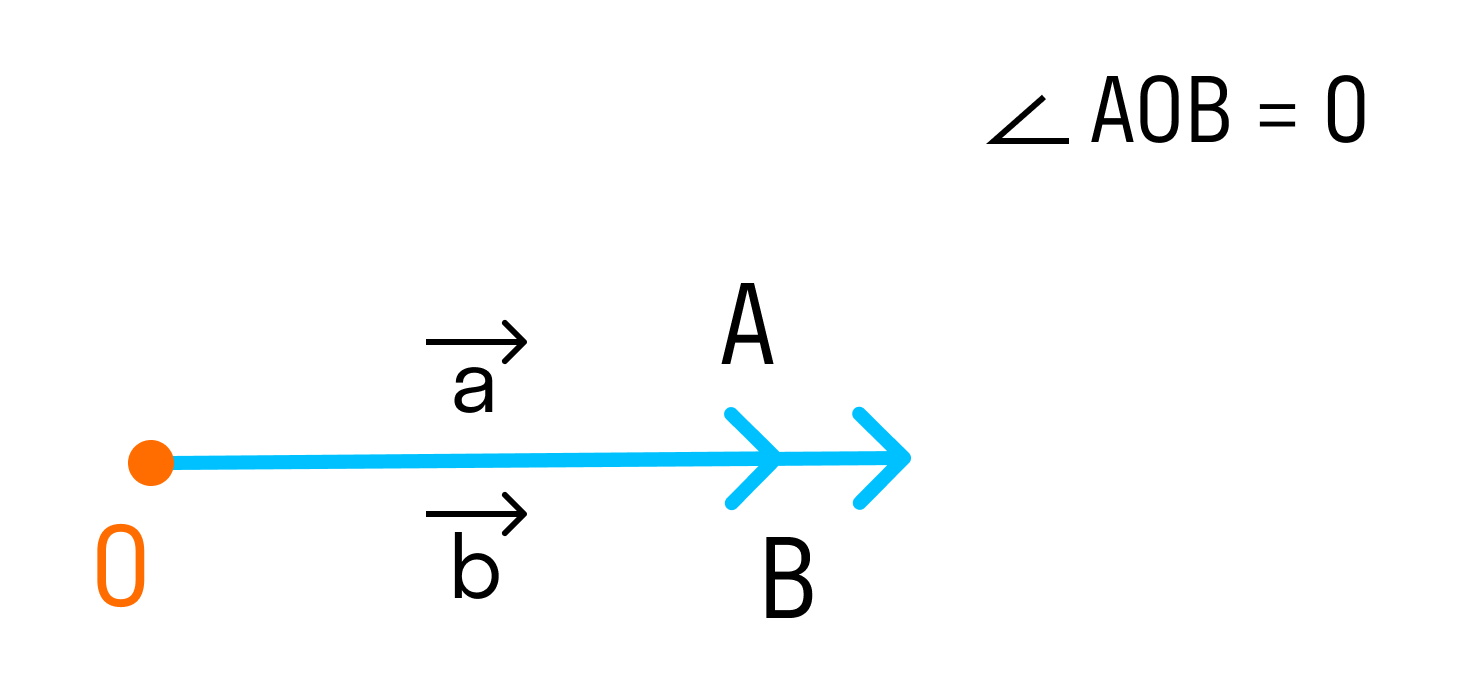
Так как косинус угла в 0° равен единице, то скалярное произведение сонаправленных векторов является произведением их длин. Если два вектора равны, то такое скалярное произведение называют скалярным квадратом.

Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.

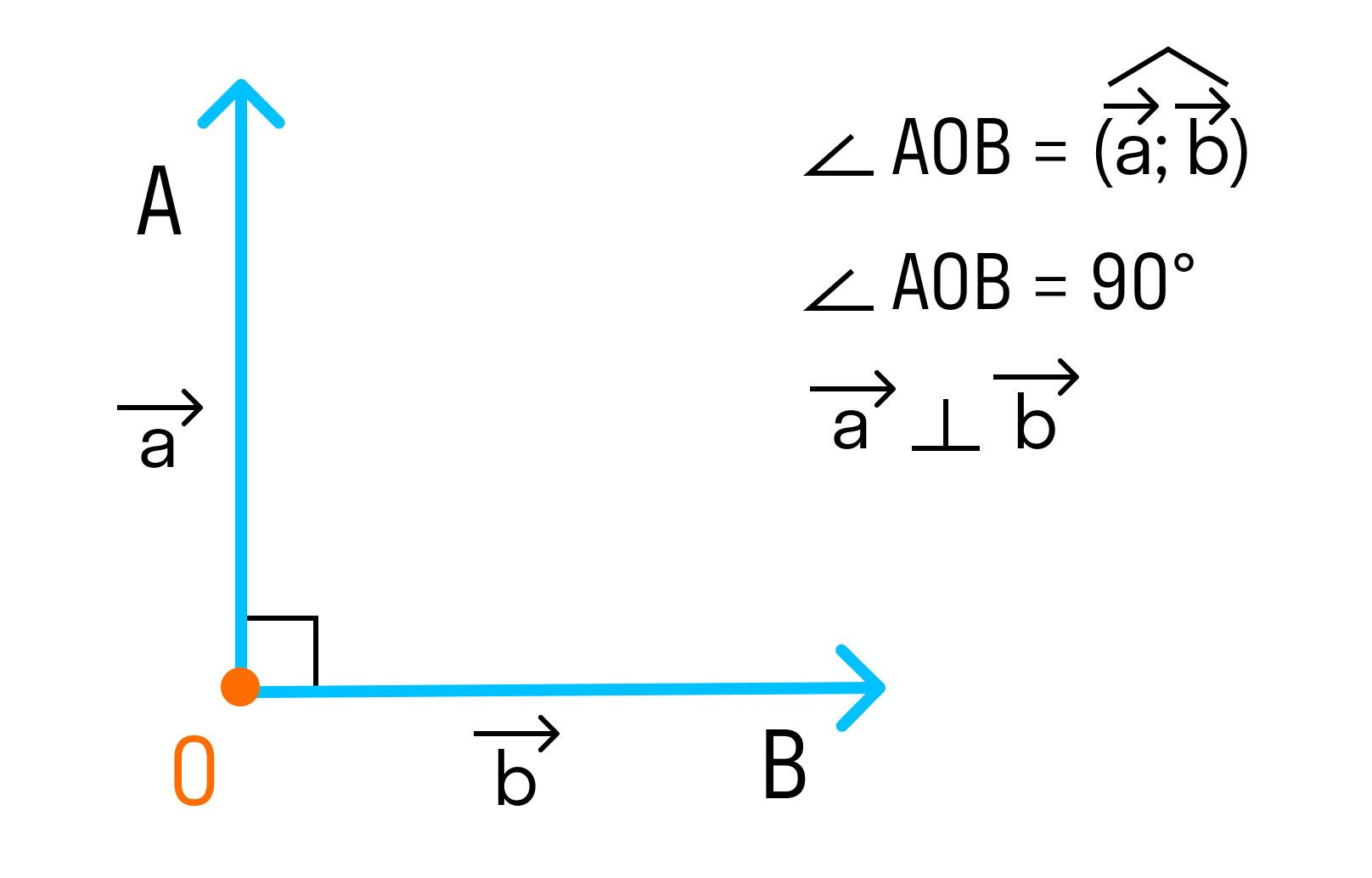
Так как косинус прямого угла равен 0, то скалярное произведение перпендикулярных векторов равно 0.

Если векторы направлены в разные стороны, тогда угол между ними 180°.

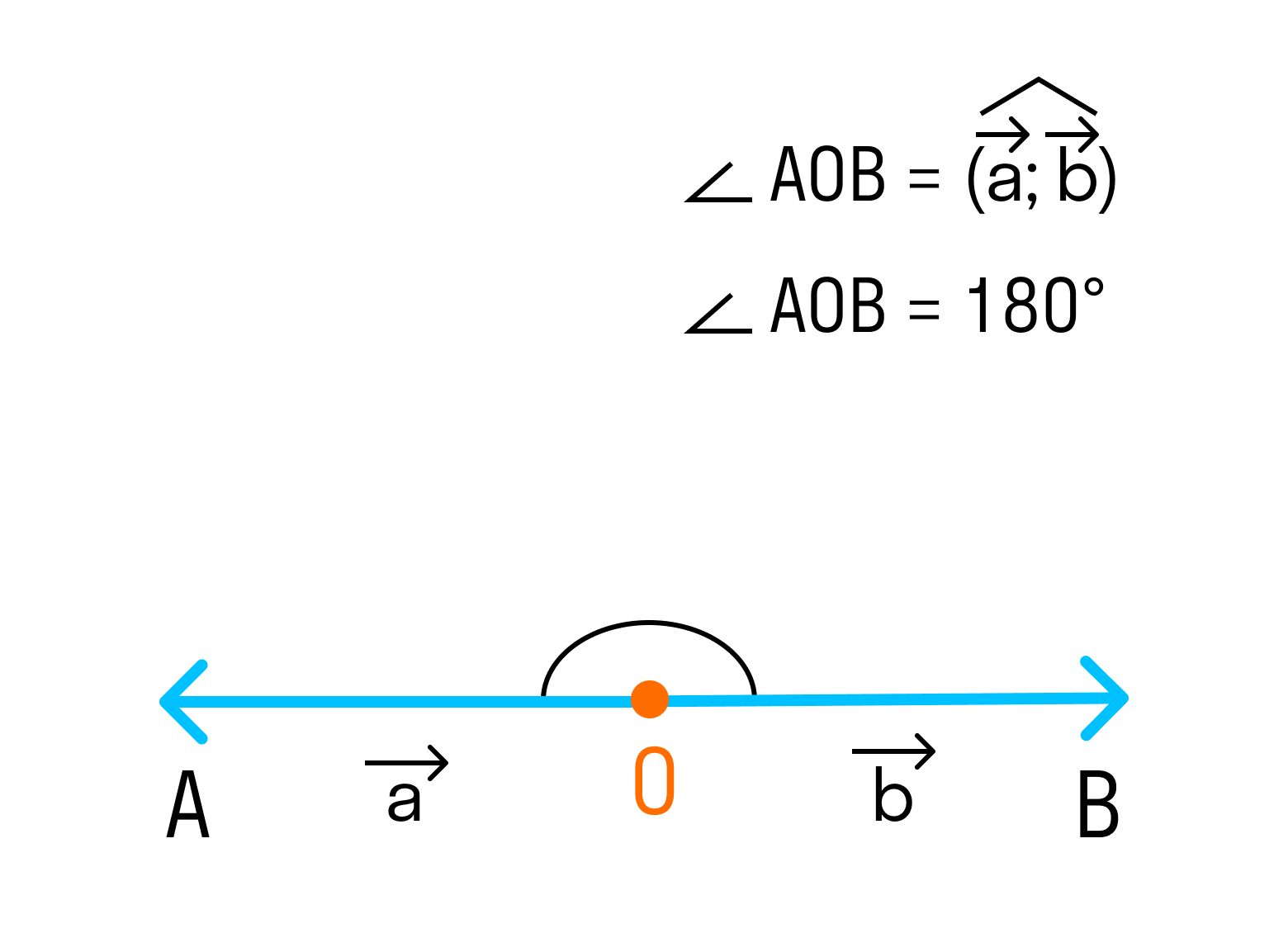
Так как косинус угла в 180° равен -1, то скалярное произведение противоположно направленных векторов равно отрицательному произведению их длин.

Также векторы могут образовывать тупой угол. Это выглядит так:

2 Вектор на плоскости и в пространстве

Вектором
называется направленный отрезок с началом и концом, изображаемым на
рисунке стрелкой. Произвольная точка пространства может считаться
нулевым вектором. Нулевой вектор не имеет конкретного направления,
так как начало и конец совпадают, поэтому ему можно придать любое
направление.

Длина
(модуль) ненулевого вектора

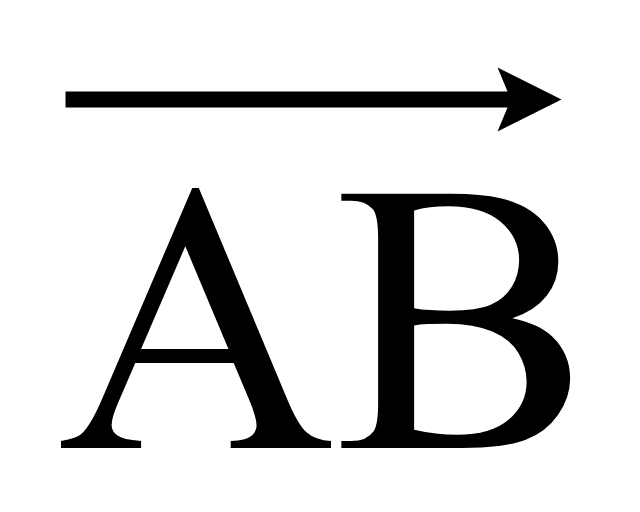
— это длина отрезка AB, которая
обозначается

.
Длина вектора

обозначается

.
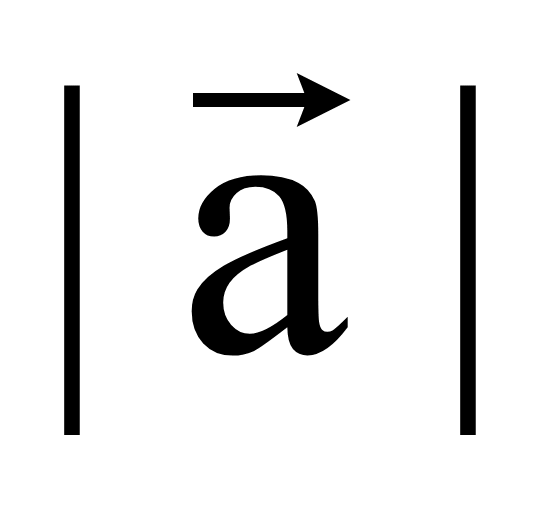
Нулевой вектор имеет длину равную нулю

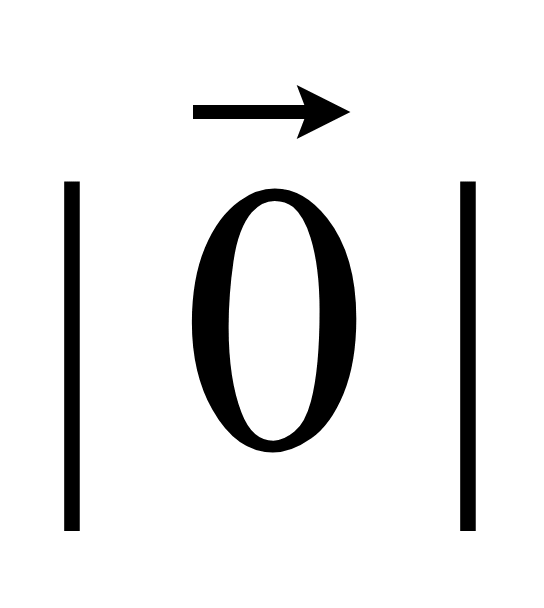
= 0.

Коллинеарными
называются ненулевые векторы, лежащие на одной прямой или на
параллельных прямых. На рисунках ниже изображены коллинеарные векторы

,

.

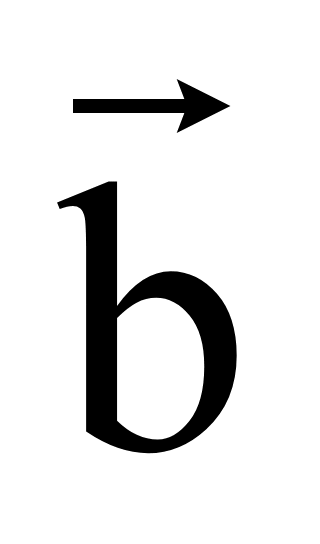
На
рисунке ниже также изображены коллинеарные векторы

,
и
.

Нулевой
вектор коллинеарен любому вектору.

Нулевой
вектор сонаправлен с любым вектором.

Равными
называются сонаправленные векторы равной длины. На рисунке ниже
изображены равные векторы

=
.

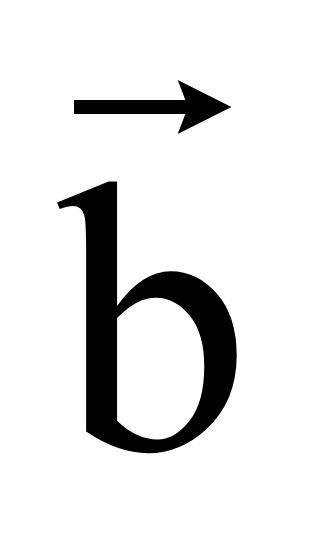
Противоположными
называются два ненулевых противоположно направленных вектора равной
длины. Вектор —

является противоположным вектору

Противоположные
векторы противоположно направленные и равны по модулю. Если даны
точки A и B,
то следующие векторы противоположные

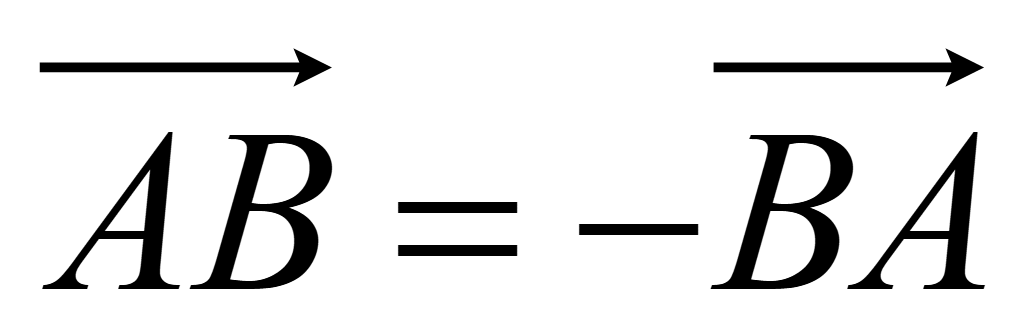
Равные
по модулю равные или противоположные, или нулевые векторы.

Многие
физические величины являются векторными величинами: сила, скорость,
электрическое поле и т.д.

Если
не задана точка приложения (начала) вектора, то она выбирается
произвольно.

Если
в точку O поместить начало вектора, то
считается, что вектор отложен от точки O.
Из любой точки можно отложить единственный вектор, равный данному
вектору.

Скалярное произведение в ортонормированной системе координат[править]

Пусть заданы координаты двух векторов a={a1,a2,a3}{\displaystyle \mathbf {a} =\{a_{1},a_{2},a_{3}\}} и b={b1,b2,b3}{\displaystyle \mathbf {b} =\{b_{1},b_{2},b_{3}\}} в ортонормированной системе координат.

a⋅b=(a1e1+a2e2+a3e3)⋅(b1e1+b2e2+b3e3)==a1b1e1⋅e1+a2b2e2⋅e2+a3b3e3⋅e3+(a1b2+a2b1)e1⋅e2+(a1b3+a3b1)e1⋅e3+(a2b3+a3b2)e2⋅e3{\displaystyle {\begin{aligned}\mathbf {a} \cdot \mathbf {b} &=(a_{1}\mathbf {e} _{1}+a_{2}\mathbf {e} _{2}+a_{3}\mathbf {e} _{3})\cdot (b_{1}\mathbf {e} _{1}+b_{2}\mathbf {e} _{2}+b_{3}\mathbf {e} _{3})=\\&=a_{1}b_{1}\mathbf {e} _{1}\cdot \mathbf {e} _{1}+a_{2}b_{2}\mathbf {e} _{2}\cdot \mathbf {e} _{2}+a_{3}b_{3}\mathbf {e} _{3}\cdot \mathbf {e} _{3}+(a_{1}b_{2}+a_{2}b_{1})\mathbf {e} _{1}\cdot \mathbf {e} _{2}+(a_{1}b_{3}+a_{3}b_{1})\mathbf {e} _{1}\cdot \mathbf {e} _{3}+(a_{2}b_{3}+a_{3}b_{2})\mathbf {e} _{2}\cdot \mathbf {e} _{3}\end{aligned}}}

В ортонормированной системе координат e1⋅e1=e2⋅e2=e3⋅e3=1{\displaystyle \mathbf {e} _{1}\cdot \mathbf {e} _{1}=\mathbf {e} _{2}\cdot \mathbf {e} _{2}=\mathbf {e} _{3}\cdot \mathbf {e} _{3}=1} и e1⋅e2=e1⋅e3=e2⋅e3={\displaystyle \mathbf {e} _{1}\cdot \mathbf {e} _{2}=\mathbf {e} _{1}\cdot \mathbf {e} _{3}=\mathbf {e} _{2}\cdot \mathbf {e} _{3}=0}, так как cos⁡=1,cos⁡π2={\displaystyle \cos 0=1,\;\cos {\tfrac {\pi }{2}}=0}.
Поэтому

a⋅b=a1b1+a2b2+a3b3{\displaystyle \mathbf {a} \cdot \mathbf {b} =a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}}

12 Координаты вектора в пространстве

В
пространстве зададим прямоугольную систему координат Oxyz.
От начала координат в положительных направлениях осей Ox,
Oy, Oz проведем
соответствующие единичные векторы

,

,

,
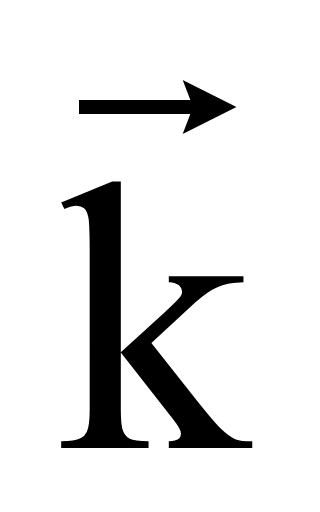
которые называются координатными векторами, неколлинеарны и
некомпланарны. Поэтому любой вектор

,
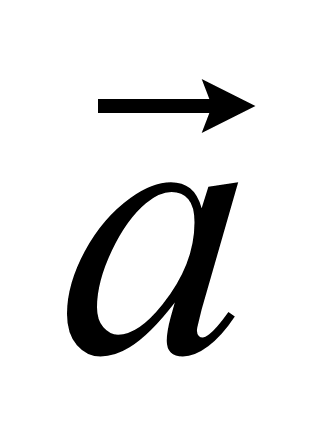
проведенный из начала координат, разлагается по трем заданным
некомпланарным координатным векторам

,

и

с единственными коэффициентами разложения x,
y, z:

=
x

+ y
+
z
.

Коэффициенты
разложения x, y,
z являются координатами вектора

,
проведенного из начала заданной прямоугольной системы координат,
которые записываются в скобках

(x;
y; z). Координаты
конца такого вектора являются и координатами вектора. Нулевой вектор
имеет координаты равные нулю

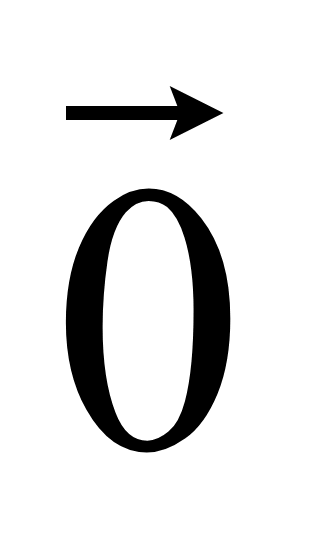
(0;
0; 0). У равных векторов соответствующие координаты равны.

Если
вектор начинается не из начала координат, то для определения его
координат можно провести его из начала координат, совместив с точкой
O начало вектора.

Правила
нахождения координат результирующего вектора:

1.
При суммировании двух и более векторов каждая координата
результирующего вектора равна сумме соответствующих координат
заданных векторов. Если даны два вектора

(x₁; y₁;
z₁) и

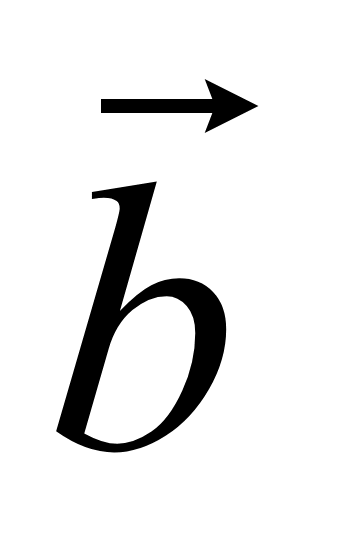
(x₂; y₂;
z₂), то сумма векторов

+

дает вектор с координатами (x₁ +
x₂; y₁
+ y₂; z₁
+ z₂)

+

= (x₁ + x₂;
y₁ + y₂;
z₁ + z₂).

2.
Разность является разновидностью суммы, поэтому разность
соответствующих координат дает каждую координату вектора, полученного
при вычитании двух заданных векторов. Если даны два вектора

(x_a;
y_a;
z_a) и

(x_b;
y_b;
z_b),
то разность векторов

—

дает вектор с координатами (x_a
— x_b;
y_a —
y_b; z_a
— z_b)

—
= (x_a
— x_b;
y_a —
y_b; z_a
– z_b).

3.
При умножении вектора на число каждая координата результирующего
вектора равна произведению этого числа на соответствующую координату
заданного вектора. Если даны число k и
вектор

(x;
y; z), то
умножение вектора на число k дает вектор k

с координатами

k

= (kx; ky; kz).

Задача.
Найти координаты вектора

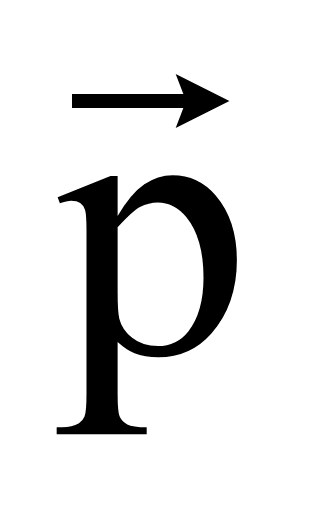
= 2

— 3
+
4
,
если координаты векторов

(1; -2; -1),

(-2; 3; -4),

(-1; -3; 2).

Решение

=
2

+ (-3
)
+ 4

2

= (2·x_a;
2·y_a;
2·z_a)
= (2·1; 2·(-2); 2·(-1)) = (2; -4; -2);

-3
=
(-3·x_b;
-3·y_b;
-3·z_b)
= (-3·(-2); -3·3; -3·(-4)) = (6; -9; 12);

4
=
(4·x_c;
4·y_c;
4·z_c)
= (4·(-1); 4·(-3); 4·2) = (-4; -12; 8).

=
(2 + 6 — 4; -4 — 9 -12; -2 + 12 + = (4; -25; 18).

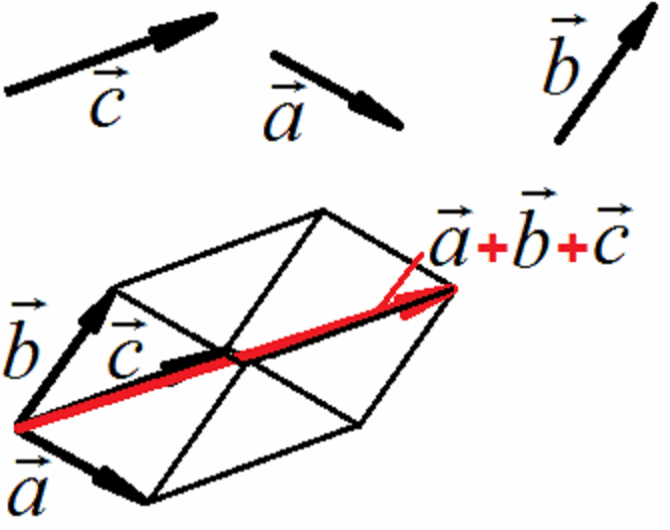
9 Правило параллелепипеда

Параллелепипед
— это объемная фигура, противоположные грани которой состоят из двух
равных параллелограммов, лежащих в параллельных плоскостях.

Правило
параллелепипеда позволяет складывать три некомпланарных вектора,
которые откладываются из одной точки и строится параллелепипед так,
чтобы суммируемые векторы образовывали его ребра, а остальные ребра
параллелепипеда были соответственно параллельны и равны длинам ребер,
образованных суммируемыми векторами. Диагональ параллелепипеда
образует вектор, являющийся суммой заданных трех векторов, который
начинается из точки начала складываемых векторов.

Свойства скалярного произведения векторов

Алгебраические свойства

1.   (переместительное свойство: от перемены местами перемножаемых векторов величина их скалярного произведения не меняется).

2.   (сочетательное относительно числового множителя свойство: скалярное произведение вектора, умноженного на некоторый множитель, и другого вектора, равно скалярному произведению этих векторов, умноженному на тот же множитель).

3.   (распределительное относительно суммы векторов свойство: скалярное произведение суммы двух векторов на третий вектор равно сумме скалярных произведений первого вектора на третий вектор и второго вектора на третий вектор).

4. (скалярный квадрат вектора больше нуля),
если — ненулевой вектор, и ,
если — нулевой вектор.

Геометрические свойства

В определениях изучаемой операции мы уже касались понятия угла между двумя векторами.
Пора уточнить это понятие.

На рисунке выше видны два вектора, которые приведены к общему началу

И первое, на что нужно
обратить внимание: между этими векторами существуют два угла —
и. Какой из этих углов фигурирует в определениях и свойствах
скалярного произведения векторов? Сумма рассмотренных углов равна и поэтому
косинусы этих углов равны

В определение скалярного произведения входит только косинус угла, а не значение его выражения.
Но в свойствах рассматривается только один угол. И это тот из двух углов, который не превосходит ,
то есть 180 градусов. На рисунке этот угол обозначен как .

1. Два вектора называют ортогональными и угол между этими векторами — прямой (90 градусов или ), если скалярное произведение этих векторов равно нулю:

.

Ортогональностью в векторной алгебре называется перпендикулярность двух векторов.

2. Два ненулевых вектора составляют острый угол (от 0 до 90 градусов, или, что тоже самое — меньше ) тогда и только тогда, когда их скалярное произведение
положительно.

3. Два ненулевых вектора составляют тупой угол (от 90 до 180 градусов, или, что то же самое — больше ) тогда и только тогда, когда их скалярное произведение отрицательно.

Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)

Пример 3. В координатах даны векторы:

.

Вычислить скалярные произведения всех пар данных векторов. Какой угол (острый, прямой, тупой) образуют эти пары векторов?

Решение. Вычислять будем путём сложения произведений соответствующих координат.

.

Получили отрицательное число, поэтому векторы образуют тупой угол.

.

Получили положительное число, поэтому векторы образуют острый угол.

.

Получили положительное число, поэтому векторы образуют острый угол.

.

Получили нуль, поэтому векторы образуют прямой угол.

.

Получили положительное число, поэтому векторы образуют острый угол.

.

Получили положительное число, поэтому векторы образуют острый угол.

Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.

Пример 4. Даны длины двух векторов и угол между ними:

.

Определить, при каком значении числа
векторы и
ортогональны (перпендикулярны).

Решение. Перемножим векторы по правилу умножения многочленов:

.

Теперь вычислим каждое слагаемое:

.

Составим уравнение (равенство произведения нулю), приведём подобные члены и решим уравнение:

Ответ: мы получили значение ,
при котором векторы ортогональны.

Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)

Пример 5. Доказать, что вектор
ортогонален (перпендикулярен) вектору

Решение. Чтобы проверить ортогональность, перемножим векторы
и
как многочлены, подставляя
вместо его выражение, данное
в условии задачи:

.

Для этого нужно каждый член (слагаемое) первого многочлена умножить на каждый член
второго и полученные произведения сложить:

.

В полученном результате дробь за счёт
сокращается. Получается следующий результат:

.

Вывод: в результате умножения получили нуль, следовательно, ортогональность (перпендикулярность) векторов доказана.

Решить задачу самостоятельно, а затем посмотреть решение

Пример 6. Даны длины векторов
и
, a
угол между этими векторами равен . Определить, при каком значении
векторы и
взаимно перпендикулярны.

Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.

Основные определения

Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.

Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.

Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.

Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.

Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.

Результат операции является число. То есть при умножении вектор на вектор получается число. Если длины векторов |→a|, |→b| — это числа, косинус угла — число, то их произведение |→a|*|→b|*cos∠(→a, →b) тоже будет числом.

Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.