Примеры применения формул сокращенного умножения
Пример 1.
Вычислить 51^2.
Решение.
Если есть калькулятор то без проблем находите
Это я пошутил — с калькулятором мудрые все, без него… (не будем о грустном).
Не имея калькулятора и зная приведенные выше правила квадрат числа находим по правилу
Пример 2.
Найти 99^2.
Решение.
Применим вторую формулу
Пример 3.
Возвести в квадрат выражение (x+y-3).
Решение.
Сумму первых двух слагаемых мысленно считаем одним слагаемым и по второй формуле сокращенного умножения имеем
Пример 4.
Найти разность квадратов 11^2-9^2.
Решение.
Поскольку числа небольшие то можно просто подставить значения квадратов
Но цель у нас совсем другая — научиться использовать формулы сокращенного умножения для упрощения вычислений. Для этого примера применим третью формулу
Пример 5.
Найти разность квадратов17^2-3^2
.
Решение.
На этом примере Вы уже захотите изучить правила чтобы вычисления свести к одной строке
Как видите — ничего удивительного мы не делали.
Пример 6.
Упростить выражение(x-y)^2-(x+y)^2.
Решение.
Можно раскладывать квадраты, а позже сгруппировать подобные слагаемые. Однако можно прямо применить разность квадратов
Просто и без длинных решений.
Пример 7.
Возвести в куб многочлен x^3-4.
Решение
. Применим 5 формулу сокращенного умножения
Пример 8.
Записать в виде разности квадратов или их сумме а) x^2-8x+7 б) x^2+4x+29
Решение.
а) Перегруппируем слагаемые
б) Упрощаем на основе предыдущих рассуждений
Пример 9.
Разложить рациональную дробь
Решение.
Применим формулу разности квадратов
Составим систему уравнений для определения констант
К утроенному первому уравнению добавим второе. Найденное значение подставляем в первое уравнение
Окончательно разложение примет вид
Разложить рациональную дробь часто необходимо перед интегрированием, чтобы снизить степень знаменателя.
Пример 10.
Используя бином Ньютона расписать выражение (x-a)^7.
Решение.
Что такое бином Ньютона Вы вероятно уже знаете. Если нет то ниже приведены биномиальные коэффициенты
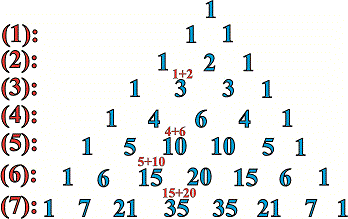
Они образуются следующим образом: по краю идут единицы, коэффициенты между ними в нижней строке образуют суммированием соседних верхних. Если ищем разницу в каком-то степени, то знаки в расписании чередуются от плюса к минусу. Таким образом для седьмого порядка получим такой расклад
Внимательно также посмотрите как меняются показатели — для первой переменной они уменьшаются на единицу в каждом следующем слагаемом, соответственно для второй — на единицу растут. В сумме показатели всегда должны быть равны степени разложения (=7
).
Думаю на основе приведенного выше материала Вы сможете решить задачи на бином Ньютона. Изучайте формулы сокращенного умножения и применяйте везде, где это может упростить вычисления и сэкономит время выполнения задания.
В предыдущем уроке мы разобрались с разложением на множители. Освоили два способа: вынесение общего множителя за скобки и группировку. В этом уроке — следующий мощный способ: формулы сокращённого умножения
. В краткой записи — ФСУ.
Формулы сокращённого умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) крайне необходимы во всех разделах математики. Они применяются в упрощении выражений, решении уравнений, умножении многочленов, сокращении дробей, решении интегралов и т.д. и т.п. Короче, есть все основания разобраться с ними. Понять откуда они берутся, зачем они нужны, как их запомнить и как применять.
Разбираемся?)
Откуда берутся формулы сокращённого умножения?
Равенства 6 и 7 записаны не очень привычно. Как бы наоборот. Это специально.) Любое равенство работает как слева направо, так и справа налево. В такой записи понятнее, откуда берутся ФСУ.
Они берутся из умножения.) Например:
(a+b) 2 =(a+b)(a+b)=a 2 +ab+ba+b 2 =a 2 +2ab+b 2
Вот и всё, никаких научных хитростей. Просто перемножаем скобки и приводим подобные. Так получаются все формулы сокращённого умножения.
Сокращённое
умножение — это потому, что в самих формулах нет перемножения скобок и приведения подобных. Сокращены.) Сразу дан результат.
ФСУ нужно знать наизусть. Без первых трёх можно не мечтать о тройке, без остальных — о четвёрке с пятёркой.)
Зачем нужны формулы сокращённого умножения?
Есть две причины, выучить, даже зазубрить эти формулы. Первая — готовый ответ на автомате резко уменьшает количество ошибок. Но это не самая главная причина. А вот вторая…
Квадрат суммы двух выражений
Существует ряд случаев, когда умножение многочлена на многочлен можно значительно упростить. Таковым к примеру является случай (2x
+ 3y
) 2
.
Выражение (2x
+ 3y
) 2
это перемножение двух многочленов, каждый из которых равен (2x
+ 3y
)
(2x
+ 3y
) 2 = (2x
+ 3y
)(2x
+ 3y
)
Получили умножение многочлена на многочлен. Выполним его:
(2x
+ 3y
) 2 = (2x
+ 3y
)(2x
+ 3y
) = 4x
2 + 6xy
+ 6xy
+ 9y
2 = 4x
2 + 12xy
+ 9y
2
То есть выражение (2x
+ 3y
) 2
равно 4x
2 + 12xy
+ 9y
2
(2x
+ 3y
) 2 = 4x
2 + 12xy
+ 9y
2
Решим аналогичный пример, который попроще:
(a + b
) 2
Выражение (a + b
) 2
это перемножение двух многочленов, каждый из которых равен (a + b
)
(a + b
) 2 = (a + b
)(a + b
)
Выполним это умножение:
(a + b
) 2 = (a + b
)(a + b
) = a
2 + ab
+ ab
+ b
2 = a
2 + 2ab
+ b
2
То есть выражение (a + b
) 2 равно a
2 + 2ab
+ b
2
(a + b
) 2 = a
2 + 2ab
+ b
2
Оказывается, что случай (a + b
) 2
можно распространить для любых a
и b
. Первый пример, который мы решили, а именно (2x
+ 3y
) 2
можно решить с помощью тождества (a + b
) 2 = a
2 + 2ab
+ b
2
. Для этого нужно подставить вместо переменных a
и b
соответствующие члены из выражение (2x
+ 3y
) 2
. В данном случае переменной a
соответствует член 2x
, а переменной b
соответствует член 3y
a
= 2x
b
= 3y
И далее можно воспользоваться тождеством (a + b
) 2 = a
2 + 2ab
+ b
2
, но вместо переменных a
и b
нужно подставлять выражения 2x
и 3y
соответственно:
(2x
+ 3y
) 2 = (2x
) 2 + 2 × 2x
× 3y
+ (3y
) 2 = 4x
2 + 12xy
+ 9y
2
Как и в прошлый раз получили многочлен 4x
2 + 12xy
+ 9y
2
. Решение обычно записывают покороче, выполняя в уме все элементарные преобразования:
(2x
+ 3y
) 2 = 4x
2 + 12xy
+ 9y
2
Тождество (a + b
) 2 = a
2 + 2ab
+ b
2
называют формулой квадрата суммы двух выражений. Эту формулу можно прочитать так:
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Рассмотрим выражение (2 + 3) 2
. Его можно вычислить двумя способами: выполнить сложение в скобках и возвести полученный результат в квадрат, либо воспользоваться формулой квадрата суммы двух выражений.
Первый способ:
(2 + 3) 2 = 5 2 = 25
Второй способ:
(2 + 3) 2 = 2 2 + 2 × 2 × 3 + 3 2 = 4 + 12 + 9 = 25
Пример 2
. Преобразовать выражение (5a
+ 3) 2
в многочлен.
Воспользуемся формулой квадрата суммы двух выражений:
(a + b
) 2 = a
2 + 2ab
+ b
2
(5a +
3) 2 = (5a
) 2 + 2 × 5a ×
3 + 3 2 = 25a
2 + 30a
+ 9
Значит, (5a +
3) 2 = 25a
2 + 30a
+ 9.
Попробуем решить данный пример, не пользуясь формулой квадрата суммы. У нас должен получиться тот же результат:
(5a +
3) 2 = (5a +
3)(5a +
3) = 25a
2 + 15a
+ 15a
+ 9 = 25a
2 + 30a
+ 9
Формула квадрата суммы двух выражений имеет геометрический смысл. Мы помним, что для вычисления площади квадрата нужно возвести во вторую степень его сторону.
Например, площадь квадрата со стороной a
будет равна a
2
. Если увеличить сторону квадрата на b
, то площадь будет равна (a + b
) 2
Рассмотрим следующий рисунок:
Представим, что сторону квадрата, изображённого на данном рисунке увеличили на b
. У квадрата все стороны равны. Если его сторону увеличить на b
, то остальные стороны тоже увеличатся на b
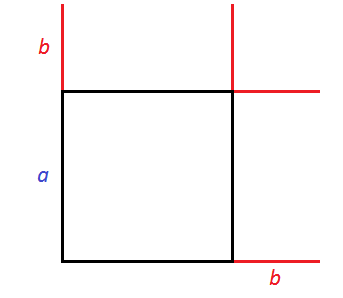
Получился новый квадрат, который больше предыдущего. Чтобы хорошо увидеть его, достроим отсутствующие стороны:
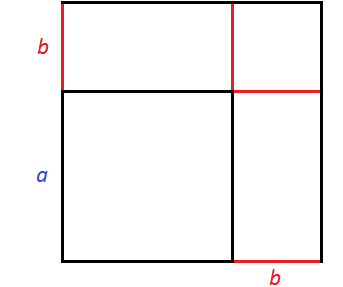
Чтобы вычислить площадь этого квадрата, можно по отдельности вычислить квадраты и прямоугольники, входящие в него, затем сложить полученные результаты.
Сначала можно вычислить квадрат со стороной a
— его площадь будет равна a
2
. Затем можно вычислить прямоугольники со сторонами a
и b
— они будут равны ab
. Затем можно вычислить квадрат со стороной b
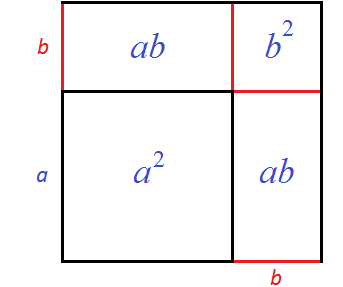
В результате получается следующая сумма площадей:
a
2 + ab + ab
+ b
2
Сумму площадей одинаковых прямоугольников можно заменить на умножение 2ab
, которое буквально будет означать «повторить два раза площадь прямоугольника ab»
. Алгебраически это получается путём приведения подобных слагаемых ab
и ab
. В результате получается выражение a
2 + 2ab
+ b
2
, которое является правой частью формулы квадрата суммы двух выражений:
(a + b
) 2
= a
2 + 2ab
+ b
2
Преобразование (упрощение) произведения одночлена и многочлена
С помощью распределительного свойства умножения можно преобразовать (упростить) в многочлен произведение одночлена и многочлена. Например:
\(9a^2b(7a^2 — 5ab — 4b^2) = \)
\(= 9a^2b \cdot 7a^2 + 9a^2b \cdot (-5ab) + 9a^2b \cdot (-4b^2) = \)
\(= 63a^4b — 45a^3b^2 — 36a^2b^3 \)
Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена.
Этот результат обычно формулируют в виде правила.
Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый из членов многочлена.
Мы уже неоднократно использовали это правило для умножения на сумму.
Распределительный закон
Распределительный закон в математике – это формальное определение для свойства алгебраических операций, которое говорит о том, что произведение двух скобок равно сумме произведений каждого элемента в первой скобке с каждым элементом во второй скобке. Если проще, то можно умножать на число либо всю сумму, либо отдельно каждое слагаемое, и результат будет один и тот же.
Распределительный закон может быть описан формулой:
(a+b)c = ac + bc
А еще можете запомнить другие формулы распределительного закона:
- ab + ac = a(b + c)
- a(b + c) = ab + ac
- ab – ac = a(b – c)
- ab + ac + ad + … = a (b + c + d + …)
Давайте посмотрим на действие этого закона на примере.
Как мы помним, распределительный закон можно применить к следующему выражению:
a(b + c) = ab + ac
Здесь мы распределяем множитель «а» над слагаемыми «b» и «c» внутри скобок. Это означает, что мы умножаем «а» на «b» и «а» на «c» и получаем ab и ac соответственно. Например:
3(4 + 5) = 3 × 4 + 3 × 5 = 12 + 15 = 27
Также можно использовать распределительный закон наоборот, т.е. (a + b)c = ac + bc, и тогда мы получим:
(3 + 2)5 = 3 × 5 + 2 × 5 = 15 + 10 = 25
В обоих случаях результат совпадает, даже если мы распределили умножение до или после сложения.
Распределительный закон может быть применен и к сложным выражениям с несколькими скобками и сложными множителями. Например:
a(b + c + d) – e(f + g) = a(b + c + d) – ef – eg = ab + ac + ad – ef – eg
Здесь мы распределяем множитель «а» над слагаемыми «b», «c» и «d» внутри первых скобок, а множитель «e» над слагаемыми «f» и «g» внутри вторых скобок. Это означает, что мы умножаем «a» Начало формы
на «b», «a» на «c» и «a» на «d» и получаем ab, ac и ad соответственно. Также мы умножаем «e» на «f» и «e» на «g» и получаем ef и eg соответственно. Например:
2(3 + 4 + 5) – 3(2 + 1) = 2 × 3 + 2 × 4 + 2 × 5 – 3 × 2 – 3 × 1 = 6 + 8 + 10 – 6 – 3 = 15
В этом примере сначала мы раскрываем скобки и применяем распределительный закон, а затем складываем и вычитаем соответствующие члены, получая результат.
Важно отметить, что применение распределительного закона может помочь упростить и ускорить решение математических задач, но необходимо быть внимательными и тщательно проверять правильность решения, особенно в сложных выражениях
Дополнительные формулы сокращенного умножения
Есть три основные дополнительные ФСУ – это бином Ньютона, формула возведения в квадрат суммы трех, четырех и более слагаемых, а также формула разности n-ых степеней двух слагаемых. Коротко о каждой из них.
Бином Ньютона
Бином Ньютона – это формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Выглядит она следующим образом:
Ck в степени n – это биноминальные коэффициенты, стоящие в строке под номером n в треугольнике Паскаля. Вычисляются эти коэффициенты по формуле:
Иначе говоря, ФСУ для квадрата и куба разности и суммы являются частными случаями формулы бинома Ньютона при n=2 и n=3 соответственно.
Однако может быть так, что слагаемых в сумме, которую нужно возвести в степень, больше, чем два. В таком случае подойдет формула квадрата суммы трех, четырех и более слагаемых.
Формула возведения в квадрат суммы трех, четырех и более слагаемых
Как и было сказано, формула возведения в квадрат суммы трех, четырех и более слагаемых нужна, когда слагаемых в сумме, которую нужно возвести в степень, больше, чем два.
Выглядит она так:
Читать и запоминать эту формулу нужно следующим образом: квадрат суммы n слагаемых равен сумме квадратов всех слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Формула разности n-ых степеней двух слагаемых
И последняя формула – это формула разности n-ых степеней двух слагаемых, выглядящая вот так:
Как правило, данную формулу разделяют на две отдельные: для четных и нечетных степеней.
Формула для четных показателей 2m:
Формула для нечетных показателей 2m + 1:
Несложно догадаться, что ФСУ разности квадратов и кубов являются частными случаями данной формулы при n=2 и n=3 соответственно. А для разности кубов b заменяется на –b.
Рассмотренные нами ФСУ и дополнительные ФСУ обязательно помогут вам быстрее справляться с математическими задачами и занимать свой мозг полезной деятельностью.
Вопросы и ответы
И напоследок несколько ответов на часто задаваемые вопросы.
Для чего нужны формулы сокращенного умножения?
Формулы сокращенного умножения нужны, чтобы упростить и ускорить вычисления, а также для улучшения наглядности и понимания математических выражений.
В настоящее время ФСУ широко используются в образовании и науке, а также в практической жизни. Они применяются в различных областях, таких как математика, физика, химия и инженерия, плюс могут применяться к решению различных задач, например, в области финансов, менеджмента и исследования данных.
Как появились формулы сокращенного умножения?
Формулы сокращенного умножения появились в результате исследований математиков в области алгебры и арифметики и основаны на использовании их свойств, таких как коммутативность, ассоциативность и дистрибутивность.
Если обратиться к истории, можно узнать, что такими формулами пользовались еще в Древнем Вавилоне и Древнем Египте. Первым же, кто доказал математическую закономерность квадрата суммы, был древнегреческий ученый Евклид, живший в III веке до н.э. А на общепринятом языке математические формулы были обоснованы Исааком Ньютоном.
Сколько всего формул сокращенного умножения?
Не существует точного количества формул сокращенного умножения, т.к. их можно создавать неограниченное количество. Но в основном изучают и используют семь основных формул. Это квадрат суммы, квадрат разности, разность квадратов, сумма кубов, разность кубов, куб суммы и куб разности. Также распространено применения трех дополнительных ФСУ, таких как бином Ньютона, формула возведения в квадрат суммы трех, четырех и более слагаемых и формула разности n-ых степеней двух слагаемых.
Почему формулы сокращенного умножения изучают на алгебре в 7 классе?
Формулы сокращенного умножения изучаются на алгебре в 7 классе, потому что именно на этом этапе школьники знакомятся с понятием многочлена и действиям с ним. Кроме того, ФСУ являются важным и основным инструментом для решения математических задач и упрощения вычислений.
Формулы помогают ученикам развить навыки в решении простых задач, а также дают им навыки для решения более сложных задач в будущем, что в перспективе способно помочь молодым людям в их дальнейшем обучении и карьере.
Можно ли не использовать формулы сокращенного умножения?
Конечно, при решении математических задач можно и не использовать формулы сокращенного умножения. Однако без них процесс решения может оказаться очень трудоемким и долгим. ФСУ же заметно упрощают его и помогают справляться с заданиями намного быстрее.
Помимо прочего, ФСУ входят в обязательную школьную программу, вследствие чего преподаватели часто требуют от учеников, во-первых, знать эти формулы наизусть, а во-вторых, решать задания именно с их помощью.
Если Вам нравится этот сайт…
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Для того что бы упростить алгебраические многочлены, существуют формулы сокращенного умножения
. Их не так уж и много и они легко запоминаются, а запомнить их нужно. Обозначения которые используются в формулах, могут принимать любой вид (число или многочлен).
Первая формула сокращенного умножения называется разность квадратов
. Она заключается в том что из квадрата одного числа отнимается квадрат второго числа равен величине разности данных чисел, а также их произведению.
а 2 — b 2 = (а — b)(a + b)
Разберем для наглядности:
22 2 — 4 2 = (22-4)(22+4)=18 * 26 = 468
9а 2 — 4b 2 c 2 = (3a — 2bc)(3a + 2bc)
Вторая формула о сумме квадратов
. Звучит она как, сумма двух величин в квадрате равняется квадрату первой величины к ней прибавляется двойное произведение первой величины умноженное на вторую, к ним прибавляется квадрат второй величины.
(а + b) 2 = a 2 +2ab + b 2
Благодаря данной формуле, становится намного проще вычислять квадрат от большого числа, без использования вычислительной техники.
Так к примеру:
квадрат от 112 будет равен
1) В начале разберем 112 на числа квадраты которых нам знакомы
112 = 100 + 12
2) Вписываем полученное в скобки возведенные в квадрат
112 2 = (100+12) 2
3) Применяя формулу, получаем:
112 2 = (100+12) 2 = 100 2 + 2 * 100 * 12 + 122 = 10000 + 2400+ 144 = 12544
Третья формула это квадрат разности
. Которая гласит о том, что две вычитаемые друг друга величины в квадрате равняются, тому что, от первой величины в квадрате отнимаем двойное произведение первой величины умноженное на вторую, прибавляя к ним квадрат второй величины.
(а +b) 2 = а 2 — 2аb + b 2
где (а — b) 2 равняется (b — а) 2 . В доказательство чему, (а-b) 2 = а 2 -2аb+b 2 = b 2 -2аb + а 2 = (b-а) 2
Четвертая формула сокращенного умножения называется куб суммы
. Которая звучит как: две слагаемые величины в кубе равны кубу 1 величины прибавляется тройное произведение 1 величины в квадрате умноженное на 2-ую величину, к ним прибавляется тройное произведение 1 величины умноженной на квадрат 2 величины, плюс вторая величина в кубе.
(а+b) 3 = а 3 + 3а 2 b + 3аb 2 + b 3
Пятая, как вы уже поняли называется куб разности
. Которая находит разности между величинами, как от первого обозначения в кубе отнимаем тройное произведение первого обозначения в квадрате умноженное на второе, к ним прибавляется тройное произведение первого обозначения умноженной на квадрат второго обозначения, минус второе обозначение в кубе.
(а-b) 3 = а 3 — 3а 2 b + 3аb 2 — b 3
Шестая называется — сумма кубов
. Сумма кубов равняется произведению двух слагаемых величин, умноженных на неполный квадрат разности, так как в середине нет удвоенного значения.
а 3 + b 3 = (а+b)(а 2 -аb+b 2)
По другому можно сказать сумму кубов можно назвать произведение в двух скобках.
Седьмая и заключительная, называется разность кубов
(ее легко перепутать с формулой куба разности, но это разные вещи). Разность кубов равняется произведению от разности двух величин, умноженных на неполный квадрат суммы, так как в середине нет удвоенного значения.
а 3 — b 3 = (а-b)(а 2 +аb+b 2)
И так формул сокращенного умножения всего 7, они похожи друг на друга и легко запоминаются, единственно важно не путаться в знаках. Они так же рассчитаны на то, что их можно использовать в обратном порядке и в учебниках собрано довольно много таких заданий
Будьте внимательны и все у вас получится.
Применяют для упрощения вычислений, а также разложение многочленов на множители, быстрого умножения многочленов. Большинство формул сокращенного умножения можно получить из бинома Ньютона — в этом Вы скоро убедитесь.
Формулы для квадратов
применяют в вычислениях чаще. Их начинают изучать в школьной программе начиная с 7 класса и до конца обучения формулы для квадратов и кубов школьники должны знать на зубок.
Формулы для кубов
не сильно сложные и их нужно знать при сведении многочленов к стандартному виду, для упрощения подъема суммы или разности переменной и числа к кубу.
Формулы обозначены красным получают из предыдущих группировкой подобных слагаемых.
Формулы для четвертого и пятого степени
в школьном курсе мало кому пригодятся, однако есть задачи при изучении высшей математики где нужно вычислять коэффициенты при степенях.
Формулы для степени
n
расписаны
через биномиальные коэффициенты с использованием факториалов следующие
Формулы сокращенного умножения
При выполнении различных алгебраических преобразований встречаются часто некоторые частные случаи умножения. Получающиеся при этом произведения полезно запомнить наизусть, чтобы в дальнейшем, когда эти случаи встретятся, можно было сразу написать результат, не производя каждый раз почленного умножения. Равенства, выражающие эти частные случаи умножения, называются формулами сокращенного умножения.
1. Квадрат суммы. Возведем в квадрат сумму двух чисел a и b.
(a + b)2 = (a+b)(a+b) = a2 + ab + ab + b2
Приведя подобные члены получим:
(a + b)2 = a2 + 2ab + b2.
Эту формулу следует запомнить как в приведенной записи, так и в словесном выражении.
Квадрат суммы двух чисел равен квадрату первого числа, плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа.
Примеры:
1)
(3a + 2b)2 = (3a)2 + 2 * 3a * 2b + (2b)2 = 9a2 + 12ab + 4b2.
Следует приобрести навык писать сразу окончательный результат, не проводя промежуточной записи, которая показана в этом примере.
2) Эта формула применяется при устном возведении в квадрат чисел, немного больших «круглого» числа, например:
412 = (40 + 1)2 = 402 + 2 * 40 * 1 + 12 = 1681;
322 = (30 + 2)2 = 302 + 2 * 2 * 30 + 22 = 900 + 120 + 4 = 1024.
3) Особенно легко запомнить прием возведения в квадрат чисел, оканчивающихся пятеркой. Положим, число имеет a десятков и 5 единиц. Тогда его можно записать так:
10a + 5.
Возведем это число в квадрат по формуле:
(10a + 5)2 = 100a2 + 2 * 5 * 10a + 52 = 100a2 + 100a + 25 = 100a(a + 1) + 25.
Полученное выражение показывает, что для возведения в квадрат числа, оканчивающегося пятеркой, надо число его десятков умножить на число, единицей большее, и к произведению приписать 25. Например:
652 = 6 * 7 * 100 + 25 = 4225;
852 = 8 * 9 (сотен) + 25 = 7225;
3,52 = 3 * 4 + 0,25 = 12,25.
Последний пример можно записать так:
Значит, чтобы возвести в квадрат смешанное число, дробная которого равна , достаточно целую часть умножить на число, единицей большее, и к произведению прибавить .2. Квадрат разности.
(a – b)2 = (a – b)(a – b) = a2 – ab – ab + b2.(a – b)2 = a2 – 2ab + b2.
Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа.
Эта формула отличается от ранее выделенной формулы только знаком среднего члена. Поэтому часто пишут сразу обе формулы так:Примеры:
1)
(4a2b – ab)2 = 16a4b2 – 8a2b * ab + a2b2 = 16a4b2 – 8a3b2 + a2b2.
И здесь следует стараться написать сразу результат, производя промежуточные вычисления в уме.
2) Эта формула применяется при устном возведении в квадрат чисел, немного меньших «круглого» числа, например:
392 = (40 – 1)2 = 402 – 2 * 40 + 1 = 1521;
482 = (50 – 2)2 = 2500 – 2 * 2 * 50 + 4 = 2304;
792 = (80 – 1)2 = 6400 – 160 + 1 = 6241.
3. Произведение суммы двух чисел на их разность.
(a + b)(a – b) = a2 + ab – ab – b2.(a + b)(a – b) = a2 – b2.
Произведение суммы двух чисел на их разность равно разности квадратов этих чисел.
Примеры.
1) (5a + 2b)(5a – 2b) = 25a2 – 4b2.
2) (2a2 + 3b3)(2a2 – 3b3) = 4a4 – 9b6.
3) Эта формула применяется при устном умножении двух чисел, из которых одно на несколько единиц больше «круглого» числа, на сколько другое меньше его, например: 47 и 53, 68 и 72.
47 * 53 = (50 – 3)(50 + 3) = 502 – 32 = 2491;
68 * 72 = 702 – 4 = 4896;
33 * 27 = 900 – 9 = 891.
4) Но иногда бывает полезно поступить наоборот: для вычисления разности квадратов двух чисел заменить эту разность произведением суммы оснований на их разность, например:
1022 — 1012 = (102 – 101)(102 + 101) = 203;
542 — 462 = (54 – 46)(54 + 46) = 800;
4. Куб суммы.
(a + b)3 = (a + b)2(a + b) = (a2 + 2ab + b2)(a + b) = a3 + 2a2b + ab2 + a2b + 2ab2 + b3;(a + b)3 = a3 + 3a2b + 3ab2 + b3.
Куб суммы двух чисел равен кубу первого числа, плюс утроенное произведение квадрата первого на второе, плюс утроенное произведение первого на квадрат второго, плюс куб второго числа.
Примеры.
1) (2a + 3b)3 = 8a3 + 3 * 4a2 * 3b + 3 * 2a * 9b2 + 27b3 = 8a3 + 36a2b + 54ab2 + 27b3.
2) 113 = 103 + 3 * 102 + 3 * 10 + 1 = 1331.
5. Куб разности.
(a – b)3 = (a – b)2(a – b) = (a2 – 2ab + b2)(a – b).
Произведя умножение и приведя подобные члены, получим:
(a – b)3 = a3 – 3a2b + 3ab2 – b3.
Куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого на второе, плюс утроенное произведение первого на квадрат второго, минус куб второго числа.
Примеры.
1) (x – 2)3 = x3 – 6×2 + 12x – 8.
2) (3a – 2b)3 = 27a3 – 54a2b + 36ab2 – 8b3.






























