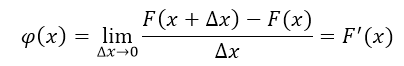Когда нельзя ограничиваться только математическим ожиданием
В большинстве случаев только математическое ожидание не может в
достаточной степени характеризовать случайную величину.
Пусть случайные величины X и Y заданы
следующими законами распределения:
| Значение X | Вероятность |
| Значение Y | Вероятность |
Математические ожидания этих величин одинаковы — равны нулю:
Однако характер распределения их различный. Случайная величина
X может принимать только значения, мало отличающиеся от математического
ожидания, а случайная величина Y может принимать значения, значительно
отклоняющиеся от математического ожидания. Аналогичный пример: средняя заработная плата
не даёт возможности судить об удельном весе высоко- и низкооплачиваемых рабочих.
Иными словами, по математическому ожиданию нельзя судить о том, какие отклонения
от него, хотя бы в среднем, возможны. Для этого нужно найти дисперсию случайной величины.
Дисперсия дискретной случайной величины.
Возможные значения случайных величин с равными математическими ожиданиями могут по-разному рассеиваться вокруг своих средних значений. Например, в двух студенческих группах средний балл за экзамен по теории вероятностей оказался равным 4, но в одной группе все оказались хорошистами, а в другой группе — только троечники и отличники. Поэтому возникает необходимость в такой числовой характеристике случайной величины, которая бы показывала разброс значений случайной величины вокруг своего математического ожидания. Такой характеристикой является дисперсия.
Дисперсия дискретной случайной величины
$X$ равна:
$$D\left(X\right)=\sum^n_{i=1}{p_i{\left(x_i-M\left(X\right)\right)}^2}.\ $$
В англоязычной литературе используются обозначения $V\left(X\right),\ Var\left(X\right)$. Очень часто дисперсию $D\left(X\right)$ вычисляют по формуле $D\left(X\right)=\sum^n_{i=1}{p_ix^2_i}-{\left(M\left(X\right)\right)}^2$.
Свойства дисперсии
$D\left(X\right)$:
- Дисперсия всегда больше или равна нулю, т.е. $D\left(X\right)\ge 0$.
- Дисперсия от константы равна нулю, т.е. $D\left(C\right)=0$.
- Постоянный множитель можно выносить за знак дисперсии при условии возведения его в квадрат, т.е. $D\left(CX\right)=C^2D\left(X\right)$.
- Дисперсия суммы независимых случайных величин равна сумме их дисперсий, т.е. $D\left(X+Y\right)=D\left(X\right)+D\left(Y\right)$.
- Дисперсия разности независимых случайных величин равна сумме их дисперсий, т.е. $D\left(X-Y\right)=D\left(X\right)+D\left(Y\right)$.
Пример 6
. Вычислим дисперсию случайной величины $X$ из примера $2$.
$$D\left(X\right)=\sum^n_{i=1}{p_i{\left(x_i-M\left(X\right)\right)}^2}={{1}\over {6}}\cdot {\left(1-3,5\right)}^2+{{1}\over {6}}\cdot {\left(2-3,5\right)}^2+\dots +{{1}\over {6}}\cdot {\left(6-3,5\right)}^2={{35}\over {12}}\approx 2,92.$$
Пример 7
. Известно, что дисперсия случайной величины $X$ равна $D\left(X\right)=2$. Найти дисперсию случайной величины $4X+1$.
Используя вышеуказанные свойства, находим $D\left(4X+1\right)=D\left(4X\right)+D\left(1\right)=4^2D\left(X\right)+0=16D\left(X\right)=16\cdot 2=32$.
Пример 8
. Известно, что дисперсия случайной величины $X$ равна $D\left(X\right)=3$. Найти дисперсию случайной величины $3-2X$.
Используя вышеуказанные свойства, находим $D\left(3-2X\right)=D\left(3\right)+D\left(2X\right)=0+2^2D\left(X\right)=4D\left(X\right)=4\cdot 3=12$.
Понятие плотности распределения вероятностей непрерывной случайной величины
Пусть $X$ — непрерывная случайная величина с функцией распределения вероятностей $F(x)$. Напомним определение функции распределения:
Определение 1
Функцией распределения называется функция $F(x)$ удовлетворяющая условию $F(x) = P(X⩽x)$.
Так как случайная величина является непрерывной, то, как нам уже известно, что функция распределения вероятностей F(x) будет непрерывной функцией. Пусть F(x) также дифференцируема на всей области определения.
Рассмотрим интервал (x,x+△x) (где △x — приращение величины x на нем).
Теперь устремляя значения приращения △x к нулю, получим:
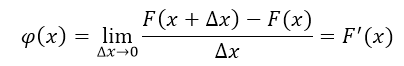Рисунок 1.
Получи помощь с рефератом от ИИ-шки
ИИ ответит за 2 минуты
Таким образом, получаем:
Определение 2
Плотность распределения (плотность вероятности) φ(x) — это производная функции распределения непрерывной случайной величины.
Плотность распределения, как и функция распределения, — это одна из форм закона распределения случайной величины. Однако закон распределения может быть записан через плотность распределения только для непрерывных случайных величин.
Функция распределения дискретной случайной величины.
Способ представления дискретной случайной величины в виде ряда распределения не является единственным, а главное он не является универсальным, поскольку непрерывную случайную величину нельзя задать с помощью ряда распределения. Существует еще один способ представления случайной величины — функция распределения.
Функцией распределения
случайной величины $X$ называется функция $F\left(x\right)$, которая определяет вероятность того, что случайная величина $X$ примет значение, меньшее некоторого фиксированного значения $x$, то есть $F\left(x\right)=P\left(X
Свойства функции распределения
:
- $0\le F\left(x\right)\le 1$.
- Вероятность того, что случайная величина $X$ примет значения из интервала $\left(\alpha ;\ \beta \right)$, равна разности значений функции распределения на концах этого интервала: $P\left(\alpha
- $F\left(x\right)$ — неубывающая.
- ${\mathop{lim}_{x\to -\infty } F\left(x\right)=0\ },\ {\mathop{lim}_{x\to +\infty } F\left(x\right)=1\ }$.
Пример 9
. Найдем функцию распределения $F\left(x\right)$ для закона распределения дискретной случайной величины $X$ из примера $2$.
$\begin{array}{|c|c|}
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline
1/6 & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 \\
\hline
\end{array}$
Если $x\le 1$, то, очевидно, $F\left(x\right)=0$ (в том числе и при $x=1$ $F\left(1\right)=P\left(X
Если $1
Если $2
Если $3
Если $4
Если $5
Если $x > 6$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)+P\left(X=5\right)+P\left(X=6\right)=1/6+1/6+1/6+1/6+1/6+1/6=1$.
Итак, $F(x)=\left\{\begin{matrix}
0,\ при\ x\le 1,\\
1/6,при\ 1
1/3,\ при\ 2
1/2,при\ 3
2/3,\ при\ 4
5/6,\ при\ 4
1,\ при\ x > 6.
\end{matrix}\right.$
Дисперсия дискретной случайной величины
Дисперсией дискретной случайной величины X называется
математическое ожидание квадрата отклонения её от математического ожидания:
Средним квадратическим отклонением
случайной величины X называется арифметическое значение квадратного корня
её дисперсии:
.
Пример 5. Вычислить дисперсии и средние
квадратические отклонения случайных величин X и Y, законы
распределения которых приведены в таблицах выше.
Решение. Математические ожидания случайных величин X и Y,
как было найдено выше, равны нулю. Согласно формуле дисперсии при Е(х)=Е(y)=0
получаем:
Тогда средние квадратические отклонения случайных величин X и Y
составляют
,
.
Таким образом, при одинаковых математических ожиданиях дисперсия
случайной величины X очень мала, а случайной величины Y —
значительная. Это следствие различия в их распределении.
Пример 6. У инвестора есть 4 альтернативных проекта инвестиций. В таблице
обобщены данные об ожидаемой прибыли в этих проектах с соответствующей вероятностью.
| Проект 1 | Проект 2 | Проект 3 | Проект 4 |
| 500, P=1 | 1000, P=0,5 | 500, P=0,5 | 500, P=0,5 |
| 0, P=0,5 | 1000, P=0,25 | 10500, P=0,25 | |
| 0, P=0,25 | 9500, P=0,25 |
Найти для каждой альтернативы математическое ожидание, дисперсию и среднее квадратическое
отклонение.
Решение. Покажем, как вычисляются эти величины для 3-й альтернативы:
.
.
В таблице обобщены найденные величины для всех альтернатив.
| Проект 1 | Проект 2 | Проект 3 | Проект 4 | |
| 500 | 500 | 500 | 500 | |
| 2500 | 1250 | 500000 | ||
| 500 | 354 | 7071 |
У всех альтернатив одинаковы математические ожидания. Это означает, что в долгосрочном
периоде у всех — одинаковые доходы. Стандартное отклонение можно интерпретировать как единицу измерения
риска — чем оно больше, тем больше риск инвестиций. Инвестор, который не желает большого риска, выберет
проект 1, так как у него наименьшее стандартное отклонение (0). Если же инвестор отдаёт предпочтение
риску и большим доходам в короткий период, то он выберет проект наибольшим стандартным отклонением —
проект 4.
Математическое ожидание дискретной случайной величины
Подойдём к понятию математического ожидания. Пусть масса некоторого вещества распределена между точками оси абсцисс x 1 , x 2 , . x n . При этом каждая материальная точка имеет соответствующую ей массу с вероятностью из p 1 , p 2 , . p n . Требуется выбрать одну точку на оси абсцисс, характеризующую положение всей системы материальных точек, с учётом их масс. Естественно в качестве такой точки взять центр массы системы материальных точек. Это есть среднее взвешенное значение случайной величины X, в которое абсцисса каждой точки x i входит с «весом», равным соответствующей вероятности. Полученное таким образом среднее значение случайной величины X называется её математическим ожиданием.
Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных её значений на вероятности этих значений:
Пример 1. Организована беспроигрышная лотерея. Имеется 1000 выигрышей, из них 400 по 10 руб. 300 — по 20 руб. 200 — по 100 руб. и 100 — по 200 руб. Каков средний размер выигрыша для купившего один билет?
Решение. Средний выигрыш мы найдём, если общую сумму выигрышей, которая равна 10*400 + 20*300 + 100*200 + 200*100 = 50000 руб, разделим на 1000 (общая сумма выигрышей). Тогда получим 50000/1000 = 50 руб. Но выражение для подсчёта среднего выигрыша можно представить и в следующем виде:
С другой стороны, в данных условиях размер выигрыша является случайной величиной, которая может принимать значения 10, 20, 100 и 200 руб. с вероятностями, равными соответственно 0,4; 0,3; 0,2; 0,1. Следовательно, ожидаемый средний выигрыш равен сумме произведений размеров выигрышей на вероятности их получения.
Пример 2. Издатель решил издать новую книгу. Продавать книгу он собирается за 280 руб., из которых 200 получит он сам, 50 — книжный магазин и 30 — автор. В таблице дана информация о затратах на издание книги и вероятности продажи определённого числа экземпляров книги.
| Число проданных экземпляров | Вероятность | Затраты |
| 500 | 0,20 | 225000 |
| 1000 | 0,40 | 250000 |
| 2000 | 0,25 | 300000 |
| 3000 | 0,10 | 350000 |
| 4000 | 0,05 | 400000 |
Найти ожидаемую прибыль издателя.
Решение. Случайная величина «прибыль» равна разности доходов от продажи и стоимости затрат. Например, если будет продано 500 экземпляров книги, то доходы от продажи равны 200*500=100000, а затраты на издание 225000 руб. Таким образом, издателю грозит убыток размером в 125000 руб. В следующей таблице обобщены ожидаемые значения случайной величины — прибыли:
| Число | Прибыль x i | Вероятность p i | x i p i |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Всего: | 1,00 | 25000 |
Таким образом, получаем математическое ожидание прибыли издателя:
Пример 3. Вероятность попадания при одном выстреле p = 0,2 . Определить расход снарядов, обеспечивающих математическое ожидание числа попаданий, равное 5.
Решение. Из всё той же формулы математического ожидания, которую мы использовали до сих пор, выражаем x — расход снарядов:
Дискретные случайные величины
Биномиальное распределение ДСВ
Пусть дискретная случайная величина $X$ — количество «успехов» в последовательности из $n$ независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна $p$ («неуспеха» — $q=1-p$).
Закон распределения $X$ имеет вид:
| $x_k$ | 1 | . | k | . | n |
| $p_k$ | $q^n$ | $n\cdot p \cdot q^ $ | $C_n^k \cdot p^k \cdot q^ $ | $p^n$ |
Здесь вероятности находятся по формуле Бернулли:
$$ P(X=k) = C_n^k \cdot p^k \cdot (1-p)^ = C_n^k \cdot p^k \cdot q^ , k=0,1,2. n. $$
Числовые характеристики биномиального распределения:
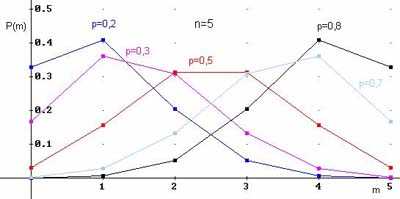
Примеры многоугольников распределения для $n=5$ и различных вероятностей:
Пуассоновское распределение ДСВ
Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
При условии $p\to 0$, $n \to \infty$, $np \to \lambda = const$ закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность $p$ события $A$ в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.
Ряд распределения по закону Пуассона имеет вид:
| $x_k$ | 1 | . | k | . | |
| $p_k$ | $e^ $ | $\lambda e^ $ | . | $\frac \cdot e^ $ | . |
Вероятности вычисляются по формуле Пуассона:
Числовые характеристики для распределения Пуассона:
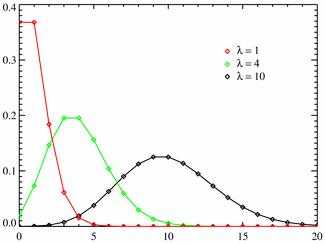
Разные многоугольники распределения при $\lambda = 1; 4; 10$.
Геометрическое распределение ДСВ
Пусть происходит серия независимых испытаний, в каждом из которых событие может появится с одной и той же вероятностью $p$. Тогда случайная величина $X$ — количество испытаний до первого появления события, имеет геометрическое распределение вероятностей.
Ряд распределения геометрического закона:
| $x_k$ | 1 | 2 | . | k | . | |
| $p_k$ | $p$ | $q\cdot p$ | $q^2 \cdot p$ | . | $q^k \cdot p$ | . |
Гипергеометрическое распределение ДСВ
Из урны, в которой находятся $N$ шаров ($K$ белых и $N-K$ чёрных шаров), наудачу и без возвращения вынимают $n$ шаров ($n \le N$). Найти закон распределения случайной величины $X$ — равной числу белых шаров среди выбранных.
Случайная величина $X$ может принимать целые значения от $0$ до $K$ (если $n \lt K$, то до $n$). Вероятности вычисляются по формуле: $$ P(X=k)=\frac ^ > , \quad 0\le k \le K. $$
$$M(X)=\frac \cdot n, \quad D(X)=\frac \cdot n \cdot \frac \cdot \frac .$$
2.2 Функция распределения
После разговора о распределении вероятностей пришло время поговорить о функции распределения. Эта функция распределения является упрощенной версией! Должно называться полное имяФункция распределения понятий。
Посмотрите на закон распределения на рисунке ниже. Закон распределения здесь явно является «функцией вероятности», о которой мы только что говорили, и это всего лишь одно. Но я знаю, что многие учебники называются законами о распределении.
Функция распределения вероятностей — это накопление функций вероятности
Давайте посмотрим на формулу на графике, где F (x) представляет собой функцию распределения вероятностей. Справа от этого символа находится длинная формула, которая напоминает функцию вероятности, но знак равенства становится формулой, которая меньше или равна знаку. Если вы посмотрите вправо, это скопление функций вероятности одна за другой!
Вы открыли секрет функции распределения вероятностей? Это совсем не новость, это совокупный результат значения функции вероятности! Поэтому ее еще называют кумулятивной функцией вероятности!
Функция вероятности и функция распределения вероятности похожи на две стороны медали, они просто разные средства описания вероятности!
3 Функция вероятности и функция распределения непрерывных случайных величин
«Функция вероятности» непрерывных случайных величин имеет другое название.Это называется «Функция плотности вероятности».
Почему это так называется? Воспользуемся словами мастера, чтобы сказать вам, что в книге Чэнь Сиру «Теория вероятностей и математическая статистика»
Если вы все еще не понимаете этот анализ, взгляните на следующую формулу:
Функция плотности вероятности, выраженная математической формулой, является функцией определенного интеграла. Определенный интеграл используется для определения площади в математике, и здесь вы можете выразить вероятность как площадь!
Слева представлен график, построенный функцией распределения непрерывной случайной величины F (x), а справа — график, построенный функцией плотности вероятности непрерывной случайной величины f (x). Между ними существует следующее соотношение:Функция плотности вероятности — это производная функция функции распределения。
Сравнивая два изображения, вы обнаружите, что если вы используете область на правом рисунке для представления вероятности, вы можете использовать график, чтобы четко увидеть, какие значения имеют большую вероятность!Следовательно, когда мы выражаем вероятность непрерывной случайной величины, очень хорошо использовать функцию плотности вероятности f (x) для ее выражения!
Однако у читателей могут возникнуть такие вопросы:
В: Каково значение значения функции плотности вероятности в определенной точке?
A: Значение легче понять в определенный моментФункция плотности вероятности А именноСкорость изменения вероятности в этой точке(Или производная). В этом месте значение плотности вероятности легко принять за значение вероятности.
Например: соотношение между расстоянием (вероятностью) и скоростью (плотностью вероятности).
- Скорость определенной точки нельзя рассматривать как расстояние до определенной точки.
- Это не имеет смысла, потому что расстояние — это понятие от ХХ до ХХ.
- Следовательно, вероятность также должна иметь интервал.
- Этот интервал может быть окрестностью x (он может бесконечно приближаться к 0). Интегрируя f (x) в окрестности x, вы можете найти площадь этой окрестности, которая представляет вероятность возникновения этого события, представленного этой окрестностью.
Примеры решения задач по теме «Закон распределения дискретной случайной величины»
Задача 1.
Выпущено 1000 лотерейных билетов: на 5 из них выпадает выигрыш в сумме 500 рублей, на
10 – выигрыш в 100 рублей, на 20 – выигрыш в 50 рублей, на 50 – выигрыш в 10 рублей. Определить
закон распределения вероятностей случайной величины X – выигрыша на один билет.
Решение.
По условию задачи возможны следующие значения случайной
величины X: 0, 10, 50, 100 и 500.
Число билетов без выигрыша равно 1000 – (5+10+20+50) = 915, тогда P(X=0) = 915/1000 = 0,915.
Аналогично находим все другие вероятности: P(X=0) = 50/1000=0,05, P(X=50) = 20/1000=0,02, P(X=100) = 10/1000=0,01,
P(X=500) = 5/1000=0,005. Полученный закон представим в виде таблицы:
Найдем математическое ожидание величины Х:
М(Х) = 1*1/6 + 2*1/6 + 3*1/6 + 4*1/6 + 5*1/6 + 6*1/6 = (1+2+3+4+5+6)/6 = 21/6 = 3,5
Задача 3.
Устройство состоит из трех независимо работающих элементов.
Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа
отказавших элементов в одном опыте, построить многоугольник распределения. Найти функцию распределения
F(x) и построить ее график. Найти математическое ожидание, дисперсию и среднее квадратическое
отклонение дискретной случайной величины.
Решение.
1.
Дискретная случайная величина X={число отказавших элементов в
одном опыте} имеет следующие возможные значения: х 1 =0 (ни один из элементов устройства не
отказал), х 2 =1 (отказал один элемент), х 3 =2 (отказало два элемента) и х 4 =3 (отказали три
элемента).
Отказы элементов независимы друг от друга, вероятности отказа каждого элемента равны между собой,
поэтому применима формула
Бернулли
. Учитывая, что, по условию, n=3, р=0,1, q=1-р=0,9, определим
вероятности значений:
P 3 (0) = С 3 0 p 0 q 3-0 = q 3 = 0,9 3 = 0,729;
P 3 (1) = С 3 1 p 1 q 3-1 = 3*0,1*0,9 2 = 0,243;
P 3 (2) = С 3 2 p 2 q 3-2 = 3*0,1 2 *0,9 = 0,027;
P 3 (3) = С 3 3 p 3 q 3-3 = р 3 =0,1 3 = 0,001;
Проверка: ∑p i = 0,729+0,243+0,027+0,001=1.
Таким образом, искомый биномиальный закон распределения Х имеет вид:
По оси абсцисс откладываем возможные значения х i , а по оси ординат –
соответствующие им вероятности р i . Построим точки М 1 (0; 0,729), М 2 (1; 0,243),
М 3 (2; 0,027), М 4 (3; 0,001). Соединив эти точки отрезками прямых, получаем искомый многоугольник распределения.
3.
Найдем функцию распределения F(x) = Р(Х
График функции F(x)
4.
Для биномиального распределения Х:
— математическое ожидание М(X) = np = 3*0,1 = 0,3;
— дисперсия D(X) = npq = 3*0,1*0,9 = 0,27;
— среднее квадратическое отклонение σ(X) = √D(X) = √0,27 ≈ 0,52.
Случайной величиной
называют переменную величину, которая в результате каждого испытания принимает одно заранее неизвестное значение, зависящее от случайных причин. Случайные величины обозначают заглавными латинскими буквами: $X,\ Y,\ Z,\ \dots $ По своему типу случайные величины могут быть дискретными
и непрерывными
.
Дискретная случайная величина
— это такая случайная величина, значения которой могут быть не более чем счетными, то есть либо конечными, либо счетными. Под счетностью имеется ввиду, что значения случайной величины можно занумеровать.
Пример 1
. Приведем примеры дискретных случайных величин:
а) число попаданий в мишень при $n$ выстрелах, здесь возможные значения $0,\ 1,\ \dots ,\ n$.
б) число выпавших гербов при подкидывании монеты, здесь возможные значения $0,\ 1,\ \dots ,\ n$.
в) число прибывших кораблей на борт (счетное множество значений).
г) число вызовов, поступающих на АТС (счетное множество значений).
Математическое ожидание дискретной случайной величины
Подойдём к понятию математического ожидания. Пусть масса некоторого вещества
распределена между точками оси абсцисс .
При этом каждая материальная точка имеет соответствующую ей массу с вероятностью из .
Требуется выбрать одну точку на оси абсцисс, характеризующую положение всей системы материальных точек,
с учётом их масс. Естественно в качестве такой точки взять центр массы системы материальных точек. Это
есть среднее взвешенное значение случайной величины X, в которое абсцисса каждой точки
входит с «весом», равным соответствующей
вероятности. Полученное таким образом среднее значение случайной величины X называется её
математическим ожиданием.
Математическим ожиданием дискретной случайной величины называется сумма произведений
всех возможных её значений на вероятности этих значений:
Пример 1. Организована беспроигрышная лотерея.
Имеется 1000 выигрышей, из них 400 по 10 руб. 300 — по 20 руб. 200 — по 100 руб. и 100 —
по 200 руб. Каков средний размер выигрыша для купившего один билет?
Решение. Средний выигрыш мы найдём, если общую сумму выигрышей,
которая равна 10*400 + 20*300 + 100*200 + 200*100 = 50000 руб, разделим на 1000 (общая
сумма выигрышей). Тогда получим 50000/1000 = 50 руб. Но выражение для подсчёта
среднего выигрыша можно представить и в следующем виде:
С другой стороны, в данных условиях размер выигрыша является
случайной величиной, которая может принимать значения 10, 20, 100 и 200 руб. с
вероятностями, равными соответственно 0,4; 0,3; 0,2; 0,1. Следовательно, ожидаемый
средний выигрыш равен сумме произведений размеров выигрышей на вероятности их получения.
Пример 2. Издатель решил издать новую книгу. Продавать книгу
он собирается за 280 руб., из которых 200 получит он сам, 50 — книжный магазин и 30 — автор. В таблице
дана информация о затратах на издание книги и вероятности продажи определённого числа экземпляров книги.
| Число проданных экземпляров | Вероятность | Затраты |
| 500 | 0,20 | 225000 |
| 1000 | 0,40 | 250000 |
| 2000 | 0,25 | 300000 |
| 3000 | 0,10 | 350000 |
| 4000 | 0,05 | 400000 |
Найти ожидаемую прибыль издателя.
Решение. Случайная величина «прибыль» равна разности доходов от продажи и стоимости затрат.
Например, если будет продано 500 экземпляров книги, то доходы от продажи равны 200*500=100000, а
затраты на издание 225000 руб. Таким образом, издателю грозит убыток размером в 125000 руб. В следующей
таблице обобщены ожидаемые значения случайной величины — прибыли:
| Число | Прибыль | Вероятность | |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Всего: | 1,00 | 25000 |
Таким образом, получаем математическое ожидание прибыли издателя:
.
Пример 3. Вероятность попадания при одном выстреле .
Определить расход снарядов, обеспечивающих математическое ожидание числа попаданий, равное 5.
Решение. Из всё той же формулы математического ожидания, которую мы использовали до
сих пор, выражаем — расход снарядов:
.