Итоговый тест «электромагнитное излучение»

Санитарные нормативы электромагнитных полей

СанПиН 1.2.3685-21 «Гигиенические нормативы и требования к обеспечению безопасности и (или) безвредности для человека факторов среды обитания» устанавливает допустимые величины электромагнитных полей. В таблице 5.74 приведены предельно допустимые уровни электромагнитных полей, в том числе, в жилых помещениях.

Таблица 5.74

Наименование фактора	Наименование параметра	Нормируемые уровни
Рабочие места	Жилые, общественные помещения
Постоянное магнитное поле (ПМП)	Напряженность магнитного поля (H), кА/м	8,0	—
Магнитная индукция (B), мТл	10,0	—
Гипогеомагнитное поле	Коэффициент ослабления геомагнитного поля, Ко, условные единицы	2,0	—
Электростатическое поле (ЭСП)	Напряженность ЭСП (E), кВ/м	20,0	15,0
Электромагнитное поле (ЭМП) промышленной частоты	Напряженность электрического поля (E), кВ/м	5,0	0,5
Напряженность магнитного поля (H), А/м	80,0	8,0
Магнитная индукция (B), мкТл	100,0	10,0
ЭМП диапазона частот от 0,01 до 0,03 МГц	Напряженность электрического поля (E), В/м	500,0	—
Напряженность магнитного поля (H), А/м	50,0	—
ЭМП диапазона частот от 0,03 до 3 МГц	Напряженность электрического поля (E), В/м	42,0	25,0
(максимально допустимая)	(500,0)	—
Напряженность магнитного поля (H), А/м	4,0
(максимально допустимая)	(50,0)	—
ЭМП диапазона частот от 3 до 30 МГц	Напряженность электрического поля (E), В/м	25,0	15,0
(максимально допустимая)	(300)	—
ЭМП диапазона частот от 30 до 50 МГц	Напряженность электрического поля (E), В/м	8	10
(максимально допустимая)	(80,0)	—
Напряженность магнитного поля (H), А/м	0,25	—
(максимально допустимая)	(3,0)
ЭМП диапазона частот от 50 до 300 МГц	Напряженность электрического поля (E), В/м	8,5	3,0
(максимально допустимая)	(80,0)	—
ЭМП диапазона частот от 300 МГц до 300 ГГц	Плотность потока энергии (ППЭ), мкВт/см2	18,0	10,0
(максимально допустимый уровень)	(1000,0)	—

Нормативы также установлены Решением Комиссии Таможенного союза от 28.05.2010 № 299 «О применении санитарных мер в Евразийском экономическом союзе». На территории населенных мест предельно допустимая напряженность переменного электрического поля с частотой 50 Гц на высоте 2 м составляет 1000 В/м, а в жилых помещениях предельно допустимая напряженность переменного электрического поля с частотой 50 Гц на высоте от 0,5 до 2 м от пола составляет 500 В/м.

В жилых помещениях допустимая напряженность магнитного поля частотой 50 Гц (действующие значения) не должна превышать 5 мкТл. Напряженность электрического поля не должна превышать 25 В/м в диапазоне частот 30 — 300 кГц. Такие же нормативы установлены в СанПиН 2.1.8./2.2.4.1383-03.

Выражение энергии через характеристики магнитного поля

Формулами (11.13) и (11.14) энергия выражена через характеристики контуров с токами.

Можно показать, что в данном случае энергия распределена в магнитном поле, окружающем проводники с токами.

Для примера возьмем поле катушки с кольцевым сердечником. Если диаметр сечения сердечника много меньше диаметра самого сердечника, поле можно считать равномерным: Тогда где — объем сердечника. Энергия магнитного поля в единице объема Здесь энергия выражена через характеристики магнитного поля, что свидетельствует о ее принадлежности магнитному полю.

Задача 11.8.

Определить энергию магнитного поля в системе двух обмоток (задача 8.21) при согласном и встречном их включении, если ток в первой обмотке I1 = 5 А, а во второй I2 = З А. Решение. Для определения энергии в магнитно-связанной системе двух обмоток воспользуемся формулой (11.14). Величины индуктивностей катушек и взаимной индуктивности при неферромагнитном сердечнике не зависят от тока в них, поэтому возьмем их по результатам решения задачи 8.21:

При согласном включении обмоток При встречном включении Задача 11.9.

Общая индуктивность двух последовательно соединенных катушек (см. рис. 8.22) при согласном включении равна 1,52 мГн, при встречном — 0,88 мГн. Определить взаимную индуктивность катушек. Решение. Найдем взаимоиндуктивность катушек, решив совместно уравнения (11.15) и (11.16): Вычтем второе уравнение из первого:

. В данном случае

От чего зависит величина

Существует ряд некоторых ограничений в применении формулы для расчета энергии магнитного поля. При записи выражения выполнялось несколько условий:

• индуктивность контура, а также магнитная проницаемость вещества стабильны;
• вся энергия источника тока трансформируется в энергию магнитного поля.

Перечисленные условия справедливы лишь в случае вакуума, то есть при (mu)=1

Если контур с током поместить в вещество, то необходимо принимать во внимание следующие параметры:

• намагничивание вещества, что способствует его нагреву;
• объем и плотность вещества в магнитном поле могут изменяться даже при стабильной температуре.

Таким образом, магнитная проницаемость вещества (mu), изменяющаяся при перепадах температуры и плотности среды, не может оставаться постоянной в процессе намагничивания. Также работа источника ЭДС не полностью трансформируется в энергию магнитного поля. В том случае, когда объем вещества изменяется в малой степени, сохраняется стабильной температура среды, внешняя работа затрачивается на увеличение энергии магнитного поля и на теплоотдачу Q, чтобы поддерживать постоянную температуру.

Работа внешних сил, в нашем случае источника тока, совершаемая над телом при квазистатическом изотермическом процессе, соответствует увеличению свободной энергии тела. Таким образом, формула определяет часть свободной энергии намагниченного вещества, которая обладает связью с магнитным полем:

Выражение применимо при рассмотрении ситуаций в условиях вакуума для парамагнетиков и диамагнетиков. Но при опытах с ферромагнетиками магнитная индукция и напряженность магнитного поля связаны нелинейно, даже при T=const.

Энергия электромагнитных волн

Предположим, что в поле электромагнитной волны расположена площадка $S$ (рис.1).

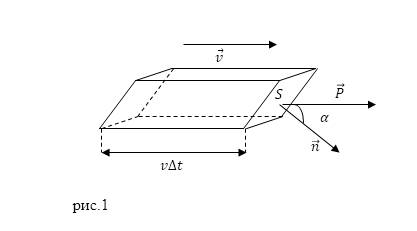Рисунок 1. Площадка, расположенная в поле электромагнитной волны. Автор24 — интернет-биржа студенческих работ

Статья: Интенсивность электромагнитой волны

Найди решение своей задачи среди 1 000 000 ответов

Определим, какая энергия ($W$) переносится электромагнитной волной сквозь эту площадку за малое время ∆t. Построим на основании площадки $S$ параллелепипед, с ребрами параллельными скорости перемещения волны $\vec{v}$. Пусть длины ребер параллелепипеда будут равны $v\Delta{}t$. Объем выделенного параллелепипеда будет:

$\Delta{}V=Sv\Delta{}t\cos{\alpha{}\ \left(1\right),}$

где α – угол между нормалью к площадке $S$ и направлением вектора скорости движения волны. Поскольку за время $\Delta{}t$ волна пробегает расстояние $v\Delta{}t$, то через выделенную нами площадь пройдет искомая нами энергия $W$, которая заключена внутри параллелепипеда.

$W=w\Delta{}V=wSv\Delta{}t\cos{\alpha{}\ \left(2\right),}$

где $w $ – объемная плотность энергии.

Электромагнитная волна имеет две составляющие, которые обладают энергией – это переменное электрическое и магнитное поля, поэтому объемную плотность нашей волны мы запишем как:

$w=\frac{\epsilon{}{\epsilon{}}_0}{2}E^2+\frac{\mu{}{\mu{}}_0}{2}H^2\left(3\right).$

Мы знаем, что напряженности полей в электромагнитной волне связывает уравнение:

$\sqrt{\epsilon{}{\epsilon{}}_0}E=\sqrt{\mu{}{\mu{}}_0}H\left(4\right),$

откуда следует, что мы можем написать:

$w=\epsilon{}{\epsilon{}}_0E^2=\mu{}{\mu{}}_0H^2=\sqrt{\epsilon{}\mu{}}\sqrt{{\epsilon{}}_0{\mu{}}_0}EH\left(5\right).$

Принимая во внимание, что скорость распространения электромагнитной волны в веществе можно представить как:

$v=\frac{1}{\sqrt{\epsilon{}\mu{}{\epsilon{}}_0{\mu{}}_0}}\left(6\right),$

учитывая формулу (5) из выражения (2) следует, что искомая энергия равна:

$W=\sqrt{\epsilon{}\mu{}}\sqrt{{\epsilon{}}_0{\mu{}}_0}EHS\frac{1}{\sqrt{\epsilon{}\mu{}{\epsilon{}}_0{\mu{}}_0}}\Delta{}t\cos{\alpha{}=EHS\Delta{}t\cos{\alpha{}}\left(7\right).}$

О системе уравнений электродинамики

Представления о природе электромагнитных волн (ЭМВ) заложены в систему уравнений, составляющую основу современной электродинамики. Эта теория разрабатывалась Дж. Максвеллом почти два десятилетия (с 1855 по 1873 годы), и в дальнейшем неоднократно правилась и преобразовывалась другими исследователями — Г. Герцем, О. Хевисайдом, А. Эйнштейном, Г. Лоренцем и другими. Существенным правкам подверглись не только уравнения, но и некоторые идеи Максвелла. Приведу лишь один вывод из сборника статей, посвященного 150-летию со дня рождения Максвелла:

Вывод о существовании ЭМВ и электромагнитной природе света является основным следствием из теории Максвелла. Сегодня трудно говорить о деталях его творческого метода. Поэтому многие высказывания о ходе мыслей Максвелла сегодня являются не более чем предположениями. Позволю себе тоже сделать одно предположение. Мне кажется, что мысль о существовании электромагнитных волн не стала следствием, а предшествовала разработке системы уравнений электродинамики, и даже больше — была одной из целей этой работы. Ещё в декабре 1861 года в письме к У. Томсону (Кельвину) Максвелл высказал предположение, что «…магнитная и светоносная среды идентичны». Есть документальные свидетельства, подтверждающие, что о существовании ЭМВ догадывался ещё Фарадей.

К середине XIX века все основные законы электродинамики были уже известны: закон Био-Савара и Ампера были открыты в 1820 году, в 1831 году Фарадей получил основной закон электромагнитной индукции, а в 1839 году Карл Гаусс сформулировал основную теорему электростатики — теорему Гаусса-Остроградского. Максвелл обобщил эти зависимости, сведя их в единую систему уравнений. Эта система состоит из семи уравнений, но основу системы составляют два уравнения:

которые описывают взаимные превращения электрического поля в магнитное (I) и наоборот (II).

На разработку этой системы Максвеллу — талантливому физику-теоретику, автору блестящих работ по молекулярной физике, механике, оптике — потребовалось почти двадцать лет! Объяснить это можно лишь тем, что при разработке системы уравнений электродинамики он столкнулся с огромными трудностями, не связанными с математикой. Основная трудность заключалась в том, что Максвелл опередил свое время: он остро ощущал дефицит знаний, необходимых для понимания физики (природы) электромагнитных взаимодействий.

Процесс генерации и распространения электромагнитных волн требовал симметрии взаимопревращений электрической и магнитной компонент волны. Так появилась максвелловская формула закона электромагнитной индукции, которая получила свое отражение во II уравнении системы (1).

Плотность импульса электромагнитной волны

При поглощении в веществе какого-нибудь тела электромагнитная волна оказывает на это тело давление, то есть сообщает ему импульс. Если обозначить плотность импульса как $\overrightarrow{G}$, то его можно определить, используя вектор Умова — Пойнтинга ($\overrightarrow{P}$):

Статья: Плотность энергии и импульса электромагнитных волн

Найди решение своей задачи среди 1 000 000 ответов

Пусть плоская волна падает перпендикулярно на плоскую поверхность тела. Положим, что $\varepsilon =1,\ \mu =1$ плохо проводящего тела. Электрическое поле волны будет возбуждать в теле ток, плотность которого ($\overrightarrow{j}$):

$\sigma $ — удельная проводимость вещества. Магнитное поле волны действует на данный ток с удельной силой (${\overrightarrow{F}}_u$) (силой на единицу объема):

Направление ${\overrightarrow{F}}_u$ совпадает с направлением распространения волны.

При этом поверхностному слою тела толщиной $\triangle l$, единичной площади волной сообщается импульс за $1 с$, ($\overrightarrow{j}\bot \overrightarrow{H}$) равный:

В том же слое за $1 с$ поглощается энергия:

которая выделяется потом, как тепло. Найдем отношение импульса (10) к энергии (11), имеем:

Воспользуемся выражением (3) при $\varepsilon =1,\ \mu =1,$ получим:

Подставим (13) в формулу (13):

Из выражения (14) следует, что электромагнитная волна, обладающая энергией $W$, имеет импульс ($G$):

Из формулы (15) получаем, что плотность импульса ($G_u$) — импульс единицы объема равен:

Воспользовавшись вектором Умова — Пойнтинга, можно выражение (16) представить как:

В формуле (17) учтено, что направление вектора импульса электромагнитной волны имеет такое же направление, что и вектор Умова — Пойнтинга.

Пример 1

Задание: Какое давление ($p$), производит плоская электромагнитная волна на тело? Она распространялась в вакууме, вдоль $оси X$, падает на тело перпендикулярно, поглощается полностью. Амплитуда напряженности магнитного поля равна $H_m$.

Решение:

В качестве основы для решения задачи примем вывод из теории Максвелла о том, что, если волна падает на тело перпендикулярно его поверхности и полностью поглощается, то:

\

где $\left\langle w\right\rangle $ — средняя объемная плотность энергии электромагнитной волны.

Уравнения колебаний модулей векторов напряженностей электрического и магнитного полей запишем в соответствии с гармоническими законами:

\ \

Плотность энергии электромагнитного поля ($w$) является суммой плотности электрического поля ($w_E$) и плотности магнитного поля ($w_H$):

\

где:

\

При этом для электромагнитной волны мы имеем соотношение между мгновенными значениями характеристик полей:

\

Следовательно, можем записать следующее:

\

Используем выражение (1.3), подставив вместо H выражение, которое находится в правой части, получим:

\

Найдем среднее от объемной плотности энергии электромагнитной волны, получим:

\

Примем во внимание, что:

\

Тогда формула (1.9) будет переписана как:

\

Ответ: $p=\frac{\mu {\mu }_0{H_m}^2}{2},\ где\ \mu =1\ .$

Пример 2

Задание: Чему равна средняя (по времени) плотность импульса электромагнитной волны ($\left\langle G_u\right\rangle $)? Если электромагнитная волна плоская, распространяется в вакууме по оси X, амплитуда ее магнитного поля равна $H_m.$

Решение:

За основу решения задачи примем формулу:

\\to G_u=\frac{1}{c^2}EH\to \left\langle G_u\right\rangle =\frac{1}{c^2}\left\langle EH\right\rangle \left(2.1\right).\]

Используя соотношение:

\

найдем амплитуду электрического поля:

\

Уравнения колебаний модулей векторов напряженностей электрического и магнитного полей запишем в соответствии с гармоническими законами:

\ \

Подставим выражения (2.3), (2.4) и (2.5) в формулу (2.1), получим:

\

Ответ: $\left\langle G_u\right\rangle =\frac{60 \pi}{c^2}{H_m}^2.$

Свойства электромагнитных волн

Современные радиотехнические устройства позволяют провести очень наглядные опыты по наблюдению свойств электромагнитных волн. При этом лучше всего пользоваться волнами сантиметрового диапазона. Эти волны излучаются специальным генератором сверхвысокой частоты (СВЧ). Электрические колебания генератора модулируют звуковой частотой. Принятый сигнал после детектирования подается на громкоговоритель.

Свойство 1 — Поглощение электромагнитных волн

Если расположить рупоры друг против друга и добиться хорошей слышимости звука в громкоговорители, а затем поместить между ними диэлектрик, звук будет менее громким.

Свойство 2 — Отражение электромагнитных волн

Если диэлектрик заменить металлической пластиной, то звук перестанет быть слышимым. Волны не достигают приемника вследствие отражения. Отражение происходит под углом, равным углу падения, как и в случае световых и механических волн. Чтобы убедиться в этом, рупоры располагают под одинаковыми углами к большому металлическому листу. Звук исчезнет, если убрать лист или повернуть его.

Свойство 3 — Преломление электромагнитных волн

Электромагнитные волны изменяют свое направление (преломляются) на границе диэлектрика. Это можно обнаружить с помощью большой треугольной призмы из парафина. Рупоры располагают под углом друг к другу, как и при демонстрации отражения. Металлический лист заменяют затем призмой. Убирая призму или поворачивая ее, наблюдают исчезновение звука.

Свойство 4 — Поперечность электромагнитных волн

Поместим между генератором и приемником решетку из параллельных металлических стержней. Решетку расположим так, чтобы стержни были горизонтальными или вертикальными. При одном из этих положений, когда электрический вектор параллелен стержням, в них возбуждаются токи, в результате чего решетка начинает отражать волны, подобно сплошной металлической пластине. Когда же вектор перпендикулярен стержням, токи в них не возбуждаются и электромагнитная волна проходит через решетку.

Приемники

Одна из четырех «Великих обсерваторий» NASA , получившая название в честь американского астрофизика индийского происхождения Субраманьяна Чандрасекара (1910–95), лауреата Нобелевской премии (1983), специалиста по теории строения и эволюции звезд.Основной инструмент обсерватории — рентгеновский телескоп косого падения диаметром 1,2 м , содержащий четыре вложенных параболических зеркала косого падения (см. схему), переходящих в гиперболические. Обсерватория выведена на орбиту в 1999 и работает в диапазоне мягкого рентгена (100 эВ -10 кэВ ). Среди множества открытий обсерватории «Чандра» — первый снимок аккреционного диска вокруг пульсара в Крабовидной туманности .

Формула зависимости плотности потока излучения от расстояния до источника

§ 50 ПЛОТНОСТЬ ПОТОКА ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ

Излучаемые электромагнитные волны несут с собой энергию.

Плотность потока излучения. Рассмотрим поверхность площадью S, через которую электромагнитные волны переносят энергию. На рисунке 7.5 изображена такая площадка.

Прямые линии указывают направления распространения электромагнитных волн. Это лучи —линии, перпендикулярные поверхностям, во всех точках которых колебания происходят в одинаковых фазах. Такие поверхности называются волновыми поверхностями (см. § 46). Плотностью потока электромагнитного излучения / называют отношение электромагнитной энергии

Фактически это мощность электромагнитного излучения (энергия в единицу времени), проходящего через единицу площади поверхности. Плотность потока излучения в СИ выражают в ваттах на квадратный метр (Вт/м 2 ). Иногда эту величину называют интенсивностью волны.

Выразим I через плотность электромагнитной энергии и скорость ее распространения с. Выберем поверхность площадью S, перпендикулярную лучам, и построим на ней как на основании цилиндр с образующей c

т. е. плотность потока излучения равна произведению плотности электромагнитной энергии на скорость ее распространения.

Найдем зависимость плотности потока излучения от расстояния до источника. Для этого надо ввести еще одно новое понятие.

Точечный источник излучения. Источники излучения электромагнитных волн могут быть весьма разнообразными. Простейшим является точечный источник.

Источник излучения считается точечным, если его размеры много меньше расстояния, на котором оценивается его действие. Кроме того, предполагается, что такой источник посылает электромагнитные волны по всем направлениям с одинаковой интенсивностью. Точечный источник — такая же идеализация реальных источников, как и другие модели принятые в физике: материальная точка, идеальный газ и т. д.

Звезды излучают свет, т. е. электромагнитные волны Так как расстояния до звезд в огромное число раз превы шают их размеры, то именно звезды представляют собой лучшее реальное воплощение точечных источников.

Зависимость плотности потока излучения от расстояния до точечного источника. Энергия, которую переносят электромагнитные волны, с течением времени распределяется по все большей и большей поверхности. Поэтому энергия, передаваемая через поверхность единичной площадки за единицу времени, т. е. плотность потока излучения, уменьшается по мере удаления от источника.

Поместим точечный источник в центр сферы радиусом R. Площадь поверхности сферы S = 4

Плотность потока излучения от точечного источника убывает обратно пропорционально квадрату расстояния до источника.

Зависимость плотности потока излучения от частоты. Излучение электромагнитных волн происходит при ускоренном движении заряженных частиц (см. § 48). Напряженность электрического поля

Плотность энергии электрического поля пропорциональна квадрату напряженности поля. Энергия магнитного поля, как это можно показать, пропорциональна квадрату магнитной индукции. Полная плотность энергии электромагнитного поля равна сумме плотностей энергий электрического и магнитного полей. С учетом формулы (7.2) плотность потока излучения

Плотность потока излучения пропорциональна четвертой степени частоты.

При увеличении частоты колебаний заряженных частиц в 2 раза излучаемая энергия возрастает в 16 раз! В антеннах радиостанций поэтому возбуждают колебания больших частот: от десятков тысяч до десятков миллионов герц.

Электромагнитные волны переносят энергию. Плотность потока излучения (интенсивность волны) равна произведению плотности энергии на скорость ее распространения. Интенсивность волны пропорциональна четвертой степени частоты и убывает обратно пропорционально квадрату расстояния от источника.

Мякишев Г. Я., Физика. 11 класс : учеб. для общеобразоват. учреждений : базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. — 17-е изд., перераб. и доп. — М. : Просвещение, 2008. — 399 с : ил.

_{Планирование по физике, учебники и книги онлайн, курсы и задачи по физике для 11 класса скачать}

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.

Установленные нормы ЭМИ для человека

Каждый орган в нашем теле вибрирует. Благодаря вибрации вокруг нас создается электромагнитное поле, содействующее гармоничной работе всего организма. Когда на наше биополе воздействуют другие магнитные поля, это вызывает в нем изменения. Иногда организм справляется с влиянием, иногда – нет. Это становится причиной ухудшения самочувствия.

Даже большое скопление людей создает электрический заряд в атмосфере. Полностью изолироваться от электромагнитного излучения невозможно. Есть допустимый уровень ЭМИ, который лучше не превышать.

Вот безопасные для здоровья нормы:

• 30-300 кГц, возникающие при напряженности поля 25 Вольт на метр (В/м),
• 0,3-3 МГц, при напряженности 15 В/м,
• 3-30 МГц – напряженность 10 В/м,
• 30-300 МГц – напряженность 3 В/м,
• 300 МГц-300 ГГц – напряженность 10 мкВт/см2.

При таких частотах работают гаджеты, радио- и телеаппаратура.

Приемники излучения

Базовым уровнем является условная поверхность Земли, на которой стоят дети и располагается ряд астрономических инструментов
, которые могут работать на Земле. Выше расположен уровень космических аппаратов, используемых для заатмосферных наблюдений. В некоторых диапазонах космические наблюдения — единственный способ получения информации о Вселенной.

Наземные астрономические инструменты
(слева направо):

• Во многих гамма-, рентгеновских и т. п. телескопах используются фотоэлектронные умножители (ФЭУ), объединенные в матрицы
• неба могут проводиться и без особых приборов или с простейшими (например, в бинокль)
• 24-метровый оптический телескоп «Магеллан» (строится; видимый, а тж. инфракрасный диапазон
  )
• Система радиотелескопов ALMA (64 телескопа, строится)

Космические инструменты
:

• Гамма-обсерватория INTEGRAL (INTErnational Gamma-Ray Astrophysics Laboratory; используется также в рентгене
  )
• (видимый диапазон, ультрафиолет, ИК
  )
• Космический гравитационный телескоп LISA (проект, )

Подземные инструменты:

(за пределами электромагнитного спектра
)