Задачи математической статистики презентация

Примеры[править]

Пример 1править

Рис. 1. Статистическое распределение выборки. Эмпирическая функция распределения для заданного распределения частотРис. 2. Решение задачи статистического распределения выборки в Mathcad

Выборка задана в виде распределения частот:

xi{\displaystyle x_{i}}	1{\displaystyle 1}	4{\displaystyle 4}	6{\displaystyle 6}	8{\displaystyle 8}
ni{\displaystyle n_{i}}	5{\displaystyle 5}	8{\displaystyle 8}	17{\displaystyle 17}	20{\displaystyle 20}

1. Найти распределение относительных частот;
2. Найти эмпирическую функцию распределения;
3. Найти моду и медиану

Решение:

1) Объем выборки равен n=50{\displaystyle n=50}. По определению относительная частота вычисляется по формуле wi=nin{\displaystyle w_{i}={\frac {n_{i}}{n}}}, следовательно, распределение относительных частот имеет вид

xi{\displaystyle x_{i}}	1{\displaystyle 1}	4{\displaystyle 4}	6{\displaystyle 6}	8{\displaystyle 8}
wi{\displaystyle w_{i}}	0.1{\displaystyle 0.1}	0.16{\displaystyle 0.16}	0.34{\displaystyle 0.34}	0.4{\displaystyle 0.4}

2) Эмпирическая функция распределения имеет вид
F(x)={,x≤1,0.1,1<x≤4,0.26,4<x≤6,0.6,6<x≤8,1,x>8.{\displaystyle F(x)={\begin{cases}0,&\quad x\leq 1,\\0.1,&\quad 1<x\leq 4,\\0.26,&\quad 4<x\leq 6,\\0.6,&\quad 6<x\leq 8,\\1,&\quad x>8.\end{cases}}}

3) Чаще всего встречается варианта x4=8{\displaystyle x_{4}=8}, поэтому она является модой распределения.
Для вычисления медианы распределения необходимо последовательно найти сумму накопленных частот ряда. Это продолжается до получения накопленной суммы частот, превышающей половину суммы частот ряда. В примере сумма частот ряда равна 50, ее половина — 25. Накопленная сумма частот, превышающих 25, равна 30. Варианта, соответствующая этой сумме, x3=6{\displaystyle x_{3}=6}, и есть медиана ряда.

xi{\displaystyle x_{i}}	1{\displaystyle 1}	4{\displaystyle 4}	6{\displaystyle 6}	8{\displaystyle 8}
ni{\displaystyle n_{i}}	5{\displaystyle 5}	8{\displaystyle 8}	17{\displaystyle 17}	20{\displaystyle 20}
Сумма накопленных частот	5	5 + 8 = 13	13 + 17 = 30	−{\displaystyle -}

Пример 2править

Рис. 3. Гистограмма относительных частот для выборки.

Дана выборка объема n=30{\displaystyle n=30}: 26; 20; 45; 50; 30; 32; 46; 45; 34; 24; 35; 42; 34; 29; 34; 36; 30; 43; 23; 38; 48; 39; 40; 42; 38; 37; 43; 28; 36; 44.

Сделать интервальную группировку этой выборки. Построить гистограмму относительных частот по данным выборки.

Решение:

Размах выборки R=50−20=30{\displaystyle R=50-20=30}. Количество частичных интервалов равно m≈1+3.322lg⁡n=5{\displaystyle m\approx =5}. Ширина интервала Δ=Rm=6{\displaystyle \Delta ={\frac {R}{m}}=6}. Таблица интервальной группировки имеет следующий вид:

Интервал	20;26){\displaystyle [20;26)}	26;32){\displaystyle [26;32)}	32;38){\displaystyle [32;38)}	38;44){\displaystyle [38;44)}
Середина интервала ui{\displaystyle u_{i}}	23{\displaystyle 23}	29{\displaystyle 29}	35{\displaystyle 35}	41{\displaystyle 41}	47{\displaystyle 47}
ni{\displaystyle n_{i}}	3{\displaystyle 3}	5{\displaystyle 5}	8{\displaystyle 8}	8{\displaystyle 8}	6{\displaystyle 6}
wi{\displaystyle w_{i}}	0.1{\displaystyle 0.1}	0.167{\displaystyle 0.167}	0.267{\displaystyle 0.267}	0.267{\displaystyle 0.267}	0.2{\displaystyle 0.2}
wiΔ{\displaystyle {\frac {w_{i}}{\Delta }}}	0.017{\displaystyle 0.017}	0.028{\displaystyle 0.028}	0.044{\displaystyle 0.044}	0.044{\displaystyle 0.044}	0.033{\displaystyle 0.033}

Для построения гистограммы необходимо вычислить wiΔ{\displaystyle {\frac {w_{i}}{\Delta }}} для каждого интервала. Гистограмма относительных частот изображена на рис. 3.

Слайд 4Статистическое распределение выборкиОпределение: Эмпирической функцией распределения (функцией распределения выборки) называется функция

F*(x), определяющая для каждого значения х относительную частоту появления события ХДля наглядности статистического распределения в случае дискретного распределения признака Х строят полигон (ломанная, где длина Х откладывается на оси абсцисс, а на оси ординат соответствующие им частоты ni). В случае непрерывного распределения признака Х строят гистограммы. Для построения гистограммы все наблюдаемые значения признака разбивают на несколько i частичных интервалов длиной h, и для каждого интервала сумму частот вариант попавших в i интервал отмечают по оси ординат. Гистограммой распределения частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению (плотность частот).

Лекция №1, ТВиМС, Лакман И.А.

Средняя скорость движения

При изучении задач на движение мы определяли скорость движения следующим образом: делили пройденное расстояние на время. Но тогда подразумевалось, что тело движется с постоянной скоростью, которая не менялась на протяжении всего пути.

В реальности, это происходит довольно редко или не происходит совсем. Тело, как правило, движется с различной скоростью.

Когда мы ездим на автомобиле или велосипеде, наша скорость часто меняется. Когда впереди нас помехи, нам приходиться сбавлять скорость. Когда же трасса свободна, мы ускоряемся. При этом за время нашего ускорения скорость изменяется несколько раз.

Речь идет о средней скорости движения. Чтобы её определить нужно сложить скорости движения, которые были в каждом часе/минуте/секунде и результат разделить на время движения.

Задача 1. Автомобиль первые 3 часа двигался со скоростью 66,2 км/ч, а следующие 2 часа — со скоростью 78,4 км/ч. С какой средней скоростью он ехал?

Сложим скорости, которые были у автомобиля в каждом часе и разделим на время движения (5ч)

Значит автомобиль ехал со средней скоростью 71,08 км/ч.

Определять среднюю скорость можно и по другому — сначала найти расстояния, пройденные с одной скоростью, затем сложить эти расстояния и результат разделить на время. На рисунке видно, что первые три часа скорость у автомобиля не менялась. Тогда можно найти расстояние, пройденное за три часа:

66,2 × 3 = 198,6 км.

Аналогично можно определить расстояние, которое было пройдено со скоростью 78,4 км/ч. В задаче сказано, что с такой скоростью автомобиль двигался 2 часа:

78,4 × 2 = 156,8 км.

Сложим эти расстояния и результат разделим на 5

Задача 2. Велосипедист за первый час проехал 12,6 км, а в следующие 2 часа он ехал со скоростью 13,5 км/ч. Определить среднюю скорость велосипедиста.

Скорость велосипедиста в первый час составляла 12,6 км/ч. Во второй и третий час он ехал со скоростью 13,5. Определим среднюю скорость движения велосипедиста:

Слайд 19Простая случайная выборкаЕдиницы выборки отбираются в случайном порядке, не зависящем

ни от последовательности расположения единиц, ни от значения признаков совокупности,

не учитывают ни принадлежность к какой –либо группе, ни к серии из единиц совокупности. Средняя ошибка повторной выборки:Где σ – среднее квадратическое отклонение изучаемого признака;n – объем выборочной совокупности.Средняя ошибка бесповторной выборки:Где σ – среднее квадратическое отклонение изучаемого признака;n – объем выборочной совокупности.N – объем генеральной совокупности.Предельная ошибка выборки определяется на основе уровня вероятности. При t=2 (p=0,954), t=3 (p=0,997), где t- статистика Стьюдента.Генеральная средняя находится в интервале:

Лекция №3, Анализ даных Лакман И.А.

Слайд 7Свойства оценокПусть имеются данные выборки, например значения некоторого признака, Х1,

Х2,…, Хn, полученные в результате n наблюдений. Для того чтобы

найти статистическую оценку θ неизвестного параметра теоретического распределения через эти данные необходимо найти функцию от наблюдаемых случайных величин, которые дают приближенное значение оцениваемого параметра. Статистическую оценку, которая определяется одним числом, называют точечной.Полученные оценки должны быть достоверными, т.е. обладать свойствами несмещенности, эффективности и состоятельности.Несмешанной называют статистическую оценку θ*, математическое ожидание которой равно оценивающему параметру θ при любом объеме выборки, т.е. М(θ*)= θ . Эффективной оценкой называют статистическую оценку θ*, которая при заданном объеме выборки n имеет наименьшую возможную дисперсию. Состоятельной называют статистическую оценку, которая при n→ ∞ и стремится по вероятности к оцениваемому параметру, т.е. .

Лекция №1, ТВиМС, Лакман И.А.

Слайд 18Методы выборочного наблюденияОпределение: Выборочным несплошным наблюдением является наблюдение, при котором

признаки регистрируются у отдельных единиц изучаемой совокупности, отобранных с помощью

специальных методов. Полученные в ходе выборочного наблюдения результаты распространяются на всю исходную совокупность с заданным уровнем доверия.Виды выборочного наблюдения:Простая случайная (собственно-случайная) выборкаСистематическая (механическая) выборка Стратификационная (типическая) выборкаГнездовая (серийная) выборкаДля каждой выборки определяют границы генеральных характеристики: средняя ошибка выборки, предельная ошибка выборки. Определяют генеральную долю и необходимый объем выборки.

Лекция №3, Анализ даных Лакман И.А.

Отбор единиц в выборочную совокупность

Повторный отбор

Бесповторный отбор

Слайд 10Описательные статистики вариацииГенеральное среднеквадратичное отклонение определяется соответственно по формулам:

, .Определение: Несмещенной оценкой среднего квадратического отклонения является стандартное отклонение, определяемое по формуле: (6)Определение: Модой называется это наиболее часто наблюдаемая величина случайной переменной, обозначается М0. Для дискретного ряда мода равна максимальной частоте, для интервального вариационного ряда определяется модальный интервал по наибольшей частоте, а мода определяется как:Здесь — частоты модального, предмодального и постмодального интервалов; а Х0 и i – нижняя граница и величина модельного интервала.

Лекция №1, ТВиМС, Лакман И.А.

7.1 Выборочное среднее

Для конкретной выборки объема n ее выборочное среднее  определяется соотношениемгде хi – значение элемента выборки.Обычно требуется описать статистические свойства произвольных случайных выборок одного объема, а не одной из них. Это значит, что рассматривается математическая модель, которая предполагает достаточно большое количество выборок объема n. В этом случае элементы выборки рассматриваются как независимые случайные величины Хi, принимающие значения хi с одной и тоже плотностью вероятностей f(x), являющейся плотностью вероятностей генеральной совокупности. Тогда выборочное среднее также является случайной величиной , равнойСреднее значение генеральной совокупности, из которой производится выборка, будем называть генеральным средним и обозначать mх. При значительном объеме выборки можно ожидать, что выборочное среднее не будет заметно отличаться от генерального среднего. Поскольку выборочное среднее является случайной величиной, то для нее можно найти математическое ожидание:Таким образом, математическое ожидание выборочного среднего равно генеральному среднему. В этом случае говорят, что выборочное среднее является несмещенной оценкой генерального среднего. В дальнейшем мы вернемся к этому термину. Так как выборочное среднее является случайной величиной, флуктуирующей вокруг генерального среднего, то желательно оценить эту флуктуацию с помощью дисперсии выборочного среднего. Рассмотрим выборку, объем которой n значительно меньше объема генеральной совокупности N (n << N). Предположим, что при формировании выборки характеристики генеральной совокупности не меняются, что эквивалентно предположению N = ¥. Тогда

Случайные величины Хi и Xj (i¹j) независимы, следовательно,Подставим полученный результат в формулу для дисперсии:, где – дисперсия генеральной совокупности. Тогда среднее квадратическое отклонение выборочного среднего  равно:.Из этой формулы следует, что с увеличением объема выборки флуктуации среднего выборочного около среднего генерального уменьшаются как . Проиллюстрируем сказанное примером. Пусть имеется случайный сигнал с математическим ожиданием и дисперсией, соответственно равными mx = 10,  = 9.Отсчеты сигнала берутся в равноотстоящие моменты времени t1, t2, … , tn.Так как отсчеты являются случайными величинами, то будем их обозначать X(t1), X(t2), … , X(tn).Определим количество отсчетов, чтобы среднее квадратическое отклонение оценки математического ожидания сигнала не превысило 1% его математического ожидания. Поскольку mx=10, то нужно, чтобы  С другой стороны  поэтому  или Отсюда получаем, что n ³ 900 отсчетов.

Мода и медиана

Модой называют элемент, который встречается в выборке чаще других.

Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров

Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.

Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат

Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.

Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.

Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:

Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:

Выпишем рост спортсменов отдельно:

180, 182, 183, 184, 185, 188, 190

В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.

Медианой упорядоченной выборки называют элемент, располагающийся посередине.

Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.

В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану

Но возможны случаи, когда количество элементов выборки чётно.

К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:

Построим этих шестерых спортсменов по росту:

Выпишем рост спортсменов отдельно:

180, 182, 184, 186, 188, 190

В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.

В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.

Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186

Найдем среднее арифметическое элементов 184 и 186

Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.

Поэтому более точное определение медианы зависит от количества элементов в выборке.

Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.

Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.

Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190

Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:

Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:

0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1

Определим среднее арифметическое для данной выборки — получим значение 2,2

По данному значению можно сказать, что в среднем у спортсменов 2,2 очка

Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:

0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 3, 4, 5, 5, 6

В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.

Графические возможности пакета STATISTICA

В пакете существуют 2 типа графиков:

1) Quick Stat Graphs — быстрые графики, позволяющие построить графики для фиксированной заранее переменной . Эти графики могут быть построены практически из любого места пакета.

2) Custom Stat Graphs — пользовательские графики, в которых переменные и диапазон случаев (Cases)zyia которых эти графики могут быть построены задается пользователем и может быть изменен в процессе выполнения  программы.

Щелчок по кнопке Graphs активизирует панель графики. Все возможности ее перечислены в пунктах меню.

Первый пункт Quick Stat Graphs позволяет строить графики только для той переменной, которая была выделена заранее. Следующая группа пунктов меню позволяет стоить пользовательские графики:

Stats 2D Graphs — двумерные графики

Stats 3D Sequenrial Graphs — трехмерные графики последовательностей

Stats 3D XYZ Graphs — трехмерные графики.

Частота

Частота это число, которое показывает сколько раз в выборке встречается тот или иной элемент.

Предположим, что в школе проходят соревнования по подтягиваниям. В соревнованиях участвует 36 школьников. Составим таблицу в которую будем заносить число подтягиваний, а также число участников, которые выполнили столько подтягиваний.

По таблице можно узнать сколько человек выполнило 5, 10 или 15 подтягиваний. Так, 5 подтягиваний выполнили четыре человека, 10 подтягиваний выполнили восемь человек, 15 подтягиваний выполнили три человека.

Количество человек, повторяющих одно и то же число подтягиваний в данном случае являются частотой. Поэтому вторую строку таблицы переименуем в название «частота»:

Такие таблицы называют таблицами частот.

Частота обладает следующим свойством: сумма частот равна общему числу данных в выборке.

Это означает, что сумма частот равна общему числу школьников, участвующих в соревнованиях, то есть тридцати шести. Проверим так ли это. Сложим частоты, приведенные в таблице:

4 + 5 + 10 + 8 + 6 + 3 = 36

Статистическое распределение выборки. Полигон. Гистограмма

Пусть из генеральной совокупности извлечена выборка, причем , наблюдалось раз, раз, раз и объем выборки. Наблюдаемые значения называются вариантами, а последовательность вариант, записанная в возрастающем порядке,— вариационным рядом. Числа наблюдений называют частотами, а их отношения к объему выборки — относительными частотами. Отметим, что сумма относительных частот равна единице:

Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (непрерывное распределение). В качестве частоты, соответствующей интервалу, принимают сумму частот вариант, попавших в этот интервал.

Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике — соответствие между наблюдаемыми вариантами и их частотами или относительными частотами.

Пример:

Перейдем от частот к относительным частотам в следующем распределении выборки объема n = 20:

Найдем относительные частоты:

Поэтому получаем следующее распределение:

Для графического изображения статистического распределения используются полигоны и гистограммы.

Для построения полигона в декартовых координатах на оси Ох откладывают значения вариант на оси Оу— значения частот (относительных частот ).

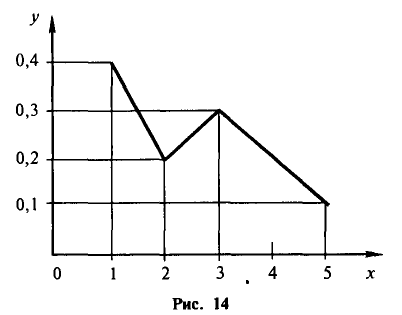
Пример:

Рис. 14 представляет собой полигон следующего распределения:

Полигоном обычно пользуются в случае небольшого количества вариант. В случае большого количества вариант и в случае непрерывного распределения признака чаще строят гистограммы. Для этого интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов шириной h и находят для каждого частичного интервала — сумму частот вариант, попавших в і-й интервал. Затем на этих интервалах как на основаниях строят прямоугольники с высотами (или , где n —объем выборки). Площадь i-го частичного прямоугольника равна

(или ). Следовательно, площадь гистограммы равна сумме всех частот (или относительных частот), т. е. объему выборки (или единице).

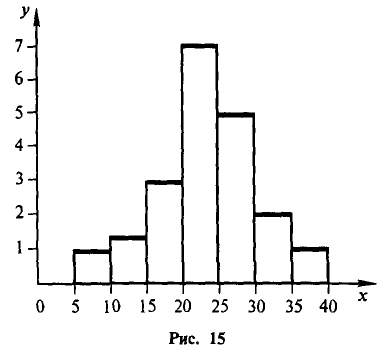
Пример:

Рис. 15 показывает гистограмму непрерывного распределения объема n =100, заданного следующей таблицей:

Слайд 19Простая случайная выборкаЕдиницы выборки отбираются в случайном порядке, не зависящем ни

от последовательности расположения единиц, ни от значения признаков совокупности, не учитывают ни принадлежность к какой –либо группе, ни к серии из единиц совокупности. Средняя ошибка повторной выборки:Где σ – среднее квадратическое отклонение изучаемого признака;n – объем выборочной совокупности.Средняя ошибка бесповторной выборки:Где σ – среднее квадратическое отклонение изучаемого признака;n – объем выборочной совокупности.N – объем генеральной совокупности.Предельная ошибка выборки определяется на основе уровня вероятности. При t=2 (p=0,954), t=3 (p=0,997), где t- статистика Стьюдента.Генеральная средняя находится в интервале:

Лекция №3, Анализ даных Лакман И.А.

Эмпирическая функция распределения[править]

Эмпирическая функция распределения — это функция, имеющая вид F∗(x)=nxn{\displaystyle F^{*}(x)={\frac {n_{x}}{n}}}, где nx{\displaystyle n_{x}} — число вариант, меньших x{\displaystyle x}.

Для группированной выборки или интервальных вариационных рядов строится гистограмма частот (относительных частот) — ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной Δ{\displaystyle \Delta }, а высоты равны niΔ{\displaystyle {\frac {n_{i}}{\Delta }}} (wiΔ{\displaystyle {\frac {w_{i}}{\Delta }}}). Верхнюю границу гистограммы относительных частот можно рассматривать как статистический аналог плотности распределения наблюдаемой случайной величины (суммарная площадь прямоугольников гистограммы равна единице).

Модой M{\displaystyle M_{0}} называется значение признака (варианта), чаще всего встречающееся в изучаемой совокупности. В дискретном ряду распределения модой будет варианта с наибольшей частотой.

Медианой Me{\displaystyle M_{e}} называется варианта, которая находится в середине вариационного ряда. Медиана делит ряд пополам, по обе стороны от нее находится одинаковое количество единиц совокупности.

Для дискретного вариационного ряда с нечетным числом членов медиана равна серединному варианту, а для ряда с четным числом членов — полусумме двух серединных вариантов.

Слайд 7Свойства оценокПусть имеются данные выборки, например значения некоторого признака, Х1, Х2,…,

Хn, полученные в результате n наблюдений. Для того чтобы найти статистическую оценку θ неизвестного параметра теоретического распределения через эти данные необходимо найти функцию от наблюдаемых случайных величин, которые дают приближенное значение оцениваемого параметра. Статистическую оценку, которая определяется одним числом, называют точечной.Полученные оценки должны быть достоверными, т.е. обладать свойствами несмещенности, эффективности и состоятельности.Несмешанной называют статистическую оценку θ*, математическое ожидание которой равно оценивающему параметру θ при любом объеме выборки, т.е. М(θ*)= θ . Эффективной оценкой называют статистическую оценку θ*, которая при заданном объеме выборки n имеет наименьшую возможную дисперсию. Состоятельной называют статистическую оценку, которая при n→ ∞ и стремится по вероятности к оцениваемому параметру, т.е. .

Лекция №1, ТВиМС, Лакман И.А.

Контрольные листки

Учитывая системный характер работ по выявлению некачественной продукции, на многих предприятиях разработаны типовые бланки для заполнения информации о наблюдениях. Такой форме регистрации данных отвечает контрольный листок – бумажный бланк, на котором заранее напечатаны контролируемые параметры, с тем, чтобы можно было легко и точно записать данные наблюдений или измерений. Его назначение имеет две цели: облегчить процесс сбора данных и упорядочить их для последующей обработки.

Рассмотрим некоторые типы контрольных листков в зависимости от назначения сбора информации.Контрольный листок для регистрации видов дефектов. Каждый раз, когда рабочий или контролер обнаруживает дефект, он делает пометку (штрих) на бланке. На том же бланке в конце рабочего дня фиксируются итоговые данные по количеству каждого типа дефектов.

Типы дефектов	Группы	Итого
Трещины	//// ////	10
Царапины	//// //// //// ////…//// //	42
Пятна	//// /	6
Деформация	//// //// //// ////…//// ////	104
Разрыв	////	4
Раковины	//// //// //// ////	20
Прочие	//// //// ////	14
Итого		200

Рис. Контрольный листок видов дефектов

К недостаткам этого листка можно отнести невозможность проведения расслоения данных.
Это недостаток можно компенсировать заполнением контрольного листка причин дефектов. Листок выполнен таким образом, чтобы из него можно было выбрать необходимую информацию о дефектах, допущенных не только по вине рабочего или по причине неправильной наладки станка, но и определить появление брака, вызванное усталостью рабочего во второй половине дня или изменением условий работы. Очевидно, что анализ причин дефектов при такой регистрации данных значительно облегчается.

Рис. Контрольный листок причин дефектов

Контрольный листок локализации дефектов позволяет оценить качество отливки на наличие раковин как вдоль оси заготовки, так и по длине ее наружной и внутренней поверхностей. Такого типа контрольные листки полезны для диагноза процесса, поскольку причины дефектов часто можно найти, только исследуя места их возникновения.

Рис. Контрольный листок локализации дефектов

Контрольный листок для регистрации распределения измеряемого параметра позволяет выявить изменения в размерах детали после проведения механической обработки. Как правило, такие листки заполняются для анализа стабильности технологического процесса путем построения гистограмм.