Плотность вещества
Плотность — скалярная физическая величина. Определяется как отношение массы тела к занимаемому этим телом объему.
Формула плотности вещества
р — плотность вещества [кг/м 3 ]
Плотность зависит от температуры, агрегатного состояния вещества и внешнего давления. Обычно если давление увеличивается, то молекулы вещества утрамбовываются плотнее — следовательно, плотность больше. А рост температуры, как правило, приводит к увеличению расстояний между молекулами вещества — плотность понижается.
Ниже представлены значения плотностей для разных веществ. В дальнейшем это поможет при решении задач.
Закон Архимеда
На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу объема жидкости или газа, вытесненного частью тела, погруженной в жидкость или газ.
Формула архимедовой силы:
Fa = ρ × g × V, где ρ — плотность жидкости, V — объем погруженной части тела, g — ускорение 9,8 м/с 2 .
Закон Архимеда помогает рассчитать, как поведет себя тело при погружении в среды разной плотности. Верны следующие утверждения:
если плотность тела выше плотности среды, оно уйдет на дно;
если плотность тела ниже, оно всплывет на поверхность.
Другими словами, тело поднимется на поверхность, если архимедова сила больше силы тяжести.
Физика 7: все формулы и определения
Формулы 8 класс Формулы 9 класс Формулы 10 класс Формулы 11 класс
В пособии «Физика 7: все формулы и определения» представлено 24 формулы
и определения за весь курс Физики 7 класса:
| Название формулы (закона, правила) | Формулировка закона (правила) | Формула |
| 1. Цена деления шкалы прибора |
Для определения цены деления (ЦД) шкалы прибора необходимо: |
ЦД = (ВГ — НГ) / N
ЦД = (Б — А) / n |
| 2. Скорость |
Скорость (ʋ) — физическая величина, численно равна пути (S), пройденного телом за единицу времени (t). |
ʋ = S / t |
| 3. Путь |
Путь (S) — длина траектории, по которой двигалось тело, численно равен произведению скорости (ʋ) тела на время (t) движения. |
S = ʋ*t |
| 4. Время движения |
Время движения (t) равно отношению пути (S), пройденного телом, к скорости (ʋ) движения. |
t = S / ʋ |
| 5. Средняя скорость |
Средняя скорость (ʋср) равна отношению суммы участков пути (S1, S2, S3, …), пройденного телом, к промежутку времени (t1 + t2+ t3+ …), за который этот путь пройден. |
ʋср = (S1 + S2 + S3 + …) / (t1 + t2 + t3 + …) |
| 6. Сила тяжести |
Сила тяжести — сила (FТ), с которой Земля притягивает к себе тело, равная произведению массы (т) тела на коэффициент пропорциональности (g) — постоянную величину для Земли. (g = 9,8 H/кг) |
FТ = m*g |
| 7. Вес |
Вес (Р) — сила, с которой тело действует на горизонтальную опору или вертикальный подвес, равная произведению массы (т) тела на коэффициент (g). |
Р = m*g |
| 8. Масса |
Масса (т) — мера инертности тела, определяемая при его взвешивании как отношение силы тяжести (Р) к коэффициенту (g). |
т = Р / g |
| 9. Плотность |
Плотность (ρ) — масса единицы объёма вещества, численно равная отношению массы (т) вещества к его объёму (V). |
ρ = m / V |
| 10. Момент силы |
Момент силы (М) равен произведению силы (F) на сё плечо (l) |
М = F*l |
| 11. Условие равновесия рычага |
Рычаг находится в равновесии, если плечи (l1, l2) действующих на него двух сил (F1, F2) обратно пропорциональны значениям сил. |
a) F1 / F2 = l1 / l2
б) F1*l1 = F2*l2 |
| 12. Давление |
Давление (р) — величина, численно равная отношению силы (F), действующей перпендикулярно поверхности, к площади (S) этой поверхности |
p = F / S |
| 13. Сила давления |
Сила давления (F) — сила, действующая перпендикулярно поверхности тела, равная произведению давления (р) на площадь этой поверхности (S) |
F = р*S |
| 14. Давление однородной жидкости |
Давление жидкости (р) на дно сосуда зависит только от её плотности (ρ) и высоты столба жидкости (h). |
p = g ρ h |
| 15.Закон Архимеда |
На тело, погруженное в жидкость (или газ), действует выталкивающая сила — архимедова сила (FВ). равная весу жидкости (или газа), в объёме (VТ) этого тела. |
FВ = ρ*g*Vт |
| 16. Условие плавания тел |
Если архимедова сила (FВ) больше силы тяжести (FТ) тела, то тело всплывает. |
FВ> FТ |
| 17. Закон гидравлической машины |
Силы (F1, F2), действующие на уравновешенные поршни гидравлической машины, пропорциональны площадям (S1, S2) этих поршней. |
F1 / F2 = S1 / S2 |
| 18. Закон сообщаю-щихся сосудов |
Однородная жидкость в сообщающихся сосудах находится на одном уровне (h) |
h = const |
| 19. Механическая работа |
Работа (A) — величина, равная произведению перемещения тела (S) на силу (F), под действием которой это перемещение произошло. |
А = F*S |
| 20. Коэффициент полезного действия механизма (КПД) |
Коэффициент полезного действия (КПД) механизма — число, показывающее, какую часть от всей выполненной работы (АВ) составляет полезная работа (АП). |
ɳ = АП / АВ *100% |
| 21. Потенциальная энергия |
Потенциальная энергия (ЕП) тела, поднятого над Землей, пропорциональна его массе (т) и высоте (h) над Землей. |
ЕП = m*g*h |
| 22. Кинетическая энергия |
Кинетическая энергия (ЕК) движущегося тела пропорциональна его массе (m) и квадрату скорости (ʋ2). |
ЕК = m*ʋ2 / 2 |
| 23. Сохранение и превращение механической энергии |
Сумма потенциальной (ЕП) и кинетической (ЕК) энергии в любой момент времени остается постоянной. |
EП + EК = const |
| 24. Мощность |
Мощность (N) — величина, показывающая скорость выполнения работы и равная:а) отношению работы (А) ко времени (t), за которое она выполнена;б) произведению силы (F), под действием которой перемещается тело, на среднюю скорость (ʋ) его перемещения. |
N = A / t
N = F*ʋ |
1 файл(ы) 549.72 KB
12 (двенадцать) самых необходимых (самых востребованных) формул по физике в 7 классе:
Формулы 8 класс Формулы 9 класс Формулы 10 класс Формулы 11 класс
Масса тела в физике
Масса тела (m) — это скалярная физическая величина, которая является мерой инертности тела и гравитационного взаимодействия.
Масса тела отображает, как оно сопротивляется изменению скорости и как сильно притягивается к Земле. Чем больше масса тела, тем меньше изменяется его скорость при воздействии на него.
В международной системе единиц (СИ) массу измеряют в килограммах.
Масса — это аддитивная (то есть добавочная) величина. Масса совокупности тел или материальных точек равна сумме масс всех отдельный тел.
Масса тела не зависит от движения тела, его расположения и воздействия других тел. Согласно закону сохранения массы, в замкнутой механической системе тел масса неизменна во времени.
Чем отличается от веса тела, связь инерции и массы
Хотя в повседневности понятие «масса» часто путают с понятием «вес», в физике они сильно отличаются.
Вес тела (P) — это сила, с которой тело действует на опору или подвес.
P = m g , где P — вес тела, m — масса тела, g — ускорение свободного падения, равное на Земле 9 , 8 м / с 2 .
Перечислим основные различия массы и веса.
- Масса отражает инертность тела или заряд гравитационного поля. Вес, в свою очередь, отражает силу, с которой тело действует на опору или подвес.
- Масса — скалярная величина, она не имеет направления. Вес — векторная величина.
- Вес определяется не внутренними свойствами объекта, а гравитационными силами. Это означает, что на разных планетах вес тела будет отличаться, а масса останется неизменной. В невесомости масса космонавта будет такой же, как на Земле, а вот вес будет равен нулю.
- Масса тела измеряется в килограммах, а вес — в ньютонах.
Определение 3
Инертность — это свойство тела препятствовать изменению своей скорости при воздействии на него внешних сил.
Инерция — это физическое явление, при котором тело сохраняет свою скорость постоянной или находится в покое, если на него не действуют другие тела или их действие скомпенсировано.
Закон инерции постулируется первым законом Ньютона. Приведем современную формулировку закона.
Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения.
Второй закон Ньютона в классической механике вводит массу как проявление инертности тела или материальной точки в определенной системе отсчета.
Согласно современной формулировке, второй закон Ньютона звучит следующим образом.
В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.
В виде формулы закон выглядит как:
где a → — ускорение материальной точки, F → — равнодействующая сил, приложенных к материальной точке, m — масса материальной точки.
Формулы по физике для ЕГЭ и 7-11 класса
Рубрика: Подготовка к ЕГЭ по физике
- Шпаргалка с формулами по физике для ЕГЭ
- и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
- Для начала картинка, которую можно распечатать в компактном виде.
- Механика
- Давление Р=F/S
- Плотность ρ=m/V
- Давление на глубине жидкости P=ρ∙g∙h
- Сила тяжести Fт=mg
- 5. Архимедова сила Fa=ρж∙g∙Vт
- Уравнение движения при равноускоренном движении
X=X0+υ0∙t+(a∙t2)/2 S=(υ2-υ02) /2а S=(υ+υ0) ∙t /2
- Уравнение скорости при равноускоренном движении υ=υ0+a∙t
- Ускорение a=(υ—υ 0)/t
- Скорость при движении по окружности υ=2πR/Т
- Центростремительное ускорение a=υ2/R
- Связь периода с частотой ν=1/T=ω/2π
- II закон Ньютона F=ma
- Закон Гука Fy=-kx
- Закон Всемирного тяготения F=G∙M∙m/R2
- Вес тела, движущегося с ускорением а↑ Р=m(g+a)
- Вес тела, движущегося с ускорением а↓ Р=m(g-a)
- Сила трения Fтр=µN
- Импульс тела p=mυ
- Импульс силы Ft=∆p
- Момент силы M=F∙ℓ
- Потенциальная энергия тела, поднятого над землей Eп=mgh
- Потенциальная энергия упруго деформированного тела Eп=kx2/2
- Кинетическая энергия тела Ek=mυ2/2
- Работа A=F∙S∙cosα
- Мощность N=A/t=F∙υ
- Коэффициент полезного действия η=Aп/Аз
- Период колебаний математического маятника T=2π√ℓ/g
- Период колебаний пружинного маятника T=2 π √m/k
- Уравнение гармонических колебаний Х=Хmax∙cos ωt
- Связь длины волны, ее скорости и периода λ= υТ
Молекулярная физика и термодинамика
- Количество вещества ν=N/ Na
- Молярная масса М=m/ν
- Cр. кин. энергия молекул одноатомного газа Ek=3/2∙kT
- Основное уравнение МКТ P=nkT=1/3nm0υ2
- Закон Гей – Люссака (изобарный процесс) V/T =const
- Закон Шарля (изохорный процесс) P/T =const
- Относительная влажность φ=P/P0∙100%
- Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
- Работа газа A=P∙ΔV
- Закон Бойля – Мариотта (изотермический процесс) PV=const
- Количество теплоты при нагревании Q=Cm(T2-T1)
- Количество теплоты при плавлении Q=λm
- Количество теплоты при парообразовании Q=Lm
- Количество теплоты при сгорании топлива Q=qm
- Уравнение состояния идеального газа PV=m/M∙RT
- Первый закон термодинамики ΔU=A+Q
- КПД тепловых двигателей η= (Q1 — Q2)/ Q1
- КПД идеал. двигателей (цикл Карно) η= (Т1 — Т2)/ Т1
https://5-ege.ru/formuly-po-fizike-dlya-ege/
Электростатика и электродинамика – формулы по физике
- Закон Кулона F=k∙q1∙q2/R2
- Напряженность электрического поля E=F/q
- Напряженность эл. поля точечного заряда E=k∙q/R2
- Поверхностная плотность зарядов σ = q/S
- Напряженность эл.
поля бесконечной плоскости E=2πkσ
- Диэлектрическая проницаемость ε=E0/E
- Потенциальная энергия взаимод.
зарядов W= k∙q1q2/R
- Потенциал φ=W/q
- Потенциал точечного заряда φ=k∙q/R
- Напряжение U=A/q
- Для однородного электрического поля U=E∙d
- Электроемкость C=q/U
- Электроемкость плоского конденсатора C=S∙ε∙ε0/d
- Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
- Сила тока I=q/t
- Сопротивление проводника R=ρ∙ℓ/S
- Закон Ома для участка цепи I=U/R
- Законы послед. соединения I1=I2=I, U1+U2=U, R1+R2=R
- Законы паралл. соед. U1=U2=U, I1+I2=I, 1/R1+1/R2=1/R
- Мощность электрического тока P=I∙U
- Закон Джоуля-Ленца Q=I2Rt
- Закон Ома для полной цепи I=ε/(R+r)
- Ток короткого замыкания (R=0) I=ε/r
- Вектор магнитной индукции B=Fmax/ℓ∙I
- Сила Ампера Fa=IBℓsin α
- Сила Лоренца Fл=Bqυsin α
- Магнитный поток Ф=BSсos α Ф=LI
- Закон электромагнитной индукции Ei=ΔФ/Δt
- ЭДС индукции в движ проводнике Ei=Вℓυsinα
- ЭДС самоиндукции Esi=-L∙ΔI/Δt
- Энергия магнитного поля катушки Wм=LI2/2
- Период колебаний кол. контура T=2π ∙√LC
- Индуктивное сопротивление XL=ωL=2πLν
- Емкостное сопротивление Xc=1/ωC
- Действующее значение силы тока Iд=Imax/√2,
- Действующее значение напряжения Uд=Umax/√2
- Полное сопротивление Z=√(Xc-XL)2+R2
Оптика
- Закон преломления света n21=n2/n1= υ 1/ υ 2
- Показатель преломления n21=sin α/sin γ
- Формула тонкой линзы 1/F=1/d + 1/f
- Оптическая сила линзы D=1/F
- max интерференции: Δd=kλ,
- min интерференции: Δd=(2k+1)λ/2
- Диф.решетка d∙sin φ=k λ
Квантовая физика
- Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=Uзе
- Красная граница фотоэффекта νк = Aвых/h
- Импульс фотона P=mc=h/ λ=Е/с
Физика атомного ядра
- Закон радиоактивного распада N=N0∙2-t/T
- Энергия связи атомных ядер
ECB=(Zmp+Nmn-Mя)∙c2
СТО
- t=t1/√1-υ2/c2
- ℓ=ℓ0∙√1-υ2/c2
- υ2=(υ1+υ)/1+ υ1∙υ/c2
- Е = mс2
Скачать эти формулы в doc: formuly-po-fizike-5-ege.ru (файл расположен на 5-ege.ru).
Рекомендуем:
- Как решать задачи по химии, готовые решения
- ЕГЭ по физике с решениями, часть А
- Решение задач по физике, ЕГЭ – часть С
Дополнительные примеры задач
На рисунке изображен кусок хозяйственного мыла в упаковке. По данным производителя размеры размеры его полиэтиленовой упаковки составляют 6 см x 9 см x 5,5 см.
Вес одного куска 200 г. Вес брутто (масса товара вместе с упаковкой) указан 211 г. Найдите объем куска мыла без упаковки. Выразите ответ в СИ.
Обозначим стороны упаковки как $a, b и с$, массу куска была $m_м$, массу куска мыла в упаковке — $m$, а общую массу мыла в упаковке — $m_$.
Объем куска мыла будем обозначать как $V_м$, а вместе с упаковкой — $V$.
Дано:$a = 6 см$$b = 9 см$$c = 5,5 см$$m_м = 200 г$$m = 211 г$
Решение:Найдем массу упаковки: $m_ = m — m_м = 211 г — 200 г = 11 г$.
Общий объем упаковки и мыла:$V = a \cdot b \cdot c = 6 см \cdot 9 см \cdot 5,5 см = 297 см^3$.
Указано, что упаковка изготовлена из полиэтилена (из таблицы 1 предыдущего параграфа его плотность $\rho_п$ равна $0,92 \frac$).
Общий объем куска мыла в упаковке складывается из объема самого куска и объема упаковки. Так мы можем найти объем куска мыла:$V_м = V — V_ = 297 см^3 — 12 см^3 = 285 см^3$.
Выразим в СИ:$285 см^3 = 285 \cdot 1 см \cdot 1 см \cdot 1 см = 285 \cdot 0,01 м \cdot 0,01 м \cdot 0,01 м = 285 \cdot 0,000001 м^3 = 0,000285 м^3$.
2. Масса чугунного шара составляет 800 г. Его объем — $125 см^3$. Будет ли этот шар сплошным (отлитым полностью из одного материала) или полым (иметь пространство внутри, заполненное, например, воздухом)?
Проверить это достаточно просто: рассчитаем плотность этого шара:
Сравним полученное значение с табличной плотностью чугуна:$\rho = 7 \frac$Сколько бы тогда весил сплошной шар?
$m = \rho V = 7 \frac \cdot 125 см^3 = 875 г$
Разница между массами реального и предполагаемого сплошного шара составляет 75 г.
Следовательно, реальный шар имеет внутри какую-то полость, он не полностью выполнен из чугуна.
3. В грузовой автомобиль загрузили 48 сосновых бревен. Масса каждого соснового бревна составляет $20 дм^3$. На сколько увеличилась масса автомобиля после загрузки?
Из таблицы 1 предыдущего параграфа возьмем плотность сухой сосны ($400 \frac$). Переведем $20 дм^3$ в $м^3$:
$20 дм^3 = 20 \cdot 0,1 м \cdot 0,1 м \cdot 0,1 м = 20 \cdot 0,001 м^3 = 0,02 м^3$
Дано:$\rho = 400 \frac$$n = 48$$V = 20 дм^3$
Решение:Рассчитаем массу одного соснового бревна:$m = \rho \cdot V = 400 \frac \cdot 0,02 м^3 = 8 кг$
Масса всех сосновых бревен (M) будет равна:$M = n \cdot m = 48 \cdot 8 кг = 384 кг$
Ответ: масса автомобиля после загрузки увеличится на 384 кг.
Сила тяжести, вес, масса, плотность
Формулы, понятия и определения, описывающие эти физические характеристики, изучают в 7 классе в рамках такого раздела физики, как динамика.
Вес тела или вещества — это физическая величина, которая характеризует, с какой силой оно действует на горизонтальную поверхность или вертикальный подвес.
Обратите внимание: вес тела измеряется в ньютонах, масса тела — в граммах и килограммах. Формула веса:
Формула веса:
P = mg, где m — масса тела, g — ускорение свободного падения.
Ускорение свободного падения возникает под действием силы тяжести, которой подвержены все находящиеся на нашей планете тела.
g = 9,806 65 м/с 2 или 9,8 Н/кг
Если тело находится в покое или в прямолинейном равномерном движении, его вес равен силе тяжести.
Но эти понятия нельзя отождествлять: сила тяжести действует на тело ввиду наличия гравитации, в то время как вес — это сила, с которой само тело действует на поверхность.
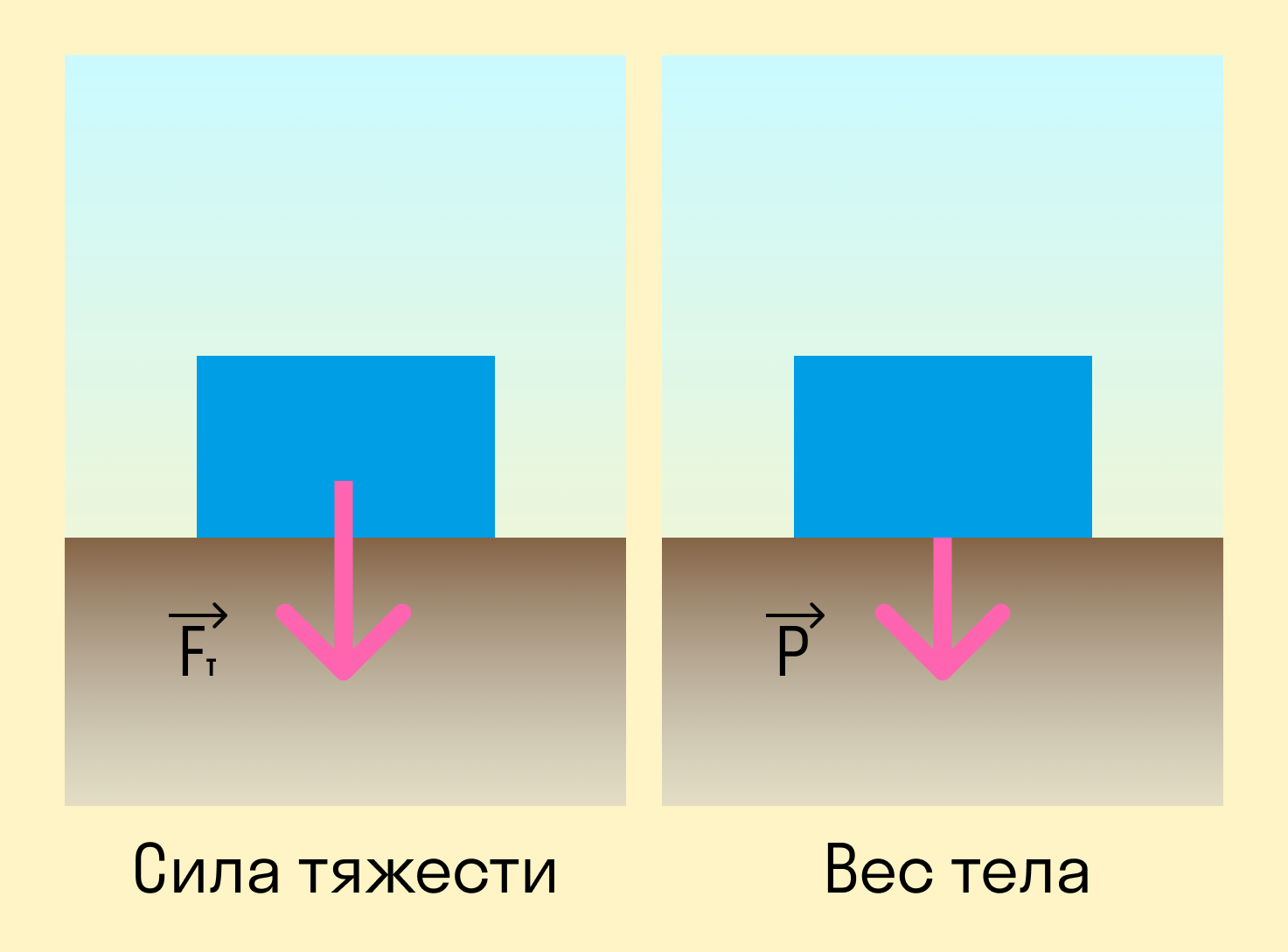
Плотность тела или вещества — величина, указывающая на то, какую массу имеет данное вещество, занимая единицу объема. Плотность прямо пропорциональна массе и обратно пропорциональна объему.
Формула плотности:
ρ = m / V, где m — масса тела или вещества, V — занимаемый объем.
Единица измерения плотности в СИ: кг/м 3 .
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Формула
Рассмотрим кубоид, погруженный в жидкость, его верхняя и нижняя грани перпендикулярны направлению силы тяжести (предполагается, что она постоянна на всем протяжении куба). Жидкость будет оказывать нормальное усилие на каждую поверхность, но только нормальные силы сверху и снизу будут способствовать плавучести. Давление разница между нижней и верхней поверхностью прямо пропорционально высоте (разница в глубине погружения в воду). Умножение разницы давлений на площадь грани дает результирующую силу на кубоид — плавучесть — равную по размеру весу жидкости, вытесненной кубоидом. Суммируя достаточно много произвольно малых кубоидов, это рассуждение может быть расширено до неправильных форм, и, таким образом, какой бы ни была форма погруженного тела, выталкивающая сила равна весу вытесненной жидкости.
- вес вытесненной жидкостизнак равновес объекта в вакууме-вес объекта в жидкости{\ displaystyle {\ text {вес вытесненной жидкости}} = {\ text {вес объекта в вакууме}} — {\ text {вес объекта в жидкости}} \,}
Вес вытесненной жидкости прямо пропорционален объему вытесненной жидкости (если окружающая жидкость равномерной плотности). Вес объекта в жидкости уменьшается из-за действующей на него силы, которая называется подъемом вверх. Проще говоря, принцип гласит, что выталкивающая сила (F b), действующая на объект, равна массе жидкости, вытесняемой объектом, или плотности ( ρ ) жидкости, умноженной на погруженный объем (V), умноженный на гравитация (г)
Мы можем выразить это соотношение в уравнении:
- Fазнак равноρграммV{\ displaystyle F_ {a} = \ rho gV}
где обозначает выталкивающую силу, приложенную к погружаемому объекту, обозначает плотность жидкости, представляет объем вытесненной жидкости и является ускорением свободного падения. Таким образом, среди полностью погруженных в воду объектов одинаковой массы объекты большего объема обладают большей плавучестью. Fа{\ displaystyle F_ {a}}ρ{\ displaystyle \ rho}V{\ displaystyle V}грамм{\ displaystyle g}
Предположим, что вес камня составляет 10 ньютонов, когда он подвешен на веревке в вакууме под действием силы тяжести. Предположим, что когда камень опускается в воду, он вытесняет воду весом 3 ньютона. Сила, которую он затем оказывает на веревку, на которой он висит, будет составлять 10 ньютонов минус 3 ньютона выталкивающей силы: 10 — 3 = 7 ньютонов. Плавучесть снижает кажущийся вес объектов, полностью опустившихся на морское дно. Как правило, легче поднять предмет через воду, чем вытащить его из воды.
Для полностью затопленного объекта принцип Архимеда можно переформулировать следующим образом:
- кажущийся погруженный весзнак равновес объекта-вес вытесненной жидкости{\ displaystyle {\ text {кажущийся погруженный вес}} = {\ text {вес объекта}} — {\ text {вес вытесненной жидкости}} \,}
затем вставляется в коэффициент весов, который был расширен на общий объем
- плотность объектаплотность жидкостизнак равномассавес вытесненной жидкости{\ displaystyle {\ frac {\ text {плотность объекта}} {\ text {плотность жидкости}}} = {\ frac {\ text {weight}} {\ text {вес вытесненной жидкости}}}}
дает формулу ниже. Плотность погружаемого объекта относительно плотности жидкости можно легко рассчитать без измерения объема.
- плотность объектаплотность жидкостизнак равномассамасса-кажущийся погруженный вес.{\ displaystyle {\ frac {\ text {плотность объекта}} {\ text {плотность жидкости}}} = {\ frac {\ text {weight}} {{\ text {weight}} — {\ text {видимый погруженная масса}}}}. \,}
(Эта формула используется, например, для описания принципа измерения дасиметра и гидростатического взвешивания. )
Пример: если вы уроните дрова в воду, плавучесть удержит их на плаву.
Пример: воздушный шар с гелием в движущейся машине. При увеличении скорости или движении по кривой воздух движется в направлении, противоположном ускорению автомобиля. Однако из-за плавучести воздушный шар отталкивается воздухом и дрейфует в том же направлении, что и автомобиль.
Когда объект погружается в жидкость, жидкость проявляет восходящую силу, известную как выталкивающая сила, которая пропорциональна весу вытесненной жидкости. Суммарная сила, действующая на объект, тогда равна разнице между весом объекта (сила «вниз») и весом вытесненной жидкости (сила «вверх»). Равновесие или нейтральная плавучесть достигается, когда эти два веса (и, следовательно, силы) равны.
Как найти массу вещества
Окружающее нас пространство наполнено разными физическими телами, которые состоят из разных веществ с различной массой. Школьные курсы химии и физики, ознакомляющие с понятием и методом нахождения массы вещества, прослушали и благополучно забыли все, кто учился в школе. Но между тем теоретические знания, приобретенные когда-то, могут понадобиться в самый неожиданный момент.
1
Вычисление массы вещества с помощью удельной плотности вещества. Пример – имеется бочка на 200 литров. Нужно заполнить бочку любой жидкостью, скажем, светлым пивом. Как найти массу наполненной бочки? Используя формулу плотности вещества p=m/V, где p – удельная плотность вещества, m – масса, V – занимаемый объем, найти массу полной бочки очень просто:
- Меры объемов – кубические сантиметры, метры. То есть бочка на 200 литров имеет объем 2 м³.
- Мера удельной плотности находится с помощью таблиц и является постоянной величиной для каждого вещества. Измеряется плотность в кг/м³, г/см³, т/м³. Плотность пива светлого и других алкогольных напитков можно посмотреть на сайте. Она составляет 1025,0 кг/м³.
- Из формулы плотности p=m/V => m=p*V: m = 1025,0 кг/м³* 2 м³=2050 кг.
Бочка объемом 200 литров, полностью наполненная светлым пивом, будет иметь массу 2050 кг.
2
Нахождение массы вещества с помощью молярной массы. M (x)=m (x)/v (x) – это отношение массы вещества к его количеству, где M (x) – это молярная масса X, m (x) – масса X, v (x) – количество вещества X. Если в условии задачи прописывается только 1 известный параметр – молярная масса заданного вещества, то нахождение массы этого вещества не составит труда. Например, необходимо найти массу йодида натрия NaI количеством вещества 0,6 моль.
- Молярная масса исчисляется в единой системе измерений СИ и измеряется в кг/моль, г/моль. Молярная масса йодида натрия – это сумма молярных масс каждого элемента: M (NaI)=M (Na)+M (I). Значение молярной массы каждого элемента можно вычислить по таблице, а можно с помощью онлайн-калькулятора на сайте: M (NaI)=M (Na)+M (I)=23+127=150 (г/моль).
- Из общей формулы M (NaI)=m (NaI)/v (NaI) => m (NaI)=v (NaI)*M (NaI)= 0,6 моль*150 г/моль=90 грамм.
Масса йодида натрия (NaI) с массовой долей вещества 0,6 моль составляет 90 грамм.
3
Нахождение массы вещества по его массовой доле в растворе. Формула массовой доли вещества ω=*100%, где ω – массовая доля вещества, а m (вещества) и m (раствора) – массы, измеряемые в граммах, килограммах. Общая доля раствора всегда принимается за 100%, иначе будут погрешности в вычислении. Несложно из формулы массовой доли вещества вывести формулу массы вещества: m (вещества)= /100%. Однако есть некоторые особенности изменения состава раствора, которые нужно учитывать при решении задач на эту тему:
- Разбавление раствора водой. Масса вещества растворенного X не изменяется m (X)=m’(X). Масса раствора увеличивается на массу добавленной воды m’ (р)=m (р)+m (H2O).
- Выпаривание воды из раствора. Масса растворенного вещества X не изменяется m (X)=m’ (X). Масса раствора уменьшается на массу выпаренной воды m’ (р)=m (р)-m (H2O).
- Сливание двух растворов. Массы растворов, а также массы растворенного вещества X при смешивании складываются: m’’ (X)=m (X)+m’ (X). m’’ (р)=m (р)+m’ (р).
- Выпадение кристаллов. Массы растворенного вещества X и раствора уменьшаются на массу выпавших кристаллов: m’ (X)=m (X)-m (осадка), m’ (р)=m (р)-m (осадка).
4
Алгоритм нахождения массы продукта реакции (вещества), если известен выход продукта реакции. Выход продукта находится по формуле η=*100%, где m (x практическая) – масса продукта х, которая получена в результате практического процесса реакции, m (x теоретическая) – рассчитанная масса вещества х. Отсюда m (x практическая)=/100% и m (x теоретическая)=/η. Теоретическая масса получаемого продукта всегда больше практической, в связи с погрешностью реакции, и составляет 100%. Если в задаче не дается масса продукта, полученного в практической реакции, значит, она принимается за абсолютную и равна 100%.
Варианты нахождение массы вещества – небесполезный курс школьного обучения, а вполне применяемые на практике способы. Каждый сможет без труда найти массу необходимого вещества, применяя вышеперечисленные формулы и пользуясь предлагаемыми таблицами. Для облегчения задания прописывайте все реакции, их коэффициенты.
Работа, энергия, мощность
Механическая работа — это скалярная величина, которая равна произведению перемещения тела на модуль силы, под действием которой было выполнено перемещение. Подразумевается, что перемещение произошло в том же направлении, в котором действует сила.
Формула работы в курсе физики за 7 класс:
A = F × S, где F — действующая сила, S — пройденный телом путь.
Единица измерения работы в СИ: джоуль (Дж).
Такое понятие, как мощность, описывает скорость выполнения механической работы. Оно говорит о том, какая работа была совершена в единицу времени.
Мощность — это скалярная величина, равная отношению работы к временному промежутку, потребовавшемуся для ее выполнения.
Формула мощности:
N = A / t, где A — работа, t — время ее совершения.
Также мощность можно вычислить, зная силу, воздействующую на тело, и среднюю скорость перемещения этого тела.
N = F × v, где F — сила, v — средняя скорость тела.
Единица измерения мощности в СИ: ватт (Вт).
Тело может совершить какую-либо работу, если оно обладает энергией — кинетической и/или потенциальной.
Кинетической называют энергию движения тела. Она говорит о том, какую работу нужно совершить, чтобы придать телу определенную скорость.
Потенциальной называется энергия взаимодействия тела с другими телами или взаимодействия между частями одного целого. Потенциальная энергия тела, поднятого над Землей, характеризует, какую работу должна совершить сила тяжести, чтобы опустить это тело снова на нулевой уровень.
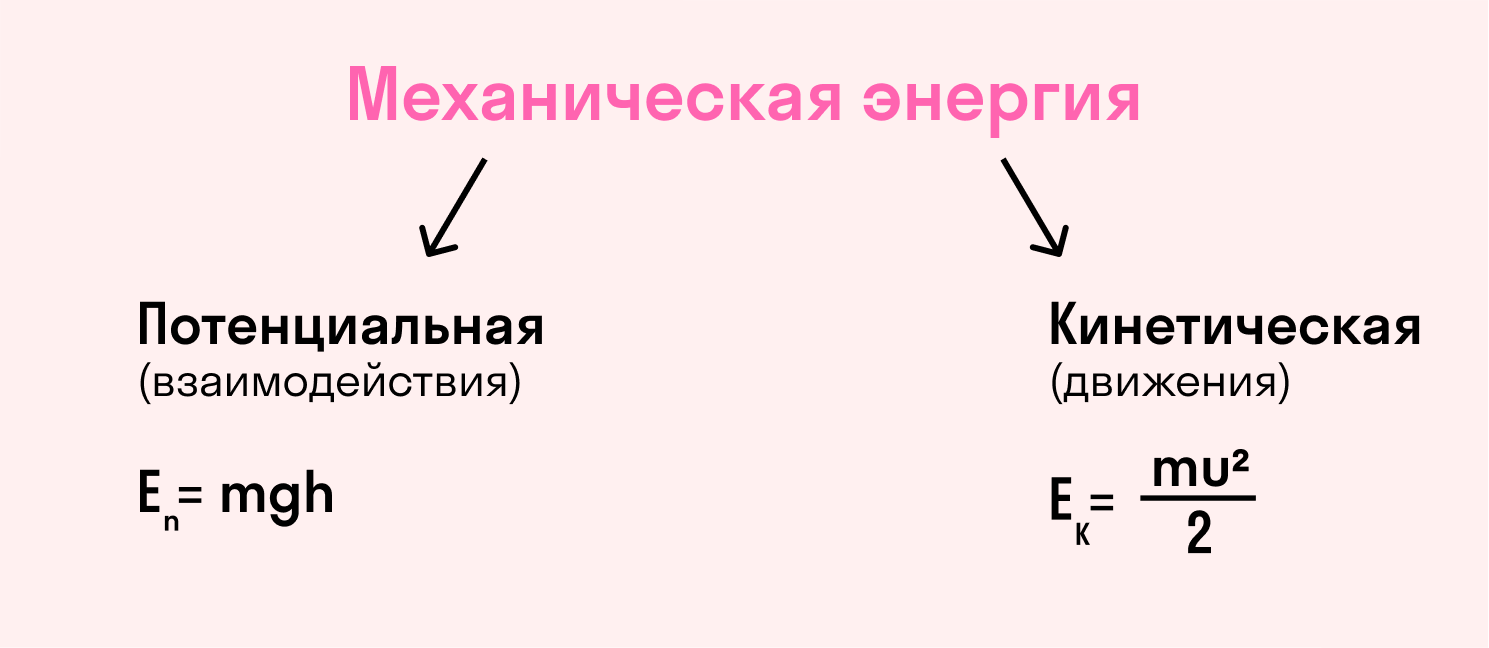
Таблица с формулами по физике за 7 класс для вычисления кинетической и потенциальной энергии:
Кинетическая энергия
Пропорциональна массе тела и квадрату его скорости.
Потенциальная энергия
Равна произведению массы тела, поднятого над Землей, на ускорение свободного падения и высоту поднимания.
Полная механическая энергия
Складывается из кинетической и потенциальной энергии.
Сохранение и превращение энергии
Если механическая энергия не переходит в другие формы, то сумма потенциальной энергии и кинетической представляет собой константу.
Для того, чтобы понять, какая часть совершенной работы была полезной, вычисляют коэффициент полезного действия или КПД. С его помощью определяется эффективность различных механизмов, инструментов и т. д.
Коэффициент полезного действия (КПД) отражает полезную часть выполненной работы. Также его можно выразить через отношение полезно использованной энергии к общему количеству полученной энергии.
Формула для расчета КПД:
где Ап— полезная работа, Аз— затраченная работа.
КПД выражается в процентах и составляет всегда меньше 100%, поскольку часть энергии затрачивается на трение, повышение температуры воздуха и окружающих тел, преодоление силы тяжести и т. д.
Источник статьи: http://skysmart.ru/articles/physics/vse-formuly-za-7-klass-po-fizike
- Свежие записи
- Где находится датчик давления масла ЯМЗ 7511?
- Разбираемся в терминах: что означает «банк 1» и «банк 2» в датчике кислорода
- Приора: последствия поломки датчика коленвала
- Что произойдет, если отключить датчик массового расхода воздуха?
- Что произойдет, если не заменить датчик кислорода?
- Правообладателям
- Политика конфиденциальности
Авто мастер на все руки 2023 Информация, опубликованная на сайте, носит исключительно ознакомительный характер
Формула плотности вещества
Плотность вещества равна отношению массы вещества к объёму, который эта масса занимает. Плотность обозначается греческой буквой $\rho$ (ро).
То есть, если объём тела обозначить буквой $V$, а массу — $m$, то формула плотности вещества примет вид:
$$\rho = {m \over V}$$
Из данной формулы можно получить единицу плотности. Поскольку масса измеряется в килограммах, а объём — в кубических метрах, то единицей измерения плотности будет килограмм на кубический метр:
$$ = {кг \over м^3}$$
Физический смысл плотности — это масса одного кубического метра данного вещества.
Рис. 1. Плотность вещества
Расчет с помощью плотности и площади
Для решения задачи по определению массы с помощью известной плотности и площади, необходимо использовать простую формулу. Для начала, определяется площадь поверхности, на которой распределена указанная плотность.
Формула для расчета массы выглядит следующим образом:
Масса = Плотность x Площадь
Для проведения расчетов необходимо знать численные значения плотности и площади. Плотность измеряется в единицах массы, деленных на единицы объема (например, кг/м³), а площадь измеряется в квадратных единицах (например, м²).
Чтобы получить результат, достаточно умножить значение плотности на значение площади. Результатом будет масса, измеряемая в соответствующих единицах.
Пример использования формулы:
Пусть плотность материала составляет 1000 кг/м³, а площадь поверхности равна 5 м². Чтобы найти массу материала, просто умножим плотность на площадь:
Масса = 1000 кг/м³ x 5 м² = 5000 кг
Таким образом, полученная масса равна 5000 кг.
Используя данную формулу, учитывайте единицы измерения плотности и площади, чтобы получить точный и правильный результат.


















