Как найти массу зная плотность и высоту

Примеры решения задач

Прежде чем приступить к примерам, следует понимать, что если данные даны в килограммах и кубических сантиметрах, то нужно либо сантиметры перевести в метры, либо килограммы перевести в граммы. По такому же принципу надо переводить и остальные данные – миллиметры, тонны и так далее.

Задача 1. Найти массу тела, состоящего из вещества, плотность которого равна 2350 кг/м³ и имеет объём 20 м³. Применяем стандартную формулу и с лёгкостью находим значение. m = p*V= 2 350 * 20 = 47 000 кг.

Задача 2. Уже известно, что плотность чистого золота без примесей равна 19,32 г/см³. Найти массу драгоценной цепочки из золота, если объём составляет 3,7 см³. Воспользуемся формулой и подставим значения. p = m / V = 19,32/3,7 = 5,22162162 гр.

Задача 3. На склад поставили металл с плотностью 9250 кг/м³. Масса составляет 1,420 тонн. Нужно найти занимаемый металлом объём. Тут нужно сначала перевести либо тонны в килограммы, либо метры в километры. Проще будет воспользоваться первым методом. V = m / p = 1420/9250 = 0.153513514 м³.

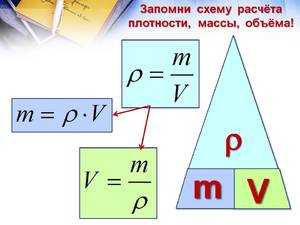
Формула зависимости массы от объема и плотности

Для того, чтобы найти плотность жидкости или твердого вещества, существует базовая формула: плотность равна массе, поделенной на объем. 

Записывается это так:

ρ = m / V

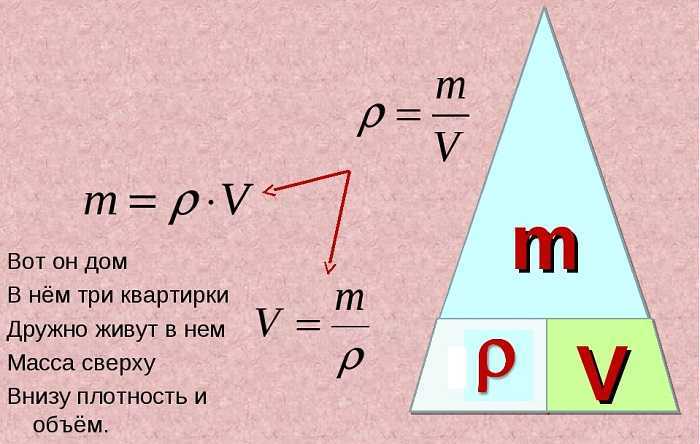
И из нее можно вывести еще две формулы.

Формулу для объема тела:

V = m / ρ

А также формулу для расчета массы:

m = V * ρ

Как видите, запомнить последнюю очень легко: это единственная формула, где две единицы нужно умножить.

Для запоминания этой зависимости можно использовать рисунок в виде «пирамидки», разделенной на три секции, в вершине которой находится масса, а в нижних углах – плотность и объем.

Несколько иначе обстоят дела с газами. Рассчитать их вес гораздо сложнее, так как у газов нет постоянной плотности: они рассеиваются и занимают весь доступный им объем. 

Для этого пригодится понятие молярной массы, которую можно найти, сложив массу всех атомов в формуле вещества при помощи данных из периодической таблицы.

Вторая единица, которая нам понадобится – количество вещества в молях. Его можно вычислить по уравнению реакции. Подробнее об этом можно узнать в рамках курса химии. 

Другой способ нахождения мольного количества – через объем газа, который нужно поделить на 22,4 литра. Последнее число – это объемная постоянная, которую стоит запомнить. 

В итоге, зная две предыдущие величины, мы можем определить массу газа:

m = n * M,

где M – это молярная масса, а n – количество вещества.

Результат получится в граммах, поэтому для решения физических задач важно не забыть перевести его в килограммы, поделив на 1000. Числа в этой формуле часто могут оказываться достаточно сложными, поэтому для вычислений может понадобиться калькулятор.

Еще один нестандартный случай, с которым можно столкнуться – необходимость найти плотность раствора

Для этого существует формула средней плотности, построенная аналогично формулам других средних величин. 

Еще один нестандартный случай, с которым можно столкнуться – необходимость найти плотность раствора. Для этого существует формула средней плотности, построенная аналогично формулам других средних величин. 

Для двух веществ посчитать ее можно так:

(m1 + m2) / V1 + V2.

Также из этой формулы можно вывести несколько других в зависимости от того, какие из величин известны по условию задачи.

Самые плотные материалы на Земле

Большую часть массы обычных атомов составляют нуклоны (протоны и нуклоны). Это означает, что на плотность обычной материи будет влиять то, насколько плотно мы можем ее упаковать, а также зависит от их внутренней атомной структуры. Металлический осмий является самым плотным материалом на Земле. Однако она намного менее плотная, чем плотность экзотических астрономических объектов, таких как нейтронные звезды и белые карлики.
Список самых плотных материалов:
Осмий — 22,6 х 10^3 кг/м^3
Иридий — 22,4 х 10^3 кг/м^3
Платина — 21,5 х 10^3 кг/м^3
Рений – 21,0 х 10^3 кг/м^3
Плутоний — 19,8 х 10^3 кг/м^3
Золото — 19,3 х 10^3 кг/м^3
Вольфрам — 19,3 х 10^3 кг/м^3
Уран — 18,8 х 10^3 кг/м^3
Тантал — 16,6 х 10^3 кг/м^3
Ртуть — 13,6 х 10^3 кг/м^3
Родий — 12,4 х 10^3 кг/м^3
Торий — 11,7 х 10^3 кг/м^3
Свинец — 11,3 х 10^3 кг/м^3
Серебро — 10,5 х 10^3 кг/м^3
Следует отметить, что плутоний, искусственный изотоп, производится из урана и ядерных реакций. Однако ученые обнаружили следовые количества встречающегося в природе плутония.
Хассий, если мы включаем промышленные элементы, является самым плотным. Хассий — это химический элемент с символом Hs и атомным номером 108. Это радиоактивный синтетический элемент, впервые синтезированный в Хассе, Германия. Самый длинный известный стабильный изотоп 269Hs имеет период полураспада примерно 9,7 секунды. Его плотность оценивается в 40,7 x 10 ^ 3 кг / м ^ 3. Плотность хассия обусловлена его высоким атомным весом и существенным уменьшением ионных радиусов элементов ряда лантаноидов. Это известно как сокращение актинидов и сокращение лантаноидов.
Мейтнерий, элемент 109, названный в честь физика Лизы Мейтнер, следует за хассием по плотности. Его расчетная плотность составляет 37,4 x 10 ^ 3 кг / м ^ 3.

Вес тела

Вес — это сила, с которой тело действует на опору или подвес. Измеряется вес, как и любая другая сила, в Ньютонах.

«Но погодите! Вес же измеряют в килограммах — я вот вешу 50»

Это не совсем верно. В быту мы часто подменяем понятие «масса» понятием «вес» и говорим: вес чемодана — десять килограммам. В физике это два совершенно разных понятия, которые при этом взаимосвязаны.

Если у вас неподалеку есть весы — приглашаем в эксперимент! Один нюанс: наша затея сработает именно с механическими весами, но не с электронными. Поехали!

Шаг 1. Если встать на весы ровно и не двигаться — ваш вес будет высчитываться по формуле:

P = mg P — вес тела m — масса g — ускорение свободного падения [м/с2] На планете Земля g = 9,8 м/с2

Здесь может возникнуть два возражения:

1. Это же сила тяжести, а не вес. Формула такая же!
2. На весах масса отображается в килограммах. И если я свою массу умножу на ускорение свободного падения, то явно получу число почти в 10 раз больше, чем показывают весы.

Точка приложения силы. Эта формула и правда аналогична силе тяжести. Вес тела в состоянии покоя численно равен массе тела, разница состоит лишь в точке приложения силы.

Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.

Весы измеряют силу. Весы работают таким образом, что измеряют вес тела — силу, с которой мы на них действуем, а показывают — массу. Можно сделать вывод, что весы — это динамометр (прибор, измеряющий силу).

Продолжаем эксперимент.

Шаг 2. Теперь пошалим и резко встанем на носочки! Стрелка резко отклонилась влево, а потом вернулась на место. Вы придали себе ускорение, направленное вверх — в то время, как ускорение свободного падения всегда направлено к центру Земли (вниз).

Теперь вес тела вычисляем по формуле:

P = m (g-a) P — вес тела m — масса g — ускорение свободного падения [м/с2] a — ваше ускорение [м/с2] На планете Земля g = 9,8 м/с2

Шаг 3. Последняя часть эксперимента — резко опуститься на пятки. Теперь вы сильнее давите на весы, потому что придали ускорение, направленное вниз. Стрелка весов отклонится вправо и вернется на место, когда вы придете в состояние покоя.

Формула веса примет вид:

P = m (g+a) P — вес тела m — масса g — ускорение свободного падения [м/с2] a — ваше ускорение [м/с2] На планете Земля g = 9,8 м/с2

Кстати, если ровно стоять на весах, но взвешиваться в лифте — все будет работать наоборот. Если лифт едет вверх, то он как будто давит весами на человека, стоящего на них, а это как раз ситуация с увеличением веса. А если вниз — весы как будто бы от вас «убегают», чтобы показать меньшее значение.

Этот случай мы можем описать через 2 закон Ньютона. Возьмем лифт, который едет вниз. Обозначим силы на рисунке.

N – сила реакции опоры ;

mg – сила тяжести ;

a – ускорение, с которым движется лифт [м/с2].

N + mg = ma

При проецировании на ось y, направленную вниз, мы получаем:

-N + mg = ma

А теперь нам понадобится третий закон Ньютона — по нему сила реакции опоры равна весу тела:

P = N

-P + mg = ma

P = m(g-a)

Проект: «Работа и энергия»

Выполнив проект, мы узнаем, что такое энергия и работа, как их измерить, как наклонная поверхность, вес объекта влияют на расстояние, до которого скатиться предмет.

Чтобы понять, что такое энергия, в ходе эксперимента будем изменять угол наклона поверхности и вес объекта.

Для того чтобы рассчитать энергию воспользуемся формулой: E = HxW, где E – энергия, H – высота, а W – вес.

Единицы измерения энергии — граммы на сантиметры: в граммах измеряем вес выбранной вещи, сантиметрах — высоту.

В качестве предмета удобно взять банку, вес которой можно регулировать, наполняя водой. Что даст совершенно разные результаты, поскольку при плескании воды в банке часть энергии теряется.

Что нам понадобится:

• гладкая, ровная доска, шириной минимум 30 см, длиной около 120 см;
• две банки (одну большего размера, другую меньшего) цилиндрической формы с крышкой и широким горлышком. Например, банки из-под томатной пасты, майонеза, чипсов и т.д.;
• вода;
• карандаш;
• книги, учебники или другие вещи для подпорки доски;
• фотоаппарат;
• скотч.

Ход эксперимента:

1. С использованием книг устанавливаем доску под наклоном так, чтобы расстояние от поднятой стороны до поверхности было 8 см. В этом месте начертим линию на доске.
2. Приклеиваем скотч по длине доски, для того чтобы потом быть уверенными, что банка катиться по прямой.
3. Десять раз скатываем большую банку по доске, начиная от размеченной линии. После каждого скатывания измеряем расстояние от нижнего края доски до места остановки банки. Подсчитываем средний результат.
4. Увеличиваем угол наклона доски, подложив под нее еще одну книгу. Находим участок на доске, расстояние от которого до поверхности 8 см, чертим на этом месте линию. Далее повторяем действия из пункта 3. Изменились ли результаты? Что будет, если скатывать банку не с отмеченной линии, а выше или ниже?
5. Теперь повторяем шаги 2-4 с маленькой банкой. Есть ли разница между полученными результатами, если рассчитывать энергию по вышеописанной формуле.

Для сравнения повторим шаги 2-4 для большой банки, наполненной водой. Как объяснить полученные результаты?

Вывод:

Результаты проекта показали, что неважно, на каком расстоянии над поверхностью земли мы начинаем скатывать предмет, независимо от угла наклона банка всегда останавливалась на одном расстоянии от конца доски. Как вы думаете, почему так происходит и, причем здесь энергия?. Такие результаты легко объяснимы, если рассчитать количество энергии, которое необходимо для скатывания банки

Расстояние, на которое прокатиться банка напрямую зависит от энергии, которой она будет обладать, когда докатиться до нижнего края доски

Такие результаты легко объяснимы, если рассчитать количество энергии, которое необходимо для скатывания банки. Расстояние, на которое прокатиться банка напрямую зависит от энергии, которой она будет обладать, когда докатиться до нижнего края доски.

Проделанный опыт подтверждает, что энергия у банки становится больше, если увеличиваются наклон доски или вес банки за счет наполнения ее водой.

За счет изменения энергии совершается работа всех внутренних и внешних сил, действующих на банку с разной мощностью.

Объём клина и обелиска

Клин в технике часто является пятигранником, в основании которого лежит прямоугольник, а боковые грани являются равнобедренными треугольниками или трапециями. Формула для расчёта объёма клина имеет вид:

• а – сторона основания подножия клина;
• а₁ – ширина верхушки клина;
• b – толщина клина;
• h –  высота клина.

Обелиск – это шестигранник, основанием которого являются прямоугольники, которые расположены в параллельных плоскостях. Противоположные грани при этом симметрично наклонены к основанию обелиска. Объём данного геометрического тела:

• а и b – размеры длины и ширины большего основания обелиска;
• а а₁ и b₁ – меньшего основания обелиска;
• h – высота обелиска.

Расчёт массы по плотности и объёму: теория, формулы, примеры задач

Все замечали, что одинаковые тела, сделанные из различных материалов, обладают разной массой. В единице объёма, например, древесины, концентрируется меньший вес, чем в металле. Литровая банка гречневой крупы весит около 800 г, а воды – 1 кг. Объясним подобное явление, покажем, как проводить расчет массы тел по плотности и объему.

Теоретическая выкладка

Ещё в Древней Греции учёные знали формулу определения объема вещей в зависимости от массы и плотности. Так Архимед открыл закон, названный его именем. Почему же ведро с водой поднять заметно легче, чем с песком? Всё объясняется различной плотностью веществ. В единице объёма песка больше вещества, чем в воде, значит, он плотнее жидкой субстанции.

Структура практически всех окружающих субстанций неравномерна, а значит, и концентрация массы в единице веществ отличается, но незначительно. В задачах этой разницей пренебрегают.

Плотностью называется величина, получаемая вследствие разделения массы объекта на занимаемое им пространство. В физике имеет вид:

ρ = m/V, ρ – читается как «ро».

В системе СИ измеряется в кг/м³, на практике применяются кратные и дольные единицы измерения, например, см/кг 3 .

В физике существует несколько трактовок или типов плотностей:

• объёмная – рассматриваемая величина;
• поверхностная – отношение веса к площади;
• линейная – указывает на обратную пропорциональность массы к длине, применяется в двухмерных вычислениях;
• плотность электрического заряда.

Относительно к газам формула видоизменяется:

ρ = M / Vm, здесь, M и Vm – молярные масса с объёмом соответственно.

Особенности

• истинную – с вычетом пустот, заполненных воздухом либо жидкостью;
• насыпную – определяется описанным выше способом, когда в объём пористого/сыпучего материала входят пустоты.

Реальную плотность вычисляют из кажущейся (насыпной) через определённый на практике коэффициент – исключает пустоты.

С ростом температуры плотность вещества снижается, хотя есть исключения, например, вода. При 4 °C она наиболее плотная, при охлаждении и нагреве значение снижается, причём лёд легче воды в жидком состоянии.

Задачи

Определите, сколько весит кусок среднего по прочности мела объёмом 34,8 cм 3 .

Воспользуемся формулой массы через её плотность и объем:

ρ – табличная величина, для прочного мела принимается равной 2400 кг/м 3 .

Кубические сантиметры переведём в метры: 34,8 cм 3 = 0,00348 м 3 – запятая переносится на 4 знака левее или число делится на 10 000.

m = 2400 * 0,00348 = 8,352 кг.

Вычислить вес сухого дубового бруса длиной 3 м с квадратным сечением 10 × 10 см.

Для формулы массы тела (вещества) через плотность нужно высчитать объём бруса – параллелепипеда.

V = S * l = a * a * l.

ρ дуба зависит от его влажности, сухим принято считать пиломатериал с влажностью ниже 20%. Из таблицы ρ равняется не более 720 кг/м3.

Как найти массу вещества

Окружающее нас пространство наполнено разными физическими телами, которые состоят из разных веществ с различной массой. Школьные курсы химии и физики, ознакомляющие с понятием и методом нахождения массы вещества, прослушали и благополучно забыли все, кто учился в школе. Но между тем теоретические знания, приобретенные когда-то, могут понадобиться в самый неожиданный момент.

1

Вычисление массы вещества с помощью удельной плотности вещества. Пример – имеется бочка на 200 литров. Нужно заполнить бочку любой жидкостью, скажем, светлым пивом. Как найти массу наполненной бочки? Используя формулу плотности вещества p=m/V, где p – удельная плотность вещества, m – масса, V – занимаемый объем, найти массу полной бочки очень просто:

• Меры объемов – кубические сантиметры, метры. То есть бочка на 200 литров имеет объем 2 м³.
• Мера удельной плотности находится с помощью таблиц и является постоянной величиной для каждого вещества. Измеряется плотность в кг/м³, г/см³, т/м³. Плотность пива светлого и других алкогольных напитков можно посмотреть на сайте. Она составляет 1025,0 кг/м³.
• Из формулы плотности p=m/V => m=p*V: m = 1025,0 кг/м³* 2 м³=2050 кг.

Бочка объемом 200 литров, полностью наполненная светлым пивом, будет иметь массу 2050 кг.

2

Нахождение массы вещества с помощью молярной массы. M (x)=m (x)/v (x) – это отношение массы вещества к его количеству, где M (x) – это молярная масса X, m (x) – масса X, v (x) – количество вещества X. Если в условии задачи прописывается только 1 известный параметр – молярная масса заданного вещества, то нахождение массы этого вещества не составит труда. Например, необходимо найти массу йодида натрия NaI количеством вещества 0,6 моль.

• Молярная масса исчисляется в единой системе измерений СИ и измеряется в кг/моль, г/моль. Молярная масса йодида натрия – это сумма молярных масс каждого элемента: M (NaI)=M (Na)+M (I). Значение молярной массы каждого элемента можно вычислить по таблице, а можно с помощью онлайн-калькулятора на сайте: M (NaI)=M (Na)+M (I)=23+127=150 (г/моль).
• Из общей формулы M (NaI)=m (NaI)/v (NaI) => m (NaI)=v (NaI)*M (NaI)= 0,6 моль*150 г/моль=90 грамм.

Масса йодида натрия (NaI) с массовой долей вещества 0,6 моль составляет 90 грамм.

3

Нахождение массы вещества по его массовой доле в растворе. Формула массовой доли вещества ω=*100%, где ω – массовая доля вещества, а m (вещества) и m (раствора) – массы, измеряемые в граммах, килограммах. Общая доля раствора всегда принимается за 100%, иначе будут погрешности в вычислении. Несложно из формулы массовой доли вещества вывести формулу массы вещества: m (вещества)= /100%. Однако есть некоторые особенности изменения состава раствора, которые нужно учитывать при решении задач на эту тему:

• Разбавление раствора водой. Масса вещества растворенного X не изменяется m (X)=m’(X). Масса раствора увеличивается на массу добавленной воды m’ (р)=m (р)+m (H2O).
• Выпаривание воды из раствора. Масса растворенного вещества X не изменяется m (X)=m’ (X). Масса раствора уменьшается на массу выпаренной воды m’ (р)=m (р)-m (H2O).
• Сливание двух растворов. Массы растворов, а также массы растворенного вещества X при смешивании складываются: m’’ (X)=m (X)+m’ (X). m’’ (р)=m (р)+m’ (р).
• Выпадение кристаллов. Массы растворенного вещества X и раствора уменьшаются на массу выпавших кристаллов: m’ (X)=m (X)-m (осадка), m’ (р)=m (р)-m (осадка).

4

Алгоритм нахождения массы продукта реакции (вещества), если известен выход продукта реакции. Выход продукта находится по формуле η=*100%, где m (x практическая) – масса продукта х, которая получена в результате практического процесса реакции, m (x теоретическая) – рассчитанная масса вещества х. Отсюда m (x практическая)=/100% и m (x теоретическая)=/η. Теоретическая масса получаемого продукта всегда больше практической, в связи с погрешностью реакции, и составляет 100%. Если в задаче не дается масса продукта, полученного в практической реакции, значит, она принимается за абсолютную и равна 100%.

Варианты нахождение массы вещества – небесполезный курс школьного обучения, а вполне применяемые на практике способы. Каждый сможет без труда найти массу необходимого вещества, применяя вышеперечисленные формулы и пользуясь предлагаемыми таблицами. Для облегчения задания прописывайте все реакции, их коэффициенты.