Как найти плотность планеты

Значения масс планет Солнечной системы

Итак, мы разобрались с общими методиками расчета масс разных небесных тел и посчитали значения для Луны, Земли и Галактики. Давайте теперь составим рейтинг планет нашей системы по их массе.

Возглавляет рейтинг с наибольшей массой планет Солнечной системы – Юпитер, которому не хватило одного порядка чтобы наша система стала двойной. Еще чуть-чуть и у нас могло быть два Солнца, второе вместо Юпитера. Итак, масса этого газового гиганта равняется 1,9 × 10²⁷ кг.

Интересно, что Юпитер – единственная планета нашей системы, центр масс вращения с Солнцем которой расположен вне поверхности звезды. Он отстоит примерно на 7% расстояния между ними от поверхности Солнца.

Вторая по массе планета – Сатурн, его масса 5,7 × 10²⁶ кг. Следующим идет Нептун – 1 × 10²⁶. Четвёртая по массе планета, газовый гигант Уран, масса которого – 8,7 × 10²⁵ кг.

Далее идут планеты земной группы, каменистые тела, в отличие от газовых гигантов с их большим радиусом и относительно малой плотностью.

Самой тяжелой из этой группы является наша планета, ее массу мы уже рассчитали. Далее идет Венера, масса этой планеты равняется 4,9 × 10²⁴ кг. После нее в рейтинге идет Марс, он почти в 10 раз легче – 6,4 × 10²³кг. И замыкает его, как планета самой маленькой массы, Меркурий – 3,3 × 10²³кг. Что интересно, Меркурий даже легче, чем два спутника в Солнечной системе – Ганимед и Каллисто.

4. Определение географической широты по астрономическим наблюдениям

2.3.1 Уравнение Адамса Вильямсона

Допустим, что изменение давления вызвано исключительно весом лежащего выше слоя толщиной , тогда , или . Переходя от конечных приращений к бесконечно малым, получим искомое уравнение Адамса-Вильямсона

Чтобы определить плотность внутри планеты, необходимо

определить продольную и поперечную скорости распространения упругих волн,

вычислить сейсмический параметр,

задать предварительную модель Земли и вычислить силу тяжести,

численно решить дифференциальное уравнение, следовательно, уточнить модель Земли.

В заключение приведем основные формулы для построения сейсмологической модели Земли.

Закон всемирного тяготения

Согласно закону всемирного тяготения, каждое небесное тело притягивает другие тела силой, пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними. Это значит, что две планеты с большой массой будут оказывать более сильное влияние друг на друга, чем две планеты с меньшей массой. Также, чем ближе планеты находятся друг к другу, тем сильнее будет их взаимное притяжение.

Используя закон всемирного тяготения, можно вычислить среднюю плотность планеты. Для этого необходимо знать ее массу и радиус. Для расчета плотности применяется следующая формула:

Формула для вычисления средней плотности планеты:

Плотность = Масса / Объем

Массу планеты можно определить, измерив ее массу и силу притяжения, которую она оказывает на другие тела. Радиус планеты можно измерить наблюдательно или с помощью спутников. Используя эти значения, можно рассчитать объем планеты и, затем, среднюю плотность.

Закон всемирного тяготения является одним из важных инструментов астрономии, позволяющим узнать больше о строении и свойствах планет. Понимание этого закона помогает ученым исследовать и предсказывать множество астрономических явлений и движение небесных тел.

Немного размышлений

Как известно, средняя плотность планеты равна средней плотности Земли, т. е. эти показатели находятся в соотношении 1:1. Чтобы выяснить точные размеры: массу, вес и другие габариты, используют самые разные формулы.

Земля – это уникальная планета. Здесь есть множество неразгаданных тайн. Одной из загадок является то, что находится под поверхностью земли, в глубинах океанов, и какова плотность на глубине свыше семнадцати километров под поверхностью.

Ученых всего мира интересуют вопросы о возникновении Вселенной и ее истинном устройстве. Изучение космоса не дает ответы на все возникающие вопросы, но на некоторые уже нашлись ответы.

Определение масс звезд и галактик

Для того чтобы найти характеристики одинарных звездных систем применяется гравиметрический метод. Его суть в измерении гравитационного красного смещения света звезды. Оно измеряется по формуле ∆V=0,635 M/R, где M и R – масса и радиус звезды, соответственно.

Косвенно можно также вычислить массу звезды по видимому спектру и светимости. Сначала определяется ее класс светимости по диаграмме Герцшпрунга-Рассела, а потом вычисляется зависимость масса/светимость. Такой способ не подходит для белых карликов и нейтронных звезд.

Масса галактик вычисляется в основном по скорости вращения ее звезд (или просто по относительной скорости звезд, если это не спиральная галактика). Все тот же всемирный закон тяготения Ньютона нам гласит, что центробежную силу звезд в галактике можно выразить в формуле:

Только в этот раз в формулу мы подставляем расстояние от Солнца до центра нашей галактики и его массу. Так можно рассчитать массу Млечного Пути, которая равняется 2,2 × 10⁴⁴г.

Не забываем, что эта цифра – это масса галактики без учета звезд, орбиты которых располагаются вне орбиты вращения Солнца. Поэтому для более точных расчетов берутся самые внешние звезды рукавов спиральных галактик.

Для эллиптических галактик способ нахождения массы схож, только там берется зависимость между угловым размером, скоростью движения звезд и общей массой.

62.69. Формулы для любого космического тела

Любое космическое тело для удобства расчетов можно считать шаром, плотность которого одинакова в любой точке и равна некоторому среднему значению плотностей всех отдельных точек. В таком случае формула эквивалентности массы, плотности и объема с учетом геометрической формул объема шара будет иметь вид:

Связь массы, плотности и радиуса любого космического тела: $M = \frac \pi \rho R^3$

R – Примерный радиус тела

ρ – Средняя плотность

Для удобства оценки массы двух космических тел на предмет отличий стоит заметить, что согласно формуле, масса зависит от плотности и третьей степени радиуса тела.

Также высокую применимость имеют все формулы гравитации, поэтому есть необходимость напомнить их:

Ускорение свободного падения на поверхности любого космического тела: $g = \frac $

Первая космическая скорость вблизи поверхности любого космического тела: $V_1 = \sqrt >$

G – Гравитационная постоянная, равная $6,7 \cdot 10^ H \cdot \text ^2/\text ^2 $

R – Примерный радиус тела

Комбинация этих формул может дать еще одну применимую на ЕГЭ формулу:

Первая космическая скорость вблизи поверхности любого космического тела выраженная через ускорениесвободного падения на поверхности этого тела: $V_1 =\sqrt $

Для получения последней формулы необходимо внести определение эксцентриситета орбиты.

Эксцентриситет – мера отличия эллипса от окружности, существует в границах 0 e1, то второй эллипс будет более вытянут в горизонтальной плоскости и сильнее сжат в вертикальной.

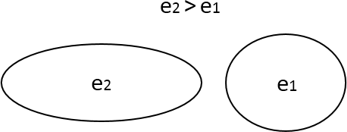
Чем меньше значение эксцентриситета, тем сильнее орбита похожа на окружность, а чем больше – тем сильнее отличается. При эксцентриситете, равном единице, орбита тела становится параболой.

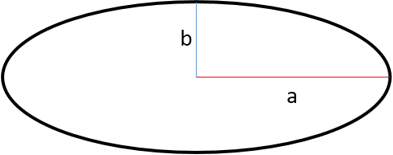
Эксцентриситет эллиптической орбиты можно найти по следующей формуле: $\varepsilon = \sqrt >, \text \; b — \text , a — \text $

Замкнутость орбиты вызвана попыткой тела покинуть гравитационное притяжение своего небесного тела (планеты/спутника/астероида). Если телу удается покинуть гравитационное притяжение планеты (то есть эксцентриситет тела стал равен 1), значит тело достигло второй космической скорости (скорость убегания) — наименьшей скорости, которую необходимо придать объекту для преодоления гравитационного притяжения этого небесного тела и покидания замкнутой орбиты вокруг него.

Формула второй космической скорости: $V_ = \sqrt V_1 = \sqrt = \sqrt >$, где все величины уже были введены в формулах выше.

Плотность

Впервые плотность Земли была выявлена И. Ньютоном в 1736 году. Он доказал, что этот показатель находится в пределах от 5 до 6 г/см3. Последующие измерения позволили выявить более точные данные, которые получили название средней плотности планеты Земля. Эта величина превышает плотность верхних горизонтов земной коры, которая на основе многочисленных измерений выходит на поверхность горных пород и может быть определена более точно.

Вычислить плотность поверхности Земли ученым еще как-то удалось, а вот решить, каким будет это значение на глубине свыше 16 километров, невозможно. Для определения этих показателей учитывается скорость сейсмических волн, сила тяжести и ряд других параметров.

Общие методики определения масс планет

Наиболее классический способ, как узнать массу планет – расчет при помощи формул третьего закона Кеплера. Он гласит, что квадраты периодов обращения планет соотносятся так же, как кубы больших полуосей орбит. Ньютон немного уточнил этот закон, внеся в формулу массы небесных тел. На выходе получилась такая формула –

Таким способом можно найти массу всех планет Солнечной системы и самого Солнца.И периоды обращения, и большие полуоси орбит планет Солнечной системы легко измеряются астрономическими методиками, доступными даже без сложных инструментов. А так как массу Земли мы уже рассчитали, можно все цифры подставить в формулу и найти конечный результат.

В отношении же экзопланет и других звезд (но только двойных) в астрономии обычно применяется метод анализа видимых возмущений и колебаний. Он основан на том факте, что все массивные тела “возмущают” орбиты друг друга.

Такими расчетами были открыты планеты Нептун и Плутон, еще до их визуального обнаружения, как говорят “на кончике пера”.

§ 31. Вычисление массы Солнца, Земли и планет

Массу Солнца можно найти из условия, что тяготение Земли к Солнцу проявляется в качестве центростремительной силы, удерживающей Землю на ее орбите (орбиту Земли для упрощения мы будем считать окружностью)

Здесь масса Земли, среднее расстояние Земли от Солнца. Обозначая продолжительность года в секундах через имеем. Таким образом

откуда, подставляя числовые значения , находим массу Солнца:

Ту же формулу можно применить для вычисления массы какой-либо планеты, имеющей спутника. В этом случае среднее расстояние спутника от планеты, время его обращения вокруг планеты, масса планеты. В частности, по расстоянию Луны от Земли и числу секунд в месяце указанным способом можно определить массу Земли.

Массу Земли можно определить также, приравнивая вес какого-либо тела к тяготению этого тела к Земле, за вычетом той составляющей тяготения, которая проявляется динамически, сообщая данному телу, участвующему в суточном вращении Земли, соответствующее центростремительное ускорение (§ 30). Необходимость указанной поправки отпадает, если для такого вычисления массы Земли мы воспользуемся тем ускорением тяжести, которое наблюдается на полюсах Земли Тогда, обозначив через средний радиус Земли и через массу Земли, имеем:

откуда масса Земли

Если среднюю плотность земного шара обозначить через то, очевидно, Отсюда средняя плотность земного шара получается равной

Средняя плотность минеральных пород верхних слоев Земли равна примерно Стало быть, ядро земного шара должно иметь плотность, значительно превышающую

Исследование вопроса о плотности Земли на различных глубинах было предпринято Лежандром и продолжено многими учеными. По выводам Гутенберга и Гаалька (1924 г.) на различных глубинах имеют место примерно следующие значения плотности Земли:

62.69. Формулы для любого космического тела

Любое космическое тело для удобства расчетов можно считать шаром, плотность которого одинакова в любой точке и равна некоторому среднему значению плотностей всех отдельных точек. В таком случае формула эквивалентности массы, плотности и объема с учетом геометрической формул объема шара будет иметь вид:

Связь массы, плотности и радиуса любого космического тела: $M = \frac{4}{3}\pi \rho R^3$

M – Масса тела

R – Примерный радиус тела

ρ – Средняя плотность 

Для удобства оценки массы двух космических тел на предмет отличий стоит заметить, что согласно формуле, масса зависит от плотности и третьей степени радиуса тела.

Также высокую применимость имеют все формулы гравитации, поэтому есть необходимость напомнить их:

Ускорение свободного падения на поверхности любого космического тела: $g = \frac{GM}{R^2}$

Первая космическая скорость вблизи поверхности любого космического тела: $V_1 = \sqrt{\frac{GM}{R}}$

G – Гравитационная постоянная, равная $6,7 \cdot 10^{-11} H \cdot \text{м}^2/\text{кг}^2 $

M – Масса тела

R – Примерный радиус тела

Комбинация этих формул может дать еще одну применимую на ЕГЭ формулу:

Первая космическая скорость вблизи поверхности любого космического тела выраженная через ускорениесвободного падения на поверхности этого тела: $V_1 =\sqrt{gR}$

Для получения последней формулы необходимо внести определение эксцентриситета орбиты.

Эксцентриситет – мера отличия эллипса от окружности, существует в границах 0

Так, если сравнить два эллипса с эксцентриситетами e2 > e1, то второй эллипс будет более вытянут в горизонтальной плоскости и сильнее сжат в вертикальной.

Чем меньше значение эксцентриситета, тем сильнее орбита похожа на окружность, а чем больше – тем сильнее отличается. При эксцентриситете, равном единице, орбита тела становится параболой.

Эксцентриситет эллиптической орбиты можно найти по следующей формуле: $\varepsilon = \sqrt{1 — \frac{b^2}{a^2}}, \text{где} \; b — \text{малая полуось}, a — \text{большая полуось эллипса}$

Замкнутость орбиты вызвана попыткой тела покинуть гравитационное притяжение своего небесного тела (планеты/спутника/астероида). Если телу удается покинуть гравитационное притяжение планеты (то есть эксцентриситет тела стал равен 1), значит тело достигло второй космической скорости (скорость убегания) — наименьшей скорости, которую необходимо придать объекту для преодоления гравитационного притяжения этого небесного тела и покидания замкнутой орбиты вокруг него.

Формула второй космической скорости: $V_{11} = \sqrt{2}V_1 = \sqrt{2gR} = \sqrt{\frac{2GM}{R}}$, где все величины уже были введены в формулах выше.

Прочитано
Отметь, если полностью прочитал текст

Решение задачи:

Тело на экваторе вращается вместе с планетой по окружности радиуса \(R\) (радиус планеты). Применим второй закон Ньютона:

Тело на полюсе лежит на оси вращения планеты, поэтому оно вращается лишь вокруг себя. Первый закон Ньютона для этого тела даст такое равенство:

По третьему закону Ньютона сила реакции опоры (\(N_э\) и \(N_п\)) равна весу тела (\(P_э\) и \(P_п\) соответственно). Учтите, что эти силы хоть и равны по величине, но противоположны по направлению и приложены к разным телам. С учетом этого запишем равенства (1) и (2) в такой системе:

Поделим нижнее равенство на верхнее. Так как \(P_п=2P_э\), то получим:

Поскольку в задаче нужно узнать среднюю плотность планеты \(\rho\), то запишем такие формулы: во-первых, формулу определения ускорения свободного падения \(g\) на поверхности планеты, во-вторых, формулу определения массы через плотность и объем, в-третьих, формулу определения объема шара.

Подставив (6) в (5), а полученное в (4), получим:

Чтобы выразить центростремительное ускорение \(a_ц\) через период вращения планеты \(T\) запишем такие формулы: формулу определения ускорения \(a_ц\) через угловую скорость \(\omega\) и формулу связи последней с периодом вращения \(T\).

Подставим выражения (7) и (8) в ранее полученное равенство (3):

Переведем данный в условии период вращения \(T\) в систему СИ (в секунды):

\

Планеты и спутники

Планеты и спутники Солнечной системы представляют собой шарообразные тела. К ним применимы многие формулы из геометрии. Одно из таких выражений — объем V = 4/3 • πR3 = πd3 / 6. Зная среднюю плотность небесного тела, можно вычислить ее массу m = 4/3 • ρπR3 = ρπd3 / 6

Еще одно важное определение — первая космическая скорость. При ее достижении небесное тело приобретает круговую орбиту и становится спутником

Если тело приобретет вторую космическую скорость, оно победит силу гравитационного притяжения, сможет покинуть свою орбиту и улететь в пространство на бесконечность. Важная характеристика — период вращения, показывающий отношение радиуса планеты к ее скорости. Период вращения определяет длительность суток или года.

Радиус планеты

Измерение радиуса планеты является сложной задачей и может выполняться различными способами. Один из распространенных методов — использование радиолокации. В этом методе используются радары, которые отправляют сигналы на поверхность планеты и затем измеряют время, которое требуется для возврата отраженного сигнала. На основе данной информации можно вычислить расстояние до поверхности планеты и, следовательно, ее радиус.

Также радиус планеты может быть измерен с помощью космических зондов. Космический зонд может быть отправлен на планету, чтобы пролететь вокруг нее или сесть на ее поверхность. В процессе выполнения этих миссий можно собрать данные о форме поверхности и измерить радиус планеты.

Знание радиуса планеты позволяет узнать ее объем и, в сочетании с ее массой, вычислить ее среднюю плотность. Средняя плотность планеты является важным параметром для понимания ее внутренней структуры и состава. Измерение радиуса планеты является одним из основных шагов в определении ее физических характеристик.

62.69. Формулы для любого космического тела

Любое космическое тело для удобства расчетов можно считать шаром, плотность которого одинакова в любой точке и равна некоторому среднему значению плотностей всех отдельных точек. В таком случае формула эквивалентности массы, плотности и объема с учетом геометрической формул объема шара будет иметь вид:

Связь массы, плотности и радиуса любого космического тела: $M = \frac\pi \rho R^3$

R – Примерный радиус тела

ρ – Средняя плотность

Для удобства оценки массы двух космических тел на предмет отличий стоит заметить, что согласно формуле, масса зависит от плотности и третьей степени радиуса тела.

Также высокую применимость имеют все формулы гравитации, поэтому есть необходимость напомнить их:

Ускорение свободного падения на поверхности любого космического тела: $g = \frac$

Первая космическая скорость вблизи поверхности любого космического тела: $V_1 = \sqrt>$

G – Гравитационная постоянная, равная $6,7 \cdot 10^ H \cdot \text^2/\text^2 $

R – Примерный радиус тела

Комбинация этих формул может дать еще одну применимую на ЕГЭ формулу:

Первая космическая скорость вблизи поверхности любого космического тела выраженная через ускорениесвободного падения на поверхности этого тела: $V_1 =\sqrt$

Для получения последней формулы необходимо внести определение эксцентриситета орбиты.

Эксцентриситет – мера отличия эллипса от окружности, существует в границах 0 e1, то второй эллипс будет более вытянут в горизонтальной плоскости и сильнее сжат в вертикальной.

Чем меньше значение эксцентриситета, тем сильнее орбита похожа на окружность, а чем больше – тем сильнее отличается. При эксцентриситете, равном единице, орбита тела становится параболой.

Эксцентриситет эллиптической орбиты можно найти по следующей формуле: $\varepsilon = \sqrt>, \text \; b — \text, a — \text$

Замкнутость орбиты вызвана попыткой тела покинуть гравитационное притяжение своего небесного тела (планеты/спутника/астероида). Если телу удается покинуть гравитационное притяжение планеты (то есть эксцентриситет тела стал равен 1), значит тело достигло второй космической скорости (скорость убегания) — наименьшей скорости, которую необходимо придать объекту для преодоления гравитационного притяжения этого небесного тела и покидания замкнутой орбиты вокруг него.

Формула второй космической скорости: $V_ = \sqrtV_1 = \sqrt = \sqrt>$, где все величины уже были введены в формулах выше.

Еще факты

1. Стоя на одном месте, человек считает, что он стоит. На самом деле он двигается, но вместе с Землей. Это происходит из-за вращения планеты вокруг Солнца и вокруг своей оси. В зависимости от места, где стоит объект, скорость его движения в пространстве может составлять 1600 км/ч. На экваторе люди двигаются быстрее, а вот те, кто живет в северных и южный районах планеты, практически стоят на месте.
2. Земля движется вокруг Солнца со скоростью 107826 км/ч.
3. Считается, что возраст Земли около 4,5 млн лет.
4. В центре планеты располагается магма.
5. На планете происходят водные приливы и отливы. Это явление возникает из-за воздействия Луны – естественного спутника Земли.
6. Самая холодная точка на планете – Антарктида. Здесь температура может опускаться до -80 и более градусов Цельсия.
7. Некоторые ученые предполагают, что когда-то у Земли было два спутника.

На планете есть множество загадочных мест, где происходят странные явления. Ученые пытались их объяснить: что-то им раскрыть удалось, а что-то все так же остается тайной. Одной из таких тайн являются движущиеся камни на плато Плайя в США. На этом участке горные породы совершают перемещения по пескам, оставляя следы в виде борозд. Это уникальное явление не имеет аналогов, и нет другого места, где происходило бы подобное.

Есть мнения, что когда-то, планета была фиолетовой. Этот окрас ей придавали бактерии, проживающие на всей территории Земли. Позже планета стала зелено-голубой.

Интересные факты

Есть мнения, что Земля – это единственная планета во всей Вселенной со сложной формой жизни, хотя это утверждение пока не доказано. Почему-то ученые считают, что формы жизни могут развиваться только такими, которые привычно видеть людям на нашей планете, и никто не допускает, что есть формы, способные расти и развиваться при совершенно других условиях. Это утверждение полностью никто не опроверг, а значит, оно имеет право на существование. Хотя ученые мира выяснили много интересного о планете:

1. Средняя плотность планеты Земля выше, чем у других планет.
2. Среди планет земной группы только она имеет наибольшую гравитацию и наисильнейшее магнитное поле.
3. Хотя все люди и представляют планету в форме ровного шара, на самом деле это не совсем так. Она больше похожа на два приплюснутых полукруга, имеющих выпуклости в зоне экватора. Эту особую форму связывают с вращением планеты.
4. Изначально существовал один континент под названием Пангея. По мере движения земной коры образовались известные сегодня континенты.
5. В защитном слое имеются озоновые дыры: самая крупная располагается над Антарктидой. Ее обнаружили в 2006 году.

Общий итог

Средняя плотность является важным параметром для изучения космических объектов. Она позволяет определить их массу и размеры, понять, как они формировались и на какой стадии развития находятся. Расчет средней плотности может быть произведен по массе и объему космического объекта. Знание средней плотности помогает изучать процессы, протекающие во Вселенной, и определять материал, из которого состоят космические тела.

• Средняя плотность выражает количество массы в единице объема.
• Вычисляется по формуле ρ = m/V.
• Для определения средней плотности необходимо знать массу и объем объекта.
• Средняя плотность важна для определения массы, размеров и стадии развития космических объектов.
• Знание средней плотности позволяет изучать процессы, протекающие во Вселенной.

Итог

Средняя плотность в астрономии является важной характеристикой, которая помогает ученым лучше понять небесные объекты и их структуру. Вычисление средней плотности планет, звезд и галактик может осуществляться различными способами, но как правило, определяется отношением массы объекта к его объему

Кроме того, плотность играет важную роль в космических исследованиях, так как она влияет на гравитационное и электромагнитное взаимодействие между небесными объектами и управляет их движением и эволюцией.

Изучение плотности помогает нам лучше понимать вселенную и расширять наши знания о ее устройстве. Таким образом, средняя плотность небесных объектов является ключевым показателем в астрономии, который может помочь в решении многих важных вопросов.