Идеальный газ

Введение

Модель идеального газа — это простейшая статистическая модель, неплохо описывающая физику реальных газов.
Рассмотрим сосуд объёмом $V$ в котором движутся небольшие шарики массы $m$.
При движении они упруго сталкиваются друг с другом (подобно бильярдным шарам, но без вращения)
и не теряя энергии, отражаются от стенок сосуда.
Далее эти шарики будут называться одноатомными молекулами.

В реальных газах молекул очень много.
В результате столкновений, они быстро
«забывают» начальные условия (положение и скорость)
и их движение становится случайным.
В частности, независимо от начальных условий, концентрация частиц в различных частях объёма со временем
оказывается примерно
одинаковой, а средняя скорость (по всем частицам) равной нулю.
Такое состояние называется равновесным.

Примеры решения задач

Задание	Вычислите плотность по хлору смеси 55 л азота и 180 л кислорода.
Решение	Найдем объемные доли веществ в смеси:

φ (N₂) = 55 / (55 + 180) = 55 / 235 = 0,23.

φ (O₂) = 180 / (180 + 55) = 180 / 235 = 0,77.

Объемные доли газов будут совпадать с молярными, т.е. с долями количеств веществ, это следствие из закона Авогадро. Найдем условную молекулярную массу смеси:

M_r conditional (mixture) = 0,23 × 28 + 0,77 × 32 = 6,44 + 24,64 = 31,08.

Найдем относительную плотность смеси по водороду:

Ответ Плотность по хлору смеси, состоящей из азота и кислорода равна 0,44.

Задание	Рассчитайте плотности газов хлористого нитрозила NOCl и бутана C4H10 по воздуху.
Решение	Отношение массы данного газа к массе другого газа, взятого в том же объеме, при той же температуре и том же давлении, называется относительной плотностью первого газа по второму. Данная величина показывает, во сколько раз первый газ тяжелее или легче второго газа.

Относительную молекулярную массу воздуха принимают равной 29 (с учетом содержания в воздухе азота, кислорода и других газов). Следует отметить, что понятие «относительная молекулярная масса воздуха» употребляется условно, так как воздух – это смесь газов.

M_r(NOCl) = A_r(N) + Ar(O) + Ar(Cl) = 14 + 16 + 35,5 = 65,5.

Давление идеального газа

Найдём давление, оказываемое идеальным газом на неподвижный поршень (или стенку сосуда).
Для этого рядом с поршнем выделим тонкий слой газа ширины $\Delta L$,
в котором можно пренебречь столкновениями молекул друг с другом (но их там должно быть по-прежнему много).
Если $S$ — это площадь поршня, то объём слоя равен $V=S\,\Delta L$.

Рассмотрим $N_{v}$ молекул, которые имеют примерно одинаковую компоненту скорости $v_x$
и движутся в направлении поршня $(v_x \gt 0)$.
За время $\Delta t = \Delta L/v_x$ эти молекулы из слоя шириной $\Delta L$,
успеют столкнутся с поршнем (последними — молекулы, находящиеся на границе слоя).
После упругого столкновения (поршень неподвижен),
компонента импульса $p_x$ молекул
меняет знак и полное изменение их импульса, переданное поршню, равно $\Delta p_x=2\,p_x$.
Поэтому суммарное давление со стороны этих молекул на поршень равно:
$$
P ~=~ \frac{F_x}{S} ~=~ N_{v}\,\frac{\Delta p_x}{\Delta t}\,\frac{1}{S}
~=~ N_v\,\frac{2\,p_x}{S\,\Delta t} ~=~ 2\,\frac{N_v}{V}\,p_x\,v_x.
$$

Молекулы газа движутся с различными скоростями $\mathbf{v}=\{v_x,v_y,v_z\}$, в различных направлениях.
В результате столкновений молекул друг с другом, их скорости постоянно изменяются, становясь случайными величинами.
Пусть $f(v_x)$ — это плотность распределения вероятностей для скоростей $v_x$.
Оно нормировано на единицу (интеграл от него по $dv_x$ равен $1$).
Естественно считать это распределение симметричным.
Число молекул $N_v$, имеющих компоненту скорости $v_x$ с небольшим разбросом $dv_x$, по определению,
равно $N_v~=~N\,f(v_x)\,dv_x$, где $N$ — общее число молекул (с любыми скоростями):

$$
\int\limits^\infty_{-\infty} f(v_x)\,dv_x = 1,~~~~~~~~~~~~~~~~~~~~f(-v_x)=f(v_x).
$$

Полное давление равно сумме давлений со стороны молекул, движущихся со всеми возможными скоростями $v_x$
в направлении поршня ($v_x \gt 0$):
$$
P~=~
2\,\frac{N}{V}\,\int\limits^\infty_{0} p_x\,v_x\,f(v_x)\,dv_x
~=~ \frac{N}{V}\,\int\limits^\infty_{-\infty} p_x\,v_x\,f(v_x)\,dv_x = \frac{N}{V}\,\langle p_xv_x \rangle,
$$
где учтена симметричность распределения и угловыми скобками обозначено среднее значение (интеграл).
Так как направления в пространстве равноправны:
$\langle \mathbf{p}\mathbf{v} \rangle = \langle p_x v_x + p_y v_y + p_zv_z \rangle = 3\, \langle p_xv_x \rangle$,
окончательно имеем:
$$
P ~=~ n\,\frac{\langle \mathbf{p}\mathbf{v} \rangle}{3},~~~~~~~~~~~~~~~~~~~n=\frac{N}{V}.
$$
Отношение числа молекул $N$ к объёму $n = N/V$ называется концентрацией молекул
(число в единице объёма).
Обратная величина $v=V/N$, называемая удельным объёмом,
— это часть объёма сосуда, приходящаяся на одну молекулу.
Усреднение по всем направлениям скорости производится при помощи тройного
интеграла с весами равными распределению каждой компоненты скорости: $f(v_x)f(v_y)f(v_z)\,dv_x\,dv_y\,dv_z$.

Для нерелятивистского газа импульс молекул равен $\mathbf{p}=m\mathbf{v}$, поэтому
полученное соотношение можно переписать следующим образом:
$$
P\,V ~=~\frac{2}{3}\,N\,\left\langle \frac{m\mathbf{v}^2}{2} \right\rangle,
$$
где под знаком среднего находится кинетическая энергия поступательного движения молекулы.

Второй способ записи основного уравнения МКТ

Определение

В середине 30-х годов XIX столетия французскому инженеру Эмилю Клапейрону удалось обобщить накопленный до этого времени экспериментальный опыт изучения поведения газов во время разнообразных изопроцессов и получить формулу, которую в будущем назвали универсальным уравнением состояния идеального газа:

\(P*V = n*R*T \)

n является количеством вещества в молях; T представляет собой температуру по абсолютной шкале и обозначается в кельвинах.

Величина R является универсальной газовой постоянной. Этот термин был введен в уравнение русским химиком Д.И. Менделеевым. Исходя из этого, запись уравнения называют законом Клапейрона-Менделеева.

Определение

С помощью данного выражения можно определить формулу для расчета давления газа:

\(P=\frac{n*R*T}{V}\)

Полученное уравнение объясняет линейный рост давления при увеличении температуры в условиях стабильности объема. Если объем уменьшается с сохранением температуры, то давление увеличивается по гиперболе. Данные закономерности явления отражены в законах Гей-Люссака и Бойля-Мариотта.

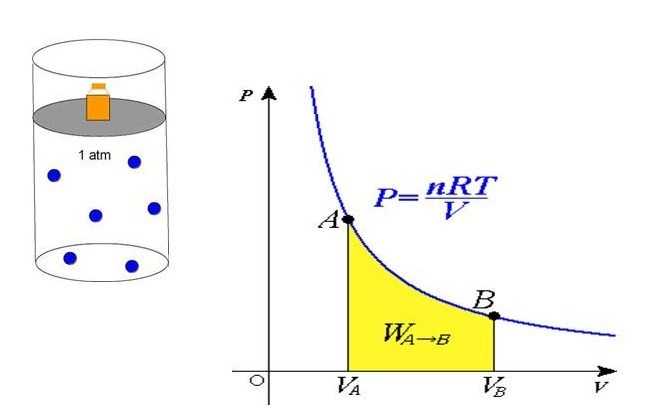
Сравнивая представленное выражение с записью формулы, которая вытекает из положений молекулярно-кинетической теории, можно установить связь кинетической энергии одной частицы, либо системы в общем, и абсолютной температуры.

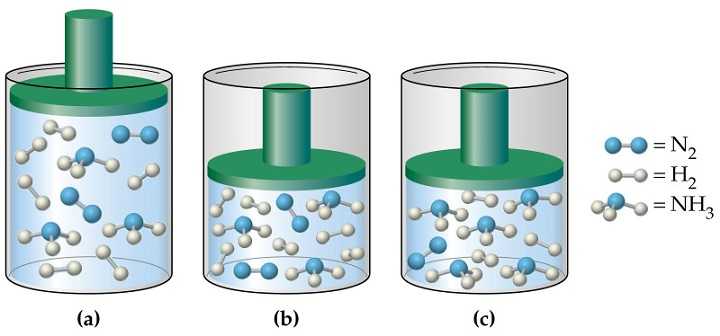
Важно отметить, что при расчетах с использованием формулы для Р, вытекающей из уравнения Клапейрона, связь с химическим составом газа отсутствует. Если давление определяют с помощью выражения, согласно понятию молекулярно-кинетической теории, то данную связь следует учитывать в виде параметра m

В том случае, когда определяют давление смеси идеальных газов, применяют один из следующих методов:

1. Расчет средней массы частиц m, либо среднего значения молярной массы М с учетом атомных процентов каждого газа в смеси.
2. Применение закона Дальтона, согласно которому давление в системе равно сумме парциальных давлений всех ее компонентов.

Пример

Предположим, что молекулы кислорода движутся со средней скоростью в 500 м/с. Требуется рассчитать, каково давление в сосуде, объем которого равен 10 литров, содержащий 2 моль молекул.

Для того чтобы найти ответ, следует применить формулу для Р из молекулярно-кинетической теории:

\(P=\frac{N*m*v^{2}}{3*V}\)

Из-за неизвестных параметров m и N требуется выполнить некоторые преобразования формулы:

\(m=\frac{M}{NA}\)

\(n=\frac{N}{NA}\)

\(m*N= M*n\)

\(P=\frac{M*n*v^{2}}{3*V}\)

Давление в газовой смеси

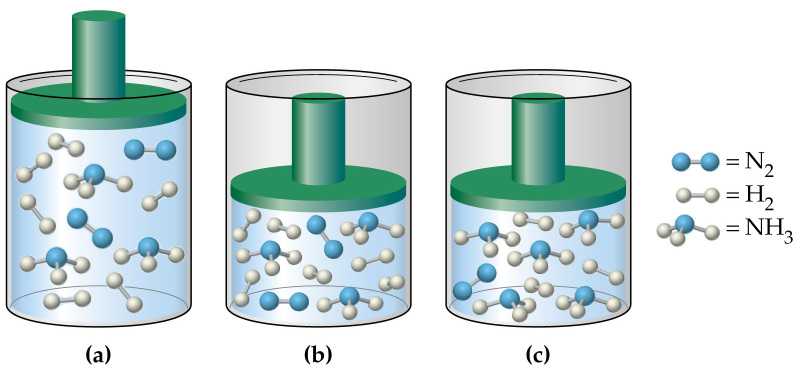
Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.

Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:

• Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
• Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.

Слайд 21Опр. Соприкосновение тел, при котором возможна лишь передача тепла от одного

тела к другому, будем наз. тепловым контактом этих тел. Мы говорим, две системы имеют равные температуры, если при тепловом контакте их состояния не меняются.Впервые понятие температуры возникло из субъективных ощущений в области восприятия «степени нагретости» тела. Объективная возможность введения понятия температуры связана с важным постулатом термоди­намики: «Если две термодинамические системы находятся в тепловом равновесии с третьей, то они должны быть в равновесии и между собой». Указанное равновесие не зависит от объема, давления, плотности и других (помимо температуры) величин, определяющих состояние систем.

Слайд 34Термометрические шкалыУвеличение объема термического тела при нагревании и дает косвенную информацию

об изменении температуры. Если зависимость объема от температуры линейна, то достаточно выбрать две реперные точки, приписать этим точкам определенные значения температуры t l и t 2 и разделить полученный интервал на некоторое число промежутков (делений температурной шкалы). Наличие такой шкалы и позволяет измерять значение температуры в интервале между реперными точками. Очевидно, что подобные единицы измерения температур и температурные шкалы являются эмпирическими и условными. Наиболее известны три эмпирические шкалы температур: Цельсия, Реомюра и Фаренгейта, отличающиеся значениями температур реперных точек. В качестве реперных точек Цельсий выбрал температуру таяния льда (t1 = 0°С) и ки­пения воды (t2 = 100°С) при нормальном давлении и разделил промежуток t2-tl на 100 интервалов — градусов. (Приведен современный вариант шкалы Цельсия).

Теплоемкость идеальных газов

Рисунок 4. Теплоемкость идеального газа. Автор24 — интернет-биржа студенческих работ

Экспериментально измеренные теплоемкости идеальных газов при обычных внешних условиях практически идеально согласуются с другими постулатами классической термодинамики. Однако, в целом классическая гипотеза теплоемкости данных веществ не может считаться вполне удовлетворительной и подходящей для всех систем. Существует много различных примеров весомых расхождений между экспериментом и теорией. Это обуславливается тем, что существующая теория не в состоянии в полной мере учесть энергию, непосредственно связанную с внутренними движениями в самой молекуле.

Гипотезу о равномерном и прямолинейном распределении тепловой энергии по степеням свободы возможно применить и к движению частиц в твердом теле. Атомы, которые входят в состав кристаллической решетки, совершают определенные колебания возле положений равновесия. Энергетический потенциал таких вибраций представляет собой внутреннюю силу физического вещества.

Замечание 2

Опыт доказывает, что практически все идеальные газы имеют молярную теплоемкость, возникающую при обычных температурах.

Но, при нулевой температуре сразу появляются значительные расхождения между движущимися элементами. Следует отметить, что «количество теплоты» и «теплоемкость» — достаточно неудачные термины. Они достались современной науке в наследство от устаревших принципов теории теплорода, которая господствовала в начале XVIII столетия.

Эта гипотеза рассматривала теплоту и энергию идеальных газов как универсальное невесомое вещество, содержащееся во всех физических телах. Считалось, что такие параметры не могут быть ни созданы, ни уничтожены. Нагревание материальных веществ объяснялось увеличением, а охлаждение – уменьшением содержащегося внутри них теплорода. Однако теория теплорода не совсем состоятельна. Она не может описать, почему одинаковые изменения внутренней энергии тела возможно получить, передавая ему абсолютно разное количество теплоты в зависимости от совершаемой системой работы. Поэтому лишено физического смысла и само утверждение, что «в физическом теле содержится определенный запас теплоты».

Пример задачи

Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.

Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:

Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:

Объем сосуда в кубических метрах равен 0,01 м 3 . Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.

Единицы измерений

Молекул в макроскопических системах очень много, поэтому
их количество принято измерять в молях.
Один моль содержит $N_A=6.022~140~76\cdot 10^{23}$ штук молекул (число Авогадро — это точное целое число).
Произведение $N_A$
на постоянную Больцмана $k=1.380~649\cdot 10^{-23}\,Дж/K$ (точно)
называют газовой постоянной:
$$
R = k\,N_A = 8.314~462~618~153~24 \, Дж/ моль\cdot K.
$$
Если число молекул $N$ измеряют в молях, а не в штуках, то уравнение состояния идеального
газа принимает вид:
$$
P\,V ~=~ N\,R\,T.
$$

Молекулярная масса — это масса одной молекулы.
Её измеряют в единицах массы $m_u=1.660~565\cdot 10^{-27}\,кг$, равной
одной двенадцатой массы атома углерода $^6_{12}\text{C}$, где
верхний индекс у элемента — это число протонов (заряд ядра), нижний — общее количество протонов и нейтронов
Удобно помнить, простое соотношение:
$$
m_u\,N_A\approx 1\,г/моль.
$$

Молярная масса — это масса одного моля вещества.
Молярная масса двухатомного водорода $^1_1\text{H}_2$ примерно равна $2\,г/моль$,
у воды $\text{H}_2 (\,^8_{16}\text{O})$ — это $\approx ~(2+16)\,г/моль ~=~ 18\,г/моль$.
Воздух, которым мы дышим, является смесью газов:
$0.76\cdot \,^7_{14}\text{N}_2+ 0.23\,\cdot \,^8_{16}\text{O}_2 + 0.01\cdot \,^{18}_{40}\text{Ar} +…$ (по массе).

В системе Си давление измеряется в паскалях: $Па = Н/м^2$,
а объём иногда измеряют в литрах: $1\,л \,=\, 10^{-3}\,м^3$ (кубик со стороной $10\,см$).
Тепловую энергию измеряют в калориях: $1\,кал~=~4.1868\,Дж$.
Нормальным давлением и температурой
принято считать:
$$
P~=~1\,атм~=~1.01325 \cdot 10^5\,Па~~~~~~~~~и~~~~~~~~~T ~=~ 273.15\,K.
$$
В этих условиях в одном кубическом метре
содержится $44.6$ моля молекул газа: $1.01\cdot10^5\cdot 1/(8.31\cdot 273.15$).

Молекулы имеют размеры порядка ангстрема $1\,Å ~=~10^{-8}\,см~=~10^{-10}\,м$.
Например, диаметр атома водорода $2\,r_B=1.06\,Å$. Разброс диаметров молекул
простых газов невелик:
$$
d(\text{H}_2)~=~2.7\,Å,~~~~~d(\text{O}_2)~=~3.6\,Å,~~~~~~d(\text{H}_2\text{O})~=~2.9\,Å,~~~~~~~
d(\text{N}_2)~=~3.7\,Å.
$$
Расстояние между молекулами газа при нормальных условиях порядка $30\,Å~=~(1\,м^3/44.5\cdot 6.02\,10^{23})^{1/3}$
(в $10$ раз больше их типных размеров).
В жидкости и твёрдых телах молекулы «упакованы» достаточно плотно.
Например плотность воды $10^3\,кг/м^3$, поэтому при молярной массе $18\,г/моль$,
в кубическом метре находится $55\cdot 10^3\,N_A$ молекул.
Типичное расстояние между ними равно $3.1\,Å~=~(1\,м^3/55\cdot 10^3\cdot 6.02\,10^{23})^{1/3}$.
Это приводит к тому, что вода оказывается практически несжимаемой.

Физика 7 класс. Давление газа и жидкости. Закон Паскаля.

Физика 7 класс. Конспект. Давление газаДавление газа. Передача давления жидкостями и газами. Закон Паскаля. Расчет давления жидкости.

Задачи на тему Давление

Газы, в отличие от твердых тел и жидкостей, заполняют весь сосуд, в котором находятся.

Газ, находясь в каком-либо сосуде, оказывает давление на стенки, дно и крышку тела, в котором находится. Молекулы газа беспорядочно движутся, сталкиваясь друг с другом и со стенками сосуда, внутри которого находятся. Давление газа на стенки сосуда (и на помещенное в газ тело) вызывается ударами молекул газа.

При уменьшении объема газа его давление увеличивается, а при увеличении объема давление уменьшается при условии, что масса и температура газа остаются неизменными.

Давление газа в закрытом сосуде тем больше, чем выше температура газа, при условии, что масса газа и объем не изменяются.

Из опытов получен общий вывод, что давление газа тем больше, чем чаще и сильнее молекулы ударяют о стенки сосуда.

Закон Паскаля:

Давление, производимое на жидкость или газ, передается в любую точку без изменений во всех направлениях.

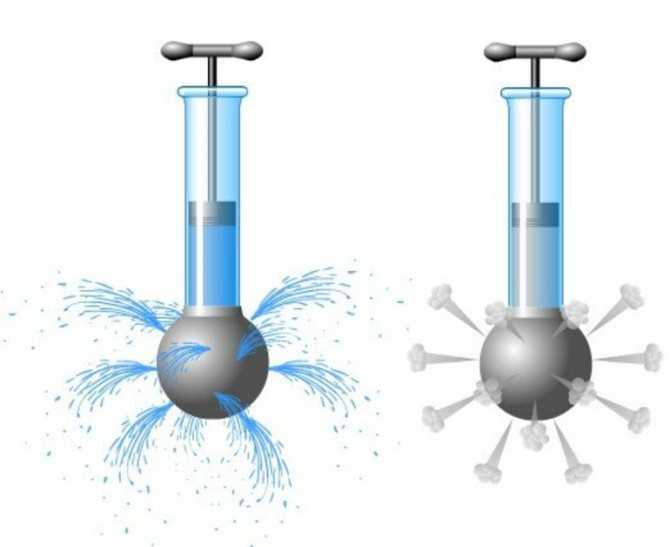
Опыт иллюстрирует закон Паскаля

Свойство газов передавать давление используют в технике при устройстве различных пневматических машин и инструментов.

На жидкости, как и на все тела на Земле, действует сила тяжести. Поэтому каждый слой жидкости, налитой в сосуд, своим весом создает давление на другие слои, которое по закону Паскаля передается по всем направлениям. Следовательно, внутри жидкости существует давление.

Опыты подтверждают, что внутри жидкости существует давление и на одном и том же уровне оно одинаково по всем направлениям. С глубиной давление увеличивается.

Давление жидкости на дно и стенки сосуда зависит только от плотности и высоты столба жидкости.

Расчет давления жидкости на дно и стенки сосуда:

где p – давление (Па), ρ – плотность жидкости (кг/м3), h– высота столб жидкости (м), g– ускорение свободного падения (Н/кг).

Сосуды, соединенные между собой (например, чайник, лейка и т.п.), называют сообщающимися.

В сообщающихся сосудах любой формы и сечения поверхности однородной жидкости устанавливаются на одном уровне (при условии, что давление воздуха над жидкостью одинаково).

При равенстве давлений высота столба жидкости с большей плотностью будет меньше высоты столба с меньшей плотностью.

Конспект составлен на основании теоретического материала учебника «Физика 7 класс» А.В. Перышкин

Задачи

Атмосферное давление

Скачать конспект:

teoriya_7_davleniegaza

Для выпуска расплавленного металла из литейного ковша делают на дне ковша отверстие, закрываемое спе…

Почему футбольные и баскетбольные мячи помещают в прочные кожаные чехлы?

Поршневой насос может произвести давление 5·10 5 Па. На какую высоту можно поднять воду этим насосом…

При сжатии поршнем кислорода в закрытом сосуде изменяется ли: а) Масса кислорода; б) объем кислорода…

Давление газа

Как уже неоднократно отмечалось, давление газа возникает в результате ударов молекул о стенки сосуда. Если мы считаем, что молекулы взаимодействуют со стенкой по законам абсолютно упругого удара, то частица передает стенке импульс, равный изменению импульса самой молекулы. Направим ось Х перпендикулярно стенке (рис.1), в этом случае изменение импульса стенки при ударе одной молекулой:

Получи помощь с рефератом от ИИ-шки

ИИ ответит за 2 минуты

где $m_0$- масса молекулы.

Рис. 1

Поток импульса, который передается стенке за счет ударов молекулами, которые движутся со скоростями близкими к v, направлен к стенке, равен $nf(v)m_0{v_x\ }^2dv$, отсюда:

где

В результате непосредственного интегрирования получаем:

Так как мы уже отмечали, что рассматриваем единичную площадку стены в течение времени. равном 1с, то можно записать, что давление будет равно:

Давление газа изотропно, это величина скалярная.

При постоянном объеме давление газа массы m подчиняется закону Шарля:

где $p_0$- давление газа при температуре $T_0=273\ К$.

Давление смеси идеальных газов равно сумме их парциальных давлений:

\

Уравнение (7) имеет название — это закон Дальтона.

Парциальным давлением называют давление компоненты смеси газа, каким оно бы было, если бы других газов в смеси не было.

Ряд важных уравнений молекулярной физики, в которые входит давление:

1. Уравнение состояния идеального газа(1):

   $p=nkT$(8).

2. Уравнение состояния идеального газа(2) в виде уравнения Менделеева — Клайперона:

   $pV=\nu RT$(9).

3. Основное уравнение МКТ:

   \

4. Работа газа:

   \

Пример 1

Задание: В процессе сжатия 1-2 с линейной зависимостью р(V). Давление идеального газа возросло в 3 раза. Затем газ сжали в изобарном процессе 2-3 до первоначального объема. Найти отношение работ, совершенных газом в процессах расширения и сжатия. Температуры в состояниях 1 и 2 считать одинаковыми.

Рис. 2

Решение:

Работу газа (или над газом) можно рассчитать по формуле:

\

Если мы рассматриваем процесс (как в условиях нашей задачи) в осях p(V), то исходя из геометрического смысла интеграла работа A будет равна площади криволинейной трапеции (в общем случае), а в нашем площади прямоугольника, когда газ расширяется и площади трапеции, когда газ сжимают. Найдем эти площади.

Площадь прямоугольника:

\

Площадь трапеции:

\

Из условий задачи имеем:

\

Найдем отношение $\frac{A_{2\to 3}}{A_{1\to 2}}$:

\

Ответ: Работа, которую совершает газ в процессе 2-3 в 1,5 больше, чем работа по сжатию газа при заданных условиях.

Пример 2

Задание: Определите, как изменяется давление постоянной массы идеального газа, если в процессе объем увеличивают, температура уменьшается?

Решение:

За основу решения возьмем уравнение Менделеева — Клайперона:

\

Выразим из него давление:

\

Ответ: В данном процессе давление уменьшается.

Пример 3

Задание: В процессе, график которого приведен на рисунке (рис.3) давление $p\sim T^n.\ $Найти значение n, если масса газа постоянна.

Рис. 3

Решение:

Из рисунка имеем зависимость p(V):

\

Из уравнения Менделеева — Клайперона:

\

Используем (3.1) заменив объем, получим:

\

Ответ: Получили $p\sim T^{\frac{1}{2}}$, следовательно, $n=\frac{1}{2}.$

Внутренняя энергия

Энергия «точечной» молекулы, движущейся без вращения, равна $m\mathbf{v}^2/2$.
Определим внутреннию энергию газа одноатомных молекул
как суммарное значение
средних энергий $N$ молекул такого газа:
$$
U ~=~ N\,\left\langle \frac{m\mathbf{v}^2}{2} \right\rangle ~=~ N\,\frac{3}{2}\,k\,T ~=~ N\,\frac{3}{2}\,\Theta.
$$

В общем случае связь внутренней
энергии и температуры зависит от «устройства» молекул. Поэтому её
удобно записать в следующем виде:
$$
U ~=~ \frac{N\,\Theta}{\gamma-1} ~=~\frac{P\,V}{\gamma-1},
$$
где для одноатомного нерелятивистского идеального газа $\gamma=5/3$. В случае сложных молекул
или при релятивистских скоростях параметр $\gamma$ может отличаться от значения $5/3$, но он всегда больше единицы.

Например, кванты излучения с энергией $E$, движутся со скоростью света $|\mathbf{v}|=c$.
Для них справедливо соотношение $\mathbf{p}\mathbf{v}=E$,
поэтому $P\,V ~=~ N\,\langle\mathbf{p}\mathbf{v}\rangle/3 ~=~ N\,E/3=U/3$, т.е. $\gamma=4/3$.

◊ В комнате включили обогреватель и её температура повысилась со значения $T_1$ до значения $T_2$.
Как изменилась при этом внутренняя энергия воздуха?

Объём и давление в комнате неизменны: $P\,V=k\,N\,T=\text{const}$.
При нагревании уменьшается концентрация молекул воздуха $n=N/V$.
Внутренняя энергия воздуха в комнате не меняется: $U=k\,N\,T/(\gamma-1)=\text{const}$.

Выравнивание кинетических энергий

Пусть сосуд разделён на две части лёким подвижным поршнем.
В одной части, объёмом $V_1$, находится $N_1$ молекул с массами $m_1$,
а во второй части $V_2$ есть $N_2$ молекул массами $m_2$.
Так как поршень подвижен, в равновесии давление в обоих частях должно быть одинаковым.
Совпадают также и средние значения кинетических энергий молекул:
$$
\left\langle \frac{m_1\mathbf{v}^2_1}{2} \right\rangle~=~
\left\langle \frac{m_2\mathbf{v}^2_2}{2} \right\rangle.
$$

Действительно, молекула из одной половины сосуда, налетая на поршень,
передаёт ему часть своего импульса (поршень подвижен).
Поршень начинает двигаться навстречу молекулам из другой части сосуда.
Сталкиваясь с ними, он передаёт им этот импульс. Его «подёргивания» туда-сюда
приводят к выравниванию средней кинетической энергии молекул слева и справа от поршня.

Отметим, что при столкновении молекулы с поршнем, она передаёт ему свой импульс,
но не может передать момент вращения или внутреннюю колебательную энергию.
Поэтому в результате выравниваются именно кинетические энергии
поступательного движения молекул.

В качестве второго примера рассмотрим газовую смесь, состоящую из молекул двух типов с массами $m_1$ и $m_2$.
Пусть две такие молекулы движутся со скоростями $\mathbf{v}_1$ и $\mathbf{v}_2$.
В равновесном состоянии скорости молекул имеют произвольные направления и нескоррелированы друг с другом.
Это означает, что совместная плотность распределения вероятностей равна произведению распределений для
каждой молекулы: $f(\mathbf{v}_1,\mathbf{v}_2)=f_1(\mathbf{v}_{1})\,f_2(\mathbf{v}_2)$,
поэтому: $\langle\mathbf{v}_1\mathbf{v}_2\rangle = \langle\mathbf{v}_1\rangle\langle \mathbf{v}_2\rangle = 0$:
$$
\langle\mathbf{v}_1\mathbf{v}_2\rangle = \int f(\mathbf{v}_1,\mathbf{v}_2)\,\mathbf{v}_1\mathbf{v}_2\,d^3\mathbf{v}_1\,d^3\mathbf{v}_2
~=~
\int f_1(\mathbf{v}_{1})\,\mathbf{v}_1\,d^3\mathbf{v}_1 \cdot \int f_1(\mathbf{v}_{2})\,\mathbf{v}_2\,d^3\mathbf{v}_2
~=~\langle\mathbf{v}_1\rangle\langle \mathbf{v}_2\rangle.
$$

В силу закона сохранения импульса, суммарный импульс $m_1\mathbf{v}_1+m_2\mathbf{v}_2$ молекул
при столкновении не изменяется, а меняется относительная скорость $\mathbf{v}_2-\mathbf{v}_1$.
В системе отсчёта центра масс (где суммарный импульс равен нулю), распределение вектора
относительной скорости должно быть изотропным (нет выделенных направлений).
Поэтому, суммарный импульс и относительная скорость также должны быть нескоррелированными:
$$
0 = \langle(\mathbf{v}_2-\mathbf{v}_1)(m_1\mathbf{v}_1+m_2\mathbf{v}_2)\rangle
= \langle m_2\mathbf{v}^2_2\rangle~-~\langle m_1\mathbf{v}^2_1\rangle,
$$
откуда следует равенство средних кинетических энергий молекул в смеси двух газов.

В общем случае, даже если молекулы вращаются или обладают внутренними колебаниями,
в результате столкновений друг с другом или перегородками,
выравниваются именно их средние кинетические энергии поступательного движения.