2.4.10 Спектральная плотность некоторых тестовых сигналов
Условие абсолютной интегрируемости функции ограничивает класс сигналов, для которых существует формула для спектральной плотности, выраженная обычными функциями. К таким сигналам относятся важные для анализа прохождения сигналов через электронные цепи функции, как гармоническое колебание, заданное при единичный скачок (функция Хевисайда), постоянный сигнал и др. Это позволяет сделать так называемая дельта-функция (функция Дирака)- бесконечно короткий импульс с единичной площадью.
а) Дельта-импульс во временной области.
При =0 дельта-импульс обозначается d (t) . Площадь импульса равна 1,т.е.
Одно из важных свойств d — функции – избирательность:
Спектральную плотность d -импульса определим обычным способом:
Таким образом, модуль спектральной плотности d — импульса равен 1[Сигн/Гц] на всех частотах и не зависит от положения на оси времени. ФЧХ спектральной плотности равна () , т.е. линейна (рис. 10).
Это означает, что бесконечное число гармонических составляющих с одинаковыми амплитудами и фазами, соответствующими ФЧХ, суммируясь, образуют пик очень большой величины в момент времени t, а в остальные моменты времени суммируются не в фазе, в результате чего получается ноль. Обратное преобразование Фурье может быть записано в виде
Понятие d — импульса широко используется при исследовании воздействия коротких импульсов на линейные цепи, при этом достаточно, чтобы амплитуда реального импульса была бы большой, а длительность – малой по сравнению с характерными параметрами цепи,
б) Дельта – функция в частотной области
В соответствии с теоремой взаимности можно записать (заменив t на w ):
Таким образом спектральной плотности d ( w ) соответствует постоянный сигнал, действующий при
в) Периодическая последовательность d -импульсов.
В соответствии со свойствами преобразований Фурье огибающая спектра периодического сигнала равна
Так как для одиночного d -импульса , то огибающая спектра периодической последовательности будет равна
Сигнал и его спектр при изображены на рис.11
При наличии сдвига относительно начала отсчета t=0 следует добавить ФЧХ, огибающая которой равна ( — w t ).
г) Единичный скачок.
Математически эта функция записывается следующим образом:
Запишем соотношение для спектральной плотности:
На рис.12 показаны временная и частотная характеристики единичного скачка при =0.
д) Спектральная плотность гармонического сигнала бесконечной длительности.
Такой сигнал на частотной плоскости легко отображается спектром с составляющими на частотах .
Найдем формально спектральную плотность такого сигнала Для этого запишем интеграл Фурье:
Таким образом, спектральная функция гармонического сигнала равна нулю везде, кроме w = , при которых она обращается в бесконечность. Аналогично можно ввести понятие спектральной плотности для любого периодического сигнала, состоящего из суммы гармонических составляющих. Действительно, пусть
Такое описание сигналов бывает полезным при рассмотрении смеси импульсного и периодического сигналов.
Андреевская Т.М., РЭ, МГИЭМ, 2004
Спектральная плотность сигнала, смещённого во времени
Для практических приложений является важным установление связи между преобразованием сигнала и соответствующим этому преобразованию изменением спектральных характеристик.
Предположим, что сигнал u1(t) произвольной формы, существующий на интервале от t1 до t2 , имеет спектральную плотность S1(jω) . Найдём спектральную плотность этого же сигнала при условии его задержки на интервал t , например преобразователем, называемым линией задержки. Функция времени задержанного сигнала при сохранении его формы запишется в виде:
Спектральная плотность задержанного сигнала S2(jω) очевидно имеет вид:
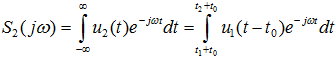
Вводя новую переменную интегрирования τ = t − t , получим:
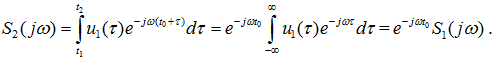
Из этого соотношения видно, что задержка во времени сигнала u1(t) на интервал t приводит к изменению фазовой характеристики спектра S1(jω) (спектра фаз) на величину (−ωt) . Очевидно, что в общем случае при сдвиге сигнала во времени на величину (±t) его фазовый спектр изменится на величину (±ωt) . Спектр амплитуд этого сигнала (модуль спектральной плотности) от положения сигнала на временной оси не зависит.
2.4 Спектр одиночного импульса
Задан одиночный видеоимпульс
(рисунок 5):
Рисунок 5
Метод рядов Фурье допускает глубокое
и плодотворное обобщение, позволяющее
получать спектральные характеристики
непериодических сигналов. Для этого
мысленно дополним одиночный импульс
такими же импульсами, периодически
следующими через некоторый интервал
времени
, и получим изученную ранее периодическую
последовательность:
Представим одиночный импульс как сумму
периодических импульсов с большим
периодом
.
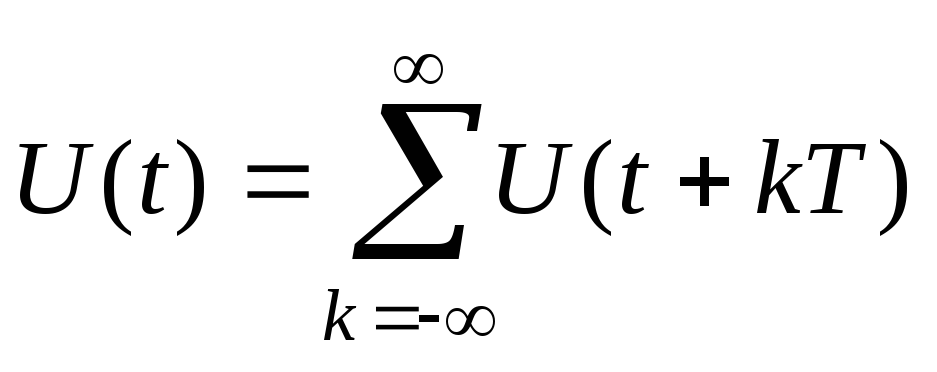 ,
,
(14)
где
—
целые числа.
Для периодического колебания
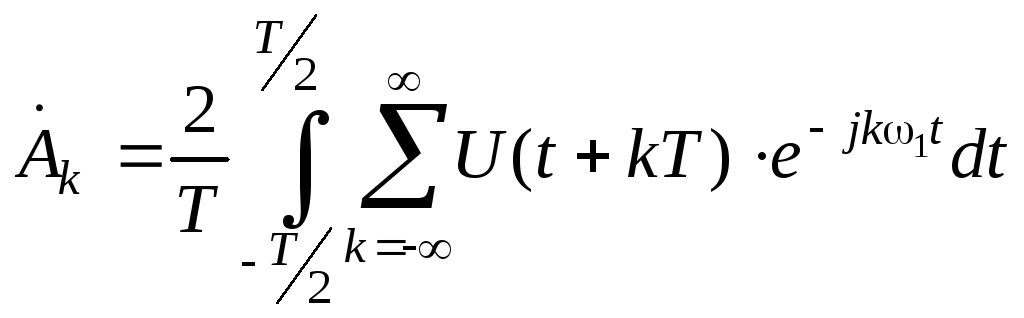 .
.
(15)
Для того, чтобы вернуться к одиночному
импульсу, устремим к бесконечности
период повторения:
.
При этом, очевидно:
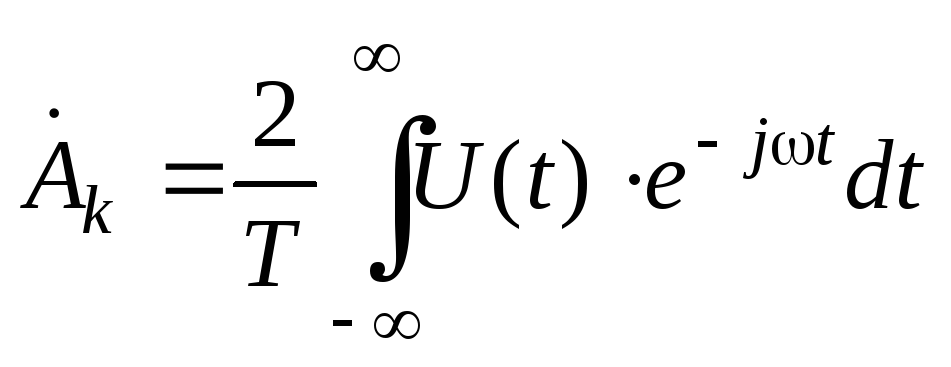 ,
,
(16)
Обозначим
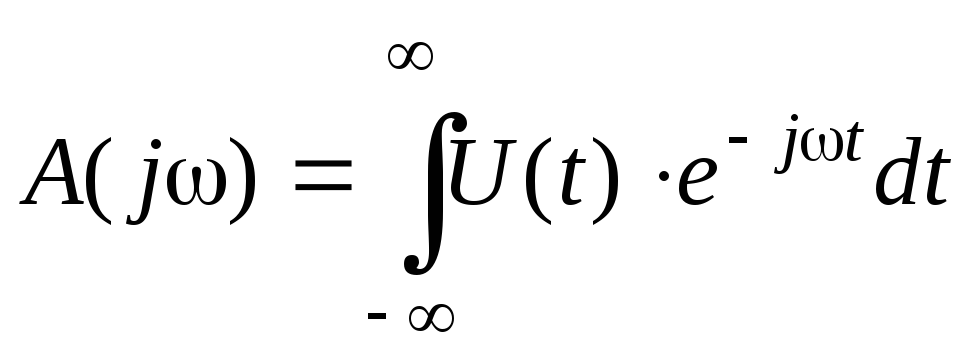 .
.
(17)
Величиной
называется спектральная характеристика
(функция) одиночного импульса (прямое
преобразование Фурье). Она зависит
только от временного описания импульсаи в общем виде является комплексной:
,
(18) где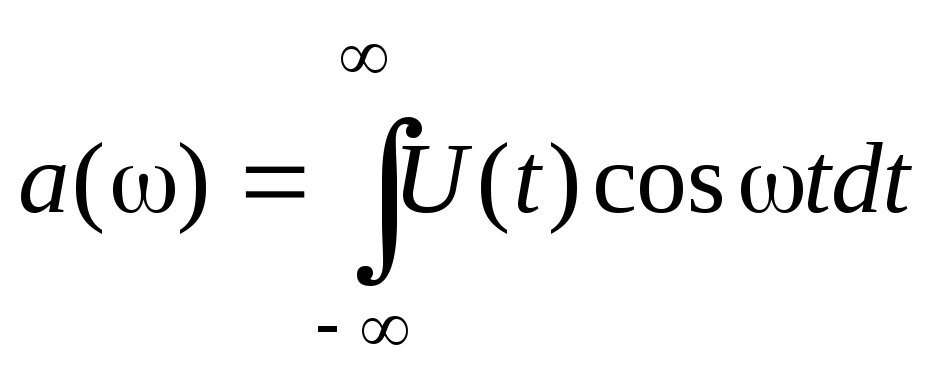 ; (19)
; (19)
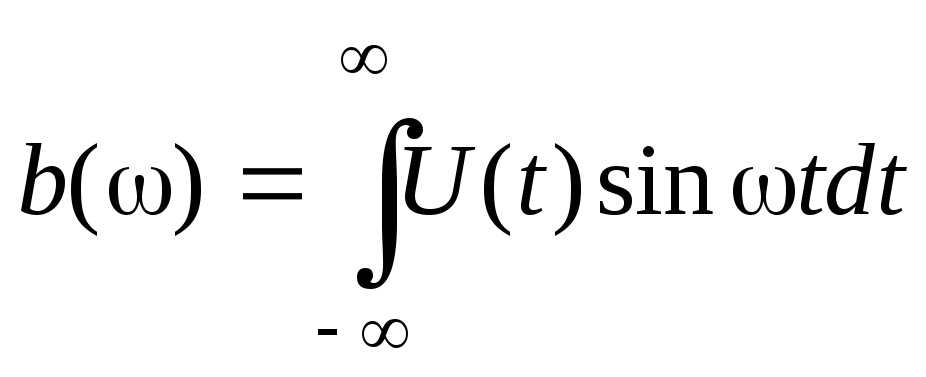 ; (20)
; (20)
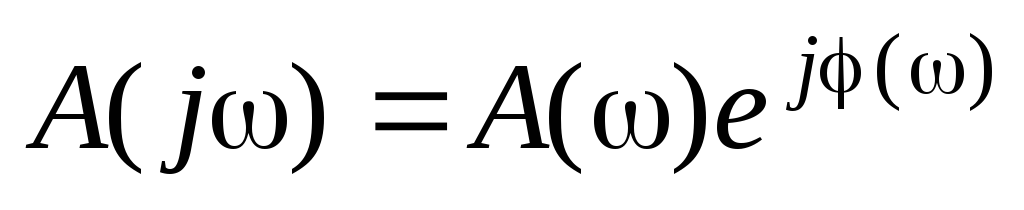 ,
,
где
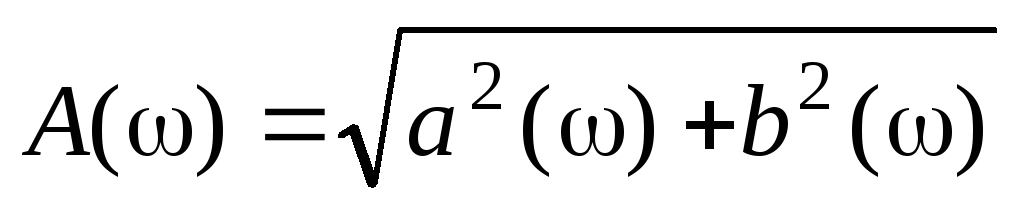 —
—
модуль спектральной функции
(амплитудно-частотная характеристика
импульса);
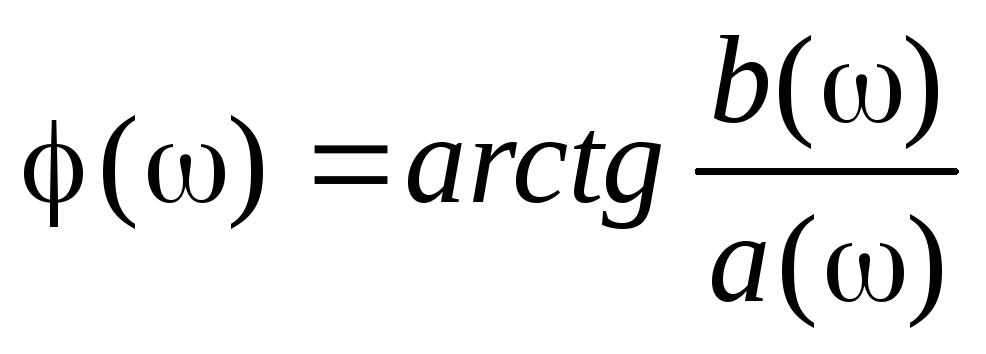 —
—
фазовый угол, фазо-частотная характеристика
импульса.
Найдем
для одиночного импульса по формуле (8),
используя спектральную функцию:
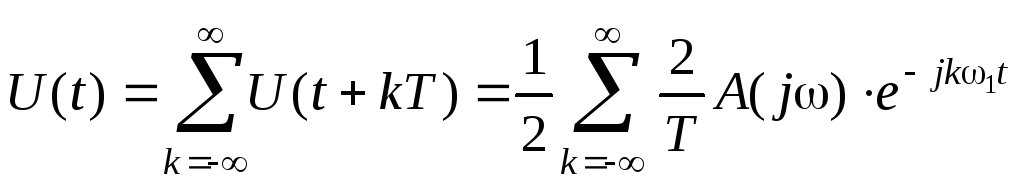 .
.
Если
,
получим:
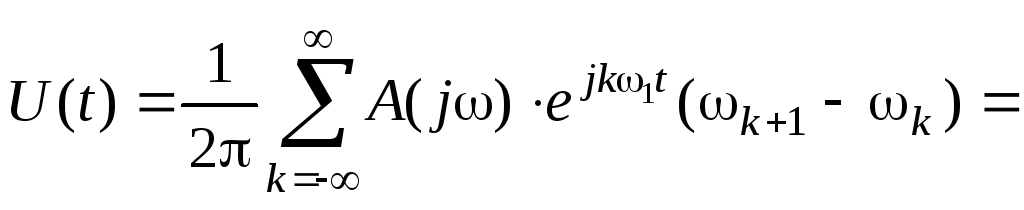
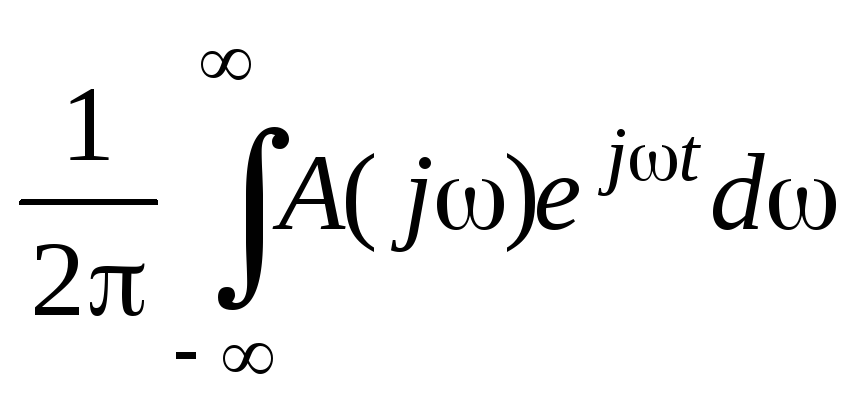 .
.
(21)
Полученное выражение называется обратным
преобразованием Фурье.
Интеграл Фурье определяет импульс в
виде бесконечной суммы бесконечно малых
гармонических составляющих, расположенных
на всех частотах.
На этом основании говорят о непрерывном
(сплошном) спектре, которым обладает
одиночный импульс.
Полная энергия импульса (энергия,
выделяемая на активном сопротивлении
Ом)
равна
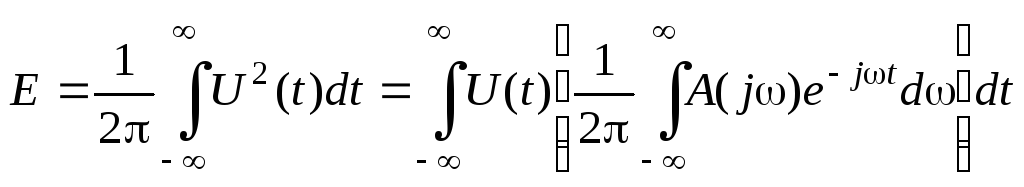 (22)
(22)
Изменяя порядок интегрирования, получим
.
Внутренний интеграл есть спектральная
функция импульса
,
взятая при аргументе -,
т.е. представляет собой комплексно
сопряженную свеличину:
Следовательно
Квадрат модуля (произведение двух
сопряженных комплексных чисел равно
квадрату модуля).
В этом случае условно говорят, что спектр
импульса является двусторонним, т.е.
размещается в полосе частот от
до.
Приведенное соотношение (23), устанавливающее
связь между энергией импульса (на
сопротивлении 1 Ом) и модулем его
спектральной функции известно под
названием равенство Парсеваля.
Оно утверждает, что энергия, заключенная
в импульсе
,
равна сумме энергий всех составляющих
его спектра
Равенство Парсеваля
характеризует важное свойство сигналов.
Если некоторая избирательная система
пропускает только часть спектра сигнала,
ослабляя другие её составляющие, то это
означает, что часть энергии сигнала
теряется
Так как квадрат модуля является четной
функцией переменной интегрирования
,
то удвоив значение интеграла можно
ввести интегрирование в пределах от 0
до:
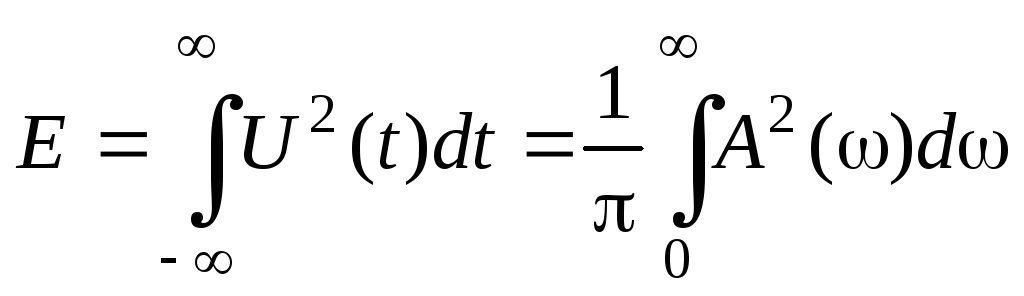 .
.
(24)
При этом говорят, что спектр импульса
размещается в полосе частот от 0 до
и
называется односторонним.
Подынтегральная величина в (23) называется
энергетическим спектром (спектральная
плотность энергии) импульса
Она характеризует распределение энергии
по частоте, и её значение на частоте
равно
энергии импульса, приходящейся на полосу
частот, равной 1 Гц. Следовательно,
энергия импульса есть результат
интегрирования энергетического спектра
сигнала по всему диапазону частот отдо.Иначе
говоря, энергия равна площади, заключённой
между кривой, изображающей энергетический
спектр сигнала и осью абсцисс.
Для оценки распределения энергии по
спектру пользуются относительной
интегральной функцией распределения
энергии (энергетической характеристикой)
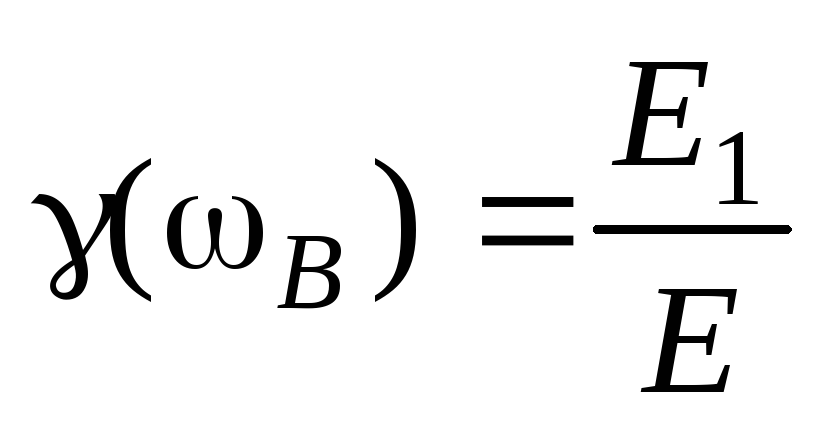 ,
,
(25)
где
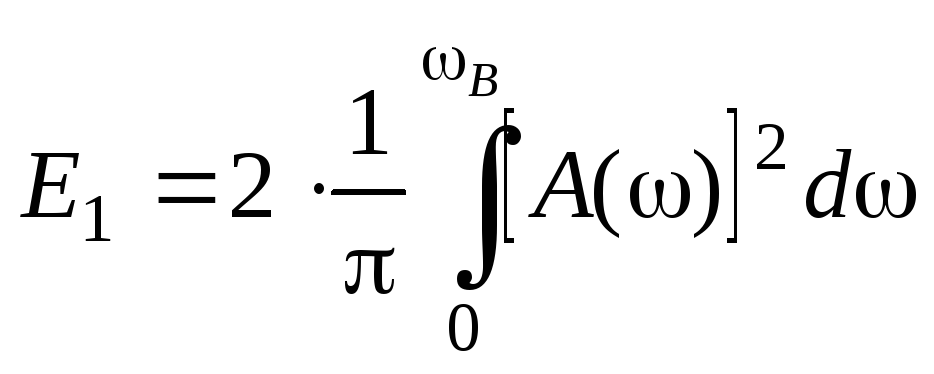 —
—
энергия импульса в заданной полосе
частот от 0 до,
которая характеризует долю энергии
импульса, сосредоточенную в интервале
частот от 0 до.
Для одиночных импульсов различной формы
выполняются следующие закономерности:
Приложения
Электротехника
FM-радио
Концепция и использование спектра мощности сигнала является фундаментальным в электротехнике, особенно в системах электронной связи, включая радио связь, радары и связанные с ними системы, а также технология пассивного дистанционного зондирования. Электронные инструменты, называемые анализаторами спектра, используются для наблюдения и измерения спектров мощности сигналов.
Анализатор спектра измеряет величину кратковременного преобразования Фурье (STFT) входного сигнала. Если анализируемый сигнал можно рассматривать как стационарный процесс, STFT представляет собой хорошую сглаженную оценку его спектральной плотности мощности.
Космология
Изначальные флуктуации, вариации плотности в ранней Вселенной, количественно оцениваются спектром мощности, который дает мощность вариаций как функцию пространственного масштаба.

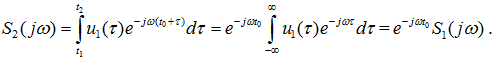









![2.2. спектры случайных процессов [1986 зюко а.г., кловский д.д., назаров м.в., финк л.м. - теория передачи сигналов]](http://dvorik56.ru/wp-content/uploads/3/b/1/3b1192b687695d1909c8005d77589713.jpeg)
![2.9. примеры определения спектров непериодических колебаний [1977 гоноровский и.с. - радиотехнические цепи и сигналы]](http://dvorik56.ru/wp-content/uploads/9/2/d/92df49f8a9349c7b16adfde25c4497d4.jpeg)
















