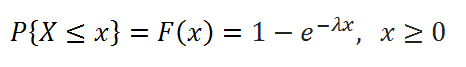Время безотказной работы двигателя автомобиля распределено по показательному закону

Показательный (экспоненциальный) закон распределения

Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения, если её плотность вероятности имеет вид:

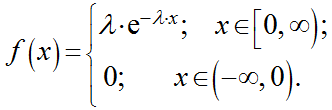
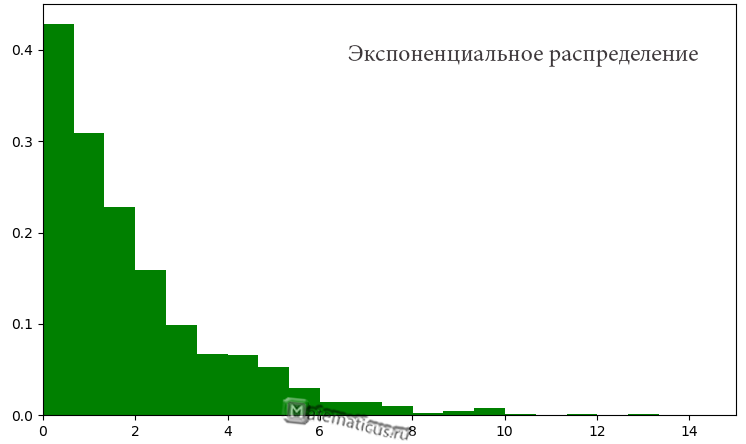
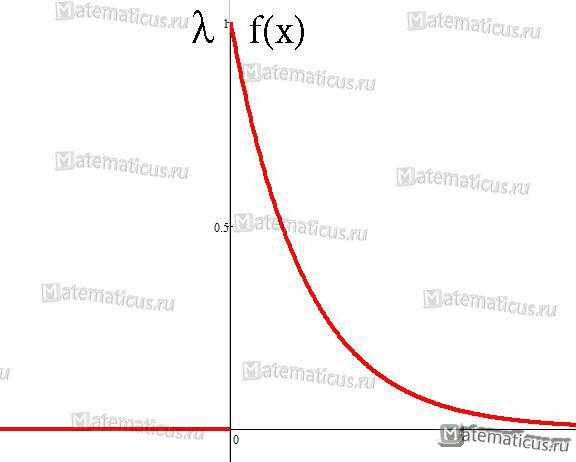
График плотности распределения случайной величины по показательному (экспоненциальному) закону

Функция распределения F(X) случайной величины X, распределенной по показательному закону, выражается формулой:

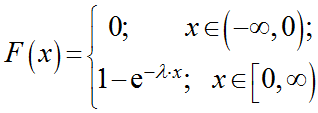
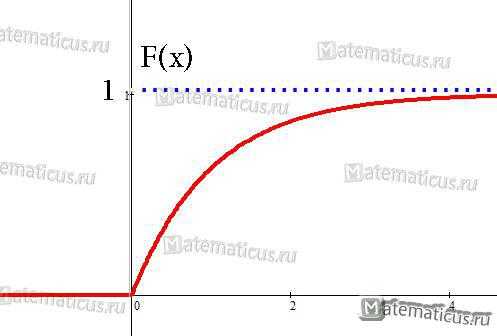
График функции распределения случайной величины по показательному (экспоненциальному) закону

λ — параметр распределения.

Математическое ожидание равно:

Дисперсия равна:

Среднеквадратическое отклонение (СКО) σ(X) равно:

Вероятность того, что случайная величина X примет значение, принадлежащее интервалу (a, b), находится по формуле:

Вероятность безотказной работы определяется по формуле:

а вероятность отказа (или интенсивность отказов) равна

Среднее время безотказной работы T:

Показательное распределение применяют в теории массового обслуживания и надёжности, для моделирования времени безотказной работы, длительности безаварийной работы приборов и машин, демографии и т. д. Пример, устройство после включения ломается через короткий промежуток времени.

Случайная величина X – время работы лампы накаливания. Случайная величина подчинена показательному распределению. Определить вероятность того, что время работы лампы накаливания будет не меньше 800 часов, если среднее время работы лампы накаливания 400 часов.

В соответствии с условием задачи, математическое ожидание M(x) случайной величины X равно 400 часам, отсюда следует, что

Подставляя в формулу выше, получаем вероятность

Дисперсия дискретной случайной величины

Дисперсией дискретной случайной величины X называется математическое ожидание квадрата отклонения её от математического ожидания:

Средним квадратическим отклонением случайной величины X называется арифметическое значение квадратного корня её дисперсии:

Пример 5. Вычислить дисперсии и средние квадратические отклонения случайных величин X и Y, законы распределения которых приведены в таблицах выше.

Решение. Математические ожидания случайных величин X и Y, как было найдено выше, равны нулю. Согласно формуле дисперсии при Е(х)=Е(y)=0 получаем:

Тогда средние квадратические отклонения случайных величин X и Y составляют

Таким образом, при одинаковых математических ожиданиях дисперсия случайной величины X очень мала, а случайной величины Y — значительная. Это следствие различия в их распределении.

Пример 6. У инвестора есть 4 альтернативных проекта инвестиций. В таблице обобщены данные об ожидаемой прибыли в этих проектах с соответствующей вероятностью.

Проект 1	Проект 2	Проект 3	Проект 4
500, P=1	1000, P=0,5	500, P=0,5	500, P=0,5
0, P=0,5	1000, P=0,25	10500, P=0,25
0, P=0,25	9500, P=0,25

Найти для каждой альтернативы математическое ожидание, дисперсию и среднее квадратическое отклонение.

Решение. Покажем, как вычисляются эти величины для 3-й альтернативы:

В таблице обобщены найденные величины для всех альтернатив.

У всех альтернатив одинаковы математические ожидания. Это означает, что в долгосрочном периоде у всех — одинаковые доходы. Стандартное отклонение можно интерпретировать как единицу измерения риска — чем оно больше, тем больше риск инвестиций. Инвестор, который не желает большого риска, выберет проект 1, так как у него наименьшее стандартное отклонение (0). Если же инвестор отдаёт предпочтение риску и большим доходам в короткий период, то он выберет проект наибольшим стандартным отклонением — проект 4.

Построение оптимальной оценки методом максимального правдоподобия

      Пусть
Х – непрерывная случайная величина,
которая в результате n испытаний приняла
значения х₁,
х₂, …,
х_n.

      Функцией 
правдоподобия случайной величины
Х называют функцию аргумента θ:

      Найдем 
оценку параметра λ экспоненциального
распределения методом максимального
правдоподобия.

 при 

      Составим 
функцию правдоподобия:

      Отсюда 
следует:

      Найдем 
логарифмическую функцию правдоподобия:

      Найдем 
первую производную по λ:

      Напишем
уравнение правдоподобия, для чего
приравняем первую производную нулю:

      Найдем 
критическую точку. Для этого 
решим полученное уравнение относительно
λ:

      Найдем 
вторую производную по λ:

      Заметим,
что при  вторая производная отрицательна;
следовательно, — точка максимума и, значит, в качестве
оценки максимального правдоподобия параметра
λ экспоненциального распределения надо
принять величину, обратную средней:

Дистрибутивы

Минимумом среди независимых случайных величин с экспоненциальным распределением параметров остается случайная величина с экспоненциальным распределением параметров .

Параллелью экспоненциального распределения, как распределения без памяти, между дискретными распределениями вероятностей является геометрическое распределение . В частности, если следует экспоненциальное распределение , то для каждой случайной величины ( целая часть ) следует геометрическое распределение :

Распределение Пуассона описывает количество последовательных событий, произошедших в интервале времени, где время ожидания между двумя последовательными событиями не зависит и подчиняется экспоненциальному распределению одного и того же параметра .

Экспоненциальное распределение соответствует распределению хи-квадрат с двумя степенями свободы ,.

Лапласово распределение параметров управляет случайной величиной , где есть две независимые случайные величины с одинаковым экспоненциальным распределением .

Гамма-распределение обобщает показательное распределение: оно совпадает с . В частности, сумма независимых случайных величин одного и того же экспоненциального закона с параметром соответствует гамма-распределению . Кроме того, в байесовском выводе , если параметр экспоненциального распределения следует априори из наблюдения за гамма-распределением, то гамма-распределение также следует апостериорно .

Экспоненциально распределенная случайная величина

На странице Непрерывная случайная величина мы разобрали примеры решений для произвольно заданных законов распределения (многочлены, логарифмы и т.п.). Здесь же мы разберем примеры только для одного типа СВ — распределенных по показательному (или экспоненциальному) закону.

Плотность распределения величины $X$ с экспоненциальным законом распределения задается формулой:

Функция распределения величины $X$:

Здесь $\lambda$ — единственный параметр данного распределения, полностью определяющий его свойства. В частности, числовые характеристики выражаются через этот параметр: $M(X)=1/\lambda$, $D(X)=1/\lambda^2$.

Экспоненциальное распределение моделирует время между двумя последовательными свершениями события, а параметр $\lambda$ описываетс среднее число наступлений события в единицу времени. Обычно с помощью этого закона описывают: продолжительность обслуживания покупателя, время жизни оборудования до отказа, промежуток времени между поломками и т.п.

В этом разделе мы приведем разные примеры задач с полным решением, где используются показательно распределенные случайные величины.

Примеры решения задач

Пример 1

Случайная величина

 задана функцией распределения

Найдите математическое
ожидание и среднее квадратическое отклонение этого
распределения.

Найдите вероятность того,
что случайная величина примет значение от 0,2 до 1.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте WhatsAppTelegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Математическое
ожидание случайной величины, распределенной по показательному закону:

Среднее
квадратическое отлонение:

Вероятность того, что
случайная величина примет значение от 0,2 до 1

Ответ

Пример 2

На шоссе установлен контрольный пункт для
проверки технического состояния автомобилей. Найти математическое ожидание и
среднее квадратическое отклонение случайной величины T – время ожидания
очередной машины контролером, если поток машин простейший и время (в часах)
между прохождениями машин через контрольный пункт распределено по
показательному закону f(t)=5e-5t.

Указание: Время ожидания машины
контролером и время прохождения машин через контрольный пункт распределены
одинаково.

Решение

В нашем случае
параметр показательного распределения

Математическое
ожидание:

Дисперсия:

Среднее
квадратическое отклонение:

Ответ:

Пример 3

Постройте
интегральную и дифференциальную функции распределения случайной величины X.
Найдите математическое ожидание M(X), дисперсию D(X),
среднее квадратическое отклонение σ(X), моду x_mod, медиану x_med, если известно, что
случайная величина X имеет показательное распределение с параметром λ=1.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте WhatsAppTelegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Плотность
распределения случайной величины

, распределенной по
показательному закону:

Функция
распределения:

Построим
графики дифференциальной и интегральной функций распределения:

График дифференциальной функции распределения

График интегральной функции распределения

Математическое
ожидание показательно распределенной случайной величины

Дисперсия:

Среднее
квадратическое отклонение:

 найдем, исходя из условия: 

Пример 4

Случайная
величина

 распределена показательно с дисперсией 0,25.
Найти математическое ожидание и вероятность попадания

 в интервал (0,5;1).

Решение

Дисперсия
случайной величины, распределенной по показательному закону:

Математическое
ожидание случайной величины, распределенной по показательному закону:

Вероятность
попадания в интервал

 непрерывной случайной величины

, распределенной по
показательному закону:

В нашем
случае:

Ответ:

Показательный закон надежности

Показательное распределение широко используется в теории надежности.

Пусть продолжительность Т безотказной работы элемента является случайной величиной. Ее функция распределения F(t)=P(T t, равна:

Функцию

функцией надежности

Часто длительность времени безотказной работы имеет показательное распределение:

где

Тогда функция надежности имеет вид

Она и определяет показательный закон надежности.

Пусть время безотказной работы моста (ненарушение первого предельного состояния) распределено по показательному закону

Вероятность того, что мост проработает безотказно 100 лет или 50 лет, равна соответственно:

Показательный закон надежности обладает очень важным свойством: вероятность безотказной работы элемента в некоторый промежуток времени не зависит от того, были ли отказы в предшествующий период.

Источник статьи: http://studopedia.ru/11_110140_pokazatelniy-zakon-nadezhnosti.html

Математическое ожидание непрерывной случайной величины. Пример решения

Чтобы найти функцию распределения дискретной случайной величины, необходимо использовать данный калькулятор.

Задание 1. Плотность распределения непрерывной случайной величины Х имеет вид: Найти: а) параметр A ; б) функцию распределения F(x) ; в) вероятность попадания случайной величины X в интервал ; г) математическое ожидание MX и дисперсию DX . Построить график функций f(x) и F(x) .

Задание 2. Найти дисперсию случайной величины X , заданной интегральной функцией.

Задание 3. Найти математическое ожидание случайной величины Х заданной функцией распределения.

Задание 4. Плотность вероятности некоторой случайной величины задана следующим образом: f(x) = A/x 4 (x = 1; +∞) Найти коэффициент A , функцию распределения F(x) , математическое ожидание и дисперсию, а также вероятность того, что случайная величина примет значение в интервале . Построить графики f(x) и F(x) .

Задача. Функция распределения некоторой непрерывной случайной величины задана следующим образом:

• Решение
• Видео решение

Найдем функцию плотности распределения, как производную от функции распределения. F′=f(x)=a Зная, что найдем параметр a :

или 3a=1, откуда a = 1/3 Параметр b найдем из следующих свойств: F(4) = a*4 + b = 1 1/3*4 + b = 1 откуда b = -1/3 Следовательно, функция распределения имеет вид: F(x) = (x-1)/3

Математическое ожидание.

1 /₉•4 3 — ( 1 /₉•1 3 ) — ( 5 /₂) 2 = 3 /₄Найдем вероятность того, что случайная величина примет значение в интервале P(2

1. Определить коэффициент A .
2. найти функцию распределения F(x) .
3. схематично построить графики F(x) и f(x) .
4. найти математическое ожидание и дисперсию X .
5. найти вероятность того, что X примет значение из интервала (2;3).

Найдем параметр A из условия:

Функцию распределения можно найти по формуле.

Математическое ожидание находится по следующей формуле:

Дисперсия выражена формулой:

3 /₄₉•4 7/ ₂ — ( 3 /₄₉•1 7/ ₂) — ( 93 /₃₅) 2 = 876 /₁₂₂₅Вероятность того, что X примет значение из интервала (2;3): Скачать пример №1 Пример №2 . Случайная величина X задана функцией распределения F(x). Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины. Схематично построить графики функций F(x) и f(x).

Экспоненциальное распределение в MS EXCEL

В MS EXCEL, начиная с версии 2010, для Экспоненциального распределения имеется функция ЭКСП.РАСП() , английское название — EXPON.DIST(), которая позволяет вычислить плотность вероятности (см. формулу в начале статьи) и интегральную функцию распределения (вероятность, что случайная величина X, распределенная по экспоненциальному закону , примет значение меньше или равное x). Вычисления в последнем случае производятся по следующей формуле:

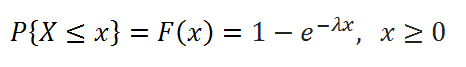
Экспоненциальное распределение имеет обозначение Exp ( λ ).

Примечание : До MS EXCEL 2010 в EXCEL была функция ЭКСПРАСП() , которая позволяет вычислить кумулятивную (интегральную) функцию распределения и плотность вероятности . ЭКСПРАСП() оставлена в MS EXCEL 2010 для совместимости.

В файле примера на листе Пример приведены несколько альтернативных формул для вычисления плотности вероятности и интегральной функции экспоненциального распределения :

• =1-EXP(- λ *x) ;
• =ГАММА.РАСП(x;1;1/ λ ;ИСТИНА) , т.к. экспоненциальное распределение является частным случаем Гамма распределения ;
• =ВЕЙБУЛЛ.РАСП(x;1;1/ λ ;ИСТИНА) , т.к. экспоненциальное распределение является частным случаем распределения Вейбулла ;

Примечание : Для удобства написания формул в файле примера создано Имя для параметра распределения — λ .

Показательный (экспоненциальный) закон распределения

Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения, если её плотность вероятности имеет вид:

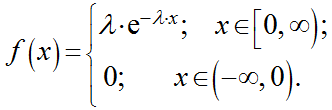
График плотности распределения случайной величины по показательному (экспоненциальному) закону

Функция распределения F(X) случайной величины X, распределенной по показательному закону, выражается формулой:

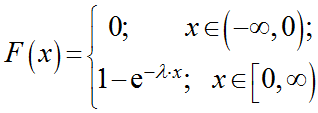
График функции распределения случайной величины по показательному (экспоненциальному) закону

λ — параметр распределения.

Математическое ожидание равно:

Дисперсия равна:

Среднеквадратическое отклонение (СКО) σ(X) равно:

Вероятность того, что случайная величина X примет значение, принадлежащее интервалу (a, b), находится по формуле:

Вероятность безотказной работы определяется по формуле:

а вероятность отказа (или интенсивность отказов) равна

Среднее время безотказной работы T:

Показательное распределение применяют в теории массового обслуживания и надёжности, для моделирования времени безотказной работы, длительности безаварийной работы приборов и машин, демографии и т. д. Пример, устройство после включения ломается через короткий промежуток времени.

Случайная величина X – время работы лампы накаливания. Случайная величина подчинена показательному распределению. Определить вероятность того, что время работы лампы накаливания будет не меньше 800 часов, если среднее время работы лампы накаливания 400 часов.

В соответствии с условием задачи, математическое ожидание M(x) случайной величины X равно 400 часам, отсюда следует, что

Подставляя в формулу выше, получаем вероятность

Приближенный метод проверки нормальности распределения

Приближенный метод проверки нормальности распределения значений выборки основан на
следующем свойстве нормального распределения: коэффициент асимметрии
и коэффициент эксцесса равны нулю.

Коэффициент асимметрии
численно характеризует симметрию эмпирического распределения относительно среднего. Если коэффициент
асимметрии равен нулю, то среднее арифметрического значение, медиана и мода равны:
и кривая плотности
распределения симметрична относительно среднего. Если коэффициент асимметрии меньше нуля (),
то среднее арифметическое меньше медианы, а медиана, в свою очередь, меньше моды
() и кривая сдвинута
вправо (по сравнению с нормальным распределением). Если коэффициент асимметрии больше нуля (),
то среднее арифметическое больше медианы, а медиана, в свою очередь, больше моды
() и кривая сдвинута
влево (по сравнению с нормальным распределением).

Коэффициент эксцесса
характеризует концентрацию эмпирического распределения вокруг арифметического среднего в направлении
оси и степень островершинности кривой плотности распределения.
Если коэффициент эксцесса больше нуля, то кривая более вытянута (по сравнению с нормальным распределением)
вдоль оси (график более островершинный). Если коэффициент
эксцесса меньше нуля, то кривая более сплющена (по сравнению с нормальным распределением)
вдоль оси (график более туповершинный).

Коэффициент асимметрии можно вычислить с помощью функции MS Excel СКОС. Если вы
проверяете один массив данных, то требуется ввести диапазон данных в одно окошко «Число».

Коэффициент эксцесса можно вычислить с помощью функции MS Excel ЭКСЦЕСС. При проверке
одного массива данных также достаточно ввести диапазон данных в одно окошко «Число».

Итак, как мы уже знаем, при нормальном распределении коэффициенты асимметрии и эксцесса
равны нулю. Но что, если мы получили коэффициенты асимметрии, равные -0,14, 0,22, 0,43, а коэффициенты
эксцесса, равные 0,17, -0,31, 0,55? Вопрос вполне справедливый, так как практически мы имеем дело лишь с
приближенными, выборочными значениями асимметрии и эксцесса, которые подвержены некоторому неизбежному,
неконтролируемому разбросу. Поэтому нельзя требовать строгого равенства этих коэффициентов нулю, они
должны лишь быть достаточно близкими к нулю. Но что значит — достаточно?

Требуется сравнить полученные эмпирические значения с
допустимыми значениями. Для этого нужно проверить следующие неравенства (сравнить значения коэффициентов
по модулю с критическими значениями — границами области проверки гипотезы).

Для коэффициента асимметрии :

,

где

—
квантиль стандартного нормального распределения уровня ,

—
среднеквадратическое отклонение для выборки с числом наблюдений .

Для коэффициента эксцесса :

,

где

—
квантиль стандартного нормального распределения уровня ,

—
среднеквадратическое отклонение для выборки с числом наблюдений .

Так как коэффициенты асимметрии и эксцесса могут оказаться и положительными, и отрицательными,
то в приближенном методе проверки нормальности распределения используется двусторонний квантиль
стандартного нормального распределения; он задаёт интервал, в который случайная величина попадает
с определённой вероятностью. Приведём значения двусторонних квантилей стандартного нормального
распределения определённых уровней
(слева — уровень, справа — значение квантиля):

• 0,90: 1,645
• 0,95: 1,960
• 0,975: 2,241
• 0,98: 2,326
• 0,99: 2,576
• 0,995: 2,807
• 0,999: 3,291
• 0,9995: 3,481
• 0,9999: 3,891

Например, для выборки с числом наблюдений и
,
пользуясь этими значениями и ранее приведёнными формулами, можно получить границу области принятия гипотезы для
коэффициента асимметрии 0,62 и для коэффициента эксцесса 1,15. Поэтому приведённые ранее примеры эмпирических
значений коэффициента асимметрии -0,14, 0,22, 0,43 попадают в область принятия гипотезы. То же самое
относится к значениям коэффициента эксцесса 0,17, -0,31, 0,55. Следовательно, если получены такие
эмпирические значения, то с вероятностью 95% данные выборки подчиняются нормальному закону распределения.

Построение алгоритма проверки параметрической статистической гипотезы

      По 
выборке объемом , подчиненной экспоненциальному закону
распределения, проверим гипотезу о равенстве
параметра конкретному значению . Пусть нулевая гипотеза – . Тогда конкурирующая – . Чтобы проверить нулевую гипотезу
необходимо:

      1.
Задать уровень значимости α 
и конкретное значение ;

      2.
Из доверительного интервала выразить (найти критерий проверки);

      3.
Вычислить нижнюю и верхнюю 
границы критерия проверки, используя 
конкретное значение ;

      4.
Если при конкретном значении  принадлежит неравенству, полученному
в пункте 2 (критерию проверки) – нет оснований
отвергнуть нулевую гипотезу. В противном
случае нулевую гипотезу отвергают.

Задачи

Экспоненциальное распределение широко используется в такой дисциплине как Техника обеспечения надежности (Reliability Engineering). Параметр λ называется интенсивность отказов , а 1/ λ – среднее время до отказа .

Предположим, что электронный компонент некой системы имеет срок полезного использования, описываемый Экспоненциальным распределением с интенсивностью отказа равной 10^(-3) в час, таким образом, λ = 10^(-3). Среднее время до отказа равно 1000 часов. Для того чтобы подсчитать вероятность, что компонент выйдет из строя за Среднее время до отказа, то нужно записать формулу:

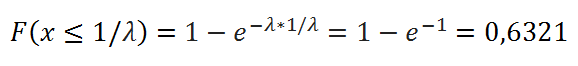
Т.е. результат не зависит от параметра λ .

В MS EXCEL решение выглядит так: =ЭКСП.РАСП(10^3; 10^(-3); ИСТИНА)

Задача . Среднее время до отказа некого компонента равно 40 часов. Найти вероятность, что компонент откажет между 20 и 30 часами работы. =ЭКСП.РАСП(30; 1/40; ИСТИНА)- ЭКСП.РАСП(20; 1/40; ИСТИНА)

СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .

Экспоненциальное распределение в MS EXCEL

В MS EXCEL, начиная с версии 2010, для Экспоненциального распределения имеется функция ЭКСП.РАСП() , английское название — EXPON.DIST(), которая позволяет вычислить плотность вероятности (см. формулу в начале статьи) и интегральную функцию распределения (вероятность, что случайная величина X, распределенная по экспоненциальному закону , примет значение меньше или равное x). Вычисления в последнем случае производятся по следующей формуле:

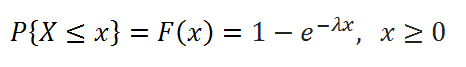
Экспоненциальное распределение имеет обозначение Exp ( λ ).

Примечание : До MS EXCEL 2010 в EXCEL была функция ЭКСПРАСП() , которая позволяет вычислить кумулятивную (интегральную) функцию распределения и плотность вероятности . ЭКСПРАСП() оставлена в MS EXCEL 2010 для совместимости.

В файле примера на листе Пример приведены несколько альтернативных формул для вычисления плотности вероятности и интегральной функции экспоненциального распределения :

• =1-EXP(- λ *x) ;
• =ГАММА.РАСП(x;1;1/ λ ;ИСТИНА) , т.к. экспоненциальное распределение является частным случаем Гамма распределения ;
• =ВЕЙБУЛЛ.РАСП(x;1;1/ λ ;ИСТИНА) , т.к. экспоненциальное распределение является частным случаем распределения Вейбулла ;

Примечание : Для удобства написания формул в файле примера создано Имя для параметра распределения — λ .

Примеры решений

Задача 1. Среднее время безотказной работы прибора равно 80 часов. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти: а) выражение его плотности вероятности и функции распределения; б) вероятность того, что в течение 100 часов прибор не выйдет из строя.

Задача 2. Известно, что время работы прибора до первого отказа подчиняется показательному распределению со средним значением 1 год. Какова вероятность, что до первого отказа пройдет не менее 2 лет?

Задача 3. Установлено, что время ремонта телевизоров есть случайная величина $X$, распределенная по показательному закону с параметром $\lambda=1/3$ (1/день). Определить вероятность того, что на ремонт телевизора потребуется не менее 5 дней.

Задача 4. Время в годах безотказной работы прибора подчинено показательному закону, т.е. плотность распределения этой случайной величины такова: $f(t)=2e^$ при $t\ge 0$ и $f(t)=0$ при $t\lt 0$. 1) Найти формулу функции распределения этой случайной величины. 2) Определить вероятность того, что прибор проработает не более года. 3) Определить вероятность того, что прибор безотказно проработает 3 года. 4) Определить среднее ожидаемое время безотказной работы прибора.

Задача 5. Предполагая, что случайное время обслуживания абонента службой «09» распределено по показательному закону и средняя продолжительность обслуживания составляет 1,5 минуты, найдите вероятность того, что абонент будет обслужен более, чем за 2 минуты.

Задача 6. Длительность телефонного разговора подчиняется показательному закону. Найти среднюю длительность разговора, если вероятность того, что разговор продлится более 5 минут, равна 0,4.

Задача 7. Случайная величина задана плотностью распределения $p(x)=ce^$ при $x \gt 0$, и ноль в остальных случаях. Найти постоянную $c$, математическое ожидание, дисперсию и среднее квадратическое отклонение.

Задача 8. Непрерывная случайная величина $\xi$ распределена по показательному закону с параметром $\lambda$, равному номеру варианта 9. Найти плотность распределения случайной величины $\xi$, функцию распределения, построить графики этих функций. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины $\xi$ и вероятность того, что $\xi$ принимает значения, меньшие своего математического ожидания.

Задача 9. Случайная величина $\xi$ распределена по показательному закону с параметром 2. Найти $M_$, $D_$ вероятность попадания $\xi$ в интервал $(-1;2)$. Нарисовать графики плотности распределения и функции распределения $\xi$.

Задача 10. Известно, что $Х$ распределено по экспоненциальному закону $Exp(\lambda)$. Найдите вероятность события $|Х — МХ | \lt 3\sigma$ («правило $3\sigma$» для показательного распределения).

Построение интервальной оценки параметра экспоненциального закона распределения

      Интервальной
называют оценку, которая определяется
двумя числами – концами интервала, покрывающего
оцениваемый параметр.

      Пусть , где λ – скалярный параметр, подлежащий
интервальной оценке.

      Примем 
в качестве опорной случайной 
величины:

      Опорная
случайная величина V монотонно убывает
и непрерывна по λ для любых и не зависит от λ.

      Построим 
центральный γ-доверительный интервал
(γ₁= γ₂)

      Для
определения границ доверительного
интервала воспользуемся уравнениями:

               
(1)

(2)

      Решив
первое уравнение, получим нижнюю границу 
γ-доверительного интервала:

       .. .. 

        ..

      Аналогично,
решив второе уравнение, получим 
верхнюю границу γ-доверительного
интервала:

      Таким
образом, двусторонний γ-доверительный 
интервал имеет вид:

Метод взятия обратной функции

Допустим, что нам задан интегральный закон распределения вероятности
F(x),
где
f(x)
функция плотности вероятности и

Тогда достаточно разыграть случайное число, равномерно распределенное в интервале
от 0 до 1. Поскольку функция
F
тоже изменяется в данном интервале, то случайное событие
x
можно определить взятием обратной функции по графику или аналитически:
x = F1(r).
Здесь
r
число, генерируемое эталонным ГСЧ в интервале от 0 до 1,
x₁
сгенерированная в итоге случайная величина. Графически суть метода изображена на
рис. 24.6.

Рис. 24.6. Иллюстрация метода обратной функции для генерации случайныхсобытий x, значения которых распределены непрерывно. На рисунке показаныграфики плотности вероятности и интегральной плотности вероятности от х

Данным методом особенно удобно пользоваться в случае, когда интегральный закон
распределения вероятности задан аналитически и возможно аналитическое взятие
обратной функции от него, как это и показано на следующем примере.

Пример 1.
Примем к рассмотрению экспоненциальный закон распределения вероятности случайных
событий
f(x) = λ · eλx.
Тогда интегральный закон распределения плотности вероятности имеет вид:
F(x) = 1  eλx.

Так как
r
и
F
в данном методе предполагаются аналогичными и расположены в одном интервале, то,
заменяя
F
на случайное число
r,
имеем:
r = 1  eλx.

Выражая искомую величину
x
из этого выражения (то есть, обращая функцию exp()), получаем:
x = 1/λ · ln(1  r).

Так как в статическом смысле
(1  r)
и
r
это одно и тоже, то
x = 1/λ · ln(r).

На
рис. 24.7
показан фрагмент алгоритма, реализующего метод обратной функции для
экспоненциального закона.

Рис. 24.7. Фрагмент блок-схемы алгоритма,реализующей метод обратной функциидля экспоненциального закона

Примеры решений

Задача 1. Среднее время безотказной работы прибора равно 80 часов. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти:
а) выражение его плотности вероятности и функции распределения;
б) вероятность того, что в течение 100 часов прибор не выйдет из строя.

Задача 2. Известно, что время работы прибора до первого отказа подчиняется показательному распределению со средним значением 1 год. Какова вероятность, что до первого отказа пройдет не менее 2 лет?

Задача 3. Установлено, что время ремонта телевизоров есть случайная величина $X$, распределенная по показательному закону с параметром $lambda=1/3$ (1/день). Определить вероятность того, что на ремонт телевизора потребуется не менее 5 дней.

Задача 4. Время в годах безотказной работы прибора подчинено показательному закону, т.е. плотность распределения этой случайной величины такова: $f(t)=2e^{-2t}$ при $tge 0$ и $f(t)=0$ при $tlt 0$.
1) Найти формулу функции распределения этой случайной величины.
2) Определить вероятность того, что прибор проработает не более года.
3) Определить вероятность того, что прибор безотказно проработает 3 года.
4) Определить среднее ожидаемое время безотказной работы прибора.

Задача 5. Предполагая, что случайное время обслуживания абонента службой «09» распределено по показательному закону и средняя продолжительность обслуживания составляет 1,5 минуты, найдите вероятность того, что абонент будет обслужен более, чем за 2 минуты.

Задача 6. Длительность телефонного разговора подчиняется показательному закону. Найти среднюю длительность разговора, если вероятность того, что разговор продлится более 5 минут, равна 0,4.

Задача 7. Случайная величина задана плотностью распределения $p(x)=ce^{-3x}$ при $x gt 0$, и ноль в остальных случаях. Найти постоянную $c$, математическое ожидание, дисперсию и среднее квадратическое отклонение.

Задача 8. Непрерывная случайная величина $xi$ распределена по показательному закону с параметром $lambda$, равному номеру варианта 9. Найти плотность распределения случайной величины $xi$, функцию распределения, построить графики этих функций. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины $xi$ и вероятность того, что $xi$ принимает значения, меньшие своего математического ожидания.

Задача 9. Случайная величина $xi$ распределена по показательному закону с параметром 2. Найти $M_{xi}$, $D_{xi}$ вероятность попадания $xi$ в интервал $(-1;2)$. Нарисовать графики плотности распределения и функции распределения $xi$.

Задача 10. Известно, что $Х$ распределено по экспоненциальному закону $Exp(lambda)$. Найдите вероятность события $|Х — МХ | lt 3sigma$ («правило $3sigma$» для показательного распределения).

Мы отлично умеем решать задачи по теории вероятностей

Другие задачи по теории вероятности

Двумерная случайная величина (X,Y) имеет равномерное распределение вероятностей в треугольнике ABC. Определить маргинальные плотности распределения f₁(x) и f₂(y), математические ожидания M(X), M(Y), дисперсии D(X), D(Y), коэффициент корреляции r_xy. Являются ли случайные величины независимыми? Вершины треугольника: A(0,0), B(-2;2), С(2;2).

Три стрелка выстрелили по одному разу по мишени. Вероятности попадания при одном выстреле у них соответственно равны 0,75, 0,95, 0,8. Найти вероятность, что в мишени будет: а) ровно одно попадание; б) не менее одного попадания.

Бросают два кубика. Суммируют число очков, выпавших на верхних гранях кубиков. Построить множество элементарных событий и его подмножество, соответствующее событию A={сумма очков больше 2}. Найти вероятность события A. Построить подмножество, соответствующее событию Ā (дополнение A). Найти его вероятность.

Закон распределения двумерной дискретной случайной величины (X,Y) задан таблицей:

Найти условные законы распределения случайной величины X при условии, что Y=3 случайной величины Y при условии, что Х=1.

Дан закон распределения дискретной случайной величины:

Найти: недостающее значение p₅, М(Х), D(X), σ(X). Построить многоугольник, функцию распределения X. Чему равны М(Y), D(Y), если Y=25X+834?

Случайная величина X распределена по биномиальному закону с параметрами 5, 0,3. Найти p(X=4), p(X=0), p(X=5).