Плотность вещества

Электростатика

Электрический заряд может быть найден по формуле:

Линейная плотность заряда:

Поверхностная плотность заряда:

Объёмная плотность заряда:

Закон Кулона (сила электростатического взаимодействия двух электрических зарядов):

Где: k — некоторый постоянный электростатический коэффициент, который определяется следующим образом:

Напряжённость электрического поля находится по формуле (хотя чаще эту формулу используют для нахождения силы действующей на заряд в данном электрическом поле):

Принцип суперпозиции для электрических полей (результирующее электрическое поле равно векторной сумме электрических полей составляющих его):

Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра:

Напряженность электрического поля, которую создает заряженная плоскость:

Потенциальная энергия взаимодействия двух электрических зарядов выражается формулой:

Электрическое напряжение это просто разность потенциалов, т.е. определение электрического напряжения может быть задано формулой:

В однородном электрическом поле существует связь между напряженностью поля и напряжением:

Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:

Работа электрического поля в общем случае может быть вычислена также и по одной из формул:

В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:

Определение потенциала задаётся выражением:

Потенциал, который создает точечный заряд или заряженная сфера:

Принцип суперпозиции для электрического потенциала (результирующий потенциал равен скалярной сумме потенциалов полей составляющих итоговое поле):

Для диэлектрической проницаемости вещества верно следующее:

Определение электрической ёмкости задаётся формулой:

Ёмкость плоского конденсатора:

Заряд конденсатора:

Напряжённость электрического поля внутри плоского конденсатора:

Сила притяжения пластин плоского конденсатора:

Энергия конденсатора (вообще говоря, это энергия электрического поля внутри конденсатора):

Объёмная плотность энергии электрического поля:

Кинематика

Путь при равномерном движении:

Перемещение S (расстояние по прямой между начальной и конечной точкой движения) обычно находится из геометрических соображений. Координата при равномерном прямолинейном движении изменяется по закону (аналогичные уравнения получаются для остальных координатных осей):

Средняя скорость пути:

Средняя скорость перемещения:

Определение ускорения при равноускоренном движении:

Выразив из формулы выше конечную скорость, получаем более распространённый вид предыдущей формулы, которая теперь выражает зависимость скорости от времени при равноускоренном движении:

Средняя скорость при равноускоренном движении:

Перемещение при равноускоренном прямолинейном движении может быть рассчитано по нескольким формулам:

Координата при равноускоренном движении изменяется по закону:

Проекция скорости при равноускоренном движении изменяется по такому закону:

Скорость, с которой упадет тело падающее с высоты h без начальной скорости:

Время падения тела с высоты h без начальной скорости:

Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):

Формула для тормозного пути тела:

Время падения тела при горизонтальном броске с высоты H может быть найдено по формуле:

Дальность полета тела при горизонтальном броске с высоты H:

Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту:

Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):

Время подъема до максимальной высоты при броске под углом к горизонту:

Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):

Определение периода вращения при равномерном движении по окружности:

Определение частоты вращения при равномерном движении по окружности:

Связь периода и частоты:

Линейная скорость при равномерном движении по окружности может быть найдена по формулам:

Угловая скорость вращения при равномерном движении по окружности:

Связь линейной и скорости и угловой скорости выражается формулой:

Связь угла поворота и пути при равномерном движении по окружности радиусом R (фактически, это просто формула для длины дуги из геометрии):

Центростремительное ускорение находится по одной из формул:

Формула расчета массы через объем и плотность

В физике массу можно вычислить, зная объем и плотность тела. Для этого используется следующая формула:

Масса = объем × плотность

Эта формула основана на определении плотности как отношения массы тела к его объему:

Таким образом, выражая массу через объем и плотность, получаем:

Пример:

У нас есть куб со стороной 10 см, с плотностью 2 г/см³. Найдем его массу.

Сначала найдем объем куба:

Затем, используя формулу, найдем массу:

Таким образом, масса куба со стороной 10 см и плотностью 2 г/см³ равна 2 кг.

Для удобства расчетов можно использовать таблицу плотностей различных веществ:

Вещество	Плотность, г/см³
Вода	1
Железо	7,87
Алюминий	2,7
Серебро	10,5
Золото	19,3

Таким образом, формула расчета массы через объем и плотность позволяет быстро и удобно определить массу тела, зная его объем и плотность. Для удобства расчетов можно использовать таблицу плотностей различных веществ.

Понятие насыпной плотности

Вводят для анализа сыпучих строительных материалов (песка, гравия, керамзита и др.). Показатель важен для расчета экономически выгодного применения тех или иных компонентов строительной смеси. Он показывает отношение массы вещества к объему, который оно занимает в состоянии рыхлой структуры.

Например, если известна материала зернистой формы и средняя плотность зерен, то легко определить параметр пустотности. При изготовлении бетона целесообразнее применять наполнитель (гравий, щебень, песок), обладающий меньшей пористостью сухого вещества, так как на его заполнение пойдет базовый цементный материал, что увеличит себестоимость.

Первый закон И. Ньютона

Идеи Г. Галилея были развиты И.Ньютоном, и оформились в виде Первого Закона Движения, в настоящее время носящее его имя.

Рис. 2. Ньютон.

Первый Закон Ньютона гласит, что любое тело сохраняет свое состояние покоя или равномерного прямолинейного движения, пока равнодействующая всех сил, действующих на него, равна нулю.

В математическом виде формула закона инерции описывается выражением:

$$\overrightarrow v=const, при \overrightarrow F_{равнод}=0$$

Отметим векторный характер этого закона. Тело сохраняет скорость постоянной и по модулю и по направлению. То есть, наличие силы и тела, со стороны которого бы эта сила воздействовала, требуется не только для изменения модуля скорости, но и для изменения направления движения, хотя модуль скорости при этом может не меняться. Любое криволинейное движение возможно только при воздействии на материальную точку со стороны других тел.

Например, равномерное движение материальной точки по окружности невозможно без воздействия на нее других материальных точек. Точки вращающегося диска движутся по окружности только потому, что на них постоянно действуют силы со стороны оси вращения и точек на противоположном конце диска. Если диск распадется на части, и эти силы исчезнут, то осколки разлетятся в разные стороны, доказывая справедливость Первого закона Ньютона.

Примеры решения задач

Задача 1

Условие: имеется алюминиевый брусок со сторонами 3, 5 и 7 сантиметров. Какова его масса?

Табличное значение плотности алюминия: 2800 кг/м 3 или 2,8 г/см 3 ;

Задача 2

Условие: сколько энергии потребуется для того, чтобы довести воду комнатной температуры (20 градусов Цельсия) из стакана (ёмкость 200 мл) до температуры кипения?

Найдем недостающую информацию: температура кипения воды t2 = 100 градусов Цельсия, удельная теплоемкость воды с = 4200 Дж/кг * С, плотность воды 1 г/см 3 , 1 мл воды = 1 см 3 ;

Q = 4200 * 0,2 * (100 – 20) = 67200 Дж = 67,2 кДж.

Задача 3

Условие: найдите массу CO2 при объеме в 5,6 л.

Найдем молярную массу CO2 :

Найдем количество вещества через объем:

Движение По Инерции своими словами для детей

Движение по инерции — это движение, которое происходит без воздействия силы или без каких-либо внешних воздействий. Когда мы говорим о движении по инерции, мы имеем в виду, что объект продолжает двигаться в том же направлении и со скоростью, пока на него не действует сила.

Давай представим, что у тебя есть игрушечная машинка, которую ты толкаешь по полу. Когда ты перестаешь толкать машинку, она не останавливается сразу же, а продолжает движение некоторое время. Это происходит из-за инерции. Инерция — это свойство тела сохранять свое состояние движения или покоя.

Другим примером движения по инерции может быть катание на велосипеде. Когда ты начинаешь педалировать, велосипед набирает скорость. Когда ты перестаешь педалировать, велосипед не останавливается сразу же, а продолжает двигаться по инерции. Чтобы остановить велосипед, тебе нужно применить силу торможения.

Инерция важна не только для понимания движения объектов, но и для безопасности. Например, когда мы едем в автомобиле и внезапно тормозим, наше тело продолжает двигаться вперед из-за инерции. Поэтому нам необходимо пристегиваться ремнем безопасности, чтобы предотвратить травмы.

В заключение, движение по инерции — это движение, которое происходит без воздействия силы или без внешних воздействий. Инерция позволяет объектам сохранять свое состояние движения или покоя. Понимание этого концепта помогает нам объяснить, почему объекты продолжают двигаться без воздействия силы и как мы можем использовать инерцию в нашу пользу.

Используемая литература:1. Бутенин Н. В., Лунц Я. Л., Меркин Д. Р. Курс теоретической механики. т. 1, 2; М., 1985 и предыдущие издания.2. Добронравов В. В., Никитин Н. Н. Курс теоретической механики. М., 1983.3. Лойцянский Л.Г., Лурье А.И. Курс теоретической механики, ч. 1 – М.: 1954 и последующие издания, 342 с.4. Лойцянский Л.Г., Лурье А.И. Курс теоретической механики, ч. 2. – М.: 1955 и последующие издания, 598 с.5. Тарг С. М. Краткий курс теоретической механики. М., 1986 и предыдущие издания.6. Яблонский А. А., Никифорова В. М. Курс теоретической механики. т. 1, 2; М., 1984 и предыдущие издания.7. Мещерский И. В. Сборник задач по теоретической механике. М., 1986 и предыдущие издания.8. Сборник задач по теоретической механике // Под ред. К. С. Колесникова. М., 1983.Значение термина Движение По Инерции на academic.ru

Формула и удивительная история её возникновения

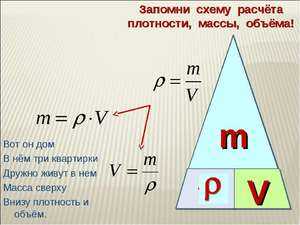
Самая обычная формула для большинства случаев имеет вид: m = pV , где m – масса тела, p и V – плотность вещества и его объём, занимаемый в пространстве соответственно. Можно, конечно, не заморачиваться и посчитать всё на онлайн-ресурсах, но знать формулу всё же полезно. Соответственно V = m / p , p = m / V .

Самое интересное – это то, что формулу нашёл мужик, который бегал голышом по улице и был при этом другом царя. Интересно? Тогда следующие три абзаца для вас.

Был в Древней Греции такой царь-тиран, как Гиерон II. Он начал подозревать, что его корону сделали не из чистого золота и ювелиры его облапошили. Но Гиерон не знал, как можно это доказать. Тогда он обратился к умнейшему человеку того времени – Архимеду

Получив приказ разобраться с делами государственной важности, Архимед день за днём стал искать решение вопроса

Ох, и нелёгкая же задачка выпала учёному. Ведь на то время не было ни нужных формул, ни современных девайсов, ни гугла, чтобы быстренько найти решение. И вот однажды, придя в баню и погрузившись в неё, Архимед заметил, что выливающаяся вода равна по объёму тому, что погружено в воду.

Эврика! – Прокричал Архимед и нагишом поспешил в свою лабораторию проводить опыты. Учёный сложил все данные в своей голове и позже проделал следующий опыт: он взял корону и опустил её в воду. Затем он взял кусок золота такого же веса и опустил его также в воду. Объём вытесненной воды получился разным. Если бы корона была сделана из чистого золота, то её объём и слитка совпали. Это доказывало то, что ювелиры обманули царя. Кто бы мог подумать, что одно из величайших открытий появилось благодаря обманщикам, тирану и учёному.

Примеры решения задач

Прежде чем приступить к примерам, следует понимать, что если данные даны в килограммах и кубических сантиметрах, то нужно либо сантиметры перевести в метры, либо килограммы перевести в граммы. По такому же принципу надо переводить и остальные данные – миллиметры, тонны и так далее.

Задача 1. Найти массу тела, состоящего из вещества, плотность которого равна 2350 кг/м³ и имеет объём 20 м³. Применяем стандартную формулу и с лёгкостью находим значение. m = p*V= 2 350 * 20 = 47 000 кг.

Задача 2. Уже известно, что плотность чистого золота без примесей равна 19,32 г/см³. Найти массу драгоценной цепочки из золота, если объём составляет 3,7 см³. Воспользуемся формулой и подставим значения. p = m / V = 19,32/3,7 = 5,22162162 гр.

Задача 3. На склад поставили металл с плотностью 9250 кг/м³. Масса составляет 1,420 тонн. Нужно найти занимаемый металлом объём. Тут нужно сначала перевести либо тонны в килограммы, либо метры в километры. Проще будет воспользоваться первым методом. V = m / p = 1420/9250 = 0.153513514 м³.

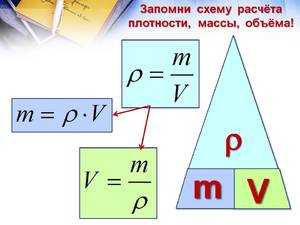
Плотность тела — зависимость массы и объема

Например, железный куб с ребром 10 см имеет массу 7,8 кг, алюминиевый куб тех же размеров имеет массу 2,7 кг, а масса такого же куба изо льда 0,9 кг. Величина, характеризующая массу, приходящуюся на единичный объём данного вещества, называется плотностью. Плотность равна частному от массы тела и его объёма, т.е.

ρ = m/V, где ρ (читается «ро») плотность тела, m — его масса, V объём.

В Международной системе единиц СИ плотность измеряется в килограммах на кубический метр (кг/м3); также часто используются внесистемные единицы, например, грамм на кубический сантиметр (г/см3). Очевидно, 1 кг/м3 = 0,001 г/см3. Заметим, что при нагревании веществ их плотность уменьшается или (реже) увеличивается, но это изменение так незначительно, что при расчётах им пренебрегают.

Сделаем оговорку, что плотность газов непостоянна; когда говорится о плотности какого-нибудь газа, обычно имеется ввиду его плотность при 0 градусов по Цельсию и нормальном атмосферном давлении (760 миллиметров ртутного столба).

Свойства массы

Масса обладает несколькими основополагающими свойствами:

• она всегда положительная;
• масса системы тел равна сумме масс тел, которые входят в эту систему;
• масса в классической механике не зависит от скорости движения тела и его характера;
• масса замкнутой системы сохраняется в случае различных взаимодействий тел друг с другом.

Для измерения величины массы на международном уровне был принят эталон массы. Он получил название килограмм. Эталон хранится во Франции и представляет собой металлический цилиндр, высота и диаметр которого составляет 39 миллиметров. Эталон – величина, которая отражает способность тела притягиваться к другому телу.

Массу в системе СИ обозначают в виде латинской маленькой буквы $m$. Масса является скалярной величиной.

Существует несколько способов определения массы на практике. Чаще всего используют метод взвешивания тела на конструкции весов. Таким способом измеряется гравитационная масса. Весы бывают различных видов:

• электронные:
• рычажные;
• пружинные.

Измерение массы тела путем взвешивания на весах – наиболее древний способ. Им пользовались жители Древнего Египта еще 4 тысячи лет назад. В наше время конструкции весов имеют различные очертания и размеры. Они позволяют определять массу тела сверхмалых форм, а также многотонных грузов. Такие весы обычно используются на транспорте или промышленных предприятиях.

Примеры решения задач

ПРИМЕР 1

Задание	Чугунный шар при объеме 125 см имеет массу 800 г. Является этот шар сплошным или полым?
Решение	Вычислим плотность шара по формуле: Переведем единицы в систему СИ: объем см м; масса г кг. По таблице плотность чугуна 7000 кг/м 3 . Так как полученное нами значение меньше табличного, шар является полым.
Ответ	Шар является полым.

ПРИМЕР 2

Задание	Во время аварии танкера в заливе образовалось пятно диаметром 640 м при средней толщине 208 см. Сколько нефти оказалось в море, если ее плотность 800 кг/м ?
Решение	Считая нефтяное пятно круглым, определим его площадь: C учетом того, что Объем нефтяного слоя равен произведению площади пятна на его толщину: Плотность нефти: откуда масса разлитой нефти: Переводим единицы в систему СИ: средняя толщина см м.
Ответ	В море оказалось кг нефти.

ПРИМЕР 3

Задание	Сплав состоит из олова массой 2,92 кг и свинца массой 1,13 кг. Какова плотность сплава?
Решение	Плотность сплава:

Плотность веществ

Плотностью тела называется масса единицы объема:

Единица измерения плотности в системе СИ кг/м
.

Разные вещества обладают различной плотностью. Плотность вещества зависит от массы атомов, из которых оно состоит, и от плотности упаковки атомов и молекул в веществе. Чем больше масса атомов, тем больше плотность вещества. В различных агрегатных состояниях плотность упаковки атомов вещества различна. В твердых телах атомы очень плотно упакованы, поэтому вещества в твердом состоянии имеют наибольшую плотность. В жидком состоянии плотность вещества несущественно отличается от его плотности в твердом состоянии, так как плотность упаковки атомов все еще велика. В газах молекулы слабо связаны друг с другом и удаляются друг от друга на большие расстояния, плотность упаковки атомов в газообразном состоянии очень низкая, поэтому в этом состоянии вещества обладают наименьшей плотностью.

Основываясь на данных астрономических наблюдений, определили среднюю плотность вещества во Вселенной, результаты расчетов говорят о том, что в среднем космическое пространство чрезвычайно разрежено. Если «размазать» вещество по всему объему нашей Галактики, то средняя плотность материи в ней окажется равной примерно 0,000 000 000 000 000 000 000 000 5 г/см 3 . Средняя плотность материи во Вселенной — приблизительно шесть атомов на кубический метр.

Масса и плотность

Любое тело «сопротивляется» попытке изменить его скорость. Это свойство тел называется инертностью. Так, например, шофер не может мгновенно остановить автомобиль, увидев перед собой внезапно выскочившего на дорогу пешехода. По той же причине трудно сдвинуть с места шкаф или диван. При одинаковом воздействии со стороны окружающих тел одно тело может быстро изменять свою скорость, а другое в тех же условиях – значительно медленнее. Говорят, что второе тело является более инертным или обладает большей массой.

Таким образом, мерой инертности тела является его инертная масса. Если два тела взаимодействуют друг с другом, то в результате изменяется скорость обоих тел, т.е. в процессе взаимодействия оба тела приобретают ускорения.

Отношение модулей ускорений взаимодействующих тел равно обратному отношению их масс:

Мерой гравитационного взаимодействия является гравитационная масса.

Экспериментально установлено, что инертная и гравитационная массы пропорциональны друг другу. Выбрав коэффициент пропорциональности равный единице, говорят о равенстве инертной и гравитационной масс.

В системе СИ единицей измерения массы является кг.

Масса обладает следующими свойствами:

1. масса всегда положительна;
2. масса системы тел всегда равна сумме масс каждого из тел, входящих в систему (свойство аддитивности);
3. в рамках классической механики масса не зависит от характера и скорости движения тела (свойство инвариантности);
4. масса замкнутой системы сохраняется при любых взаимодействиях тел системы друг с другом (закон сохранения массы).

Молекулярная физика

Химическое количество вещества находится по одной из формул:

Масса одной молекулы вещества может быть найдена по следующей формуле:

Связь массы, плотности и объёма:

Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:

Определение концентрации задаётся следующей формулой:

Для средней квадратичной скорости молекул имеется две формулы:

Средняя кинетическая энергия поступательного движения одной молекулы:

Постоянная Больцмана, постоянная Авогадро и универсальная газовая постоянная связаны следующим образом:

Следствия из основного уравнения МКТ:

Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева):

Газовые законы. Закон Бойля-Мариотта:

Закон Гей-Люссака:

Закон Шарля:

Универсальный газовый закон (Клапейрона):

Давление смеси газов (закон Дальтона):

Тепловое расширение тел. Тепловое расширение газов описывается законом Гей-Люссака. Тепловое расширение жидкостей подчиняется следующему закону:

Для расширения твердых тел применяются три формулы, описывающие изменение линейных размеров, площади и объема тела:

Вес тела и масса тела: формула подсчета

Масса это мера инертности тела, это то, каким образом тело реагирует на приложенное к нему воздействие, либо же само воздействует на другие тела. А вес тела это сила, с которой тело действует на горизонтальную опору или вертикальный подвес под влиянием притяжения Земли.

Масса измеряется в килограммах, а вес тела, как и любая другая сила в ньютонах. Вес тела имеет направление, как и любая сила, и является величиной векторной. А масса не имеет никакого направления и является величиной скалярной.

Стрелочка, которой обозначается вес тела на рисунках и графиках, всегда направлена вниз, так же, как и сила тяжести.

Формула веса тела в физике
записывается следующим образом:

где m — масса тела

g — ускорение свободного падения = 9,81 м/с^2

Но, несмотря на совпадение с формулой и направлением силы тяжести, есть серьезное различие между силой тяжести и весом тела. Сила тяжести приложена к телу, то есть, грубо говоря, это она давит на тело, а вес тела приложен к опоре или подвесу, то есть, здесь уже тело давит на подвес или опору.

Но природа существования силы тяжести и веса тела одинакова притяжение Земли. Собственно говоря, вес тела является следствием приложенной к телу силы тяжести. И, так же как и сила тяжести, вес тела уменьшается с увеличением высоты.

Понятие плотности вещества

Определение 2

Плотность является скалярной физической величиной, которая определяется массой единичного объема конкретного вещества.

$\rho = \frac{m}{V}$

Плотность вещества ($\rho$) — отношение массы тела $m$ или вещества к объёму $V$, которое занимает это тело или вещество.

Единицей плотности тела в системе измерения СИ является кг/м $^{3}$.

Замечание 2

Плотность вещества зависит от массы атомов, из которых состоит вещество, а также плотности упаковки молекул в веществе.

Плотность тела увеличивается под влиянием большого количества атомов. Различные агрегатные состояния вещества существенно изменяют плотность определенного вещества.

Твердые вещества обладают большой степенью плотности, так как в таком состоянии атомы очень плотно упакованы. Если рассматривать то же самое вещество в жидком агрегатном состоянии, то его плотность уменьшится, но останется примерно на сопоставимом уровне. В газах молекулы вещества максимально далеко находятся друг от друга, поэтому упаковка атомов на этом уровне агрегатного состояния очень низка. Вещества будут иметь наименьшую плотность.

В настоящее время исследователи составляют специальные таблицы плотности различных веществ. Наибольшие показатели по плотности имеют металлы осмий, иридий, платина, золото. Все эти материалы славятся своей безупречной прочностью. Средние показатели по плотности у алюминия, стекла, бетона – эти материалы имеют особые технические характеристики и часто используются в строительстве. Наименьшие показатели по плотности имеют сухая сосна и пробка, поэтому они не тонут в воде. Вода обладает плотностью в 1000 килограммов на кубический метр.

Ученые смогли новыми методами вычислений определить среднюю плотность вещества во Вселенной. Результаты экспериментов показали, что в основном космическое пространство разрежено, то есть там практически отсутствует плотность – примерно шесть атомов на кубический метр. Это означает, что значения массы в такой плотности также будут уникальными.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Плотность железа 7,8 г/см3. Чему равна плотность железа в кг/м3?

1) 0,078 кг/м3
2) 7,8 кг/м3
3) 7800 кг/м3
4) 7 800 000 кг/м3

2. Две тележки массами 200 г и 400 г соединены сжатой пружиной и скреплены нитью. После того, как нить пережгли, пружина распрямилась, и тележки разъехались. Первая тележка приобрела скорость, равную 0,5 м/с. Какую скорость приобрела вторая тележка?

1) 0,25 м/с
2) 0,5 м/с
3) 1 м/с
4) 2 м/с

3. При взаимодействии двух тел каждое из них приобретает ускорение. Ускорение одного тела массой 200 г равно 1 м/с2. Ускорение другого тела массой 500 г равно

1) 2,5 м/с2
2) 1 м/с2
3) 0,5 м/с2
4) 0,4 м/с2

4. Массу тела измеряют,

А. взвешивая его на рычажных весах
Б. приведя во взаимодействие с телом известной массы

Правильный ответ

1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б

5. Три тела имеют одинаковый объём. Плотности веществ, из которых изготовлены эти тела, соотносятся как ​\( \rho_1<\rho_2<\rho_3 \)​. Как соотносятся массы этих тел?

1) ​\( m_1=m_2=m_3 \)​
2) ​\( m_1>m_2>m_3 \)
3) ​\( m_1<m_2<m_3 \)
4) ​\( m_1<m_2>m_3 \)

6. На рисунке приведена столбчатая диаграмма, на которой представлены значения массы двух тел равного объёма. Какой вывод можно сделать из анализа диаграммы?

1) ​\( \rho_1=2\rho_2 \)​
2) \( \rho_1=1,5\rho_2 \)​
3) \( \rho_1=\rho_2 \)​
4) \( \rho_1=0,5\rho_2 \)​

7. Три кубика одинакового объёма сделаны из разных материалов. Плотности этих материалов соотносятся как ​\( \rho_1>\rho_2>\rho_3 \)​. Как соотносятся массы этих тел?

1) ​\( m_1<m_2<m_3 \)
2) \( m_1=m_2=m_3 \)
3) \( m_1>m_2>m_3 \)
4) \( m_1>m_2<m_3 \)

8. На рисунке приведены графики зависимости массы двух тел от их объёма. Сравните значения плотности этих тел.

1) ​\( \rho_1<\rho_2 \)​
2) \( \rho_1=\rho_2 \)
3) \( \rho_1>\rho_2 \)
4) \( \rho_1\leq\rho_2 \)

9. Чему равна масса льдины объёмом 0,2 м3, если плотность льда 0,9 г/см3?

1) 0,18 кг
2) 4,5 кг
3) 18 кг
4) 180 кг

10. Отвечая на вопрос учителя о том, какую величину называют плотностью вещества, учащиеся давали разные ответы, среди которых были следующие:

А. Плотность вещества — физическая величина, прямо пропорциональная массе тела и обратно пропорциональная его объёму.
Б. Плотность вещества — физическая величина, рав-
ная отношению массы тела к его объёму.

Правильный ответ:

1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б

11. Ниже приведены таблица плотности веществ и четыре утверждения. Из приведённых ниже утверждений выберите два правильных и запишите их номера

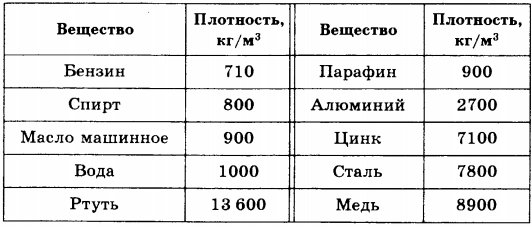
1) Масса 6 м3 машинного масла равна массе 2 м3 алюминия
2) Объём стальной детали больше объёма алюминиевой детали при их одинаковой массе
3) Объём 0,5 кг машинного масла примерно в 2 раза меньше объёма 0,8 кг спирта
4) Масса 5 м3 цинка меньше массы 30 м3 воды

12. Установите соответствие между физическими величинами в левом столбце и их зависимостью от выбора системы отсчёта в правом столбце. В таблице под номером
физической величины левого столбца запишите соответствующий номер выбранного вами элемента из правого столбца.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) масса
Б) время
B) скорость

ПОНЯТИЕ
1) относительная
2) инвариантная

Часть 2

13. Два мяча: один массой 200 г, другой массой 250 г после столкновения разлетелись в разные стороны. Мяч меньшей массы в результате столкновения приобрёл скорость 5 м/с. Чему равен путь, который пролетит за 2 с мяч большей массы? Считать, что скорость мяча за это время не изменится.

Изменение скорости движения

Плотность веществ

Плотностью тела называется масса единицы объема:

Единица измерения плотности в системе СИ кг/м .

Разные вещества обладают различной плотностью. Плотность вещества зависит от массы атомов, из которых оно состоит, и от плотности упаковки атомов и молекул в веществе. Чем больше масса атомов, тем больше плотность вещества. В различных агрегатных состояниях плотность упаковки атомов вещества различна. В твердых телах атомы очень плотно упакованы, поэтому вещества в твердом состоянии имеют наибольшую плотность. В жидком состоянии плотность вещества несущественно отличается от его плотности в твердом состоянии, так как плотность упаковки атомов все еще велика. В газах молекулы слабо связаны друг с другом и удаляются друг от друга на большие расстояния, плотность упаковки атомов в газообразном состоянии очень низкая, поэтому в этом состоянии вещества обладают наименьшей плотностью.

Основываясь на данных астрономических наблюдений, определили среднюю плотность вещества во Вселенной, результаты расчетов говорят о том, что в среднем космическое пространство чрезвычайно разрежено. Если «размазать» вещество по всему объему нашей Галактики, то средняя плотность материи в ней окажется равной примерно 0,000 000 000 000 000 000 000 000 5 г/см 3 . Средняя плотность материи во Вселенной — приблизительно шесть атомов на кубический метр.

Ключевые различия между массой и плотностью

Следующие пункты являются существенными, как разница между массой и плотностью:

1. Термин «масса» используется для обозначения количества вещества, содержащегося в объекте. Плотность намекает на близость атомов в веществе, то есть на то, насколько плотно атомы упакованы.
2. Масса является мерой количества инерции. И наоборот, плотность – это степень компактности.
3. Масса объекта – это внешнее свойство, которое зависит от вещества, присутствующего в веществе. Напротив, плотность объекта подразумевает внутреннее свойство объекта, которое не основано на количестве вещества, существующего в образце.
4. Масса представляет количество вещества, присутствующего в объекте. В отличие от этого, плотность указывает массу, присутствующую на единицу объема.
5. Единицей измерения массы является килограмм, тогда как стандартной единицей измерения плотности в соответствии с международным стандартом является килограмм на кубический метр.

Плотность веществ

Плотностью тела называется масса единицы объема:

Единица измерения плотности в системе СИ кг/м
.

Разные вещества обладают различной плотностью. Плотность вещества зависит от массы атомов, из которых оно состоит, и от плотности упаковки атомов и молекул в веществе. Чем больше масса атомов, тем больше плотность вещества. В различных агрегатных состояниях плотность упаковки атомов вещества различна. В твердых телах атомы очень плотно упакованы, поэтому вещества в твердом состоянии имеют наибольшую плотность. В жидком состоянии плотность вещества несущественно отличается от его плотности в твердом состоянии, так как плотность упаковки атомов все еще велика. В газах молекулы слабо связаны друг с другом и удаляются друг от друга на большие расстояния, плотность упаковки атомов в газообразном состоянии очень низкая, поэтому в этом состоянии вещества обладают наименьшей плотностью.

Основываясь на данных астрономических наблюдений, определили среднюю плотность вещества во Вселенной, результаты расчетов говорят о том, что в среднем космическое пространство чрезвычайно разрежено. Если «размазать» вещество по всему объему нашей Галактики, то средняя плотность материи в ней окажется равной примерно 0,000 000 000 000 000 000 000 000 5 г/см 3 . Средняя плотность материи во Вселенной — приблизительно шесть атомов на кубический метр.

Второй закон Ньютона

Всякое тело оказывает сопротивление при попытке привести его в движение, т.е. придать ему некоторое ускорение. Такое свойство тел называется инертностью. Мера инертности — масса.

Система тел, на которую не оказывают влияние другие тела, называется замкнутой системой или изолированной системой. В таких системах тела могут взаимодействовать только друг с другом.Пусть замкнутая система состоит из двух тел (двух материальных точек). Скорость тел и , а и приращение этих скоростей за один и тот же промежуток времени . Векторы и имеют противоположные направления и связаны соотношением . Коэффициенты и постоянны и имеют одинаковые знаки и называются массами или инертными массами тел 1 и 2.

Импульс или количество движения материальной точки — вектор, равный произведению массы точки на её скорость.

Импульс системы — векторная сумма импульсов отдельных материальных точек, из которых состоит система: для системы состоящей из материальных точек.

Импульс изолированной системы остаётся постоянным во времени – Закон сохранения импульса.

Сила (в механике) — всякая причина, которая меняет импульс тела (это качественная характеристика). Количественная характеристика выражается уравнением:

Это уравнение справедливо только в том случае, если m не зависит от скорости.

В инерциальной системе отсчёта производная импульса материальной точки по времени равна действующей на неё силе.

ИЛИ

В инерциальной системе отсчёта ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе

Приведённые выше высказывания есть ничто иное как две формулировки второго закона Ньютона. Соответствующее определению закона уравнение — уравнение движения материальной точки.