Скрещивающиеся прямые — определение, теорема и примеры

Понятие скрещивающихся прямых

В пространстве можно построить две прямые так, что они не будут пересекаться, но и параллельными они также являться не будут. Для этого достаточно, чтобы прямые НЕ находились в одной плоскости. В этом случае их именуют скрещивающимися прямыми.

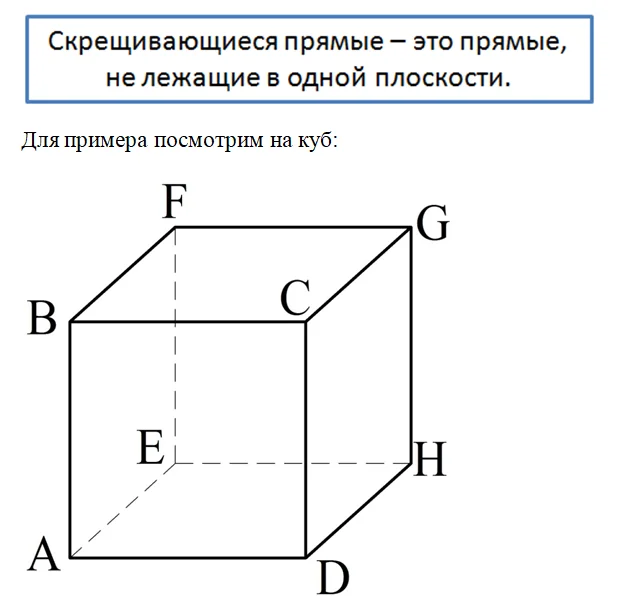
Здесь ребра ВС и АЕ как раз лежат на двух скрещивающихся прямых. Поэтому их можно так и называют – скрещивающиеся отрезки. По аналогии можно ввести понятие и скрещивающихся лучей.

Существует теорема, представляющая собой признак скрещивающихся прямых.

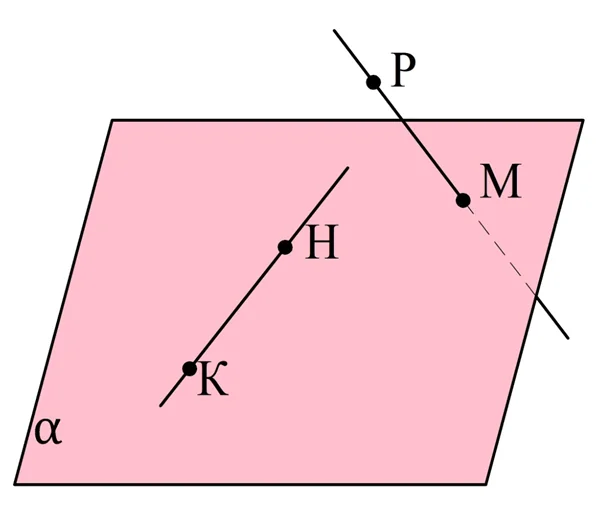
Действительно, пусть есть две прямые, НК и РМ. Обозначим как α плос-ть, проходящую через НК и точку М. Если РМ пересекает α, то это означает, что М – единственная общая точка у α и РМ. Получается, что Н, К, М и Р – это точки в различных плос-тях, и через них нельзя провести одну плос-ть. Значит, и прямые НК и РМ – скрещивающиеся.

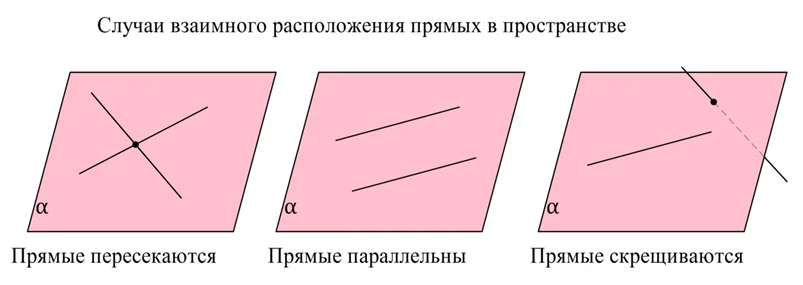
Таким образом, в стереометрии возможно всего три случая взаимного расположения двух прямых в пространстве:

1) прямые пересекаются, и тогда они обязательно находятся в одной плос-ти;

2) прямые располагаются в одной плос-ти, но не пересекаются – случай параллельных прямых;

3) прямые находятся в разных плос-тях – случай скрещивающихся прямых.

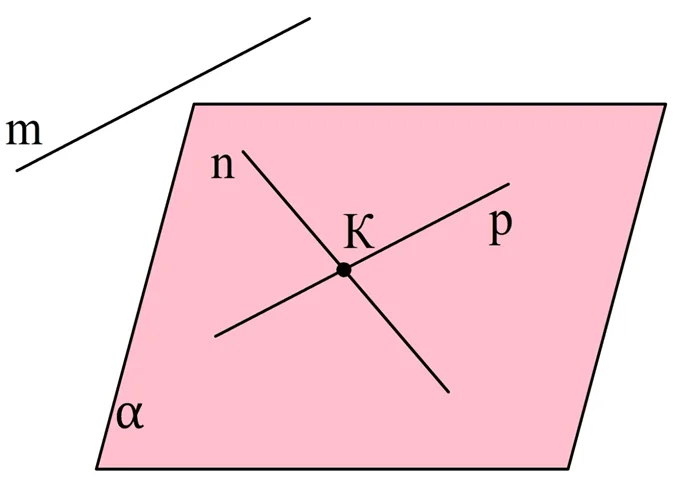
Докажем одну теорему:

Для доказательства возьмем произвольные скрещивающиеся прямые m и n. Отметим на n точку К и проведем через К прямую р, параллельную m:

Через пересекающиеся прямые nи p можно провести единственную плос-тьα. По признаку параллельности прямой и плос-ти можно заключить, что m||α.

Покажем, что кроме α нет других плос-тей, проходящих через n и параллельных m. Действительно, если бы такая плос-ть β существовала, то р имела бы с ней общую точку К, но полностью в β она бы не могла находиться, иначе α и β совпадали бы. Значит, р пересекала бы β. Но тогда ее обязательно пересекала бы и m по одну из свойств параллельных прямых. В этом случае m и β не были бы параллельными.

window.yaContextCb.push(()=>{ Ya.Context.AdvManager.render({ renderTo: ‘yandex_rtb_R-A-483726-15’, blockId: ‘R-A-483726-15’ }) })

Задание. Прямые m и n скрещиваются. M – точка на m, N – точка на n. Через m и N проведена плос-ть α, а через n и M – плос-ть β. Пересекаются ли плос-ти α и β, и если да, то по какой линии?

Решение.

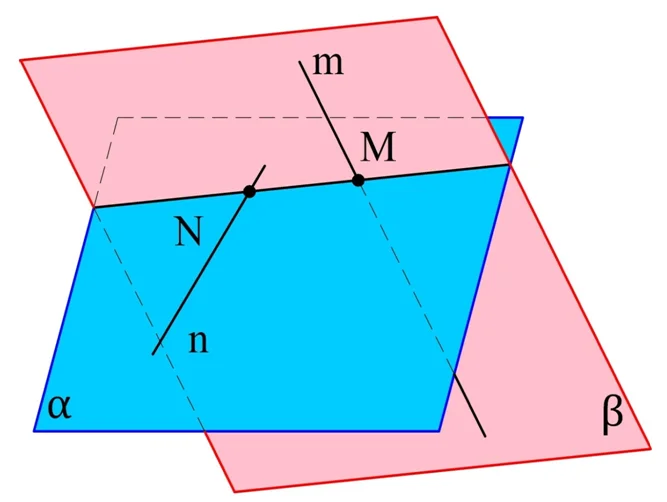
Посмотрим, есть ли у α и β общие точки. Плос-ть α проходит через n, то есть и через точку N тоже. Плос-ть β также проходит через N. Значит, N – общая точка. Аналогично можно показать, что и М – это общая точка. В итоге α и β пересекаются, причем на линии пересечения находятся точки M и N. Значит, именно прямая МN является границей этих двух плос-тей.

Задание. Известно, что MНКЕ – параллелограмм, а МНРТ – трапеция (РТ – её основание), причем они располагаются в разных областях. Каково расположение отрезков КЕ и РТ друг относительно друга.

Решение. Задачу можно решить и без рисунка. Если РТ – основание трапеции, то второе основание – это МН, и МН||РТ. В параллелограмме МНКЕ параллельны стороны МН и КЕ, ведь они противоположные. Тогда по свойству транзитивности параллельности из того факта, что МН||РТ и МН||КЕ, вытекает, что и РТ||КЕ.

Аксиомы стереометрии и следствия из них

Упростить решение множества задач и изучение стереометрии позволяет знание основных положений и правил. К примеру, существуют аксиомы, которые не нуждаются в доказательстве. С их помощью достаточно просто выполнять построение классических и сложных фигур, производить разнообразные вычисления. Перечислим их.

Аксиома 1: Если 3 точки не принадлежат общей прямой, то через них допустимо построить плоскость в единственном экземпляре.

Аксиома 2: При нахождении 2 точек какой-то прямой в некой плоскости можно сделать вывод о расположении в этой же плоскости остальных точек рассматриваемой прямой.

Аксиома 3: В том случае, когда пара плоскостей обладает общей точкой, можно сделать вывод о наличии у таких плоскостей одной прямой, содержащей каждую из точек пересечения рассматриваемых плоскостей.

Аксиома 4: В какой-либо пространственной плоскости справедлива каждая из аксиом планиметрии.

При анализе перечисленных аксиом можно сформулировать некоторые закономерности. Такие утверждения называют следствиями. Перечислим их.

Следствие 1

Если имеется какая-то прямая и точка, ей не принадлежащая, то через данные элементы допустимо провести единственную плоскость.

Следствие 2

Если 2 прямые линии пересекаются между собой, то с их помощью допустимо построить единственную плоскость.

Следствие 3

В том случае, когда имеется пара прямых, расположенных параллельно относительно друг друга, через них допустимо провести единственную плоскость.

Следствие 4

Когда прямая не расположена на некоторой плоскости, данные элементы обладают максимум одной единой точкой.

Нахождение угла между скрещивающимися прямыми.

Так как угол между скрещивающимися прямыми определяется через угол между пересекающимися прямым, то нахождение угла между скрещивающимися прямыми сводится к нахождению угла между соответствующими пересекающимися прямыми в трехмерном пространстве.

Несомненно, для нахождения угла между скрещивающимися прямыми подходят методы, изучаемые на уроках геометрии в средней школе. То есть, выполнив необходимые построения, можно связать искомый угол с каким-либо известным из условия углом, основываясь на равенстве или подобии фигур, в некоторых случаях поможет теорема косинусов
, а иногда к результату приводит определение синуса, косинуса и тангенса угла
прямоугольного треугольника.

Однако очень удобно решать задачу нахождения угла между скрещивающимися прямыми методом координат. Именно его и рассмотрим.

Пусть в трехмерном пространстве введена Oxyz
(правда, во многих задачах ее приходится вводить самостоятельно).

Поставим перед собой задачу: найти угол между скрещивающимися прямыми a
и b
, которым соответствуют в прямоугольной системе координат Oxyz
некоторые уравнения прямой в пространстве .

Решим ее.

Возьмем произвольную точку трехмерного пространства М
и будем считать, что через нее проходят прямые a 1
и b 1
, параллельные скрещивающимся прямым a
и b
соответственно. Тогда искомый угол между скрещивающимися прямыми a
и b
равен углу между пересекающимися прямыми a 1
и b 1
по определению.

Таким образом, нам осталось найти угол между пересекающимися прямыми a 1
и b 1
. Чтобы применить формулу для нахождения угла между двумя пересекающимися прямыми в пространстве нам нужно знать координаты направляющих векторов прямых a 1
и b 1
.

Как же мы их можем получить? А очень просто. Определение направляющего вектора прямой позволяет утверждать, что множества направляющих векторов параллельных прямых совпадают. Следовательно, в качестве направляющих векторов прямых a 1
и b 1
можно принять направляющие векторы и прямых a
и b
соответственно.

Итак, угол между двумя скрещивающимися прямыми a
и b
вычисляется по формуле
, где и — направляющие векторы прямых a
и b
соответственно.

Формула для нахождения косинуса угла между скрещивающимися прямыми
a
и b
имеет вид .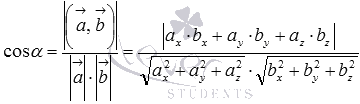

Позволяет найти синус угла между скрещивающимися прямыми, если известен косинус: .

Осталось разобрать решения примеров.

Пример.

Найдите угол между скрещивающимися прямыми a
и b
, которые определены в прямоугольной системе координат Oxyz
уравнениями и .

Решение.

Канонические уравнения прямой в пространстве позволяют сразу определить координаты направляющего вектор этой прямой – их дают числа в знаменателях дробей, то есть, . Параметрические уравнения прямой в пространстве также дают возможность сразу записать координаты направляющего вектора – они равны коэффициентам перед параметром, то есть, — направляющий вектор прямой . Таким образом, мы располагаем всеми необходимыми данными для применения формулы, по которой вычисляется угол между скрещивающимися прямыми: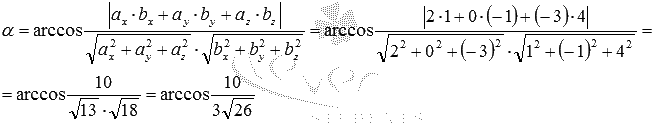

Ответ:

Угол между заданными скрещивающимися прямыми равен .

Пример.

Найдите синус и косинус угла между скрещивающимися прямыми, на которых лежат ребра AD
и BC
пирамиды АВСD
, если известны координаты ее вершин: .

Решение.

Направляющими векторами скрещивающихся прямых AD
и BC
являются векторы и . Вычислим их координаты как разность соответствующих координат точек конца и начала вектора: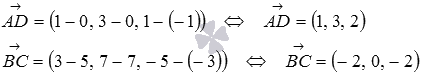

По формуле мы можем вычислить косинус угла между указанными скрещивающимися прямыми:

Теперь вычислим синус угла между скрещивающимися прямыми: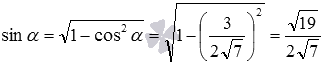

Ответ:

Параллельные прямые в пространстве

Параллельные прямые пространства, как и пересекающиеся прямые тоже лежат в одной плоскости:

Что сразу можно сказать? Они не пересекаются, и у них один и тот же направляющий вектор.

В начале этой статьи я зарубил четырёхглавого дракона, ловите мой меч-кладенец, вас поджидает стандартный шестиглазый зверь:

Пример 17

Дана прямая . Требуется:

а) построить прямую , параллельную данной и проходящую через точку

б) будут ли параллельные прямые  однозначно определять плоскость в пространстве? Если да, то составить уравнение данной плоскости;

в) найти расстояние между параллельными прямыми.

Постарайтесь самостоятельно, не заглядывая в образец решения, выполнить предложенные задания.

Вот, пожалуй, и все основные задачи с пространственными прямыми. После изучения уравнения плоскости и уравнений прямой в пространстве, можно приступить к рассмотрению задач на прямую и плоскость, они вряд ли покажутся вам сложнее.

Желаю успехов!

Решения и ответы:

Пример 12: Решение: 1) Находим направляющие векторы и точки, принадлежащие данным прямым. Для нахождения точек удобно использовать нулевые значения параметров :2) Найдём вектор: 3) Вычислим смешанное произведение векторов: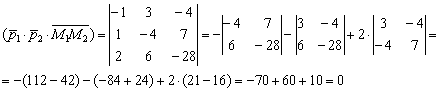Таким образом, прямые  могут пересекаться, быть параллельными или совпадать.4) Исследуем направляющие векторы  на коллинеарность:, следовательно, направляющие векторы не коллинеарны, и прямые пересекаются.Ответ

Пример 16: Решение: 1) Выполним схематический чертёж: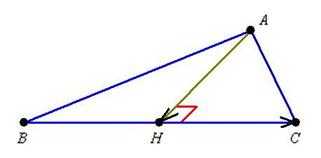2) Найдём вектор .3) Запишем параметрические уравнения прямой  по точке  и направляющему вектору : 4) Точка , поэтому её координаты удовлетворяют параметрическим уравнениям данной прямой: .5) Найдём вектор .6) Так как  – высота треугольника, то  и:7) Найдём точку:   Точка  совпала с точкой , значит, высота  совпадает со стороной , и треугольник является прямоугольным.8) Найдём вектор .9) Составим уравнения высоты  (катета ) по точке  и направляющему вектору : 10) Найдём длину высоты  как длину вектора :Ответ

Пример 17: Решение: а) Из уравнений прямой  найдём её направляющий вектор: . Уравнения прямой  составим по точке  и направляющему вектору :б) Да, две параллельные прямые однозначно определяют плоскость, в которой они лежат. Точка  принадлежит первой прямой.Найдём вектор: Уравнение искомой плоскости составим по точке  и двум неколлинеарным векторам :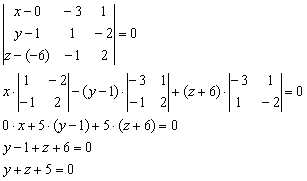в) Расстояние между параллельными прямыми   найдём как расстояние от точки до прямой:  (формула из Примера № 15).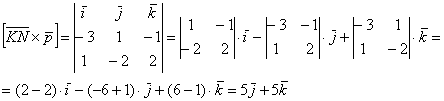

Таким образом: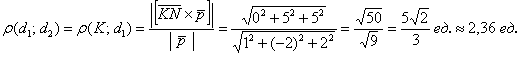 Ответа) б) да,

в)

(Переход на главную страницу)

Теорема 1 (признак скрещивающихся прямых) и ее доказательство

Теорема (признак скрещивающихся прямых)

Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на этой прямой, то эти прямые скрещивающиеся.

Доказательство

Пусть нам дана плоскость α. Прямая АВ лежит в плоскости α, а прямая DC пересекается с плоскостью α в точке С, которая не лежит на прямой АВ (Рис. 1.). Докажем, что прямые АВ и DC являются скрещивающимися.

Рис. 1.

Используем метод от противного. Предположим, что существует плоскость β, в которой лежит, и прямая АВ и прямая DC. Тогда в плоскости β лежит прямая АВ и точка С. Через прямую и точку, не лежащую на ней проходит единственная плоскость — α. Значит, такой плоскости β, в которой лежит, и прямая АВ и прямая DC, не существует. То есть, прямые АВ и DC – скрещивающиеся. Теорема доказана.

Взаимное расположение прямых в пространстве

Две прямые  пространства могут:

1) скрещиваться;

2) пересекаться в точке ;

3) быть параллельными ;

4) совпадать.

Случай № 1 принципиально отличается от других случаев. Две прямые скрещиваются, если они не лежат в одной плоскости. Поднимите одну руку вверх, а другую руку вытяните вперёд – вот вам и пример скрещивающихся прямых. В пунктах же № 2-4 прямые обязательно лежат в одной плоскости.

Как выяснить взаимное расположение прямых в пространстве?

Рассмотрим две прямые пространства:

– прямую , заданную точкой  и направляющим вектором ;
– прямую , заданную точкой  и направляющим вектором .

Для лучшего понимания выполним схематический чертёж: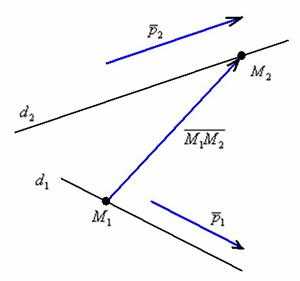
На чертеже в качестве примера изображены скрещивающиеся прямые.

Как разобраться с этими прямыми?

Так как известны точки , то легко найти вектор .

Если прямые скрещиваются, то векторы  не компланарны (см. урок Линейная (не) зависимость векторов. Базис векторов), а, значит, определитель, составленный из их координат, ненулевой. Или, что фактически то же самое, смешанное произведение векторов будет отлично от нуля: .

В случаях № 2-4 наша конструкция «падает» в одну плоскость, при этом векторы  компланарны, а смешанное произведение линейно зависимых векторов равняется нулю: .

Раскручиваем алгоритм дальше. Предположим, что , следовательно, прямые либо пересекаются, либо параллельны, либо совпадают.

Если направляющие векторы  не коллинеарны, то прямые пересекаются. Как проверить два вектора на коллинеарность, подробно рассмотрено в той же статье Линейная (не) зависимость векторов. Базис векторов.

Если направляющие векторы  коллинеарны, то  прямые либо параллельны, либо совпадают. Финальным гвоздём предлагаю следующий приём: берём какую-либо точку одной прямой и подставляем её координаты в уравнение второй прямой; если координаты «подошли», то прямые совпадают, если «не подошли», то прямые параллельны.

Ход алгоритма незатейлив, но практические примеры всё равно не помешают:

Пример 11

Выяснить взаимное расположение двух прямых

Решение: как и во многих задачах геометрии, решение удобно оформить по пунктам:

1) Вытаскиваем из уравнений точки и направляющие векторы:

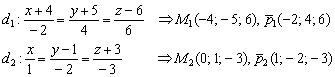
2) Найдём вектор:

3) Вычислим смешанное произведение векторов:

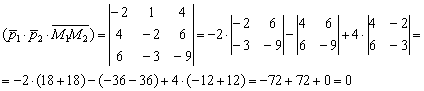
Таким образом, векторы  компланарны, а значит, прямые  лежат в одной плоскости и могут пересекаться, быть параллельными или совпадать.

4) Проверим направляющие векторы  на коллинеарность.

Составим систему из соответствующих координат данных векторов:

Из каждого уравнения следует, что , следовательно, система совместна, соответствующие координаты векторов пропорциональны, и векторы коллинеарны.

Вывод: прямые  параллельны либо совпадают.

5) Выясним, есть ли у прямых общие точки. Возьмём точку , принадлежащую первой прямой, и подставим её координаты в уравнения прямой :

Таким образом, общих точек у прямых нет, и им ничего не остаётся, как быть параллельными.

Ответ:

Интересный пример для самостоятельного решения:

Пример 12

Выяснить взаимное расположение прямых

Обратите внимание, что у второй прямой в качестве параметра выступает буква. Логично

В общем случае – это же две различные прямые, поэтому у каждой прямой свой параметр.

И снова призываю не пропускать примеры, пороть буду предлагаемые мной задачи далеко не случайны

Задачи с прямой в пространстве

В заключительной части урока я постараюсь рассмотреть максимальное количество различных задач с пространственными прямыми. При этом будет соблюдён начатый порядок повествования: сначала мы рассмотрим задачи со скрещивающимися прямыми, затем с пересекающимися прямыми, и в конце поговорим о параллельных прямых в пространстве. Однако должен сказать, что некоторые задачи данного урока можно сформулировать сразу для  нескольких случаев расположения прямых, и в этой связи разбиение раздела на параграфы несколько условно. Есть более простые примеры, есть более сложные примеры, и, надеюсь, каждый найдёт то, что нужно.

Разновидности уравнений прямой

Канонические уравнения прямой.Пусть задана точка $M_{0} \left(x_{0} ,y_{0} ,z_{0} \right)$, через которую проходит прямая, а также направляющий вектор $\overline{R}=m\cdot \overline{i}+n\cdot \overline{j}+p\cdot \overline{k}$, которому она параллельна. Уравнения $\frac{x-x_{0} }{m} =\frac{y-y_{0} }{n} =\frac{z-z_{0} }{p}$ называются каноническими уравнениями прямой.

Параметрические уравнения прямой. Введем обозначения: $\frac{x-x_{0} }{m} =t$, $\frac{y-y_{0} }{n} =t$, $\frac{z-z_{0} }{p} =t$. Здесь $t$ — параметр. Из этих равенств получаем: $x=x_{0} +m\cdot t$, $y=y_{0} +n\cdot t$, $z=z_{0} +p\cdot t$. Эти уравнения называются параметрическими уравнениями прямой.

Уравнение прямой, которая проходит через две заданные точки $M_{1} \left(x_{1} ,y_{1} ,z_{1} \right)$ и $M_{2} \left(x_{2} ,y_{2} ,z_{2} \right)$. Уравнения $\frac{x-x_{1} }{x_{2} -x_{1} } =\frac{y-y_{1} }{y_{2} -y_{1} } =\frac{z-z_{1} }{z_{2} -z_{1} } $, аналогичные каноническим, называются уравнениями прямой, проходящей через две заданные точки.

Статья: Взаимное расположение прямых в пространстве

Найди решение своей задачи среди 1 000 000 ответов

Общие уравнения прямой. Прямую линию в пространстве можно определить как линию пересечения двух не параллельных между собой плоскостей: $A_{1} \cdot x+B_{1} \cdot y+C_{1} \cdot z+D_{1} =0$ и $A_{2} \cdot x+B_{2} \cdot y+C_{2} \cdot z+D_{2} =0$. Решение системы уравнений, состоящей из уравнений плоскостей, называются общими уравнениями прямой.

window.yaContextCb.push(()=>{ Ya.Context.AdvManager.render({ renderTo: ‘yandex_rtb_R-A-483726-17’, blockId: ‘R-A-483726-17’ }) })

Задание. Дан куб, вершины которого обозначены так, как это показано на рисунке:

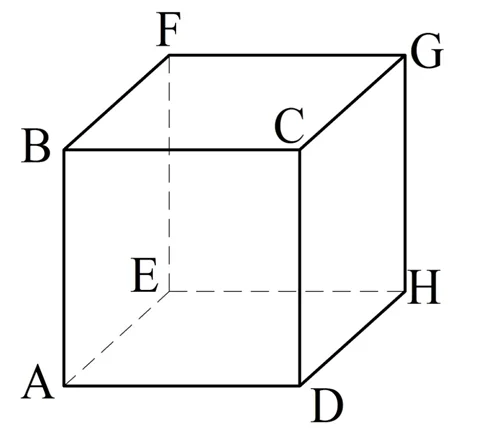
Найдите угол между прямыми:

Решение. Во всех трех случаях нам даны скрещивающиеся прямые. Для вычисления угла надо найти такие параллельные им прямые, которые будут пересекаться.

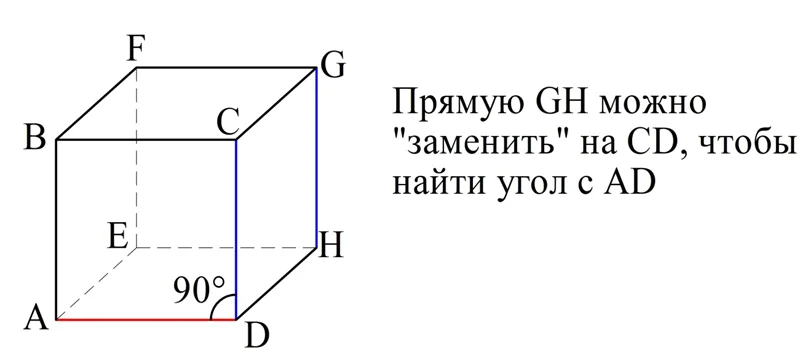
а) AD и GH. Заметим, что GH||СD, ведь это противоположные стороны квадрата СDHG, поэтому мы можем определить угол между AD и CD. Другими словами, мы просто заменяем в задаче GH на CD, так как эти отрезки параллельны. Так как отрезки AD и CD в свою очередь являются уже смежными сторонами в квадрате АВСD, то ∠ADC, который нам надо найти, составляет 90°.

б) BD и FG. Здесь уже уместно заменить FG на ВС. Это можно сделать, ведь FG||ВС (это стороны квадрата). Тогда нам необходимо вычислить ∠СВD. Он составляет 45°, ведь диагональ квадрата делит его угол пополам.

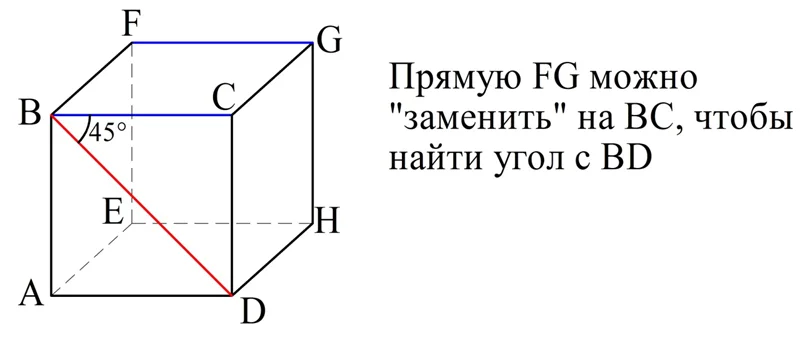
в) BD и AF. Здесь есть смысл AF заменить на GD. Но для этого надо сначала показать, что AF||DG.Рассмотрим отрезки AD и FG. Каждый из них параллелен ВС (по свойству квадратов ABCD и ВСGH). Значит, по свойству транзитивности AD||FG, то есть эти отрезки располагаются в одной плос-ти. Тогда AFGD – плоский четырехугольник.

Заметим, что отрезки AD и FG ещё и одинаковы, так каждый из них равен ВС (вообще в кубе все ребра одинаковы). Получается, что в четырехугольнике AFGD стороны AD и FG одинаковы и параллельны, а потому AFGD – параллелограмм, по одному из его признаков. Отсюда и вытекает, что AF||DG.

Мы поняли, искомый нами угол между прямыми равен∠BDG. Как его вычислить? Для этого надо рассмотреть ∆BDG. Можно заметить, что он равносторонний. Действительно, отрезки BG, GD и BD – это диагонали в равных квадратах ВСGH, СDHG, АВСD, поэтому и сами эти диагонали также одинаковы. В любом равностороннем треугольнике все углы составляют по 60°, поэтому и ∠BDG равен этому же значению, то есть 60°.

Ответ: а) 90°; б) 45°; в) 60°.

Понятия стереометрии

Стереометрия представляет собой раздел в науке геометрии, нацеленный на исследование свойств, которые характерны для фигур, расположенных в пространстве.

Ознакомимся с основными понятиями и теориями данной области научных знаний. Предмет изучает разнообразные фигуры. Рассмотрим основные из них, с которыми часто можно столкнуться в процессе решения задач и в продолжении обучения темам из курса стереометрии повышенного уровня сложности.

Многогранником называют некое тело в геометрии, границы которого сформированы с помощью определенного количества плоских многоугольников, какая-либо пара из которых обладает единой стороной и не расположена в общей плоскости.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Многогранники имеют следующие составные элементы:

• грани в виде многоугольников, которые упоминаются в определении;
• стороны, то есть ребра рассматриваемого многогранника;
• вершины, которые совпадают с вершинами данного многогранника.

Примеры многогранников:

Поверхность многогранника представляет собой фигуру, которая сформирована с помощью каждой из граней этого многогранника. При этом площади граней рассматриваемой фигуры в сумме дают площадь полной поверхности.

Кубом называют такой многогранник, который состоит из 6 граней в виде идентичных квадратов.

Куб обладает следующими компонентами:

• стороны являются ребрами фигуры;
• вершинами обозначают вершины рассматриваемого куба.

Пример куба:

Параллелепипед является одним из видов многогранника, обладает 6 гранями в форме параллелограмма.

Перечислим компоненты параллелепипеда:

• стороны, то есть ребра;
• вершины, то есть вершины этих сторон.

В прямом параллелепипеде грани с боков являются прямоугольниками. Прямоугольным называют такой параллелепипед, у которого каждая из граней обладает формой прямоугольника.

Призма представляет собой разновидность многогранника с парой граней в виде идентичных многоугольников и остальными гранями, изображенными, как параллелограммы.

Введем определения для элементов призмы:

• основания, то есть многоугольники, которые равны между собой;
• боковые грани в виде параллелограммов.

Призма может быть следующих типов:

• прямая, с боковыми гранями в форме прямоугольников;
• правильная, в виде прямой призмы, в основаниях которой расположены правильные многоугольники.

Пример призмы:

Пирамидой называют многогранник с одной гранью в виде некого многоугольника и остальными гранями, изображенными в форме треугольников, обладающих единой вершиной.

В состав пирамиды включены такие элементы, как:

• основание, то есть многоугольник;
• боковые грани треугольной формы;
• вершина, совпадает с единой вершиной треугольников.

Условия идентификации правильной пирамиды:

• в основании расположен правильный многоугольник;
• равенство боковых ребер.

Пример пирамиды:

Тетраэдр представляет собой треугольную пирамиду с гранями, изображенными в форме правильных треугольников, которые равны друг другу.

Практическое применение

Теоретические основы, понятия на уроках геометрии в режиме онлайн понятны, но для закрепления материала в классе решаются разные задачи с доказательствами. Сначала нужно найти в пространстве линии, углы и охарактеризовать их вид.

Типовые задачи

Чтобы на практике понять действие теорем, нужно использовать пример решения и наглядный рисунок. Например, точка D не лежит в плоскости АВС, точки M, N, P будут центром DA, DB и DC. Точка К расположена на прямой ВС. Требуется определить взаимное расположение линий.

1) ND, АВ.

Линии будут обозначаться буквами АВ и BD, они находятся в плоскости АВD и пересекаются.

2) PK и ВС.

Эти две линии расположены в единой плоскости, поэтому являются параллельными или пересекающимися. Нужно провести среднюю линию NP, где N, P являются серединой отрезка DB и DC. По свойству средней линии, NP II (знак параллельности) ВС. Через т. Р проводится отрезок, II ВС, и это NP. Любая другая линия, проходящая через т. Р, не II ВС, поэтому PK и ВС пересекаются.

3) MN и AB.

В треугольнике ABD точки M и N являются центрами сторон АD и ВD, значит, МN — средняя линия. Основываясь на типовых свойствах, МN II АВ.

4) МР и АС.

В ADС точки M и Р будут серединами АD и СD. Значит, МР является средней линией. МР IIАС.

5) КN и АС.

Прямопроходящая линия КN и ВD являются одной и той же прямой. АС располагается в плоскости АВС, линия ВD пересекает АВС в точке, не расположенной на АС. По признаку ВD и АС являются скрещивающимися, КN и АС — такая же.

6) МD и ВС.

MD и АD будут одинаковой ПЛ по всем характеристикам и параметрам. Линия ВС располагается в плоскости АВС, прямая АD пересекает АВС в точке, расположенной в стороне от ВС. АD и ВС относятся к скрещиванию, а МD и ВС такие же.

Сложные задания

В нижней части пирамиды SABC расположена геометрическая фигура с прямым углом при вершине С, гипотенузой АВ = 13 и катетом АС = 12 (когда 1 из 2 сторон прямоугольного треугольника образует прямой угол). Максимальная точка пирамиды S проектируется в основании В. Боковое ребро CS равняется 5*корень из 5. Требуется выяснить расстояние между ребрами AS и ВС.

Для решения нужно определить расстояние между отрезками AS и ВС. Они лежат на скрещивающихся прямых (СП). Точка s не принадлежит отрезку АВС, а точка А принадлежит АВС. AS пересекает АВС, ВС включает отрезок АВС и А не принадлежит ВС.

Расстояние между 1 из СП и плоскостью, проложенной через другую II первой, называется промежутком между СП. Нужно построить такое пространство, проходящее через 1 из СП, параллельно другой, и добавить перпендикуляр к пространству из точки, принадлежащей другой линии.

Пирамиду нужно достроить до параллелепипеда, через т. А на плоскости АВС проведя параллельную ВС и через т. В — АС. Точку пересечения ПЛ обозначают буквой D. Через А, С, D нужно провести прямые II SB, на каждой отложить отрезки, равные BS, а точки соединить линиями.

Определение скрещивающихся прямых подтверждено теоремами, также существует условие, описывающее, что через каждую пару ПЛ, которые скрещены, проложена плоскость, II другой линии. Изучены случаи расположения ПЛ в пространстве: они пересекаются, являются параллельными или скрещиваются.

Общая характеристика

Алгоритм определения того, что прямые линии (ПЛ) могут называться скрещивающимися, описывает расположение вне бесконечной поверхности. Существует несколько теорем и доказательств пересечения прямых в одной точке.

Основные понятия и теоремы

Из курса планиметрии известно, что две ПЛ в плоскости пересекаются, имеют одну точку или располагаются параллельно по отношению друг к другу.

Произвести вычисления, необходимые расчеты и графическое построение можно, изучив главные особенности и характеристику понятий. Когда прямые заданы векторными параметрическими уравнениями, выполняется равенство (формула) р = р0+SU и r = r0+tv.

Вычисление удаленности между ними определяется смешанным и векторным произведением D = (r 0 — p 0, u, v)/u, v.

Существует первая теорема, доказывающая признаки скрещивающихся ПЛ. Ее смысл заключается в теоретическом аспекте, указывающим на то, что когда одна из двух ПЛ расположена в плоскости, а другая ПЛ пересекает пространство в точке, не находящейся на отрезке, то эти ПЛ являются скрещивающимися. Данные можно доказать графически, используя методы черчения и рисования фигур, углов и перпендикуляров.

Например, дана плоскость α, в ней находится АВ, а прямая CD пересекается с плоскостью в т. С, расположенной на АВ. Для доказательства скрещивания прямых используется метод от обратного. Предполагается, что существует вторая плоскость, в которой расположены AB и DC. Во второй плоскости лежит отрезок АВ и т. С. Через ПЛ и точку, не лежащую на ней, проходит плоскость альфа. Второй плоскости бета не существует. Прямые скрещиваются.

Существует три положения прямых. В первом случае линии a и b пересекаются в т. С. Сквозь 2 ПЛ, которые пересекаются, проходит плоскость. ПЛ А II В, лежат в едином пространстве и не смогут пересечься. Прямые скрещиваются, когда не находятся в едином поле.

Вторая теорема о скрещивающихся прямых гласит, что через каждую из пары скрещивающихся ПЛ проходит одна плоскость, параллельная другой. Для подтверждения даны две ПЛ AB и CD. Требуется доказать, что через линию АВ проложена плоскость, параллельная СД.

Для этого через точку А проводится линия АЕ, расположенная параллельно DC. Согласно теореме о параллельных ПЛ, эта линия является единственной. Пересечение двух линий АВ и АЕ позволяет проложить плоскость альфа. Прямая DC, не лежащая в пространстве альфа, II АЕ, значит, DC параллельна пространству α.

Для доказательства единства такого пространства предполагается, что существует другая плоскость бета (β), проходящая через АВ, и является параллельной по отношению к DC.

Особенности ПЛ:

• Отрезок АЕ пересекает пространство бета, линия DC пересекает β.
• Отрезок DC не расположен параллельно бета.

Прочие условия

У отрезков, которые скрещиваются, нет общей точки соприкосновения, потому что тогда они бы располагались в едином пространстве.

Признаки скрещивающихся прямых:

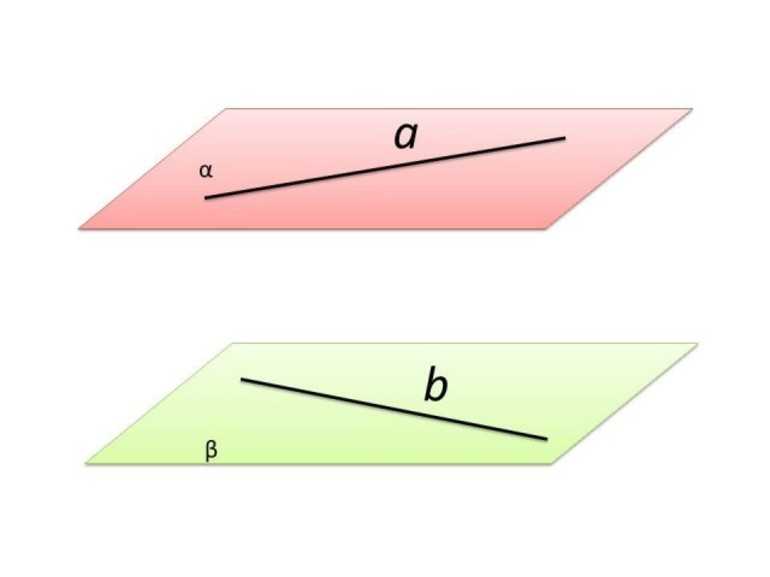
• Если на двух ПЛ имеются 4 точки, не находящиеся в одной плоскости, то линии будут скрещены. Если бы данные ПЛ были пересекающимися или параллельными по отношении друг к другу, то они лежали в единой плоскости.
• Чтобы сонаправить линии (сделать их параллельными по отношению друг к другу), угол между скрещивающимися прямыми должен быть 0 градусов. Величина, наименьшая из 2 пересекающихся линий, представляет собой угол. Когда все углы одинаковы, образуется его 90-градусный параметр и перпендикулярность.

В тригонометрии еще существует понятие обозначения косинуса — это отношение длины стороны, прилежащей к острому углу, к гипотенузе. Осуществить нахождение ПЛ параллельно скрещивающимся можно через произвольную точку. Это официальное утверждение. Две ПЛ могут быть параллельными или пресекать плоскость, значит, они находятся в едином пространстве координат.

https://youtube.com/watch?v=jEQseQZnERg

Итоги урока

Итак, мы познакомились со скрещивающимися прямыми: дали определение, доказали признак скрещивающихся прямых. Также мы доказали теорему о том, что через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна. Теперь нам известны все случаи взаимного расположения прямых в пространстве: они могут пересекаться, быть параллельными, быть скрещивающимися.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/10-klass/parallelnost-pryamyh-i-ploskostej/skreschivayuschiesya-pryamye-provedenie-cherez-odnu-iz-skreschivayuschihsya-pryamyh-ploskosti-parallelnoy-drugoy-pryamoy?seconds=0&chapter_id=210

http://www.metod-kopilka.ru/images/doc/54/49016/hello_html_m1b2a5d9c.png

http://festival.1september.ru/articles/593938/

http://www.proektant.ru/i/content/2014_II/4526_transportnaia_razviazka_02.jpg