Нормальное распределение в статистике
История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.
Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.
Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.
Кривая нормального распределения Гаусса имеет следующий вид.
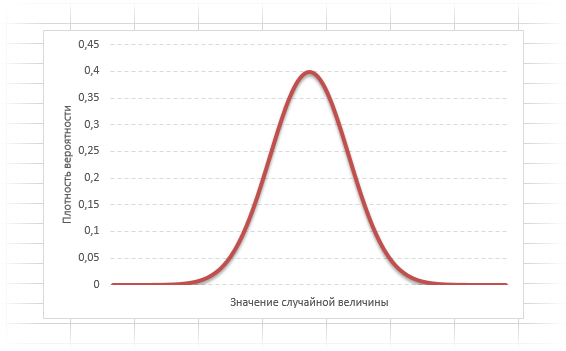
График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.
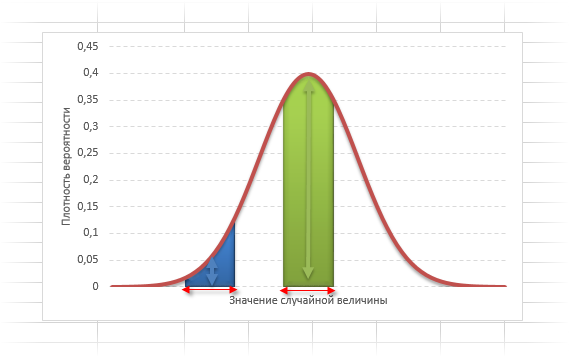
На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.
Формула нормального распределения (плотности) следующая.
Формула состоит из двух математических констант:
π – число пи 3,142;
е – основание натурального логарифма 2,718;
двух изменяемых параметров, которые задают форму конкретной кривой:
m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);
σ2 – дисперсия;
ну и сама переменная x, для которой высчитывается плотность вероятности.
Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ2). Кратко обозначается N(m, σ2) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ2 характеризует размах вариации, то есть «размазанность» данных.
Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.
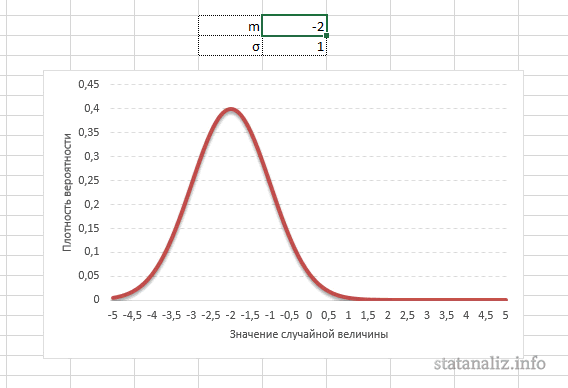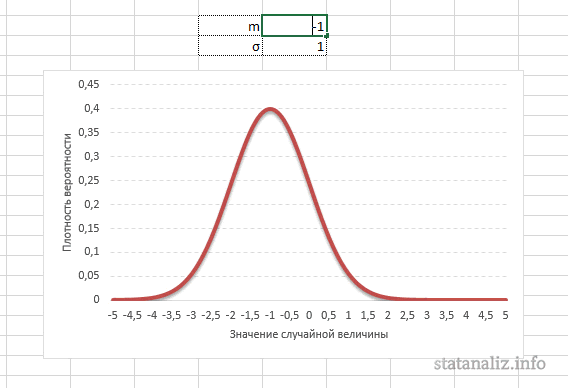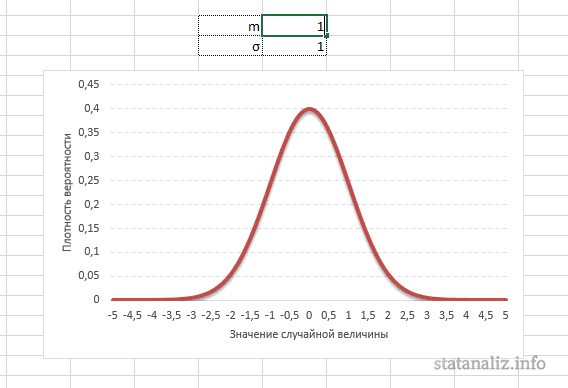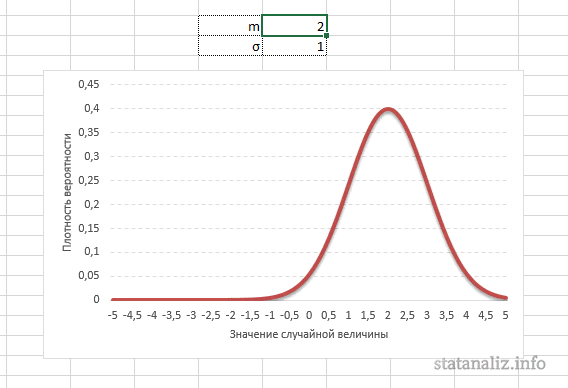
А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.
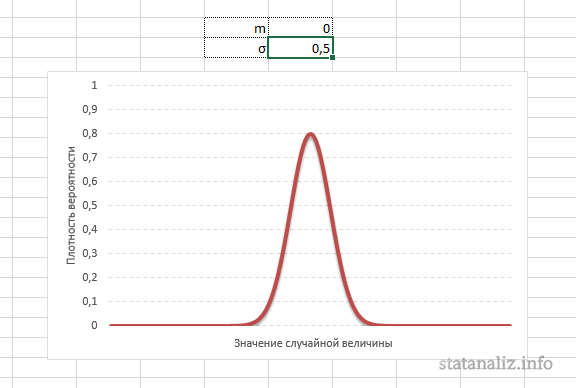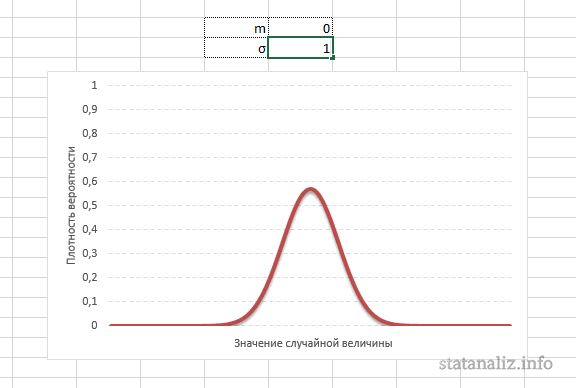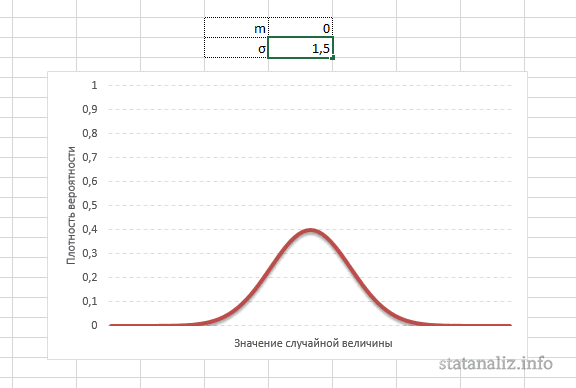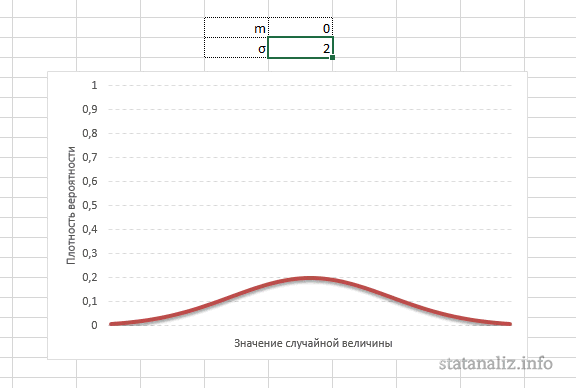
Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.
Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:
![]()
P(a ≤ X < b) = Ф(b) – Ф(a)
Гистограмма
Для построения гистограммы по оси абсцисс указывают значения границ интервалов и на их основании строят прямоугольники, высота которых пропорциональна частотам (или частостям).
На рис. 6.2. изображена гистограмма распределения населения России в 1997 г. по возрастным группам.
Рис. 6.2. Распределение населения России по возрастным группам
Условие
: Приводится распределение 30 работников фирмы по размеру месячной заработной платы
Задача
: Изобразить интервальный вариационный ряд графически в виде гистограммы и кумуляты.Решение
:
- Неизвестная граница открытого (первого) интервала определяется по величине второго интервала: 7000 — 5000 = 2000 руб. С той же величиной находим нижнюю границу первого интервала: 5000 — 2000 = 3000 руб.
- Для построения гистограммы в прямоугольной системе координат по оси абсцисс откладываем отрезки, величины которых соответствуют интервалам варицонного ряда.Эти отрезки служат нижним основанием, а соответствующая частота (частость) — высотой образуемых прямоугольников.
- Построим гистограмму:
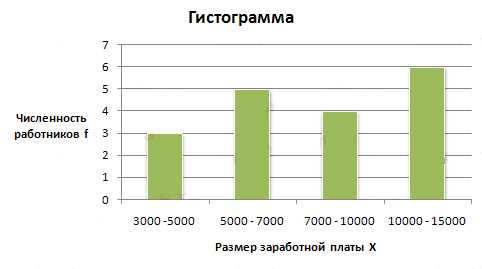
Для построения кумуляты необходимо рассчитать накопленные частоты (частости). Они определяются путем последовательного суммирования частот (частостей) предшествующих интервалов и обозначаются S. Накопленные частоты показывают, сколько единиц совокупности имеют значение признака не больше, чем рассматриваемое.
В какой программе можно создавать полигональную графику?
Трехмерная графика.
На этот вопрос нет однозначного ответа. Мастера 3D, предпочтут, несомненно, делать это в 3D max, Maya, или Cinema 4D. Последнее ПО настолько дружелюбно, что в нем может рисовать даже ребенок. В целом, полигональная графика достаточно проста в создании, особенно если сравнивать с фотореалистичной визуализацией. Она напоминает ранние дни компьютерного моделирования и анимации с налетом современных техник. Чем меньше полигонов вы используете на стадии моделирования, тем более абстрактным будет результат. Для выраженного эффекта можно отключить функцию сглаживания в настройках рендеринга, и тогда вы получите четкие грани. Здесь все зависит от эффекта, которого вы хотите достичь. Использование низкополигональной техники совсем не означает, что сцена будет простой. Вы можете использовать сложные текстуры, реалистичные настройки отражений и преломлений в окружающей среде и т. д.
2D графика.
Можно создавать полигональные шедевры в таких программах как Adobe Illustrator , и даже Adobe Photoshop . Эти программы, в отличие от специфичных 3D пакетов, хорошо знакомы большинству дизайнеров. Таким методом можно создавать стилизованные, декоративные изображения с потрясающими
А еще можно дополнять полигональную графику фотографиями, создавая удивительные коллажи, напоминающие дополненную реальность и намекающие о связях между реальным и виртуальными мирами. Некоторые работы дополняются типографикой.



История нормального распределения
В главе посвященной вероятности мы увидели, что биномиальное распределение можно использовать для таких проблем, как: «Если подбросить честную монету 100 раз, какова вероятность выпадения 60 и более орлов?» Вероятность выпадения ровно x орлов за N подбрасываний рассчитывается по формуле:
$$P(X) = \frac{N!}{x!(N-x!)}p^x(1-p)^{N-x}$$
Где \(x\) это число орлов (60), \(N\) – количество подбрасываний монеты (100), а \(p\) это вероятность выпадения орла (0.5). Таким образом, чтобы решить эту проблему вам нужно вычислить вероятность 60 орлов, затем вероятность 61 орла, 62 и т.д. и сложить эти вероятности. Представьте, сколько времени потребовалось бы для вычисления биномиальных вероятностей до появления калькуляторов и компьютеров.
Абрахам де Муавр, статистик 18-го века и консультант азартных игроков, часто привлекался к проведению этих длительных вычислений. Де Муавр заметил, что, когда число событий (подбрасываний монет) увеличивается, форма биномиального распределения приближается к очень плавной кривой. Биномиальное распределение для 2, 4 и 12 подбрасываний показаны на рис. 2.
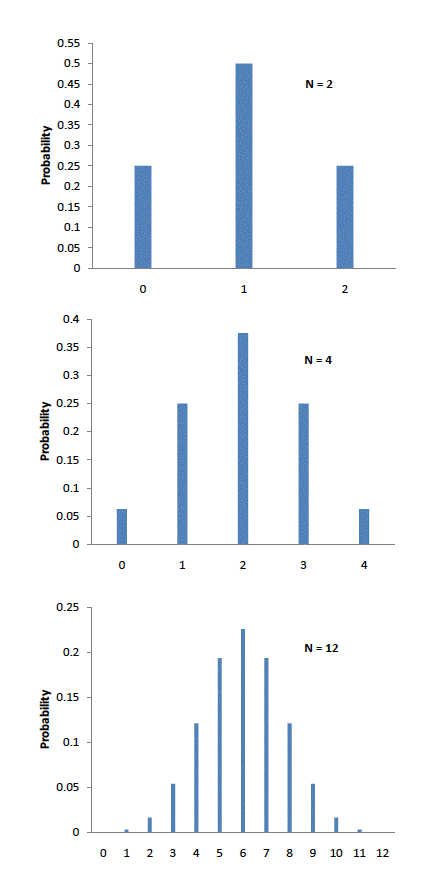 Рисунок 2. Примеры биномиальных распределений. Высоты синих столбцов являются вероятностями
Рисунок 2. Примеры биномиальных распределений. Высоты синих столбцов являются вероятностями
Де Муавр рассуждал, что, если бы он мог найти математическое выражение для этой кривой, он мог бы гораздо легче решать такие проблемы, как нахождение вероятности 60 и более орлов из 100 бросков монет. В точности это он и сделал, и кривая, которую он открыл, теперь называется «нормальной кривой».
Рисунок 3. Нормальное приближение биномиального распределения для 12 бросков монет. Гладкая кривая – это нормальное распределение
Обратите внимание, насколько хорошо она аппроксимирует биномиальные вероятности представленные высотой синих линий.
Важность нормальной кривой обусловлена тем, что распределения многих природных явлений, по крайней мере приблизительно, нормально распределены. Одно из первых применений нормального распределения было к анализу ошибок измерений, сделанных при астрономических наблюдениях, ошибок произошедших из-за несовершенства инструментов и наблюдателей
Галилео в 17 веке отметил, что эти ошибки были симметричными и что небольшие ошибки возникали чаще, чем большие. Это привело к нескольким гипотезам о распределении ошибок, но только в начале 19-го века было установлено, что эти ошибки соответствуют нормальному распределению. Независимо друг от друга математики Адрейн в 1808 г. и Гаусс в 1809 г. разработали формулу для нормального распределения и показали, что ошибки хорошо соответствуют этому распределению.
Это же распределение было обнаружено Лапласом в 1778 г., когда он вывел чрезвычайно важную центральную предельную теорему, тему одного из следующих разделов. Лаплас показал, что даже если распределение не является нормальным, средние повторяющихся выборок из распределения будут распределены почти нормально, и чем больше размер выборки, тем ближе к нормальному будет распределение средних.
Большинство статистических процедур для проверки между средними значениями предполагают нормальное распределение. Поскольку распределение средних близко к нормальному, эти тесты работают хорошо даже если само распределение только приблизительно нормально. Кетле был первым, кто применил нормальное распределение к человеческим характеристикам. Он отметил, что такие характеристики, как рост, вес и сила были нормально распределены.
Симметричное многомерное распределение Лапласа
Типичная характеристика симметричного многомерного распределения Лапласа имеет характеристическая функция:
- φ(т;μ,Σ)=exp(яμ′т)1+12т′Σт,{ displaystyle varphi (t; { boldsymbol { mu}}, { boldsymbol { Sigma}}) = { frac { exp (я { boldsymbol { mu}} ‘ mathbf {t}) } {1 + { tfrac {1} {2}} mathbf {t} ‘{ boldsymbol { Sigma}} mathbf {t}}},}
куда μ{ displaystyle { boldsymbol { mu}}} вектор средства для каждой переменной и Σ{ displaystyle { boldsymbol { Sigma}}} это ковариационная матрица.
в отличие от многомерное нормальное распределение, даже если ковариационная матрица имеет нулевой ковариация и корреляция переменные не независимы. Симметричное многомерное распределение Лапласа имеет вид эллиптический.
Функция плотности вероятности
Если μ={ displaystyle { boldsymbol { mu}} = mathbf {0}}, то функция плотности вероятности (pdf) для k-мерное многомерное распределение Лапласа принимает вид:
- жИкс(Икс1,…,Иксk)=2(2π)k2|Σ|0.5(Икс′Σ−1Икс2)v2Kv(2Икс′Σ−1Икс),{ displaystyle f _ { mathbf {x}} (x_ {1}, ldots, x_ {k}) = { frac {2} {(2 pi) ^ {k / 2} | { boldsymbol { Sigma}} | ^ {0.5}}} left ({ frac { mathbf {x} ‘{ boldsymbol { Sigma}} ^ {- 1} mathbf {x}} {2}} right) ^ {v / 2} K_ {v} left ({ sqrt {2 mathbf {x} ‘{ boldsymbol { Sigma}} ^ {- 1} mathbf {x}}} right),}
куда:
v=(2−k)2{ Displaystyle v = (2-к) / 2} и Kv{ displaystyle K_ {v}} это модифицированная функция Бесселя второго рода.
В коррелированном двумерном случае, т. Е. k = 2, причем μ1=μ2={ Displaystyle му _ {1} = му _ {2} = 0} PDF-файл сокращается до:
- жИкс(Икс1,Икс2)=1πσ1σ21−ρ2K(2(Икс12σ12−2ρИкс1Икс2σ1σ2+Икс22σ22)1−ρ2),{ displaystyle f _ { mathbf {x}} (x_ {1}, x_ {2}) = { frac {1} { pi sigma _ {1} sigma _ {2} { sqrt {1- rho ^ {2}}}}} K_ {0} left ({ sqrt { frac {2 left ({ frac {x_ {1} ^ {2}} { sigma _ {1} ^ { 2}}} — { frac {2 rho x_ {1} x_ {2}} { sigma _ {1} sigma _ {2}}} + { frac {x_ {2} ^ {2}} { sigma _ {2} ^ {2}}} right)} {1- rho ^ {2}}}} right),}
куда:
σ1{ displaystyle sigma _ {1}} и σ2{ displaystyle sigma _ {2}} являются Стандартное отклонение из Икс1{ displaystyle x_ {1}} и Икс2{ displaystyle x_ {2}}соответственно и ρ{ displaystyle rho} это коэффициент корреляции из Икс1{ displaystyle x_ {1}} и Икс2{ displaystyle x_ {2}}.
Для независимого двумерного случая Лапласа, то есть k = 2, μ1=μ2=ρ={ Displaystyle му _ {1} = му _ {2} = rho = 0} и σ1=σ2=1{ Displaystyle sigma _ {1} = sigma _ {2} = 1}, PDF-файл становится:
- жИкс(Икс1,Икс2)=1πK(2(Икс12+Икс22)).{ displaystyle f _ { mathbf {x}} (x_ {1}, x_ {2}) = { frac {1} { pi}} K_ {0} left ({ sqrt {2 (x_ {1 } ^ {2} + x_ {2} ^ {2})}} right).}
Виды статистических группировок
Вариационный ряд
-
Типологическая группировка
– это разделение исследуемой качественно разнородной совокупности на классы, социально–экономические типы, однородные группы единиц. Для построения данной группировки используйте параметр Дискретный вариационный ряд. -
Структурной называется группировка
, в которой происходит разделение однородной совокупности на группы, характеризующие ее структуру по какому–либо варьирующему признаку. Для построения данной группировки используйте параметр Интервальный ряд. - Группировка, выявляющая взаимосвязи между изучаемыми явлениями и их признаками, называется аналитической группировкой
(см. аналитическая группировка ряда).
Наиболее популярные методы статистического анализа
Наибольшее применение в задачах принятия решений получили следующие методы:
- регрессионный анализ (методы восстановления зависимости и построения моделей, прежде всего линейных);
- планирование эксперимента;
- методы классификации (дискриминантный анализ, кластерный анализ, распознавание образов, систематика и типология, теория группировок);
- многомерный статистический анализ экономической информации (анализ главных компонент и факторный анализ);
- методы анализа и прогнозирования временных рядов;
- теория робастности, т.е. устойчивости статистических процедур к допустимым отклонениям исходных данных и предпосылок модели;
- теория индексов, в частности, индекса инфляции.
Наиболее популярны регрессионные уравнения и их системы. Обычно используют уравнения не выше второго порядка, линейные по параметрам:
- Yi — переменная отклика;
- xij — факторы, от которых зависит;
- Bi — коэффициенты, которые характеризуют взаимодействие между и;
- Bif — отражают взаимодействие между и;
- ei- ошибка модели;
- i – номер наблюдения (измерения, опыта, анализа, испытания), i= 1, 2, n;
- j – номер фактора (независимой переменной), j = 1,2,…, k.
- Коэффициенты Bi, Bif находятся методом наименьших квадратов.
Применение вероятностно-статистического описания
Традиционное вероятностно-статистическое описание с интуитивной точки зрения применимо лишь к массовым событиям. Для единичных событий целесообразно применять теорию субъективных вероятностей и теорию нечетких множеств
(fuzzy sets). которая развивалась ее основателем Л.Заде для описания суждений человека, для которого переход от «принадлежности» к множеству к «непринадлежности» не скачкообразен, а непрерывен.
В последнее время можно заметить, что область статистических методов приобретает всё больший вес в системном анализе. Эта область посвящена анализу статистических данных нечисловой природы (её ещё называют статистикой нечисловых данных, или нечисловой статистикой). Выборка — это исходный объект в прикладной статистике, который означает совокупность одинаково распределенных случайных элементов, которые также являются независимыми между собой.
Необходимо различать выборку в математической статистике (выборка — это числа) и многомерном статистическом анализе (выборка — это вектора). Также стоит отметить, что в нечисловой статистике элементы выборки — это объекты нечисловой природы (нельзя складывать и умножать на числа). То есть, объекты нечисловой природы лежат в пространствах, которые не имеют векторную структуру.
Примеры объектов нечисловой природы являются:
- значения качественных признаков, т.е. результаты кодировки объектов с помощью заданного перечня категорий (градаций);
- упорядочения (ранжировки) экспертами образцов продукции (при оценке её технического уровня и конкурентоспособности) или заявок на проведение научных работ (при проведении конкурсов на выделение грантов);
- классификации, т.е. разбиения объектов на группы сходных между собой (кластеры);
- толерантности, т.е. бинарные отношения, описывающие сходство объектов между собой, например, сходства тематики научных работ, оцениваемого экспертами с целью рационального формирования экспертных советов внутри определенной области науки;
- результаты парных сравнений или контроля качества продукции по альтернативному признаку («годен» — «брак»), т.е. последовательности из 0 и 1;
- множества (обычные или нечеткие), например, зоны, пораженные коррозией, или перечни возможных причин аварии, составленные экспертами независимо друг от друга;
- слова, предложения, тексты;
- вектора, координаты которых — совокупность значений разнотипных признаков, например, результат составления статистического отчета о научно-технической деятельности организации или анкета эксперта, в которой ответы на часть вопросов носят качественный характер, а на часть — количественный;
- ответы на вопросы экспертной, маркетинговой или социологической анкеты, часть из которых носит количественный характер (возможно, интервальный), часть сводится к выбору одной из нескольких подсказок, а часть представляет собой тексты; и т.д.
Одно из основных применений статистики объектов нечисловой природы — теория и практика экспертных оценок, связанные с теорией статистических решений и проблемами голосования.
Методы анализа статистических данных
В анализе статистических данных можно выделить аналитический этап и описательный. Описательный этап — последний, он включает представление собранных данных в удобном графическом виде – в графиках, диаграммах, дашбордах. Аналитический этап — это анализ, заключающийся в использовании одного из следующих методов:
- статистического наблюдения – систематического сбора данных по интересующим характеристикам;
- сводки данных, в которой можно обработать информацию после наблюдения; она описывает отдельные факты как часть общей совокупности или создает группировки, делит информацию по группам на основании каких-либо признаков;
- определении абсолютной и относительной статистической величины; абсолютная величина придает данным количественные характеристики в индивидуальном порядке, в независимости от других данных; относительные величины описывают одни объекты или признаки относительно других;
- метода выборки – использовании при анализе не всех данных, а только их части, отобранной по определенным правилам (выборка может быть случайной, стратифицированной, кластерной и квотной);
- корреляционного и регрессионного анализа — выявляет взаимосвязи данных и причины, по которым данные зависят друг от друга, определяет силу этой зависимости;
- метода динамических рядов — отслеживает силу, интенсивность и частоту изменений объектов и явлений; позволяет оценить данные во времени и дает возможность прогнозирования явлений.
Примеры задачи на построение полигона и гистограммы
Пример 1
Пусть распределение частот имеет вид:
Рисунок 7.
Построить полигон относительных частот.
Построим сначала ряд распределения относительных частот по формуле $W_i=\frac{n_i}{n}$
Представляются в виде рядов распределения и оформляются в виде .
Ряд распределния является одним из видов группировок.
В зависимости от признака, положенного в основу образования ряда распределения различают атрибутивные и вариационные
ряды распределения:
-
Атрибутивными
— называют ряды распределения, построенные по качественными признакам. - Ряды распределения, построенные в порядке возрастания или убывания значений количественного признака называются вариационными
.
Вариационный ряд распределения состоит из двух столбцов:
В первом столбце приводятся количественные значения варьирующегося признака, которые называются вариантами
и обозначаются . Дискретная варианта — выражается целым числом. Интервальная варианта находится в пределах от и до. В зависимости от типа варианты можно построить дискретный или интервальный вариационный ряд.Во втором столбце содержится количество конкретных вариант
, выраженное через частоты или частости:
Графическое изображение рядов распределения
Наглядно ряды распределения представляются при помощи графических изображений.
Ряды распределения изображаются в виде:
- Полигона
- Гистограммы
- Кумуляты
- Огивы
Вероятностно-статистическое моделирование
При применении статистических методов в конкретных областях знаний и отраслях народного хозяйства получаем научно-практические дисциплины типа «статистические методы в промышленности», «статистические методы в медицине» и др. С этой точки зрения эконометрика — это «статистические методы в экономике». Эти дисциплины группы б) обычно опираются на вероятностно-статистические модели, построенные в соответствии с особенностями области применения. Весьма поучительно сопоставить вероятностно-статистические модели, применяемые в различных областях, обнаружить их близость и вместе с тем констатировать некоторые различия. Так, видна близость постановок задач и применяемых для их решения статистических методов в таких областях, как научные медицинские исследования, конкретные социологические исследования и маркетинговые исследования, или, короче, в медицине , социологии и маркетинге . Они часто объединяются вместе под названием «выборочные исследования».
Отличие выборочных исследований от экспертных проявляется, прежде всего, в числе обследованных объектов или субъектов — в выборочных исследованиях речь обычно идет о сотнях, а в экспертных — о десятках. Зато технологии экспертных исследований гораздо изощреннее. Еще более выражена специфика в демографических или логистических моделях, при обработке нарративной (текстовой, летописной) информации или при изучении взаимовлияния факторов.
Вопросы надежности и безопасности технических устройств и технологий, теории массового обслуживания подробно рассмотрены, в большом количестве научных работ.



























