Презентация на тему "объём пирамиды" по математике

Правильные многогранники

1. Найдите площадь поверхности правильного
тетраэдра, если сторона основания равнаа.

а)а2√͞͞͞͞͞3; б)2а2√͞͞͞͞͞3;

в)а2√͞͞͞͞͞2; г)2а2√͞͞͞͞͞2.

2. Найдите площадь поверхности правильного
тетраэдра, если апофема равнаl.

3. Найдите площадь поверхности правильного
тетраэдра, если высота равна h.

4. Найдите ребро октаэдра, если площадь его поверхности
равна 24√͞͞͞͞͞3 см2.

а) 2√͞͞͞͞͞2 см; б)2√͞͞͞͞͞3 см;

в) 2√͞͞͞͞͞6 см; г) 2 см.

5. Ребро куба равно а. Найдите площадь поверхности многогранника, вершинами
которого являются центры граней куба.

а) 3а2; б) 4а2;

в) 2а2; г) а2.

6. Ребро
правильного тетраэдра равно а. Найдите площадь поверхности многогранника, вершинами
которого являются центры граней данного тетраэдра.

7. Ребро
правильного октаэдра равно а. Найдите площадь поверхности многогранника, вершинами
которого являются центры граней данного октаэдра.

а) 3а2; б) 4а2;

в) 2а2; г) а2.

8. Найдите площадь поверхности правильного додекаэдра,
ребро которого равно m.

9. Отрезок
ОН –
высота тетраэдра ОАВС. Выясните взаимное расположение сферы радиуса R с центром
О и плоскости
АВС,
если R= 5 дм, ОА = 45 см.

а) пересекаются по окружности;

б) не
имеют общих точек;

в) нельзя
определить;

г) касаются.

10. Чему равен
двугранный угол при ребре правильного икосаэдра ?

11. Два ребра
тетраэдра равны b, а остальные четыре ребра равны а.
Найдите объём тетраэдра, если рёбра длины
b имеют общие точки.

12. Сечением
правильного икосаэдра является правильный десятиугольник. Найдите его площадь,
если ребро данного икосаэдра равно а.
Задания к уроку 18

Задание 1
Задание 3

8.2. Тетраэдр, гексаэдр, октаэдр window.top.document.title = «8.2. Тетраэдр, гексаэдр, октаэдр»;

Предъявим теперь многогранники каждого вида, доказывая тем самым их существование.

Тетраэдр (tetra – четыре, hedra – грань). Правильный тетраэдр – правильный четырехгранник, то есть тетраэдр с равными ребрами, представляет собой правильный многогранник, все грани которого – правильные треугольники и из каждой вершины которого выходит ровно три ребра. Очевидно, что тетраэдр с заданной длиной ребра единственен. Все остальные тетраэдры подобны ему и определяются длиной ребра, что следует из теоремы 8.1.

Чертеж 8.2.1

Гексаэдр (куб, hexa – шесть). Гексаэдр – правильный многогранник, все грани которого – квадраты, и из каждой вершины выходит три ребра.

Чертеж 8.2.2

Октаэдр (okto – восемь). Это правильный многогранник, все грани которого – правильные треугольники и к каждой вершине прилегают четыре грани. Покажем, что этот многогранник имеет восемь граней, указав способ его построения.

Чертеж 8.2.3

Рассмотрим квадрат ABCD и построим на нем, как на основании, по обе стороны от его плоскости четырехугольные пирамиды, боковые ребра которых равны сторонам квадрата. Полученный многогранник и будет октаэдром (рис. 8.2.1).

Рисунок 8.2.1

Чтобы это доказать, нам остается проверить, что у него равны все двугранные углы. Действительно, пусть O – центр квадрата ABCD. Соединив точку O со всеми вершинами нашего многогранника, мы получим восемь треугольных пирамид с общей вершиной O. Рассмотрим одну из них, например ABEO. AO = BO = EO и, кроме того, эти ребра попарно перпендикулярны. Пирамида ABEO правильная, так как ее основание – правильный треугольник ABE. Значит, все двугранные углы при основании равны. Аналогично, все восемь пирамид с вершиной в точке O и основаниями – гранями восьмигранника ABCDEG – являются правильными и более того, равны между собой. Значит, все двугранные углы этого восьмигранника равны, так как каждый из них в два раза больше двугранного угла при основании каждой из пирамид.

Отметим интересный факт, связанный с гексаэдром (кубом) и октаэдром. Куб имеет 6 граней, 12 ребер и 8 вершин, а октаэдр – 8 граней, 12 ребер и 6 вершин. То есть число граней одного многогранника равно числу вершин другого и наоборот. Как говорят, куб и гексаэдр являются двойственными друг к другу. Это также проявляется в том, что если взять куб и построить многогранник с вершинами в центрах его граней, то, как несложно убедиться, получится октаэдр. Верно и обратное – центры граней октаэдра служат вершинами куба. В этом-то и состоит двойственность октаэдра и куба (рис. 8.2.2).

Несложно сообразить, что если взять центры граней правильного тетраэдра, то мы вновь получим правильный тетраэдр (рис. 8.2.3). Таким образом, тетраэдр двойственен самому себе.

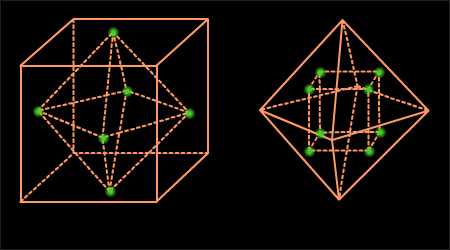Рисунок 8.2.2

Рисунок 8.2.3

Пять правильных многогранников

Вероятно, куб и правильный тетраэдр являются первыми правильными многогранниками, открытыми человечеством. Уже во времена Пифагора люди знали и о третьем правильном многограннике – октаэдре. Каждая его грань – это равносторонний треуг-к, но, в отличие от тетраэдра, из каждой его вершины исходит уже не три, а четыре ребра. Выглядит правильный октаэдр так:

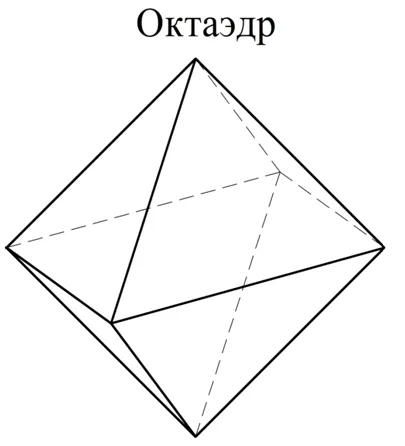
Можно доказать, что октаэдр состоит из двух правильных пирамид, у которых общее основание, но вершины располагаются по разные стороны от плоскости основания. Название октаэдра происходит от греческого слова «окта», означающее число 8. Легко увидеть, что у октаэдра как раз 8 граней. Также видно, что он имеет 6 вершин и 12 ребер.

Следующие два правильных многогранника как раз и были открыты Теэтетем Афинским. Это икосаэдр и додекаэдр. Икосаэдр также состоит из равносторонних треуг-ков, но каждая его вершина принадлежит сразу 5 ребрам.Правильный икосаэдр довольно сложно нарисовать на плоскости, поэтому его внешний вид мы покажем с помощью анимации:

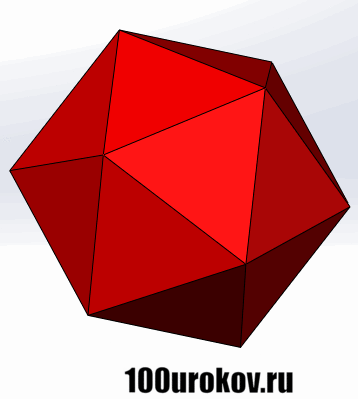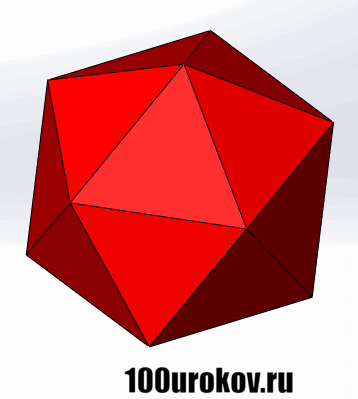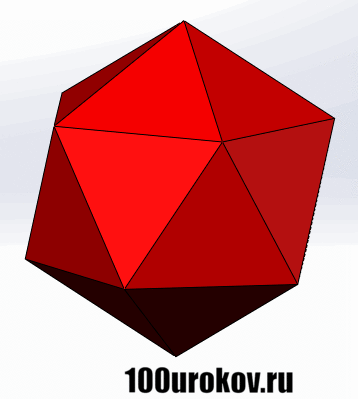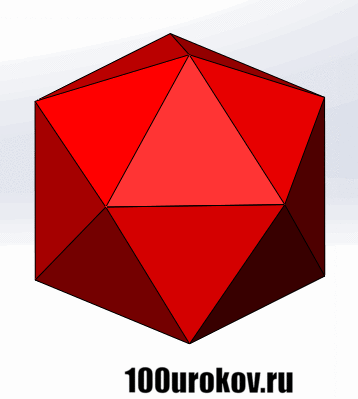
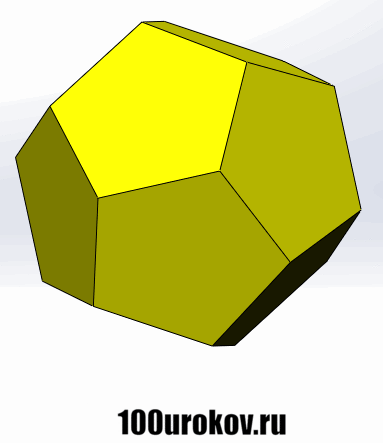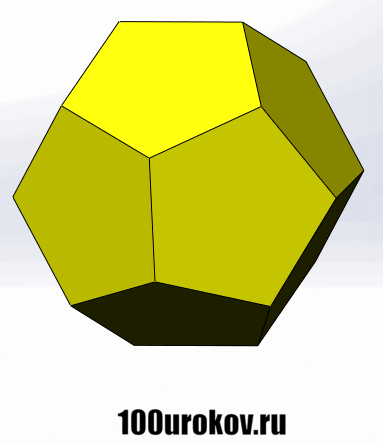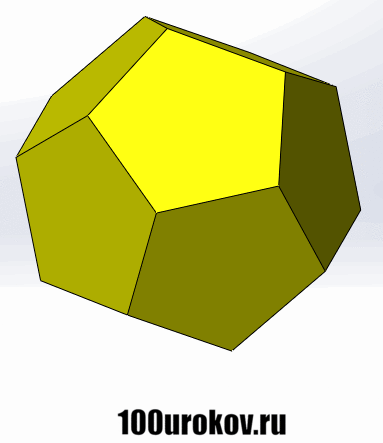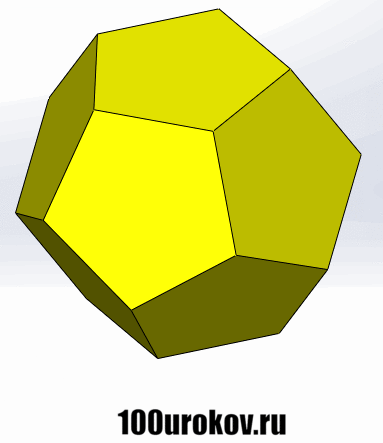
Гранями додекаэдра являются правильные пятиугольники, причем в каждой его вершине соприкасаются ровно 3 грани, и, соответственно, сходятся 3 ребра. Нарисовать правильный додекаэдр ещё тяжелее, поэтому снова посмотрим на него с помощью gif-анимации:

Для подсчета количества ребер, граней и вершин у додекаэдра и икосаэдра можно применить теорему Эйлера. Начнем с икосаэдра. Обозначим количество его граней буквой Г. Теперь подсчитаем ребра (Р), принадлежащие каждой грани. Так как эти грани являются треуг-ками, то получится 3Г ребер. Но при этом каждое ребро мы посчитали дважды, ведь ребра принадлежат строго двум граням. То есть у икосаэдра количество ребер равно 3Г/2 = 1,5Г.

Также подсчитаем и вершины (В), находящиеся вокруг граней. На каждую грань приходится 3 вершины, но при этом каждая вершины принадлежит уже 5 граням. Тогда общее количество вершин составит 3Г/5 = 0,6Г.

Записываем теорему Эйлера и подставляем в ней полученные значения:

Теперь проведем аналогичные расчеты для додекаэдра. Его грани – пятиугольники, поэтому количество его ребер составляет 5Г/2. В каждой вершине додекаэдра сходятся три грани, а потому количество вершин составит 5Г/3. Используем теорему Эйлера:

Теперь составим таблицу, в которой отразим основные сведения о пяти известным нам правильных многогранниках:

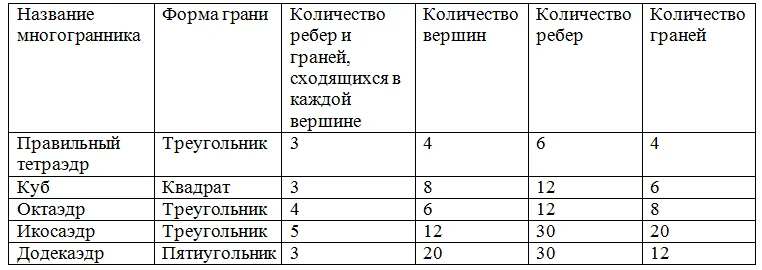
Возникает вопрос – существуют ли ещё какие-нибудь правильные многогранники? Оказывается, что нет. Действительно, каждая вершина правильного многогранника является одновременно и вершиной многогранного угла. Напомним, что сумма плоских углов в многогранном угле всегда меньше 360°. Легко подсчитать, что в правильном шестиугольнике каждый угол составляет 120°, а в многоуг-ках с большим количеством сторон (семиугольник, восьмиугольник…) этот угол ещё больше. Это значит, что если трехгранный угол образован тремя шестигранниками, то сумма его плоских углов составит ровно 120°•3 = 360°, что невозможно. Также невозможно, чтобы трехгранный угол и любой другой многогранный угол был образован правильными семиугольниками, восьмиугольниками и т. д. То есть грани правильного многогранника могут быть исключительно треуг-ками, четырехуг-ками или пятиугольниками.

Рассмотрим случай, когда грани – это треуг-ки. У равностороннего треуг-ка угол составляет 60°. У тетраэдра в вершине смыкаются 3 грани, у октаэдра – 4 грани, а у икосаэдра – 5 граней. А 6 треуг-ков уже не могут образовать многогранный угол, ведь сумма углов составит 6•60° = 360°.

Теперь рассмотрим случай с четырехуг-ком. Правильный четырехуг-к – это квадрат с углом 90°. Варианту с 3 смыкающимися квадратами соответствует куб, а 4 квадрата уже не образуют многогранный угол, ведь сумма углов снова составит 4•90° = 360°.

Остался случай с пятиугольником. У правильного пятиугольника угол равен 108°. Значит, 4 таких фигуры не смогут сомкнуться и образовать многогранный угол, а варианту с тремя пятиугольниками соответствует додекаэдр.

Итак, мы рассмотрели все возможные варианты, и оказалось, что никаких других правильных многогранников, кроме пяти описанных, существовать не может, ч. т. д. Отметим также, что этот факт можно доказать и без применения свойства многогранного угла, используя только теорему Эйлера.

Уроки арифметики на українській мові

Урок №2. Додавання натуральних чисел
Урок №3. Віднімання натуральних чисел
Урок №4. Таблиця множення
Урок №5. Множення натуральних чисел
Урок №6. Ділення натуральних чисел
Урок №8. Величини та їх вимірювання
Урок №10. Подільність чисел
Урок №13. Звичайні дроби
Урок №15. Додавання дробів
Урок №16. Віднімання дробів
Урок №17. Множення дробів
Урок №18. Ділення дробів
Урок №21. Кінечни десяткові дроби
Урок №22. Додавання десяткових дробів
Урок №23. Віднимання десяткових дробів
Урок №24. Множення десяткових дробів
Урок №25. Ділення десяткових дробів
Урок №18. Нескінченний десятковий дріб
Урок №19. Відношення величин
Урок №20. Пропорції
Урок №6. Відсотки
Урок №7. Відсотки (2)
Урок №12. Середнє арифметичне
Урок №14. Масштаб

Центр — грань — октаэдр

Центры граней октаэдра являются вершинами куба. Поэтому группы куба и октаэдра изоморфны. Каждому вращению куба — соответствует подстановка его четырех диагоналей. Произведению вращений соответствует прбй & веДение соответствующих подстановок. Рассмотрим все вращения куба.

Центры граней октаэдра являются вершинами куба. Поэтому группы куба и октаэдра изоморфны. Каждому вращению куба соответствует подстановка его четырех диагоналей. Произведению вращений соответствует произведение соответствующих подстановок. Рассмотрим все вращения куба.

Докажите, что центры граней куба являются вершинами октаэдра, а центры граней октаэдра — вершинами куба.

Мы можем, очевидно, вписать в сферу единичного радиуса куб таким образом, чтобы радиусы, идущие в центры грани октаэдра, имели своими концами вершины куба. Отсюда непосредственно следует, что группа вращения для куба будет той же самой, что и для октаэдра. Положим, что мы иначе выбрали положение октаэдра, а именно, что новое положение октаэдра получается из первоначального при помощи вращения, осуществляемого некоторой матрицей U. Если V есть некоторое вращение, при котором прежний октаэдр переходил сам в себя, то, очевидно, UVU — l будет давать такое вращение, при котором новый октаэдр будет переходить в себя, и наоборот. Иначе говоря, получается подобная группа. Вообще, если совокупность некоторых матриц Vk образует группу, то совокупность подобных матриц UVkU — — при любой фиксированной матрице U также образует группу. Это нетрудно непосредственно доказать из определения группы, что мы и предлагаем проделать читателю. Вторая группа называется обычно подобной первой.

Цифра 3 на второй позиции в символе 23 или 432 означает наличие четырех осей 3 проходящих через вершины куба или центры граней октаэдра или через вершину и центр противоположной грани тетраэдра. Цифра 2 на третьей позиции означает шесть диагональных осей 2 октаэдра или куба.

Ребро правильного октаэдра равно а. Центры граней октаэдра служат вершинами другого правильного многогранника. Установить вид многогранника и вычислить длины его ребер.

Соединив отрезками прямых центры граней куба, имеющих общее ребро, мы получим октаэдр. Соединив отрезками прямых центры граней октаэдра, имеющих общее ребро, мы получим куб. Такие многогранники называют взаимными. Взаимны не только куб и октаэдр. Взаимны также икосаэдр и додекаэдр.

Значительно более выгодными в энергетическом отношении оказываются 12 направлений к серединам ребер октаэдра; они проходят между лигандами. В этих направлениях ориентируются оси электронных облаков dxy, dxz и dyi. Еще более выгодными оказываются направления к центрам граней октаэдра.

Последние же присоединены к отдельным молекулам воды при помощи водородных связей. Такое своеобразное расположение ионов хлора в окру г тетраэдра молекулы воды, естественно, приводит к весьма сложной кристаллической структуре. В этих соединениях, обладающих структурой флюорита, ион Ni ( NH3) 6 также окружен восемью, ионами галоида, но каждый из них находится против центра грани октаэдра аммония, что создает возможность более простого расположения в кристалле. Каждый из галоидов окружен четырьмя группами Ni ( NH3), расположенными в вершинах правильного тетраэдра.

Уроки арифметики на русском языке

Урок №2. Сложение натуральных чисел
Урок №3. Вычитание натуральных чисел
Урок №4. Таблица умножения
Урок №5. Умножение натуральных чисел
Урок №6. Деление натуральных чисел
Урок №8. Величины и их измерение
Урок №10. Делимость чисел
Урок №13. Обыкновенные дроби
Урок №15. Сложение дробей
Урок №16. Вычитание дробей
Урок №17. Умножение дробей
Урок №18. Деление дробей
Урок №21. Конечные десятичные дроби
Урок №22. Сложение десятичных дробей
Урок №23. Вычитание десятичных дробей
Урок №24. Умножение десятичных дробей
Урок №25. Деление десятичных дробей
Урок №26. Округление чисел
Урок №1. Отношение величин
Урок №2. Пропорции
Урок №6. Проценты
Урок №7. Нахождение процентов данного числа
Урок №12. Среднее арифметическое
Урок №14. Масштаб

Центры граней куба ребро которого равно 2а служат вершинами октаэдра

Центры граней куба, ребро которого равно 2а ,служат вершинами октаэдра.Найдите его объем

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Октаэдр состоит из 2-х правильных пирамид,В основании квадрат ,диагональ которого равна стороне куба,а высота равна 1/2 стороне кубаV=2*1/3*Sосн*hV=2/3*(2a*2a)/2*a=4a³/3

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
Использовать мат — это неуважительно по отношению к пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Алгебра.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.