Единичная тригонометрическая окружность
Единичная тригонометрическая окружность — это окружность с центром в точке (0; 0) на координатной плоскости, радиус которой равен 1
Так как длина всей окружности равна 2π, сделаем вывод, что половина окружности — это π, а четверть — это π2.
Теперь разделим окружность сначала на восемь частей, а потом ту же окружность на двенадцать частей. Рассчитаем значения полученных точек.
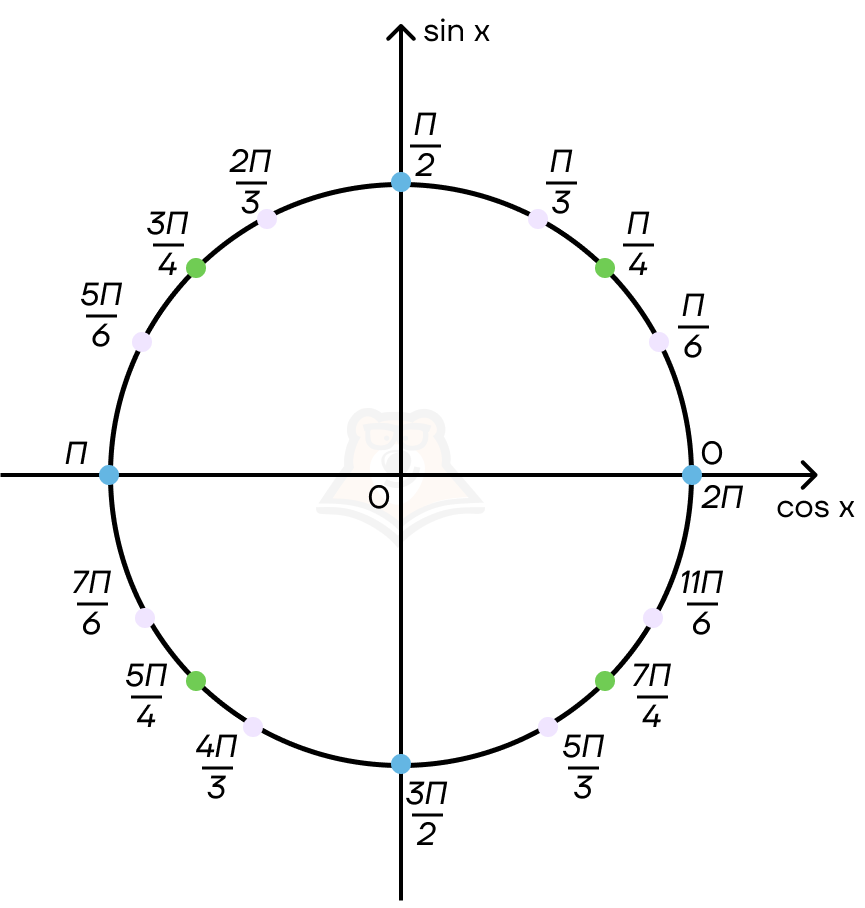
Заметим, что точка 0 совпадает с точкой 2π. Это означает, что мы сделали один оборот по окружности. Но мы можем продолжать идти так и дальше: тогда эта же точка будет принимать значения 4π, 6π, 8π.
| Как найти углы у апельсина?Для удобства представим, что окружность — это половинка апельсина. Длина корочки апельсина равна 2π. А теперь будем делить 2π на 4, 8 и 12. Таким образом, получившиеся кусочки апельсина будут являться углами на тригонометрической окружности. |
Движение по тригонометрической окружности можно сравнить с движением по числовой прямой, закрученной в спираль.
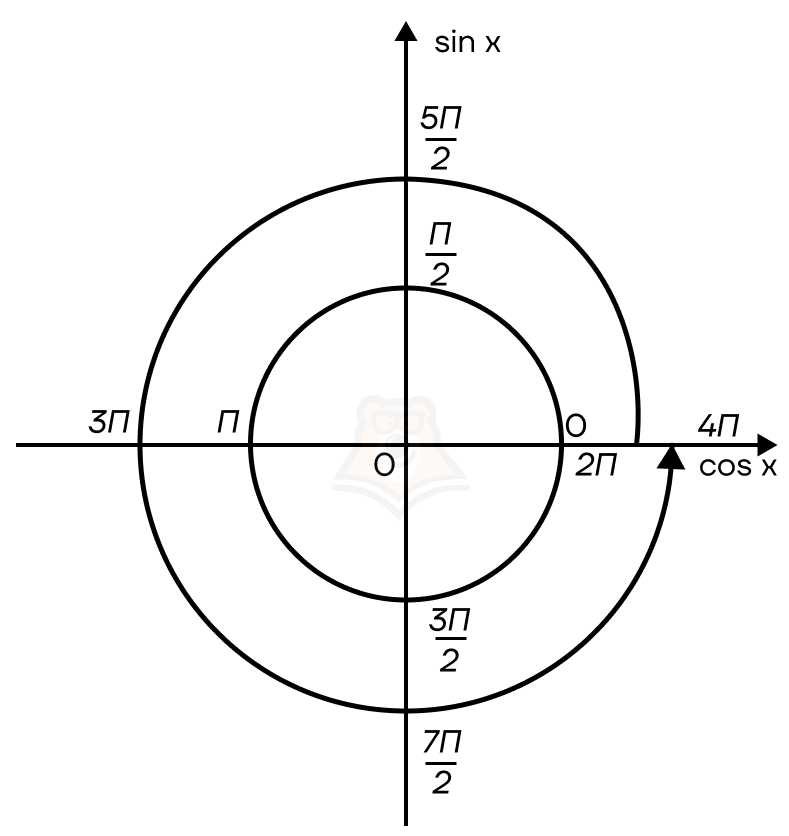
Аналогично можно двигаться и против движения часовой стрелки, но это уже будет отрицательная спираль.
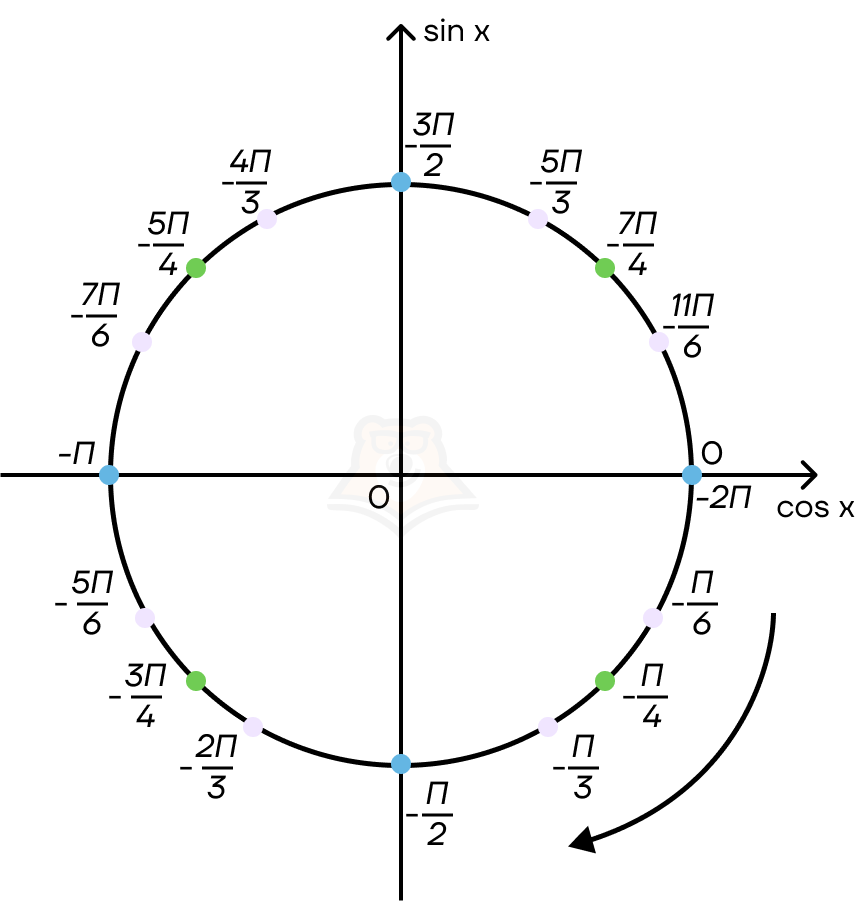
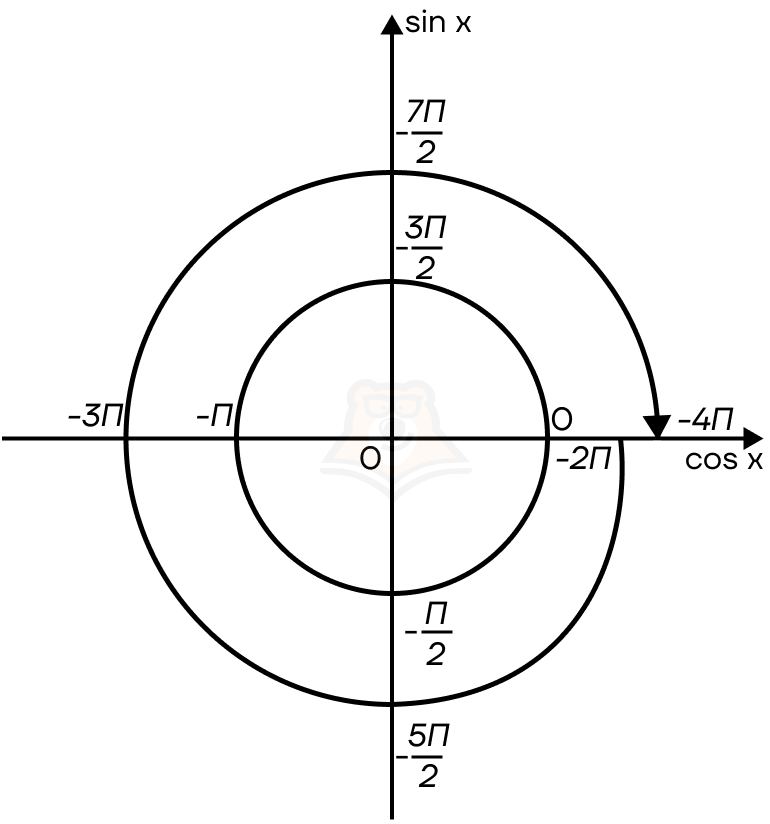
Как записать множество точек, находящихся в одной точке окружности, но на разных витках спирали?
Так как тригонометрические функции — это периодические функции, то и значения в точках будут повторяться с определенным интервалом: то есть с интервалом 2πk, где k принадлежит множеству целых чисел.
Пример: π + 2πk, k ∈ Z
Теперь рассмотрим значения синусов и косинусов, определенных на окружности точек.
На положительных частях осей они представлены как \(\frac{1}{2}\), \(\frac{\sqrt{2}}{2}\), \(\frac{\sqrt{3}}{2}\), а на отрицательных — \(-\frac{1}{2}\), \(-\frac{\sqrt{2}}{2}\), \(-\frac{\sqrt{3}}{2}\).
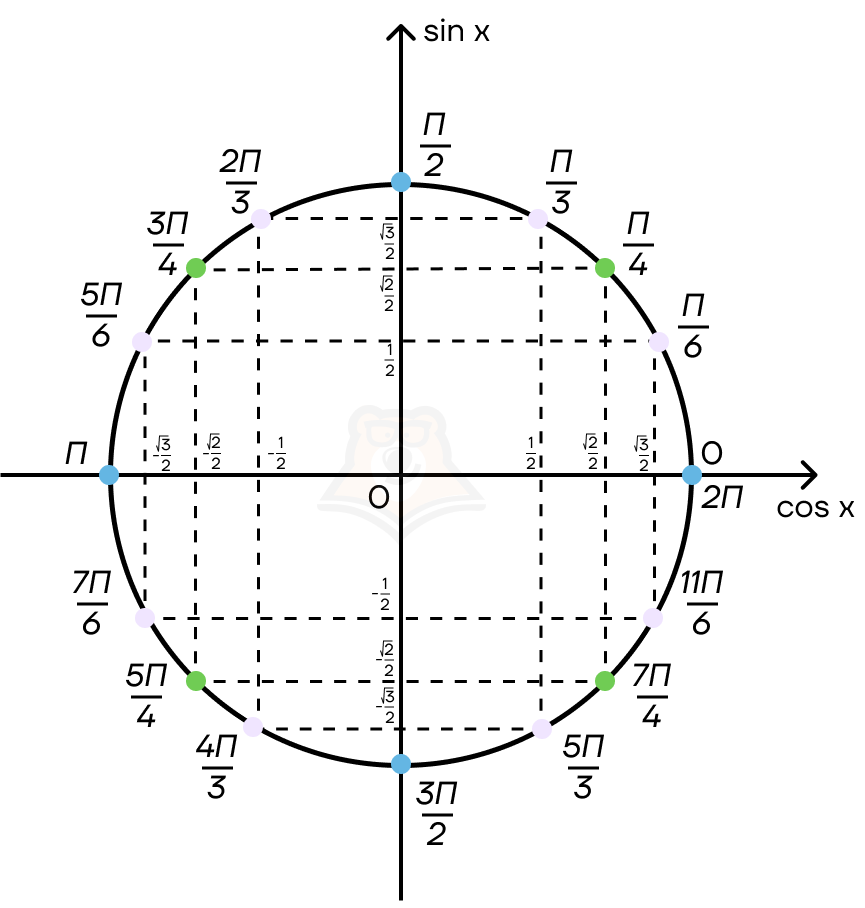
Для нахождения значения синуса или косинуса известного угла нужно провести перпендикулярную прямую к прямой, предназначенной этой функции. Значение, в котором она пересечет прямую функции будет являться значением этой тригонометрической функции от известного числа.
Пример:Нужно узнать чему равно \(sin \frac{\pi}{3}\)
Сначала найдем \(\frac{\pi}{3}\) на окружности, затем проведем перпендикулярную прямую к прямой синусов. Ответом является значение в точки пересечения.
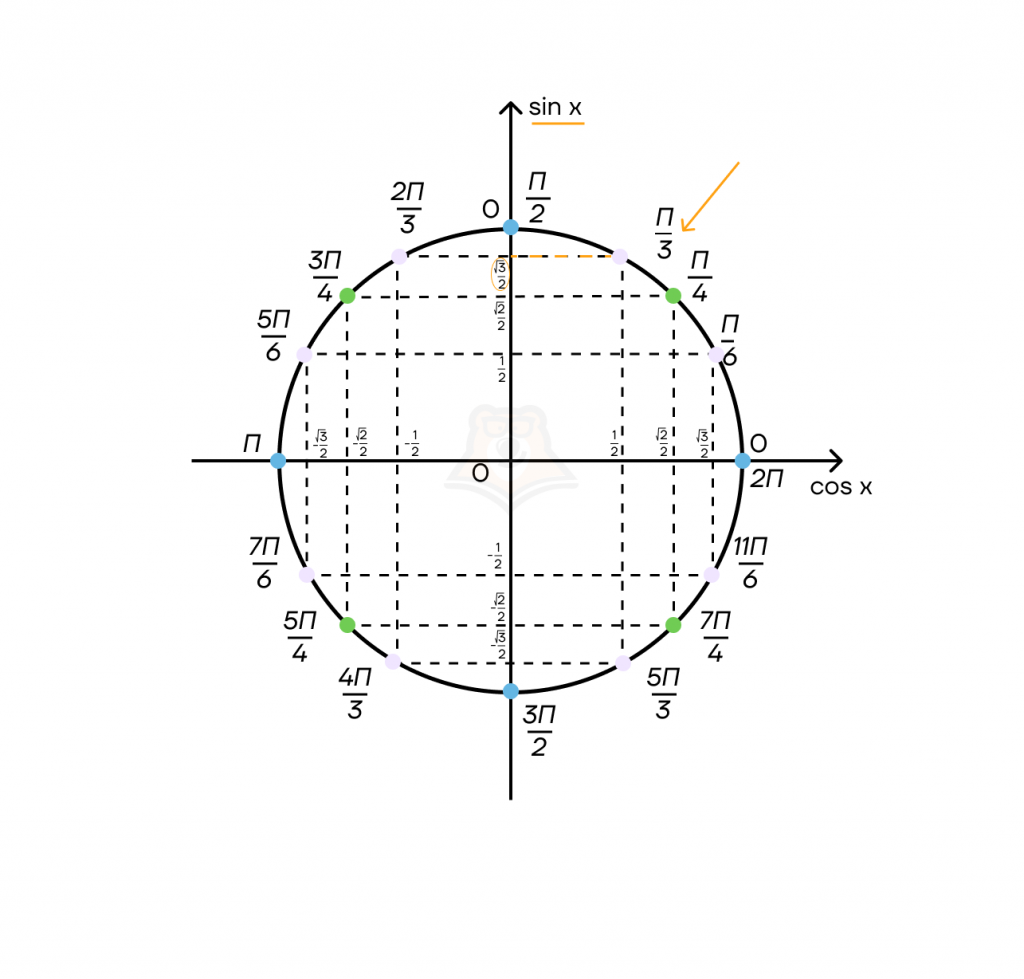
\(sin \frac{\pi}{3} = \frac{\sqrt{3}}{2}\)
Теперь проведём ещё две прямые для обозначения прямых тангенса и котангенса. Отметим на них значения для точек окружности.
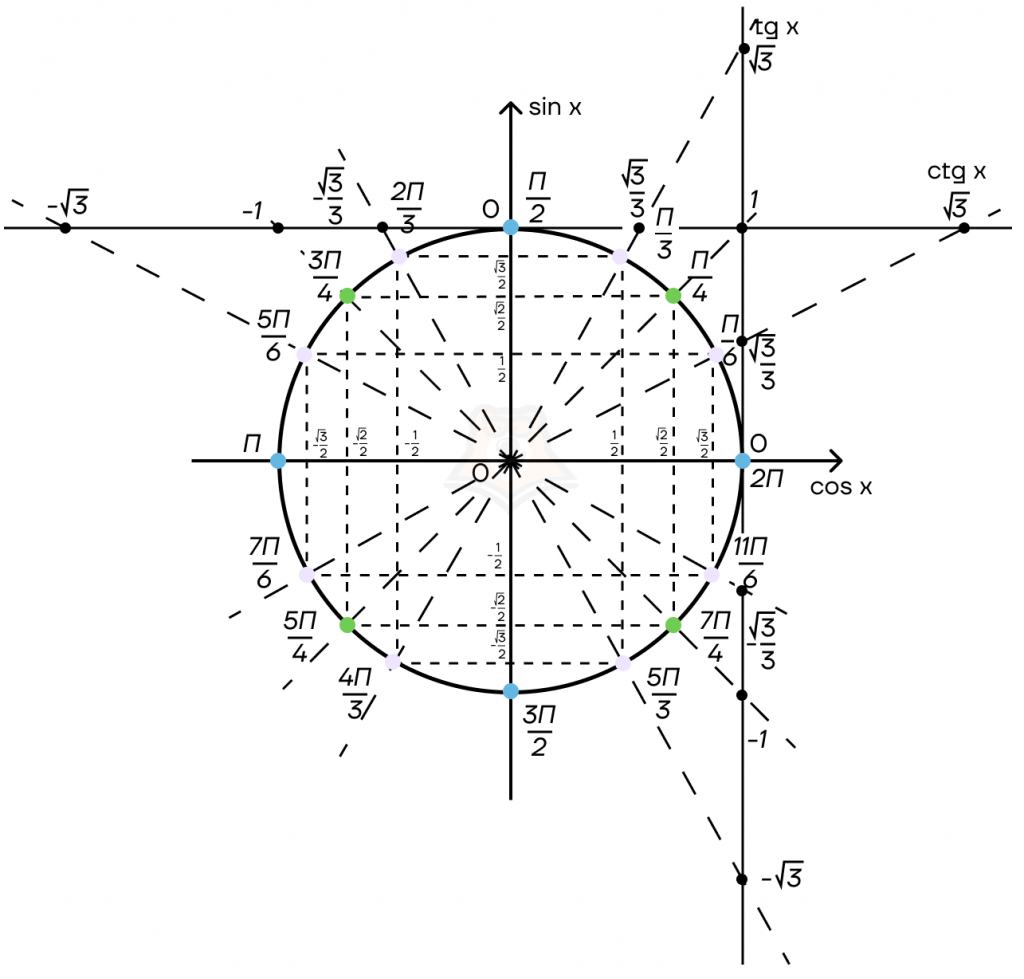
Для нахождения значения тангенса или котангенса известного угла нужно провести прямую через точку (0; 0) и это число на окружности. Значение, в котором она пересечет прямую данной функции, будет являться значением этой тригонометрической функции от известного числа.
Пример:
Нужно узнать чему равно \(ctg \frac{2 \pi}{3}\)
Сначала найдем \(\frac{2 \pi}{3}\) на окружности, затем проведём прямую через (0; 0) и эту точку на окружности. Ответом является значение в точки пересечения проведенной прямой и прямой котангенсов.
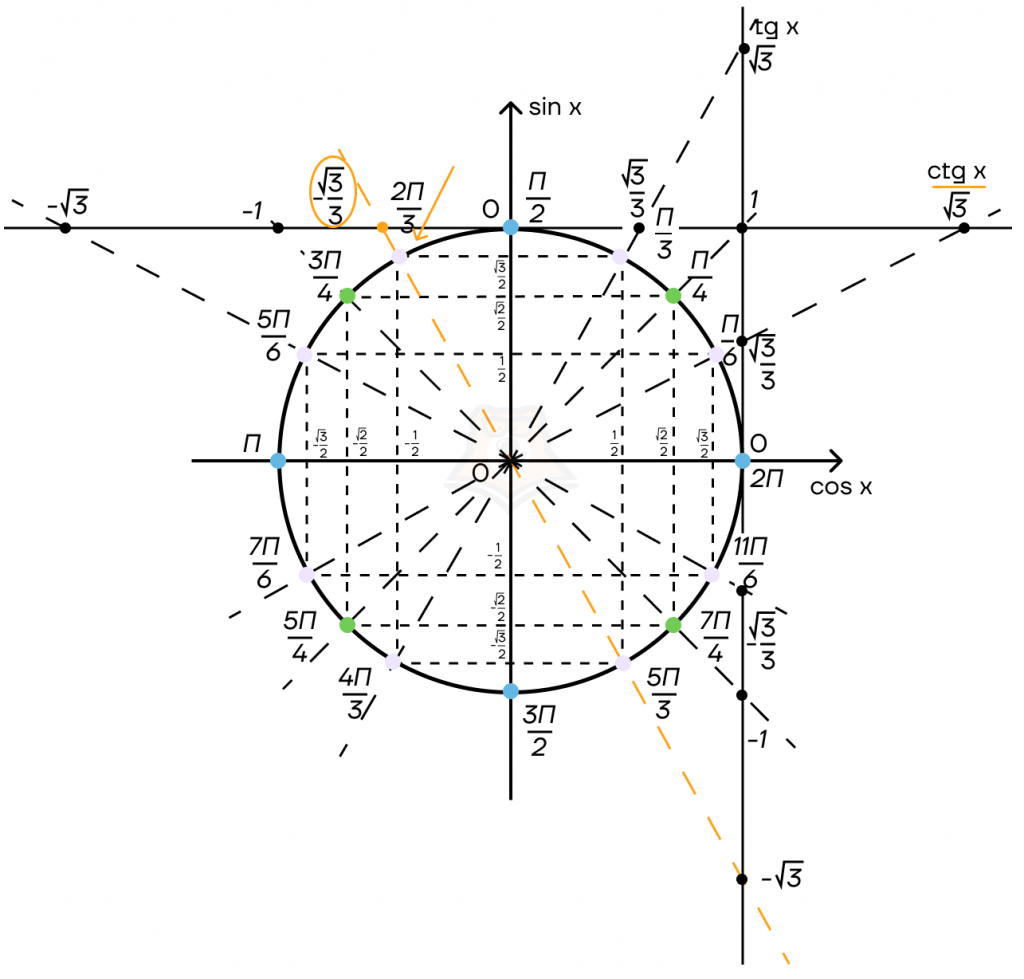
\(ctg \frac{2 \pi}{3} = -\frac{\sqrt{3}}{3}\)
Примеры тригонометрии можно найти и в жизни. Например: когда мы режем морковку, нож находится под углом \(\frac{\pi}{2}\) к поверхности доски.
История[]
Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива»), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
Современное обозначение синуса sin и косинуса cos введено Леонардом Эйлером в XVIII веке.
Термины «тангенс» (от лат. «tangens» — касающийся) и «секанс» (лат. «secans» — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583)
Сумма, разность и произведение синуса и косинуса
Нам осталось разобрать еще несколько формул. В этот раз они связаны с действиями, производимыми с самими функциями. Например, с произведением синуса и косинуса.
Рассмотрим формулы:
\(sin\alpha+sin \beta =2sin(\frac{\alpha+\beta}{2})*cos(\frac{\alpha-\beta}{2})\)\(sin \alpha-sin \beta=2sin(\frac{\alpha-\beta}{2})*cos(\frac{\alpha+\beta}{2})\)\(cos \alpha+cos \beta =2cos(\frac{\alpha-\beta}{2})*cos(\frac{\alpha+\beta}{2})\)\(cos \alpha-cos \beta =-2sin(\frac{\alpha+\beta}{2})*sin(\frac{\alpha-\beta}{2})\)\(sin \alpha*sin \beta =\frac{1}{2}(cos(\alpha-\beta)-cos(\alpha+\beta))\)\(cos \alpha*cos \beta =\frac{1}{2}(cos(\alpha-\beta)+cos(\alpha+\beta))\)\(sin \alpha*cos \beta=\frac{1}{2}(sin(\alpha-\beta)+sin(\alpha+\beta))\)
Заметим, что в формулах разные аргументы. Если они не табличные, то посчитать значение выражения почти нереально. Поэтому, если это возможно, с помощью этих формул мы можем упростить выражение до табличных углов.
Например, попробуем преобразовать выражение \(sin(\frac{3\pi}{8})*cos(\frac{\pi}{8})\).
Рассчитать значение не представляется возможным: в аргументе стоят нетабличные значения. Попробуем преобразовать это выражение с помощью формулы \(sin \alpha*cos\beta =\frac{1}{2}(sin(\alpha-\beta)+sin(\alpha+\beta))\):
\(sin(\frac{3\pi}{8})*cos(\frac{\pi}{8})=\frac{1}{2}(sin(\frac{3\pi}{8}-\frac{\pi}{8})+sin(\frac{3\pi}{8}+\frac{\pi}{8}))\)
Преобразуем выражения в аргументах синусов отдельно:
\(\frac{3\pi}{8}-\frac{\pi}{8}=\frac{3\pi-\pi}{8}=\frac{2\pi}{8}=\frac{\pi}{4}\)\(\frac{3\pi}{8}+\frac{\pi}{8}=\frac{3\pi+\pi}{8}=\frac{4\pi}{8}=\frac{\pi}{2}\)
Получаем выражение:
\(\frac{1}{2}(sin(\frac{3\pi}{8}-\frac{\pi}{8})+sin(\frac{3\pi}{8}+\frac{\pi}{8}))=\frac{1}{2}(sin(\frac{\pi}{4})+sin(\frac{\pi}{2}))\)
Теперь подставим значения из таблицы:
\(\frac{1}{2}(sin(\frac{\pi}{4})+sin(\frac{\pi}{2}))=\frac{1}{2}(\frac{\sqrt2}{2}+1)=\frac{1}{2}*\frac{2+\sqrt2}{2}=\frac{2+\sqrt2}{4}\)
Значение выражения найдено.
Подведем итог. Формулы тригонометрии необходимы для преобразования сложных выражений. А чтобы они были в одном месте, мы составили для вас таблицу.


Итак, мы разобрались, как преобразовывать выражения с тригонометрическими функциями. Какой следующий шаг? Правильно, решение уравнений.
График синуса и косинуса
Заметим, что координаты точек, лежащей на единичной окружности, варьируются в пределах от – 1 до 1. Это означает, что значение синуса и косинуса также может находиться только в интервале между этими числами. Получается, что область значения этих ф-ций – это промежуток .
Вычислить синус и косинус можно для абсолютно любого угла поворота, поэтому область определения этих тригонометрических ф-ций – вся числовая прямая, то есть промежуток (– ∞; + ∞).
Изучение графиков тригонометрических функций начнем с синуса. В тригонометрии при построении графика синуса принято по оси Ох откладывать значение угла в радианах, а не в градусах. Из-за этого в школьной тетради тяжело точно отметить точки, через которые проходит этот график. Например, возьмем угол, равный 90°. Его величина в радианах π/2, а sinπ/2 = 1. Получается, график должен пройти через точку (π/2; 1). Однако число π/2 – иррациональное, равное примерно 1,5708…, и точно отложить отрезок длиной π/2 невозможно.
Поэтому в учебных целях график строят приближенно (естественно, что на практике точный график можно построить с помощью компьютера с любой требуемой точностью). Считают, что величина π/2 примерно равна 1,5, то есть дроби 3/2. Если выбрать масштаб, при котором единице равны 2 клеточки, то π/2 – это 3 клеточки. Тогда π/6 – это одна клеточка, а π/3 – две.
Мы знаем, что
sin 0 = 0
sin π/6 = 1/2
sin π/2 = 1
Значит, график синуса должен проходить через точки (0; 0), (π/6; 1/2) и (π/2; 1). Отметим их на координатной плоскости:
С помощью некоторых соображений симметрии можно вычислить ещё несколько точек в диапазоне от 0 до 2π. Не будем перечислять их координаты, а просто отметим их на рисунке:
Теперь соединим их плавной кривой:
Мы получили график синуса на промежутке от 0 до 2π. Но ведь мы можем вычислить синус для любого другого угла! При этом мы используем тот факт, что углам, отличающимся на 2π (на один полный оборот), на единичной окружности соответствует одинаковая точка. То есть этим двум углам будут соответствовать точки на графике с одинаковой ординатой (координатой у), но абсциссами, отличающимися на 2π. Другими словами, точку графика можно перенести на 2π (то есть 12 клеточек) влево или вправо:
Перенести можно не одну точку, а сразу всё множество точек, лежащих между 0 и 2π:
Получили ещё два участка графика, на промежутках и . Эти участки также можно переместить влево и вправо. Продолжая этот процесс бесконечно, мы получим весь график у = sinx:
В результате мы получили кривую, которую называют синусоидой.
Теперь построим график косинуса. Мы знаем что
cos 0 = 1
cos π/3 = 1/2
cos π/2 = 1
Получается, что график должен проходить через точки (0;1), (π/3; 1/2) и (π/2; 0). Отметим их на плоскости:
Можно вычислить, используя симметрию на единичной окружности, ещё несколько точек, которые должны лежать на графике. Не приводя этих вычислений, просто отметим эти точки на плоскости:
Соединяем эти точки плавной линией:
Как и в случае с синусом, участок графика косинуса можно перенести на 2π (12 клеточек влево и вправо). В результате таких действий получим окончательный вид ф-ции у = cosх:
Можно заметить несколько особенностей полученных графиков. Во-первых, все точки обоих графиков лежат в «полосе» между прямыми у = 1 и у = – 1. Это следствие того, что и у синуса, и у косинуса область значений – это промежуток :
Во-вторых, график косинуса очень похож на синусоиду. Он имеет такую же форму, но просто смещен на π/2 (3 клеточки) влево. Это не случайно, в будущих уроках мы узнаем причину этого явления. Но, так как график косинуса – это просто смещенная синусоида, то термин «косинусоида» для его обозначения почти не используется – он просто избыточен.
В-третьих, графики обладают периодичностью. Они «повторяются» с периодом 2π. Дело в том, что углам, отличающимся друг от друга на 2π (то есть ровно на один полный поворот в 360°), на единичной окружности соответствует одна и та же точка. То есть справедливы формулы:
sin (x+ 2π) = sinx
cos (x+ 2π) = sinx
В-четвертых, можно заметить, что график косинуса симметричен относительно оси Ох, а график синуса симметричен относительно начала координат. Это значит, что синус является , а косинус – . Напомним, что ф-ция f(x) является нечетной, если справедливо условие
f(x) = – f(– x)
Если f(x) – четная ф-ция, то должно выполняться условие:
f(x) = f(– x)
Действительно, если отложить на единичной окружности углы α и (– α), то можно заметить, что их косинусы будут равны друг другу, и синусы окажутся противоположными:
Поэтому верны формулы:
sin (– α) = – sinα
cos (– α) = cosα
Общая информация
Раздел математики, который занимается изучением тригонометрических функций, называется тригонометрией. К функциям относятся следующие: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg). Существуют также и обратные им функции: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg).
Для нахождения знаков тригонометрических функций по четвертям рекомендуется применять специальный «инструмент». Он называется окружностью синусов и косинусов. Однако по ней можно находить не только функции, которые соответствуют ее названию, но и другие. Делается это с помощью тригонометрических тождеств.
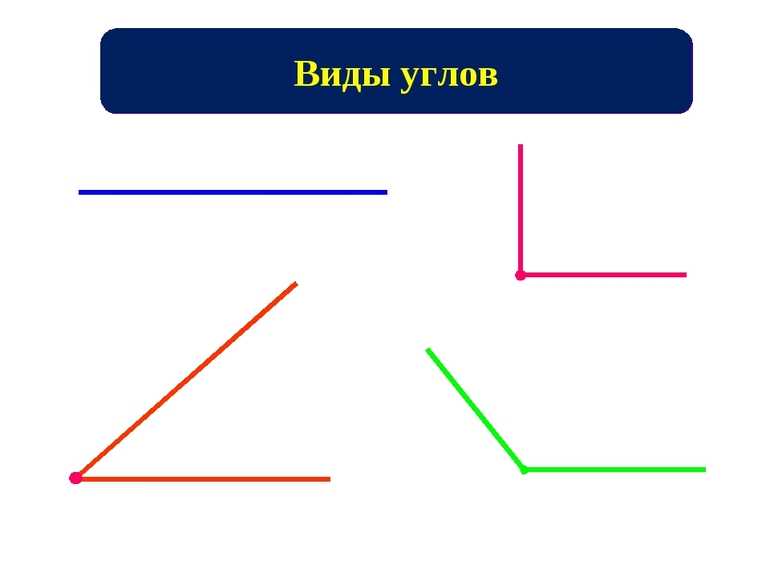
Виды углов
Важной «ступенью» в освоении тригонометрии является идентификация углов. Они делятся на 7 видов
Кроме того, существует еще два типа классификации по знаку: положительные и отрицательные.
Для составления критериев, по которым математики классифицируют углы, необходимо ввести некоторую переменную. Пусть существует некоторый угол a, градусная мера которого составляет x градусов. Необходимо рассмотреть 7 случаев, в которых он измеряется только в градусной размерности:
- При х < 90 угол считается острым.
- Если х = 90, то является прямым.
- В случае, когда выполняется неравенство, он считается тупым: 90 < x < 180.
- Развернутый: х = 180.
- Выпуклый: 180 < x < 360.
- Полный: х = 360.
- Свыше 360: x > 360.
Градус — это не единственная единица измерения размерности угла. Существует также и радиан, который пользуется большей популярностью, чем предыдущая единица. Согласно статистике, которая составлена математиками, при решении задач с тригонометрическим уклоном многие используют радиан (около 95,88%). Это объясняется удобством, поскольку в основном применяется тригонометрическая окружность для быстрого нахождения значений функций. Перевод одной единицы в другую осуществляется с помощью двух простых соотношений:
- В радианы: P = (a * ПИ) / 180.
- В градусы: а = (P * 180) / ПИ.
Существует 2 метода перевода: автоматизированный и ручной. В первом случае следует применять специальные радианные таблицы, программы и тригонометрическую окружность. Во втором — пользоваться формулами для преобразований. Если очень часто приходится решать задачи подобного типа, то можно создать свой инструмент. Для этого потребуется табличный процессор EXCEL. Необходимо вбить в ячейки две формулы, и тогда ручной метод «превратится» в автоматизированный.
Смысл функций
Тригонометрические функции используются не только в математике, но и в других дисциплинах (физике, электронике, микросхемотехнике, акустике и так далее). С их помощью можно описывать законы изменения различных периодических величин.

Синус угла — значение, которое вычисляется отношением линейного размера противолежащего катета к гипотенузе прямоугольного треугольника. Если выразить величину через отношение прилежащего катета к гипотенузе, то она называется косинусом угла. Величина, полученная при отношении двух катетов — противолежащего к прилежащему, называется тангенсом. В случае с котангенсом, необходимо поменять числитель и знаменатель местами, то есть отношение прилежащего к противолежащему. Следует также напомнить, что все четыре функции обладают периодичностью. Для sin и cos период соответствует 2 ПИ, а для tg и ctg — ПИ.
Обратными тригонометрическими функциями являются arcsin, arccos, arctg и arcctg. Их необходимо использовать в том случае, когда нужно найти угол по заданному значению. Для этих целей применяются таблицы Брадиса, тригонометрический калькулятор и программное обеспечение, а также круг синусов и косинусов.
Поиск тангенса на квадратной решетке
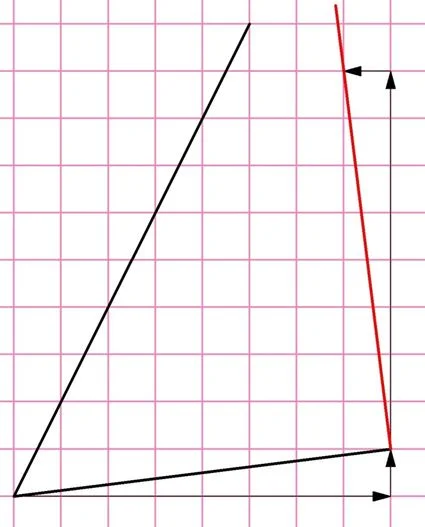
Рассмотрим задание, которое часто встречается на экзаменах и вызывает большие затруднения. На рисунке показан угол, требуется высчитать его тангенс:
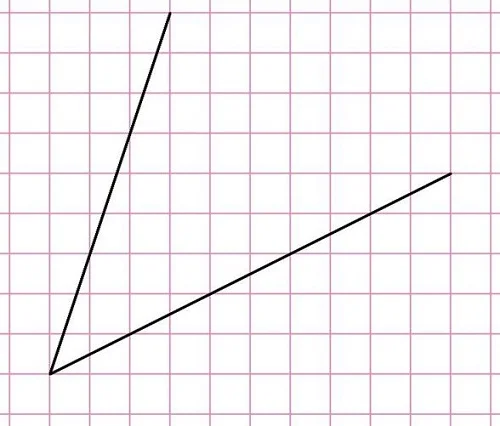
Ясно, что для нахождения тангенса надо построить какой-нибудь прямоугольный треугольник, однако проблема заключается в том, что обе стороны угла не являются ни горизонтальными, ни вертикальными линиями, а потому провести к ним перпендикуляр у многих не получается. Рассмотрим, как это делается.
Посмотрим на нижнюю линию. Она представляет собой поднимающуюся прямую, причем на каждые 2 клеточки, которые эта прямая проходит вправо, приходится подъем на 1 клеточку вверх.
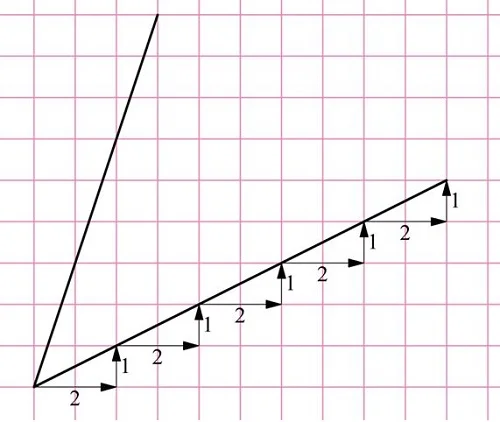
Оказывается, что для построения перпендикуляра к ней необходимо от какой-нибудь ее точки вести наклонную прямую, у которой, наоборот, на каждые две клеточки подъема будет приходиться 1 клетка движения вбок, причем не вправо, а влево:
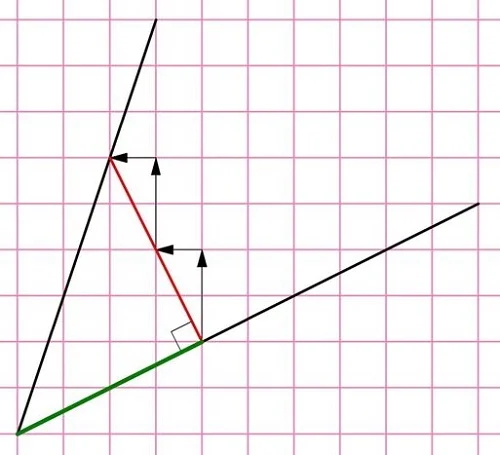
Теперь, чтобы найти тангенс, надо просто поделить длину красного отрезка (он здесь оказывается противолежащим катетом) на длину зеленого отрезка. Несложно заметить, что эти отрезки одинаковы, так как являются гипотенузами в двух равных прямоугольных ∆АBС и ∆CDF:
Естественно, что отношение одинаковых отрезков равно единице, поэтому и тангенс также равен единице. Заметим, что прямой угол можно было получить, проведя перпендикуляр к нижней линии в другой точке:
Более того, перпендикуляр можно провести и к верхней стороне угла. Она представляет собой линию, которая поднимается вправо, и на каждые три клетки движения вверх приходится одна клетка смещения вправо:
Соответственно, чтобы построить к ней перпендикуляр, надо от одной из ее точек начать двигаться вправо и вниз, причем на 3 клетки движения вбок будет приходиться только 1 клетка движения вниз:
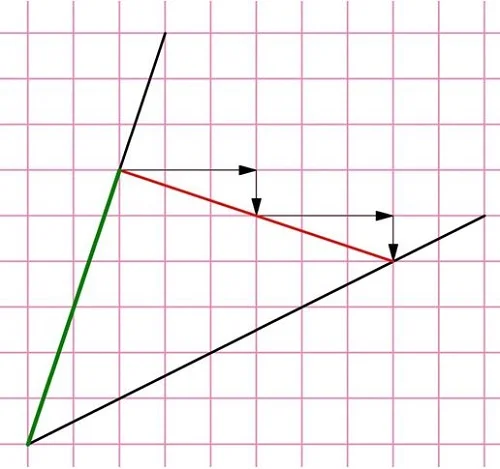
Во всех этих случаях зеленые и красные отрезки одинаковы, а потому тангенс равен единице.
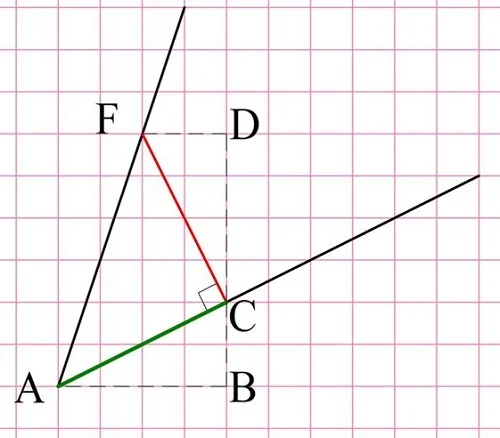
Объясним, почему для построения перпендикуляра надо использовать именно такой метод. Пусть на квадратной решетке начерчена прямая АС, к которой надо провести перпендикуляр. Построив горизонтальную (показана зеленым цветом) линию АB и вертикальную (показана красным) линию ВС, мы достоим ее до прямоугольного ∆АBС. Далее отложим от точки С уже вертикально отрезок CD, равный АB, а далее от D – горизонтальный отрезок, равный ВС:
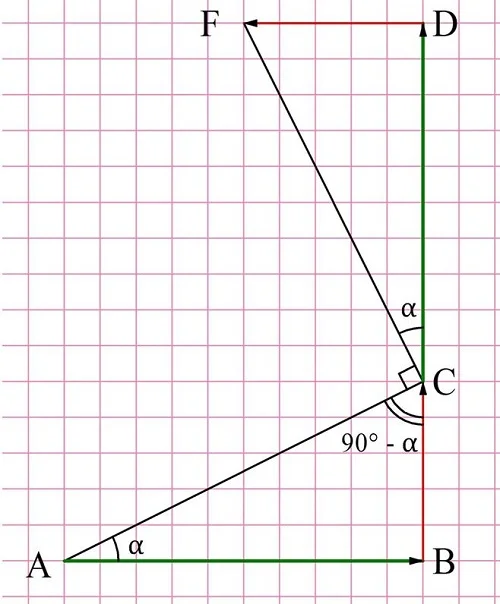
Обозначим∠А как α, тогда ∠АСВ будет составлять 90° – α. Заметим, что ∆АBС и ∆СDF – равные, так как они прямоугольные и у них одинаковы катеты:

Теперь обратим внимание на три угла, вершины которых лежат в точке С. Это ∠АСВ, ∠FCD и ∠АСF
Они вместе образуют развернутый угол ВСD, то есть их сумма составляет 180°. Но ∠АСВ и ∠FCD мы уже выразили через величину α. Тогда можно вычислить и третий угол ∠АСF:
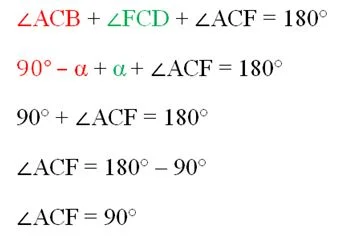
Получили, что отрезки АС и СF действительно перпендикулярны.
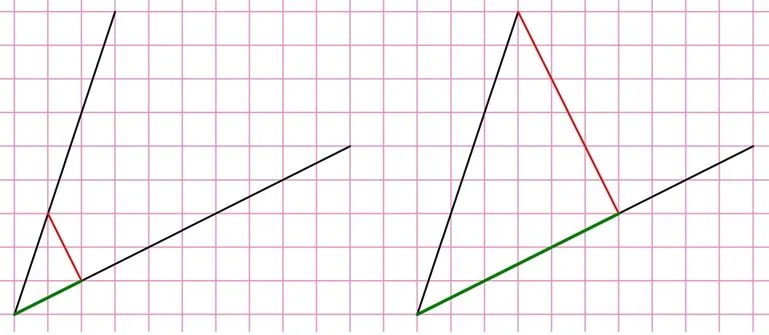
Задание. Найдите тангенс угла, показанного на рисунке:
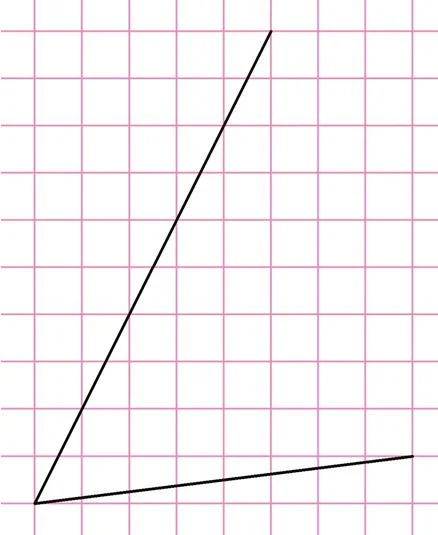
Решение. Если попытаться провести прямую, перпендикулярную нижней стороне угла, то в результате этот перпендикуляр просто не пересечется со второй стороной:
Поэтому перпендикуляр следует проводить к верхней стороне:
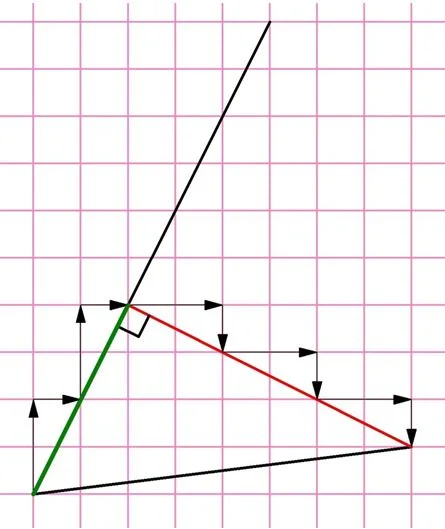
Теперь осталось найти отношение длин красного (здесь это противолежащий катет) зеленого отрезка. Конечно, и длины можно найти по теореме Пифагора, однако есть и более простой метод. Возьмем в качестве единичного отрезок, который получается, если на квадратной решетке сделать два шага вбок и один вверх. Этот отрезок будет укладываться на красном катете ровно 3 раза, а на зеленом – ровно 2 раза, то есть прилежащий катет равен трем единичным отрезкам, а противолежащий – двум. Тогда их отношение составляет 3/2 = 1,5
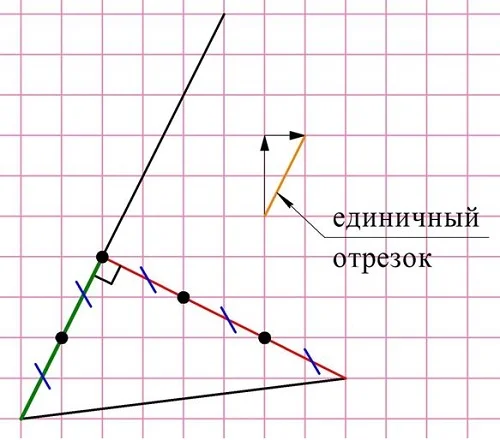
Ответ: 1,5
Свойства синуса, косинуса, тангенса и котангенса
В этой статье будут рассмотрены три основных свойства тригонометрических функций: синуса, косинуса, тангенса и котангенса.
Первое свойство — знак функции в зависимости от того, какой четверти единичной окружности приналдежит угол α . Второе свойство — периодичность. Согласно этому свойству, тигонометрическая функция не меняет значения при изменении угла на целое число оборотов. Третье свойсто определяет, как меняются значения функций sin, cos, tg, ctg при противоположных углах α и — α .
Знаки тригонометрических функций по четвертям
Часто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это такое?
Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку A 0 ( 1 , 0 ) и, поворачивая ее вокруг точки O на угол α , попадем в точку A 1 ( x , y ) . В зависимости от того, в какой четверти будет лежать точка A 1 ( x , y ) , угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно.
Для наглядности приведем иллюстрацию.
Угол α = 30 ° лежит в первой четверти. Угол — 210 ° является углом второй четверти. Угол 585 ° — угол третьей четверти. Угол — 45 ° — это угол четвертой четверти.
При этом углы ± 90 ° , ± 180 ° , ± 270 ° , ± 360 ° не принадлежат ни одной четверти, так как лежат на координатных осях.
Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.
Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус — это ордината точки A 1 ( x , y ) . Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной — отрицательна.
Косинус — это абсцисса точки A 1 ( x , y ) . В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.
Для определения знаков тангенса и котангенса по четвертям также вспоминаем определения этих тригонометрических функций. Тангенс — отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки — отрицательным. Аналогично определяются знаки котангенса по четвертям.
- Синус угла α имеет знак плюс в 1 и 2 четвертях, знак минус — в 3 и 4 четвертях.
- Косинус угла α имеет знак плюс в 1 и 4 четвертях, знак минус — в 2 и 3 четвертях.
- Тангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
- Котангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
Свойство периодичности
Свойство периодичности — одно из самых очевидных свойств тригонометрических функций.
При изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными.
Действительно, при изменении угла на целое число оборотов мы всегда будем попадать из начальной точки A на единичной окружности в точку A 1 с одними и теми же координатами. Соответственно, не будут меняться и значения синуса, косинуса, тангенса и котангенса.
Математически данное свойство записывается так:
sin α + 2 π · z = sin α cos α + 2 π · z = cos α t g α + 2 π · z = t g α c t g α + 2 π · z = c t g α
Какое применение на практике находит это свойство? Свойство периодичности, как и формулы приведения, часто используется для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов.
sin 13 π 5 = sin 3 π 5 + 2 π = sin 3 π 5
t g ( — 689 ° ) = t g ( 31 ° + 360 ° · ( — 2 ) ) = t g 31 ° t g ( — 689 ° ) = t g ( — 329 ° + 360 ° · ( — 1 ) ) = t g ( — 329 ° )
Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов
Вновь обратимся к единичной окружности.
Точка A 1 ( x , y ) — результат поворота начальной точки A 0 ( 1 , 0 ) вокруг центра окружности на угол α . Точка A 2 ( x , — y ) — результат поворота начальной точки на угол — α .
Точки A 1 и A 2 симметричны относительно оси абсцисс. В случае, когда α = 0 ° , ± 180 ° , ± 360 ° точки A 1 и A 2 совпадают. Пусть одна точка имеет координаты ( x , y ) , а вторая — ( x , — y ) . Вспомним определения синуса, косинуса, тангенса, котангенса и запишем:
sin α = y , cos α = x , t g α = y x , c t g α = x y sin — α = — y , cos — α = x , t g — α = — y x , c t g — α = x — y
Отсюда следует свойство синусов, косинусов, тангенсов и котангенсов противоположных углов.
Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов
sin — α = — sin α cos — α = cos α t g — α = — t g α c t g — α = — c t g α
Согласно этому свойству, справедливы равенства
sin — 48 ° = — sin 48 ° , c t g π 9 = — c t g — π 9 , cos 18 ° = cos — 18 °
Рассмотренное свойство часто используется при решении практических задач в случаях, когда нужно избавиться от отрицательных знаков углов в агрументах тригонометрических функций.
Определение тригонометрических функций через окружность[]
Пусть на плоскости задана прямоугольная система координат с началом в точке O{\displaystyle O} и с осями OX{\displaystyle {OX}} и OY{\displaystyle {OY}} . Возьмём в этой системе координат окружность с центром в точке O{\displaystyle O} и радиусом, равным единице. Пусть отрезок OA{\displaystyle {OA}} поворачивается на произвольный угол ϑ{\displaystyle \vartheta} вокруг центра O.{\displaystyle O.}
Синусом угла ϑ{\displaystyle \vartheta} называется отношение ординаты точки A{\displaystyle A} к длине отрезка OA.{\displaystyle {OA}.} Обозначают sinϑ=ACOA.{\displaystyle \sin\vartheta=\frac{AC}{OA}.} Так как длина отрезка OA{\displaystyle {OA}} равна 1{\displaystyle 1}, то sinϑ=AC.{\displaystyle \sin\vartheta={AC}.}
Косинусом угла ϑ{\displaystyle \vartheta} называется отношение абсциссы точки A{\displaystyle A} к длине отрезка OA.{\displaystyle {OA}.} Обозначают cosϑ=OCOA.{\displaystyle \cos\vartheta=\frac{OC}{OA}.} Так как длина отрезка OA{\displaystyle {OA}} равна 1, то cosϑ=OC.{\displaystyle \cos\vartheta={OC}.}
Тангенсом угла ϑ{\displaystyle \vartheta} называется отношение ординаты точки A{\displaystyle A} к абсциссе точки A{\displaystyle A}. Обозначают tgϑ=ACOC{\displaystyle \operatorname{tg}\,\vartheta=\frac{AC}{OC}} (в англоязычной литературе tanϑ).{\displaystyle \tan\vartheta ).} Так как AC=sinϑ{\displaystyle {AC}=\sin \vartheta} и OC=cosϑ,{\displaystyle {OC}=\cos\vartheta,} то tgϑ=sinϑcosϑ.{\displaystyle \operatorname{tg}\,\vartheta=\frac{\sin\vartheta}{\cos\vartheta}.}
Котангенсом угла ϑ{\displaystyle \vartheta} называется отношение абсциссы точки A{\displaystyle A} к ординате точки A{\displaystyle A}. Обозначают ctgϑ=OCAC{\displaystyle \operatorname{ctg}\,\vartheta=\frac{OC}{AC}} (в англоязычной литературе cotϑ).{\displaystyle \cot\vartheta ).} Так как AC=sinϑ{\displaystyle {AC}=\sin \vartheta} и OC=cosϑ,{\displaystyle {OC}=\cos\vartheta,} то ctgϑ=cosϑsinϑ.{\displaystyle \operatorname{ctg}\,\vartheta=\frac{\cos\vartheta}{\sin\vartheta}.} Котангенс равен обратному значению тангенса: ctgϑ=1tgϑ.{\displaystyle \operatorname{ctg}\,\vartheta=\frac{1}{\operatorname{tg}\,\vartheta}.}
Секансом угла ϑ{\displaystyle \vartheta} называется отношение длины отрезка OA{\displaystyle {OA}} к абсциссе точки A{\displaystyle A}. Обозначают secϑ=OAOC.{\displaystyle \sec\vartheta=\frac{OA}{OC}.} Так как длина отрезка OA{\displaystyle {OA}} равна 1, то secϑ=1OC.{\displaystyle \sec\vartheta=\frac{1}{OC}.} Секанс равен обратному значению косинуса: secϑ=1cosϑ.{\displaystyle \sec\vartheta=\frac{1}{\cos\vartheta}.}
Косекансом угла ϑ{\displaystyle \vartheta} называется отношение длины отрезка OA{\displaystyle {OA}} к ординате точки A{\displaystyle A}. Обозначают cosecϑ=OAAC{\displaystyle \operatorname{cosec}\,\vartheta=\frac{OA}{AC}} (в англоязычной литературе cscϑ).{\displaystyle \csc \vartheta ).} Так как длина отрезка OA{\displaystyle {OA}} равна 1{\displaystyle 1}, то cosecϑ=1AC.{\displaystyle \operatorname{cosec}\,\vartheta=\frac{1}{AC}.} Косеканс равен обратному значению синуса: cosecϑ=1sinϑ.{\displaystyle \operatorname{cosec}\,\vartheta=\frac{1}{\sin\vartheta}.}
Из определения следует: если косинус угла равен нулю, то тангенс и секанс этого угла не существуют. Аналогично для котангенса и косеканса: если синус угла равен нулю, то котангенс и косеканс этого угла не существуют.
Тангенс
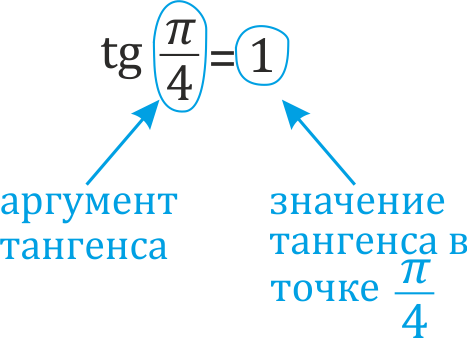
Аргументом тангенса может быть: — как число или выражение с Пи: \(1,3\), \(\frac\), \(π\), \(-\frac\) и т.п. — так и угол в градусах: \(45^°\), \(360^°\),\(-800^°\), \(1^° \) и т.п.
Для обоих случаев тангенс вычисляется одинаковым способом – либо через значения синуса и косинуса, либо через тригонометрический круг (см. ниже).
Тангенс острого угла
1) Пусть дан угол и нужно определить тагенс этого угла.
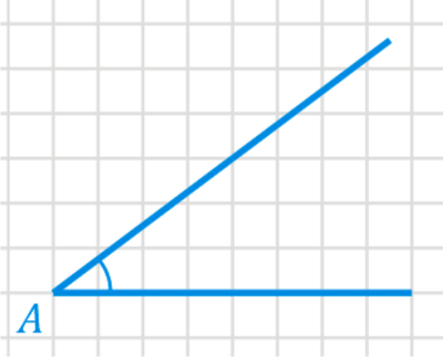
2) Достроим на этом угле любой прямоугольный треугольник.
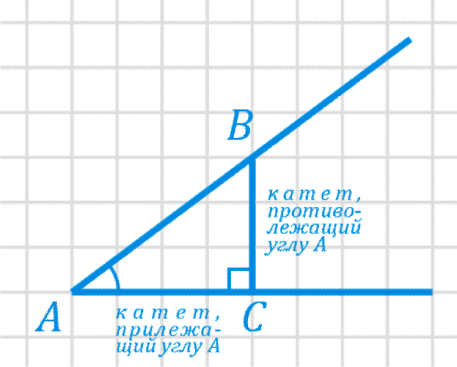
3) Измерив, нужные стороны, можем вычислить тангенс.
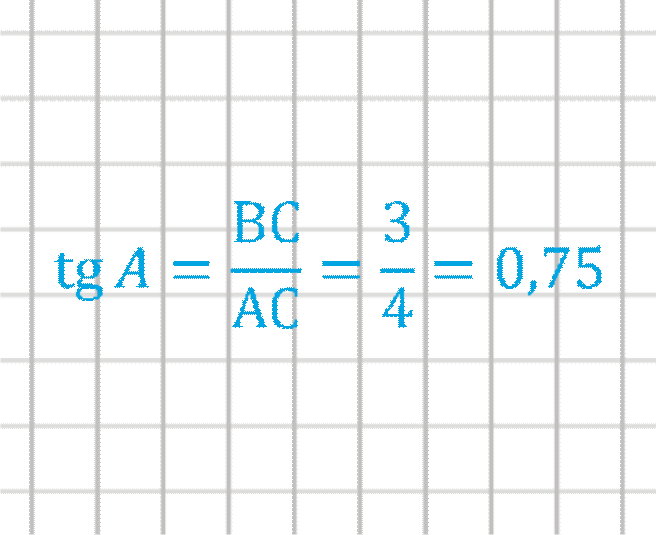
Вычисление тангенса числа или любого угла
Пример. Вычислите \(tg\:0\). Решение: Чтобы найти тангенс нуля нужно найти сначала синус и косинус \(0\). И то, и другое найдем с помощью тригонометрического круга :
Точка \(0\) на числовой окружности совпадает с \(1\) на оси косинусов, значит \(cos\:0=1\). Если из точки \(0\) на числовой окружности провести перпендикуляр к оси синусов, то мы попадем в точку \(0\), значит \(sin\:0=0\). Получается: \(tg\:0=\) \(\frac\) \(=\) \(\frac\) \(=0\).
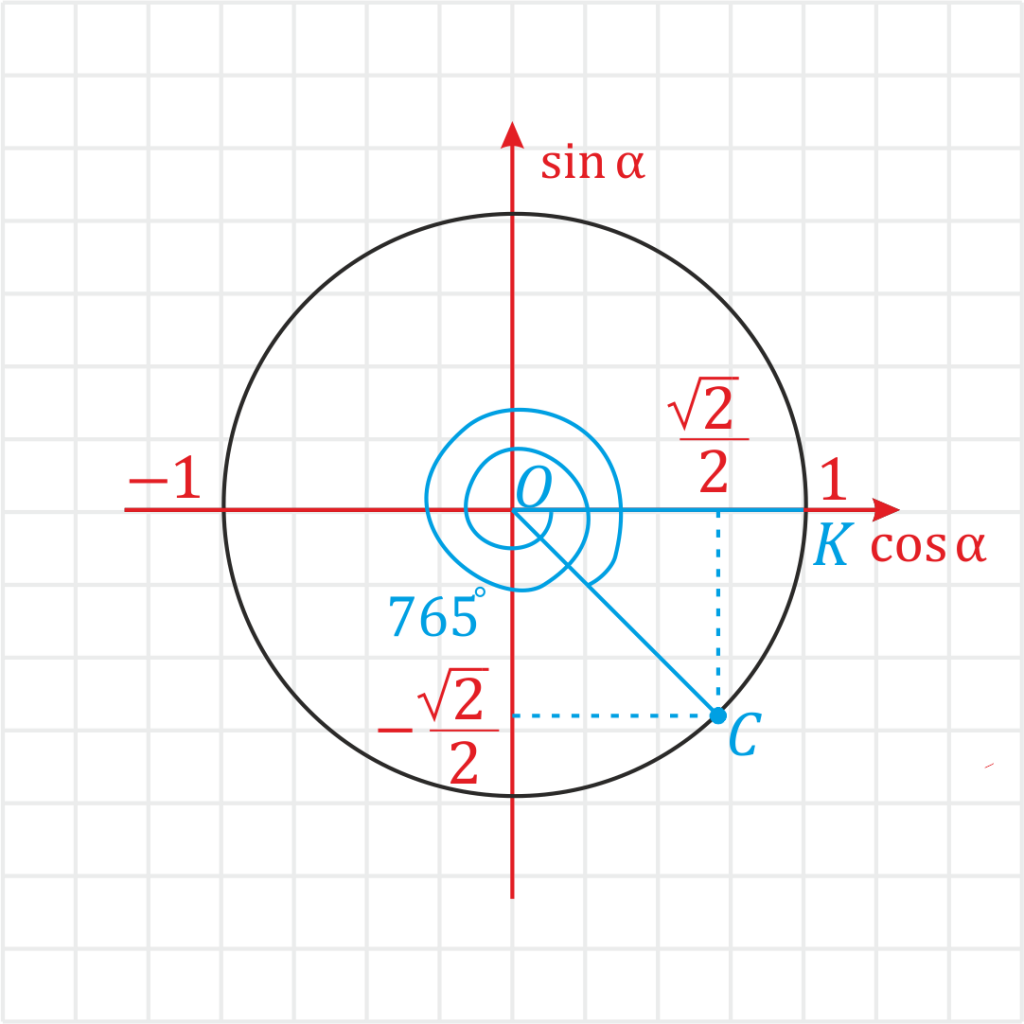
Пример. Вычислите \(tg\:(-765^\circ)\). Решение: \(tg\: (-765^\circ)=\) \(\frac\) Что бы вычислить синус и косинус \(-765^°\). Отложим \(-765^°\) на тригонометрическом круге. Для этого надо повернуть в отрицательную сторону на \(720^°\) , а потом еще на \(45^°\).
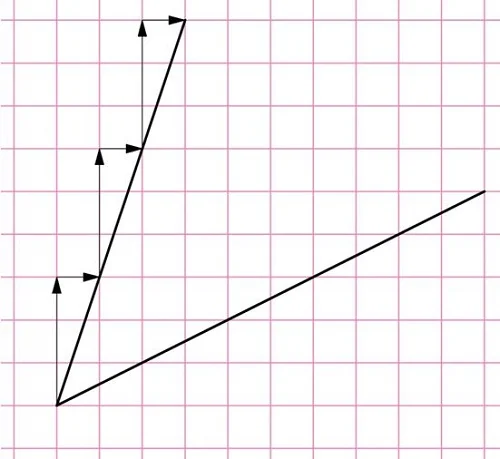
Однако можно определять тангенс и напрямую через тригонометрический круг — для этого надо на нем построить дополнительную ось:
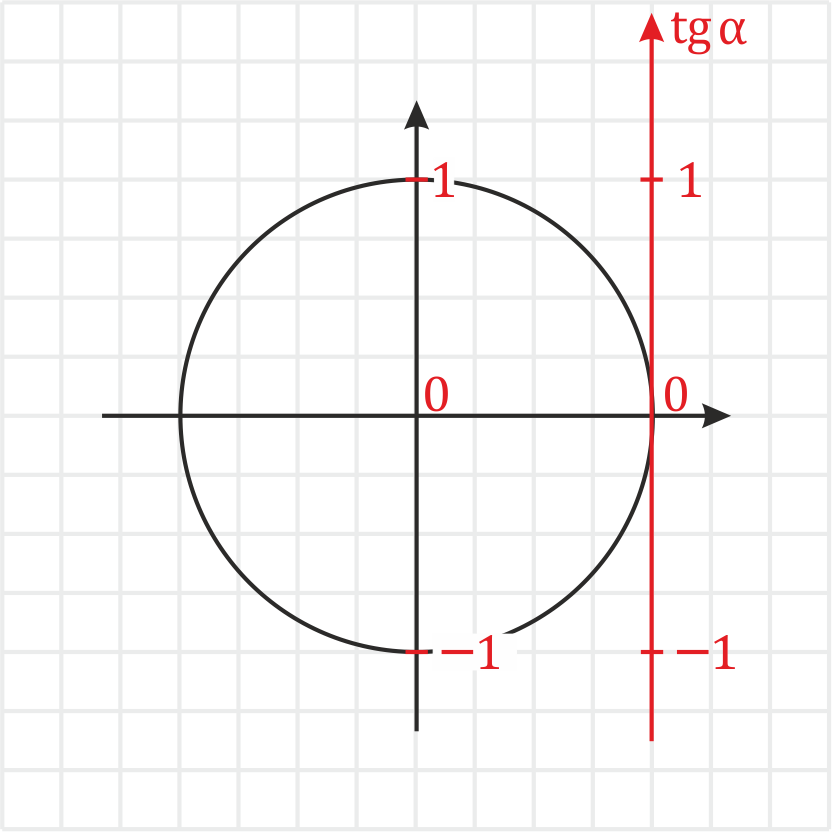
Ось тангенсов – это фактически копия оси синусов, только сдвинутая. Поэтому все числа на ней расставляются так же как на оси синусов.
Чтобы определить тангенс с помощью числовой окружности, нужно: 1) Отметить соответствующую аргументу тангенса точку на числовой окружности. 2) Провести прямую через эту точку и начало координат и продлить её до оси тангенсов. 3) Найти координату пересечения этой прямой и оси тангенсов.
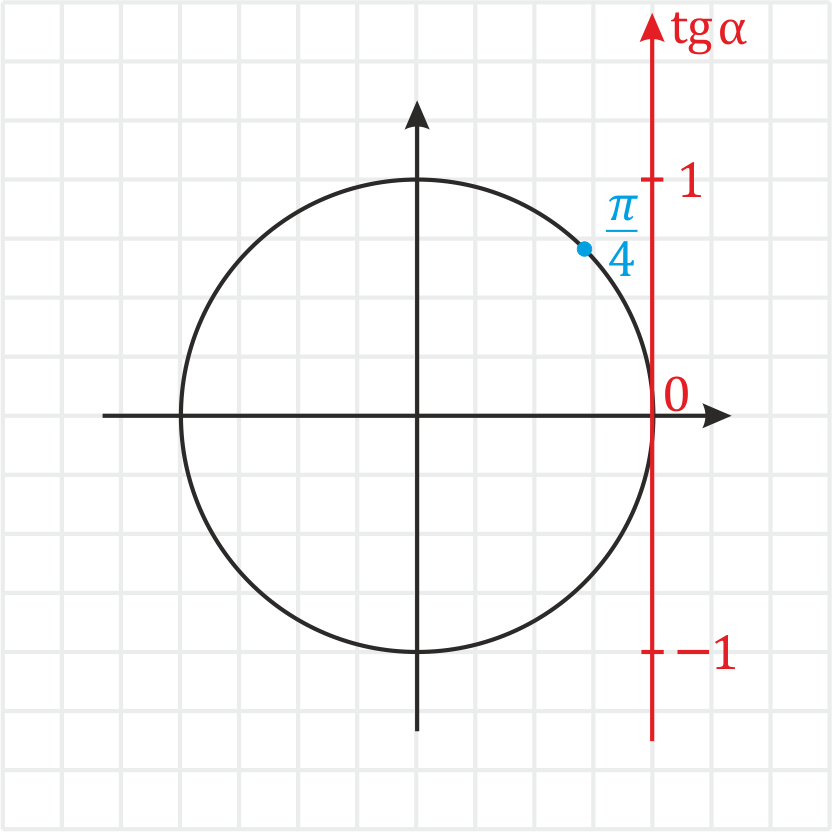
Пример. Вычислите \(tg\:\frac\). Решение: 1)Отмечаем \(\frac\) на окружности.
2) Проводим через данную точку и начало координат прямую.
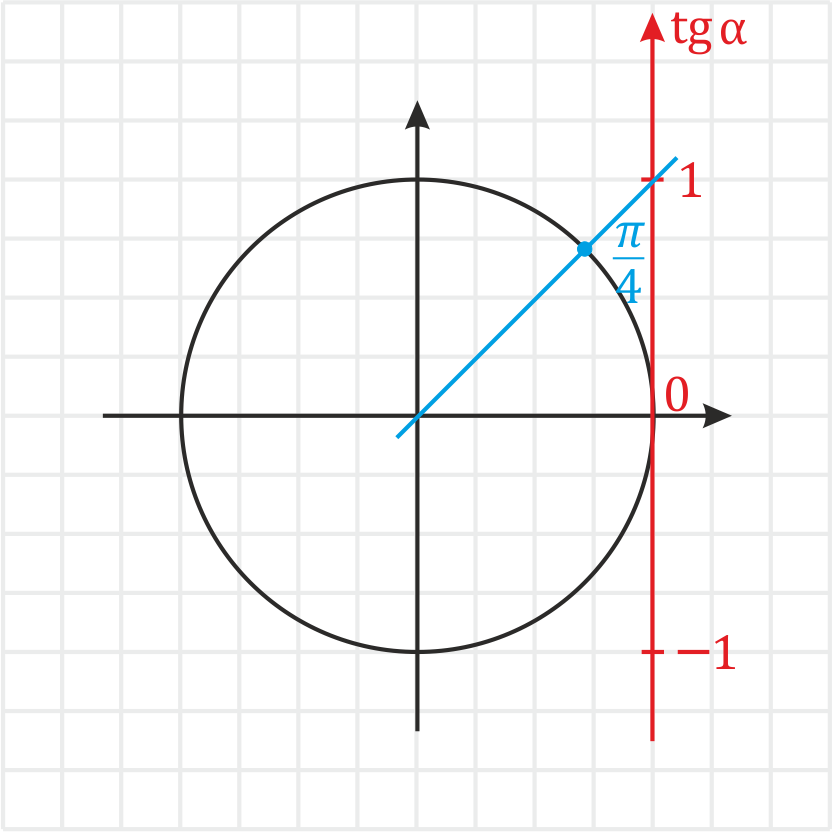
3) В данном случае координату долго искать не придется – она равняется \(1\).
Пример. Вычислите \(tg\: 45°\) и \(tg\: (-240°)\). Решение: Для угла \(45°\) (\(∠KOA\)) тангенс будет равен \(1\), потому что именно в таком значении сторона угла, проходящая через начало координат и точку \(A\), пересекает ось тангесов. А для угла \(-240°\) (\(∠KOB\)) тангенс равен \(-\sqrt\) (приблизительно \(-1,73\)).
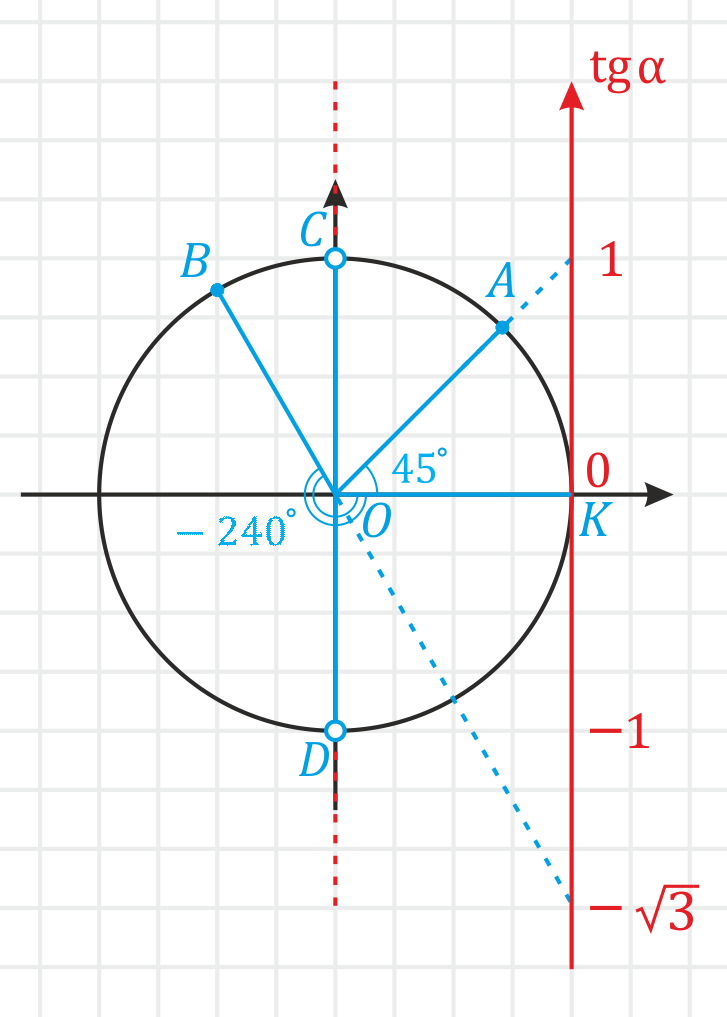
Значения для других часто встречающихся в практике углов смотри в тригонометрической таблице.
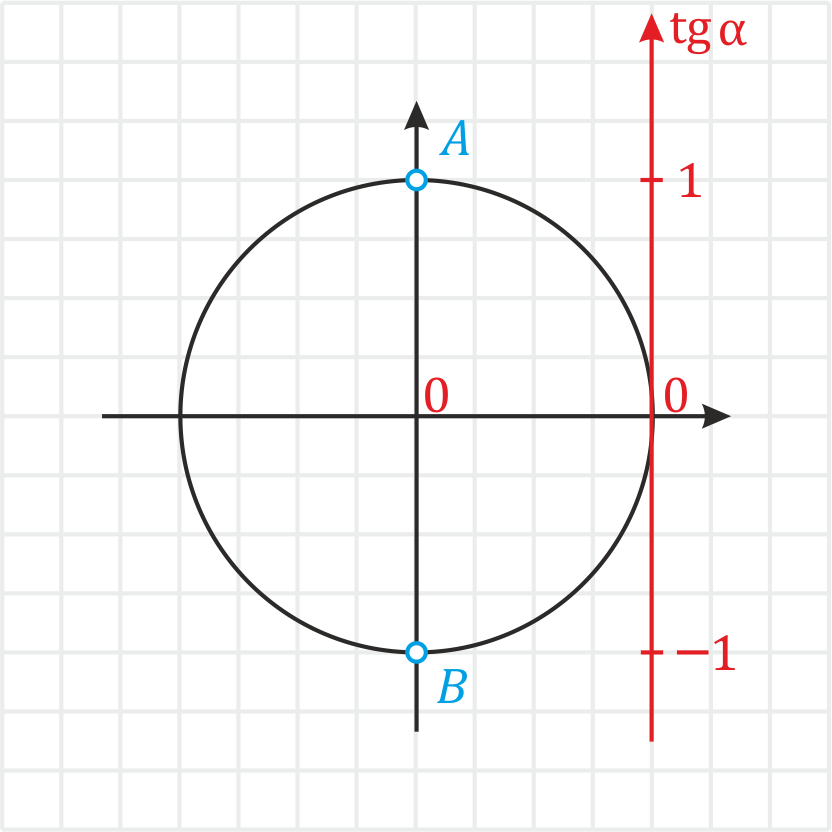
При этом тангенс не определен для: 1) всех точек \(A\) (значение в Пи: …\(-\) \(\frac\) ,\(-\) \(\frac\) , \(\frac\) , \(\frac\) , \(\frac\) …; и значение в градусах: …\(-630°\),\(-270°\),\(90°\),\(450°\),\(810°\)…) 2) всех точек \(B\) (значение в Пи: …\(-\) \(\frac\) ,\(-\) \(\frac\) ,\(-\) \(\frac\) , \(\frac\) , \(\frac\) …; и значение в градусах: …\(-810°\),\(-450°\),\(-90°\),\(270°\)…) .
Так происходит потому, что прямая проходящая через начало координат и любую из этих точек никогда не пересечет ось тангенсов, т.к. будет идти параллельно ей. Поэтому в этих точках тангенс – НЕ СУЩЕСТВУЕТ (для всех остальных значений тангенс может быть найден).
Из-за этого при решении тригонометрических уравнений и неравенств с тангенсом необходимо учитывать ограничения на ОДЗ .
Знаки по четвертям
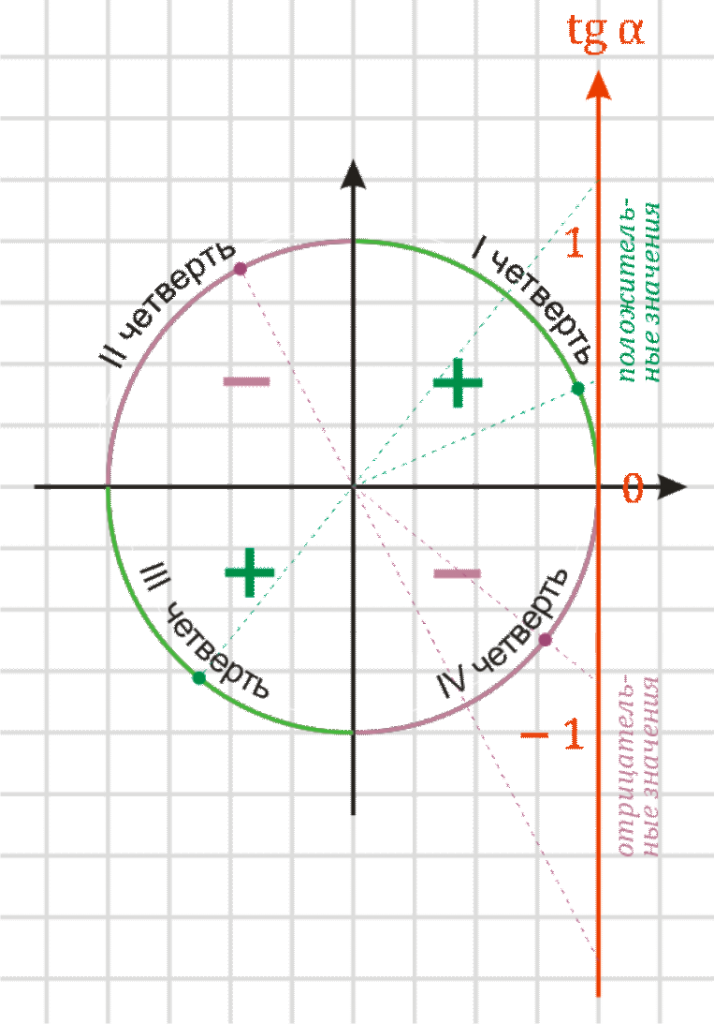
С помощью оси тангенсов легко определить знаки по четвертям тригонометрической окружности. Для этого надо взять любую точку на четверти и определить знак тангенса для нее описанным выше способом. У всей четверти знак будет такой же.
Для примера на рисунке нанесены две зеленые точки в I и III четвертях. Для них значение тангенса положительно (зеленые пунктирные прямые приходят в положительную часть оси), значит и для любой точки из I и III четверти значение тангенса будет положительно (знак плюс). С двумя фиолетовыми точками в II и IV четвертях – аналогично, но с минусом.
— котангенсом того же угла: формулой \(ctg\:x=\) \(\frac\) Другие наиболее часто применяемые формулы смотри здесь .




























