Модуль числа. что такое модуль в математике?

Решение неравенств с модулем

Чтобы лучше понять, как раскрыть модуль в разных типах равенств и неравенств, нужно проанализировать примеры.

Уравнения вида |x| = a

Пример 1 (алгебра 6 класс). Решить: |x| + 2 = 4.

Решение.

Такие уравнения решаются так же, как и равенства без абсолютных значений. Это означает, что, перемещая неизвестные влево, а константы – вправо, выражение не меняется.

После перемещения константы вправо получено: |x| = 2.

Поскольку неизвестные связаны с абсолютным значением, это равенство имеет два ответа: 2 и −2.

Ответ: 2 и −2.

Пример 2 (алгебра 7 класс). Решить неравенство |x + 2| ≥ 1.

Решение.

Первое, что нужно сделать, это найти точки, где абсолютное значение изменится. Для этого выражение приравнивается к 0. Получено: x = –2.

Это означает, что –2 – поворотная точка.

Далее определяется знак на интервалах: на промежутке  величина будет отрицательной, а на интервале  будет положительной.

Разделим интервал на 2 части:

1. для x + 2 ≥ 0

Общим ответом для этих двух неравенств является интервал [−1, + ∞).

1. для х + 2 &lt, 0

Общим ответом для этих двух неравенств является интервал (−∞, –3].

Окончательное решение – объединение ответов отдельных частей:

x ∈ (–∞, –3] ∪ [–1, + ∞).

Ответ: x ∈ (–∞, –3] ∪ [–1, + ∞).

Уравнения вида |x| = |y|

Пример 1 (алгебра 8 класс). Решить уравнение с двумя модулями: 2 * |x – 1| + 3 = 9 – |x – 1|.

Решение:

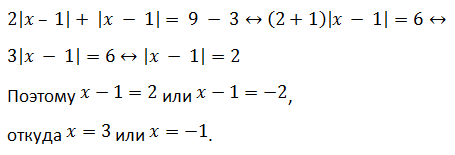
Ответ: x1 = 3, x2 = − 1.

Пример 2 (алгебра 8 класс). Решить неравенство:

Решение:

Уравнения вида |x| = y

Пример 1 (алгебра 10 класс). Найти x:

Решение:

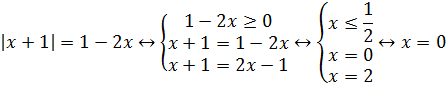
Очень важно провести проверку правой части, иначе можно написать в ответ ошибочные корни. Из системы видно, что  не лежит в промежутке. Ответ: x = 0

Ответ: x = 0.

График модуля

Как изобразить функцию с модулем? Для начала разберемся, что делает модуль с графиком функции. 

Рассмотрим функцию y = x — это прямая. При этом у может быть и положительным, и отрицательным. 

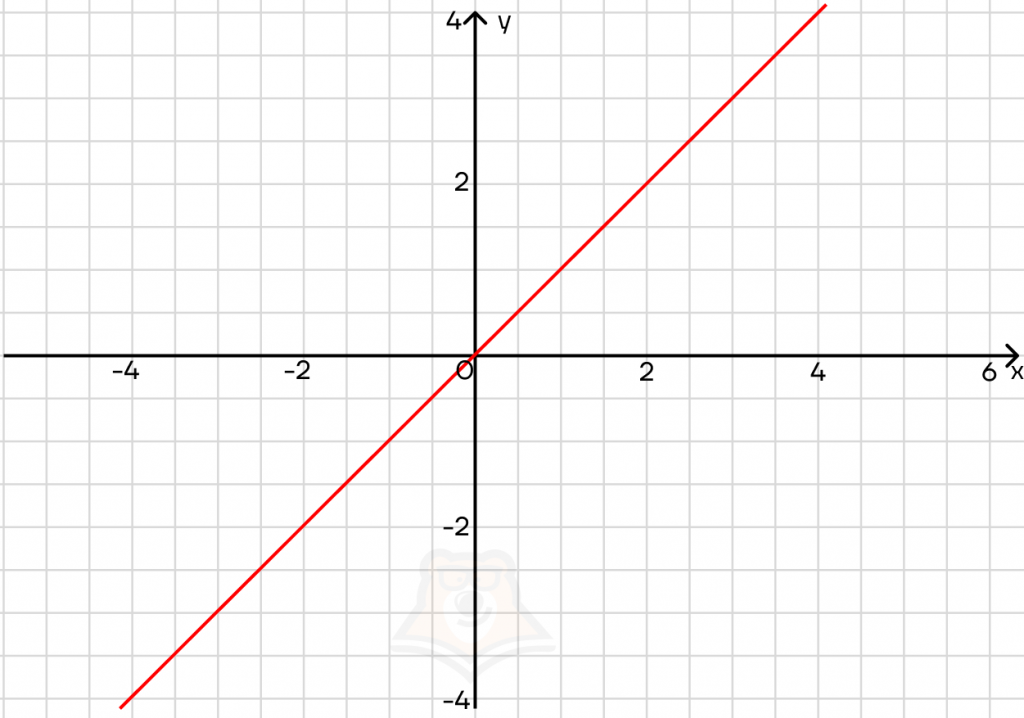
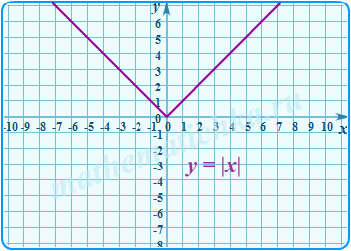
Занесем х под знак модуля: y = |x|. Теперь у может быть только положительным. Что происходит с частью графика, которая лежит ниже оси х? Она зеркально отражается. В итоге мы получаем галочку: 

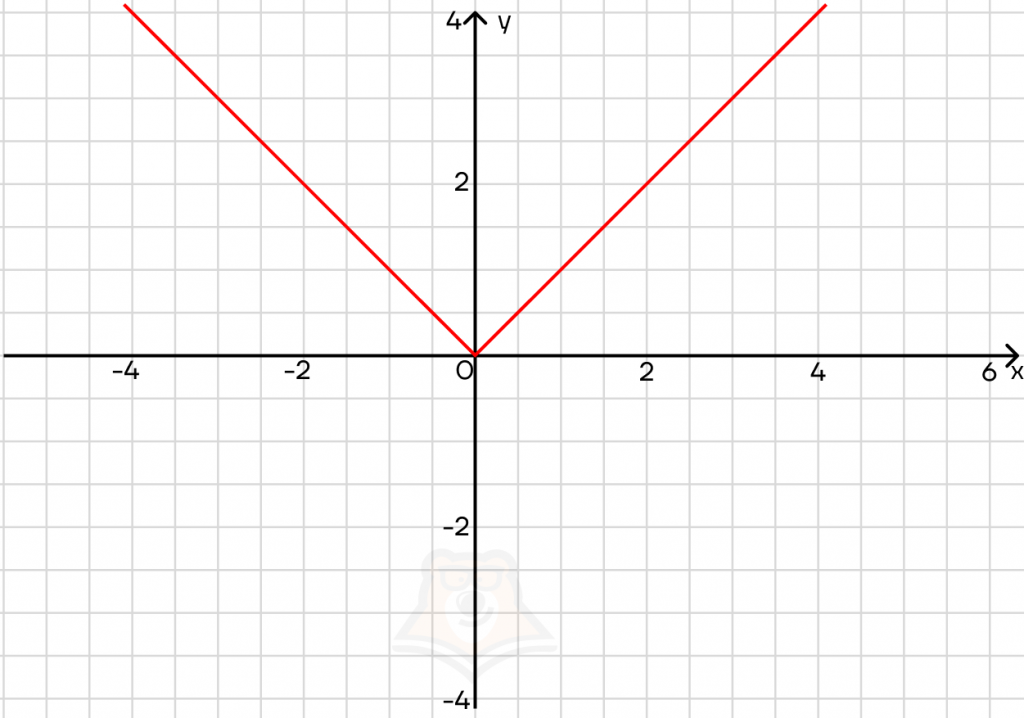
Модуль отражает любой график относительно оси х. 

Что будет, если перед х будет стоять коэффициент? Построим графики: 

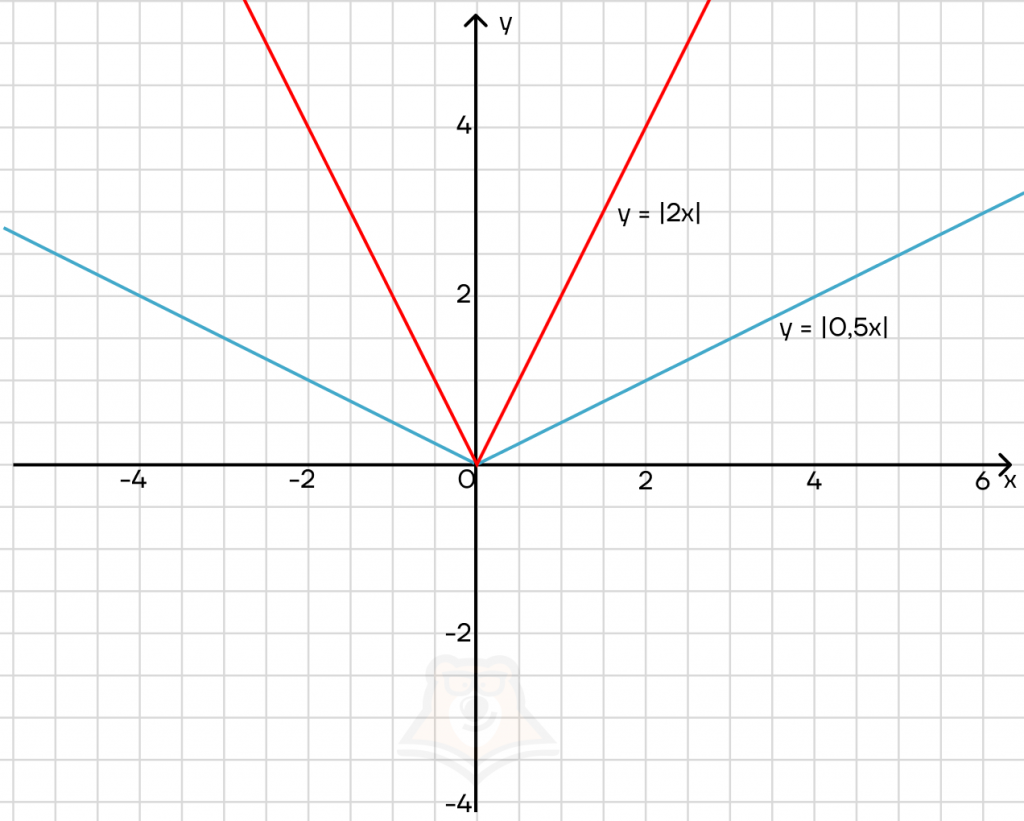
Галочка будет сужаться и расширяться. Причем чем больше коэффициент перед х, тем ýже будет галочка. 

Попробуем добавить слагаемое к подмодульному выражению. 

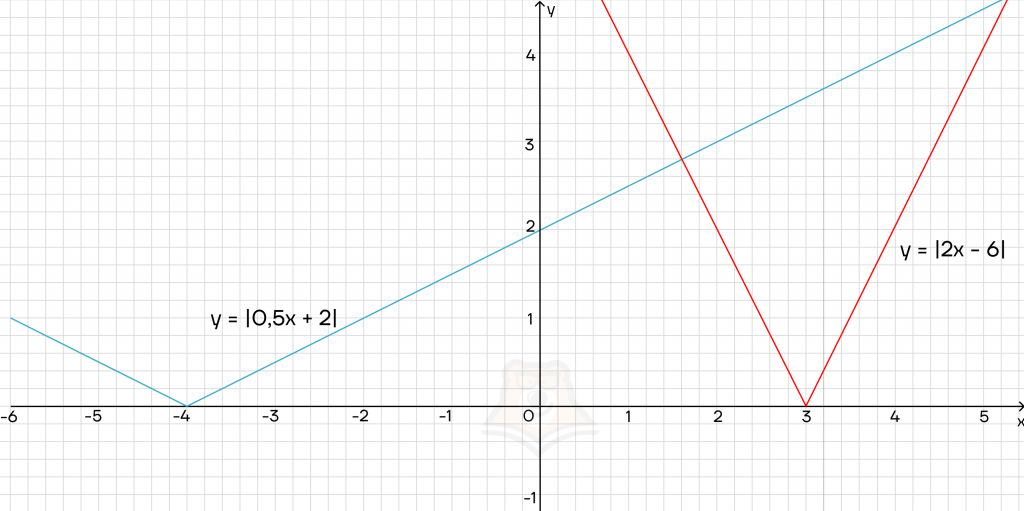
График модуля будет двигаться вдоль оси х. Причем:

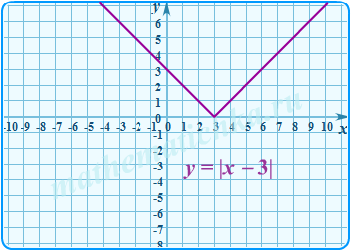
• если мы прибавляем число, то график сдвигается влево;
• если мы вычитаем число, то график сдвигается вправо. 

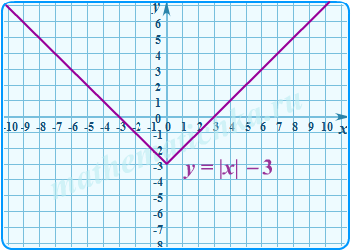
Добавим число к модулю, а не подмодульному выражению:

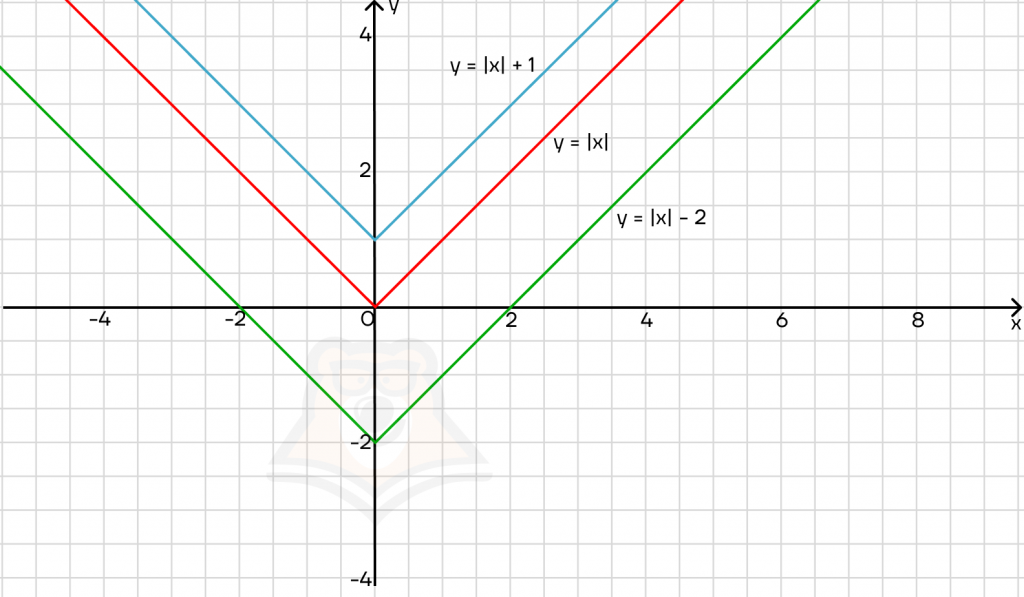
График будет двигаться вдоль оси у. 

Как перевернуть график модуля?Для этого достаточно добавить перед модулем минус

Важно, чтобы минус стоял именно перед модулем, а не внутри него. Тогда график будет отзеркален относительно оси х и лежать только ниже нее. Это легко проследить с помощью уравнений: если y = -|x|, то, при x = 3 получаем:y = -|3| = -3

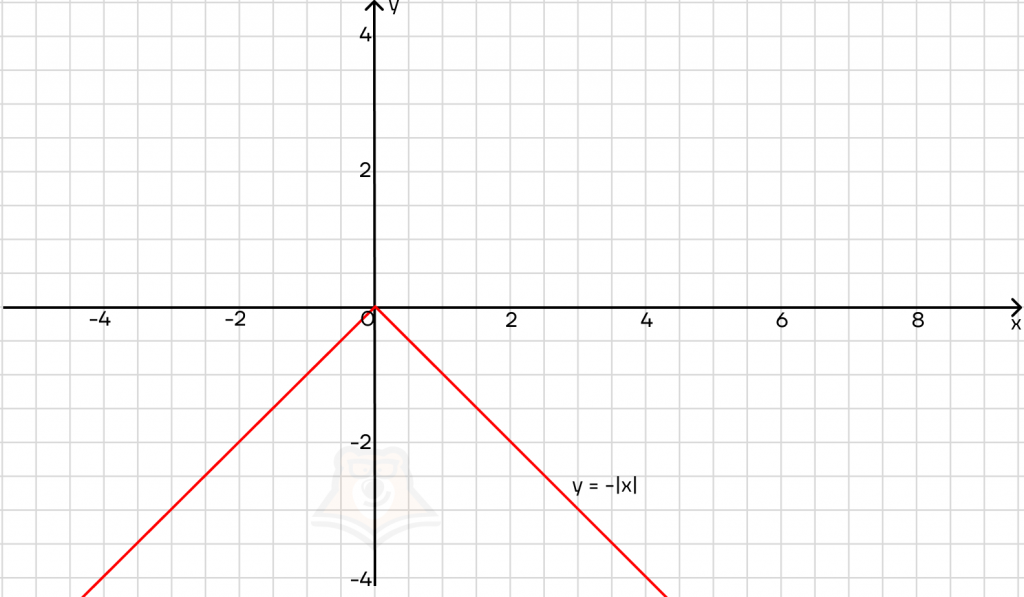
Свойства модуля (абсолютной величины)

Точка O на координатной прямой — это точка, из которой шар покатился — начальная точка.

Один отрезок прямой линии равен 1 делению — 1 метру.

Точка A на координатной прямой A (+ 3 ) — это момент удара мяча о стену.

Точка B с координатой B ( 0 ) — совпадает с начальной точкой.

Можно ли сказать, что мяч не прошел никакого расстояния, пока покоился в начале координат, потому что он приземлился в точке 0 м (ни один единичный отрезок не подходит от точки 0 до начала координат O)? Конечно, нет!

Шарик прошел бы путь, равный нулю, если бы его вообще не толкали и он оставался бы в состоянии покоя в точке O.

Однако следует учитывать, что путь (расстояние), пройденный мячом, состоит из 3 единичных отрезков справа и 3 единичных отрезков слева; если мы все

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Длина такого отрезка всегда является неотрицательной величиной.

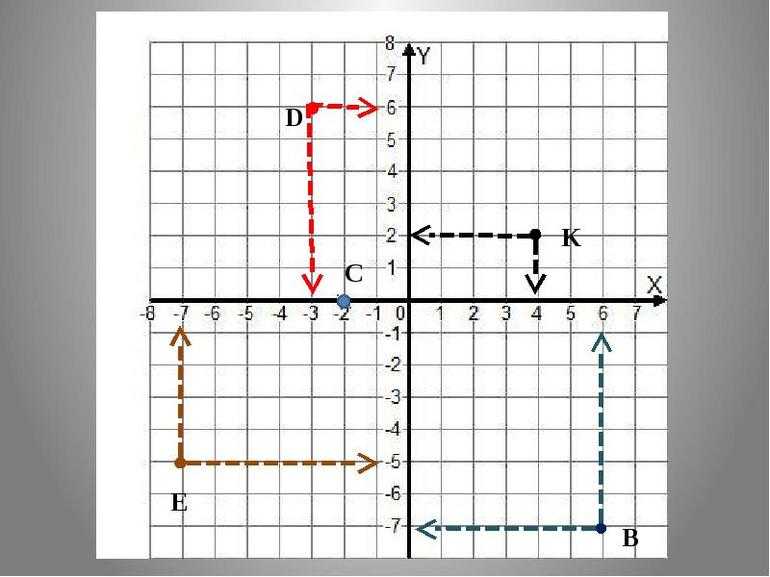
Два шарика катятся по прямой линии. Первый шар покатился на 4 м вправо от начальной точки, второй шар покатился на 6 м влево от начальной точки.

Проведите координатную линию и отметьте на ней координаты точек остановки двух шаров.

Проблема 1.

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Решение:

Проведем координатную линию с началом координат в точке O.

Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!

Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?

Эта информация доступна для зарегистрированных пользователей

Мы знаем, что мерой числа является расстояние (количество единичных отрезков) от нуля до данной точки.

Мы можем отложить 142 единичных отрезка вправо на координатной прямой и получить точку с координатами 142.

Мы также можем отложить 142 единичных отрезка влево от нуля и получить точку с координатами 142.

На координатной прямой есть два числа, которые по модулю равны 142, и расстояние между этими точками содержит по 142 единичных отрезка.

|142| = 142

Длина такого отрезка всегда является неотрицательной величиной.

Два шарика катятся по прямой линии. Первый шар покатился на 4 м вправо от начальной точки, второй шар покатился на 6 м влево от начальной точки.

Проведите координатную линию и отметьте на ней координаты точек остановки двух шаров.

Расположите числа — 15 ; — 1 ; — 1 ? 4 ; 7 в порядке возрастания по модулю.

Как построить графики для задач

Графики для задач, которые мы привели в предыдущем разделе, могут быть построены в программе, которая может строить графики функций. Например, можно воспользоваться такими программами, как Desmos, GeoGebra или MATLAB.

Для построения графика функции y = |x|, можно использовать любую из перечисленных программ, создать график, задав функцию y = |x| и построить график на интервале от -5 до 5.

Для функции y = , где — это наибольшее целое число, которое не превосходит x, можно использовать функцию floor в программе, которая округляет x вниз до ближайшего целого числа. Таким образом, функцию можно записать как y = floor(x), и построить график на интервале от -5 до 5.

Для функции y = {x}, где {x} — это дробная часть числа x, можно использовать функцию fract в программе, которая вычисляет дробную часть числа. Таким образом, функцию можно записать как y = fract(x), и построить график на интервале от -5 до 5.

Для функции y = sign(x), где sign(x) возвращает знак числа x, можно использовать функцию sign в программе. Таким образом, функцию можно записать как y = sign(x), и построить график на интервале от -5 до 5.

Система координат

Прежде чем говорить о расстоянии между точками по координатам, следует ввести систему отчета, в которой каждый геометрический объект можно будет однозначно определять. Для этой цели часто используют декартову систему координат. Она представляет собой взаимно перпендикулярные прямые, на каждой из которых отмечены единичные отрезки. Именно в них определяется положение тел в пространстве, на плоскости или на прямой линии.

Для названных трех случаев декартова система координат отличается количеством осей:

• 3 для определения положения пространственных объектов;
• 2 для фигур на плоскости;
• 1 для вычисления координат точек.

Единичные отрезки на координатных осях в общем случае могут иметь разную длину.

Как выглядит знак модуля и как его найти на клавиатуре?

Знак модуля обозначается символом «| |» или двумя вертикальными линиями, расположенными рядом друг с другом. Он используется в математике для обозначения модуля числа, то есть его абсолютной величины без учета знака.

На клавиатуре знак модуля может находиться на разных местах, в зависимости от языка и раскладки клавиатуры. Рассмотрим несколько способов найти его:

1. Некоторые клавиатуры имеют специальные клавиши с символами модуля. Они могут находиться под числами или в верхнем ряду клавиш. В таком случае, символ модуля будет нанесен на соответствующую клавишу, и его можно найти вместе с другими специальными символами.
2. Если на клавиатуре нет отдельной клавиши с символом модуля, можно воспользоваться сочетанием клавиш для ввода специальных символов. На операционных системах Windows это комбинация клавиш «Alt» + «124» (набирается на дополнительной клавиатуре справа, при включенном Num Lock). На MacOS можно использовать комбинацию клавиш «Option» + «Shift» + «Backslash» (находится на клавиатуре слева от буквы Z).
3. Альтернативным способом является использование символов модуля из символьной таблицы. Для этого нужно открыть таблицу символов, выбрать символ модуля и скопировать его в буфер обмена. Затем его можно вставить в нужное место, нажав сочетание клавиш «Ctrl» + «V».

Независимо от способа нахождения знака модуля, он может быть использован в различных программных средствах или веб-приложениях, где требуется обозначить абсолютное значение числа.

Задачи на модуль в старшей школе (10-11 классы)

Задачи на модуль очень часто встречаются в программе старшей школы, поэтому важно понимать, как с ними работать. Вот несколько примеров типов задач

Для этого нужно разбить уравнение на два случая: когда выражение в модуле положительное и когда оно отрицательное. Затем решить каждый случай отдельно и найти объединение решений.

Если выражение содержит модуль, его можно разбить на два случая: когда выражение внутри модуля положительное и когда оно отрицательное. Затем найти минимальное и максимальное значения для каждого случая и выбрать меньшее минимальное значение и большее максимальное значение.

Если множество задано как интервал, его можно представить как неравенство с модулем. Затем решить это неравенство и проверить, лежит ли заданное число в интервале.

Если в неравенстве есть модуль, его можно разбить на два случая: когда выражение внутри модуля положительное и когда оно отрицательное. Затем доказать неравенство для каждого случая отдельно и объединить результаты.

Вопрос-ответ:

Что такое модуль в математике?

Модуль числа — это его абсолютная величина, то есть расстояние от нуля до этого числа на числовой прямой. Модуль отрицательного числа равен его абсолютной величине.

Какие математические операции можно выполнять с модулями чисел?

С модулями чисел можно выполнять основные математические операции — сложение, вычитание, умножение и деление. В случае сложения и умножения модулей результат будет равен модулю соответствующего числа, при вычитании и делении результат зависит от знаков чисел и может быть как положительным, так и отрицательным.

Как использовать модули в математических задачах?

Модули в математических задачах позволяют упростить вычисления и обработку данных. Например, можно использовать модуль для определения расстояния между двумя точками на плоскости или вычисления площади треугольника.

Можно ли вычислять модуль комплексного числа?

Да, модуль комплексного числа вычисляется по формуле |z| = sqrt(x^2 + y^2), где x и y — это соответственно вещественная и мнимая части комплексного числа z.

Как модули могут быть использованы в программировании?

В программировании модули могут быть использованы для организации кода в отдельные блоки, которые можно переиспользовать в разных частях программы. Также модули могут использоваться для импортирования и использования уже существующих модулей, написанных другими программистами.

Могут ли модули быть отрицательными?

Модуль числа всегда неотрицательный, поскольку он является его абсолютной величиной. Модуль отрицательного числа равен его абсолютной величине, то есть положительному числу с такой же абсолютной величиной.

Применение модуля в реальной жизни

Модуль – это один из важных математических понятий, которое находит свое отражение в многих областях жизни. Он широко применяется в физике, технике, программировании и других сферах деятельности.

В программировании модуль является одним из основных инструментов в поиске ошибок, отладки и создании программ. Модули используются при написании сложных программных комплексов и для облегчения работы программиста.

Ведущие интернет-компании, такие как Google и Facebook, используют модули для повышения безопасности своих сайтов и приложений. Использование модулей позволяет защитить данные пользователя и улучшить работу сайта в целом.

Решение задач с применением модуля числа

Решение:

Следует понимать, что мы не располагаем числа — 15 ; — 1 ; в порядке возрастания. 4 ; 7, но их модули.

Для этого мы должны определить модули каждого из них:

|-15| = 15

|-1| = 1

Длина такого отрезка всегда является неотрицательной величиной.

Два шарика катятся по прямой линии. Первый шар покатился на 4 м вправо от начальной точки, второй шар покатился на 6 м влево от начальной точки.

Проведите координатную линию и отметьте на ней координаты точек остановки двух шаров.

Расположите эти числа в порядке возрастания (от наименьшего к наибольшему):

1, 4, 7, 15 .

Это дает следующую последовательность уравнений,

|-1| = 1

|4| = 4

|7| = 7

|-15| = 15

Следовательно, числа должны располагаться в порядке возрастания их модуля: -1, 4, 7, 7, -15

Ответ: — 1, 4, 4, 7, 7, — 15

|-15| = 15

На координатной прямой мы отметили две точк и-73 и 68. Какой коэффициент числа больше?

Решение:

Представьте, что на координатной прямой на определенном расстоянии от точки O (начало координат) отмечены две точки.

Слева от начала координат находится точка с координатам и-73.

Справа от начала координат находится точка с координатой 68.

Мы знаем, что модуль — это расстояние от данной точки до начала координат, выраженное в единичных отрезках.

Понятие модуля числа часто кажется студентам пугающим и непонятным. На самом деле, в этой теме по математике 6 класса нет ничего сложного. Чтобы лучше понять вопрос, давайте рассмотрим основные моменты, связанные с понятием коэффициента.

Мы начнем с понятия числовой линии и вектора. Прямая линия — это линия, на которой можно увидеть направление движения, точку 0 (начало координат) и величину единичного перехвата.

Каждое из действительных чисел может быть отмечено на числовой прямой. Независимо от подмножества, размер числа и его десятичные знаки. Прямая линия бесконечна и поэтому подходит абсолютно ко всем числам, кроме комплексных.

Числовая линия часто используется для сравнения различных типов чисел. Если отметить на линии два числа, то число справа будет больше, а число слева — меньше.

Слева от начала координат находится точка с координатам и-73.

Справа от начала координат находится точка с координатой 68.

Мы знаем, что модуль — это расстояние от данной точки до начала координат, выраженное в единичных отрезках.

Представьте, что на координатной прямой на определенном расстоянии от точки O (начало координат) отмечены две точки.

Модуль — это размер сегмента вектора. То есть, если число обозначено символом модуля, то вычитается параметр направления вектора. В геометрии это необходимо для нахождения сумм векторов и вообще для любых алгебраических операций с векторами. В этом примере невозможно указать и учесть направление, поэтому был придуман модуль.

В алгебре модуль числа означает, что при вычислениях учитывается только размер отрезка, без учета направления. На практике это означает, что

повороты модуля:

Возникает вопрос, почему отрицательное число становится положительным? Знак минус указывает только направление вектора. Символ знака минус указывает направление знака. А знак модуля отменяет параметр направления. Может ли размер сегмента быть отрицательным? Нет, конечно, нет. Таким образом, коэффициент отрицательного числа всегда является положительным числом.

|-15| = 15

В этом уроке мы более подробно рассмотрим понятие коэффициента числа.

Модуль — это расстояние между началом координат и числом на координатной прямой. Поскольку расстояние никогда не бывает отрицательным, модуль всегда неотрицателен. Поэтому модуль числа 3 равен 3, так же как модуль числ а-3 равен 3.

Предположим, что на координатной прямой расстояние между целыми числами равно одному шагу. Если теперь обозначить числ а-3 и 3, то их расстояние от начала координат равно трем шагам:

Коэффициент — это не только расстояние между началом координат и числом. Модулем также является расстояние между любыми двумя числами на координатной прямой. Это расстояние выражается как разность между этими числами с помощью символа модуло:

Функция y = sign(x)

Функция y = sign(x) обозначает знак числа x и определяется следующим образом:

y = sign(x) = { -1, x 0 }

Свойства функции y = sign(x):

Функция является ступенчатой и постоянна на интервалах (-∞, 0), (0, +∞). Функция не является непрерывной и не дифференцируемой в точке x = 0.

Построение графика функции y = sign(x): График функции y = sign(x) представляет собой две горизонтальные линии: y = -1 на интервале (-∞, 0) и y = 1 на интервале (0, +∞). В точке x = 0 график функции имеет разрыв.

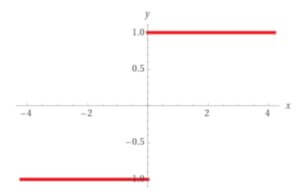
Примеры применения функции y = sign(x):

Использование в физике для определения направления силы или скорости. Использование в анализе данных для определения направления изменения значения переменной.

В заключении можно отметить, что функции y = |x|, y = , y = {x} и y = sign(x) являются важными и широко используемыми математическими функциями. Знание и понимание свойств их графиков позволяет более глубоко понимать многие явления и процессы, которые возникают в нашей жизни и в различных областях знаний.

Свойства модуля

Модуль, как и все понятия в математике, обладает своими свойствами. 

Свойство 1. |a| >= 0. 

Как мы уже говорили, модуль всегда будет положительным числом, поскольку он не обращает внимания на знак числа. 

Свойство 2. |a| = |-a|. 

Это свойство также подтверждает рассуждения выше. Модули противоположных чисел, то есть чисел с разными знаками, равны. 

Свойство 3. |a| >= a. 

Если число а будет положительным, например, 5, то неравенство |5| >= 5 \(\rightarrow\) 5 >= 5  выполняется, поскольку знак неравенства нестрогий. 

Если число а будет отрицательным, например, -5, то неравенство |-5| >= -5 \(\rightarrow\) 5 >= -5  выполняется, поскольку положительное число всегда больше отрицательного. 

Свойство 4. |a * b| = |a| * |b|. 

Пусть a = 5, b = -2, тогда |5 * (-2) | = |-10| = 10, и |5| * |-2| = 5 * 2 = 10, то есть выражения равны между собой. 

Свойство 5. \(|\frac{a}{b}| = \frac{|a|}{|b|}\). 

Рассуждения такие же, как и в предыдущем свойстве. Пусть a = 10, b = -5, тогда \(|\frac{10}{(-5)}| = |-2| = 2 и \frac{|10|}{|-5|} = \frac{10}{5} = 2\). 

Свойство 6. |a + b| <= |a| + |b|.

Почему появилось неравенство, а не уравнение, как в предыдущих двух свойствах? Разберем два примера. 

Пусть a = 1, b = 2, тогда |1 + 2| = |3| = 3 и |1| + |2| = 1 + 2 = 3 — неравенство выполняется, поскольку знак нестрогий.

Но если a = -1, b = 2, тогда |-1 +2| = |1| = 1 и |-1| + |2| = 1 + 2 = 3, откуда получаем 1 < 3. 

Свойство 7. \(\sqrt{a^2} = |a|\). 

Докажем это свойство. Пусть \(\sqrt{a^2} = x\), тогда x, поскольку квадратный «Корень» не может быть отрицательным. Возведем полученное уравнение в квадрат: a2 = x2 a2 — x2 = 0(a — x)(a + x) = 0

Из уравнения x = a,  из-за ограничений на x получаем a >= 0.

И x = -a,  из-за ограничений на x получаем a < 0. 

То есть получается выражение модуля. 

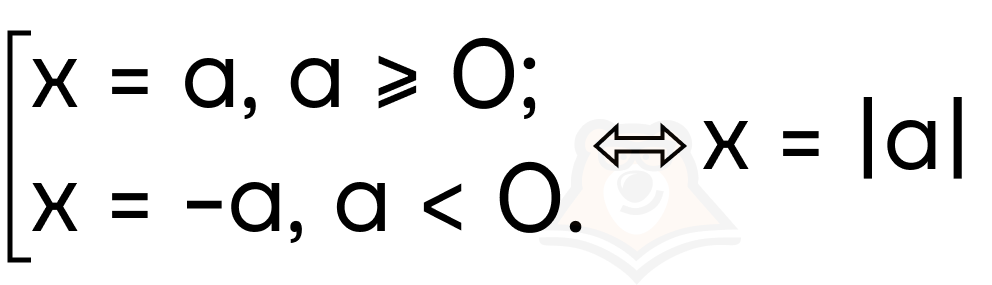
Свойство 8. |a|2 = a2.

Поскольку и модуль, и квадрат числа дают положительный результат, модуль в квадрате можно заменить просто квадратом числа. 

Модуль аргумента и модуль функции

Внимание: мелкие рисунки увеличиваются щелчком левой клавиши мыши.

Если Вы попали на эту страницу из поисковика, миновав предыдущие разделы темы «Графики функций и их преобразования», то рекомендую сначала повторить графики основных элементарных функций и общие правила преобразования графиков функций.

Модуль переменной (абсолютная величина значения) определяется следующим образом:

• если если

В контексте построения графиков это означает использование преобразования симметрии относительно осей координат.

   

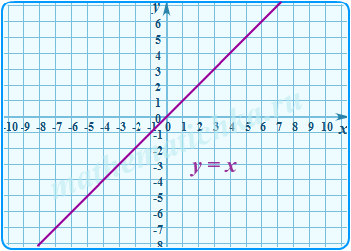
Iy = f(|x|)

1. Построить график функции .
2. Исключить его часть, расположенную в отрицательной половине оси абсцисс. (Например, просто стереть ластиком, если график был построен карандашом.)
3. Построить левую ветвь графика (при отрицательных x) симметричным отображением его правой ветви относительно оси Oy.

II

1. Построить график функции .
2. Участок графика, расположенный ниже оси абсцисс (при отрицательных y) развернуть на верхнюю половину координатной сетки преобразованием симметрии относительно оси Ox.

Пример 1.

   

В этом примере оба графика получены из графика функции Первый — преобразованием Гf(x) → Гf(|x|), второй — преобразованием Гf(x) → Г|f(x)|.

Пример 2.

   

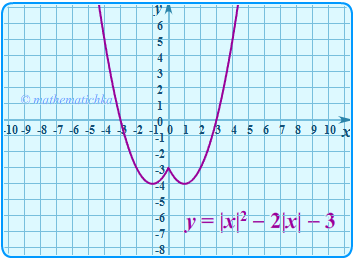
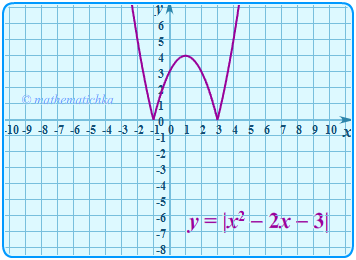
В этом примере оба графика получены из графика функции Первый — преобразованием Гf(x) → Гf(|x|), второй — преобразованием Гf(x) → Г|f(x)|.

Один из способов быстро и точно построить исходную параболу по характерным точкам показан в видео на канале Mathematichka.

IIIпоследовательность преобразований

• 1. 
  2. 
  3. 
  4. 
  5.

1.

2.

3.

4.

5.

IV  Равенство вида по определению не является функцией, так как допускает неоднозначность при вычислении значения y. Однако линию на координатной плоскости оно задает, и эту линию тоже можно построить, исходя из графика функции . Для этого нужно:

1. Построить график функции .
2. Исключить его часть, расположенную ниже оси абсцисс, поскольку указанное равенство возможно только для положительных значений f(x).
3. Построить нижнюю часть линии (при отрицательных y) симметричным отображением относительно оси Ox.

• 6. 
  7. 
  8.

6.

7.

8.

Пример 3.

Задан график функции . Построить кривые, удовлетворяющие уравнению, .

Заметим, что (значение четной степени, как и значение модуля, всегда неотрицательно). Поэтому, выделяя полный квадрат, преобразуем функцию к виду
и строим её график последовательными преобразованиями.

Строим график функции переносом на 1 вправо вдоль оси Ox, а затем переносом вниз на 6 единиц вдоль оси Oy.
Строим график функции с использованием преобразования симметрии относительно оси Oy.
Строим линии, удовлетворяющие уравнению с использованием преобразования симметрии относительно оси Ox.

• 1. 
  2. 
  3. 
  4. 5. 
  6.

1.	2.	3.	4.
5.	6.

Следующий график постройте самостоятельно, чтобы убедиться, что вы правильно поняли материал.

Пример 4.

Задан график функции . Построить график функции .

Показать ответ

Примеры использования этих функций

Изучение функций $y=|x|$, $y=$, $y={x}$ и $y=\text{sign}(x)$ может быть полезным для решения различных задач в различных областях, таких как физика, экономика, математика и т.д. Рассмотрим несколько примеров использования этих функций.

Задача на вычисление длины отрезка на координатной плоскости, заданного двумя точками $(x_1,y_1)$ и $(x_2,y_2)$.

Длина отрезка может быть вычислена с помощью функции $y=|x|$. Для этого нужно вычислить расстояние между координатами точек $x_1$ и $x_2$, затем применить функцию $y=|x|$ к этому расстоянию:

Длина отрезка=∣x2−x1∣Длина отрезка=∣x2​−x1​∣

Задача на определение максимального значения функции при заданных условиях.

Рассмотрим функцию $y=\sin(x)+\cos(x)$ на отрезке $$. Чтобы найти максимальное значение функции на этом отрезке, нужно найти ее производную и приравнять ее к нулю:

ddx(sin⁡(x)+cos⁡(x))=cos⁡(x)−sin⁡(x)=0dxd​(sin(x)+cos(x))=cos(x)−sin(x)=0

Отсюда получаем $x=\frac{\pi}{4}$ или $x=\frac{5\pi}{4}$. Подставляя эти значения в функцию, получаем максимальное значение $y=\sqrt{2}$.

Задача на нахождение пересечения двух функций.

Рассмотрим функции $y=x$ и $y=2-x$. Чтобы найти их точки пересечения, нужно приравнять их друг к другу:

x=2−x⇒x=1x=2−x⇒x=1

Точка пересечения будет иметь координаты $(1,1)$.

Задача на определение целочисленного значения функции.

Рассмотрим функцию $y=$. Чтобы найти ее значение для целого числа $x$, достаточно взять любое число на отрезке $[x,x+1)$:

=⌊x⌋=⌊x⌋

Задача на определение медианы выборки.

Предположим, что у нас есть выборка чисел $x_1,x_2,\dots,x_n$. Медиана этой выборки может быть вычислена с помощью функции $y=$, где $x$ — это середина отсортированной выборки:

Медиана=Медиана=

Проблемы при изучении функций y=|x|, y=[x], y={x}, y=sign(x) и их графиков

Несколько советов для тех, кто сталкивается с проблемами при изучении функций y=|x|, y=, y={x}, y=sign(x) и их графиков:

1. Внимательно изучите определения и свойства каждой из этих функций. Это поможет вам понять, как они работают и как они отличаются друг от друга.
2. Начните с простых задач и графиков, чтобы понять основные принципы работы каждой функции. Затем переходите к более сложным примерам.
3. Не бойтесь задавать вопросы. Если вы не понимаете какую-то часть материала, спросите своего преподавателя или коллегу за помощью.
4. Изучайте материал постепенно, посвящая каждой функции достаточное количество времени. Не пытайтесь изучать все сразу.
5. Применяйте каждую функцию на практике, решая задачи. Это поможет вам лучше понять, как каждая функция работает и как ее можно использовать.
6. Рисуйте графики, чтобы лучше визуализировать каждую функцию. Это поможет вам лучше понять, как она работает и как ее свойства влияют на ее график.
7. Практикуйтесь в решении задач, которые требуют применения нескольких функций. Это поможет вам понять, как функции могут взаимодействовать друг с другом и как их свойства могут влиять на результат.
8. Используйте различные источники информации для изучения этой темы, включая учебники, онлайн-курсы и видеоуроки.
9. Не забывайте повторять материал и решать задачи, чтобы закрепить свои знания.
10. Наконец, не забывайте, что понимание этих функций требует времени и усилий. Не отчаивайтесь, если что-то не получается с первого раза. Старайтесь улучшать свои навыки и продолжайте изучение этой темы.

Случай переменной правой части

А теперь рассмотрим вот такое уравнение:

\

Это уравнение принципиально отличается от всех предыдущих. Чем? А тем, что справа от знака равенства стоит выражение $2x$ — и мы не можем заранее знать, положительное оно или отрицательное.

Как быть в таком случае? Во-первых, надо раз и навсегда понять, что если правая часть уравнения окажется отрицательной, то уравнение не будет иметь корней — мы уже знаем, что модуль не может быть равен отрицательному числу.

А во-вторых, если права часть всё-таки положительна (или равна нулю), то можно действовать точно так же, как раньше: просто раскрыть модуль отдельно со знаком «плюс» и отдельно — со знаком «минус».

Таким образом, сформулируем правило для произвольных функций $f\left( x \right)$ и $g\left( x \right)$ :

\

Применительно к нашему уравнению получим:

\

Ну, с требованием $2x\ge 0$ мы как-нибудь справимся. В конце концов, можно тупо подставить корни, которые мы получим из первого уравнения, и проверить: выполняется неравенство или нет.

Поэтому решим-ка само уравнение:

\

Ну и какой их этих двух корней удовлетворяет требованию $2x\ge 0$? Да оба! Поэтому в ответ пойдут два числа: $x=2$ и $x={2}/{5}\;$. Вот и всё решение.:)

Подозреваю, что кто-то из учеников уже начал скучать? Что ж, рассмотрим ещё более сложное уравнение:

\

Хоть оно и выглядит злобно, по факту это всё то же самое уравнение вида «модуль равен функции»:

\

И решается оно точно так же:

\

С неравенством мы потом разберёмся — оно какое-то уж слишком злобное (на самом деле простое, но мы его решать не будем). Пока лучше займёмся полученными уравнениями. Рассмотрим первый случай — это когда модуль раскрывается со знаком «плюс»:

\

Ну, тут и ежу понятно, что нужно всё собрать слева, привести подобные и посмотреть, что получится. А получится вот что:

\

Выносим общий множитель ${{x}^{2}}$ за скобку и получаем очень простое уравнение:

\

\

Тут мы воспользовались важным свойством произведения, ради которого мы и раскладывали исходный многочлен на множители: произведение равно нулю, когда хотя бы один из множителей равен нулю.

Теперь точно так же разберёмся со вторым уравнением, которое получается при раскрытии модуля со знаком «минус»:

\

Опять то же самое: произведение равно нулю, когда равен нулю хотя бы один из множителей. Имеем:

\

\

Ну вот мы получили три корня: $x=0$, $x=1,5$ и $x={2}/{3}\;$. Ну и что из этого набора пойдёт в окончательный ответ? Для этого вспомним, что у нас есть дополнительное ограничение в виде неравенства:

\

Как учесть это требование? Да просто подставим найденные корни и проверим: выполняется неравенство при этих $x$ или нет. Имеем:

\

Таким образом, корень $x=1,5$ нас не устраивает. И в ответ пойдут лишь два корня:

\

Как видите, даже в этом случае ничего сложного не было — уравнения с модулями всегда решаются по алгоритму. Нужно лишь хорошо разбираться в многочленах и неравенствах. Поэтому переходим к более сложным задачам — там уже будет не один, а два модуля.

Нахождение расстояния между точками на числовой оси

Расстояние между точками на числовой оси может быть вычислено с помощью модуля разности координат этих точек. Модуль числа, также известный как абсолютная величина числа, обозначается через символ вертикальной черты » | | » и возвращает неотрицательное значение.

Пусть у нас есть две точки на числовой оси: точка A с координатой x_A и точка B с координатой x_B. Тогда расстояние между этими точками можно вычислить по следующей формуле:

| x_A — x_B |

Например, если точка A имеет координату 5, а точка B -3, то расстояние между ними будет:

| 5 — (-3) | = | 5 + 3 | = | 8 | = 8

Таким образом, расстояние между точкой A и точкой B на числовой оси равно 8.

Этот метод вычисления расстояния между точками на числовой оси имеет множество применений в математике. Он может быть использован для определения расстояния между двумя значениями на временной шкале, например, разница во времени между двумя событиями. Также он может быть применен в физике для вычисления перемещения тела в пространстве.

Примеры решения задач на нахождение расстояния между точками

Исходные данные: задана координатная прямая и точки, лежащие на ней с заданными координатами A (1 — 2) и B (11 + 2) . Необходимо найти расстояние от точки начала отсчета O до точки A и между точками A и B .

Решение

1. Расстояние от точки начала отсчета до точки равно модулю координаты этой точки, соответственно O A = 1 — 2 = 2 — 1
2. Расстояние между точками A и B определим как модуль разности координат этих точек: A B = 11 + 2 — (1 — 2) = 10 + 2 2

Ответ: O A = 2 — 1 , A B = 10 + 2 2

Пример 2

Исходные данные: задана прямоугольная система координат и две точки, лежащие на ней A (1 , — 1) и B (λ + 1 , 3) . λ – некоторое действительное число. Необходимо найти все значения этого числа, при которых расстояние А В будет равно 5 .

Решение

Чтобы найти расстояние между точками A и B , необходимо использовать формулу A B = (x B — x A) 2 + y B — y A 2

Подставив реальные значения координат, получим: A B = (λ + 1 — 1) 2 + (3 — (- 1)) 2 = λ 2 + 16

А также используем имеющееся условие, что А В = 5 и тогда будет верным равенство:

λ 2 + 16 = 5 λ 2 + 16 = 25 λ = ± 3

Ответ: А В = 5 , если λ = ± 3 .

Пример 3

Исходные данные: задано трехмерное пространство в прямоугольной системе координат O x y z и лежащие в нем точки A (1 , 2 , 3) и B — 7 , — 2 , 4 .

Решение

Для решения задачи используем формулу A B = x B — x A 2 + y B — y A 2 + (z B — z A) 2

Подставив реальные значения, получим: A B = (- 7 — 1) 2 + (- 2 — 2) 2 + (4 — 3) 2 = 81 = 9

Ответ: | А В | = 9

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Пусть задана прямоугольная система координат.

Теорема 1.1.
Для любых двух точек М 1 (х 1 ;у 1) и М 2 (х 2 ;у 2) плоскости расстояние d между ними выражается формулой

d = . (3)

Доказательство.
Опустим из точек М 1 и М 2 перпендикуляры М 1 В и М 2 А соответственно на оси Оу и Ох и обозначим через К точку пересечения прямых М 1 В и М 2 А (рис.1.4). Возможны следующие случаи:

1)Точки М 1 , М 2 и К различны. Очевидно, что точка К имеет координаты (х 2 ;у 1). Нетрудно заметить что М 1 К = ôх 2 – х 1 ô, М 2 К = ôу 2 – у 1 ô. Т.к. ∆М 1 КМ 2 прямоугольный, то по теореме Пифагора d = М 1 М 2 = = =.

2) Точка К совпадает с точкой М 2 , но отлична от точки М 1 (рис.1.5). В этом случае у 2 = у 1 и

d = М 1 М 2 = М 1 К = ôх 2 – х 1 ô= = =.

3) Точка К совпадает с точкой М 1 , но отлична от точки М 2 . В этом случае х 2 = х 1 и

d =М 1 М 2 = КМ 2 = ôу 2 — у 1 ô= =.

4) Точка М 2 совпадает с точкой М 1 . Тогда х 1 = х 2 , у 1 = у 2 и

d = М 1 М 2 = О =.

—

Пусть задана прямоугольная система координат.
Теорема 1.1.Для любых двух точек М1(х1;у1) и М2(х2;у2) плоскости расстояние d между ними выражается формулой
d = . (3)
Доказательство.Опустим из точек М1 и М2 перпендикуляры М1В и М2А соответственно на оси Оу и Ох и обозначим через К…

— Расстояние между двумя точками

— Расстояние между двумя точками

Определение расстояний
Лекция № 6. МЕТРИЧЕСКИЕ ЗАДАЧИ
(определение расстояний, определение величины части плоскости,
определение величины угла)
План лекции
1. Определение расстояний.
1.1. Расстояние между двумя точками:
а) без преобразования чертежа;
б)…

— Модуль вектора. Расстояние между двумя точками

Дан вектор в пространстве

Модуль вектора вычисляется по формуле: .
Важной задачей является нахождение расстояния между двумя точками:
1) расстояние между точками и на прямой равно длине вектора:
;
2) расстояние между двумя точками и на плоскости равно длине вектора:
;
…

— Теорема Шаля для отрезков. Координата направленного отрезка, заданного двумя точками декартовой оси координат. Расстояние между двумя точками, лежащими на оси координат

Теорема (1) Шаля. (Для отрезков). Если А, В, С три любые точки оси, то. (Число число числу).
Доказательство. (1). Предположим, что точки А, В, С попарно различны. Если точки В лежит между точками А и С, то длина отрезка АС равна сумме длин отрезков АВ и ВС:
;
но так как в…

Расстояние от точки до точки
— это длина отрезка, соединяющего эти точки, в заданном масштабе. Таким образом, когда речь идет об измерении расстояния, то требуется знать масштаб (единицу длины), в котором будут проводиться измерения. Поэтому, задачу нахождения расстояния от точки до точки обычно рассматривают либо на координатной прямой, либо в прямоугольной декартовой системе координат на плоскости или в трехмерном пространстве. Другими словами, наиболее часто приходится вычислять расстояние между точками по их координатам.

В этой статье мы, во-первых, напомним, как определяется расстояние от точки до точки на координатной прямой. Далее получим формулы для вычисления расстояния между двумя точками плоскости или пространства по заданным координатам. В заключении, подробно рассмотрим решения характерных примеров и задач.

Навигация по странице.

Функция y = [x]

Функция y = обозначает наибольшее целое число, не превышающее x. Например, = 3, = -3. Функция y = может быть определена следующим образом:

y = = max{k ∈ ℤ | k ≤ x}

Свойства функции y = :

Функция является ступенчатой и постоянна на интервалах между целыми числами. Функция не является непрерывной и не дифференцируемой на множестве действительных чисел.

Построение графика функции y = : График функции y = представляет собой последовательность горизонтальных линий на уровне каждого целого числа.

Примеры применения функции y = :

Использование в комбинаторике для определения числа возможных вариантов перестановок и сочетаний. Вычисление суммы целых чисел от 1 до n: 1 + 2 + … + n = /2.

В следующих разделах мы рассмотрим еще две функции и их графики.