Правильные и полуправильные многогранники. теорема эйлера–декарта

Архимедовы тела (полурегулярные) от W6 до W18

Индекс	Имя	Изображение	Двойное имя	Двойное изображение	Символ Wythoff	Вершина	Группа симметрии	U #	K #	V	E	F	Грани по типу
6	Усеченный тетраэдр		триакис-тетраэдр		2 3 | 3	. 3.6.6	Td	U02	K07	12	18	8	4 {3} + 4 {6}
7	Усеченный октаэдр		тетракис-шестигранник		2 4 | 3	. 4.6.6	Oh	U08	K13	24	36	24	6 {4} + 8 {6}
8	Усеченный шестигранник		триакис октаэдр		2 3 | 4	. 3.8.8	Oh	U09	K14	24	36	14	8 {3} + 6 {8}
9	Усеченный икосаэдр		пентакис додекаэдр		2 5 | 3	. 5.6.6	Ih	U25	K30	60	90	32	12 {5} + 20 {6}
10	Усеченный додекаэдр		триакисикосаэдр		2 3 | 5	. 3.10.10	Ih	U26	K31	60	90	32	20 {3} + 12 {10}
11	Кубооктаэдр		ромбический додекаэдр		2 | 3 4	. 3.4.3.4	Oh	U07	K12	12	24	14	8 {3} + 6 {4}
12	икосододекаэдр		ромбический триаконтаэдр		2 | 3 5	. 3.5.3.5	Ih	U24	K29	30	60	32	20 {3} + 12 {5}
13	Малый ромбокубооктаэдр		дельтоидный икоситетраэдр		3 4 | 2	. 3.4.4.4	Oh	U10	K15	24	48	26	8 {3} + (6 + 12) {4}
14	Малый ромбикосододекаэдр		дельтоидальный гексеконтаэдр		3 5 | 2	. 3.4.5.4	Ih	U27	K32	60	120	62	20 {3} + 30 {4} + 12 {5}
15	Усеченный кубооктаэдр. (Большой ромбокубооктаэдр)		дисдиакис додекаэдр		2 3 4 |	. 4.6.8	Oh	U11	K16	48	72	26	12 {4} + 8 {6} + 6 {8}
16	Усеченный икосододекаэдр. (Большой ромбикосододекаэдр)		дисдякис триаконтаэдр		2 3 5 |	. 4.6.10	Ih	U28	K33	120	180	62	30 {4} + 20 {6} + 12 {10}
17	Плосконосый куб		пятиугольный икоситетраэдр		| 2 3 4	. 3.3.3.3.4	O	U12	K17	24	60	38	(8 + 24) {3} + 6 {4}
18	Плоский додекаэдр		пятиугольный шестигранник		| 2 3 5	. 3.3.3.3.5	I	U29	K34	60	150	92	(20 + 60) {3} + 12 {5}

Звездчатые формы: модели от W19 до W66

Звездчатые формы октаэдра

Индекс	Имя	Группа симметрии	Изображение	Грани
2	Октаэдр. (правильный)	Oh
19	Звездчатый октаэдр. (Соединение двух тетраэдров)	Oh

Звёздчатые формы додекаэдра

Индекс	Название	Группа симметрии	Изображение	Грани
5	Додекаэдр (регулярный)	Ih
20	Маленькая стелла звездчатый додекаэдр (правильный). (Первая звездчатая форма додекаэдра)	Ih
21	Большой додекаэдр (правильный). (Вторая звездчатая форма додекаэдра)	Ih
22	Большая звездчатая додекаэдр (правильный). (Третья звёздчатая форма додекаэдра)	Ih

Звёздчатая форма икосаэдра

Индекс	Название	Группа симметрии	Изображение	Грани
4	Икосаэдр (правильный)	Ih
23	Соединение пяти октаэдров. (Первая составная звездчатая форма икосаэдра)	Ih
24	Соединение пяти тетраэдров. (Вторая составная звездчатая форма икосаэдра)	I
25	Соединение десяти тетраэдров. (Третья составная звездчатая форма икосаэдра)	Ih
26	Малый триамбический икосаэдр. (Первая звездчатая форма икосаэдра). (Триакисикосаэдр)	Ih
27	Вторая звездчатая форма икосаэдра	Ih
28	Додекаэдр с выемками. (Третья звездчатость икосаэдра)	Ih
29		Ih
30		Ih
31		Ih
32		Ih
33		Ih
34	Девятая звездчатая форма икосаэдра. Большой триамбический икосаэдр.	Ih
35	Десятая звездчатость икосаэдра	I
36		I
37		Ih
38		I
39		I
40		I
41	Большой икосаэдр (правильный). (Шестнадцатая звездчатая форма икосаэдра)	Ih
42	Конечная звездчатость икосаэдра	Ih

Звездчатость кубооктаэдра

Индекс	Имя	Группа симметрии	Изображение	Грани (восьмигранные плоскости)	Грани (кубические плоскости)
11	Кубооктаэдр (правильный)	Oh
43	Соединение куба и октаэдра. (Первая звездчатая форма кубооктаэдра)	Oh
44		Oh
45		Oh
46		Oh

Звездчатость икосододекаэдра

Индекс	Имя	Группа симметрии	Изображение	Грани (плоскости икосаэдра)	Грани (плоскости додекаэдра)
12	Икосододекаэдр. (обычный)	Ih
47	(Первая звездчатая форма икосододекаэдра). Соединение додекаэдра и икосаэдра	Ih
48		Ih
49		Ih
50	. (соединение малого звездчатого додекаэдра. и триакисикосаэдра)	Ih
51	. (соединение малого звездчатого додекаэдра. и пяти октаэдров)	Ih
52		Ih
53		Ih
54	. (Соединение пяти тетраэдров. и большого додекаэдра)	I
55		Ih
56		Ih
57		Ih
58		Ih
59		Ih
60		Ih
61	Соединение большого звездчатого додекаэдра и большого икосаэдра	Ih
62		Ih
63		Ih
64		Ih
65		Ih
66		Ih

Чем обусловлена популярность шестиугольников?

Снежинки, органические молекулы, кристаллы кварца и столбчатые базальты представляют собой шестиугольники. Причиной тому является присущая им симметрия. Наиболее ярким примером служат соты, шестиугольная структура которых сводит к минимуму пространственный недостаток, так как вся поверхность расходуется весьма рационально. Зачем делиться на идентичные ячейки? Пчелы создают в природе правильные многогранники для того, чтобы использовать их для своих нужд, в том числе для хранения меда и откладки яиц. Почему природа предпочитает шестиугольники? Ответ на этот вопрос может дать элементарная математика.

• Треугольники. Возьмем 428 равносторонних треугольников со стороной около 7,35 мм. Их общая длина составляет 3*7,35 мм*428/2 = 47,2 см.
• Прямоугольники. Возьмем 428 квадратов со стороной около 4,84 мм, их общая длина составляет 4*4,84 м *428/2 = 41,4 см.
• Шестиугольники. И, наконец, возьмем 428 шестиугольников со стороной 3 мм, их общая длина составляет 6*3 мм*428/2 = 38,5 см.

Очевидной является победа шестиугольников. Именно эта форма помогает предельно минимизировать пространство и позволяет на меньшей территории поместить как можно больше фигур. Соты, в которых пчелы хранят свой янтарный нектар, являются чудесами точной инженерии, массивом призмовидных клеток с идеально шестиугольным поперечным сечением

Восковые стены выполнены с соблюдением очень точной толщины, ячейки осторожно наклонены, чтобы предотвратить выпадение вязкого меда, а вся конструкция выравнивается в соответствии с магнитным полем Земли. Удивительным образом пчелы работают одновременно, координируя свои усилия

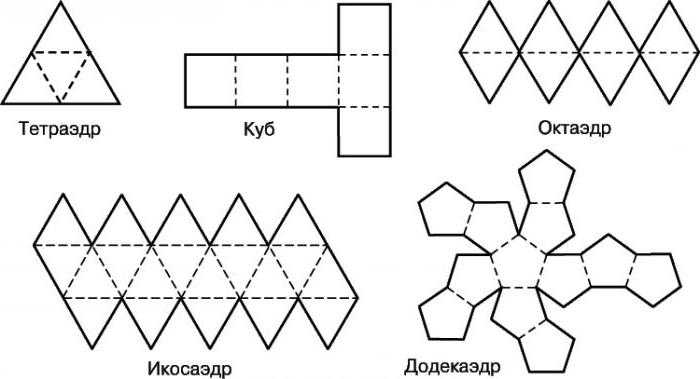
Как построить развертку самостоятельно?

Пожалуй, помимо склеивания многогранника — хоть звездчатого, хоть платоновского, — еще интереснее построить развертку будущей модели собственными силами, оценив свои способности к черчению, конструированию и пространственному вообжению. Простые платоновсткие тела состоят из простых многоугольников, которые в одной фигуре идентичны друг другу. Так, тетраэдр — это три равнобедренных треугольника. Прежде чем простроить развертку, нужно представить себе, как правильно сложить плоские многоугольники между собой, чтобы получить многогранник. Треугольники можно соединить между собой по ребрам, прочертив один рядом с другим. Для склеивания развертки многогранников схемы должны быть снабжены специальными кармашками или клапанами, которые позволят соединить все части в единое целое. Тетраэдр — простейшая фигура из четырех граней. Октаэдр можно представить как двойной тетраэдр, у него восемь гарней — равнобедренных треугольников. Гексаэдром называют знакомый всем с детства куб. Икосаэдр представляет собой соединение 20 равнобедренных треугольников в правильный выпуклый многогранник. Додекаэдр — это объемная фигура из 12 граней, каждая из которых представляет собой правильный пятиугольник.

Правильные пузырьки

Предположим, что вы можете сделать «идеальную» пену, в которой все пузырьки имеют одинаковый размер. Какова же совершенная форма ячейки, которая делает общую площадь стенки пузырька настолько малой, насколько это возможно. Это обсуждалось много лет, и долгое время считалось, что идеальная форма ячейки представляет собой 14-гранный многогранник с квадратными и шестиугольными сторонами.

В 1993 году была обнаружена более экономичная, хотя и менее упорядоченная структура, состоящая из повторяющейся группы из восьми различных форм ячеек. Эта более сложная модель использовалась как вдохновение для пенообразного дизайна плавательного стадиона во время Олимпийских игр 2008 года в Пекине.

Правила формирования клеток в пене также контролируют некоторые закономерности, наблюдаемые в живых клетках. Не только составной глаз мух показывает ту же гексагональную упаковку фасетов, что и плоский пузырь. Светочувствительные клетки внутри каждой из отдельных линз тоже соединяются в группы, которые выглядят так же, как мыльные пузыри.

Природе виднее

Растительный и животный мир изобилуют примерами многогранников в живой природе, как и неживой мир камней и минералов. С чисто эволюционной точки зрения, шестиугольная структура является лидером по оптимизации энергопотребления. Помимо очевидных преимуществ (экономия пространства), полиэдральные сетки обеспечивают большое количество граней, следовательно, увеличивается количество соседей, что благотворно сказывается на всей конструкции. Конечным результатом этого является то, что информация распространяется гораздо быстрее. Почему правильные шестиугольные и неправильные звездчатые многогранники в природе встречаются так часто? Наверное, так нужно. Природе виднее, она знает лучше.

Разные грани — разные формы

Многогранники — это особая сфера геометрии. Они бывают простые — к примеру кубики, которыми дети играют с раннего возраста, — а бывают очень и очень сложные. Простроение развертки многогранников для склеивания считается
достаточно сложной областью конструирования и творчества: нужно не только знать основы черчения, геометрические особенности пространства, но и иметь пространственное воображение, позволяющее оценить правильность решения еще на стадии проектирования. Но и одной фантазией не обойтись. Чтобы сделать развертки не достаточно просто представить, как в конце концов должна выглядеть работа. Нужно уметь правильно ее просчитать, сконструировать, а также грамотно начертить.

Слайды и текст этой презентации

Слайд 1Тела Архимеда
Работу выполнилУченик 10-11 класса Самохвалов Андрей

Слайд 2Определение Архимедово тело — выпуклый многогранник, имеющий в

граней два или более типов правильных многоугольников, примыкающих к

идентичным вершинам. Здесь «идентичные вершины» означают, что для любых двух вершин существует изометрия всего тела, переводящая одну вершину в другую.

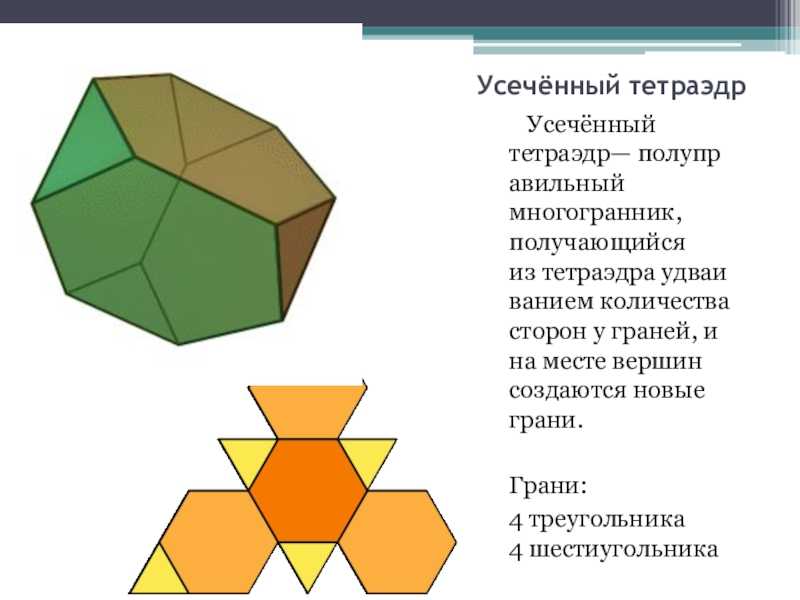
Слайд 3Усечённый тетраэдр Усечённый тетраэдр— полуправильный многогранник, получающийся из тетраэдра удваиванием количества сторон

у граней, и на месте вершин создаются новые грани.Грани:4 треугольника
4 шестиугольника

Слайд 4Кубоктаэдр Полуправильный многогранник, состоящий из 14 граней (8 правильных треугольников

и 6 квадратов). В кубоктаэдре 12 одинаковых вершин, в которых

сходятся два треугольника и два квадрата, а также 24 одинаковых ребра, каждое из которых разделяет треугольник и квадрат.

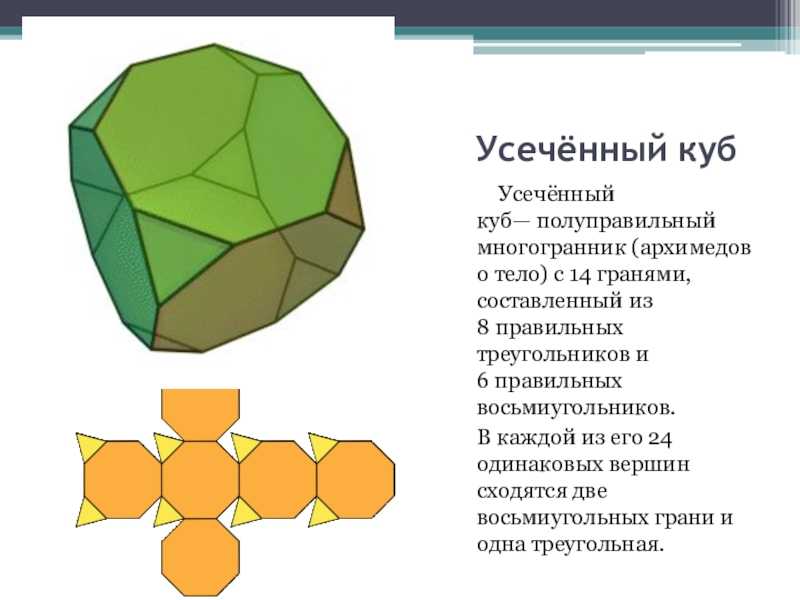
Слайд 5Усечённый куб Усечённый куб— полуправильный многогранник (архимедово тело) с 14 гранями,

одинаковых вершин сходятся две восьмиугольных грани и одна треугольная.

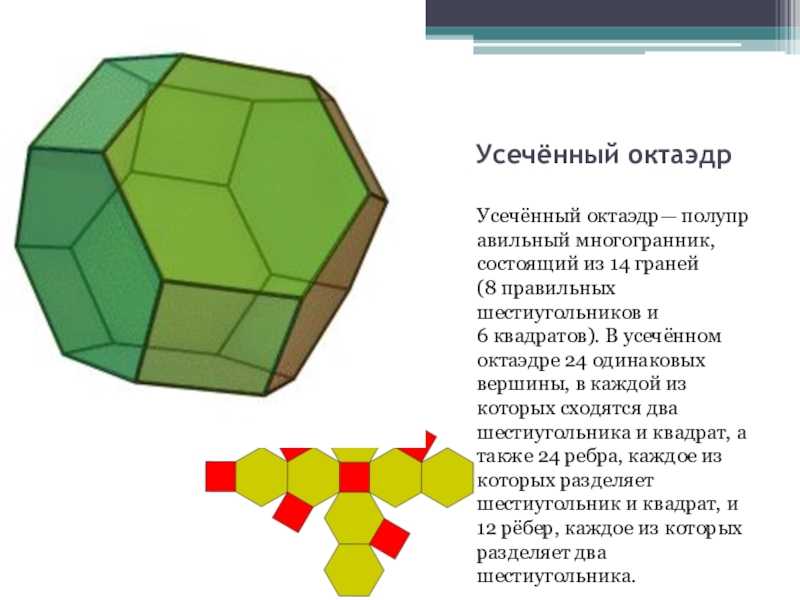
Слайд 6Усечённый октаэдр Усечённый октаэдр— полуправильный многогранник, состоящий из 14 граней (8 правильных

шестиугольников и 6 квадратов). В усечённом октаэдре 24 одинаковых вершины, в каждой

из которых сходятся два шестиугольника и квадрат, а также 24 ребра, каждое из которых разделяет шестиугольник и квадрат, и 12 рёбер, каждое из которых разделяет два шестиугольника.

Слайд 7Ромбокубооктаэдр Ромбокубооктаэдр или ромбокубоктаэдр— полуправильный многогранник, гранями которого являются 18 квадратов и 8 треугольников.

Слайд 8Усечённый кубооктаэдр Усечённый кубооктаэдр усечённый кубоктаэдр— полуправильный многогранник (архимедово тело) с 12 квадратными гранями,

8 гранями в виде правильного шестиугольника, 6 гранями в виде правильного восьмиугольника,

48 вершинами и 72 рёбрами. Поскольку каждая из граней многогранника имеет центральную симметрию (что эквивалентно повороту на 180°), усечённый кубооктаэдр является зоноэдром.

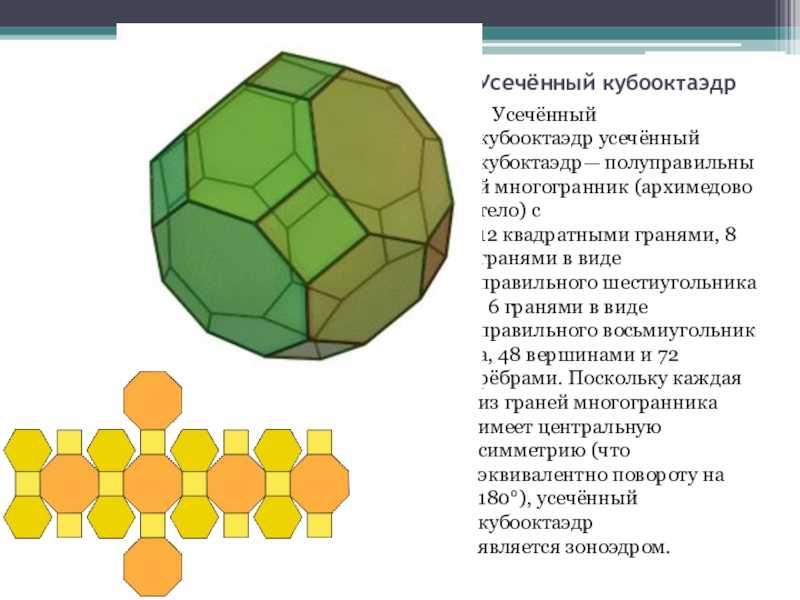
Слайд 9Плосконосый куб  Полуправильный многогранник (архимедово тело) с 38 гранями, составленный

из 6 квадратов и 32 правильных треугольников. В каждой из его 24 одинаковых

вершин сходятся одна квадратная грань и четыре треугольных. Треугольные грани делятся на две группы: 8 из них окружены только другими треугольными, остальные 24 — квадратной и двумя треугольными.Имеет 60 рёбер равной длины.

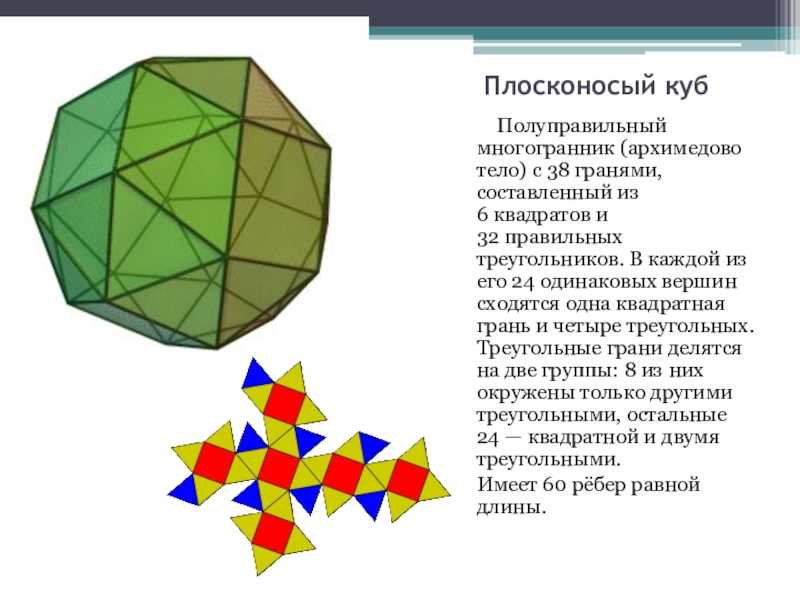
Слайд 10Икосододекаэдр Полуправильный многогранник, состоящий из 32 граней (12 правильных пятиугольников и

20 правильных треугольников). В икосододекаэдре 30 одинаковых вершин, в которых сходятся

два треугольника и два пятиугольника, а также 60 одинаковых рёбер, каждое из которых разделяет треугольник и пятиугольник. 

Слайд 11Усечённый додекаэдр  Усечённый додекаэдр — полуправильный многогранник (архимедово тело) с 32 гранями,

составленный из 20 правильных треугольников и 12 правильных десятиугольников В каждой из его

60 одинаковых вершин сходятся две десятиугольных грани и одна треугольная.

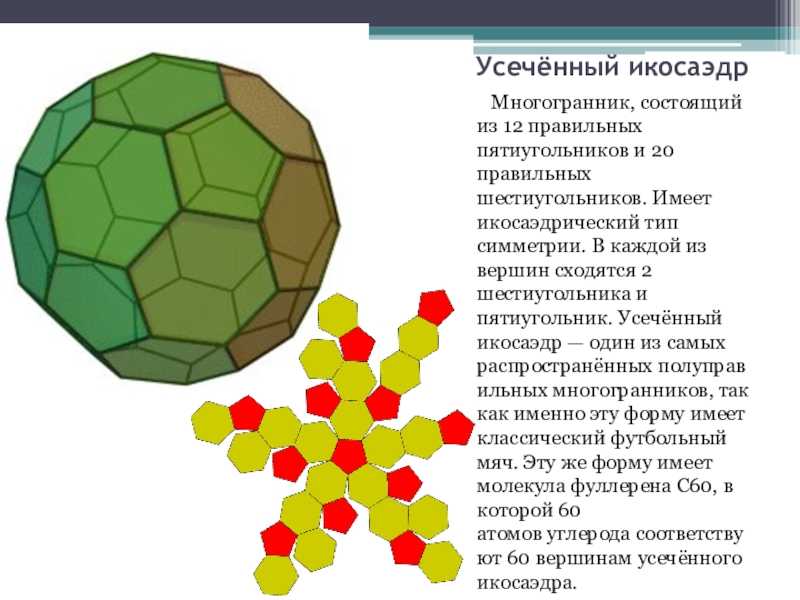
Слайд 12Усечённый икосаэдр Многогранник, состоящий из 12 правильных пятиугольников и 20

правильных шестиугольников. Имеет икосаэдрический тип симметрии. В каждой из вершин

сходятся 2 шестиугольника и пятиугольник. Усечённый икосаэдр — один из самых распространённых полуправильных многогранников, так как именно эту форму имеет классический футбольный мяч. Эту же форму имеет молекула фуллерена C60, в которой 60 атомов углерода соответствуют 60 вершинам усечённого икосаэдра.

Слайд 13Ромбоикосододекаэдр Полуправильный многогранник, состоящий из 12 правильных пятиугольников, 30

квадратов и 20 треугольников. Имеет икосаэдрический тип симметрии. В каждой

из вершин сходятся треугольник, пятиугольник и 2 квадрата.

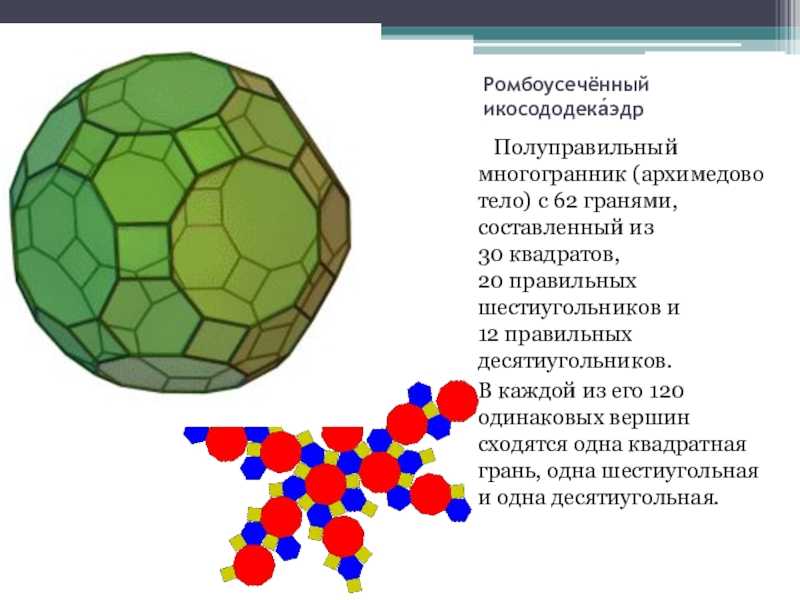
Слайд 14Ромбоусечённый икосододека́эдр Полуправильный многогранник (архимедово тело) с 62 гранями, составленный

одинаковых вершин сходятся одна квадратная грань, одна шестиугольная и одна десятиугольная. 

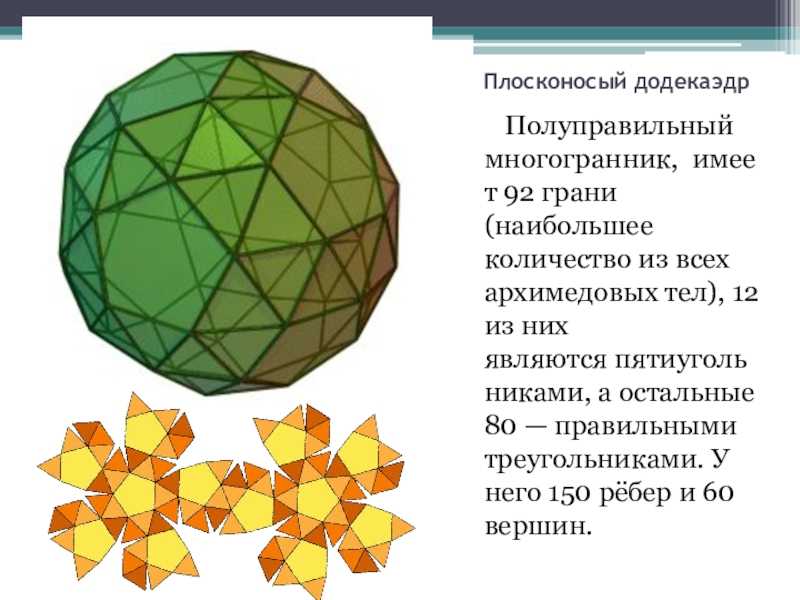
Слайд 15Плосконосый додекаэдр Полуправильный многогранник,  имеет 92 грани (наибольшее количество

из всех архимедовых тел), 12 из них являются пятиугольниками, а остальные

80 — правильными треугольниками. У него 150 рёбер и 60 вершин.

Красивая геометрия

Украшать интерьер дома, создавая своими руками необычные, стильные вещи, — это увлекательное творчество. Смастерить самостоятельно из плотной бумаги различные многогранники — значит создать уникальные вещи, которые могут стать просто занятием на день или два, а могут превратиться в дизайнерские интерьерные украшения. К тому же с развитием техники, способной к пространственному моделированию всевозможных вещей, стало возможным создание стильных и современных 3D-моделей. Есть мастера, которые при помощи простроения разверток по законам геометрии делают из бумаги макеты животных и различных предметов. Но это достаточно сложное математическое и чертежное творчество. Начать работать в подобной технике поможет

Примеры многогранников в природе

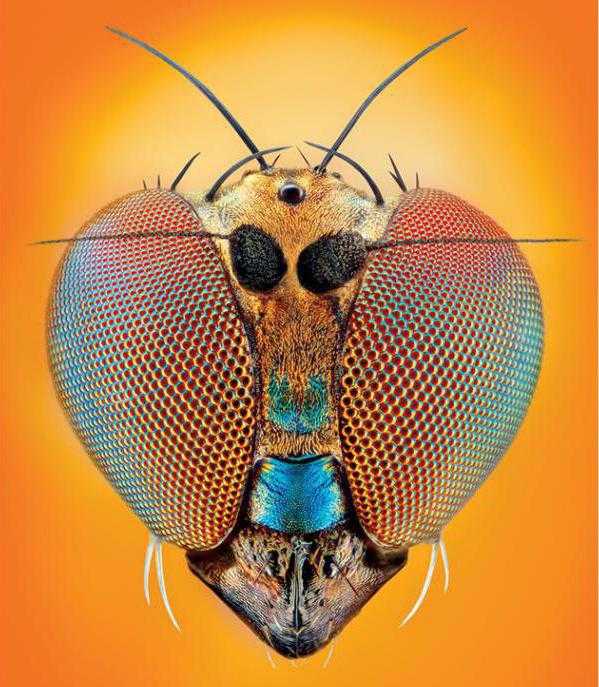
Составные глаза некоторых насекомых упакованы в гексагональ, где каждая грань – это линза, соединенная с длинной тонкой клеткой сетчатки. Структуры, которые образуются кластерами биологических клеток, часто имеют формы, управляемые по тем же правилам, что и пузырьки в мыльном растворе. Микроскопическая структура грани глаза – один из лучших примеров. Каждый фасет содержит кластер из четырех светочувствительных клеток, которые имеют ту же форму, что и кластер из четырех обычных пузырьков.

Что определяет эти правила мыльных пленок и формы пузырьков? Природа еще больше обеспокоена экономией, чем пчелы. Пузырьки и мыльные пленки сделаны из воды (с добавлением мыла), и поверхностное натяжение тянет поверхность жидкости таким образом, чтобы придать ей как можно меньшую площадь. Вот почему капли являются сферическими (более или менее), когда они падают: сфера имеет меньшую площадь поверхности, чем любая другая форма с тем же объемом. На восковом листе капли воды втягиваются в маленькие бусины по той же причине.

Это поверхностное натяжение объясняет модели пузырьковых плотов и пенопластов. Пена будет искать структуру, которая имеет самое низкое общее поверхностное натяжение, что обеспечит наименьшую площадь стенки. Хотя геометрия мыльных пленок продиктована взаимодействием механических сил, она не говорит нам, какова будет форма пены. Типичная пена содержит многогранные ячейки разных форм и размеров. Если присмотреться внимательнее, то правильные многогранники в природе – не такие уж правильные. Их края редко бывают идеально прямыми.

Виды правильных многоугольников

Какое минимальное количество сторон может иметь правильный многоугольник? У одной линии не может быть много сторон. Две стороны также не могут встретиться и сформировать закрытую форму. А три стороны могут – так получится треугольник. И поскольку мы говорим о правильных многоугольниках, где все стороны и углы равны, мы имеем в виду равносторонний треугольник.

Если добавить еще одну сторону, получится квадрат. Может ли прямоугольник, где стороны не равны, являться правильным многоугольником? Нет, эта фигура будет называться прямоугольником. Если добавить пятую сторону, то получится пятиугольник. Соответственно, есть и шестиугольники, семиугольники, восьмиугольники и так до бесконечности.

Кусудама из правильных пятиугольников

Схема сборки додекаэдра-оригами из пентагонов – равносторонних пятиугольников, разработана американским дизайнером Дэвидом Брилом. Для модулей он использует 12 листов формата А6, то есть 10,5х14,8 см.

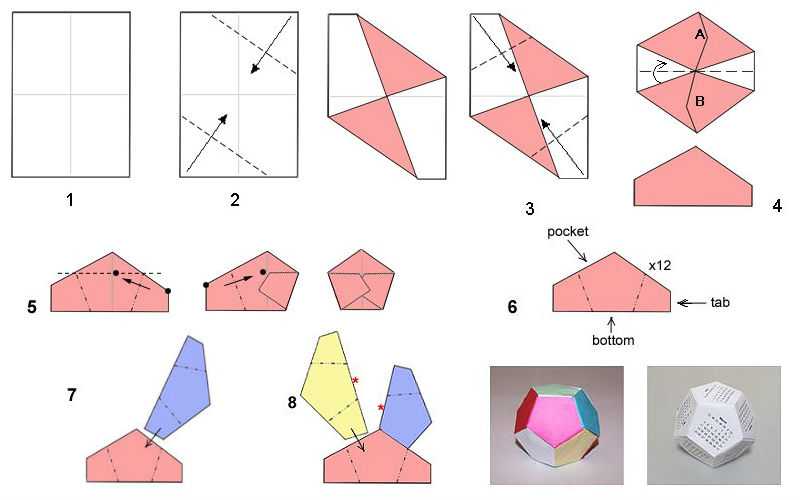
Пошаговая инструкция:

1. Исходный прямоугольник складываем пополам в продольном и поперечном направлении, намечая серединные оси.
2. Правый верхний и левый нижний угол сгибаем к центру. Получаем своего рода полуконверт.
3. Аналогично складываем противоположные углы.
4. Пятиугольную заготовку, «закрываем» сверху вниз «долиной».
5. Верхний угол опускаем вниз и возвращаем обратно. На месте пересечения получившейся линии с вертикальной осью фигуры, образуется точка. К ней поочерёдно сгибаем внешние углы.
6. Модуль-пентагон готов. Последние два сгиба раскрываем – это будут детали крепления элементов между собой.
7. Боковые «ушки» одной детали вставляем в «карманы» другой. Места соединения для надёжности фиксируем клеем.
8. Продолжаем сборку, пока не используем все 12 модулей.

Из подобных додекаэдров часто делают настольные календари. На каждой грани как раз размещается по месяцу. Соответствующие распечатки с числами и днями недели, можно скачать из интернета и наклеить на стенки модели. Получится не только красиво, но и практично.

Многогранники в природе и жизни человека

В то время как пятиугольными узорами изобилуют многие живые формы, минеральный мир предпочитает двойную, тройную, четырехкратную и шестикратную симметрию. Шестиугольник представляет собой плотную форму, которая обеспечивает максимальную структурную эффективность. Он очень распространен в области молекул и кристаллов, в которых пятиугольные формы почти не встречаются. Стероиды, холестерин, бензол, витамины С и D, аспирин, сахар, графит – это все проявления шестикратной симметрии. Где в природе встречаются правильные многогранники? Самая известная гексагональная архитектура создается пчелами, осами и шершнями.

Шесть молекул воды формируют ядро ​​каждого кристалла снега. Так получается снежинка. Грани глазка мухи образуют плотно упакованное шестиугольное расположение. Какие еще есть правильные многогранники в природе? Это кристаллы воды и алмаза, базальтовые колонны, эпителиальные клетки в глазу, некоторые растительные клетки и многое другое. Таким образом, многогранники, созданные природой, как живой, так и неживой, присутствуют в жизни человека в огромном количестве и многообразии.

Построение чертежа

Развертка пирамиды усеченной выполняется в несколько этапов. Боковой гранью усеченной пирамиды является трапеция, а основаниями – подобные многогранники. Допустим, что это квадраты. На листе бумаги выполняем чертеж трапеции с заданными размерами. Боковые стороны полученной фигуры продлеваем до пересечения. В результате получаем равнобедренный треугольник. Его сторону измеряем циркулем. На отдельном листе бумаги строим окружность, радиусом которой будет измеренное расстояние.

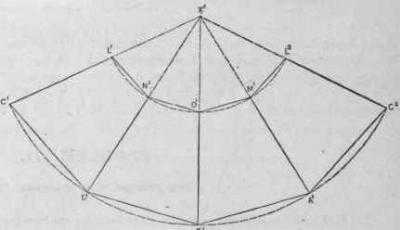
Следующий этап – это построение боковых ребер, которые имеет усеченная пирамида. Развертка выполняется внутри нарисованной окружности. Циркулем измеряют нижнее основание трапеции. На окружности отмечаем пять точек, которые соединяют линии с ее центром. Получаем четыре равнобедренных треугольника. Циркулем измеряем сторону трапеции, нарисованной на отдельном листе. Данное расстояние откладываем на каждой стороне нарисованных треугольников. Полученные точки соединяем. Боковые грани трапеции готовы. Остается только нарисовать верхнее и нижнее основания пирамиды. В данном случае это подобные многогранники – квадраты. К верхнему и нижнему основаниям первой трапеции дорисовываем квадраты. На чертеже изображены все части, которые имеет пирамида. Развертка практически готова. Остается только дорисовать соединительные клапаны на сторонах меньшего квадрата и одной из граней трапеций.

17

Многие формы звездчатых многогранников подсказывает сама природа. Снежинки — это звездчатые многогранники. С древности люди пытались описать все возможные типы снежинок, составляли специальные атласы. Сейчас известно несколько тысяч различных типов снежинок.

18

Оригами в нашей школе.

Мы создаём красоту своими руками.

19

20

Заключение.

Мы достигли цели. Выполнили все поставленные задачи.

«Наглядное понимание играет первенствующую роль в геометрии, и притом не только как обладающеебольшей доказательной силой при исследовании, но и для понимания и оценки результатов исследования». (Д.Гильберт, 1932г.)

Эти слова как нельзя лучше подводят итог тому, что мы делали:

Узнали больше о применении многогранников в жизни, сделали вывод, о том, что многогранные формы окружают нас в повседневной жизни повсюду: спичечный коробок, книга, комната, молочные пакеты в форме тетраэдра или параллелепипеда, здания. Почти все сооружения, возведённые человеком, от древнеегипетских пирамид до современных небоскрёбов, имеют форму многогранников. Изготовили модели многогранников своими руками.

Проверили теорему Аполлония Пергского.

Показали красоту и истинность математики.

Сделали следующие выводы: 1. проблема исследования многогранников была насущной всегда.Философы-математики в попытке описать и объяснить устройство Вселенной и природу пространства обращались к понятию многогранников.Таким образом, математическое понятие «многогранники» становится своего рода философской категорией. Эта тема актуальна всегда. 2. Современные формулы для вычисления объёмов сложных многогранников дают, весьма, приближённое значение. Если нужно более точное значение, то вычислять его нужно по закону Архимеда. Всякая научная гипотеза, даже неверная, способствует в конечном итоге общему научному прогрессу.

«Когда мы стремимся искать неведомое нам, то становимся лучше, мужественнее и деятельнее тех, кто полагает, будто неизвестное нельзя найти и незачем искать».

Эта мысль Платона должна сопровождать вас на всем жизненном пути.

21

Использованные материалы.

1. Интернет – ресурсы.

2. Математическая энциклопедия. Издательство «Советская энциклопедия» Москва 1977 г.

3. Учебник Л. С. Атанасяна «Геометрия 10 – 11»

4. Глейзер Г.И. «История математики в школе». IX-X классы. Пособие для учителей. – М.: Просвещение, 1983

5. Веннинджер М. «Модели многогранников». Перевод с англ. В.В.Фирсова. под ред. И послесл. И.М.Яглома., М.: Мир, 1974

22

23

Ажурная модель

Существует несколько типов оригами-додекаэдров, но сделать эту прозрачную конструкцию из бумажных модулей проще всего. Хорошее задание для детей, желающих познакомиться с азами пространственной геометрии и взрослых, ищущих эффективное средство для снятия стресса. Желательно использовать для игрушки бумагу ками с рисунком, она придаст особый шарм и колорит.

Пошаговая инструкция:

1. Для создания кусудамы понадобится 30 одинаковых модулей. Их складывают из прямоугольников, имеющих соотношение сторон 3:4. Например, размером 6х8 см, 9х12 см и так далее. Можно брать как одно-, так и двухсторонние листы.
2. Складываем каждый прямоугольник пополам вдоль длинной стороны. После чего делаем Z-образный сгиб.
3. Располагаем получившуюся полоску длинной стороной к себе. Загибаем правый нижний угол вверх. Переворачиваем заготовку на 180°. И повторяем действие для правого нижнего угла (другого).
4. Складываем фигуру по диагонали, как показано на рис 4.
5. Модули для додекаэдра-кусудамы готовы.

Остаётся соединить их в пространственную композицию. Для этого короткую часть одного модуля вставляем к «карман» длинной части другого. И располагаем так, чтобы внутренние углы и грани обоих элементов совпали.

Аналогичный образом добавляем третий модуль, соединяя его с предыдущими двумя и формируя устойчивый конструктивный узел.

Продолжаем крепить детали друг к другу, пока не получится объёмная фигура.

За счёт необычной бумаги с принтом, получается стильный предмет декора. Чтобы кусудама не распадалась, лучше соединить узловые элементы с помощью клея.

Подробная сборка ажурного додекаэдра представлена и в видео-МК:

Определение параметров

Прежде всего определим, какой будет пирамида. Развертка данной фигуры является основой для изготовления объемной фигуры. Выполнение работы потребует предельной точности. При неправильном чертеже геометрическую фигуру собрать будет невозможно. Допустим, необходимо изготовить макет правильной треугольной пирамиды.

Любое геометрическое тело обладает определенными свойствами. Данная фигура имеет основанием правильный многоугольник, а ее вершина спроецирована в его центр. В качестве основания выбран равносторонний треугольник. Данное условие определяет название. Боковые ребра у пирамиды – это треугольники, количество которых зависит от выбранного для основания многогранника. В данном случае их будет три

Также важно знать размеры всех составных частей, из которых будет составлена пирамида. Развертки из бумаги выполняются в соответствии с учетом всех данных геометрической фигуры

Параметры будущей модели оговариваются заранее. От этих данных зависит выбор используемого материала.

Почему шестиугольники? Это простая геометрия

Если вы хотите собрать вместе одинаковые по форме и размеру ячейки, чтобы они заполнили всю плоскость, то будут работать только три регулярные фигуры (со всеми сторонами и с одинаковыми углами): равносторонние треугольники, квадраты и шестиугольники. Из них гексагональные ячейки требуют наименьшей общей длины стены по сравнению с треугольниками или квадратами одной и той же области.

Поэтому выбор пчелами шестиугольников имеет смысл. Еще в XVIII веке ученый Чарльз Дарвин заявил, что гексагональные соты «абсолютно идеальны в экономии труда и воска». Он считал, что естественный отбор наделял пчел инстинктами для создания этих восковых камер, которые имели преимущество, предусматривающее меньшие затраты энергии и времени, чем при создании других форм.

Пирамида – развертка. Развертка пирамиды для склеивания. Развертки из бумаги

Прямоугольник, квадрат, треугольник, трапеция и другие – геометрические фигуры из раздела точной науки. Пирамида – это многогранник. Основанием этой фигуры является многоугольник, а боковыми гранями треугольники, имеющие общую вершину, или трапеции. Для полного представления и изучения любого геометрического объекта изготавливают макеты. Используют самый разнообразный материал, из которого выполняется пирамида. Поверхность многогранной фигуры, развернутая на плоскости, называется ее разверткой. Создать макет поможет метод преобразования плоских предметов в объемные многогранники и определенные знания из геометрии. Развертки из бумаги или картона изготовить непросто. Потребуется умение выполнять чертежи по заданным размерам.