Стереометрия

Понятия стереометрии

Стереометрия представляет собой раздел в науке геометрии, нацеленный на исследование свойств, которые характерны для фигур, расположенных в пространстве.

Ознакомимся с основными понятиями и теориями данной области научных знаний. Предмет изучает разнообразные фигуры. Рассмотрим основные из них, с которыми часто можно столкнуться в процессе решения задач и в продолжении обучения темам из курса стереометрии повышенного уровня сложности.

Многогранником называют некое тело в геометрии, границы которого сформированы с помощью определенного количества плоских многоугольников, какая-либо пара из которых обладает единой стороной и не расположена в общей плоскости.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Многогранники имеют следующие составные элементы:

• грани в виде многоугольников, которые упоминаются в определении;
• стороны, то есть ребра рассматриваемого многогранника;
• вершины, которые совпадают с вершинами данного многогранника.

Примеры многогранников:

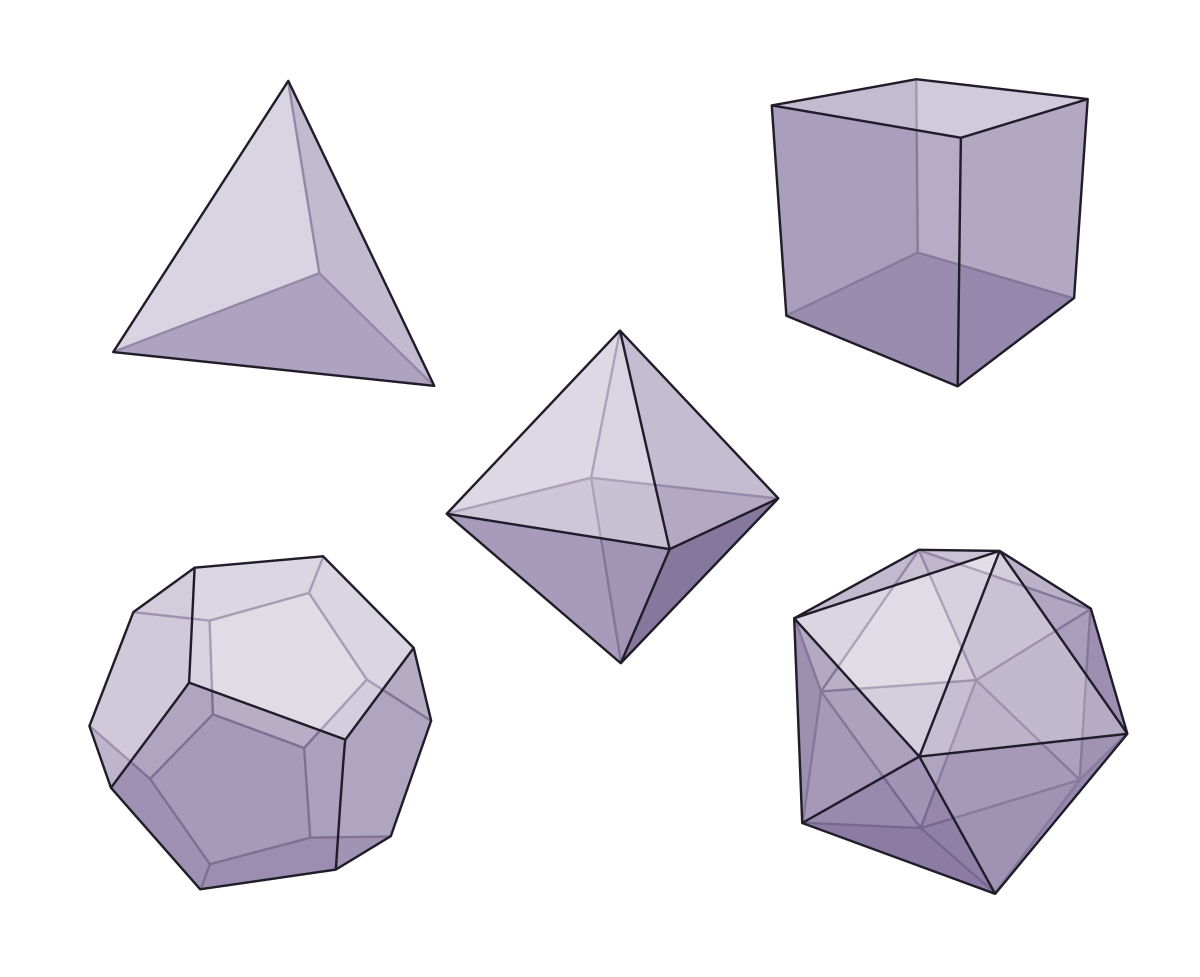
Поверхность многогранника представляет собой фигуру, которая сформирована с помощью каждой из граней этого многогранника. При этом площади граней рассматриваемой фигуры в сумме дают площадь полной поверхности.

Кубом называют такой многогранник, который состоит из 6 граней в виде идентичных квадратов.

Куб обладает следующими компонентами:

• стороны являются ребрами фигуры;
• вершинами обозначают вершины рассматриваемого куба.

Пример куба:

Параллелепипед является одним из видов многогранника, обладает 6 гранями в форме параллелограмма.

Перечислим компоненты параллелепипеда:

• стороны, то есть ребра;
• вершины, то есть вершины этих сторон.

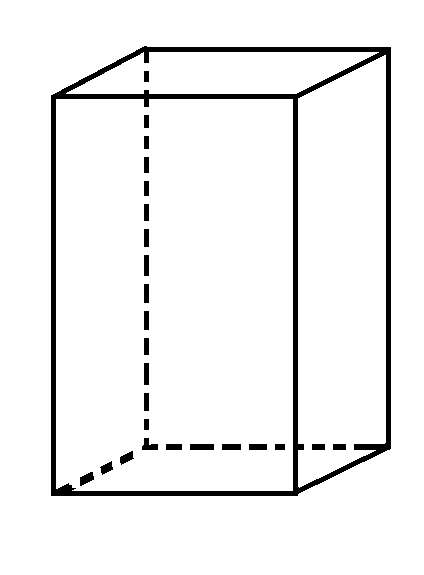
В прямом параллелепипеде грани с боков являются прямоугольниками. Прямоугольным называют такой параллелепипед, у которого каждая из граней обладает формой прямоугольника.

Призма представляет собой разновидность многогранника с парой граней в виде идентичных многоугольников и остальными гранями, изображенными, как параллелограммы.

Введем определения для элементов призмы:

• основания, то есть многоугольники, которые равны между собой;
• боковые грани в виде параллелограммов.

Призма может быть следующих типов:

• прямая, с боковыми гранями в форме прямоугольников;
• правильная, в виде прямой призмы, в основаниях которой расположены правильные многоугольники.

Пример призмы:

Пирамидой называют многогранник с одной гранью в виде некого многоугольника и остальными гранями, изображенными в форме треугольников, обладающих единой вершиной.

В состав пирамиды включены такие элементы, как:

• основание, то есть многоугольник;
• боковые грани треугольной формы;
• вершина, совпадает с единой вершиной треугольников.

Условия идентификации правильной пирамиды:

• в основании расположен правильный многоугольник;
• равенство боковых ребер.

Пример пирамиды:

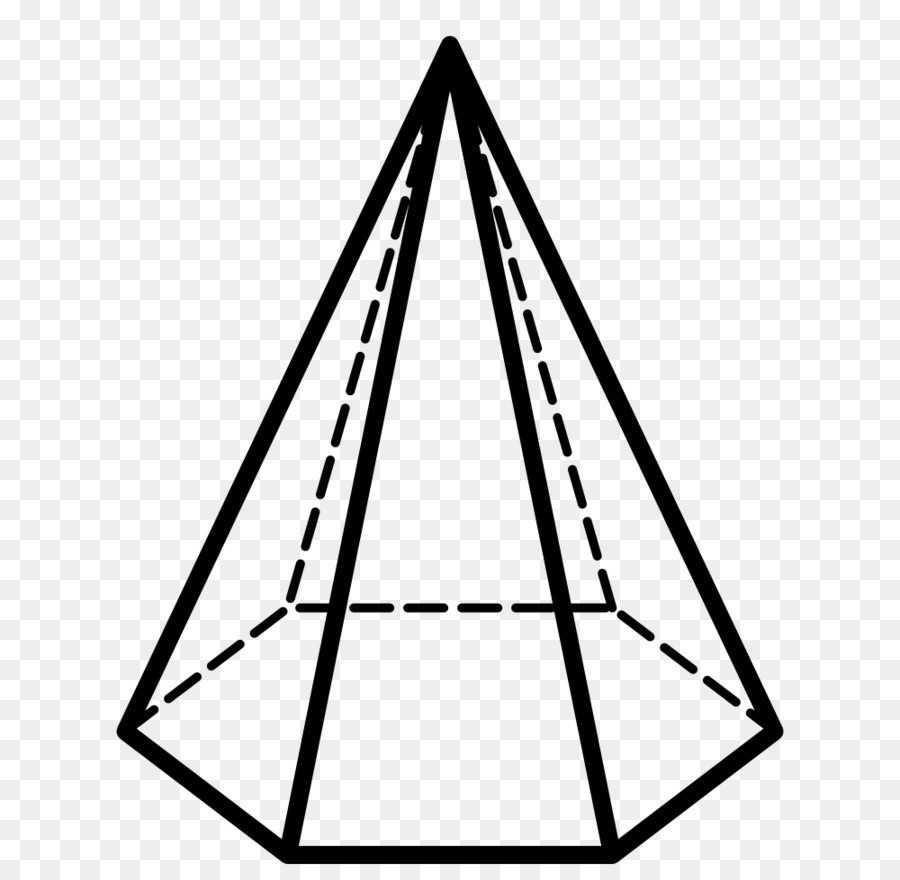
Тетраэдр представляет собой треугольную пирамиду с гранями, изображенными в форме правильных треугольников, которые равны друг другу.

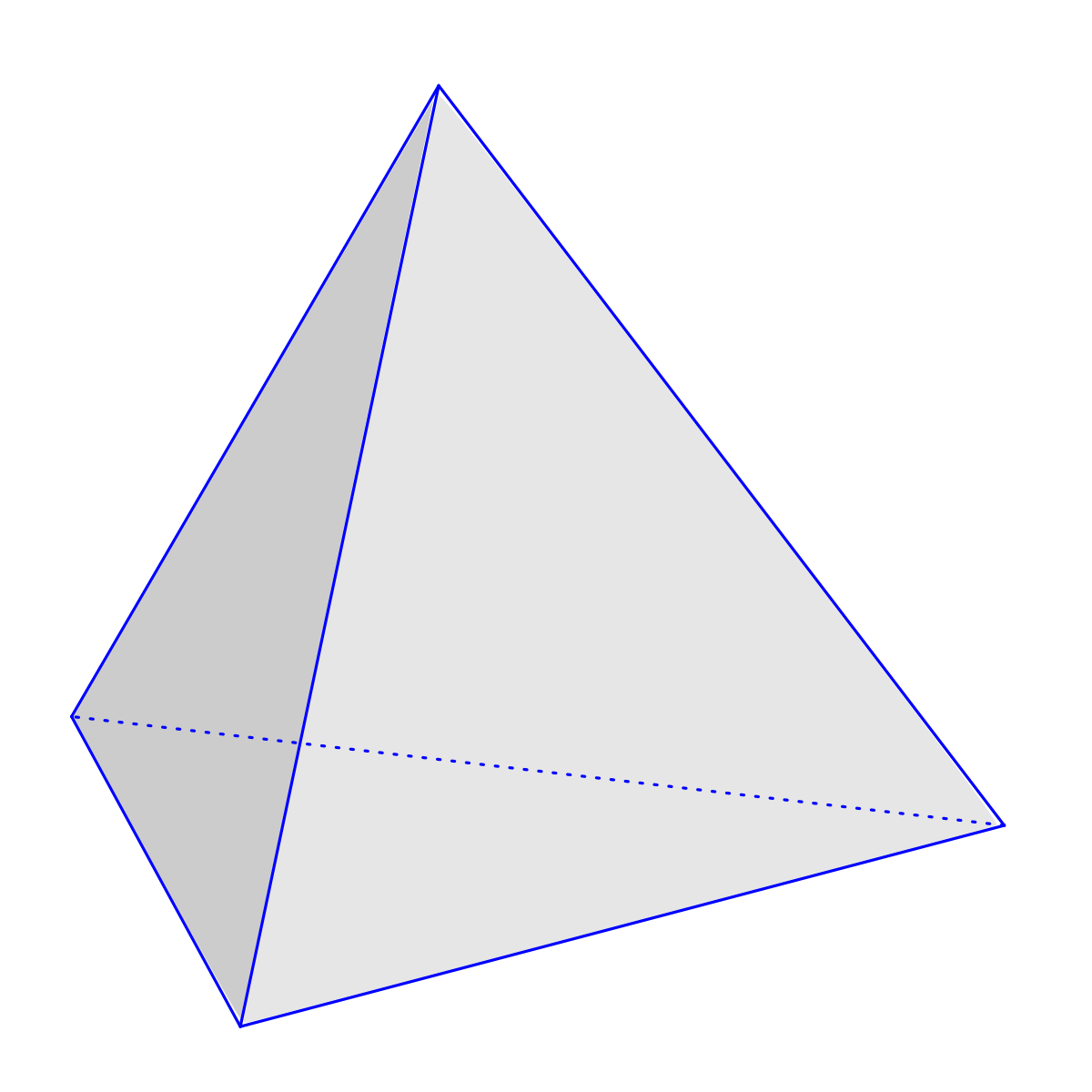
Решение задачи 7

а) Верно ли, что любые 3 точки лежат в одной плоскости?

Рис. 12.

Через 3 точки, если они не лежат на одной прямой, можно провести плоскость, и притом только одну, в силу аксиомы А1.

Ответ: да.

б) Верно ли, что любые 4 точки лежат в одной плоскости?

Рис. 13.

Через 3 точки можно провести плоскость, а 4 точку можно взять и в этой плоскости, и вне нее. Значит, ответ отрицательный.

Ответ: нет.

в) Верно ли, что любые 4 точки не лежат в одной плоскости?

Рис. 14.

Приведем конкретный пример. Рассмотрим плоский четырехугольник, в плоскости этого четырехугольника лежат 4 точки. Итак, ответ на этот вопрос отрицательный, нет.

Ответ: нет.

г) Верно ли, что через любые 3 точки проходит плоскость, и притом только одна?

Рис. 15.

Приведем пример. Возьмем 3 точки А, В, С, лежащие на одной прямой. Через них можно провести плоскость , плоскость . Через 3 точки, лежащие на одной прямой, можно провести бесконечное количество плоскостей.

Ответ: нет

Решение задачи 3

Две смежные вершины и точка пересечения диагоналей параллелограмма лежат в плоскости . Лежат ли 2 другие вершины параллелограмма в плоскости ?

Решение:

Рис. 8.

Пусть дан параллелограмм АВСD. Известно: точка А, точка В, точка О – точка пересечения диагоналей, лежат в плоскости . Нужно проверить, лежат ли вершины С и D лежат также в этой плоскости.

Через три точки А, В и О проходит плоскость, и притом только одна. Это плоскость . Прямая АО целиком лежит в этой плоскости, потому что две ее точки лежат в плоскости. Значит, точка С, точка прямой АО, лежит в плоскости .

Аналогично, прямая ВО целиком лежит в плоскости , значит, точка D этой прямой тоже лежит в плоскости .

Ответ: Да, вершины С и D лежат в плоскости .

Аксиомы стереометрии

Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Аксиома 2. Если две точки прямой лежат в плоскости, то все точки данной прямой лежат в этой плоскости. В этом случае говорят, что прямая лежит в плоскости или что плоскость проходит через прямую.

Из аксиомы 2 следует, что прямая, не лежащая в плоскости, не может иметь с плоскостью более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что прямая пересекает плоскость.

Аксиома 3.  Если две плоскости имеют общую точку, то они имеют общую прямую, которой принадлежат все общие точки этих плоскостей. В этом случае говорят, что плоскости пересекаются по прямой.

Аксиома 4. В любой плоскости пространства выполняются все аксиомы планиметрии. Таким образом, в любой плоскости пространства можно использовать все доказанные теоремы и формулы из планиметрии.

Решение задачи 1

Задача 1.

Даны две прямые, которые пересекаются в точке М. Докажите, что все прямые, не проходящие через точку М и пересекающие данные прямые, лежат в одной плоскости (Рис. 6.).

Рис. 6.

Решение:

Нам даны две прямые а и b, которые пересекаются в некоторой точке М. Возьмем произвольную прямую с, которая не проходит через точку М, но пересекает исходные прямые а и b в точках А, В, соответственно.

Через две пересекающиеся прямые проходит плоскость, и притом только одна, согласно 2 теореме. Значит через пересекающиеся прямые а и b проходит единственная плоскость, обозначим ее .

Две разные точки А и В  прямой с принадлежат плоскости . А из того, что две точки прямой принадлежат плоскости, вытекает, что все точки прямой принадлежат плоскости, т.е. вся прямая лежит в плоскости. Значит, прямая с принадлежит этой плоскости.

Таким образом, мы доказали, что все прямые, пересекающие А и В, но не проходящие через М, лежат в одной плоскости. 

Зачем нужны аксиомы

Математику изучают в школе не просто так. Большинство забудет все эти уравнения, графики и аксиомы сразу после ЕГЭ в 11 классе.

Задача школьного курса математики состоит в том, чтобы вы освоили научное мышление. Чтобы поняли, как работает наука, как проверяются гипотезы и как доказываются утверждения. И чем отличается частный жизненный опыт от универсальных знаний.

Подробнее о том, чем научное знание отличается от обывательского (и почему это так важно), смотрите в цикле уроков «Как работает наука». Однако в любой науке есть «стартовый» набор утверждений, которые принимаются без доказательств

Эти утверждения и есть аксиомы. Обычно они наглядны и «очевидны» даже для начинающих

Однако в любой науке есть «стартовый» набор утверждений, которые принимаются без доказательств. Эти утверждения и есть аксиомы. Обычно они наглядны и «очевидны» даже для начинающих.

Простой пример «очевидного» утверждения. Биссектриса треугольника пересекает его противоположную сторону:

Спасибо, Капитан Очевидность. Однако напрямую этот факт ниоткуда не следует. Его можно доказать, например, через тригонометрию или координаты. Но потребовать такое доказательство — отличная задача-гроб на устном экзамене в университет.

Создание системы аксиом — долгий и кропотливый процесс. Классическая евклидова геометрия, которую изучают в школе, основана на аксиомах, которые формировались более двух тысяч лет. Основоположник этих аксиом — Евклид — жил в III веке до н.д. Собственно, потому геометрия и называется евклидовой.

Зато когда система аксиом построена, все последующие теоремы выводятся из неё через логические рассуждения. Без привлечения наглядных иллюстраций и «очевидных соображений». Вот здесь и начинается настоящая наука.:)

Решение задачи 4

Дана прямая и точка, не лежащая на этой прямой. Докажите, что все прямые, проходящие через данную точку и пересекающие данную прямую, лежат в одной плоскости.

Рис. 9.

Решение:

Нам дана прямая а и некоторая точка М, которая не лежит на этой прямой. Нам нужно доказать, что все прямые, которые проходят через точку М и пересекают прямую а лежат в некоторой единственной плоскости.

Мы знаем, что в силу 1 теоремы через прямую а и точку М проходит единственная плоскость, обозначим через . Теперь возьмем произвольную прямую, которая проходит через точку М и пересекает прямую а, например, в точке А. Прямая МА лежит в плоскости , потому что две ее точки М и А, лежат в этой плоскости. Значит, и вся прямая лежит в плоскости , в силу 2 аксиомы.

Итак, мы взяли произвольную прямую, которая удовлетворяет условиям задачи, и доказали, что она лежит в плоскости . Значит, все прямые, проходящие через точку М и пересекающие прямую а лежат в плоскости , что и требовалось доказать.

Решение задач

Слайды и текст этой презентации

Слайд 2Данная презентация посвящена аксиомам стереометрии и следствиям из них.Может быть

использована: в виде диагностики знаний обучающихся при завершении темы «Аксиомы

стереометрии и следствия из них»;при организации работы по готовому чертежу, что способствует развитию быстрого интуитивного логического мышления;для развития устной и письменной математической речи.

обучающихся: — при решении задач на готовом чертеже; — путём

проведения самостоятельной работы контролирующего характера

вершин треугольника?

Слайд 13 АДВСКМНазовите плоскости, в которых лежат точка К,

одна

грани куба.

Слайд 24Сколько граней проходит через:а) одну,б) две,в) три,г) четыре точки, выделенные

на рисунке куба?Сколько плоскостей можно провести через те же точки?

Определится ли при этом положение плоскости однозначно? Ответ обоснуйте.

Слайд 321.Какое из следующих утверждений верно?а) любые четыре точки лежат в

одной плоскости;б) любые три точки не лежат в одной плоскости;в)

любые четыре точки не лежат в одной плоскости;г) через любые три точки проходит плоскость;д) через любые три точки проходит плоскость, и притом только одна.Д

Слайд 332. Сколько общих точек могут иметь две различные плоскости?а) 2;

б) 3; в) несколько;

г) бесконечно много;д) бесконечно много или ни одной. Д

Слайд 343. Точки А, В, С лежат на одной прямой, точка

Д не лежит на ней. Через каждые три точки проведена

одна плоскость. Сколько различных плоскостей при этом получилось?а) 2; б) 3; в) 1; г) 4; д) бесконечно много. В

Слайд 354. Если три точки не лежат на одной прямой, то

положение плоскости в пространстве они:а) не определяют в любом случае;б)

определяют, но при дополнительных условиях;в) определяют в любом случае;г) ничего сказать нельзя;д) другой ответ. В

Слайд 365. Выберите верное утверждение:а) если одна точка прямой лежит в

плоскости, то все точки прямой лежат в этой плоскости;б) через

прямую и не лежащую на ней точку проходит плоскость, и притом только одна;в) через две пересекающиеся прямые плоскость провести нельзя;г) любые две плоскости не имеют общих точек;д) если четыре точки не лежат в одной плоскости, то какие-нибудь три из них лежат на одной прямой. Б

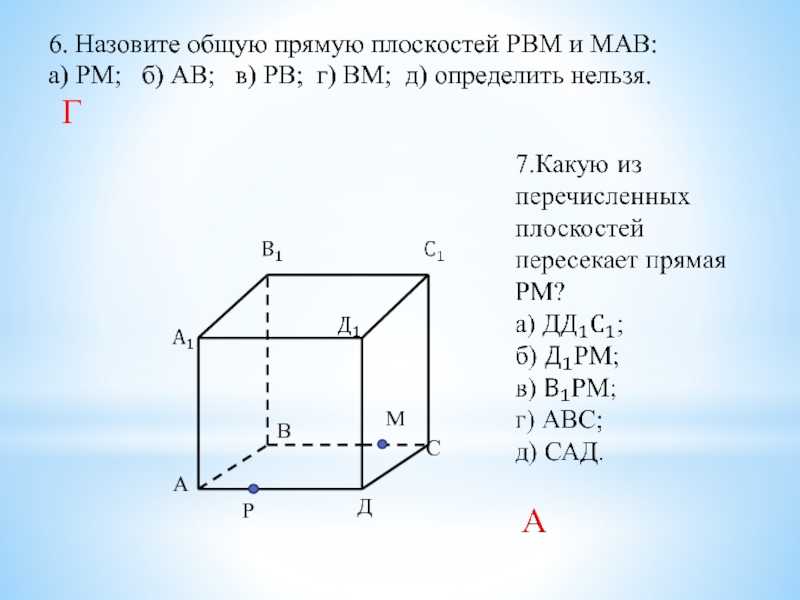
Слайд 376. Назовите общую прямую плоскостей РВМ и МАВ:а) РМ;

б) АВ; в) РВ; г) ВМ; д) определить нельзя.

Г

В

С

А

Д

Р

М

Слайд 388. Две плоскости пересекаются по прямой с. Точка М лежит

только в одной из плоскостей. Что можно сказать о взаимном

положении точки М и прямой с?а) никакого вывода нельзя сделать;б) на прямой с лежит точка М;в) через точку М прямая с не проходит;г) другой ответ. Г

Слайд 399. Прямые а и в пересекаются в точке М. Прямая

с, не проходящая через точку М, пересекает прямые а и

в. Что можно сказать о взаимном положении прямых а, в и с?а) все прямые лежат в разных плоскостях;б) прямые а и в лежат в одной плоскости, а прямая с в ней не лежит;в) все прямые лежат в одной плоскости;г) ничего сказать нельзя;д) прямая с совпадает с одной из прямых: или са, или св. В

Слайд 4010. Точки А, В, С не лежат на одной прямой.

МϵАВ, КϵАС, ХϵМК. Выберите верное утверждение:а) ХϵАВ, б)

ХϵАС, в) ХϵАВС;г) точки Х и М совпадают; д) точки Х, К совпадаютВ

Отметьте произвольно точки М, Н, К на рёбрах многогранника. Постройте сечение многогранника плоскостью (МНК).

Основные аксиомы стереометрии

Рассмотрим четыре основные аксиомы стереометрии. 

1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и при том только одна.
2. Если две точки прямой лежат в плоскости, то каждая точка данной прямой лежит в этой плоскости. В таком случае говорят, что прямая лежит в плоскости или, что плоскость проходит через прямую.
3. Если две плоскости имеют общую точку, то они имеют общую прямую, которой принадлежат все общие точки этих плоскостей. Тогда считается, что плоскости пересекаются по прямой.
4. В любой плоскости пространства выполняются все аксиомы планиметрии. То есть для любой плоскости пространства справедливы все доказанные теоремы и формулы из планиметрии.

Аксиома прямой и плоскости (основная)

Это интуитивно понятное утверждение, но его нельзя вывести из предыдущих аксиом.

Итак, есть прямая, две точки которой лежат на плоскости:

Следовательно, вся прямая лежит на этой плоскости:

Записывается это так: если точки $\color{red}{A}\in \alpha $ и $\color{red}{B}\in \alpha $, то прямая $l\in \alpha $. Хотя в некоторых учебниках с более строгим изложением предлагают писать $l\subset \alpha $, где знак $\subset $ означает «включение». При этом говорят, что прямая $l$ является подмножеством плоскости $\alpha $.

В этом уроке мы не будем давать строгие теоретико-множественные определения. Потому что сейчас наша цель — максимальная наглядность, а не научная красота. Кому интересно, см. учебник «Геометрия 10» Потоскуева и Звавича.

Вообще существует три варианта взаимного расположения прямой и плоскости в пространстве:

1. Прямая принадлежит плоскости — как раз этот вариант описывает аксиома.
2. Прямая параллельна плоскости, т.е. не имеет с ней общих точек.
3. Прямая пересекает плоскость, т.е. имеет с ней ровно в одну общую точку.

Простой пример: на столе, выполняющем роль плоскости $\alpha $, стоит кирпич $ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}$.

Прямая $\color{red}{AB}$ лежит в плоскости $\alpha $. Прямая $\color{red}{B{{B}_{1}}}$ пересекает эту плоскость в точке $\color{red}{B}$ (и тут удобна теоретико-множественная запись $\color{red}{B{{B}_{1}}}\cap \alpha =\color{red}{B}$). Наконец, прямая $\color{red}{{{A}_{1}}{{D}_{1}}}$ параллельна плоскости $\alpha $ (пишут $\color{red}{A{{A}_{1}}}\parallel \alpha $).

Аксиомы стереометрии и следствия из них

Упростить решение множества задач и изучение стереометрии позволяет знание основных положений и правил. К примеру, существуют аксиомы, которые не нуждаются в доказательстве. С их помощью достаточно просто выполнять построение классических и сложных фигур, производить разнообразные вычисления. Перечислим их.

Аксиома 1: Если 3 точки не принадлежат общей прямой, то через них допустимо построить плоскость в единственном экземпляре.

Аксиома 2: При нахождении 2 точек какой-то прямой в некой плоскости можно сделать вывод о расположении в этой же плоскости остальных точек рассматриваемой прямой.

Аксиома 3: В том случае, когда пара плоскостей обладает общей точкой, можно сделать вывод о наличии у таких плоскостей одной прямой, содержащей каждую из точек пересечения рассматриваемых плоскостей.

Аксиома 4: В какой-либо пространственной плоскости справедлива каждая из аксиом планиметрии.

При анализе перечисленных аксиом можно сформулировать некоторые закономерности. Такие утверждения называют следствиями. Перечислим их.

Следствие 1

Если имеется какая-то прямая и точка, ей не принадлежащая, то через данные элементы допустимо провести единственную плоскость.

Следствие 2

Если 2 прямые линии пересекаются между собой, то с их помощью допустимо построить единственную плоскость.

Следствие 3

В том случае, когда имеется пара прямых, расположенных параллельно относительно друг друга, через них допустимо провести единственную плоскость.

Следствие 4

Когда прямая не расположена на некоторой плоскости, данные элементы обладают максимум одной единой точкой.

Решение задачи 5

Верно ли утверждение:

а) если две точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости;

б) если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости?

Рис. 10.

Решение:

а) Пусть дана окружность и точки А, В, С. В случае если только две точки В и С принадлежат некоторой плоскости, то совсем необязательно, что и любая другая точка окружности лежит в этой плоскости. Поэтому, данное утверждение неверно. 

Ответ: нет.

б) Даны три точки окружности  А, В, и С. В силу аксиомы 1, через эти три различные точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. Назовем эту плоскость .

Теперь докажем, что любая точка М окружности лежит в плоскости . Соединим М с А, получим точку D. Вся прямая АD лежит в плоскости , потому что две ее точки А и D лежат в плоскости . Значит, и точка Мокружности лежит в плоскости . Значит, данное утверждение верно. 

Ответ: да.

Рекомендации по оцениванию работ

Задания тестов разделены на три уровня сложности: А, В, С.

Задания уровня А (базового) предполагают выбор правильного ответа из четырех предложенных.

Для заданий уровня В (повышенной сложности) требуется привести краткий ответ.

В заданиях уровня С (творческих заданиях) необходимо изложить обоснованное решение.

Тематический тест содержит три задания уровня А (каждое оценивается в 1 балл), два задания уровня В (каждое оценивается в 2 балла) и одно задание уровня С (3 балла).

На выполнение теста отводится 15–20 мин. Рекомендуем следующее соответствие количества баллов и оценки: 2–3 балла – «3», 4–5 баллов – «4», 6–10 баллов – «5».

Решение задачи 2

Три данные точки соединены попарно отрезками. Докажите, что все отрезки лежат в одной плоскости.

Решение:

Пусть нам даны три точки: А, В, и С. Нужно доказать, что отрезки АВ, ВС, СА лежат в одной плоскости (Рис. 7.).

Рис. 7.

Если точка С лежит на прямой АВ, то ответ очевиден. Предположим, что точка С не принадлежит прямой АВ. Тогда через три точки A, B, C, не лежащие на одной прямой, проходит плоскость, и притом только одна, в силу аксиомы 1. Обозначим эту плоскость 

Прямая АВ целиком лежит в плоскости , потому что две ее точки лежат в этой плоскости. Но, значит, и отрезок АВ лежит в плоскости .

Аналогично и с другими отрезками. Прямая ВС лежит в плоскости , потому что две ее точки В и С лежат в плоскости, значит, и отрезок ВС лежит в плоскости .

И аналогично, отрезок АС лежит в плоскости . Что и требовалось доказать. 

Что такое стереометрия

Определение

Стереометрия — раздел евклидовой геометрии, в котором изучаются свойства фигур в пространстве.

Если основными фигурами планиметрии являются точка и прямая, то в стереометрии к изучению добавляется плоскость.

Примеры стереометрических фигур:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

• шар;
• сфера;
• конус;
• цилиндр;
• призма и так далее.

Нередко основным способом решения задач в стереометрии является рассмотрение разнообразных плоскостей при выполнении планиметрических законов.

В стереометрии используются следующие обозначения: 

• прописные буквы A,B,C,D обозначают точки;
• строчные буквы обозначают прямые, например, AB = a; 
• плоскости, как правило, обозначаются такими буквами как \(\alpha,\;\beta,\;\gamma\) и подобными;
• принадлежность точек к прямой или точек и прямых к плоскости обозначается стандартно: \(A\;\in\;a\) или \(b\;\in\;\alpha.\)

Напоминание аксиом стереометрии и теорем, которые следуют из них

Аксиомы стереометрии и следствия из них устанавливают взаимоотношения между основными фигурами стереометрии: точкой, прямой и плоскостью.

Точка может лежать на прямой, может не лежать на прямой.

Прямая может принадлежать плоскости, может не принадлежать плоскости.

Плоскость может проходить через прямую, не проходить через нее, содержать точку, не содержать точку. 

Подобные задачи мы решали для пирамиды и для параллелепипеда. Теперь мы будем решать задачи в общем виде.

Вспомним для этого сначала аксиомы и теоремы-следствия.

Аксиома 1 (А1)

Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. 

Иллюстрация аксиомы А1.

Рис. 1.

Рассмотрим три точки: А, В, С, причем точка С не принадлежит прямой АВ: (Рис. 1.). Тогда через три точки А, В, С, не лежащие на одной прямой, проходит плоскость , и притом только одна. Плоскость  можно также обозначить через три точки АВС.

Аксиома 2 (А2)

Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. 

Иллюстрация аксиомы А2. (Рис. 2.)

Рис. 2.

Аксиома 3 (А3).

Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей (плоскости пересекаются по прямой).

Иллюстрация аксиомы А3. (Рис. 3.)

Рис. 3.

Повторение теорем, которые следуют из аксиом стереометрии.

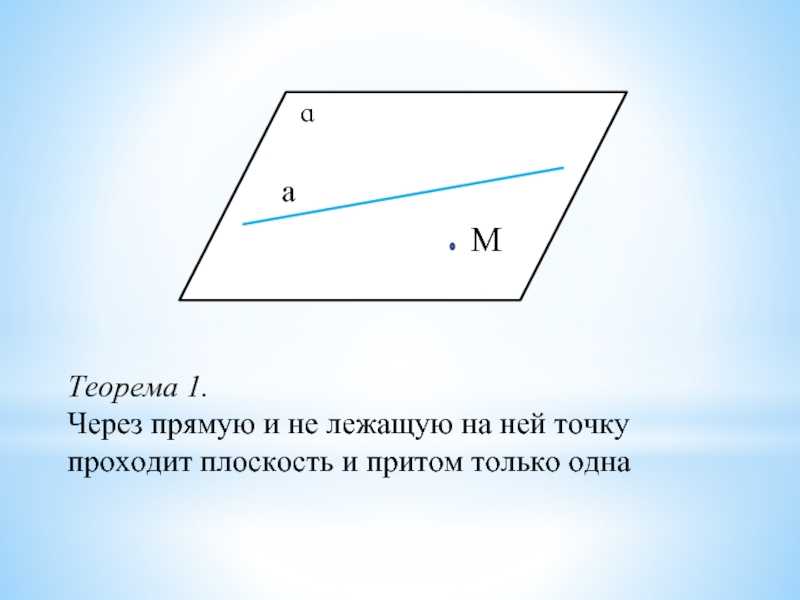
Теорема 1

Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

Иллюстрация теоремы 1. (Рис. 4.)

Рис. 4. 

   единственная

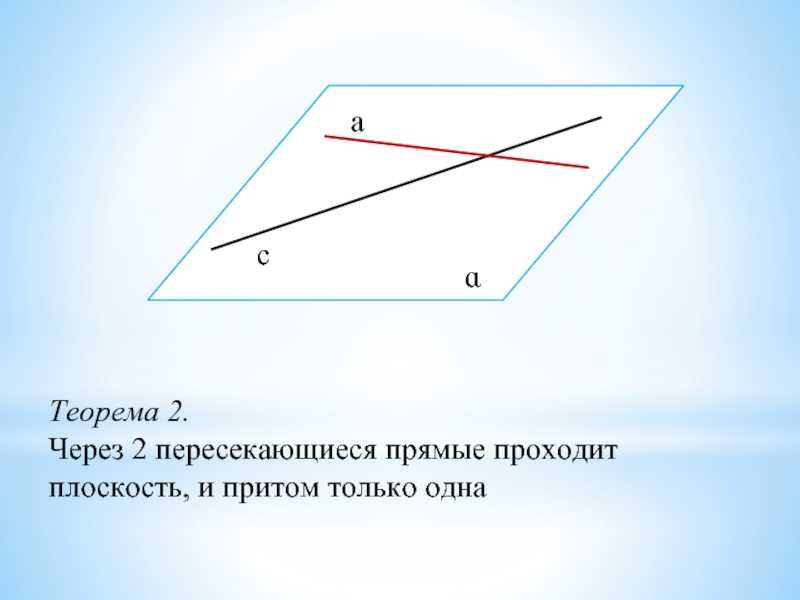
Теорема 2

Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Иллюстрация теоремы 2. (Рис. 5.)

Рис. 5.

Основные теоремы стереометрии

Теоремы о параллельности прямых и плоскостей

1. Если прямая AB параллельна какой-нибудь прямой CD, расположенной в плоскости P, то она параллельна самой плоскости.

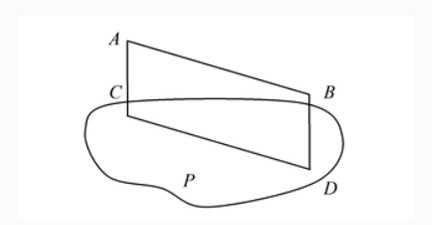
2. Если плоскость R проходит через прямую AB, параллельную другой плоскости P, и пересекает эту плоскость, то линия пересечения CD параллельна первой прямой AB.

3. Если две параллельные плоскости P и Q пересекаются третьей плоскостью R, то линии пересечения AB и CD параллельны.

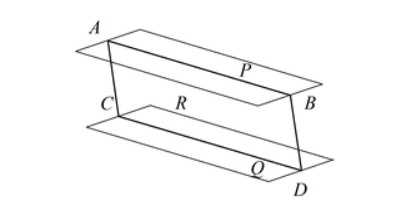
4. Если две пересекающиеся прямые AB и DC одной плоскости соответственно параллельны двум прямым A₁B₁ и C₁D₁ другой плоскости, то эти плоскости параллельны.

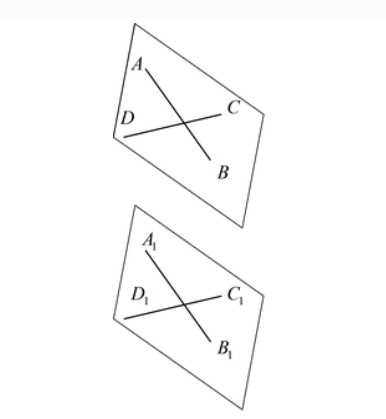
Теоремы о перпендикулярности прямых и плоскостей

1. Для того что бы прямая AB была перпендикулярна плоскости P, необходимо и достаточно, чтобы она была перпендикулярна двум произвольным непараллельным прямым CD и EF, лежащим в этой плоскости.

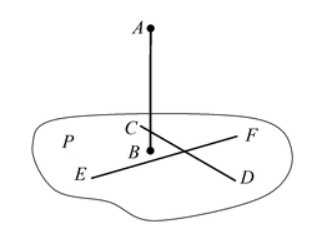
2. Для того, чтобы прямая DE проведенная на плоскости P через основание наклонной AC была ей перпендикулярна, необходимо и достаточно, чтобы эта прямая была перпендикулярна к проекции BC, наклонной на плоскость P (достаточное условие этой теоремы называется «Теоремой о трех перпендикулярах»: AC, BC, DE).

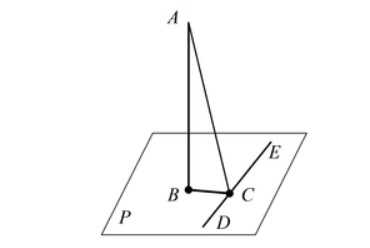
3. Если две прямые AB и CD перпендикулярны одной плоскости P, то они параллельны между собой.

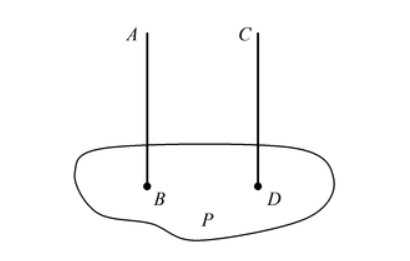
4. Если две плоскости P и Q перпендикулярны одной прямой AB, то они параллельны друг другу.

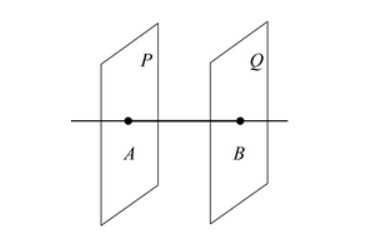
Теоремы о перпендикулярности плоскостей

1. Если плоскость P проходит через перпендикуляр к другой плоскости Q, то плоскость P перпендикулярна плоскости Q.

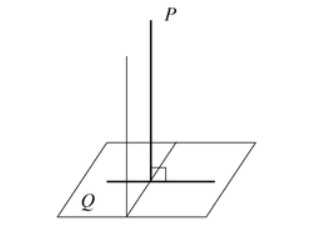
2. Если две плоскости P и Q взаимно перпендикулярны, то прямая, проведенная в одной плоскости перпендикулярно линии пересечения плоскостей, перпендикулярна другой плоскости.

Теорема о скрещивающихся прямых

1. Угол \(\alpha\) между скрещивающимися прямыми AB и CD определяется как угол между одной из этих прямых (например, CD) и любой прямой A₁B₁, проходящей через ее произвольную точку E параллельно другой прямой.

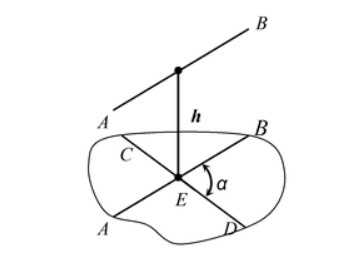
2. Расстояние h между скрещивающимися прямыми AB и CD определяется как кратчайшее расстояние от одной из этих прямых и может быть найдено как расстояние от одной их этих прямых (например, AB) до плоскости P, проходящей через другую прямую CD параллельно первой.

Базовые теоремы, аксиомы и определения стереометрии

Сечения многогранников

При решении задач по стереометрии нередко придется строить сечения многогранников на определенной плоскости. Далее приведены базовые определения, которые относятся к сечению.

Определение

Секущей плоскость будет называться в случае, если по обе стороны от нее будут находиться точки пирамиды, куба, параллелепипеда или же призмы.

Сечением пирамиды, куба, параллелепипеда или же призмы будет являться фигура, которая состоит из всех точек, являющихся общими фигуры и секущей плоскости.

Секущая плоскость будет пересекать грани пирамиды, куба, параллелепипеда или же призмы по отрезкам, исходя из этого, сечение является многоугольником, который лежит в секущей плоскости, со сторонами — указанными отрезками.

Чтобы построить сечение указанных выше фигур стереометрии, необходимо построение точек пересечения секущей плоскости и ребер фигуры, а после соединяться каждые две из них, которые лежат в одной грани.

Симметрия фигур

1. Точки A и B будут являться симметричными относительно точки O в тех случаях, когда O — середина отрезка AB.
2. Точки A и B будут являться симметричными относительно прямой C в тех случаях, когда прямая C будет проходить через середину отрезка AB и будет ему перпендикулярна.
3. Точки A и B будут являться симметричными относительно плоскости \(\beta\) в тех случаях, когда плоскость α будет проходить через середину отрезка AB и будет ему перпендикулярна.
4. Точка О (прямая c, плоскость \(\beta\)) будет являться центром симметрии фигуры в тех случаях, когда все точки фигуры симметричны относительно точки O (прямой C, плоскости \(\beta\)) какой-либо точке этой же фигуры.
5. Выпуклый многогранник будет являться правильным в тех случаях, когда все его грани — равные между собой правильные многоугольники и в каждой вершине сходится одно и то же количество ребер.

Взаимное расположение прямых в пространстве

В пространстве прямые лежат либо в одной плоскости, либо в разных плоскостях.

1. Две прямые в пространстве будут являться параллельными в тех случаях, когда они лежат в одной и той же плоскости и не имеют общих точек.
2. Две прямые в пространстве будут являться пересекающимися в тех случаях, когда они лежат в одной и той же плоскости и имеют общую точку.
3. Две прямые в пространстве будут являться скрещивающимися в тех случаях, когда они не лежат в одной и той же плоскости.

Расстояние между фигурами

1. Расстоянием между фигурами будет называться самое маленькое среди расстояний между их точками.
2. Расстояние между двумя прямыми, которые скрещиваются, будет соответствовать величине отрезка с концами на этих прямых, который перпендикулярен им обеим. Для каждых двух скрещивающихся прямых такой отрезок существует и единственен.
3. Расстояние между двумя прямыми, которые скрещиваются, будет равняться расстоянию между параллельными плоскостями, в которых они лежат.
4. Расстояние между двумя прямыми, которые скрещиваются, будет равняться расстоянию от одной из них до параллельной ей плоскости, которая проходит через вторую прямую.
5. Расстояние между двумя прямыми, которые скрещиваются, будет равняться расстоянию между их проекциями на плоскость, которая перпендикулярна одной из них.

Тест 2

Вариант 1

1. Точки М и К являются серединами рёбер ВВ₁ и СС₁ параллелепипеда ABCDA₁B₁C₁D₁. Сколько плоскостей, содержащих грани куба, параллельны прямой МК?

2. Точки А и В принадлежат рёбрам LL₁ и ММ₁ куба KLMNK₁L₁M₁N₁. Сколько существует прямых, содержащих рёбра куба, и скрещивающихся с прямой АВ?

3. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ угол BC₁B₁ равен 65°. Найдите угол между прямыми С₁В и DD₁.

4. На каком рисунке изображено сечение куба плоскостью PRT?

5. В тетраэдре MNPT NMT = 90°, PNT = 60°, MN = 3, МТ = 4, NP = 6. Найдите площадь грани NPT.

6. Сумма трёх измерений прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ равна 32, АВ:АА₁:AD = 2:1:5. Найдите наибольшую из диагоналей граней параллелепипеда.

7. Через точку К на ребре AD тетраэдра DABC проведено сечение параллельно грани ABC. Площадь сечения равна 27, АК:KD =1:3. Найдите площадь грани ABC.

Вариант 2

1. Точки Р и Т являются серединами рёбер LL₁ и ММ₁ параллелепипеда KLMNK₁L₁M₁N₁. Сколько плоскостей, содержащих грани параллелепипеда, параллельны прямой РТ?

2. Точки Н и Р принадлежат рёбрам АА₁ и DD₁ куба ABCDA₁B₁C₁D₁. Сколько существует прямых, содержащих рёбра куба и скрещивающихся с прямой HP?

3. Основание прямого параллелепипеда KLMNK₁L₁M₁N₁ — ромб, K₁L₁M₁ = 150°. Найдите угол между прямыми NL и L₁М₁.

4. На каком рисунке изображено сечение куба плоскостью ABC?

5. В тетраэдре DABC BAD = 90°, CBD = 60°, AD = 4, АВ = 4, ВС =7. Найдите площадь грани BCD.

6. Сумма трёх измерений прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ равна 40, АВ:АА₁:AD = 2:2:4. Найдите наибольшую из диагоналей граней параллелепипеда.

7. Через точку К на ребре AD тетраэдра DABC проведено сечение параллельно грани BCD. Площадь грани BCD равна 50, АК:KD = 2:3. Найдите площадь сечения.

Итоги урока

Итак, мы еще раз подытожили наши знания о стереометрии, а именно: прокомментировали три аксиомы, и два следствия из нее. И, кроме того, решили самые разнообразные задачи с использованием этих знаний.

Далее и аксиомы, и следствия будут использованы на следующих уроках при решении вопросов параллельности прямых и плоскостей.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/10-klass/aksiomy-stereometrii-i-ih-sledstviya/reshenie-zadach-na-primenenie-aksiom-i-ih-sledstviy-raznye-zadachi?seconds=0&chapter_id=209

https://www.youtube.com/watch?v=ffn2AgoFkRY

http://mypresentation.ru/documents/6d9ed536a22eb1004a1537fe519f1650/img3.jpg

http://mypresentation.ru/documents/6d9ed536a22eb1004a1537fe519f1650/img4.jpg

http://mypresentation.ru/documents/6d9ed536a22eb1004a1537fe519f1650/img5.jpg

http://russkiy-gdz.com/f/homework/9103/173733.jpg

http://five-points.ru/img/108/exercises/62693.jpg

http://mcvouo.ru/images/files/gdz/9103/173741.jpg

http://static.zoobrilka.com/files/gdz/9103/173734.jpg