Таблица квадратов натуральных чисел

Как на калькуляторе посчитать в квадрате?

Найти с помощью калькулятора квадрат числа 11052:

1. Шаг 1. Набрать на калькуляторе число, которое нужно возвести в квадрат. В нашем случае — это число 11052.
2. Шаг 2. Нажать кнопку умножить: «*».
3. Шаг 3. Нажать кнопку равно: «=». Полученное число и будет квадратом числа.

Чтобы найти квадрат числа, введите это число в калькулятор, а затем нажмите кнопку “x 2 “. “1/X” – деление числа 1 на текущее число. Чтобы разделить число 1 на текущее число, введите это число в калькулятор, а затем нажмите кнопку “1/X”.”%” – вычисление процента от числа.” √” – вычисление квадратного корня. Чтобы найти квадратный корень числа, введите это число в калькулятор, а затем нажмите кнопку “√”.

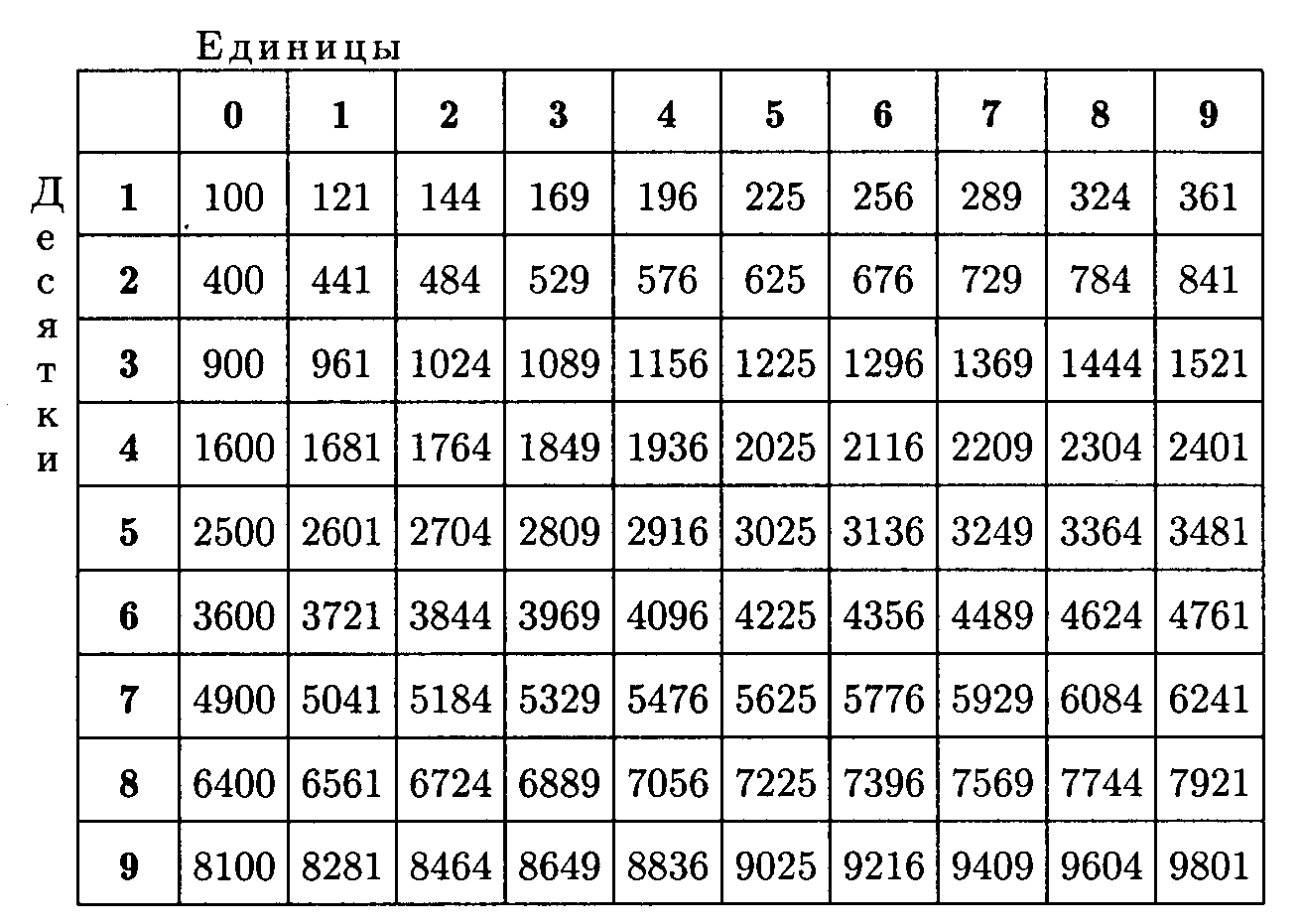
Квадраты чисел от 10 до 99

РАЗ	ЕДИНИЦЫ
	1	2	3	4	5	6	7	8	9
1	100	121	144	169	196	225	256	289	324	361
2	400	441	484	529	576	625	676	729	784	841
3	900	961	1024	1089	1156	1225	1296	1369	1444	1521
4	1600	1681	1764 г	1849 г	1936 г	2025	2116	2209	2304	2401
5	2500	2601	2704	2809	2916	3025	3136	3249	3364	3481
6	3600	3721	3844	3969	4096	4225	4356	4489	4624	4761
7	4900	5041	5184	5329	5476	5625	5776	5929	6084	6241
8	6400	6561	6724	6889	7056	7225	7396	7569	7744	7921
9	8100	8281	8464	8649	8836	9025	9216	9409	9604	9801

Как пользоваться таблицей:

Уровень в первом столбце, один в верхнем ряду. Квадрат определенного числа находится на пересечении искомых десятков и единиц.

Допустим, что нам нужно найти квадрат числа 45. В столбце десятков ищем число 4, в ряду единиц — число 5. Их пересечение соответствует числу 2025 — ответ, который мы хотели найти.

Что такое степени?

Начиная с первого класса, вы знакомились с несколькими арифметическими действиями, использовали их при решении задач и заданий. Принято считать, что в математике существует 4 основных действия: сложение, вычитание, умножение, деление. Оказывается, существуют и другие действия. Сегодня рассмотрим новое и очень интересное.

Рассмотрим ситуацию.

Дети получили домашнее задание по математике – решить три столбика уравнений, по три уравнения в каждом. Сколько всего уравнений задали детям?

Чтобы ответить на вопрос задачи, суммируем уравнения во всех столбиках. Мы знаем, что в одном столбике три уравнения, а в трех столбиках:

3+3+3.

В данном случае слагаемое повторяется три раза. Сумму одинаковых компонентов можно заменить произведением. Для этого повторяющуюся составляющую умножаем на количество повторов.

3×3

Составленное произведение запишем короче. Для этого, запомним значение множителей, количество множителей.

Сначала, записываем значение множителя. Рядом с записанной цифрой, записываем их численность.

Получается: 32

То есть: 3+3+3=3×3=32=9.

Получен ответ на главный вопрос задачи. Ученикам задали девять уравнений.

Решая задачу, мы познакомились с новым математическим действием — возведением в степень.

Давайте дадим правильное определение рассмотренному действию.

Степень числа – это произведение одинаковых множителей, взятых определенное количество раз: 𝑎 × 𝑎 × 𝑎 …= 𝑎b .

Произносят: а в степени б.

К примеру, запись 64, нужно читать: «шесть в четвертой степени», «четвертая степень шести».

Разберем еще одну задачу.

Работникам городского парка необходимо засеять травой клумбу прямоугольной формы. Чтобы правильно рассчитать необходимое количество семян, нужно знать посадочную площадь. Найдите площадь клумбы, зная, что её ширина и длина по четыре метра.

Чтобы ответить на главный вопрос, вспомним, правило нахождения площади прямоугольника: для нахождения площади прямоугольника необходимо длину умножить на ширину. Зная длину и ширину клумбы, найдем произведение:

Получим, 4×4 – площадь клумбы.

В данном произведении составляющая четыре, использована два раза. На основании изученного определения рассматриваемое произведение запишем иначе: 

Посадочная площадь клумбы равна 16 м2.

Основание и показатель

 Математика – точная наука. Каждый компонент имеет определенное наименование, определенное место. Давайте вспомним наименования составляющих в различных математических действиях:

У изученного действия, составляющие имеют свои отличные от других наименования. Их называют: основание и показатель.

Запишем правильную формулировку для составляющих рассмотренного действия.

Числовое значение дублирующейся составляющей, называют основанием степени.

Цифра, стоящая справа, обозначает, численность повторяющихся множителей,называется показателем степени

В выражении 89, основанием является 8, а показателем 9. Значит, чтобы найти значение рассматриваемого выражения, нужно умножить число 8 само на себя 9 раз.

Найдем значение выражения 55.

Для верного проведения необходимых вычислений определим основание   (дублирующийся компонент) — пять, и показатель (численность составляющих)  – пять.

Имеем:

Исходя из рассмотренных примеров, можно сделать вывод как возвести число в степень:

для возведения числа в степень достаточно это число умножить само на себя несколько раз (на численность повторов указывает показатель степени).

Вычислим: 26

Нам необходимо возвести два в шестую степень. Главное – нужно умножить  два, само на себя шесть раз:

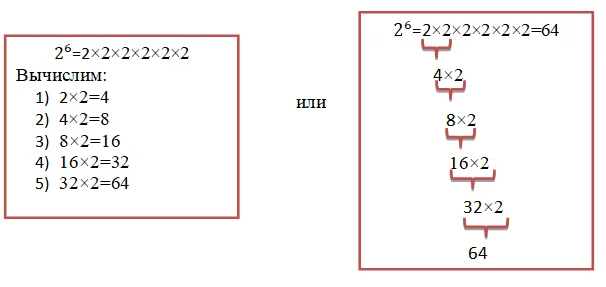
Получается, 26=64

Все очень просто! Главное – запомнить, что для возведения числа в степень, нужно умножить его само на себя, а сколько раз это сделать, вам подскажет показатель!

Квадрат и куб числа.

Таблица квадратов натуральных чисел от $10$ до $99$

Другой популярной таблицей является таблица квадратов чисел от $10$ до $99$ (табл. 4), то есть всех десятичных чисел.

Необходимо найти значения из этой таблицы следующим образом: В первом столбце находим количество десятков интересующего нас числа. Запомните число в этой строке. Итак, в первом слагаемом находим количество единиц интересующего числа и запоминаем найденный столбец. Пересечение найденной строки и столбца даст нам ответ.

Пример 3

Найдите $37^2$

Решение.

Находим число $3$ в первом столбце: получаем 4 строку.

Находим число $7$ в первой строке: получаем восьмой столбец.

Мы видим, что на их пересечении число $1369$. Поэтому

37$^2=1369$

Таблица квадратов натуральных чисел 1 до 100

12 = 1 22 = 4 32 = 9 42 = 16 52 = 25 62 = 36 72 = 49 82 = 64 92 = 81 102 = 100	112 = 121 122 = 144 132 = 169 142 = 196 152 = 225 162 = 256 172 = 289 182 = 324 192 = 361 202 = 400	212 = 441 222 = 484 232 = 529 242 = 576 252 = 625 262 = 676 272 = 729 282 = 784 292 = 841 302 = 900	312 = 961 322 = 1024 332 = 1089 342 = 1156 352 = 1225 362 = 1296 372 = 1369 382 = 1444 392 = 1521 402 = 1600	412 = 1681 422 = 1764 432 = 1849 442 = 1936 452 = 2025 462 = 2116 472 = 2209 482 = 2304 492 = 2401 502 = 2500
512 = 2601 522 = 2704 532 = 2809 542 = 2916 552 = 3025 562 = 3136 572 = 3249 582 = 3364 592 = 3481 602 = 3600	612 = 3721 622 = 3844 632 = 3969 642 = 4096 652 = 4225 662 = 4356 672 = 4489 682 = 4624 692 = 4761 702 = 4900	712 = 5041 722 = 5184 732 = 5329 742 = 5476 752 = 5625 762 = 5776 772 = 5929 782 = 6084 792 = 6241 802 = 6400	812 = 6561 822 = 6724 832 = 6889 842 = 7056 852 = 7225 862 = 7396 872 = 7569 882 = 7744 892 = 7921 902 = 8100	912 = 8281 922 = 8464 932 = 8649 942 = 8836 952 = 9025 962 = 9216 972 = 9409 982 = 9604 992 = 9801 1002 = 10000

Кто создал таблицу квадратов?

Иногда изобретение таблицы умножения приписывают Пифагору, в честь которого она названа в различных языках, включая французский, итальянский и русский. В 493 году Викторий Аквитанский создал таблицу из 98 столбцов, которая представляла в римских числах результат перемножения чисел от 2 до 50.

Пифагор изучил в Египте, а потом привез в Европу цифровые матрицы, известные ранее только узкому кругу избранных. В адаптированном варианте тайные таблицы дошли до наших дней и ныне известны как квадрат Пифагора. Пифагор не оставил после себя собрания сочинений, он держал своё учение в тайне и передавал ученикам устно. Учёные утверждают, что квадрат Пифагора дает возможность точно определить сильные и слабые стороны человеческой натуры.

Специфические характеристики применения таблицы квадратных и кубических корней

Таблицы корней в кубе и в квадрате применяются совершенно одинаково. Но из-за того, что степени могут быть как четные, так и нечетные, появляются определенные отличия в расчете значений подобных корней.

Исходя из дефиниции термина «квадратный корень» получается, что число, которое находится под корнем, никогда не является неположительным числом. Данную особенность стали использовать потому, что требовалось привести к однозначности термин «корень в квадрате». Но существует расширенная дефиниция корня в квадрате в математике.

Согласно ей корень в квадрате является корнем, возведенным во вторую степень. Для подобного вида корня не нужно вычленять неотрицательное выражение, а также положительную величину непосредственно корня.

В процессе работы со всеми таблицами стоит понимать, что за корень в квадрате необходимо рассчитать — корень алгебраический или же корень арифметический. В случае арифметического корня необходимо нужно брать величину из корневой таблицы, не совершая никаких иных операций.

В случаях, когда совершаются операции с алгебраическим вариантом корня, итог будет основываться на величине, величине, которая находится под корнем. В случае, когда величина под корнем является величиной более нуля, тогда корней в результате получится два корня — один неотрицательный, а другой отрицательный. В случае, когда величина, которую возвели в степень, является неположительной, тогда у уравнения не будет никаких вариантов решения. Четной будет вторая степень, потому что не существует подобной величины, что при возведении в квадрат привело бы к неположительному значению.

Пример 

\(\sqrt{47}=\pm6.85565\)

Величина 47 является величиной, которая не равняется нулю, из-за этого корня будет два: 6.85565 и -6.85565. \(\sqrt{-35}\neq5.91608\), \(\sqrt{-35}\neq-5.91608\). -35 является величиной неположительной, из-за этого решения не будет.

Корень в третьей степени является нечетной степенью, из-за этого величина под корнем способна быть как неотрицательной, так и отрицательной. У подобного выражения будет решение. Таким образом, к итогу, взятому из таблицы корней, необходимо прибавить знак «минус», при условии, что корень, который нужно найти, возводится в величину менее нуля.

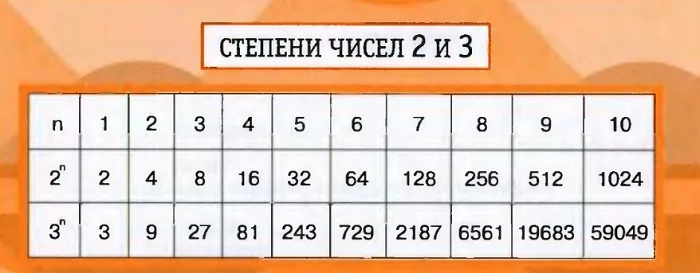
Таблица степеней первых натуральных чисел

Начнем с таблицы для нахождения степеней натуральных чисел от $2$ до $12$ по степеням от $1$ до $10$ (таблица 1)

Обратите внимание, что мы не приводим степени $1$, потому что единица будет равна самой себе в любой степени

Нужно найти значения из этой таблицы следующим образом: В первом столбце находим число, степень которого нас интересует. Запоминаем номер этой строки. Итак, в первом члене находим показатель степени и запоминаем найденный столбец. Пересечение найденной строки и столбца даст нам ответ.

Тренируйте свой мозг с удовольствием Развивайте память, внимание и мышление с помощью онлайн-тренажеров. Выберите программуПример 1. Найдите $8^7$

Найдите $8^7$

Решение.

Находим число $8$ в первом столбце: получаем восьмую строку.

Находим число $7$ в первой строке: получаем восьмой столбец.

Мы видим, что число $2097152$ находится на их пересечении. Поэтому

$8^7=2097152$

Куб числа

В выходной день бабушка пекла пирожки с малиной, клубникой и вишней. До прихода внуков она успела испечь по три пирожка с каждой начинкой. По рецепту пирожков должно получиться в три раза больше, чем выпеченных. Вычислите, сколько пирожков должно получиться по рецепту? 

Чтобы понять на сколько пирогов рассчитан рецепт бабушки, нужно знать, сколько пирогов бабуля успела испечь. Мы знаем, что готовы по три штуки с каждой начинкой – малина, клубника, вишня. Поэтому три готовых пирожка повторяем три раза, то есть: 3×3.

Зная сколько выпеченных изделий, можем найти, сколько пирогов получится согласно рецепту. Для этого, готовые пироги увеличиваем в три раза (умножаем на три):

3×3×3.

Мы видим, составляющая три использована три раза. Пользуясь изученным определением, можем записать иначе:  33

Составленное выражение произносится «три в кубе».

Вычислим: 

Бабушкин рецепт рассчитан на приготовление 27 пирожков.

Показатель степени числа равен 3, то говорят «число в кубе».

73 – семь в кубе;

93 – девять в кубе;

113 – одиннадцать в кубе.

Запомните:

Чтобы возвести число в куб, его нужно умножить само на себя три раза!

И в заключение урока рассмотрим таблицу, которая станет верным другом на протяжении учебного процесса.

Правила пользования таблицей!

На верхней горизонтальной строке записаны основания, в первом вертикальном столбце – показатели. Для нахождения нужного значения квадрата, куба числа, в верхней строке находим требуемое число и опускаемся на вторую, третью строку (зависит от показателя).

Вот и все! Благодаря табличке, не нужно выполнять вычисления, а просто держать её под рукой!

Интересные факты.

• 1) Человеческий мозг содержит 2×1010 нервных клеток, имеет ежедневную возможность сохранять 8,6×107  бит различной информации. У взрослых людей память хранит множество информации –  1018 бит.
• 2) Ежесекундно человеческий мозг выполняет 105 химических процессов. Сплетение нейронов головного мозга в 1,4×103  раз сложнее, всей мировой сети телефонной связи.
• 3) Все человечество на планете можно поместить в куб, имеющий длину ребра 1 километр.
• 4) Самое маленькое число, состоящее из четырех знаков и являющееся суммой двух кубов натуральных чисел.
• 5) В древние времена славяне использовали своеобразную запись чисел,  большого значения.

103 называли «тысяща»;

106 имело название «тьма»

1012 прозвали «легион»

1024 называлось «леодр»

1048 читалось «ворон»

1049 произносили, «колода»

Корень n-ой степени, арифметический корень степени n

Обобщим понятие корня из числа – введем определение корня n-ой степени
для n
.

Определение

Корень n
-ой степени из числа a

– это число, n
-я степень которого равна a
.

Из данного определения понятно, что корень первой степени из числа a
есть само число a
, так как при изучении степени с натуральным показателем мы приняли a 1 =a
.

Выше мы рассмотрели частные случаи корня n
-ой степени при n=2
и n=3
– квадратный корень и кубический корень. То есть, квадратный корень – это корень второй степени, а кубический корень – корень третьей степени. Для изучения корней n
-ой степени при n=4, 5, 6, …
их удобно разделить на две группы: первая группа – корни четных степеней (то есть, при n=4, 6, 8, …
), вторая группа – корни нечетных степеней (то есть, при n=5, 7, 9, …
). Это связано с тем, что корни четных степеней аналогичны квадратному корню, а корни нечетных степеней – кубическому. Разберемся с ними по очереди.

Начнем с корней, степенями которых являются четные числа 4, 6, 8, …
Как мы уже сказали, они аналогичны квадратному корню из числа a
. То есть, корень любой четной степени из числа a
существует лишь для неотрицательного a
. Причем, если a=0
, то корень из a
единственный и равен нулю, а если a>0
, то существует два корня четной степени из числа a
, причем они являются противоположными числами.

Обоснуем последнее утверждение. Пусть b
– корень четной степени (обозначим ее как 2·m
, где m
– некоторое натуральное число) из числа a
. Предположим, что существует число c
– еще один корень степени 2·m
из числа a
. Тогда b 2·m −c 2·m =a−a=0
. Но мы знаем вида b 2·m −c 2·m =
(b−c)·(b+c)·
(b 2·m−2 +b 2·m−4 ·c 2 +b 2·m−6 ·c 4 +…+c 2·m−2)
, тогда (b−c)·(b+c)·
(b 2·m−2 +b 2·m−4 ·c 2 +b 2·m−6 ·c 4 +…+c 2·m−2)=0
. Из этого равенства следует, что b−c=0
, или b+c=0
, или b 2·m−2 +b 2·m−4 ·c 2 +b 2·m−6 ·c 4 +…+c 2·m−2 =0
. Первые два равенства означают, что числа b
и c
равны или b
и c
– противоположны. А последнее равенство справедливо лишь при b=c=0
, так как в его левой части находится выражение, которое неотрицательно при любых b
и c
как сумма неотрицательных чисел.

Что касается корней n
-ой степени при нечетных n
, то они аналогичны кубическому корню. То есть, корень любой нечетной степени из числа a
существует для любого действительного числа a
, причем для данного числа a
он является единственным.

Единственность корня нечетной степени 2·m+1
из числа a
доказывается по аналогии с доказательством единственности кубического корня из a
. Только здесь вместо равенства a 3 −b 3 =(a−b)·(a 2 +a·b+c 2)
используется равенство вида b 2·m+1 −c 2·m+1 =
(b−c)·(b 2·m +b 2·m−1 ·c+b 2·m−2 ·c 2 +… +c 2·m)
. Выражение в последней скобке можно переписать как b 2·m +c 2·m +b·c·(b 2·m−2 +c 2·m−2 +
b·c·(b 2·m−4 +c 2·m−4 +b·c·(…+(b 2 +c 2 +b·c))))
. Например, при m=2
имеем b 5 −c 5 =(b−c)·(b 4 +b 3 ·c+b 2 ·c 2 +b·c 3 +c 4)=
(b−c)·(b 4 +c 4 +b·c·(b 2 +c 2 +b·c))
. Когда a
и b
оба положительны или оба отрицательны их произведение является положительным числом, тогда выражение b 2 +c 2 +b·c
, находящееся в скобках самой высокой степени вложенности, является положительным как сумма положительных чисел. Теперь, продвигаясь последовательно к выражениям в скобках предыдущих степеней вложенности, убеждаемся, что они также положительны как суммы положительных чисел. В итоге получаем, что равенство b 2·m+1 −c 2·m+1 =
(b−c)·(b 2·m +b 2·m−1 ·c+b 2·m−2 ·c 2 +… +c 2·m)=0
возможно только тогда, когда b−c=0
, то есть, когда число b
равно числу c
.

Пришло время разобраться с обозначениями корней n
-ой степени. Для этого дается определение арифметического корня n
-ой степени
.

Определение

Арифметическим корнем n
-ой степени из неотрицательного числа a

называется неотрицательное число, n
-я степень которого равна a
.

About curly numbers

A full square is the most common example of a classic figurative number, that is, a number that can be graphically expressed using geometric shapes. The concept of figurative numbers arose, according to researchers, as early as the 6th-4th centuries BC and is directly related to the Pythagoreans. Ancient Greek philosophers learned algebra, largely relying on geometric foundations, so natural numbers were associated with a set of points on the plane and in space. Actually, the very name «full square» owes its appearance to this particular approach to the study of mathematics.

Figured numbers are traditionally generalized to multidimensional spaces. For example, on a plane, curly numbers are associated with polygons according to certain rules, and in three-dimensional space they are associated with various polyhedra.

The Pythagoreans attached great importance and greatness to the concept of curly numbers, so such well-known ancient mathematicians as, for example, Diophantus of Alexandria, Hypsicles of Alexandria and Eratosthenes of Cyrene were engaged in their study. Entire scientific papers and studies were devoted to the comprehension and structuring of the theory of curly numbers. So, fragments of the book of Diophantus of Alexandria «On Polygonal Numbers», written, according to some estimates, in the 3rd century BC, have survived to our time.

By the way, curly numbers were of interest not only to ancient mathematicians. Many mathematicians of the Middle Ages were also engaged in them: Gerolamo Cardano, Fibonacci, and even the great scientists of modern times — Leonard Euler, Joseph Louis Lagrange, Pierre de Fermat, Carl Friedrich Gauss.

Таблица степеней по алгебре: числа в квадрате

Расписать абсолютно каждое число и найти его значение во всех степенях — невозможно. В сложных примерах рекомендуется использовать онлайн калькуляторы. Мы же рассматриваем наиболее примитивные и распространенные случаи. В основном, в средней школе (вплоть до 11 класса) рассматриваются примеры с перемножением незначительное количество раз. Часто используется квадрат (a2). Некоторые числа мы уже возводили в него (от 1 до 25). Значения больших чисел же можно искать тут:

_{*Для лучшего понимания примеры подсвечены голубым.}

С левой стороны указаны десятки, а сверху — единицы. Т.е., для возведения в квадрат числа 24 ищем пересечение его десятка и единицы (2 — десяток, 4 — единица). Получаем показатель 576. Таким образом данная таблица степеней натуральных чисел может использоваться для возведения в квадрат цифр до 99.

Пример 3. Возводим большие значения в квадрат.

Задача. Найти 632.

Решение. В числе «63» 6 десятков и 3 единицы. Десятки у нас находятся с левой стороны, а единицы — в верхней строчке. Ищем нужные значения в таблице степеней по алгебре и находим число, находящееся на их пересечении.

Ответ. 3969.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Как пользоваться таблицей

Если все упростить, что в итоге является квадратным корнем? Для четкого понимания этого термина стоит привести пример, который используется в рамках школьной программе по алгебре. Возьмем обычное школьное выражение: \(x^{2}=4\). Для решения необходимо осознать, что за величину необходимо возвести в квадрат, чтобы получить в итоге — 4. Согласно классической таблице умножения получается, что итог может быть в двух вариантах — 2 или -2. Для того, чтобы сделать проще решение задачи, вводят термин «корень в квадрате», а также используются специализированный значок: \(\sqrt{}\).

Корень в квадрате неотрицательной величины x станет исключительно неотрицательной величиной, квадрат от которого эквивалентен x. \(\sqrt{x}=a, a^{2}=x; a,x\geq0\).

Из-за чего возможно сказать, что x способно быть исключительно неотрицательной величиной? Следует снова вернуться к образцу выше, рассчитать корневую величину для -9. Таким образом, получится, что 32=-9. Однако это неверный вариант, потому что не получится -9. Если рассматривать величину -3, тогда получится просто 9. Величина без знака «минус» не подходит для решения задачи. Таким образом, не бывает величин, что в процессе возведения во вторую степень, производили величину со знаком «минус».

Возможно увидеть, что корень в квадрате в ответе способен быть исключительно неотрицательной величиной, однако вспоминаем, что в первом выражении говорилось об ответе 2 и -2. Все дело в том, что типы корней различные — одни являются квадратными, а другие — арифметическими квадратными корнями. К примеру, \(a^{2}=4\) не является эквивалентом a=?4.

Для того чтобы быстрее, точнее рассчитывать величины-ответы на задачи, изобрели корневую таблицу, в которой возможно найти рассчитанные ранее корни. В корневой таблице в строчке находятся единицы, в столбиках находятся десятки. Приведем пример использования таблицы: нужно рассчитать корень в квадрате величины 54. Для начала нужно взглянуть на столбики, ищем нужное нам число, то есть 5, потом необходимо взглянуть на строчку, найти там нужное число, то есть 4. После необходимо рассмотреть место, в котором эти цифры пересекаются. В этой ячейке располагается необходимый для задачи результат, то есть 6,7082.

Существует также таблица квадратов — ее нельзя сопоставлять с корневой таблицей. Таблица квадратов выглядит таким образом:

Таблицей квадратов уместно пользоваться в тех случаях, когда необходимо рассчитать величину двухзначной величины, возведенной в квадрат. Приведем пример: необходимо возвести в двойную степень число 89. Нужно найти в данной таблице 8 в столбике, а 9 в строчке, находим ячейку, на которой они соприкасаются. Ответ будет 7921.  

Значения в таблице достаточно быстро запоминаются, поэтому возможно после продолжительного времени использования этой таблицы, перестать использовать ее.

Традиционная таблица степеней натуральных чисел: от 1 до 10

Проще всего находить значение многократного перемножения небольших натуральных чисел. Для поиска решения можно использовать следующую подсказку:

По методу вычисления эта таблица натуральных степеней схожа с таблицей умножения. Чтобы найти результат произведения числа нужное количество раз, достаточно найти соответствующую формулу в столбике.

Пример 1. Используем простую таблицу степеней по алгебре.

Задача. Найти 79.

Решение. Находим 79. Расположено значение во втором столбике нижней строки.

Ответ. 40353607.

Пример 2. Используем простую таблицу по алгебре.

Задача. Найти 17.

Решение. В данном случае найти значение выражения можем без использования вспомогательных инструментов. Достаточно вспомнить одно из свойств степеней: единица всегда остается единицей.

Ответ. 1.

Таблица степеней чисел до 100 в кубе

Часто в примерах требуется возвести двузначное число в куб. Сделать это будет проще со следующей таблицей:

_{*Для лучшего понимания примеры подсвечены голубым.}

Пример 4. Работаем с таблицей натуральных степеней чисел в кубе.

Задача. Найти 453.

Решение. Делим число на десятки и единицы. Находим 4 десятка (левый столбец) и 5 единиц (верхняя полоса) и ищем значение их пересечения.

Ответ. 157464.

Пример 5. Вычисляем квадрат по таблице.

Задача. Найти 403.

Решение. Найти значение можно двумя способами. Первый — руководствуясь таблицей. 4 — десятки, 0 — единицы. Ищем пересечение этих цифр. Результат — 6400. Второй способ: возводим 4 в куб и прибавляем два нуля (т.к. 10 в кубе = 100). 43=64. Прибавляем «00» и получаем идентичный ответ: 6400.

Ответ. 6400.

Пользоваться таблицами степеней по математике несложно. Но только в том случае, если речь идет о небольших цифрах. В длинных примерах, состоящих из множества чисел в степенях, можно использовать онлайн калькуляторы. Это позволит избежать ошибок, которые могут быть вызваны просмотром не той ячейки.

Таблица квадратов двузначных чисел

0 2 = 0 1 2 = 1 2 2 = 4 3 2 = 9 4 2 = 16 5 2 = 25 6 2 = 36 7 2 = 49 8 2 = 64 9 2 = 81	10 2 = 100 11 2 = 121 12 2 = 144 13 2 = 169 14 2 = 196 15 2 = 225 16 2 = 256 17 2 = 289 18 2 = 324 19 2 = 361	20 2 = 400 21 2 = 441 22 2 = 484 23 2 = 529 24 2 = 576 25 2 = 625 26 2 = 676 27 2 = 729 28 2 = 784 29 2 = 841	30 2 = 900 31 2 = 961 32 2 = 1024 33 2 = 1089 34 2 = 1156 35 2 = 1225 36 2 = 1296 37 2 = 1369 38 2 = 1444 39 2 = 1521	40 2 = 1600 41 2 = 1681 42 2 = 1764 43 2 = 1849 44 2 = 1936 45 2 = 2025 46 2 = 2116 47 2 = 2209 48 2 = 2304 49 2 = 2401
50 2 = 2500 51 2 = 2601 52 2 = 2704 53 2 = 2809 54 2 = 2916 55 2 = 3025 56 2 = 3136 57 2 = 3249 58 2 = 3364 59 2 = 3481	60 2 = 3600 61 2 = 3721 62 2 = 3844 63 2 = 3969 64 2 = 4096 65 2 = 4225 66 2 = 4356 67 2 = 4489 68 2 = 4624 69 2 = 4761	70 2 = 4900 71 2 = 5041 72 2 = 5184 73 2 = 5329 74 2 = 5476 75 2 = 5625 76 2 = 5776 77 2 = 5929 78 2 = 6084 79 2 = 6241	80 2 = 6400 81 2 = 6561 82 2 = 6724 83 2 = 6889 84 2 = 7056 85 2 = 7225 86 2 = 7396 87 2 = 7569 88 2 = 7744 89 2 = 7921	90 2 = 8 100 91 2 = 8281 92 2 = 8464 93 2 = 8649 94 2 = 8836 95 2 = 9025 96 2 = 9216 97 2 = 9409 98 2 = 9604 99 2 = 9801

02=0=0

Таблица квадратов натуральных чисел 100 до 200

1012 = 10 201 1022 = 10 404 1032 = 10 609 1042 = 10 816 1052 = 11 025 1062 = 11 236 1072 = 11 449 1082 = 11 664 1092 = 11 881 1102 = 12 100	1112 = 12 321 1122 = 12 544 1132 = 12 769 1142 = 12 996 1152 = 13 225 1162 = 13 456 1172 = 13 689 1182 = 13 924 1192 = 14 161 1202 = 14 400	1212 = 14 641 1222 = 14 884 1232 = 15 129 1242 = 15 376 1252 = 15 625 1262 = 15 876 1272 = 16 129 1282 = 16 384 1292 = 16 641 1302 = 16 900	1312 = 17 161 1322 = 17 424 1332 = 17 689 1342 = 17 956 1352 = 18 225 1362 = 18 496 1372 = 18 769 1382 = 19 044 1392 = 19 321 1402 = 19 600	1412 = 19 881 1422 = 20 164 1432 = 20 449 1442 = 20 736 1452 = 21 025 1462 = 21 316 1472 = 21 609 1482 = 21 904 1492 = 22 201 1502 = 22 500
1512 = 22 801 1522 = 23 104 1532 = 23 409 1542 = 23 716 1552 = 24 025 1562 = 24 336 1572 = 24 649 1582 = 24 964 1592 = 25 281 1602 = 25 600	1612 = 25 921 1622 = 26 244 1632 = 26 569 1642 = 26 896 1652 = 27 225 1662 = 27 556 1672 = 27 889 1682 = 28 224 1692 = 28 561 1702 = 28 900	1712 = 29 241 1722 = 29 584 1732 = 29 929 1742 = 30 276 1752 = 30 625 1762 = 30 976 1772 = 31 329 1782 = 31 684 1792 = 32 041 1802 = 32 400	1812 = 32 761 1822 = 33 124 1832 = 33 489 1842 = 33 856 1852 = 34 225 1862 = 34 596 1872 = 34 969 1882 = 35 344 1892 = 35 721 1902 = 36 100	1912 = 36 481 1922 = 36 864 1932 = 37 249 1942 = 37 636 1952 = 38 025 1962 = 38 416 1972 = 38 809 1982 = 39 204 1992 = 39 601 2002 = 40 000

Как быстро найти число в квадрате?

Как возвести число в квадрат

1. Шаг 1: Умножьте первую цифру числа на цифру, которая стоит выше в ряду с ней: 3 х 4 = 12.
2. Шаг 2: К числу, которое получилось припишите в конце число 25.
3. Шаг 1: Возьмем ближайшее число, кратное 10.
4. Шаг 2: Теперь найдем нижнее число с разницей 3 от нашего числа.

Существует способ быстрого возведения в квадрат двухзначных чисел, которые оканчиваются на цифру 5.

Первую цифру числа, возводимого в квадрат, необходимо умножить на сумму этого числа и единицы

Записать полученное число- это будут первые цифры ответа (с этих цифр начинается ответ)

Ответ всегда будет заканчиваться на 25 (т.е. в конце ответа всегда будет стоять число 25)

Приписываем к числу, полученному в п 2, число 25, получаем ответ

Таблица квадратов натуральных чисел 200 до 300

2012 = 40 401 2022 = 40 804 2032 = 41 209 2042 = 41 616 2052 = 42 025 2062 = 42 436 2072 = 42 849 2082 = 43 264 2092 = 43 681 2102 = 44 100	2112 = 44 521 2122 = 44 944 2132 = 45 369 2142 = 45 796 2152 = 46 225 2162 = 46 656 2172 = 47 089 2182 = 47 524 2192 = 47 961 2202 = 48 400	2212 = 48 841 2222 = 49 284 2232 = 49 729 2242 = 50 176 2252 = 50 625 2262 = 51 076 2272 = 51 529 2282 = 51 984 2292 = 52 441 2302 = 52 900	2312 = 53 361 2322 = 53 824 2332 = 54 289 2342 = 54 756 2352 = 55 225 2362 = 55 696 2372 = 56 169 2382 = 56 644 2392 = 57 121 2402 = 57 600	2412 = 58 081 2422 = 58 564 2432 = 59 049 2442 = 59 536 2452 = 60 025 2462 = 60 516 2472 = 61 009 2482 = 61 504 2492 = 62 001 2502 = 62 500
2512 = 63 001 2522 = 63 504 2532 = 64 009 2542 = 64 516 2552 = 65 025 2562 = 65 536 2572 = 66 049 2582 = 66 564 2592 = 67 081 2602 = 67 600	2612 = 68 121 2622 = 68 644 2632 = 69 169 2642 = 69 696 2652 = 70 225 2662 = 70 756 2672 = 71 289 2682 = 71 824 2692 = 72 361 2702 = 72 900	2712 = 73 441 2722 = 73 984 2732 = 74 529 2742 = 75 076 2752 = 75 625 2762 = 76 176 2772 = 76 729 2782 = 77 284 2792 = 77 841 2802 = 78 400	2812 = 78 961 2822 = 79 524 2832 = 80 089 2842 = 80 656 2852 = 81 225 2862 = 81 796 2872 = 82 369 2882 = 82 944 2892 = 83 521 2902 = 84 100	2912 = 84 681 2922 = 85 264 2932 = 85 849 2942 = 86 436 2952 = 87 025 2962 = 87 616 2972 = 88 209 2982 = 88 804 2992 = 89 401 3002 = 90 000

What is a full square

A perfect square is an integer that is the square of an integer. In other words, a perfect square is the product of two equal integers. Based on the definition, the square root of a full square is taken completely, so the geometric embodiment of a full square is the area of a square with a side expressed as an integer equal to the square root of the original full square.

For a more precise disclosure of the topic, let us recall the definition of integers. Integers are called all natural (used to count objects) and their opposite numbers and zero. Accordingly, the set of integers does not include finite or infinite fractions and complex numbers.

Examples of perfect squares are, for example, the following numbers: 9 (square of the number 3), 49 (square of the number 7), 676 (square of the number 26). But the number 15 cannot be represented as a product of two equal integers, so it is not a perfect square.

It is interesting that the concept of a perfect square can be extended to include, for example, rational numbers. In this case, a full square is a fraction, which is the ratio of two square integers.

Как доказать что квадрат?

Если в четырехугольник можно вписать окружность и около него описать окружность, а противолежащие углы равны, то это квадрат. Если в прямоугольник можно вписать окружность, то он квадрат. Доказательство. Исходя из теоремы (если в четырехугольник вписана окружность, то суммы противолежащих сторон равны), AB+CD = BC+AD.

С помощью признаков квадрата можно доказать, что четырехугольник — квадрат.

По сторонам и углу 90°: Если в четырехугольнике все стороны равны и один из углов 90°, то это квадрат

По диагоналям: Если диагонали четырехугольника равны, перпендикулярны и делятся пополам в точке пересечения, то это квадрат

По ромбу: Если в ромбе все углы прямые, то это квадрат

По прямоугольнику: Если в прямоугольнике все стороны равны, то это квадрат

По параллелограмму: Если в параллелограмме все стороны и углы равны, то это квадрат