Основы цифровой обработки сигнала (теория к экзамену), страница 2

Амплитудно-импульсная модуляция

Амплитудно-импульсная модуляция ( АИМ) — вид импульсной модуляции ( см.), при которой от воздействия передаваемых сигналов изменяется величина ( амплитуда) импульсов.
 

Амплитудно-импульсная модуляция и метод Делфел-да — Мерфи. Среди систем с импульсной модуляцией лучше всего изучены системы с АИМ.
 

Амплитудно-импульсная модуляция по сравнению с другими видами импульсной модуляций обладает меньшей помехозащищенностью.
 

Амплитудно-импульсная модуляция является начальным этапом всех других видов импульсной модуляции. Для ее осуществления требуются довольно простые устройства, но АИМ имеет существенный недостаток — низкую помехоустойчивость. Помехи, воздействуя на амплитуду модулированного сигнала, вызывают искажение передаваемой информации, поэтому сигналы АИМ не могут передаваться по линиям. Таким образом, АИМ может быть использована только для построения внутристанционного тракта передачи.
 

Амплитудно-импульсная модуляция применяется в связи на сантиметровых волнах, в радиотелеметрии и в системах обработки данных. Модулированные импульсы обычно применяются в проводной связи и в радиосвязи в виде поднесущего колебания, модулирующей высокочастотное или сверхвысокочастотное синусоидальное несущее колебание. Импульсное поднесущее колебание может модулировать несущее колебание по амплитуде, по фазе или по частоте.
 

Амплитудно-импульсная модуляция ( АИМ) представляет собой лишь один из способов модуляции ряда одинаковых импульсов с целью передачи информации. Во всех этих системах получающийся ряд импульсов используется для модуляции амплитуды или частоты высокочастотного синусоидального колебания.
 

Спектр видеоимпульсов при амплитудно-импульсной модуляции.

Амплитудно-импульсная модуляция, как и обычная амплитудная модуляция, не позволяет срезать наслаивающиеся на импульсы помехи путем ограничения в приемном устройстве. Поэтому был предложен ряд других видов импульсной модуляции, где амплитуда импульсов остается неизменной, а полезная информация передается путем изменения других параметров импульсов.
 

Амплитудно-импульсная модуляция не требует особых пояснений, так как эна представляет собой простую комбинацию AM и ИМ. Колебания АИМ имеют приблизительно такую же ширину спектра как и немодулированная последовательность РЧ импульсов.
 

Амплитудно-импульсная модуляция не требует особых пояснений, так как на представляет собой простую комбинацию AM и ИМ. Колебания АИМ имеют приблизительно такую же ширину спектра как и немодулированнал последовательность РЧ импульсов.
 

Амплитудно-импульсная модуляция сигнала выполняется с равными интервалами времени; амплитуда преобразуется в цифровую форму и наносится на двух наборах перфокарт. Сдвиг по оси времени достигается простым смещением одной или более карт одного набора. Умножение двух функций, появляющихся в последовательных точках двух наборов карт, и усреднение являются стандартными операциями для машины этого типа. Такой вычислительный процесс медленен, но имеет то достоинство, что при нем достижима любая требуемая точность. Если этим методом выполняется большое количество корреляционных вычислений, желательно также использовать автоматическое устройство для преобразования исходных непрерывных данных в кодиро-врнную форму на перфокартах.
 

Здесь амплитудно-импульсная модуляция осуществляется коммутатором, подвижный контакт которого вращается с постоянной скоростью и обходит одна за другой ламели, соединенные с различными датчиками. Время, в течение которого имеется контакт с ламелями, определяет длительность импульсов; частота их следования F зависит от скорости вращения и числа ламелей коммутатора.
 

При амплитудно-импульсной модуляции длительность т ( ширина) импульса постоянна ( коэффициент заполнения f t / 7lpconst), а его амплитуда изменяется в функции ( обычно пропорционально) ординат кривой входного сигнала в моменты съема.
 

В амплитудно-импульсной модуляции ( АИМ) последовательность импульсов с амплитудами, пропорциональными сигналу, передается через регулярные промежутки времени. При широтно-импульсной модуляции ( ШИМ) ширина ( длительность) импульса постоянной амплитуды пропорциональна мгновенной амплитуде сигнала.
 

При амплитудно-импульсной модуляции в соответствии с законом изменения модулирующего напряжения изменяется амплитуда высокочастотных импульсов. Применяется также модуляция импульсов по длительности ( широтно-импулъсная), сдвигом импульсов по фазе ( фазо-импульсная) и ряд других вариантов.
 

Модель сигнала с частотно-импульсной модуляцией

Модель сигнала с частотно-импульсной модуляцией можно получить с использованием предыдущей модели, внеся следующие изменения. Во-первых, зададим кодовую последовательность, одинаковую для всех уровней квантования сигнала следующим кодом (Листинг 10) и введем коэффициенты сжатия импульсов дискретизации каждого уровня, что и позволит получить различную частоту их следования в зависимости от уровня первичного сигнала

Следует сказать о том, что с изменением длительности импульсов дискретизации мы изменяем и длительности пауз, при этом скважность последовательности, как видно из кодовой последовательности, равна двум. Во-вторых, очевидно, следует внести изменения и в выражения для формирования модулированного сигнала (Листинг 11)

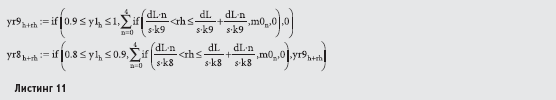
Здесь показан фрагмент измененного программного кода для формирования модулированного сигнала уровней 9 и 8. И, наконец, для заданной кодовой последовательности параметр s следует установить равным шести, тогда на протяжении каждого интервала дискретизации dS поместится три импульса и три паузы. При этом наибольшую частоту следования импульсов мы получим, когда уровень первичного сигнала y1 соответствует девятому интервалу (коэффициент сжатия импульсов дискретизации k9 = 2), наименьшую частоту следования импульсов мы получим, когда уровень первичного сигнала находится в пределах от 0 до 1 (коэффициент сжатия импульсов дискретизации k0 = 1).

В реальных системах связи полученная модулированная последовательность видеоимпульсов используется для манипуляции гармонического высокочастотного несущего колебания. Тем самым осуществляется перенос модулированных видеоимпульсов на частоту несущего колебания ?H, излучаемого непосредственно в эфир. Тогда получается вторичная или двойная модуляция. Чаще всего применяется вторичная амплитудная манипуляция. Для реализации этой операции в модели добавим следующий программный код:

Таким образом, массив s1_j есть КИМ-АТ сигнал, полученный путем первичной кодово-импульсной модуляции и вторичной амплитудной манипуляции (телеграфии). Применяя рассмотренные в статье алгоритмы формирования сигналов, читатель сможет самостоятельно создавать (или модифицировать приводимые) модели и использовать их для разработки различных радиоэлектронных устройств. В следующих статьях цикла автор планирует рассмотреть вопросы моделирования процессов взаимодействия сигналов и преднамеренных помех, используемых в аппаратуре специального назначения для радиоподавления систем связи.

Модели сигналов, рассмотренные в статье, можно посмотреть на сайте журнала http://finestreet.ru/magazine/compitech/models.rar. Для их открытия и моделирования необходимо наличие установленной на ПК системы MathCAD 2001.

Фазовая манипуляция

В современных цифровых РРЛ применяются двоичная, 4-уровневая и 8-уровневая ФМ.

При демодуляции фаза ФМ радиосигнала сравнивается с фазой восстановленного на приемном конце опорного колебания (несущей).

Из-за случайных искажений радиосигнала может иметь место неопределенность фазы восстановленной несущей, что является причиной так называемой обратной работы, при которой двоичные посылки принимаются за «негатив». Для устранения этого явления применяется разностное кодирование фазы передаваемых радиоимпульсов. Такую манипуляцию фазы называют фазоразностной или относительно фазовой манипуляцией ОФМ.

В цифровых РРЛ с ОФМ при передаче информации кодируется не сама фаза радиосигнала, а разность фаз (фазовый сдвиг) двух соседних радиоимпульсов.

Правило кодирования при ОФМ приведено на рис. 38.

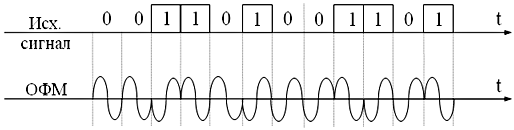
Рис.38

Здесь:	переход	1→1	— скачек фазы
		1→0	— нет скачка фазы
		0→0	— нет скачка фазы
		0→1	— скачек фазы.

При двоичной ОФМ длительность радиоимпульса τ=Т. В случае многоуровневой манипуляции (М>2) исходная последовательность двоичных элементов длительностью Т с помощью кодера модулятора преобразуется в совокупность двух (при М=4) или трех (при М=8) последовательностей двоичных элементов длительностью τ=2Т (при М=4) или τ=3Т (при М=8).

Комбинация двоичных элементов получаемых последовательностей используются при кодировании фазового сдвига при ОФМ.

Например. При 4-уровневом ОФМ, фазовый сдвиг кодируется следующим образом:

Символ первой последовательности	1	1
Символ второй последовательности	1	1
Фазовый сдвиг	π/2	π	3π/2

Применяются два способа демодуляции ОФМ радиосигналов. В первом вначале восстанавливается несущая и когерентно детектируется ОФМ радиосигнала, затем разностно (диффференциально) декодируются принимаемые сигналы рис. 39.

Рис.39

Второй способ предполагает дифференциально-когерентное (автокорреляционное) детектрирование ОФМ радиосигнала, при котором в качестве опорного колебания используется предшествующий радиоимпульс. При этом операция детектирования и декодирования совмещены рис. 40.

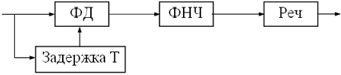
Рис.40

Модемы цифровых трактов

Модуляция обычно осуществляется по ПЧ.

Схема имеет вид (рис. 43) при ОФМ-2 и (рис. 44) при ОФМ-4.

В преобразователе кода модулятора КМ бинарный сигнал разбивается на две бинарные последовательности с удвоенной длительностью импульса, которые методом разностного кодирования преобразуются в двухуровневые последовательности. Полученные сигналы поступают через ФНЧ на ФМ, представляющие собой перемножители соответственно синфазного и квадратурного каналов. Опорные колебания, подаваемые с генератора на вторые входы этих перемножителей, сдвинуты друг относительно друга на 90° посредством фазовращателя ФВ. Каждый из перемножителей осуществляет линейную балансную АМ. Сигнал ОФМ-4 получается путем сложения модулированных сигналов синфазного и квадратурного каналов.

Рис.43

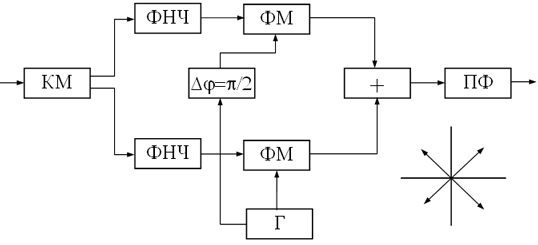
Рис.44

Сигнал КАМ-16 получают сложением двух сигналов ОФМ-4, один из которых в 2 раза больше другого по амплитуде. Структурная схема приведена на рис.45

Рис.45

Сигналы двух модулированных квадратурных составляющих ОФМ-4 складываются между собой, образуя многопозиционный сигнал с ОФМ и КАМ.

Модель сигнала с времяимпульсной модуляцией

При этом виде модуляции положение импульса на временной оси пропорционально амплитуде модулирующего сигнала, поэтому выражение для формирования временного представления Y_j следует преобразовать к виду (Листинг 7).

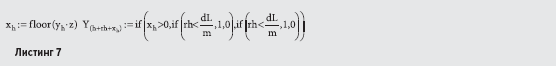
Параметр модели x_h представляет собой коэффициент, обеспечивающий сдвиг начала импульсов дискретизации, вычисляется как целое значение от амплитудного отсчета первичного сигнала, умноженного на коэффициент глубины модуляции z. Сдвиг начала импульсов дискретизации (функции Y_j) осуществляется путем приращения индексов на величину x_h. Результаты моделирования колебания с времяимпульсной модуляцией представлены на рис. 5.

Рис. 5. Результаты моделирования колебания с времяимпульсной модуляцией

На временном представлении сигнала с времяимпульсной модуляцией показаны моменты снятия амплитудных отсчетов первичного колебания, позволяющие оценить глубину модуляции.

Слайд 31МНОГОПОЗИЦИОННЫЕ СИГНАЛЫДля разных видов манипуляции существуют методы, позволяющие передавать

не только 0 и 1 в рамках одного сигнала, такие методы получили название многопозиционные. Суть этих методов в том, что один элемент линейного сигнала несет информацию о большем числе битов, чем в обычных двухпозиционных методах. Работает это очень просто. Например, в многопозиционной амплитудной манипуляции зададим не 2 амплитуды, которые будут кодировать 0 или 1, а 4, которые будут соответствовать 00, 01, 10, 11 по мере увеличения амплитуды. Для многопозиционной частотной манипуляции используется больше частот, а для многопозиционной фазовой манипуляции, соответственно, больше сдвигов. Да, это действительно позволяет повысить удельную скорость передачи информации, но при этом начинают возникать ошибки, связанные с погрешностью передачи.

Возможно, вам также будет интересно

В данной статье рассмотрены проблемы, возникающие при построении токового зеркала, и способы их решения, причины рассогласования элементов и способы их устранения. Также приведены методы построения топологии токовых зеркал и даны их сравнительные характеристики. Особое внимание уделено правилам построения топологии согласованных элементов, в частности транзисторов. Введение Токовые зеркала широко используются при проектировании интегральных микросхем, работающих в

Драйверы International Rectifier Фирма International Rectifier (IR) давно и хорошо известна в России как производитель силовых транзисторов и интегральных микросхем управления. Выпускаемые IR драйверы предназначены для работы в любых конфигурациях силовых каскадов в диапазоне мощности до 3–5 кВт. Технология производства микросхем управления HVIC вобрала в себя все достижения высоковольтных технологий, поэтому будет логично начать обзор

В предлагаемой вниманию читателей статье рассматриваются два частных вопроса работы с САПР Quartus. Фирма Altera наделила свой пакет огромным количеством разнообразных возможностей. Оборотной стороной этого является некоторая трудоемкость освоения на начальном этапе. Статья предназначена для инженеров, недавно начавших работать с пакетом Quartus. Автор будет рад, если приведенные здесь материалы помогут им сэкономить немного времени.

Слайд 19 При цифровой модуляции используют чаще всего дискретные

последовательности двоичных символов — двоичных кодов. Закодированный первичный аналоговый сигнал e(t), представляющий собой последовательность кодовых символов {еn} = еn (k)  (n = О, 1, 2, 3, … — порядковый номер символа; к — номер позиции кода; m — основание кода, т. е. число различных его элементов, которые преобразуются в последовательность элементов (посылок) сигнала {Un(t)} путем воздействия кодовых символов на высокочастотное несущее колебание UН(t). Как правило, используют двоичные коды т.е. m=2. Обычно посредством модуляции частота или фаза несущего в радиоимпульсе изменяется по закону, определяемому цифровым кодом.

ЦИФРОВАЯ МОДУЛЯЦИЯ

2.5. Спектры хаотических (шумовых) колебаний

Хаотическое
колебание

s
(t
)
—
это
случайный
процесс
.
Каждая его реализация в неизменных
условиях не повторяется, является
уникальной. В электронике хаотические
колебания связаны с шумами

— колебаниями токов и напряжений,
изменяющихся случайным образом вследствие
беспорядочного движения носителей
зарядов. В данном контексте хаотические
и шумовые колебания считаются синонимами.

Рис.
7.

Структурная
схема измерения среднего квадрата
шумового напряжения

Шумовое
колебание

можно описать в частотном представлении:
ему сопоставляют некую спектральную
характеристику, причем для случайного
процесса она непрерывна. Теоретические
основы спектрального разложения
хаотических колебаний изложены в . Не
погружаясь в строгую теорию, объясним
методику экспериментального исследования
статистических параметров шумового
напряжения

s
(t
)
по схеме, показанной на рис. 8.

Рис.
8.

Схема измерения спектральной плотности
интенсивности шумового напряжения

Пропустим
шумовое напряжение s
(t
)
через фильтр, выделяющий энергию
колебаний в узкой полосе

вблизи частоты f
.
При соблюдении условия
f

колебание на выходе фильтра будет
напоминать синусоиду с частотой f
.
Однако амплитуда и фаза этой синусоиды
подвержены хаотическим изменениям. С
уменьшением полосы пропускания фильтра
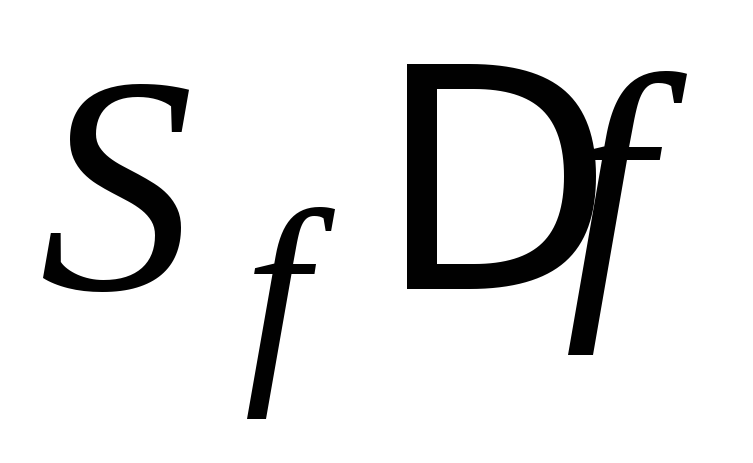форма выходного колебания все более
приближается к синусоиде. Амплитуда ее
уменьшается, но отношение среднего
квадрата напряжения, прошедшего через
фильтр (),
к ширине полосы

остается конечным и при последовательном
уменьшении полосы стремится к определенному
пределу W
(f
):

Предельную
величину W
(f
)
называют спектральной
плотностью интенсивности
процесса
s
(t
).

Она равна средней интенсивности
гармонических составляющих, приходящихся
на единичный интервал оси частот. При
измерении W
(f
)
используют узкополосный перестраиваемый
фильтр, который можно настроить на любую
частоту в заданном диапазоне измерений.
Шумовое напряжение, прошедшее сквозь
фильтр, подвергают квадратичному
детектированию и усредняют (интегрируют).
В результате получают средний квадрат:

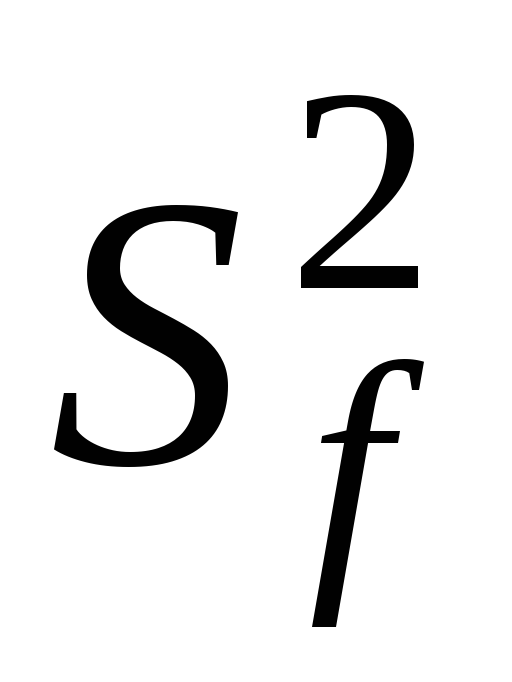
. Далее по известной полосе фильтра

вычисляют W
(f
).
Полную
интенсивность процесса

— средний квадрат

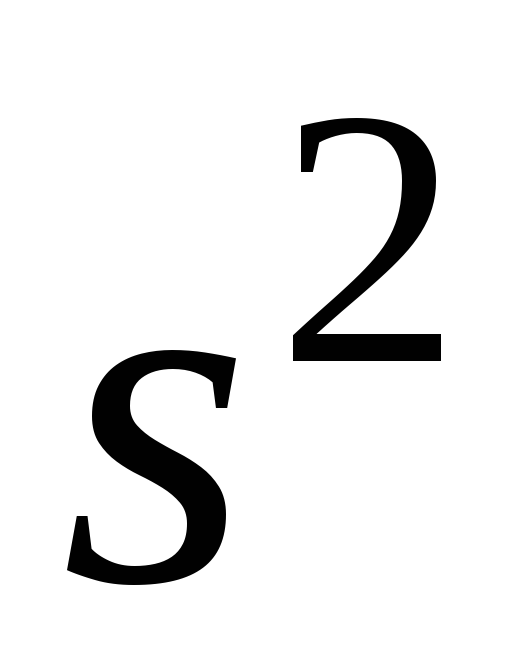
— находят интегрированием спектральных
составляющих шума по всем частотам:

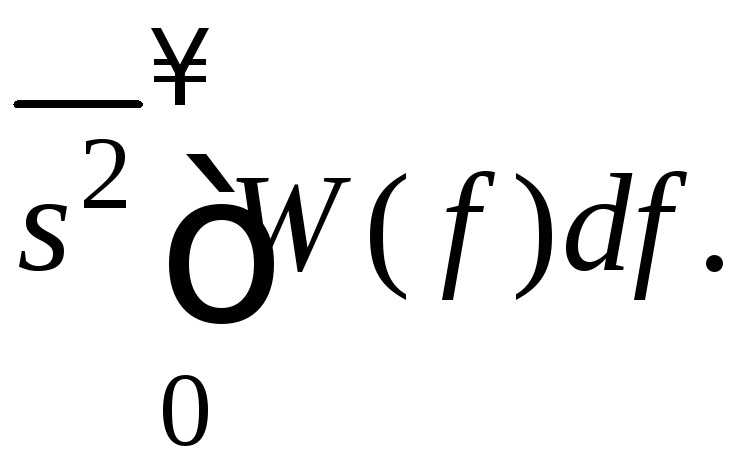(10)

Для
подготовки к работе следует изучить в
полном объеме данное пособие. Более
подробные сведения по теме лабораторной
работы можно найти в главе «Частотные
спектры электрических колебаний,
спектральный анализ» книги .

Манипуляция в цифровых РРЛ

Модуляция в цифровых РРЛ называют манипуляцией. В зависимости от числа уровней М манипулирующего сигнала различают двухуровневую (двоичную) и многоуровневую манипуляцию.

Для многих видов манипуляции, применяемых в цифровых РРЛ, предполагается использование манипулирующих сигналов, отличающихся по структуре от исходного передаваемого сигнала. Для формирования указанных манипулирующих сигналов применяется специальные кодирующие устройства — кодер модулятора.

При демодуляции осуществляется обратное преобразование, т.е. декодер. Перед декодером осуществляется регенерация посылок.

Обобщенная схема выглядит следующим образом рис.36.

Рис.36

В современных цифровых РРЛ применяются амплитудная, фазовая, частотная и комбинированная — амплитудно-фазовая манипуляция.

Сравнение PAM, PWM и PPM

Сравнение описанных выше процессов модуляции представлено в единой таблице.

PAM	ШИМ	PPM
Амплитуда варьируется	Ширина варьируется	Позиция варьируется
Полоса пропускания зависит от ширины импульса	Полоса пропускания зависит от времени нарастания импульса	Полоса пропускания зависит от времени нарастания импульса
Мгновенная мощность передатчика зависит от амплитуды импульсов.	Мгновенная мощность передатчика зависит от амплитуды и ширины импульсов.	Мгновенная мощность передатчика остается постоянной в зависимости от ширины импульсов.
Сложность системы высокая	Сложность системы низкая	Сложность системы низкая
Шумовые помехи высокие	Шумовые помехи низкие	Шумовые помехи низкие
Это похоже на амплитудную модуляцию	Это похоже на частотную модуляцию	Это похоже на фазовую модуляцию

Статические параметры

• Максимальный (Vref) и минимальный (обычно 0) уровни входного сигнала — устанавливают диапазон шкалы преобразования, относительно которой будет оцениваться входной сигнал (рис. 1). Также этот параметр может обозначаться как FS — full scale. Для дифференциального АЦП шкала определяется от -Vref до +Vref, однако для упрощения далее будем рассматривать только single-ended шкалы.
• Разрядность (N) — разрядность выходного кода, характеризующая количество дискретных значений (), которые преобразователь может выдать на выходе (рис. 1).
• Ток потребления (Idd) — сильно зависит от частоты преобразования, поэтому информацию об этом параметре лучше искать на соответствующем графике.
• МЗР (LSB) – младший значащий разряд (Least Significant Bit) — минимальное входное напряжение, разрешаемое АЦП (по сути единичный шаг в шкале преобразования). Определяется формулой: (рис. 1).
• Ошибка смещения (offset error) – определяется как отклонение фактической передаточной характеристики АЦП от передаточной характеристики идеального АЦП в начальной точке шкалы. Измеряется в долях LSB. При ошибке смещения переход выходного кода от 0 в 1 происходит при входном напряжении отличном от 0.5LSB (рис. 2).Рис. 2: Ошибка смещения
  Существует и другой вариант квантователя, когда переход осуществляется при целых значения LSB (характеристика у него будет смещена относительно первого варианта, который представлен на рисунке 2). Оба этих квантователя равноправны, и для простоты далее будем рассматривать только первый вариант.
• Ошибка усиления (gain error) – определяется как отклонение средней точки последнего шага преобразования (которому соответствует входное напряжение Vref) реального АЦП от средней точки последнего шага преобразования идеального АЦП после компенсации ошибки смещения (рис. 3).Рис. 3: Ошибка усиления
• Дифференциальная нелинейность (DNL — Differential nonlinearity) – отклонение ширины ступеньки на передаточной характеристике реального АЦП от номинальной ширины ступеньки у идеального преобразователя. Из-за дифференциальной нелинейности шаги квантования имеют различную ширину (рис. 4).
  Рис. 4: Дифференциальная нелинейность
  Для 3-х битного АЦП с рисунка 4:
• Интегральная нелинейность ( INL — Integral nonlinearity) – разница по вертикали между реальной и идеальной характеристикой преобразования (рис. 5). INL можно интерпретировать как сумму DNL. Отрицательная INL указывает на то, что реальная характеристика находится ниже идеальной в данной точке шкалы. Для положительной INL реальная характеристика находится выше идеальной. Распределение DNL определяет интегральную нелинейность АЦП.
  Рис. 5: Интегральная нелинейность
• Общая нескорректированная ошибка ( TUE — Total Unadjusted Error) – абсолютная ошибка, включающая в себя следующие ошибки: квантования, смещения, усиления и нелинейности. Другими словами, это максимальное отклонение между реальной и идеальной характеристикой преобразования. Для идеального АЦП TUE = 0.5LSB, обусловлена ошибкой квантования (или шум квантования — возникает из-за округления значения аналогового сигнала, которое соответствует цифровому коду). Ошибки усиления и смещения обычно вносят наиболее весомый вклад в абсолютную ошибку. Однако с точки зрения динамических параметров (см. ниже) ошибки смещения и усиления ничтожны, так как они не порождают нелинейных искажений.

Позиционная импульсная модуляция

Pulse Position Modulation (PPM) является аналогом схемы модулирующей, в которой амплитуда и ширина импульсов поддерживаются постоянная, в то время как положение каждого импульса, со ссылкой на позицию опорного импульса изменяется в зависимости от мгновенного дискретизированного значения сигнала сообщения.

Передатчик должен посылать синхронизирующие импульсы (или просто синхронизирующие импульсы), чтобы поддерживать синхронизацию передатчика и приемника. Эти синхроимпульсы помогают поддерживать положение импульсов. На следующих рисунках поясняется импульсная позиционная модуляция.

Позиционная импульсная модуляция выполняется в соответствии с сигналом с широтно-импульсной модуляцией. Каждое завершение сигнала с широтно-импульсной модуляцией становится отправной точкой для импульсов в сигнале PPM. Следовательно, положение этих импульсов пропорционально ширине импульсов ШИМ.

Слайд 33 КЛАССИФИКАЦИЯ ВИДОВ МОДУЛЯЦИИ С РАСШИРЕНИЕМ СПЕКТРА ФАЗОВАЯ (ОТНОСИТЕЛЬНО ФАЗОВАЯ)

МОДУЛЯЦИЯ НЕСУЩЕГО КОЛЕБАНИЯ ЦИФРОВОЙ КОДОВОЙ ПОСЛЕДОВАТЕЛЬНОСТЬЮ С ЧАСТОТОЙ СЛЕДОВАНИЯ СИМВОЛОВ, ВО МНОГО РАЗ ПРЕВОСХОДЯЩЕЙ СКОРОСТЬ ПЕРЕДАЧИ ИНФОРМАЦИОННЫХ СИГНАЛОВ.Системы связи, использующие этот метод, получили название систем с фазоманипулированными широкополосными сигналами (ФМ-ШПС). В настоящее время в различной технической литературе можно найти аналогичное название данного метода, например расширение спектра методом прямой последовательности (DSSS — Direct Sequence Spread Spectrum);МОДУЛЯЦИЯ НЕСУЩЕГО КОЛЕБАНИЯ ПУТЕМ ИЗМЕНЕНИЯ (СДВИГА) ЕГО ЧАСТОТЫ В ДИСКРЕТНЫЕ МОМЕНТЫ ВРЕМЕНИ. Такой метод называется псевдослучайной, или программной, перестройкой рабочих частот (ППРЧ), что аналогично расширению спектра методом перескока частоты (FHSS — Frequency Hopping Spread Spectrum) с точки зрения происходящих физических процессов.

Оконечная аппаратура цифрового ствола

Скремблер-дескремблер. Кроме преобразования кода в оконечном оборудовании производится операция скремблирования-дискремблирования Скр-Декр. Скремблер Скр облегчает условия выделения тактовой частоты в демодуляторе, а также устраняет дискретные компоненты в спектре передаваемого сигнала, затрудняющие выполнение требований электромагнитной совместимости. В скремблере преобразуется статистическое распределение вероятности появления нулей и единиц в бинарном сигнале для придания передаваемому по тракту цифровому сигналу свойства случайной последовательности. Для этого осуществляется сложение по модулю 2 информационного сигнала и М-последовательности (псевдослучайной последовательности с периодом 2м).

При пропадании входного сигнала или при повышении коэффициента ошибок до 10-3 в оконечном цифровом оборудовании в направлении передачи передаются сигнал индикации аварийного состояния СИАС, содержащей одни единицы рис.42.

Рис.42

РРС с цифровыми методами передачи информации

В начале (в 60-х годах) использовались РРС построенные по схеме ИКМ-ВРК-ЧМ. Эта схема передачи по сравнению с ИКМ-ВРК-АМ давала ряд преимуществ. Однако в последнее время во второй ступени модуляции стал использоваться оптимальный метод передачи — относительно фазовая манипуляция (ОФМ) или ее еще называют фазо-разностная манипуляция (ФРМ). Этот метод обеспечивает по сравнению с ЧМ выигрыш по полосе более чем в 2 раза, а по помехоустойчивости 3 дБ.

Используя этот метод строят специализированные цифровые РРС (ЦРРС) с ИКМ-ВРК-ОФМ, они в ряде случая успешно конкурируют с системами ОБП-ЧРК-ЧМ.

Основным достоинством ЦРРС является возможность регенерации сигнала на каждой ПС, что позволяет практически полностью «очистится» от помех, пока не произойдет сбой символа («грубая» аномальная ошибка). Но вероятность «сбоя» зависит от превышения уровня сигнала над пороговым. Практически ЦРРС нечувствительны к шумам, если сигнал превышает уровень шумов на 20-25 дБ.

Для ЦРРС выделен диапазон частот выше 10 ГГЦ. Суммарная полоса выделенная для ЦРРС составляет около 14 ГГц.

Основной проблемой освоения этого диапазона является большое затухание сигналов на трассе из-за влияния гидрометеоров (дождь, снег и т.д.).

Это приводит к необходимости сокращать интервалы и увеличивать количество ПС. Для ЦРРС это не является существенным, так как в отличии от аналоговых методов передачи, в цифровых за счет регенерации не происходит наполнения помех.

Для расчета ЦРРС пользуются данными по сравнительной характеристики основных методов модуляции. Эти данные приводятся при условии, что вероятность ошибки равна 10-6. По этим данным определяется минимально допустимая мощность сигнала на входе приемника Р_пор.

Нормы МККР на устойчивость ЦРРС установлены и согласно ей — среднеминутная псофометрическая мощность шума может превышать 50000 пВт в течение не более 0,1% времени любого месяца.

Дальнейший расчет проводится как для аналоговых систем, т.е. определяют условие обеспечения требуемой устойчивости связи, когда мощность сигнала на входе приемника ЦРРС превышает Р_пор в течение (1 — 0,1/п_с)% времени любого месяца (п_с — число интервала).