Разложение рациональной функции в ряд

Извлечение отрицательного корня

Существуют вещественные числа, из которых невозможно извлечь корень, т.е. решения нет. А вот из комплексных чисел можно извлекать корень. Для начала узнаем, что это за числа.

Определение

Вещественные (действительные) числа— это рациональные и иррациональные числа, которые можно записать в форме конечной или бесконечной десятичной дроби.

Комплексные числа — это выражение, в котором есть:

• вещественные числа a и b;
• i — мнимая единица.

Итак, чтобы извлечь корень из отрицательного числа, нужно помнить, что если знаменатель является нечётным, то число под знаком корня может оказаться отрицательным.

Далее, чтобы провести эту операцию с отрицательным числом, перейдем к следующим действиям:

1. Извлекаем корень из противоположного ему положительного числа.
2. Ставим перед полученным числом знак минус.

Пример 1:

1. Преобразуем выражение ⁵√-12 640/32 так, чтобы вместо отрицательного числа под корнем оказалось положительное:

⁵√-12 640/32 = -⁵√12 640/32

2. Избавимся от смешанного числа, заменив его обыкновенной дробью:

 -⁵√12 640/32= -⁵√1024/32

3. С помощью правила извлечения корней из обыкновенной дроби, начнем извлекать:

-⁵√1024/32 = — ⁵√1024/⁵√32.

4. Теперь нужно вычислить корни в числителе и знаменателе:

— ⁵√1024/⁵√32 = — ⁵√4⁵/⁵√2⁵ = — 4/2 = -2.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Квадраты натуральных чисел

Основной является таблица квадратов натуральных чисел:

	1	2	3	4	5	6	7	8	9
1	4	9	16	25	36	49	64	81
1	100	121	144	169	196	225	256	289	324	361
2	400	441	484	529	576	625	676	729	784	841
3	900	961	1024	1089	1156	1225	1296	1369	1444	1521
4	1600	1681	1764	1849	1936	2025	2116	2209	2304	2401
5	2500	2601	2704	2809	2916	3025	3136	3249	3364	3481
6	3600	3721	3844	3969	4096	4225	4356	4489	4624	4761
7	4900	5041	5184	5329	5476	5625	5776	5929	6084	6241
8	6400	6561	6724	6889	7056	7225	7396	7569	7744	7921
9	8100	8281	8464	8649	8836	9025	9216	9409	9604	9801

Она, пожалуй, самая распространенная среди школьников. Если в какой-то важный момент она вам необходима, но у вас отсутствует к ней доступ, можно воспользоваться несколькими хитростями:

1. Чтобы быстро возвести в квадрат число, на конце которого 0, можно добавить к нему парочку нулей: 80×80=6400; 30×30=900. Т.е., первые цифры умножаем и дописываем два 0 к этому числу.
2. Теперь возьмём какое-нибудь число так, чтобы вторая его цифра оканчивалась на 5. Так, например, число 75. Чтобы быстро возвести его в квадрат, прибавьте к первой цифре единицу, из чего получаются цифры 7 и 8.
3. Умножаем их и приписываем в конец число 25 и получаем конечный результат в виде числа 5625.

Поразрядное нахождение значения корня

Мы разобрали несколько методов, которые вы можете выбрать на своё усмотрение. Однако, есть еще один, который может понадобиться в таких ситуациях, когда нужно знать полное значение корня, а число, находящееся под корнем нельзя представить в виде n-ной степени определенного числа.

Для таких случаев существует алгоритм поразрядного нахождения значения корня, который нужно использовать, чтобы получить нужное количество значений определяемого числа.

Пример 1:

Итак, чтобы в этом разобраться, найдем значение квадратного корня из 7:

1. Находим значение разряда единиц, перебирая значения 0, 1, 2, …, 9, в это же время вычисляя их во 2 степени до нужного значения, которое больше подкоренного числа 7. Значение ряда единиц равняется 2 (потому как 2² < 7, а 2³ > 7).

2. Следующий на очереди — разряд десятых. Здесь мы будем возводить в квадрат числа: 2.0, 2.1, 2.2, …, 2.9, сравнивая результат с нужным нам числом 7. Так как 2.6² < 7, а 2.7² > 7, то значение десятых равняется 6.

3. Значение сотых. По аналогии находим приближенное значение к 7.

2.64² = 6,9696 подходит нам, так как 2.65²=7.0225, а это больше 7. Действуя таким же образом, можно и дальше находить значение √7 ≈ 2.64.

Теперь, когда мы разобрались с извлечением корней, перейдем к практике. Специально для вас составлены задания с ответами, чтобы вы попробовали воспользоваться приобретенными знаниями. Решайте без таблиц и калькулятора.

Задания для отработки материала

1 задание

а)√324

б)√900

в)√1369

2 задание

а)³√531,441

б)³√166,375

3 задание

а) ⁵√-14 2471/1024

б) ⁵√-5 1182/3125

4 задание

а)Найдите квадратный корень из 3.

б)Найдите квадратный корень из 5.

в)Найдите квадратный корень из 9.

Ответы с решением

1 задание

а)√324

1)2×2×3×3×3×3=2²×3⁴=√324, а чтобы извлечь, мы умножаем:

2)2×3×3=18. Получается, √324=18.

б)√900

1)2×2×3×3×5×5=2²×3²×5²=√900.

Извлекаем:

2)2×3×5=30. Мы получили √900=30.

в)√1369

1)37×37=37²=√1369.

А здесь мы оставляем 37, так как это единственное число в квадрате. Конечным ответом будет: √1369=37.

2 задание

а)³√531441.

1)3×3×3×3×3×3×3×3×3×3×3×3=3¹²=³√531441.

Разложили на простые множители, а теперь найдем квадратный корень.

2)3¹² это 3×3×3×3, т.к. 3 у нас в 12 степени. Это можно проверить, отняв из 12 столько троек, чтобы вышел 0: 12-3-3-3-3. Так что, 3⁴=81; ³√531441=81.

3)1000=10³.  

4)³√531441/³√1000=81/10=8,1.

б)³√166,375.

1) 5×5×5×11×11×11=5³×11³=³√166375.

2)5³×11³=55. Так как числа в кубе – они в степени 1.

3) 1000=10³.  

4)³√166375/³√1000=55/10=5,5.

3 задание

а)

1) ⁵√-14 2471/1024 = -⁵√14 2471/1024.

2) -⁵√14 2471/1024= -⁵√16801/1024.

3) -⁵√16801/1024 = — ⁵√16801/⁵√1024.

4) ⁵√16801/⁵√1024 = — ⁵√6⁵/⁵√4⁵ = — 6/4 = — 1,5.

б)

1) ⁵√-5 1182/3125 = -⁵√5 1182/3125.

2) -⁵√5 1182/3125= -⁵√16807/3125.

3) -⁵√16807/3125 = — ⁵√16807/⁵√3125.

4) ⁵√16807/⁵√3125 = — ⁵√7⁵/⁵√5⁵ = — 7/5 = — 1,4.

4 задание

а)√3≈1,73.

б√5≈2,23.

в)√8≈2,82.

Элементарные функции комплексного переменного.

Показательная, гиперболические и тригонометрические функции комплексного переменного \(z\) определятся соответственно формулами
$$
e^{z} = \sum_{n = 0}^{\infty} \frac{z^{n}}{n!},\label{ref42}
$$
$$
\operatorname{ch} z = \sum_{n = 0}^{\infty} \frac{z^{2n}}{(2n)!},\label{ref43}
$$
$$
\operatorname{sh} z = \sum_{n = 0}^{\infty} \frac{z^{2n + 1}}{(2n + 1)!},\label{ref44}
$$
$$
\cos z = \sum_{n = 0}^{\infty} \frac{(-1)^{n}z^{2n}}{(2n)!},\label{ref45}
$$
$$
\sin z = \sum_{n = 0}^{\infty} \frac{(-1)^{n}z^{2n + 1}}{(2n + 1)!}.\label{ref46}
$$
Радиус сходимости \(R\) каждого из рядов \eqref{ref42}-\eqref{ref46} равен \(+\infty\). Заменяя в равенстве \eqref{ref42} \(z\) на \(iz\) и \(-iz\), получаем
$$
e^{iz} = \sum_{n = 0}^{\infty} \frac{i^{n}z^{n}}{n!},\qquad e^{-iz} = \sum_{n = 0}^{\infty} \frac{(-1)^{n}i^{n}z^{n}}{n!}.\label{ref47}
$$

Используя равенства \eqref{ref47} и формулы \eqref{ref45}, \eqref{ref46}, находим
$$
\frac{e^{iz} + e^{-iz}}{2} = \cos z,\ \frac{e^{iz}-e^{-iz}}{2i} = \sin z,\label{ref48}
$$
откуда следует, что
$$
e^{iz} = \cos z + i \sin z.\label{ref49}
$$
Полагая в формуле \eqref{ref42} \(z = z_{1}\) и \(z = z_{2}\). и перемножая соответствующие ряды, можно показать, что
$$
e^{z_{1}}e^{z_{2}} = e^{z_{1} + z_{2}}.\label{ref50}
$$

Пусть \(z = x + iy\), где \(x \in R\), \(y \in R\). Тогда из равенства \eqref{ref50} и формулы \eqref{ref49} находим
$$
e^{z} = e^{x + iy} = e^{x}(\cos y + i \sin y).\label{ref51}
$$
Из формулы \eqref{ref51} следует, что
$$
e^{z + 2\pi i} = e^{z},\nonumber
$$
то есть \(e^{z}\) — периодическая функция с периодом \(2\pi i\). Поэтому для каждого комплексного \(z \neq 0\) уравнение
$$
e^{w} = z\label{ref52}
$$
имеет бесконечное множество решений вида \(w + i2\pi n\), где \(w\) — одно из решений уравнения \eqref{ref52}, \(n \in Z\).

Если \(w = u + iv\), то \(z = e^{w} = e^{u}(\cos v + i \sin v)\), откуда получаем
$$
|z| = e^{u},\quad u = \ln |z|,\quad v = \arg z.\nonumber
$$

Пусть \(\varphi\) — какое-нибудь значение аргумента числа \(z\). Тогда
$$
v = \varphi + 2\pi n,\ n \in Z.\nonumber
$$
Таким образом, все решения уравнения \eqref{ref52}, если их обозначить символом \(\operatorname{Ln}\ z\), задаются формулой
$$
\operatorname{Ln}\ z = \ln |z| + i(\varphi + 2\pi n),\label{ref53}
$$
где \(\varphi\) — одно из значений аргумента числа \(z\) \((z \neq 0)\), \(n \in Z\).

По заданному значению \(z\) значение \(w\) из уравнения \eqref{ref52} определяется, согласно формуле \eqref{ref53}, неоднозначно (говорят, что логарифмическая функция \(\operatorname{Ln}\ z\) является многозначной).

Пример 4.

Разложить в степенной ряд в окрестности точки \(z = 0\) функцию \(f(z) = e^{z}\sin z\).

\(\triangle\) Используя формулы \eqref{ref48} и \eqref{ref50}, получаем
$$
f(z) = e^{z}\left(\frac{e^{iz}-e^{-iz}}{2i}\right) = \frac{1}{2i}(e^{z(1 + i)}-e^{z(1-i)}).\nonumber
$$
Так как \(1 + i = \sqrt{2}e^{i\pi/4}\), \(1-i = \sqrt{2}e^{-i\pi/4}\), то по формуле \eqref{ref42} находим
$$
f(z) = \sum_{n = 0}^{\infty} \frac{2^{n/2}}{n!} \left(\frac{e^{i\pi n/4}-e^{-i\pi n/4}}{2i}\right)z^{n},\nonumber
$$
откуда в силу второго из равенств \eqref{ref48} следует, что
$$
e^{z}\sin z = \sum_{n = 0}^{\infty} \frac{2^{n/2}}{n!} \sin \frac{\pi n}{4}z^{n}.\nonumber
$$
Радиус сходимости ряда \(R = +\infty\). \(\blacktriangle\)

How to calculate the Taylor series?

Here is an example solved by our Taylor expansion calculator.

Example 

Find Taylor series of sinx up to order four and the center point is 3.

Solution 

Step 1: Identify the given terms.

f(x) = sin(x)n = 4a = 3

Step 2: Now write the Taylor series expansion formula for n=4 & a=3.

\(F\left(x\right)=\sum _{n=0}^4\left(\frac{f^n\left(a\right)}{n!}\left(x-a\right)^n\right)\)

\( F\left(x\right)=\frac{f\left(a\right)}{0!}\left(x-3\right)^0+\frac{f\:’\left(a\right)}{1!}\left(x-3\right)^1+\frac{f\:»\left(a\right)}{2!}\left(x-3\right)^2+\frac{f\:»’\left(a\right)}{3!}\left(x-3\right)^3+\frac{f^{iv}\left(a\right)}{4!}\left(x-3\right)^4\) …(1)

Step 3: Now calculate the derivative of sinx up to order four.

\(f\left(a\right)=sin\left(a\right)\)

\(f’\left(a\right)=cos\left(a\right)\)

\(f»\left(a\right)=-sin\left(a\right)\)

\(f»’\left(a\right)=-cos\left(a\right)\)

\(f^{iv}\left(a\right)=sin\left(a\right)\)

Step 4: Now expand the above formula up to n=4.

For n = 0

\(\frac{sin\left(3\right)}{0!}\left(x-3\right)^0=sin\left(3\right)\)

For n = 1

\(\frac{cos\left(3\right)}{1!}\left(x-3\right)^1=\left(x-3\right)cos\left(3\right)\)

For n = 2

\(\frac{-\sin \left(3\right)}{2!}\left(x-3\right)^2=-\frac{1}{2}\left(x-3\right)^2\sin \left(3\right)\)

For n = 3

\(\frac{-cos\left(3\right)}{3!}\left(x-3\right)^3=-\frac{1}{6}\left(x-3\right)^3cos\left(3\right)\)

For n = 4

\(\frac{sin\left(3\right)}{4!}\left(x-3\right)^4=\frac{1}{24}\left(x-3\right)^4sin\left(3\right)\)

Step 5: Now put the above calculated values in (1).

\(F\left(x\right)=sin\left(3\right)+\left(x-3\right)cos\left(3\right)-\frac{1}{2}\left(x-3\right)^2sin\left(3\right)-\frac{1}{6}\left(x-3\right)^3cos\left(3\right)+\frac{1}{24}\left(x-3\right)^4sin\left(3\right)\)

Формула бинома Ньютона

Данная формула, записанная таким образом, существует давно. Эти знания были доступны еще математикам Индии и Персии. Формула бинома была сформулирована и введена в использование Ньютоном с целью демонстрации обобщенного случая при показателе степени в виде некоего числа из множества действительных. Спустя время формула была распространена и на комплексные числа. Общий случай бинома является рядом, не имеющим окончания. 

Упростить и ускорить процесс, при котором раскладывают степень на слагаемые, можно, если прибегнуть к треугольнику Паскаля.

Заметим, что формула бинома Ньютона представляет собой частный случай разложения функции  в ряд Тейлора:

Здесь для r допустимы какие-либо значения из множества комплексных чисел, то есть это может быть число со знаком минус или вещественное число. Для того чтобы определить коэффициенты записанного разложения, следует воспользоваться следующей формулой:

Рассмотрим полученную последовательность элементов:

Сделаем вывод, что схождение данного ряда возможно при соблюдении условия:

Рассмотрим частный случай, когда:

В такой ситуации справедливо следующее тождество:

В том случае, когда , допустим переход к пределу. Целесообразно воспользоваться вторым замечательным пределом:

Основываясь на записанных выше свойствах, представим следующее тождество:

Данное соотношение и его объяснение первым удалось вывести Эйлеру.

Допустимо обобщение бинома Ньютона таким образом, что результатом является полином Ньютона.

Суммируются индексы , имеющие целое значение и являющиеся неотрицательными. При сложении они дают n. Таким образом, сумма берется по всем композициям числа n длины m. Применение полинома Ньютона возможно при условии, что:

Это выполняется даже в том случае, когда 

Имеется два способа доказательства мультиномиальной теоремы:

• индукция по n;
• комбинаторные соображения и комбинаторный смысл, которыми обладает мультиномиальный коэффициент.

В том случае, когда m=2, можно выразить  . В итоге получается бином Ньютона.

Предположим, что:

При этом для полных полиномов Белла характерно биномиальное разложение:

Разложение многочленов на множители по формулам суммы кубов и разности кубов.

12+

4 месяца назад

Математика от Баканчиковой255 подписчиков

Алгебра 7 класс. Как разложить многочлен на множители с помощью формул сокращенного умножения суммы кубов и разности кубов? Сегодня, продолжая говорить о разложении многочленов на множители, мы ответим на этот вопрос. А чтобы Вы легко поняли и запомнили новый материал, вначале мы напомним Вам, как получаются формулы суммы кубов и разности кубов

Обратим Ваше внимание на то, чем отличаются формулы суммы и разности кубов. Дадим подсказки, которые помогут Вам находить в упражнениях формулы суммы кубов и разности кубов

На примере 6 упражнений мы подробно объясним Вам все нюансы разложения многочленов на множители по формулам суммы кубов и разности кубов. План урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
00:00 Начало видео.
00:32 Вспомним, как получаются формулы суммы кубов и разности кубов.
03:41 Как применять формулы суммы кубов и разности кубов при разложении многочленов на множители?
05:39 Как искать формулы суммы кубов и разности кубов?
09:20 Упражнение 1.

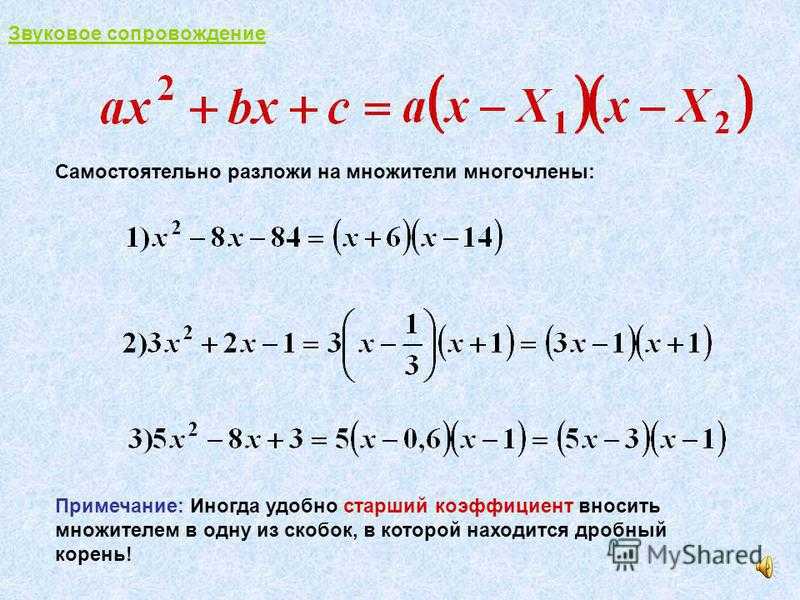
What is the Taylor series?

“In mathematics, Taylor series is an expression of a function for which the differentiation of all orders exists at a point “a” in the domain of “f” in the form of the power series.” 

The Taylor series of a function is infinite of terms that are expressed in terms of the derivatives of the function at a single point.(Source: Wikipedia)

Formula

The formula for Taylor series expansion is:

\(F\left(x\right)=\sum _{n=0}^{\infty }\left(\frac{f^n\left(a\right)}{n!}\left(x-a\right)^n\right)\)

In the formula of Taylor series, \(f^n\left(a\right)\) is the nth order of the given function, “a” is a particular point or center point of the function, and “n” is the order. The Taylor series can be finite or infinite depending on the order of the expression. This Taylor polynomial calculator works according to the above expansion formula. 

Квадратные корни

Вторая таблица — это таблица квадратных корней:

√x	1	2	3	4	5	6	7	8	9
1	1,41421	1,73205	2	2,23607	2,44949	2,64575	2,82843	3
1	3,16228	3,31662	3,4641	3,60555	3,74166	3,87298	4	4,12311	4,24264	4,3589
2	4,47214	4,58258	4,69042	4,79583	4,89898	5	5,09902	5,19615	5,2915	5,38516
3	5,47723	5,56776	5,65685	5,74456	5,83095	5,91608	6	6,08276	6,16441	6,245
4	6,32456	6,40312	6,48074	6,55744	6,63325	6,7082	6,78233	6,85565	6,9282	7
5	7,07107	7,14143	7,2111	7,28011	7,34847	7,4162	7,48331	7,54983	7,61577	7,68115
6	7,74597	7,81025	7,87401	7,93725	8	8,06226	8,12404	8,18535	8,24621	8,30662
7	8,3666	8,42615	8,48528	8,544	8,60233	8,66025	8,7178	8,77496	8,83176	8,88819
8	8,94427	9	9,05539	9,11043	9,16515	9,21954	9,27362	9,32738	9,38083	9,43398
9	9,48683	9,53939	9,59166	9,64365	9,69536	9,74679	9,79796	9,84886	9,89949	9,94987

Факторизация полиномов — Факторизация полиномов с примерами

Факторизация полиномов требуется для решения различных задач по алгебре. Множители — это числа или алгебраические выражения, которые делят другое число или выражение нацело, т. е. их деление дает в остатке 0, (или) множители считаются небольшими числами или выражениями, которые при умножении дают другие числа.

Пример: 1, 2, 4, 7, 14 и 28 являются множителями числа 28.

Аналогично, многочлен разлагается на множители, чтобы записать его как произведение двух или более многочленов. Это называется факторизацией многочлена. любое число или полином является простой факторизацией. В этом методе мы записываем число в виде произведения его простых множителей.

Пример. Найдите простые делители числа 70

Аналогично можно выразить алгебраическую выражения как произведение их множителей.

Пример:

Типы факторинговых полиномов

Факторизация — это не что иное, как запись числа как произведения меньших чисел. Это разложение ряда (или) математических объектов на меньшие или более простые числа/объекты. Факторизация различных типов алгебраических выражений очень полезна для различных целей, используемых в математике. Существуют различные методы факторизации:0028

Наибольший общий делитель

Наибольший общий делитель между двумя числами называется GCF (Greatest Common Factor). Это полезно для разложения многочленов на множители

Шаги для нахождения GCF:

• Шаг 1: Сначала разделите каждый член алгебраического выражения на неприводимые множители
• Шаг 2: Затем найдите среди них общие члены.
• Шаг 3: Теперь произведение общих членов и оставшихся членов дает требуемую форму множителя.

Пример: Факторизация 3x + 18

Решение:

Перегруппировка

Иногда члены данного выражения следует расположить в подходящие группы таким образом, чтобы все группы имели общий делитель, и тогда общий делитель выносится. Таким образом производится факторизация многочлена.

Пример: разложить на множители x 2 + yz + xy + xz

Решение:

Факторизация с использованием тождеств

Существует множество стандартных алгебраических тождеств, которые используются для факторизации различных многочленов. Некоторые из них приведены ниже:

1. (a + b) 2 = a 2 + 2ab + b 2
2. (a – b) 2 = a 2 2
3. a 2 – b 2 = (a + b) (a – b)

Example 1: Factorise x 2 + 8x + 16

Solution:

Пример 2: Фактор x 2 — 6x +

Решение:

Пример 3: Фактор 2x + 3 + 2Y + 3X

Решение:

Часто задаваемые вопросы по факторизации

Вопрос 1: Что такое факторизация и напишите ее пример?

Ответ:

Вопрос 2: Каковы основные 4 типа методов факторизации?

Ответ:

Разложение многочленов на множители в комбинации с формулами сокращённого умножения 7 класс онлайн-подготовка на

Вводная информация

На предыдущих уроках мы изучили два способа разложения многочлена на множители – способ вынесения общего множителя и способ группировки. Кроме того, мы изучили формулы сокращенного умножения и говорили, что их также можно использовать для разложения многочлена на множители.

Теперь для начала рассмотрим простейшие способы комбинирования вышеуказанных методов разложения.

Пример 1:

Теперь усложним выражение, умножив заданный многочлен на три:

Данная формула очень похожа на полный квадрат, но в таком виде свернуть ее мы не можем, но мы видим, что у всех членов есть общий множитель и можем вынести его за скобку. Получаем:

Итак, первая комбинация это формулы сокращенного умножения плюс вынесение общего множителя за скобки.

Примеры на комбинацию вынесения общего множителя и формулы квадрата разности

Пример 2:

;

Определим, что можно вынести за скобки.

Вынесем найденный общий множитель:

Определим, какие буквенные множители можно вынести. Обе переменные a и b есть во всех членах многочлена, значит, их можно выносить. Осталось определить только, в какой степени. Для этого найдем минимальную степень каждой из переменных. Это  и . Вынесем найденную буквенную часть:

Распишем полученную скобку более подробно, для этого определим, квадратами каких выражений являются первое и третье выражение, а затем проверим удвоенное произведение:

Очевидно, что в скобке стоит полный квадрат разности, так как мы помним его формулу: . Свернем его:

Комбинирование способа группировки и формулы разности квадратов

Пример 3:

;

Сгруппируем первый, третий и четвертый член, получим:

В скобках мы видим квадрат суммы. Свернем его:

Теперь мы видим разность квадратов. Вспомним формулу: .

Итак, мы рассмотрели комбинацию способа группировки и формул сокращенного умножения.

Пример 4:

Поступаем аналогично предыдущему примеру: сначала группируем члены по схеме «3+1», после этого применяем формулы сокращенного умножения:

Комбинация вынесения множителя и формулы суммы кубов

Пример 5:

Очевидно, что нужно вынести  за скобки:

В скобках мы получили формулу суммы кубов. Распишем ее:

В данном примере мы применили комбинацию вынесения общего множителя за скобки и формулы куба суммы.

Решение объемных примеров на комбинацию многих способов

Пример 6:

Распишем разность квадратов:

Пример 7:

Вынесем общий множитель за скобки:

Во второй скобке мы видим квадрат разности, можем свернуть его:

Выводы по уроку

Вывод: в данном уроке мы рассмотрели простейшие комбинации способов разложения многочлена на множители и формул сокращенного умножения и решили много различных примеров на разные варианты этих комбинаций.

Список рекомендованной литературы

1) Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.

2) Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ 

3) Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.

Рекомендованные ссылки на ресурсы интернет:

1. Школьный помощник (Источник).

2. Математика для чайников (Источник).

3. ЕГЭ по математике (Источник).

Рекомендованное домашнее задание:

Задание 1: Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7, № 890, ст.224;

Задание 2: Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7, № 897, ст.225

Задание 3: Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7, №899, ст. 225;

Вынесение минуса за скобки

При решении задач иногда может быть полезным вынесение минуса за скобки. Это позволяет упростить выражение и сделать его проще.

Рассмотрим следующий пример. Вынести минус за скобки в выражении −15 + (−5) + (−3)

Для наглядности заключим данное выражение в скобки, ведь речь идёт о том, чтобы вынести минус за эти скобки

( −15 + (−5) + (−3) )

Итак, чтобы вынести минус за скобки, нужно записать перед скобками минус и в скобках записать все слагаемые, но с противоположными знаками. Знаки операций (то есть плюсы) оставляем без изменений:

−(15 + 5 + 3)

Мы вынесли минус за скобки в выражении −15 + (−5) + (−3) и получили −(15 + 5 + 3). Оба выражения равны одному и тому же значению −23

−15 + (−5) + (−3) = −23

−(15 + 5 + 3) = −(23) = −23

Поэтому между выражениями −15 + (−5) + (−3) и −(15 + 5 + 3) можно поставить знак равенства, потому что они равны одному и тому же значению:

−15 + (−5) + (−3) = −(15 + 5 + 3)

−23 = −23

На самом деле при вынесении минуса за скобки опять же срабатывает распределительный закон умножения:

a(b + c) = ab + ac

Если поменять местами левую и правую часть этого тождества, то получится, что сомножитель a вынесен за скобки

ab + ac = a(b+c)

Тоже самое происходит, когда мы выносим общий множитель в других выражениях и когда выносим минус за скобки.

Очевидно, что при вынесении минуса за скобки, выносится не минус, а минус единица. Ранее мы говорили, что коэффициент 1 принято не записывать.

Поэтому и образуется перед скобками минус, а знаки слагаемых которые были в скобках меняют свой знак на противоположный, поскольку каждое слагаемое разделено на минус единицу.

Вернёмся к предыдущему примеру и детально увидим, как на самом деле выносился минус за скобки

Пример 2. Вынести минус за скобки в выражении −3 + 5 + 11

Ставим минус и рядом в скобках записываем выражение −3 + 5 + 11 с противоположным знаком у каждого слагаемого:

−3 + 5 + 11 = −(3 − 5 − 11)

Как и в прошлом примере, здесь за скобки вынесен не минус, а минус единица. Подробное решение выглядит следующим образом:

Сначала получилось выражение −1(3 + (−5) + (−11)), но мы раскрыли в нём внутренние скобки и получили выражение −(3 − 5 − 11). Раскрытие скобок это тема следующего урока, поэтому если данный пример вызывает у вас затруднения, можете пока пропустить его.

Остаточный член формулы Тейлора.

Пусть функция \(f(x)\) бесконечно дифференцируема в точке \(x_{0}\). Тогда ей можно поставить в соответствие ряд \eqref{ref1}. Обозначим
$$
S_{n}(x) = \sum_{k=0}^{n}\frac{f^{(k)}(x_{0})}{k!}(x-x_{0})^{k},\label{ref5}
$$
$$
r_{n}(x) = f(x)-S_{n}(x)\label{ref6}
$$
и назовем \(r_{n}(x)\) остаточным членом формулы Тейлора для функции \(f\) в точке \(x_{0}\). Если существует
$$
\lim_{x \rightarrow 0} r_{n}(x) = 0,\label{ref7}
$$
то согласно определению сходимости ряда ряд \eqref{ref1} сходится к функции \(f(x)\) в точке \(x\), то есть
$$
f(x) = \sum_{n = 0}^{\infty}\frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n}.\label{ref8}
$$

Теорема 1.

Если функции \(f(x)\), \(f'(x)\), …, \(f^{(n + 1)}(x)\) непрерывны на интервале \(\Delta = (x_{0}-\delta, x_{0} + \delta)\), где \(\delta > 0\), то для любого \(x \in \Delta\) остаточный член формулы Тейлора для функции \(f\) в точке \(x_{0}\) можно представить:

1. в интегральной форме
   $$
   r_{n}(x) = \frac{1}{n!} \int\limits_{x_{0}}^{x} (x-t)^{n}f^{(n + 1)}(t)\ dt;\label{ref9}
   $$
2. в форме Лагранжа
   $$
   r_{n}(x) = \frac{f^{(n + 1)}(\xi)}{(n + 1)!}(x-x_{0})^{n + 1},\label{ref10}
   $$
   где \(\xi\) принадлежит интервалу с концами \(x_{0}\) и \(x\).

\(\circ\) Формула \eqref{ref10} доказана в . Докажем формулу \eqref{ref9} методом индукции. В силу равенств \eqref{ref5} и \eqref{ref6} нужно показать, что
$$
f(x)-f(x_{0}) = \sum_{k=0}^{n}\frac{f^{(k)}(x_{0})}{k!}(x-x_{0})^{k} + \frac{1}{n!} \int\limits_{x_{0}}^{x} (x-t)^{n}f^{(n + 1)}(t)\ dt.\label{ref11}
$$

Воспользуемся равенством \(\displaystyle\int\limits_{x_{0}}^{x} f'(t)\ dt = f(x)-f(x_{0})\) и преобразуем его левую часть с помощью формулы интегрирования по частям:
$$
\int\limits_{x_{0}}^{x} f'(t)\ dt =-\left.\int\limits_{x_{0}}^{x} f'(t)d(x-t) = \right|_{t = x_{0}}^{t = x} + \int\limits_{x_{0}}^{x} (x-t)f″(t)\ dt =\\= f'(x_{0})(x-x_{0}) + \int\limits_{x_{0}}^{x} (x-t)f″(t)\ dt.\nonumber
$$
Таким образом,
$$
f(x)-f(x_{0}) = f'(x_{0})(x-x_{0}) + \int\limits_{x_{0}}^{x} (x-t)f″(t)\ dt,\nonumber
$$
то есть формула \eqref{ref11} верна при \(n = 1\). Предположим, что формула \eqref{ref11} является верной для номера \(n-1\), то есть
$$
f(x)-f(x_{0}) = \sum_{k=0}^{n}\frac{f^{(k)}(x_{0})}{k!}(x-x_{0})^{k} + \frac{1}{(n-1)!} \int\limits_{x_{0}}^{x} (x-t)^{n-1}f^{(n)}(t)\ dt.\label{ref12}
$$
Преобразуем интеграл в правой части формулы \eqref{ref12}, применив формулу интегрирования по частям:
$$
\frac{1}{(n-1)!} \int\limits_{x_{0}}^{x} (x-t)^{n-1}f^{(n)}(t)\ dt = -\frac{1}{n!} \int\limits_{x_{0}}^{x} f^{n}(t)dt((x-t)^{n}) =\\= \left.\left(-\frac{1}{n!}f^{n}(t)(x-t)^{n}\right)\right|_{t = x_{0}}^{t = x} + \frac{1}{n!} \int\limits_{x_{0}}^{x}(x-t)^{n}f^{(n + 1)}(t)\ dt =\\= \frac{1}{n!}f^{(n)}(x_{0})(x-x_{0})^{n} + \frac{1}{n!} \int\limits_{x_{0}}^{x}(x-t)^{n}f^{(n + 1)}(t)\ dt.\nonumber
$$
Отсюда следует, что равенство \eqref{ref12} можно записать в виде \eqref{ref11}. Формула \eqref{ref9} доказана. \(\bullet\)

Теорема 2.

Если функция \(f\) и все ее производные ограничены в совокупности на интервале \(\Delta = (x_{0}-\delta, x_{0} + \delta)\), то есть
$$
\exists M > 0: \forall x \in \Delta \rightarrow |f^{(n)}(x)| \leq M,\ n = 0,1,2,\ldots,\label{ref13}
$$
то функция \(f\) представляется сходящимся к ней в каждой точке интервала \(\Delta\) рядом Тейлора \eqref{ref8}.

\(\circ\) Пусть \(x \in (x_{0}-\delta, x_{0} + \delta)\). Тогда, используя формулу \eqref{ref10} и условие \eqref{ref13}, получаем
$$
|r_{n}(x)| \leq M \frac{|x-x_{0}|^{n + 1}}{(n + 1)!}.\label{ref14}
$$

Так как \(\displaystyle\lim_{x \rightarrow 0} \frac{a^{n}}{n!} = 0\) для любого \(a > 0\) (пример разобран ), то из \eqref{ref14} следует, что выполняется условие \eqref{ref7}, то есть в точке \(x\) справедливо равенство \eqref{ref8}. \(\bullet\)

Замечание 1.

Теорема 2 остается в силе, если условие \eqref{ref13} заменить следующим условием:
$$
\exists M > 0\ \exists C > 0: \forall x \in \Delta \rightarrow |f^{(n)}(x)| \leq MC^{n},\ n = 0, 1, 2, \ldots\nonumber
$$