Формулы, параметры и примеры решения расчета балки на прогиб

Распределенная нагрузка: определение и примеры

Распределенная нагрузка, также известная как непрерывно-распределенная нагрузка, является одним из типов нагрузок, применяемых к конструкциям, таким как балки. Она характеризуется тем, что нагрузка равномерно распределена по длине конструкции и действует на нее на протяжении всего участка.

Определение распределенной нагрузки можно представить следующим образом: это нагрузка, равномерно распределенная по длине конструкции и характеризующаяся постоянной величиной или плотностью.

Примерами распределенных нагрузок могут служить собственный вес балки, равномерно распределенная нагрузка от мебели на пол, равномерно распределенная нагрузка от снега на крышу здания и т.д.

Распределенная нагрузка может быть выражена в виде силы, действующей на единицу длины конструкции. В зависимости от применяемой системы единиц, она может выражаться, например, в Н/м (ньютонов на метр) или кН/м (килоньтонов на метр).

Для расчета напряжений, возникающих в балке под воздействием равномерно распределенной нагрузки, используются соответствующие формулы и уравнения механики. Расчет напряжений позволяет определить прочность конструкции и проверить ее на соответствие требуемым нормам и стандартам безопасности.

Расчет по допускаемым напряжениям

При данной методике материал рассматривается, как некое упругое тело, деформации которого прямо пропорциональны напряжениям.

Методика расчета по допускаемым напряжениям основана на сравнении расчетных напряжений с так называемыми допускаемыми. Допускаемые напряжения определяются как опасные, деленные на коэффициент запаса k, учитывающий все изложенные выше факторы:

= σ_o/k; = т_o/k (319.1.1)

Для пластических материалов опасным напряжением считается предел текучести, за которым следуют значительные пластические деформации:

= σ_т/k₁; = т_т/k₁(319.1.2)

По этим формулам определяются величины допускаемых напряжений при растяжении _р и при кручении тонкостенных стержней _к для сталей различных марок.

Для элементов конструкций или деталей машин, выполненных из хрупких материалов, не имеющих ярко выраженного предела текучести, за опасное напряжение принимается предел прочности:

= σ_в/k₂; = т_в/k₂(319.1.3)

При повторно-переменных нагрузках опасное состояние связано с появлением усталостных трещин, поэтому опасным напряжением считается предел выносливости:

= σ_r/k₃ (319.1.4)

Особенности работы элемента или конструкции могут учитываться введением коэффициентов снижения основных допускаемых напряжений. Ориентировочные значения допускаемых напряжений приведены в таблице 319.1:

Таблица 319.1. Ориентировочные значения допускаемых напряжений

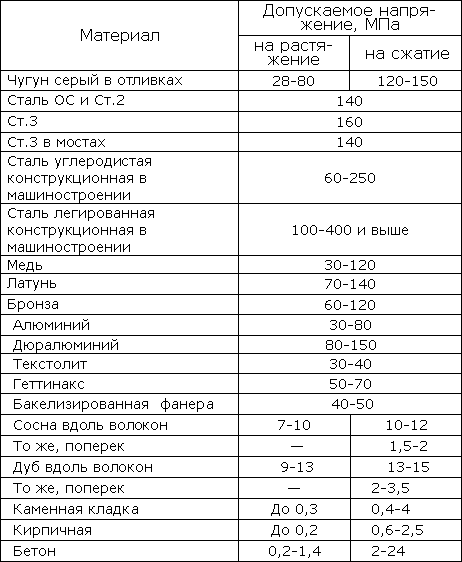
В машиностроении при определении допускаемых напряжений используется один из следующих методов.

1.Дифференцированный — запас прочности определяется как произведение коэффициентов, учитывающих качество материала, точность метода расчета, степень ответственности детали и другие факторы, определяющие условия работы детали.

2.Табличный — допускаемые напряжения принимаются по действующим нормам (по таблицам).

Второй метод менее точен, но более прост, поэтому он нашел более широкое применение в практике проектирования, особенно — в проверочных прочностных расчетах. В данной статье допускаемые напряжения, принимаемые в машиностроении, не приводятся.

В СССР в строительной отрасли методика расчета по допускаемым напряжениям использовалась для расчета железобетонных конструкций до 1938 г., металлических и деревянных конструкций до 1955 г. Тем не менее проектировщики старой закалки и сейчас еще рассчитывают металлические конструкции, пользуясь данной методикой, в частности принимая расчетное сопротивление стали 160 МПа. При расчете конструкций, производящихся в большом количестве, такая методика расчета может приводить к завышенному расходу материалов. А вот в индивидуальном строительстве, при расчете конструкций, выполняемых в количестве от 1 до 10, да еще и с учетом того, что расчет производится непрофессиональным проектировщиком, методика расчета по допускаемым напряжениям, на мой взгляд, должна применяться и сейчас.

Расчет железобетонных конструкций без учета стадии пластических деформаций приводил к повышенному запасу прочности и соответственно завышенному расходу материалов, поэтому для расчета железобетонных конструкций в 30-е годы ХХ столетия была разработана более точная методика расчета железобетонных конструкций:

Расчет прямоугольной балки на сдвиг

Расчет на сдвиг включает оценку расстояния между стержнями для обеспечения предельного сдвига. Обычно часть бетона сопротивляется сдвигающему усилию, а часть, не поддерживаемая бетоном, воспринимается сдвигающей арматурой.

Сначала вычислите предельную сдвигающую силу на расстоянии d, которое является глубиной поперечного сечения. Существуют исключения, когда для расчета на сдвиг используется сдвиг по торцу опоры. Например, когда нагрузка прикладывается к нижней части балки.
Во-вторых, оцените проектную прочность бетона на сдвиг,
Если VuVc .
Если 0,5Vc>VuVc>VuVc , то следует предусмотреть только минимальное поперечное армирование.
Усиление на сдвиг необходимо, если Vu> Vc.
В-третьих, выберите пробную площадь стального полотна, основываясь на стандартных размерах стяжек в диапазоне от NO.10 до NO.16.
Для расчета площади поперечного армирования умножьте площадь поперечного армирования на количество ножек стремянок.
Наконец, найдите расстояние между стременами для вертикальных и наклонных стремен соответственно, используя уравнения 12 и 13.
Расстояние между вертикальными стременами не должно превышать 100 мм. Таким образом, размер стяжек должен быть подобран таким образом, чтобы предотвратить более близкое расстояние между ними.
Распределяйте стремена равномерно на балках с короткими пролетами.
Однако при длинных пролетах экономичнее рассчитать необходимое расстояние на нескольких участках. И, соответственно, размещать стремена группами с разным расстоянием между ними.
Требуемое расстояние должно быть равно или меньше максимального расстояния, которое равно наименьшему из 600, d/2 и уравнения 14.
Если Vs больше 0,33fc’^0,5bwd, то эти максимальные расстояния должны быть уменьшены вдвое.
Наконец, вычертите проектную балку с продольным и сдвиговым армированием.

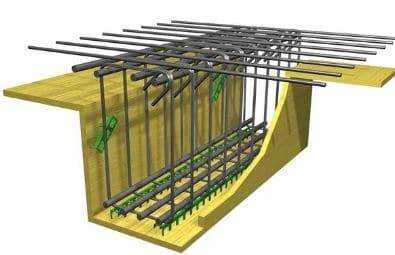
Читайте далее:

• Как спроектировать одностороннее перекрытие в соответствии с ACI 318-19? | Прилагается пример.
• Концепция проектирования высотных зданий из железобетона.
• Минимальное и максимальное соотношение армирования в различных железобетонных элементах.
• Процедура проектирования железобетонной тавровой балки с примером.
• Детализация железобетонных балок в соответствии с кодексом ACI.
• Что такое коэффициент податливости железобетонной колонны и как его рассчитать?.
• Правила и спецификации для проектирования железобетонной балки.

Расчет в Excel прогиба пластины. Пример.

Прямоугольная пластина из изотропного материала (Сталь Ст3) жестко закреплена по всему контуру. В перпендикулярном направлении к плоскости пластины приложена равномерно распределенная по всей площади нагрузка.

Требуется вычислить наибольший прогиб пластины от действия нагрузки и найти максимальные возникающие в теле листа напряжения.

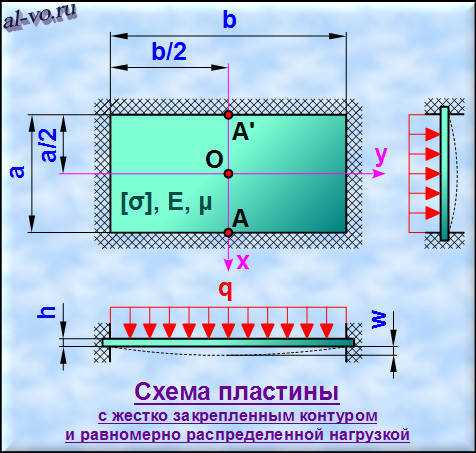
Исходные данные:

Первые три параметра являются справочными характеристиками свойств материала пластины.

1. Предел текучести для пластичных материалов или прочности для хрупких материалов в Н/мм2 записываем

в ячейку  D3: 245

Этот параметр не участвует в расчетах и нужен лишь для сравнения с полученными в результате расчета напряжениями. Правильнее вместо него использовать допускаемые напряжения материала с учетом всех запасов для конкретного случая применения.

2. Модуль упругости или модуль Юнга E в Н/мм2 заносим

в D4: 210000

3. Коэффициент Пуассона μ вписываем

в D5: 0,28

В примечаниях к ячейкам D4 и D5 приведены значения модулей упругости и коэффициентов Пуассона для некоторых материалов.

4.,5.,6. Далее вводим в таблицу размеры пластины h, a и b в мм

в ячейку  D6: 5,0

в D7: 500

в D8: 1000

В примечаниях к ячейкам D6, D7 и D8 записаны ограничения, которые должны соблюдаться. В случае их нарушения цифры окрашиваются инверсным белым цветом, а поле ячейки – красным, сообщая пользователю об ошибке ввода данных.

7. Значение распределенной равномерно по всей площади нагрузки q в Н/мм2 вносим

в D9: 0,016

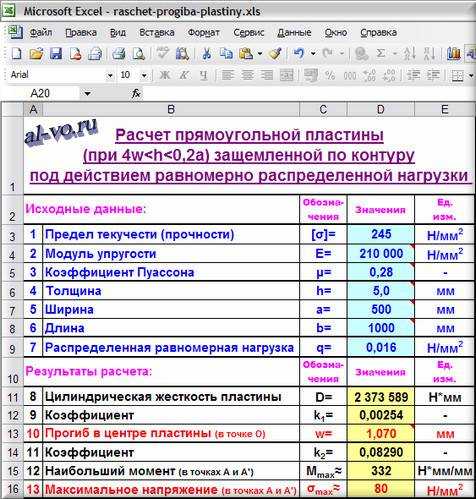
Ссылка на скачивание файла с программой: raschet-progiba-plastiny-NEW (xlsx 174KB).

Результаты расчета:

8. Цилиндрическую жесткость пластины D в Н*мм (аналог EI – линейной жесткости для стержней) вычисляем

в ячейке D11: D=(E*h3)/(12*(1- μ2)=2373589

9.,11. Безразмерные коэффициенты k₁ и k₂, зависящие от формы и размеров пластины, а также от способов закрепления контурных сторон, можно найти в таблицах старых справочников (Тимошенко С.П., Войновский-Кригер С. Пластины и оболочки; Вайнберг Д.В, Вайнберг Е.Д. Расчет пластин). Правда, k₂ зависит еще и от μ, а в таблицах приведены значения только для стали μ≈0,3 и бетона μ≈1/6, но, проанализировав ряд таблиц, можно увидеть, что эта зависимость не очень значительная…

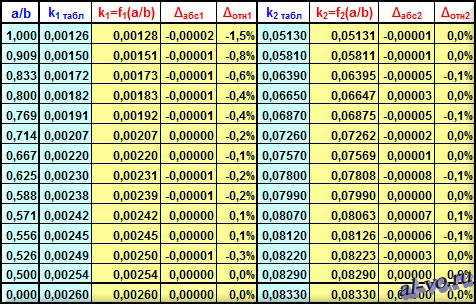
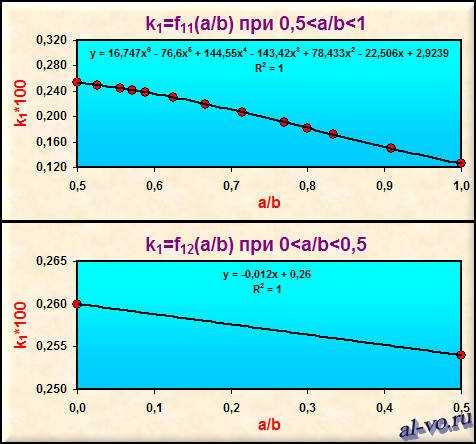
Выполнив аппроксимацию в Excel табличных данных, получим аналитические выражения для расчетов коэффициентов

в ячейке D12: при 0,5<a/b<1

k₁=0,16747*(a/b)6-0,766*(a/b)5+1,4455*(a/b)4-1,4342*(a/b)3+0,78433*(a/b)2-0,22506*(a/b)+0,029239=0,0254

при 0<a/b<0,5

k₁=-0,00012*(a/b)+0,0026=0,0254

в D14: при 0,5<a/b<1

k₂=0,71922*(a/b)6-3,1489*(a/b)5+5,6353*(a/b)4-5,1372*(a/b)3+2,3658*(a/b)2-0,50294*(a/b)+0,12003=0,0829

при 0<a/b<0,5

k₁=-0,0008*(ab)+0,0833=0,0829

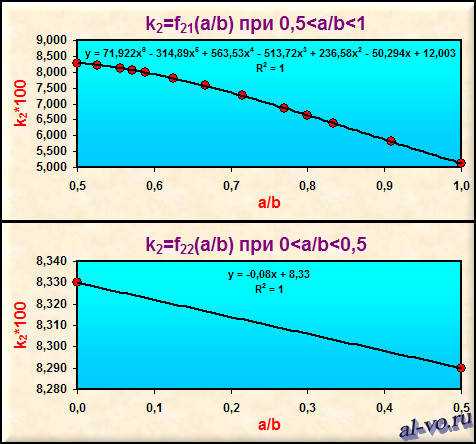
Точность аппроксимации очень и очень высокая. Об этом можно судить как по абсолютным Δ_абс и относительным Δ_отн погрешностям, так и по величине достоверности R2.

10. Максимальный прогиб пластины w в мм будет в рассматриваемой схеме в центре пластины в точке O; вычисляем его

в ячейке D13: w=k₁*q*a4D=1,07

Расчет прогиба в MS Excel выполнен. Величина прогиба не превышает четверти толщины листа, следовательно применение использованных формул правомерно.

12. Наибольшие моменты на единицу длины сечения пластины M_max возникают в рассматриваемой схеме по серединам больших сторон контура в точках A и A’. Вычисляем их в Н*мм/мм

в ячейке D15: M_max=k₂*q*a2=332

13. Наибольшие напряжения в пластине σ_max в точках действия максимального момента вычисляем в Н/мм2

в ячейке D16: σ_max=6* M_maxh2=80

Напряжения не превышают предела текучести. Деформации листа являются упругими, после снятия нагрузки пластина вернется в исходное плоское состояние.

Выбор материала для главной балки

Выбор материала для главной балки является важным этапом в процессе конструирования. От правильного выбора материала зависит прочность, устойчивость и долговечность балки.

Свойства материала

Первым шагом при выборе материала является оценка его свойств

Важно учитывать такие параметры, как прочность, упругость, плотность и устойчивость к воздействию внешних факторов, таких как влага, температура и химические вещества

Прочность материала

Прочность материала определяет его способность сопротивляться нагрузкам без разрушения. Для главной балки необходимо выбирать материал с высокой прочностью, чтобы он мог выдерживать требуемые нагрузки без деформаций или повреждений.

Упругость материала

Упругость материала определяет его способность возвращаться в исходное состояние после удаления нагрузки. Для главной балки желательно выбирать материал с высокой упругостью, чтобы он мог справляться с постоянными нагрузками и не деформироваться со временем.

Плотность материала

Плотность материала определяет его массу в единице объема. При выборе материала для главной балки следует учитывать его плотность, так как это может влиять на общую массу конструкции и ее способность выдерживать нагрузки.

Устойчивость к внешним факторам

Устойчивость материала к воздействию внешних факторов, таких как влага, температура и химические вещества, также является важным критерием при выборе материала для главной балки. Материал должен быть устойчивым к таким факторам, чтобы не терять свои свойства и не разрушаться со временем.

При выборе материала для главной балки необходимо учитывать все эти факторы и выбирать материал, который наилучшим образом соответствует требованиям конструкции и условиям эксплуатации.

Основы вычислений

Для начала следует понять, что именно требуется рассчитать. Дело в том, что деревянный брус или доска балки под нагрузкой способно изогнуться до определенного предела – эта величина называется пределом прочности – и при дальнейшем увеличении нагрузки сломаться. Под действием нагрузки изогнувшаяся балка может также выскользнуть из креплений. Чтобы избежать этого или хотя бы снизить риск такой неприятности, деревянные балки стараются заделать в кладку дома или прикрепить с помощью кронштейнов, уголков и других видов деталей к деревянной стене дома. Используют также врубку балки в венец стены. Все такие виды фиксации считаются жесткой заделкой.

Вот так примерно выглядит расчетная схема для однопролетной балки, то есть изделие, у которого закреплены только концы. Здесь L – пролет балки, расстояние между опорными точками, Q – распределенная нагрузка, f – величина прогиба.

Основой для расчета предельно допустимого прогиба, как и источником других данных о работе деревянных конструкций, является СП 64.13330.2011. Согласно этому документу, предельный прогиб балки для межэтажных перекрытий не должен превышать 1/250 часть длины пролета.

То есть для балки с длиной 6 м допустимый прогиб составит 24 мм. Если же брать более строгие значения (для штукатурки на потолке и требующих строгой плоскости пола второго этажа напольных покрытий, например, плитки) – 1/350, допустимый прогиб уменьшается до 17 мм.

В целом для вычислений используют формулу f=L/350, при этом длину пролета указывают в миллиметрах.

Таблица 1.1. Допустимый прогиб деревянных конструкций.

Соответственно, при расчете балки на прочность в онлайн-калькуляторе или вручную следует уменьшать сечение только до тех пределов прогиба, которые меньше вычисленного значения.

На иллюстрации выше показана расчетная схема для распределенной нагрузки, то есть такой, которая равномерно распределяется по всей балке. Обычно в жилых помещениях используется именно эта схема. Однако при размещении в комнате мебели или оборудования большого веса, особенно не возле стены (на которую опирается край балки), а на некотором удалении от нее, иногда бывает разумнее использовать схему расчета для сосредоточенной нагрузки.

Вот так примерно создается сосредоточенная нагрузка на балку.

Таблица 1.2. Схемы расчета деревянных балок с одной сосредоточенной нагрузкой.

Здесь и далее Е – модуль упругости древесины Е=100 000 кгс/м2), I – осевой момент инерции балки.

Таблица 1.3. Схемы расчета деревянных балок с двумя сосредоточенными нагрузками.

Таблица 1.4. Расчет балки с двусторонним жестким защемлением при равномерно-распределенной нагрузке.

В зависимости от того, куда именно приложены нагрузки и в каком количестве, используется расчетная схема соответствующего типа.

Для бруса, защемленного в стене только одним концом (консольное крепление), используются другие формулы расчета деревянной балки на прочность. Обычно такие вычисления нужны при проектировании навесов на деревянных балках-опорах, больших вылетов крыши и других подобных случаях.

Таблица 1.5. Расчет консольной балки при одной сосредоточенной нагрузке.

Таблица 1.6. Расчет консольной балки при одной неравномерно-распределенной нагрузке.

Таблица 1.7. Расчет консольной балки при одной равномерно-распределенной нагрузке.

Формулы кажутся громоздкими и сложными, но фактически обычному пользователю при расчете деревянных балок перекрытия важно просто представлять себе характер распределения действующих на балку сил и понимать – чтобы соблюсти условия прочности, необходимо правильно выбрать схему приложения нагрузок

Какие бывают виды балок?

Строительные балки, как и практически все материалы, используемые на стройках, классифицируются по различным видам, ориентированным на определённые работы.

Деревянные

В спектр балочных древесных изделий применяемых, соответственно, в деревянных постройках, попадают лаги, ригели, прогоны, перекладины, и другие элементы, составляющие каркас брускового или бревенчатого жилого загородного дома. При разделении этажей используют балки перекрытий. Для устройства крыши выстраивают балочный каркас, где применяют стропила. Главная функция деревянных балок, равномерное распределение нагрузки по плоскости верхнего покрытия (крыши). Качественные характеристики материала залог прочности и устойчивости сооружения.

Железобетонные

В строительстве, монтаж железобетона, например, на промышленных предприятиях, учитывает включение соответствующих изделий в устройство подкрановых балок, бетонных ригелей, устанавливаемых на колонны, под плиты перекрытия.

Железобетонные балки являются строительным элементом линейного типа. Выполненные из качественного бетона с расположенной внутри стальной арматурой для усиления, предназначены перераспределять нагрузку и повысить устойчивость основного конструктива.

Металлические

Металлоконструкции в строительстве включают горизонтальные и наклонные стальные балки, как важную часть жёсткого каркаса. Чаще это двутавровые балки с параллельными гранями. Основные их типы — широкие и колонные. Последние не предназначены для выдерживания повышенной нагрузки, поэтому при монтаже опорных частей, воспринимающих влияние основных действующих сил, используют широкополые балки. Применяются при устройстве подвесных путей, шахтных стволов и так далее.

Опоры

Сама балка ложится на опоры. В зависимости от конструктивных особенностей детали бывают:

• разрезными: две опоры поддерживают строительный элемент между этажами, в кровле крыши или мостовыми пролетами;
• неразрезными: несколько опор держат балку, прогиб в одном месте влияет на всю балочную нагрузку.

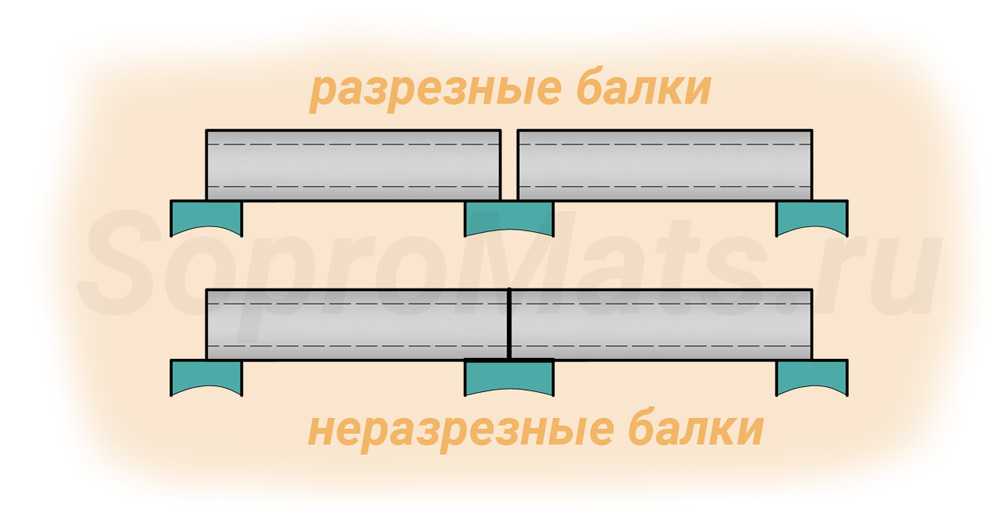
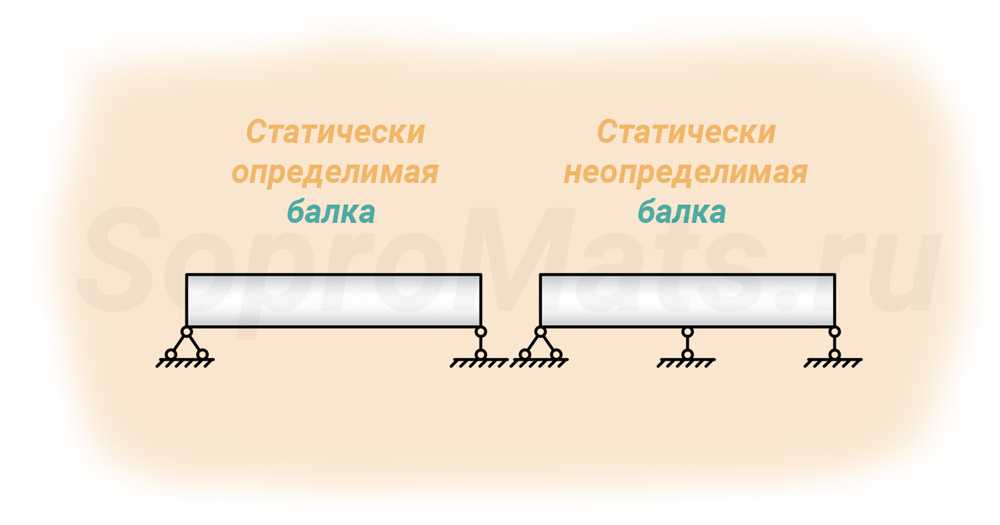
В зависимости от количества опорных связей данные элементы можно классифицировать на виды:

• статически определимые: когда количество реакций связей равно числу независимых уравнений равновесия статики;
• статически неопределимые: когда количество связей больше возможных уравнений статического равновесия.

Поперечное сечение как форма классифицирования

Стальные балки можно классифицировать по торцевому сечению. Подобная классификация в строительстве позволяет распределить соответствующие элементы в сортаменте металла и, таким образом, провести подбор изделий.

Например:

• Прямоугольное сечение. Соответствует применению в пролетах с небольшой длиной.
• Сечение типа «L». Предназначено главным образом при возведении фасадов сооружений.
• Сечение типа «Т». Принадлежит стандартным и двускатным тавровым балкам. Оптимально соответствуют проведению монтажа пролетов средней протяжённости.
• Двутавровое сечение. Балки наделены повышенной устойчивостью и используются для пролётов большой длины. В свою очередь, двутавр может иметь параллельные грани полок. Параметры их разнятся в соответствии со стандартами и установленными ГОСТами.
• Сечение типа «V». Такая строительная балка играет роль дополнительного изделия для усиления несущей конструкции.
• Сечение типа «VT». Соответствует прогонам.

Так, полые опоры обычно находят свое применение в легких постройках гаража, небольшого магазина, маленького навеса.

Цельные брусы вполне подойдут для перекрытий на чердаке простого деревянного домика. Различные «тавровые варианты» предназначены для более серьезных нагрузок в многоэтажных домах, производственных постройках. Двутавровые формы на крупных стройках самые популярные, так как они отлично справляются с нагрузкой на изгиб в кровельных конструкциях. Для придания им наибольшей прочности производят такие балки с толстой стенкой, с внутренними гранями под уклоном или параллельно.

Упрощенный расчет балок перекрытия из дерева на прочность

В частном строительстве в основном используется схема 2.1 из таблицы 1.4, то есть равномерно распределенная по всей длине балки от стены до стены нагрузка. Ее величина определяется исходя из таблиц или экспериментально.

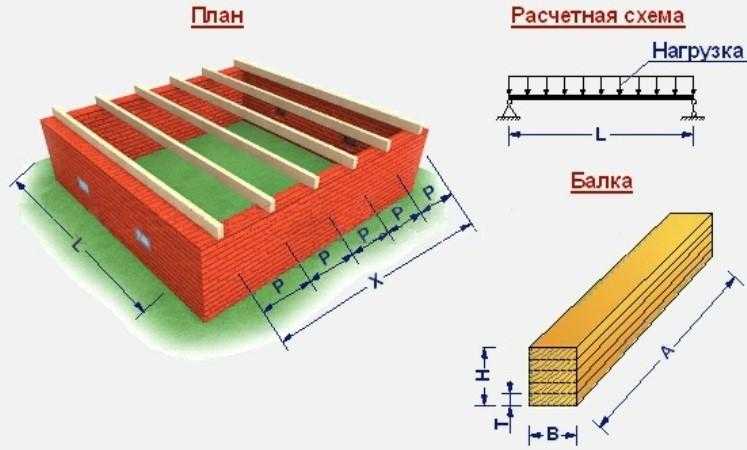
Поскольку балка работает не сама по себе, а в комплексе с другими, для расчета требуется информация о шаге расположения балок (на схеме Р).

Нагрузка на балки определяется типом перекрытия – чердачным или межэтажным. СНиП 2.01.07-85 дает такие данные (в кгс/м.кв. или в кПа, в скобках второе число):

• для чердачных перекрытий 130…245 (1,3…2,45);
• для мансарды 350 (3,5);
• для межэтажного перекрытия 400 (4).

В соответствии с планируемыми длиной пролета, шагом балок (0,5 или 1 м) и ориентировочной нагрузкой выбирается сечение балки в сантиметрах по таблице 1.8.

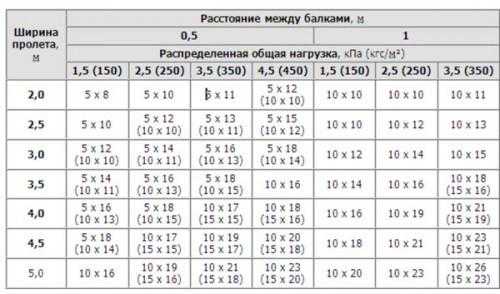
Далее расчет ведется, исходя из условия прочности – максимальный изгибающий момент, деленный на момент сопротивления балки при изгибе, должен быть меньше предельно допустимого напряжения.

σ_max= M/W≤

Для расчета момента используем формулы, приведенные в соответствующей таблице, для равномерно распределенной нагрузки на балку с защемлением в обоих концах это

M= (ql^2)/24

Момент сопротивления при изгибе прямоугольной балки

W= (bh^2)/6

Таким образом, расчет деревянной балки на прочность производим по формуле

σ= ((ql^2)/24) ⁄ ((bh^2)/6)

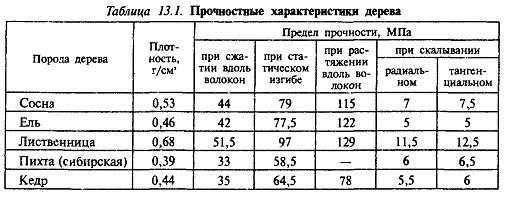
Для примера возьмем пролет 3 м, балки в межэтажном перекрытии расположены с шагом 0,5 м, сечение (по таблице 1.8) 50х180 мм. Эти цифры дадут (с учетом перевода всех составляющих в единую размерность)

σ=((45000×3^2)/24) ⁄ ((0,05×0,18^2)/6)=1687.5/0,00027=6250000 Па=6.2 МПа

Что намного меньше предела прочности для сосны на изгиб (σ_max=79 МПа). Таким образом, расчетное значение сечения балки полностью удовлетворяет условию прочности и дает возможность нагрузить перекрытие даже больше, чем это предполагает СНиП.

Конструирование соединений главной балки

При конструировании соединений главной балки необходимо учесть не только прочность и надежность соединения, но и его удобство в монтаже и демонтаже. Соединения могут быть выполнены различными способами, в зависимости от типа и формы балки, а также от требований к конструкции.

Сварные соединения

Сварные соединения являются одним из наиболее распространенных способов соединения главной балки. Они обеспечивают высокую прочность и жесткость соединения. Для сварки используются специальные электроды или полуавтоматические сварочные аппараты. При конструировании сварных соединений необходимо учитывать толщину и форму балки, а также требования к прочности и устойчивости соединения.

Болтовые соединения

Болтовые соединения представляют собой соединение балок с помощью болтов и гаек. Они обеспечивают возможность быстрого монтажа и демонтажа конструкции. Для болтовых соединений необходимо выбрать подходящие размеры болтов и гаек, а также учесть требования к прочности и надежности соединения.

Соединения с использованием фланцев

Соединения с использованием фланцев являются одним из способов соединения главной балки с другими элементами конструкции, например, с колоннами или стойками. Фланцы представляют собой плоские или выступающие части балки, которые соединяются с помощью болтов или сварки. При конструировании соединений с использованием фланцев необходимо учесть требования к прочности и устойчивости соединения, а также обеспечить правильное выравнивание и фиксацию фланцев.

Клеевые соединения

Клеевые соединения представляют собой соединение балок с помощью специальных клеевых составов. Они обеспечивают высокую прочность и надежность соединения, а также позволяют создавать более сложные формы и конструкции. При конструировании клеевых соединений необходимо выбрать подходящий клей и учесть требования к прочности и устойчивости соединения, а также к условиям эксплуатации и возможным воздействиям окружающей среды.

При конструировании соединений главной балки необходимо учитывать требования к прочности, устойчивости и надежности соединения, а также удобство в монтаже и демонтаже

Важно выбрать подходящий способ соединения, который будет соответствовать требованиям проекта и обеспечивать безопасность и надежность конструкции