Колебательные системы. антенны. выпрямители

Резонанс напряжений

Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:

и конденсатор в 1000 пФ

Из них собираю последовательный колебательный контур. Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.

Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора  падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор — это не есть хорошо, но что не сделаешь ради науки!

Ну что же, приступим ;-). Давайте сначала посчитаем  резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.

Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:

Размах амплитуды 4 Вольта

Хотя на генераторе частоты  размах  более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.

Теперь небольшой прикол

Вот этот сигнал мы подаем на наш последовательный колебательный контур:

Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.

Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:

Смотрим напряжение на конденсаторе:

Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!

Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:

Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию с конденсатора или с катушки!

Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как среднеквадратичное напряжение будет где-то Вольт 14,  и цепляю поочередно к ним лампочку:

Как видите — полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока — увы! Поэтому, последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!

Объяснение резонанса напряжения

При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.

При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение U_L = IX_L , а на конденсаторе U_C = IX_C . А так как при резонансе у нас X_L = X_C , то получаем что U_L = U_C , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.

Действующие значения силы тока и напряжения

Пусть источник тока создает переменное гармоническое напряжение

\(u=U_{m} \cdot \sin \omega \cdot t.\;\;\;(1)\)

Согласно закону Ома, сила тока в участке цепи, содержащей только резистор сопротивлением R, подключенный к этому источнику, изменяется со временем также по синусоидальному закону:

\(i = \dfrac{u}{R} =\dfrac{U_{m} }{R} \cdot \sin \omega \cdot t = I_{m} \cdot \sin \omega \cdot t,\;\;\; (2)\)

где \(I_m = \dfrac{U_{m}}{R}.\) Как видим, сила тока в такой цепи также меняется с течением времени по синусоидальному закону. Величины U_m, I_m называются амплитудными значениями напряжения и силы тока. Зависящие от времени значения напряжения u и силы тока i называют мгновенными.

Кроме этих величин используются еще одна характеристика переменного тока: действующие (эффективные) значения силы тока и напряжения.

Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.

Обозначается буквой I.

Действующим (эффективным) значением напряжения переменного тока называется напряжение такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.

Обозначается буквой U.

Действующие (I, U) и амплитудные (I_m, U_m) значения связаны между собой следующими соотношениями:

\(I = \dfrac{I_{m} }{\sqrt{2}}, \; \; \; U =\dfrac{U_{m} }{\sqrt{2}}.\)

Таким образом, выражения для расчета мощности, потребляемой в цепях постоянного тока, остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:

\(P = U\cdot I = I^{2} \cdot R = \dfrac{U^{2}}{R}.\)

Необходимо отметить, что закон Ома для цепи переменного тока, содержащей только резистор сопротивлением R, выполняется как для амплитудных и действующих, так и для мгновенных значений напряжения и силы тока, вследствие того, что их колебания совпадают по фазе.

\(I=\dfrac{U}{R}.\;\;\;(3)\)

*Вывод формулы

Зная мгновенные значения u и i, можно вычислить мгновенную мощность

\(p = u \cdot i,\)

которая, в отличие от цепей постоянного тока, изменяется с течением времени. С учетом уравнений (1) и (2) перепишем выражение для мгновенной мощности на резисторе в виде

\(p=U_{m} \cdot I_{m} \cdot \sin ^{2} \omega \cdot t=U_{m} \cdot I_{m} \cdot \dfrac{1-\cos 2\omega \cdot t}{2} =\dfrac{U_{m} \cdot I_{m} }{2} -\dfrac{U_{m} \cdot I_{m} }{2} \cdot \cos 2\omega \cdot t.\)

Первое слагаемое не зависит от времени. Второе слагаемое P₂ — функция косинуса удвоенного угла и ее среднее значение за период колебаний равно нулю (рис. 2, найдите сумму площади выделенных фигур с учетом знаков).

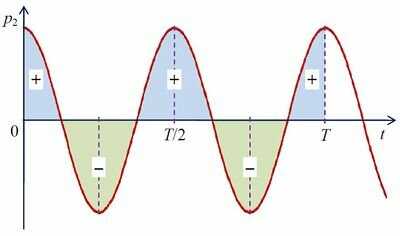
Рис. 2

Поэтому среднее значение мощности переменного электрического тока за период будет равно

\(\left\langle P \right\rangle =\dfrac{U_{m} \cdot I_{m} }{2}.\)

Тогда с учетом закона Ома \(\left(I_{m} =\dfrac{U_{m}}{R} \right)\) получаем:

\(\left\langle P \right\rangle = \dfrac{I_{m}^{2} }{2} \cdot R=\dfrac{U_{m}^{2} }{2R}. (4)\)

По определению действующих значений необходимо сравнивать мощности (количество теплоты в единицу времени) переменного и постоянного тока. Запишем уравнения для расчета мощности постоянного тока

\(P=I^{2} \cdot R=\dfrac{U^{2} }{R}\)

и сравним с уравнениями (4}:

\(\dfrac{I_{m}^{2}}{2} \cdot R = I^{2} \cdot R, \;\;\; I=\dfrac{I_{m}}{\sqrt{2}},\)

\(\dfrac{U_{m}^{2}}{2R} = \dfrac{U^{2}}{R}, \;\;\; U=\dfrac{U_{m}}{\sqrt{2}}.\)

Практические рекомендации для расчета полной энергии

Расчет полной энергии колебательного контура может показаться сложным процессом, но с помощью правильных подходов и формул он может быть достигнут с легкостью. В следующих параграфах мы предоставим практические рекомендации для эффективного расчета полной энергии контура.

1. Определите все необходимые значения: Прежде чем приступить к расчету полной энергии, убедитесь, что у вас есть все необходимые значения, такие как масса объекта, частота колебаний и амплитуда колебаний. Точные и правильные значения являются ключевыми для достижения точных результатов.

2. Используйте соответствующие формулы: Для расчета полной энергии можно использовать различные формулы, в зависимости от контекста и условий задачи. Например, для возбужденного колебательного контура формула полной энергии можно записать как W_total = 1/2L_eqC_eqV_m2, где L_eq — эквивалентная индуктивность, C_eq — эквивалентная емкость, V_m — максимальное значение напряжения.

3. Проверьте единицы измерения: При расчетах полной энергии не забудьте проверить и преобразовать единицы измерения, чтобы они были согласованы. Например, если масса объекта дана в граммах, а амплитуда колебаний в метрах, необходимо привести все значения к одной системе единиц, чтобы гарантировать правильный результат.

4. Проведите схематическую диаграмму: Визуализация колебательного контура в виде схематической диаграммы поможет вам лучше понять его структуру и связи между различными элементами. Это также может помочь в определении значений переменных и упрощении расчетов.

5. Проверьте свои расчеты: После завершения расчетов полной энергии контура всегда рекомендуется проверить свои результаты, чтобы избежать возможных ошибок. Проверка равенств и учет единиц измерения также являются важными шагами в этом процессе.

Следуя этим практическим рекомендациям, вы сможете более эффективно и точно рассчитывать полную энергию колебательных контуров и достигать более точных результатов в своих исследованиях и расчетах.

Устройство электрического конденсатора и его ёмкость

Конструкция электрического конденсатора достаточна проста. Он состоит из двух металлических пластин, которые разделены изолятором. В роли изолятора может выступать слюда, бумага или даже воздушная прослойка.

Базовое свойство конденсатора — способность к накоплению электроэнергии. Это происходит благодаря тому, что на каждой из пластин скапливаются заряды только с одним знаком («плюс» или «минус»).

Единственное значимое различие между конденсаторами разных видов — их ёмкость, то есть ограничения по количеству вмещаемых зарядов. Увеличить ёмкость конденсатора можно, если увеличить площадь пластин, а также, если разместить их как можно ближе друг к другу.

Емкость конденсатора изменяется не только в соответствии с площадью пластин и расстоянием между ними, но и согласно выбранному типу диэлектрика. Так при прочих равных условиях, если в качестве диэлектрика использовалась слюда, то ёмкость будет практически в шесть раз больше той, что продемонстрирует образец с воздушным диэлектриком. Ёмкость при использовании бумажного диэлектрика будет лишь в два раза превосходить ту, что даёт воздушный вариант.

Существуют также конденсаторы переменной ёмкости. В соответствии с названием для таких разновидностей конденсаторов свойственна возможность изменения ёмкости. Конструкция такого конденсатора включает в себя статор (неподвижную пластину) и ротор (подвижную пластину). Оба элемента закреплены на оси. Поворот оси заставляет двигаться ротор увеличивая или уменьшая площадь попадания подвижной пластины между стационарными пластинами, а значит регулируя ёмкость конденсатора.

Колебательные контуры в коммуникационных системах

В коммуникационных системах колебательные контуры играют роль фильтра, позволяющего пропустить только определенные частоты сигнала, а подавить или ослабить остальные. Такой подход позволяет повысить качество передаваемого сигнала и уменьшить влияние шумов и помех.

Колебательные контуры также используются для модуляции сигналов, то есть изменения одной или нескольких характеристик сигнала под воздействием информации, которую необходимо передать. Например, контуры часто применяются в системах радиосвязи для модуляции амплитуды, частоты или фазы сигнала.

Один из самых распространенных примеров использования колебательных контуров в коммуникационных системах — это радиоприемники. В радиоприемниках колебательный контур играет роль фильтра, который позволяет пропускать только сигналы определенной частоты, соответствующие выбранной радиостанции. Это позволяет слушателю получать четкий и чистый звук без помех.

Кроме того, колебательные контуры применяются в других коммуникационных системах, таких как телевизионные приемники, сотовые телефоны, сети передачи данных и т. д. В каждом из этих устройств контуры играют свою уникальную роль в обеспечении эффективной передачи сигнала.

Примеры применения колебательных контуров в коммуникационных системах:
— Радиоприемники;
— Телевизионные приемники;
— Сотовые телефоны;
— Сети передачи данных и интернета;
— Радиолокационные системы;
— Системы радиосвязи.

Колебательные контуры имеют широкий спектр применения в коммуникационных системах и являются неотъемлемым элементом обеспечения эффективной передачи информации.

Колебательный контур: определение и основные принципы

Основной принцип работы колебательного контура заключается в периодическом прохождении электрического заряда между индуктивностью и емкостью. Когда заряд переходит с конденсатора на индуктивность, возникают магнитные поля, которые хранят энергию. Затем, когда заряд возвращается на конденсатор, энергия магнитных полей превращается в энергию электрического поля конденсатора. Этот процесс повторяется во времени и создает электрические колебания.

Важно отметить, что сопротивление в колебательном контуре выполняет роль «тормоза», который затрудняет энергии свободно переходить между индуктивностью и емкостью. Это позволяет контролировать частоту колебаний и расход энергии в системе

Колебательные контуры широко используются в различных устройствах, таких как радиопередатчики, радиоприемники, радары и усилители сигналов.

Индуктивность	Емкость	Сопротивление
Индуктивность представляет собой катушку или катушку из провода, которая создает магнитное поле, когда через нее протекает электрический ток. Магнитное поле хранит энергию и позволяет переходу заряда между индуктивностью и емкостью.	Емкость — это устройство для хранения электрического заряда, состоящее из двух металлических пластин, разделенных диэлектриком (изолятором). Когда заряд переходит на пластины, электрическое поле создается между ними и хранит энергию.	Сопротивление представляет собой свойство материала, которое затрудняет протекание электрического тока. В колебательном контуре сопротивление имеет роль тормоза, которое регулирует энергию и частоту колебаний.

Способы расчета периода электромагнитных колебаний

Период электромагнитных колебаний в колебательном контуре можно рассчитать различными способами в зависимости от известных параметров контура. Рассмотрим несколько основных методов расчета:

Метод	Описание
1. Формула для колебательного контура с индуктивностью и емкостью	Если известны индуктивность (L) и емкость (C) колебательного контура, то период колебаний можно определить с помощью следующей формулы: T = 2π√(LC). Здесь T — период колебаний, π — число Пи.
2. Формула для колебательного контура с индуктивностью, емкостью и сопротивлением	Если известны индуктивность (L), емкость (C) и сопротивление (R) колебательного контура, то период колебаний можно рассчитать с помощью формулы: T = 2π√(LC(1 + (R/(2L))^2)).
3. Измерение периода колебаний	Если у вас есть возможность измерить период колебаний напряжения в колебательном контуре, то его можно получить путем прямого измерения с помощью осциллографа или другого измерительного устройства.
4. Метод математического моделирования	Еще одним способом расчета периода колебаний является математическое моделирование с использованием соответствующих уравнений, которые описывают поведение электромагнитных колебаний в колебательном контуре.

Выбор метода расчета периода электромагнитных колебаний зависит от доступных данных и возможностей проведения измерений. Каждый из этих способов имеет свои преимущества и ограничения и может быть применен в различных ситуациях. Используя один из этих методов, вы сможете точно определить период электромагнитных колебаний в колебательном контуре и использовать это знание для дальнейшего анализа и применения в практических задачах.

Электромагнитные колебания

Конспект для 10-11 классов. Элементы содержания ЕГЭ по физике:3.5.1. Колебательный контур. Свободные электромагнитные колебания в колебательном контуре.
Формула Томсона. Связь амплитуды заряда конденсатора с амплитудой силы тока в колебательном контуре.3.5.2. Закон сохранения энергии в колебательном контуре.3.5.3. Вынужденные электромагнитные колебания. Резонанс

Электромагнитные колебания — это повторяющийся процесс взаимного превращения электрических и магнитных полей. Электромагнитные колебания возникают в колебательном контуре.

Колебательный контур — это цепь, состоящая из конденсатора и катушки индуктивности.

Если сопротивлением проводов контура можно пренебречь, то такой контур называется идеальным. При зарядке конденсатора в идеальном колебательном контуре возникают свободные, незатухающие электромагнитные колебания заряда и напряжения на обкладках конденсатора, а также силы тока и ЭДС в катушке индуктивности. Электромагнитные колебания в идеальном колебательном контуре являются высокочастотными и гармоническими.

Электромагнитные колебания бывают двух видов — свободные и вынужденные.

Свободными колебаниями называют колебания, возникающие в колебательной системе за счет первоначально сообщенной этой системе энергии.

Вынужденные колебания — это периодические изменения заряда, силы тока и напряжения в цепи под действием переменной электродвижущей силы от внешнего источника.

На рисунке ниже изображены графики колебаний заряда, напряжения и силы тока в идеальном колебательном контуре. Внизу статьи приведены уравнения электромагнитных колебаний и волн.

Период, циклическая частота и частота свободных электромагнитных колебаний в колебательном контуре (формула Томсона):

Т = 2π√LC;   ω = 1/√LC;   v = 1/(2π√LC)

Здесь Т — период колебаний (с), L — индуктивность катушки (Гн), C — емкость конденсатора (Ф), ω — циклическая частота колебаний (рад/с), v — частота колебаний (Гц).

Свободные электромагнитные колебания в идеальном колебательном контуре подчиняются закону сохранения энергии: полная энергия электромагнитных колебаний Е_ЭЛ–М равна максимальной энергии электрического поля конденсатора Е_{эл max}, или равна максимальной энергии магнитного поля катушки индуктивости Е_{м max}, или равна сумме мгновенных электрической Е_эл и магнитной Е_м энергий поля конденсатора и катушки в любой промежуточный момент:

Е_ЭЛ–М = Е_{эл max} = Е_{м max} = Е_эл + Е_м.

Это закон можно записать, развернув значения энергии электрического и магнитного полей через их параметры:

В этом уравнении максимальную энергию электрического поля в зависимости от известных величин можно выразить как Е_{эл max} = q2_max/2C или Е_{эл max} = q_maxU_max/2, а его мгновенную энергию — соответственно как Е_эл = q2/2C или Е_эл = qu/2. Здесь q, u и i — мгновенные значения заряда, напряжения и силы тока.

Всякий реальный колебательный контур имеет сопротивление проводов R. Если ему один раз сообщить энергию, например, зарядив конденсатор С, то колебания в нем будут затухающими из-за потерь энергии на джоулево тепло. График затухающих колебаний силы тока изображен на рисунке.

Электромагнитные колебания являются затухающими, потому что происходят потери энергии. Часть энергии расходуется на преодоление сопротивления контура и превращается во внутреннюю энергию. Поэтому суммарная энергия электрического и магнитного полей с течением времени уменьшается и колебания затухают. Чтобы колебания были незатухающими, колебательный контур надо пополнять энергией, например, включив в него источник переменного напряжения.

Если частота пополнения контура энергией будет равна собственной частоте колебаний контура, то в контуре возникнет электрический резонанс — явление резкого возрастания максимальной силы тока в контуре (амплитуды силы тока), когда частота пополнения контура энергией становится равной собственной частоте колебаний в контуре.

Уравнения электромагнитных колебаний заряда,
силы тока, напряжения и ЭДС:

Конспект урока по физике для 10-11 классов «Электромагнитные колебания». Выберите дальнейшее действие:

• Вернуться к Списку конспектов по физике для 7-11 классов
• Найти конспект через Кодификатор ОГЭ по физике
• Найти конспект через Кодификатор ЕГЭ по физике

Свободные колебания, основные параметры контура

В простейшем случае реальный колебательный контур состоит всего из двух деталей – катушки индуктивности и конденсатора, но его эквивалентная схема включает три элемента — индуктивность $L,$ емкость $С$ и эквивалентное сопротивление $R$_L$ (рис. 1,а).
Основной вклад в сопротивление $R_L$ обычно вносит омическое сопротивление провода, которым намотана катушка, а добавочный — активные потери энергии в сердечнике катушки, в конденсаторе, скин–эффект в проводе катушки и рассеяние электромагнитной энергии в окружающем пространстве. Элементы $L$ и $С$ определяют собственную частоту колебаний контура $\omega _0 = 2\pi f_0$, а отношение реактивного сопротивления этих элементов к активному сопротивлению потерь — добротность контура $Q:$
\begin{equation}
f_{0} =\frac{1}{2\pi \sqrt{LC} } , \ \ Q=\frac{\omega L}{R_{L} } =\frac{1}{\omega CR_{L} } =\frac{\rho }{R_{L} } \ \ \rho =\sqrt{\frac{L}{C} } .
\end{equation}

Величина $\rho $ называется волновым (или характеристическим) сопротивлением контура. Это чисто реактивное сопротивление, которое определяет взаимосвязь реактивных токов и напряжений в контуре, а отношение реактивного сопротивления к активному определяет добротность.

Энергия может быть введена в контур самыми различными способами, например, начальной зарядкой конденсатора до некоторого напряжения $U,$ как показано на рис. 1,б. При переключении конденсатора он начнет разряжаться через индуктивность и напряжение $U_{C}$ будет уменьшаться, а ток через катушку расти. В момент полной разрядки конденсатора (уменьшения напряжения $U_{C}$ до нуля) ток в цепи достигает максимального значения и начальная электрическая энергия конденсатора $W_э = \frac 12 CU^{2}$ переходит в магнитную энергию катушки $W_м = \frac 12 LI^2$. Поскольку ток через индуктивность не может прерваться мгновенно из–за явления самоиндукции, то энергия магнитного поля начинает уменьшаться постепенно. Изменение знака производной магнитной индукции вызывает эдс самоиндукции противоположного знака по отношению к первому полупериоду (полупериоду разрядки конденсатора) и конденсатор начинает перезаряжаться. Если бы потери в контуре отсутствовали
$R_L = 0,$ то конденсатор перезарядился бы до той же величины $U_C,$ но противоположного знака заряда.

В реальном контуре часть энергии за цикл перезарядки будет рассеиваться на $R_L$ и колебания в контуре будут затухающими (рис. 2). Величина затухания $\delta$ однозначно связана с добротностью (п. 3.4 введения):
$$
\delta = \frac{\pi}{QТ} = \frac{R_L}{2L}.
$$

Какие основные характеристики имеет колебательный контур?

Основные характеристики колебательного контура:

1. Резонансная частота: это частота, при которой колебания в контуре наиболее эффективны. Резонансная частота определяется параметрами контура и вычисляется по формуле: f = 1 / (2π√(LC)), где L — индуктивность, C — емкость.
2. Период колебаний: это время, за которое колебания в контуре проходят один полный цикл. Период колебаний можно вычислить по формуле: T = 1 / f, где f — частота колебаний.
3. Резонансное сопротивление: это сопротивление, при котором в контуре достигается максимальная амплитуда колебаний. Резонансное сопротивление зависит от параметров контура и определяется по формуле: R = √(L / C).
4. Качество колебательного контура: это безразмерная характеристика, которая показывает, насколько контур малоамортезированный. Качество контура определяется по формуле: Q = ω₀ (L / R), где ω₀ — резонансная угловая частота.
5. Фазовый сдвиг: это разность фаз между напряжением на индуктивности и напряжением на емкости в колебательном контуре. Фазовый сдвиг зависит от частоты колебаний и может быть либо положительным, либо отрицательным.

Примеры колебательных контуров включают: электрические колебательные контуры в радиопередатчиках, радиоприёмниках и радарах; контуры, используемые в электро- и радиочасах; контуры LC-генераторов и другие.

Изменение заряда конденсатора колебательного контура

При работе колебательного контура внутри него наблюдается колебание электронов. Изначально, для возникновения колебаний требуется первичный энергетический импульс. Сформировать его можно всего лишь на долю секунды соединив конденсатор с электрической батареей.

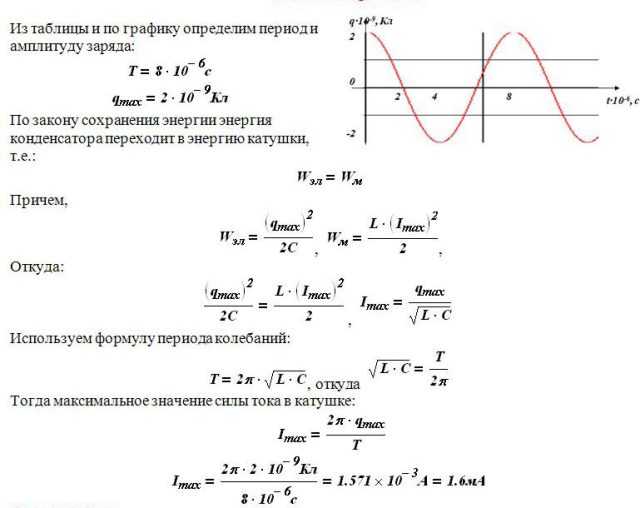
В этот момент конденсатор заряжается. Одна пластина насыщается избыточным количеством электронов, а на другой возникает их дефицит. Между этими разнозаряженными полюсами происходит формирование электрического поля, которое и является ёмкостью для запасания энергии, полученной от источника питания.

Как только конденсатор оказывается заряжен, избыточный объём электронов с одной пластины направляется в сторону другой, но перед этим проходит через катушку. В это мгновение внутри контура фиксируется наличие электрического тока.

Нужно отметить, что в момент колебаний не происходит прямого перехода электронов между обкладками конденсатора. Хотя ток и движется достаточно быстро (практически 300 000 км/с), перемещение электронов внутри проводников не превышает пары-тройки миллиметров в секунду. В ходе одного полупериода электроны способны преодолеть лишь небольшой промежуток пути.

Несмотря на то, что намотка катушки представляет собой проводку, изготовленную из металлической проволоки, она становится причиной сильного противодействия для потока электронов. Образуемое витками магнитное поле перенимает на себя часть той электроэнергии, которую конденсатор скопил в момент зарядки.

По этой причине, даже при полной разрядке конденсатора продолжается течение тока внутри контура. Направление движения не изменится, но продолжатся оно будет уже благодаря катушечной энергии.

Когда энергетические запасы катушки тоже иссякнут, исчезнет и её магнитное поле. В этот момент у конденсатора вновь появится заряд, полярность пластин поменяется (избыток электронов будет там, где прежде был дефицит). У вновь накопившего заряд конденсатора начнётся повторная разрядка. Ток снова будет проходить через катушку, но его направление сменится на противоположное.

Таким образом формируются электронные колебания, которые прекратятся только когда энергетические потери не превысят количество запасённой конденсатором энергии.

Энергия тока может теряться ввиду следующих причин:

Нагревание проводов.

Поверхностный эффект делает уровень активного сопротивления более высоким, чем уровень сопротивления постоянному току. Под поверхностным эффектом подразумевается явление при котором движение высокочастотного тока происходит не во всём проводе, а лишь вдоль тонкого поверхностного слоя. Это приводит к сокращению площади рабочего сечения. При более высоких частотах рабочий слой ещё больше истончается и сопротивление вновь растёт.

Нагревание твёрдого диэлектрика.

Диэлектрики находятся под действием переменного электрического поля, что приводит к интенсивному молекулярному колебанию и взаимному трению между молекулами.

Отсутствие идеальной изоляции.

К сожалению, даже самые хорошие диэлектрики не позволяют избежать возникновения токов утечки.

Нагревание ферромагнитного сердечника.

Ферромагнитные сердечники необходимы, чтобы увеличивать индуктивность катушек.

Возникновение вихревых токов.

На размещённые поблизости от колебательного контура предметы из металла влияет переменное магнитное поле, ввиду чего в них образуются вихревые токи, забирающие на себя часть энергии.

• Излучаемые контуром электромагнитные волны.
• Потери, связанные с подключением к другим цепям.

При возрастании частоты внутри колебательного контура увеличиваются все виды потерь. При суммировании энергетических потерь из приведённого перечня окажется, что они соответствуют потерям под влиянием активного сопротивления. Соответственно по активному сопротивлению можно судить об общих энергетических потерях.

Добротность последовательного колебательного контура

Ну раз уж мы начали задвигать тему колебательных контуров, поэтому мы не можем обойти стороной такой параметр, как добротность колебательного контура. Так как мы уже провели некоторые опыты, то нам будет проще определить добротность, исходя из амплитуды напряжений. Добротность обозначается буквой Q и вычисляется по первой простой формуле:

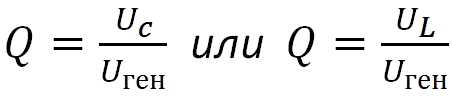
Давайте посчитаем добротность в нашем случае.

Так как цена деления одного квадратика по вертикали 2 Вольта, следовательно, амплитуда сигнала  генератора частоты 2 Вольта.

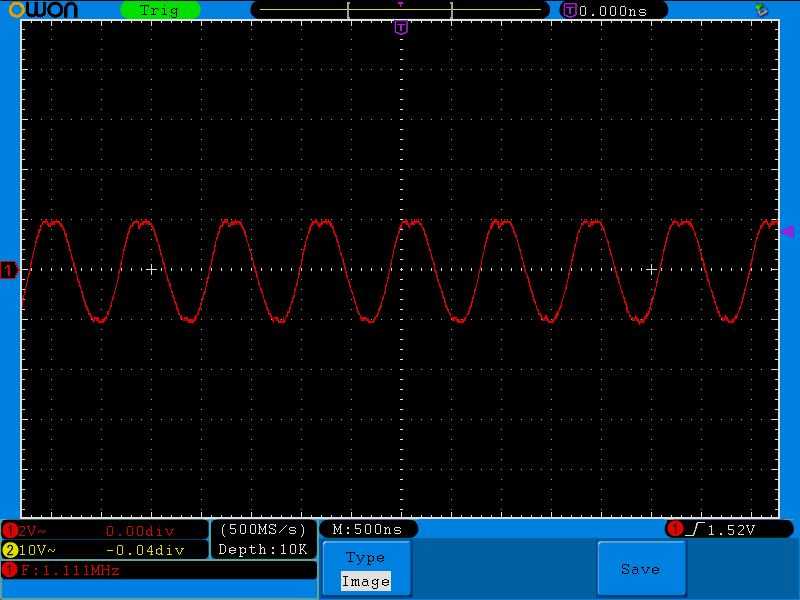
А это то, что мы имеем на зажимах конденсатора или катушки. Здесь цена деления одного квадратика по вертикали 5 Вольт. Считаем квадратики и умножаем. 5х4=20 Вольт.

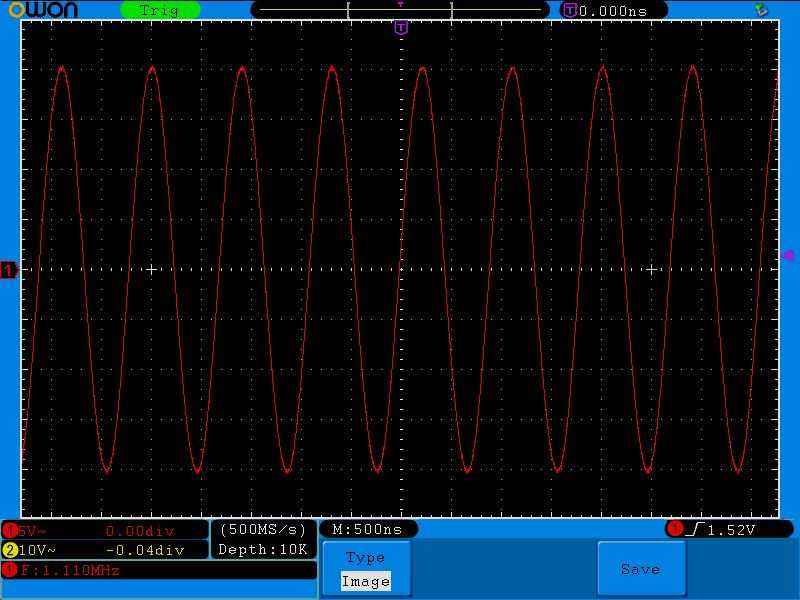
Считаем по формуле добротности:

Q=20/2=10. В принципе немного и не мало. Пойдет. Вот так вот на практике можно найти добротность.

Есть также вторая формула для вычисления добротности.

где

R — сопротивление потерь в контуре, Ом

L — индуктивность, Генри

С — емкость, Фарад

Зная добротность, можно легко найти сопротивление потерь R последовательного колебательного контура.

Также хочу добавить пару слов о добротности. Добротность контура — это качественный показатель колебательного контура. В основном его стараются всегда увеличить различными всевозможными способами. Если взглянуть на формулу выше, то можно понять, для того, чтобы увеличить добротность, нам надо как-то уменьшить сопротивление потерь колебательного контура. Львиная доля потерь относится к катушке индуктивности, так как она уже конструктивно имеет большие потери. Она намотана из провода и в большинстве случаев имеет сердечник. На высоких частотах в проводе начинает проявляться скин-эффект, который еще больше вносит потери в контур.

Видео на тему «Как работает колебательный контур. Резонанс»:

Основные компоненты колебательного контура

Колебательный контур состоит из нескольких основных компонентов, которые взаимодействуют между собой и обеспечивают возможность выполнять колебательные процессы. Вот основные компоненты колебательного контура:

1. Индуктивность (катушка) – это элемент, который создает магнитное поле при прохождении через него электрического тока. Индуктивность измеряется в генри (Гн) и обозначается символом L. Она является ключевым компонентом колебательного контура, так как сохраняет энергию в магнитном поле.
2. Емкость – это компонент, который хранит электрическую энергию в виде заряда. Емкость измеряется в фарадах (Ф) и обозначается символом C. Она играет важную роль в колебательном контуре, так как аккумулирует энергию в электрическом поле.
3. Сопротивление – это элемент, который противодействует свободному движению электрического тока в колебательном контуре. Сопротивление измеряется в омах (Ω) и обозначается символом R. Оно необходимо для ограничения тока и диссипации избыточной энергии.

Вместе индуктивность, емкость и сопротивление создают колебательный контур, который способен осуществлять колебательные процессы. При наличии энергии колебания происходят между индуктивностью и емкостью. Сопротивление же преобразует энергию в тепло и помогает поддерживать амплитуду колебаний на постоянном уровне.

Процесс возникновения и поддержания осцилляций

Осцилляции в колебательном контуре осуществляются за счет взаимодействия двух хранимых форм энергии: электрической и магнитной. Эти колебания возникают под воздействием внешнего возбуждающего источника, например, генератора переменного тока.

Процесс возникновения осцилляций в колебательном контуре можно представить следующим образом:

1. В начальный момент времени заряд на конденсаторе равен нулю, а ток в катушке равен максимальному значению. Начинает действовать закон Фарадея и заряжается конденсатор.
2. После зарядки конденсатора его заряд максимален, а ток в катушке равен нулю. В это время начинает действовать закон Ленца и происходит разрядка конденсатора.
3. Процесс разрядки конденсатора протекает до тех пор, пока его заряд не станет нулевым, а ток в катушке достигнет максимального значения.
4. После разрядки конденсатора начинается зарядка в обратном направлении.
5. Процесс зарядки и разрядки конденсатора продолжается, пока в колебательном контуре продолжается внешнее возбуждение источником.

Длительность процесса зарядки и разрядки конденсатора определяется параметрами колебательного контура и частотой внешнего источника. Если эти параметры соответствуют условию резонанса, то амплитуда колебаний будет максимальной.

Для поддержания осцилляций в колебательном контуре необходима система, которая будет постоянно передавать энергию обратно в контур. Обычно в роли такой системы выступает генератор переменного тока, который поддерживает колебания, питая их новой порцией энергии на каждом участке колебательного процесса. Таким образом, осцилляции в колебательном контуре остаются поддерживаться за счет постоянного поступления энергии.

Осцилляции в колебательном контуре широко применяются в электронике. Они используются в радиосвязи, телевидении, радарах и других системах передачи и приема сигналов.