Площадь поверхности куба

Объём и площадь куба, формулы.

Введите пожалуйста в соответствующее поле один, любой параметр куба, который Вам известен, остальные мы вычислим и предоставим подробный расчёт с указанием всех формул, по которым быдут произведены вычисления.

Формула объёма куба

Чтобы его найти, необходимо знать размеры рёбер: высоту, ширину и длинну. по формуле, размеры граней куба необходимо перемножить три раза, то есть возвести в третью степень. Объём куба равен длине ребра ‘в кубе’ ))).

Объём можно представить в литрах или куб.см., кубических миллиметрах.

Формула площади поверхности куба

По формуле площади куба необходимо найти площадь одной стороны/грани куба, а затем умножить это значение на 6. Потому, что граней у куба как раз шесть штук ;-). Все стороны куба равны между собой по площади, а все рёбра куба равны по длинне.

Грань куба

В некоторых случаях бывает известна площадь грани куба, тогда для того, что бы найти объём куба, нужно вычислить квадратный корень из площади сторогы куба — это будет длинна ребра, и умножить длинну ребра на площадь грани — получим объём куба. Или просто возвести в третью степень длинну ребра — получим объём куба опять. Два разных пути нахождения объёма дадут один и тот же результат.

• Расчёт НДС
• Сумма прописью онлайн!
• Определить сумму по НДС
• Формула площади треугольника
• Найти площадь трапеции
• Объем цилиндра
• Площадь квадрата
• Объём куба
• Найти объём параллелепипеда
• Длина окружности формула
• Площадь круга онайн
• Как найти площадь прямоугольника
• Расчёт площади стены
• Расчёт профнастила
• Расчёт забора
• Калькулятор стен дома
• Расчёт площади помещения
• Расчёт площади дома
• Расчёт объёма помещения
• Строительный объём здания
• Калькулятор НДС
• Объём воздуха в комнате
• Расчёт двускатной крыши
• Площадь квадрата со стороной 3
• Площадь квадрата со стороной 2
• Площадь квадрата если известен периметр

Как найти площадь куба — онлайн измерение площади

Используя калькулятор на сайте OnlineMSchool , можно быстро вычислить площадь куба. Достаточно ввести нужное значение стороны и сервис выдаст детальное пошаговое решение задания.

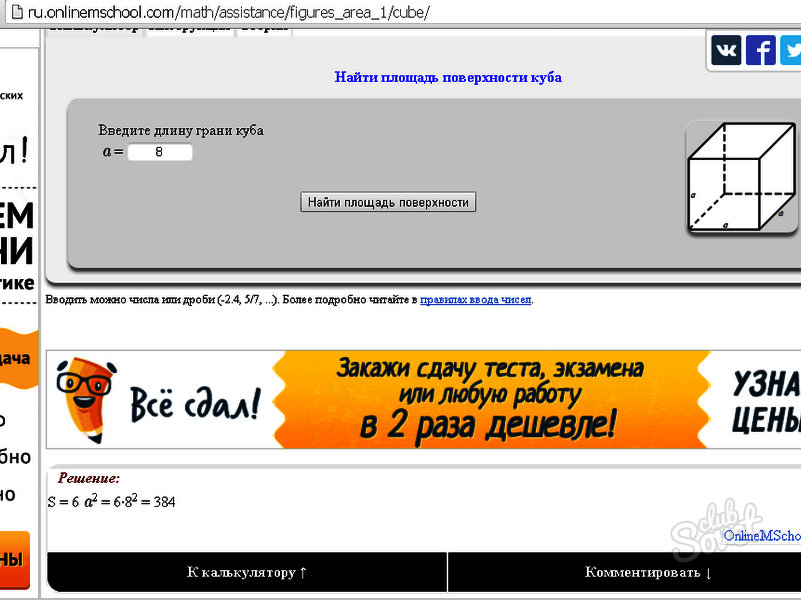
Итак, чтобы знать площадь куба, вычислите площадь одной из сторон, затем умножьте результат на 6, так как фигура имеет 6 равных сторон. Можно при подсчете использовать формулу S = 6а². Если задана площадь поверхности, возможно определить длину боковой части, проделав обратные шаги.

Геометрия
является одной из основных математических наук, базовый курс которой изучается даже в школе. На самом деле польза от знаний различных фигур и законов пригодится в жизни каждому. Очень часто встречаются геометрические задачи на нахождение площади
. Если с плоскими фигурами
особых проблем у учащихся не возникает, то вот объемные
могут вызвать определенные трудности. Вычислить площадь поверхности куба

бывает не так просто, как кажется на первый взгляд. Но при должном внимании решается даже самая сложная задача.

Площадь куба, площадь сечения куба, формула, площадь куба онлайн.

1. Для того, чтобы перейти к теме «формулы площади куба» — давайте нарисуем или предоставим, что такое куб.

   Куб — это фигура с одинаковыми сторонами, угол между которыми равен 90°.

   Если сторона куба — «а».

   Площадь куба равна 6 умноженное на а²

2. Для того, чтобы доказать формулу «площади куба» Вам потребуется

   Взглянуть на куб и вы увидите, что количество сторон куба — 6. И каждая сторона куба состоит из квадрата, со стороной «а».

   Вы знаете площадь квадрата, которая выражается формулой:

   S = a²

   Выше вы уже сказали, что сторон у куба 6, то нужно площадь одного квадрата умножить на 6.

   Вы доказали, что «Площадь куба равна 6 умноженное на а²»

3. Условие задачи :

   Найдите площадь куба. если известна сторона куба, которая равна 5см.

   Вспоминаем уже приведенную формулу куба :

   И букву a — сторону куба заменяем на наше значение — 5см

   S = 6a² = 6 * 5² = 6 * 25 = 150Ответ:

   Если сторона куба равна 5см, то площадь куба равна 150см²

   Для проверки правильности решения задачи «найдите площадь куба, если известна сторона» — воспользуйтесь онлайн калькулятором «подсчета площади куба» — см. ниже:

4. Для того чтобы найти площадь куба онлайн, вам потребуется :

   Сторона куба — заполнить значением стороны куба.

   И нажать кнопку найти площадь куба.

5. Сформулируем «формулу площади сечения куба» начнем…

   Если сторона куба — — «а».

   То формула площади сечения куба звучит так:

   Сечение площади куба равно произведению квадрата стороны на корень из двух.

6. Выше Вы рассмотрели формулу «площади сечения куба», теперь… давайте докажем «формулу площади сечения куба».

   Нам нужно найти диагональ треугольника ABC — что будет одной из сторон сечения куба.

   Вспоминаем теорию Пифагора

   с² = а² + b²

   Если мы переведем в наши буквенные обозначения, для нашего треугольника, то:

   BC² = AB² + AC²

   В нашем случае «AB = AC= a» — из чего получаем :

   BC² = а² + а² = 2а²

   Теперь извлекаем корень с двух сторон:

   √BC² = √2а²

   Мы нашли одну сторону сечения куба:

   BC = а √2

   Мы нашли сторону сечения куба это — BC

   Теперь мы можем построить сечение куба:

   Т.е нам нужно найти площадь прямоугольника BCDE.

   Площадь прямоугольника равна :

   S = BC * CD

   Выше, мы уже нашли BC = а√2

   Как мы знаем из условия, что это куб, а у куба все стороны равны, то CD = «a».

   Заменяем BC и CD.

   S = а √2 * a = a² √2

7. Для того, чтобы найти площадь сечения куба онлайн нам понадобится формула и немного вернуться к теории, чтобы…

   добавить ясности, как видим, что в формуле присутствует корень из 2, что равно:

   1.4142135623731

   И далее к форме:

   Для того, чтобы подсчитать «площадь сечения куба» вам понадобится:

   В первом поле выбираем диапазон числа(см. выше), диапазон от 1 до 13, который будет показывать ваш выбор сколько чисел после запятой оставить!

   Во втором поле вбиваем размер стороны куба.

   И далее вам остается подсчитать площадь сечения куба онлайн! Нажимаем кнопку — «найти площадь сечения куба».

8. Условие задачи :

   Найдите площадь сечения куба, если известна сторона, которая равна 10см.

   Для решения данной задачи, нам потребуется знать

   Вспоминаем площадь сечения куба:

   S = a²√2

   Заменяем а на 10, корень квадратный из 2 округлим до 1.4 :

   S = 10²√2 = 100 * 1.4 = 140см².

   Более точные вычисления «площади сечения куба » вы можете произвести в форме выше пунктом!

Не стесняемся говорить спасибо!

Как связан куб с другими фигурами и телами?

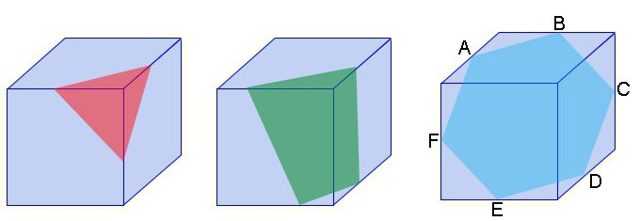
Если начертить сечение куба, которое проходит через три его грани, то оно будет иметь вид треугольника. По мере удаления от вершины сечение будет все больше.

Настанет момент, когда пересекаться будут уже 4 грани, и фигура в сечении станет четырехугольником.

Если провести сечение через центр куба так, чтобы оно было перпендикулярно его главным диагоналям, то получится правильный шестиугольник.

Внутри куба можно начертить тетраэдр (треугольную пирамиду). За вершину тетраэдра берется один из его углов. Остальные три совпадут с вершинами, которые лежат на противоположных концах ребер выбранного угла куба.

В него можно вписать октаэдр (выпуклый правильный многогранник, который похож на две соединенные пирамиды). Для этого нужно найти центры всех граней куба. Они будут вершинами октаэдра.

Возможна и обратная операция, то есть внутрь октаэдра реально вписать куб. Только теперь центры граней первого станут вершинами для второго.

Площадь поверхности куба

Площадь кубической фигуры — это сумма площадей всех граней. Каждая грань куба — это квадрат. Площадь квадрата, то есть одной грани, определяется по простой формуле как:

Куб — это гексаэдр, то есть шестигранник. Таким образом, площадь поверхности кубической фигуры представляет собой сумму шести квадратов:

Определить площадь куба можно не только при помощи длины его ребра: для расчета площади поверхности вы можете использовать диагональ самого куба или диагональ одной грани.

Диагональ куба — это отрезок, который находится внутри пространства куба и соединяет две противоположные вершины. Проведенная диагональ разделяет куб на два прямоугольных треугольника. Согласно теореме Пифагора квадрат ребра куба равен одной трети от квадрата диагонали D, следовательно, формула площади полной поверхности приобретает вид:

Площадь поверхности куба легко определить и с помощью диагонали одной грани. Площадь квадрата через диагональ равна:

Так как у куба 6 граней, общая площадь поверхности составит сумму шести граней куба, то есть:

Таким образом, чтобы определить площадь поверхности кубической фигуры вам достаточно ввести в форму-онлайн калькулятора всего один параметр на выбор:

• длину ребра;
• диагональ куба;
• диагональ квадрата.

Рассмотрим примеры использования данных формул в реальной жизни.

Куб — свойства, виды и формулы

Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.

Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:

многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;

прямая призма, все грани которой есть квадраты;

прямоугольный параллелепипед, все рёбра которого равны.

Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.

Видео:Как различать периметр и площадь?Скачать

вычисление площади куба по его ребру

Для того чтобы вычислить всю площадь поверхности куба, потребуется знание одного из его элементов. Самый простой способ решения, когда известно его ребро или, другими словами, сторона квадрата, из которого он состоит. Обычно эта величина обозначается латинской буквой «а».

Теперь нужно вспомнить формулу, по которой вычисляется площадь квадрата. Чтобы не запутаться, введено ее обозначение буквой S1.

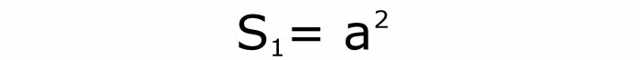
Для удобства лучше задать номера всем формулам. Эта будет первой. Но это площадь только одного квадратика. Всего их шесть: 4 по бокам и 2 снизу и сверху. Тогда площадь поверхности куба вычисляется по такой формуле: S = 6 * a2. Ее номер 2.

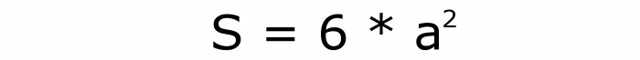
Примеры из жизни

Представьте, что вы хотите соорудить из листов ДСП ящик для хранения инструментов в форме куба. Вы знаете, что он отлично впишется в пространство на чердаке высотой 50 см. Сколько же квадратных метров ДСП вам понадобится для создания такого контейнера? Зная высоту, равную a = 0,5 м вы можете легко подсчитать площадь общей поверхности куба, введя данный параметр в онлайн-калькулятор. Вы получите ответ в виде:

Таким образом, вам понадобится всего 1,5 квадратных метра ДСП для создания ящика для инструментов. Зная всего один параметр, вы без труда порежете листы на грани куба и соорудите нужную конструкцию.

Контейнер

Допустим, вы хотите обработать антикоррозионным покрытием грузовые контейнеры, которые имеют кубическую форму. Для правильного расчета параметров покрытия вам необходимо знать площадь обрабатываемой поверхности. Вы знаете, что диагональ грани стандартного контейнера равняется d = 3 м. Зная этот параметр, вы легко рассчитаете площадь кубической поверхности, которая равна

Зная общую площадь покрытия, вы без проблем определите необходимое количество антикоррозионной жидкости.

Элементы куба

Основными элементами многогранника считаются грани, рёбра, вершины.

Грань

Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.

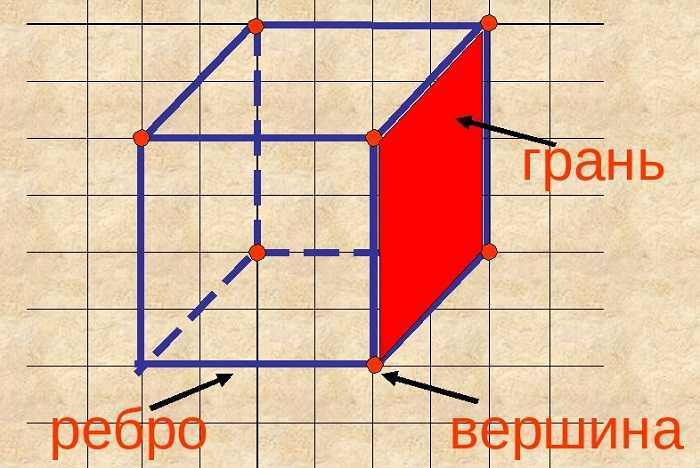
Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.

Грани куба попарно перпендикулярны, являются квадратами, равны между собой.

Ребро

Линии пересечения сторон называются рёбрами.

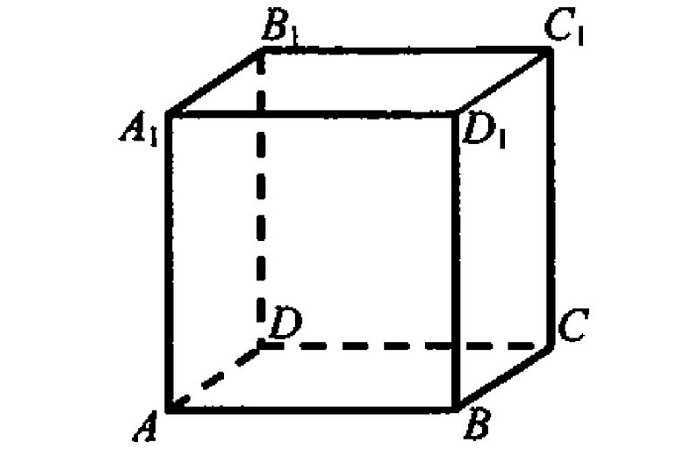
Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.

Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.

Центр грани

Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.

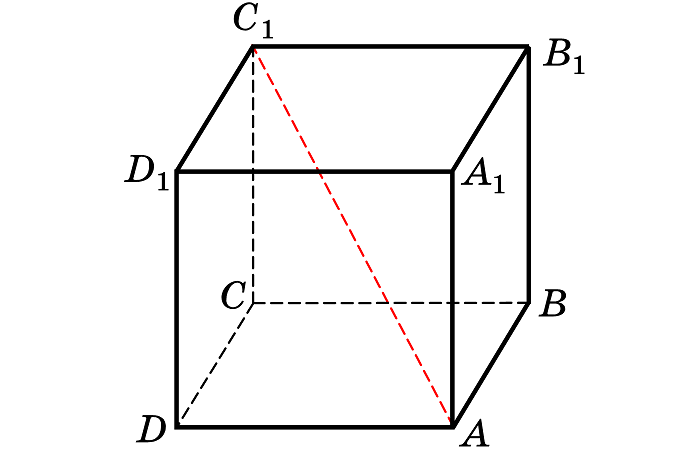
Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.

Центр куба

Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.

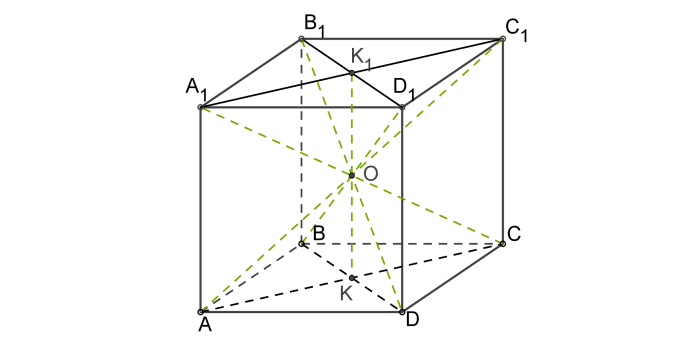
Это есть центр симметрии куба.

Ось куба

Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.

Диагональ куба

Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

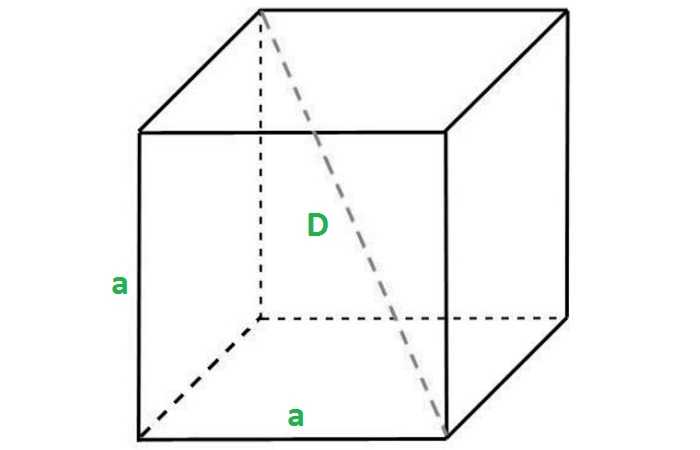
Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:

Формула доказывается с помощью дважды применённой теоремы Пифагора.

Диагональ куба — одна из осей симметрии.

Все диагонали куба равны между собой и точкой пересечения делятся пополам.

Диагональ грани куба

Длина диагонали грани в √2 раз больше ребра, то есть:

Эта формула доказывается также с помощью теоремы Пифагора.

Видео:КАК НАЙТИ ОБЪЕМ КУБА ПО РЕБРУ? Примеры | МАТЕМАТИКА 5 классСкачать

Примеры задач

Задание 1
Вычислите объем куба, если его ребро равняется 5 см.

Решение:
Подставляем в формулу заданное значение и получаем:
V = 5 см ⋅ 5 см ⋅ 5 см = 125 см 3 .

Задание 2
Известно, что объем куба равен 512 см 3 . Найдите длину его ребра.

Решение:
Пусть ребро куба – это A. Выведем его длину из формулы расчета объема:

Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.

Решение:
Применим формулу, в которой используется диагональ грани:

Публикации по теме:

Нахождение площади квадрата: формула и примеры Нахождение площади прямоугольника: формула и пример Нахождение площади треугольника: формула и примеры Нахождение площади круга: формула и примеры Нахождение площади ромба: формула и примеры Нахождение площади трапеции: формула и примеры Нахождение площади параллелограмма: формула и примеры Нахождение площади эллипса: формула и пример Нахождение площади выпуклого четырехугольника: формула и пример Нахождение периметра квадрата: формула и задачи Нахождение периметра треугольника: формула и задачи Нахождение периметра прямоугольника: формула и задачи Нахождение периметра трапеции: формула и задачи Нахождение периметра параллелограмма: формула и задачи Нахождение длины окружности: формула и задачи Теорема Пифагора для прямоугольного треугольника: формула и задачи Теорема косинусов для треугольника: формула и задачи Теорема синусов для треугольника: формула и задачи Теорема о сумме углов треугольника: формула и задачи Тригонометрические функции острого угла в прямоугольном треугольнике Нахождение объема конуса: формула и задачи Нахождение объема цилиндра: формула и задачи Нахождение объема шара: формула и задачи Нахождение площади правильного шестиугольника: формула и примеры Нахождение объема тетраэдра: формула и задачи Нахождение объема призмы: формула и задачи Нахождение объема параллелепипеда: формула и задачи Нахождение площади поверхности цилиндра: формула и задачи Нахождение площади поверхности конуса: формула и задачи Нахождение площади поверхности шара (сферы): формула и задачи Нахождение площади поверхности вписанного в цилиндр шара Нахождение радиуса шара: формула и примеры Нахождение радиуса цилиндра: формула и примеры Нахождение площади прямоугольного параллелепипеда: формула и пример Нахождение площади правильной пирамиды: формулы Формула Герона для треугольника Теорема Менелая: формулировка и пример с решением Теорема о внешнем угле треугольника: формулировка и задачи Теорема Чевы: формулировка и пример с решением Теорема Стюарта: формулировка и пример с решением Теорема о трех перпендикулярах Теорема Фалеса: формулировка и пример решения задачи Геометрическая фигура: треугольник Признаки равенства треугольников Признаки подобия треугольников Признаки равенства прямоугольных треугольников Свойства прямоугольного треугольника Свойства равнобедренного треугольника: теория и задача Определение и свойства медианы треугольника Определение и свойства медианы прямоугольного треугольника

Куб – это правильный многогранник, все грани которого являются квадратами.

Cube Formula — Что такое Cube Formula? Примеры

Формула куба помогает нам найти площадь поверхности, диагонали и объем куба. Куб числа непосредственно отражает объем куба, имеющего длину ребра, равную данному числу.

Что такое формула куба?

Куб является одним из пяти платоновых тел и также известен как правильный шестигранник.

Формула куба

Объем куба

Объем куба можно рассчитать с использованием различных формул на основе заданных параметров. Его можно рассчитать, используя длину стороны, а также размер диагонали куба.

• Объем куба (на основе длины стороны) = a 3  кубических дюймов, где a – длина стороны куба
• Объем куба (по диагонали) = (√3×d 3 )/9кубических дюймов, где d — длина диагонали куба

Боковая площадь куба

Боковая площадь куба равна сумме площадей всех боковых граней куба.

LSA куба = 4a 2

, где a — длина стороны.

Общая площадь куба

Общая площадь поверхности куба будет равна сумме площади основания и площади вертикальных поверхностей куба. Поскольку все грани куба состоят из квадратов одинакового размера, то общая площадь поверхности куба будет равна площади поверхности одной грани, сложенной с самой собой в пять раз. Таким образом, формула для нахождения площади поверхности куба:

Общая площадь поверхности (TSA) куба = 6a 2

, где a — длина стороны.

Диагональ куба

Куб имеет диагонали двух разных длин, более короткие лежат на квадратных гранях, а более длинные проходят через центр. Главной диагональю куба называется та, которая проходит через центр, который можно найти, умножив длину одной стороны на квадратный корень из 3.

Диагональ куба = a√3

Давайте лучше разберемся с формулами куба на нескольких решенных примерах.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запись на бесплатный пробный урок

Примеры с использованием формулы куба

Пример 1: Найдите объем кубика Рубика длиной 4 дюйма. Решение:

Чтобы найти объем кубика Рубика: кубик Рубика0003

Длина стороны куба = 4 дюйма (дано)

Используя формулу куба, объем = с × с × с = с 3

Поместите значения,

объем = 4 × 4 × 4 = 4 3  = 64

Ответ: Объем кубика Рубика составляет 64 кубических дюйма.

Пример 2: Размеры куба – 64 дюйма. Найдите его диагональ по формуле куба. Решение: 

Чтобы найти диагональ куба:

Размеры куба: длина (l) = ширина (w) = высота (h) = 64 дюйма (данные)

Используя формулу куба,

диагональ = a√3 

Поместите значения,

Диагональ = 64√3 = 110,848 дюйма

Ответ: Диагональ куба равна 110,848 дюйма

Пример 3: Найдите общую площадь поверхности куба, если длина стороны куба равна 25 дюймам.

Решение:

Длина стороны куба, a = 25 дюймов 

Используя формулу площади куба, а именно: A = 6a 2

Поместите значения,

A = 6 × 25 × 25 = 3750 квадратных дюймов

Ответ: Площадь поверхности куб равен 3750 квадратных дюймов.

Часто задаваемые вопросы о формуле куба

Что такое формула куба?

Формула куба помогает нам найти площадь поверхности, диагонали и объем куба. Это простые формулы, зависящие в основном от одного параметра — длины ребра или стороны куба.

Как рассчитать диагональ куба по формуле куба?

Главную диагональ куба , пересекающую центр, можно найти, умножив длину одной стороны на квадратный корень из 3. Таким образом, диагональ куба = a√3, где a – ребро куба. .

Что такое s в формуле куба?

В формуле куба s относится к ребру куба. Все формулы куба — объем, площадь поверхности и диагонали — зависят от ребра куба, представленного как s, так и a.

Как вывести формулу куба?

Чтобы вычислить объем по формуле куба,

• Шаг 1: Рассмотрим любой квадратный лист бумаги.
• Шаг 2: Теперь площадь, покрытая этим квадратным листом, будет равна площади его поверхности, т. е. его длине, умноженной на его ширину. Оба одинаковы в случае куба. Таким образом, площадь поверхности будет равна «s 2 ».
• Шаг 3: Куб получается путем складывания нескольких квадратных листов таким образом, чтобы высота стала равной длине и ширине, т. е. единицам «s». Таким образом, высота или толщина куба равна «s».

Таким образом, можно сделать вывод, что общее пространство, занимаемое кубом, то есть объем, равно площади основания, умноженной на высоту. Объем куба = s 2  × s = s 3

Чтобы вывести формулу поверхности куба,

• Шаг 1. Рассмотрим любой лист бумаги квадратной формы.
• Шаг 2: В случае квадрата, поскольку длина и ширина равны, площадь поверхности будет равна «s 2 » (длина, умноженная на ширину).
• Шаг 3: Поскольку у куба 6 граней, общая площадь поверхности куба равна площади одной грани, умноженной на 6 = 6s 2

Как найти площадь поверхности куба

Все материалы по математике для старших классов

← Предыдущая 1 2 Следующая →

Справка по математике для средней школы »
Геометрия »
Твердая геометрия »
Кубики »
Как найти площадь поверхности куба

Какова площадь поверхности куба со стороной 15?

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы найти площадь поверхности куба, мы должны подсчитать количество граней поверхности и сложить площади каждой из них.

В кубе 6 граней, каждая из которых представляет собой квадрат с одинаковыми длинами сторон.

В этом примере длины сторон равны 15, поэтому площадь каждого квадрата будет

Затем мы умножаем это число на 6, количество граней куба, чтобы получить

Наш ответ для площади поверхности: .

Сообщить об ошибке

Какова площадь поверхности куба со стороной ?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти площадь поверхности куба, мы должны подсчитать количество граней поверхности и сложить площади каждой из них. В кубе есть грани, каждая из которых представляет собой квадрат с одинаковыми длинами сторон. В этом примере длина стороны равна .

Площадь квадрата определяется уравнением . Используя нашу длину стороны, мы можем найти площадь одной грани куба.

Затем мы умножаем это число на число граней куба, чтобы найти общую площадь поверхности.

Наш ответ для площади поверхности .

Сообщить об ошибке

Если площадь поверхности куба равна 96, какова длина одной стороны куба?

Возможные ответы:

Правильный ответ:

4

Пояснение:

Площадь поверхности куба = 6a 2 , где a — длина стороны каждого ребра куба. Иными словами, поскольку все стороны куба равны, а — это просто длина одной стороны куба.

У нас есть 96 = 6a 2  → a 2 = 16, так что это площадь одной грани куба.

Решив, мы получим √16, поэтому a = 4

Сообщить об ошибке

Какова площадь поверхности куба с длиной стороны ?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти площадь поверхности куба, используйте формулу .

Сообщить об ошибке

Какова площадь поверхности в дюймах прямоугольной призмы длиной , шириной и высотой ?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти площадь поверхности прямоугольной призмы, используйте формулу .

Однако все единицы измерения должны быть одинаковыми. Все единицы измерения этой задачи указаны в дюймах, за исключением .

Преобразование в дюймы.

Теперь мы можем подставить известные значения в формулу площади поверхности, чтобы рассчитать площадь поверхности прямоугольной призмы.

Если вы вычислили площадь поверхности равной , тогда вы использовали формулу объема прямоугольной призмы, которая равна ; это неправильно.

Сообщить об ошибке

Какова площадь поверхности куба с диагональю ?

Возможные ответы:

Правильный ответ:

Объяснение:

Для решения этой задачи необходимо знать несколько фактов.

Изменить порядок решения для .

Теперь найдите площадь куба по формуле .

Сообщить об ошибке

Эта фигура представляет собой куб с одной гранью площадью 16 в 2 .

Какова площадь поверхности куба (в 2 )?

Возможные ответы:

Правильный ответ:

Объяснение:

Площадь поверхности куба равна сумме площадей каждой грани. Поскольку у куба 6 граней, площадь поверхности всего куба равна .

Сообщить об ошибке

Куб имеет высоту 4 фута.

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти площадь поверхности куба, возведите в квадрат длину одного ребра и умножьте результат на шесть:

Сообщить об ошибке

Длина стороны определенного куба . Какова площадь поверхности этого куба?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти поверхность куба, используйте стандартное уравнение: 

, где  обозначает длину стороны.

Подставьте данное значение для , чтобы найти ответ:

Сообщить об ошибке

Сара упаковывает подарок на день рождения.

Возможные ответы:

Правильный ответ:

Объяснение:

Помните, .

Для куба:

Таким образом .

Сообщить об ошибке

← Предыдущая 1 2 Следующая →

Уведомление об авторских правах

Нюансы расчета площади куба

Как и в любом другом расчете, есть определенные нюансы, которые следует учитывать при расчете площади куба:

1. Убедитесь, что все ребра куба равны.

2. Если вычисляете по диагонали, не забудьте правильно перевести ее в длину ребра.

3. Учтите, что результат будет в той же единице измерения, что и входные данные.

4. Проверьте правильность введенных вами значений перед расчетом.

5. Учитывайте округление: результат может незначительно отличаться в зависимости от количества знаков после запятой.

6. Не забудьте про погрешность измерительных инструментов, если используете их для получения данных.

7. Если используете куб в реальных проектах, учтите дополнительные факторы, такие как материал или условия окружающей среды.

8. Помните, что площадь поверхности отличается от объема куба.

9. При расчете площади для покраски или облицовки учтите запас материала на стыки и переходы.

10. Всегда проверяйте свои расчеты, особенно если они касаются значимых проектов или работ.

Вычисление объемов фигур

Радиус первого шара в \(5\) раз больше радиуса второго шара. Во сколько раз площадь поверхности второго шара меньше площади поверхности первого шара?

Площадь поверхности шара радиуса \(R\) ищется по формуле \(S=4\pi R^2\) . Следовательно, площадь поверхности первого шара относится к площади поверхности второго шара как \ Так как радиус первого шара больше радиуса второго шара в 5 раз, то \(R_1=5R_2\) . Следовательно, \ Следовательно, площадь поверхности первого шара в 25 раз больше площади поверхности второго, значит, площадь поверхности второго в 25 раз меньше.

Даны два конуса. Радиус второго конуса в \(3\) раза больше радиуса первого конуса, а высота второго конуса в \(6\) раз меньше высоты первого конуса. Найдите объем первого конуса, если объем второго конуса равен \(18\) .

Объем конуса с высотой \(h\) и радиусом основания \(R\) вычисляется по формуле \(V=\frac13\pi R^2h\) . Следовательно, объем первого конуса относится к объему второго конуса как \ Так как радиус второго в 3 раза больше радиуса первого, то \(R_2=3R_1\) . Так как высота второго в 6 раз меньше высоты первого, то \(h_1=6h_2\) . Следовательно, \

Даны два конуса: \(K_1\) и \(K_2\) . Площадь полной поверхности \(K_1\) относится к площади полной поверхности \(K_2\) как \(4:1\) . Известно, что радиус \(K_1\) в 4 раза больше образующей \(K_1\) и в 2 раза больше радиуса \(K_2\) . Найдите отношение образующей \(K_2\) к образующей \(K_1\) .

Площадь полной поверхности конуса с образующей \(l\) и радиусом основания \(R\) ищется по формуле \(S=\pi R (R+l)\) . Тогда площадь полной поверхности \(K_1\) относится к площади полной поверхности \(K_2\) как \ Из условия следует, что \(R_1=4l_1\) , \(R_2=\frac12R_1=2l_1\) , следовательно, \

Во сколько раз радиус первого шара больше радиуса второго шара, если объем первого шара в \(343\) раза больше объема второго шара?

Объем шара радиуса \(R\) ищется по формуле \(V=\dfrac43 \pi R^3\) . Следовательно, объем первого шара относится к объему второго как \=7.\] Следовательно, радиус первого шара в 7 раз больше радиуса второго шара.

Объем первого прямоугольного параллелепипеда равен 105. Найдите объем второго прямоугольного параллелепипеда, если известно, что высота первого параллелепипеда в 7 раз больше высоты второго, ширина второго в 2 раза больше ширины первого, а длина первого в 3 раза больше длины второго.

Пусть буквы \(a\) , \(b\) и \(c\) обозначают высоту, ширину и длину соответственно. Объем прямоугольного параллелепипеда ищется по формуле \(V=abc\) . Следовательно, объем первого параллелепипеда относится к объему второго как \ Из условия следует, что \(a_1=7a_2\) , \(b_2=2b_1\) , \(c_1=3c_2\) . Тогда \

Площадь боковой поверхности первого цилиндра равна \(16\) . Найдите площадь боковой поверхности второго цилиндра, если его радиус в 4 раза больше радиуса первого, а высота в 5 раз меньше высоты первого цилиндра.

Площадь боковой поверхности цилиндра с высотой \(H\) и радиусом основания \(R\) ищется по формуле \(S=2\pi RH\) . Тогда площадь бок. поверхности первого цилиндра относится к площади бок. поверхности второго как \ Из условия следует, что \(R_2=4R_1\) , \(H_1=5H_2\) , значит, \ Следовательно, \

Площадь боковой поверхности первого конуса относится к площади боковой поверхности второго конуса как \(3:7\) . Найдите отношение образующей первого конуса к образующей второго конуса, если радиус первого конуса относится к радиусу второго как \(15:7\) .

Площадь боковой поверхности конуса с образующей \(l\) и радиусом основания \(R\) ищется по формуле \(S=\pi Rl\) . Тогда площадь бок. поверхности первого конуса относится к площади бок. поверхности второго как \ Так как радиус первого конуса относится к радиусу второго как \(15:7\) , то есть \(\frac=\frac7\) , то \

Во время подготовки к сдаче ЕГЭ по математике повторение базовых формул из школьного курса геометрии в пространстве (стереометрии), в том числе и для вычисления объемов фигур, является одним из основных этапов. И хотя на изучение этого раздела отводится достаточно большое количество времени в рамках учебной программы, многим выпускникам требуется освежить в памяти основной материал.

Понимая, как осуществляется вычисление площадей объемных фигур, учащиеся значительно повышают свои шансы на получение достойных баллов по итогам сдачи ЕГЭ.

Определение куба

Куб – это правильный многогранник, все грани которого являются квадратами.

Примечание: куб является частным случаем параллелепипеда или призмы.

Определение площади поверхности куба.

Определение площади поверхности куба выполняется по формуле SA = 6а 2 . Куб (правильный гексаэдр) – это один из 5 видов правильных многогранников, который является правильным прямоугольным параллелепипедом, куб имеет 6 граней, каждая из этих граней является квадратом.

Для вычисления площади поверхности куба Вам необходимо записать формулу SA = 6а 2 . Теперь давайте разберем почему данная формула имеет такой вид. Как мы говорили ранее, куб имеет шесть равных квадратных граней. Исходя из того что стороны квадрата равны, площадь квадрата составлять – a 2 , где а – сторона куба. Так куба имеет 6 равных квадратных граней, то для определения площади его поверхности, Вам необходимо умножить площадь одной грани (квадрата) на шесть. В итоге получаем формулу для вычисления площади поверхности (SA) куба: SA = 6а 2 , где а – ребро куба (сторона квадрата).