Формула для вычисления суммы длин всех ребер куба

Часто задаваемые вопросы: что символизирует куб?

1. Что такое кубический символ в духовности?

Куб — мощный символ в духовных учениях, олицетворяющий стабильность, заземление и физическое царство. Он часто используется для обозначения элемента земли.

2. Что представляет собой куб в математике?

В математике куб представляет собой трехмерную фигуру с шестью квадратными гранями одинакового размера. Он имеет восемь вершин и 12 ребер.

3. Что символизирует куб в искусстве?

В искусстве куб может представлять разные вещи в зависимости от контекста. Он может символизировать стабильность, баланс, порядок и структуру. Он также может представлять замкнутость, ограничение и жесткость.

4. В чем смысл кубика Рубика?

Кубик Рубика — это головоломка, состоящая из кубика с разноцветными сторонами, которые можно вращать в разные стороны. Его часто используют как метафору решения проблем, настойчивости и творчества.

5. Что означает тату куб?

Тату куб может иметь разное значение для разных людей. Он может символизировать порядок, стабильность, баланс и структуру. Он также может символизировать индивидуальность, креативность и любовь к головоломкам.

6. Что во сне символизирует куб?

В снах куб может представлять разные вещи в зависимости от контекста. Он может символизировать физическое царство, стабильность, баланс, порядок и структуру. Он также может представлять замкнутость, ограничение и жесткость.

7. Что такое гиперкуб и что он символизирует?

Гиперкуб, также известный как тессеракт, представляет собой четырехмерный куб. Это сложная математическая концепция, но она может символизировать высшие измерения, творчество и бесконечность.

Кубический граф

Кубический граф
Назван в честь	Q3
Вершины	8
Ребра	12
Радиус	3
Диаметр	3
Обхват	4
Автоморфизмы	48
Хроматическое число	2
Свойства	Гамильтониан, правильный, симметричный, дистанционно-регулярный, дистанционно-транзитивный, 3-вершинно-связанный, планарный граф
Таблица графиков и параметров

скелет куб (вершины и ребра) образуют граф с 8 вершинами и 12 ребрами. Это частный случай графа гиперкуба . Это один из 5 платоновых графов, каждый из которых является скелетом своего платонового тела.

Расширением является трехмерный k-арный граф Хэмминга, который для k = 2 — куб-граф. Графики такого типа встречаются в теории параллельной обработки в компьютерах.

Куб в искусстве и архитектуре

Куб также играет роль значительную роль в искусстве и архитектуре. Это простая, но мощная форма, которая использовалась в скульптурах, зданиях и других произведениях искусства. Художник Дональд Джадд, например, создал серию скульптур, используя кубы разных размеров и материалов. Куб также использовался в архитектуре, особенно в современных зданиях, которые подчеркивают простоту и чистоту линий. Например, парижская пирамида Лувра представляет собой большой куб из стекла и металла, служащий входом в музей.

Свойства куба	Формулы
Количество граней	6
Количество вершин	8
Количество ребер	12
Объем	V = s^3
Площадь поверхности	SA = 6s^2

В целом, куб является важной фигурой в геометрии и математике, имеет множество приложений и применений в различных областях. Его простота и универсальность делают его ценным инструментом для изучения концепций и изучения математических принципов

Число 7

Число 7 ассоциировалось с совершенством, полнотой и целостностью во многих культурах и культурах. религии. Не случайно куб имеет 7 сторон, также известных как грани. Число 7 играет решающую роль в размерах куба, поскольку оно имеет духовное и символическое значение.

• В иудаизме менора, семисвечник, является символом завершенного Бога. работа творения.
• Для христиан число 7 – это символ семи дней, которые потребовались Богу для сотворения мира, и семи таинств.
• В исламе число 7 часто встречается в Коран, такие как 7 небес и 7 земель.
• 7 также считается счастливым числом во многих культурах и связано с удачей и процветанием.

Более того, куб можно разделить на меньшие кубики, и когда 7 меньших кубиков соединяются вместе, они образуют больший, олицетворяющий единство и законченность. Вот почему число 7 часто используется для обозначения размеров зданий и сооружений, таких как 7-этажные здания или двери высотой 7 футов.

Элементы композиции куба

Зная, что у куба 12 ребер, 8 вершин и 6 граней, см. следующее изображение.

• A, B, C, D, E, F, G и H — вершины куба.

• \(\overline{AB},\ \overline{AD},\ \overline{AE},\ \overline{BC},\ \overline{BF},\ \overline{CD,\ }\overline{CG}, \ \overline{DH,\ }\overline{HG},\ \overline{EH}\overline{,\ EF},\ \overline{FG}\) являются ребрами куба.

• ABCD, ABFE, BCFG, EFGH, ADHE, CDHG — грани куба.

Куб состоит из 6 квадратных граней, поэтому все его ребра равны. Поскольку его ребра имеют одинаковую меру, куб классифицируется как многогранник Правильный или твердый Платон вместе с тетраэдром, октаэдром, икосаэдром и додекаэдром.

Не останавливайся сейчас… После рекламы есть еще

Рассуждения

У параллелограмма противоположные стороны равны между собой. Получается, что напротив стороны А лежит такая же сторона А. Исходя из определения параллелограмма понятно, что верхняя грань его тоже равна А. Получается, что сумма длин всех сторон данного параллелограмма равна 4А.

Аналогичные рассуждения могут быть приведены и для стороны В — получается, что сумма сторон параллелограмма, созданного из стороны В, будет равняться 4 В.

Если внимательно присмотреться, то можно сделать вывод, что боковые грани прямоугольного параллелепипеда — это тоже параллелограммы. Причём, ребро С одновременно относится к двум соседним граням прямоугольного параллелепипеда. И аналогично представленными выше рассуждениям, сумма длин всех рёбер будет равняться 4 С.

Классификация двумерных полиэдров

Наша задача состоит в том, чтобы связать символы Шлефли {n,m} с количеством вершин, ребер и граней. Для примера рассмотрим тетраэдр и попытаемся выяснить зависимость.

1. У тетраэдра 4 грани, в каждой из которых три угла. Т.о., если умножить 4 грани на 3 угла получим 12 чего-то там, что в два раза больше, чем количество его ребер (каждое из них посчитано дважды).

2. В каждой вершине сходятся m=3 граней. Если умножить 4 вершины на 3 грани получим 12 чего-то там, что в два раза больше количества ребер (их так же считали дважды

В качестве упражнения можно посчитать для куба. В каждой из 6 граней 4 угла, отсюда (6*4)/2 = 12 ребер. В каждой из 8 вершин сходятся 3 грани, что даёт (8*3)/2 = 12 ребер.

Получили три уравнения с тремя неизвестными, которые будем сейчас решать, чтобы получить в чистом виде зависимость от составляющих символа Шлефли:

Такую систему уравнений удобно решить, воспользовавшись параметризацией через некое t. Во второй строчке подставили данные в уравнение Эйлера и затем привели дроби к одному знаменателю

Из очевидных соображений, что t > 0 , мы должны потребовать положительности знаменателя. Остается в целых числах решить соответствующее неравенство:

Не только лишь все натуральные числа при умножении дают результат, меньший 4, поэтому у нас не так много работы:

А теперь вспомните рисунок с символами Шлефли для платоновых тел! Как видите, мы получили одно и то же с помощью решения обычной системы уравнений! Алгебраизация — один из самых мощных способов исследования окружающего нас мира.

Куб и Сознание

Куб также можно рассматривать как метафора самой природы сознания. Каждая сторона куба представляет собой различное восприятие или переживание реальности, а углы представляют пересечения и перекрытия между этими разными перспективами.

Подобно тому, как куб является трехмерным объектом, наше сознание также может быть рассматривается как многомерное, с разными уровнями и слоями осознания. Изучая куб как метафору сознания, мы можем глубже понять наши отношения с миром и восприятие, которое формирует наш опыт.

Символизм	Репрезентация
Поверхности	различные аспекты нашего сознания
Углы	различные мысли, знания и переживания
Трехмерный объект	многомерное сознание

Куб — это мощный символ, который может дать нам представление о природе нашего разума и сознания. Изучая его различные грани и значения, мы можем углубить наше понимание самих себя и окружающего мира.

Примеры использования куба

1. Геометрические расчеты

Куб часто используется в геометрии для решения различных задач и расчетов. Например, можно использовать куб для определения объема или площади поверхности кубического объекта. Также куб может быть использован для вычисления длины диагонали куба или расстояния между двумя его вершинами.

2. Головоломки

Кубик Рубика — одна из самых известных головоломок, основанная на принципе куба. Цель игры — повернуть грани кубика таким образом, чтобы каждая грань состояла из квадратных блоков одного цвета. Кубик Рубика требует логического мышления и навыков вращения граней, и является популярным развлечением для детей и взрослых.

3. Моделирование и дизайн

Куб также используется в компьютерной графике для создания трехмерных моделей и дизайна. Благодаря своей форме и прямым граням, куб может служить основой для создания более сложных объектов и форм.

4. Визуализация данных

В аналитике данных кубы используются для организации многомерных данных. Они позволяют анализировать и визуализировать данные по разным измерениям и категориям. Благодаря структуре куба, можно легко фильтровать и агрегировать данные, делать срезы и сводные таблицы.

5. Тестирование программного обеспечения

Кубы часто используются в тестировании программного обеспечения для оценки функциональности и надежности системы. Такие тесты позволяют проверить различные комбинации входных данных и условий, чтобы обнаружить ошибки или несоответствия в работе программы.

Куб как представление четырех элементов

Многие культуры и системы верований на протяжении всей истории использовали куб как символ для представления четырех элементов — земли, воды, воздуха и огня. Каждая грань куба соответствует одному из этих элементов: земля — нижняя грань, вода — передняя грань, воздух — задняя грань, а огонь — верхняя грань. Куб — мощный символ, который можно найти в различных формах, включая искусство, архитектуру и религиозные ритуалы.

• Земля: элемент земли связан с физический мир, стабильность и материальные блага. Нижняя грань куба представляет собой землю, так как это основа, на которой держится все остальное.
• Вода. Элемент воды связан с эмоциями, интуицией и подсознанием. Передняя грань куба представляет собой воду, так как это ворота, через которые мы обрабатываем наши эмоции и получаем доступ к нашему внутреннему я.
• Воздух: Элемент воздуха связан с интеллектом. , общение и мышление. Задняя сторона куба представляет собой воздух, так как это платформа, через которую мы взаимодействуем с миром и делимся своими идеями.
• Огонь: стихия огня ассоциируется со страстью. , преображение и духовный рост. Верхняя грань куба представляет собой огонь, поскольку это искра, которая зажигает наши души и побуждает нас следовать нашим желаниям.

Помимо своих элементарных ассоциаций, куб также несет символическое значение, связанное с равновесие, симметрия и гармония. Его шесть сторон и равные углы предполагают стабильность и равновесие, а правильная форма символизирует симметрию и порядок. В некоторых традициях куб также используется как инструмент для гадания, где каждая грань представляет собой отдельный аспект жизни или свой путь.

В целом, куб — это многогранный символ, который можно интерпретировать. во многом в зависимости от культурного контекста и индивидуальных убеждений. Независимо от того, используется ли куб в искусстве, архитектуре или духовных практиках, он остается ярким представлением основных элементов, формирующих наш мир и нашу жизнь.

формулы куба

Для расчета площади основания, площади стороны, общей площади и объема куба будем рассматривать куб с измерением ребра .

Площадь основания куба

Так как основание образовано квадратом ребра , площадь основания куба вычисляется по формуле:

\(А_б=а^2\)

Пример:

Вычислите меру основания куба, длина ребра которого равна 12 см:

Разрешение:

\(А_б=а^2\)

\(A_b={12}^2\)

\(A_b=144\ см^2\)

площадь стороны куба

Площадь стороны куба состоит из 4 квадратов со сторонами, равными . Таким образом, для вычисления площади боковой поверхности куба формула такова:

\(А_л=4а^2\)

Пример:

Чему равна площадь стороны куба, длина ребра которого равна 8 см?

Разрешение:

\(А_л=4а^2\)

\(A_l=4\cdot8^2\)

\(A_l=4\cdot64\)

\(A_l=256\ см^2\)

общая площадь куба

Общая площадь куба или просто площадь куба сумма площадь всех граней куба. Мы знаем, что у него всего 6 сторон, образованных квадратами со стороной , то общая площадь куба рассчитывается по формуле:

\(А_Т=6а^2\)

Пример:

Какова общая площадь куба, длина ребра которого равна 5 см?

Разрешение:

\(А_Т=6а^2\)

\(A_T=6\cdot5^2\)

\(A_T=6\cdot25\)

\(A_T=150\ см^2\)

объем куба

Объем куба равен умножение мера его трех измерений. Поскольку все они имеют одинаковую меру, мы имеем:

\(V=а^3\)

Пример:

Чему равен объем куба, длина ребра которого равна 7 см?

Разрешение:

\(V=а^3\)

\(V=7^3\)

\(V=343\ см^3\)

диагонали куба

На кубе мы можем провести боковую диагональ, то есть диагональ его грани, и диагональ куба.

◦ диагональ стороны куба 

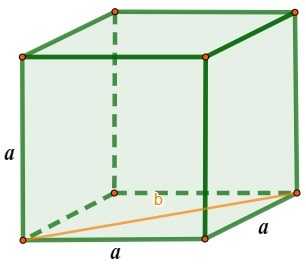
Боковая диагональ или диагональ грани куба обозначается буквой Б на изображении. Шерсть теорема Пифагора, у нас есть один прямоугольный треугольник измерения пекари и измерение гипотенузы Б:

б² = а² + а²

б² = 2а²

б = \(\sqrt{2a^2}\)

б = \(а\кв2\)

Следовательно, формула для вычисления диагонали грани куба:

\(б=а\кв2\)

◦ диагональ куба

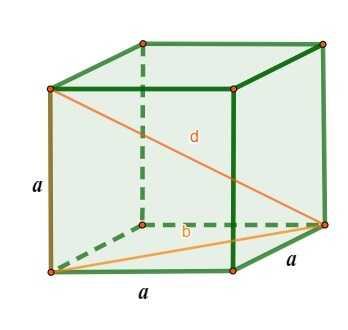
диагональ г куба можно вычислить и по теореме Пифагора, так как у нас есть прямоугольный треугольник с катетами Б, и измерение гипотенузы г:

\(д^2=а^2+б^2\)

Но мы знаем, что b =\(а\кв2\):

\(d^2=a^2+\влево (a\sqrt2\вправо)^2\)

\(д^2=а^2+а^2\cdot2\)

\(д^2=а^2+2а^2\)

\(д^2=3а^2\)

\(d=\sqrt{3a^2}\)

\(д=а\sqrt3\)

Итак, для вычисления диагонали куба воспользуемся формулой:

\(д=а\sqrt3\)

Узнать больше: Цилиндр — геометрическое тело, которое классифицируется как круглое тело.

Символы Шлефли

Задача классификация правильных многогранников в целом различных размерностей — одна из важных задач геометрии, которую проще всего оказалось решить комбинаторными средствами.

Людвиг Шлефли (1814-1895) — швейцарский математик, специалист в области многомерной геометрии и комплексного анализа. Преподавал в Бернском университете

В своей диссертации Шлефли дал полную классификацию правильных многогранников для n-размерных пространств. С тех пор в научный оборот вошел т.н. символ Шлефли {n,m}, где n — количество углов в грани, m — количество граней, которые сходятся в вершине.

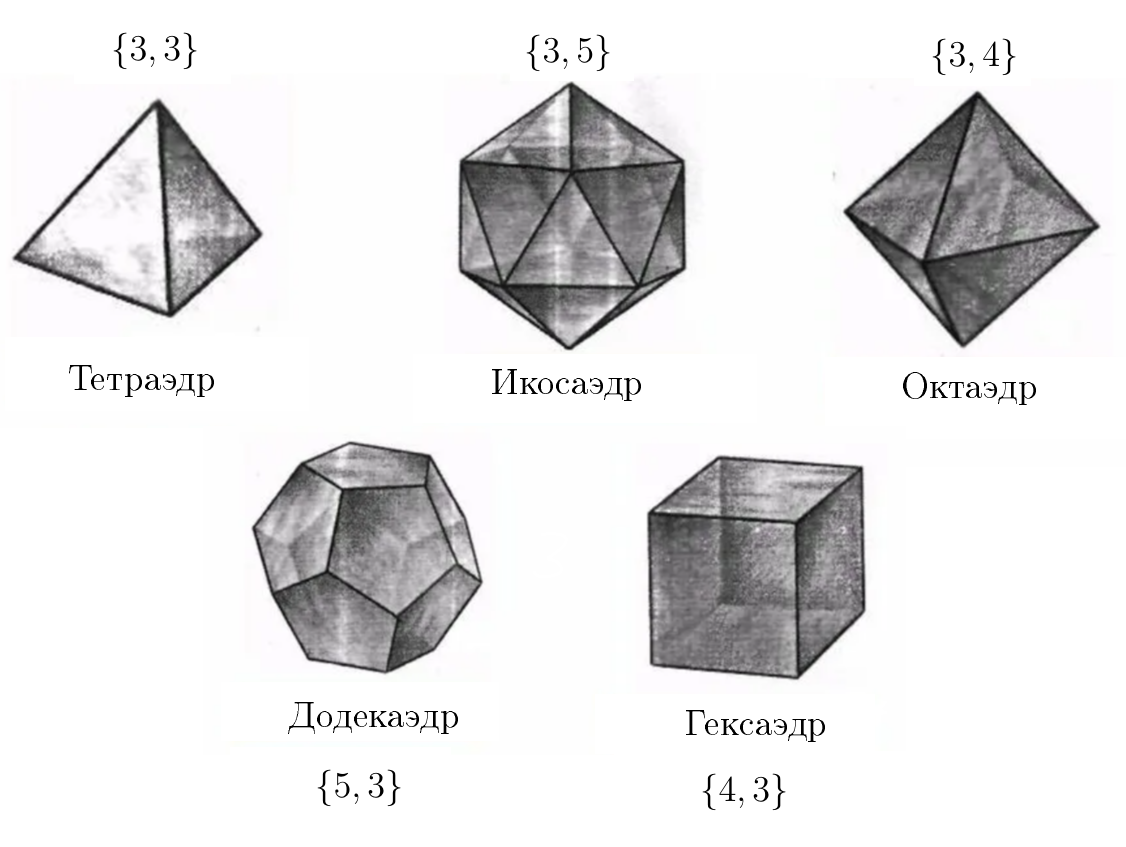Додекаэдр — это правильный многогранник, имеющий по 3 пятиугольника вокруг каждой вершины. И да, куб — это гексаэдр в том смысле, что у него восемь вершин.

Запомните эти символы. Они встретятся нам в конце повествования. Переходим к следующему инструменту.

Связанные многогранники

октаэдр

Частное куба по карте антипод дает проективный многогранник, гемикуб.

Если исходный куб имеет длину ребра 1, его двойной многогранник (октаэдр ) имеет длину ребра 2/2 {\ displaystyle \ scriptstyle {\ sqrt {2}} / 2 }.

Куб является частным случаем в различных классах общих многогранников:

Имя	Равные длины ребер?	Равные углы?	Прямые углы?
Куб	Да	Да	Да
Ромбоэдр	Да	Да	Нет
Кубоид	No	Да	Да
Параллелепипед	No	Да	Нет
четырехугольник шестигранник с гранями	No	No	Нет

Вершины куба можно сгруппировать в две группы по четыре, каждая из которых образует правильный тетраэдр ; в более общем виде это называется полукубом. Эти два вместе образуют обычное соединение, stella octangula. Их пересечение образует правильный октаэдр. Симметрии правильного тетраэдра соответствуют симметрии куба, который отображает каждый тетраэдр в себя; другие симметрии куба отображают их друг в друга.

Один такой правильный тетраэдр имеет объем 1/3 куба. Оставшееся пространство состоит из четырех равных неправильных тетраэдров, каждый из которых имеет объем 1/6 объема куба.

Ректифицированный куб — это кубооктаэдр. Если срезать меньшие углы, мы получим многогранник с шестью восьмиугольными гранями и восемью треугольными. В частности, мы можем получить правильные восьмиугольники (усеченный куб ). Ромбокубооктаэдр получается путем обрезания углов и кромок на нужную величину.

Куб можно вписать в додекаэдр так, чтобы каждая вершина куба была вершиной додекаэдра, а каждое ребро было диагональю одной из граней додекаэдра; взятие всех таких кубиков дает правильное соединение из пяти кубиков.

Если два противоположных угла куба усекаются на глубине трех вершин, непосредственно связанных с ними, получается неправильный октаэдр. Восемь из этих неправильных октаэдров могут быть присоединены к треугольным граням правильного октаэдра, чтобы получить кубооктаэдр.

Куб топологически связан с серией сферических многогранников и мозаик с фигурами вершин порядка 3 .

* n32 изменение симметрии правильных мозаик: {n, 3} [ v ]
Сферический	Евклидово	Компактная гиперб.	Парако.	Некомпактный гиперболический
{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞, 3}	{12i, 3}	{9i, 3}	{6i, 3}	{3i, 3}

Кубооктаэдр — один из семейства однородных многогранников, связанных с кубом и правильным октаэдром.

Симметрия : , (* 432)	. (432)	= . (* 332)	. (3 * 2)
{4,3}	t {4,3}	r {4,3}. r {3}	t{3,4}. t {3}	{3, 4}. {3}	rr {4,3}. s2{3,4}	tr {4,3}	sr {4,3}	h {4,3}. {3,3}	h2{4,3}. t {3,3}	s {3,4}. s {3}
		. =	. =	. =				=. или	=. или	=.
		.	.	.	.					.
Двойники к однородным многогранникам
V4	V3.8	V (3.4)	V4.6	V3	V3.4	V4. 6.8	V3.4	V3	V3.6	V3

Куб топологически связан как часть последовательности правильных мозаик, простирающихся в : {4, p}, p = 3,4,5…

* n42 мутация симметрии регулярных мозаик: {4, n} [ v ]
Сферическая	Евклидова	Компактная гиперболическая	Паракомпактная
. {4,3}.	. {4,4}.	. {4,5}.	. {4,6}.	. {4,7}.	. {4,8}….	. {4, ∞}.

При двугранной симметрии, Dih 4 куб топологически связан в виде ряда однородных многогранников ra и мозаики 4.2n.2n, простирающиеся в гиперболическую плоскость:

* n42 мутация симметрии усеченных мозаик: 4.2n.2n [ v ]
Симметрия. * n42.	Сферический	Евклидово	Компактный гиперболический	Паракомп.
* 242.	* 342.	* 442.	* 542.	* 642.	* 742.	* 842. …	* ∞42.
Усеченные. цифры
Конфиг.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4.∞.∞
н-кис. цифры
Конфиг.	V4.4.4	V4.6.6	V4.8.8	V4.10.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.∞

Все эти фигуры обладают октаэдрической симметрией.

Куб является частью последовательности ромбических многогранников и мозаик с группа Кокстера симметрия. Куб можно рассматривать как ромбический шестигранник, в котором ромбы представляют собой квадраты.

Мутации симметрии двойных квазирегулярных мозаик: V (3.n)
* n32	Сферический	Евклидов	Гиперболический
* 332	* 432	* 532	* 632	* 732	* 832…	* ∞32
Мозаика
Конф.	В (3,3)	В (3,4)	В (3,5)	В (3,6)	В (3,7)	В (3,8)

Куб представляет собой квадратную призму :

Семейство однородных призм [ v ]
Многогранник
Кокстера
Мозаика
Конфигурация	2.4.4	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11,4.4	12.4.4

Как тригональный трапецоэдр, куб относится к семейству гексагональной двугранной симметрии.

Равномерные шестиугольные двугранные сферические многогранники
Симметрия : , (* 622)	, (622)	, (2 * 3)
{6,2}	t {6,2}	r {6,2}	t {2,6}	{2,6}	rr {6,2}	tr {6,2}	sr {6,2}	s {2,6}
От двойного к униформе
V6	V12	V6	V4.4.6	V2	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

Обычные и однородные соединения кубов

. Соединение из трех кубов

. Состав из пяти кубов

Формулы объема и площади поверхности. Призма, пирамида — материалы для подготовки к ЕГЭ по Математике

Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:

1. Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
2. Элементарная логика.

Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.

Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».

Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.

Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.

Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.

Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.

Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб

Очевидно, их 6, поскольку у куба 6 граней.

Иногда в задаче  надо посчитать площадь поверхности куба или призмы.

Напомним, что площадь поверхности многогранника — это сумма площадей всех его граней.

В некоторых задачах каждое ребро многогранника увеличили, например, в три раза. Очевидно, что при этом площадь поверхности увеличится в девять раз, а объём — в раз.

Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.

Использование куба в гадании

Куб можно использовать в различных методах гадания, таких как гадание на костях, где бросок кубиков может раскрыть понимание конкретной ситуации или вопроса. Куб также можно использовать в геомантии, которая представляет собой практику гадания, в которой используются линии и точки для создания узоров и интерпретации их значений. В этом методе куб представляет собой элемент земли, который ассоциируется со стабильностью, заземлением и материальными благами.

Символ	Значение
Куб	Стабильность, заземление, физическая реальность
Круг	Единство, целостность, бесконечность
Треугольник	Гармония, равновесие, троичность

Куб также можно использовать в сочетании с другими символами, такими как круг или треугольник, чтобы получить более глубокое понимание и связи с духовным царством.

В целом, куб является универсальным и мощным инструментом в магии. и гадание, представляющее стабильность, симметрию и число три, имеющее большое значение во многих духовных традициях.

Куб как символ стабильности

Стабильность куба можно наблюдать в различных архитектурные сооружения — от древности до современности. Например, Кааба в Мекке, одно из самых священных мест в исламе, представляет собой сооружение в форме куба. Он считается самым устойчивым сооружением в мире из-за своего положения и того, как он построен. Стабильность куба влияет на веру людей в структуру и ее способность выполнять свое предназначение. Таким образом, его форма является высшим символом стабильности, представляющим непоколебимую силу веры и убеждений.

Стабильность куба распространяется и на нашу личную жизнь. Это говорит о балансе и порядке в наших действиях и решениях. Когда мы уравновешены, мы можем достичь стабильности в нашей жизни. Куб — это напоминание о том, что нужно оставаться внутри себя и быть осторожными с внешними факторами, которые могут привести к нестабильности.