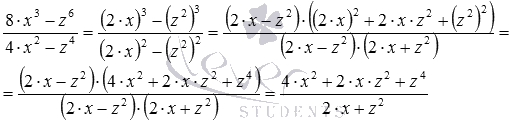Куб простыми словами для чайников
Куб — это геометрическая фигура, которая имеет форму игральной кости. Он состоит из шести квадратных граней, каждая из которых имеет одинаковую площадь. Куб также имеет 12 ребер и 8 вершин.
Куб является одним из правильных многогранников, что означает, что все его грани и углы являются равными. Это делает его особенно интересным и полезным в геометрии.
Куб используется во многих областях науки и техники. Например, в физике куб используется для моделирования кристаллической решетки, а в компьютерной графике — для создания трехмерных объектов.
Чтобы найти объем куба, нужно умножить длину одной из его сторон на себя три раза. Формула для нахождения объема куба выглядит следующим образом: V = a * a * a, где V — объем, а a — длина стороны куба.
Площадь поверхности куба можно найти, умножив площадь одной из его граней на шесть. Формула для нахождения площади поверхности куба выглядит следующим образом: S = 6 * a * a, где S — площадь поверхности, а a — длина стороны куба.
Куб часто используется в математике для изучения объема и площади поверхности. Он также является основой для изучения других геометрических фигур, таких как пирамиды и призмы.
Куб имеет много интересных свойств. Например, диагональ куба равна квадратному корню из трех умноженному на длину его стороны. Также, каждая диагональ куба является гипотенузой прямоугольного треугольника, образованного двумя его ребрами.
Куб также имеет симметрию. Если повернуть его на 90 градусов вокруг оси, проходящей через центр куба, он останется неизменным. Это свойство делает куб особенно интересным для создания симметричных и гармоничных изображений.
В заключение, куб — это геометрическая фигура, которая имеет форму игральной кости и состоит из шести квадратных граней. Он является одним из правильных многогранников и имеет много интересных свойств. Куб используется в науке, технике и математике, и его изучение помогает развивать понимание объема, площади поверхности и симметрии.
Что такое квадратный корень в математике
Квадратный корень — это операция в математике, которая позволяет найти число, которое при возведении в квадрат дает заданное число. Например, квадратный корень из числа 25 равен 5, так как 5 в квадрате равно 25.
Квадратный корень обозначается символом √ и записывается как √x, где x — число, из которого нужно извлечь корень. Например, √16 равен 4.
Квадратный корень — это обратная операция возведения в квадрат. Он широко используется в математике, физике, инженерии и других науках.
Также существуют не только квадратные корни, но и корни степени больше двух — кубические, четвертные и т.д. Однако, квадратный корень наиболее распространен и полезен в повседневной жизни.
🎥 Видео
Куб дров это сколько? Количество поленьев в одном кубометре дровСкачать
ШКОЛЬНЫЕ ВОПРОСЫ | Чему равно 3 в кубе? Биг Спрос, Big Spros #вопросы #опрос #загадки #головоломкиСкачать
№ 9.1. Кубические метры, сантиметры и т.д. (5 класс, дополнение)Скачать
5 класс, 16 урок, Степень числа. Квадрат и куб числаСкачать
Куб. Кубики. Форма, грани, ребра, объем кубаСкачать
1 куб воды — сколько это литров?Скачать
Куба 2024. Все что вы хотели знать, но боялись спросить. Часть 1.Скачать
КАК НАЙТИ ОБЪЕМ КУБА ПО РЕБРУ? Примеры | МАТЕМАТИКА 5 классСкачать
Математика 5 Объем куба Соотношения между единицами объемаСкачать
Выпускной экзамен 11 класс (03.03.2024)Скачать
Вы не представляете, сколько стоят тачки на Кубе! #погнали #shortsСкачать
СЛИВ теории вероятностей | Старт Ключевой сотки | ЕГЭ 2024Скачать
Как посчитать количество досок в кубеСкачать
Четверо в кубе — Там, где водятся витамины — 3 серия — современные обучающие мультики для детейСкачать
Сколько блоков в одном кубе?Скачать
Как рассчитать кубические метрыСкачать
Вокруг Кубы своим ходом. Ответы на вопросы часть 2.Скачать
Построение куба
Чтобы построить куб, нужно знать его размеры и следовать определенной последовательности действий. В данной статье мы рассмотрим подробное руководство для начинающих.
Шаг 1: Определение размеров куба
Прежде чем начать строительство куба, необходимо определить его размеры. Размеры куба определяются трехмерными координатами его вершин. Например, если вершины куба имеют координаты (0,0,0) и (1,1,1), то длина стороны куба равна 1 единице.
Шаг 2: Построение вершин куба
Постройте вершины куба, используя трехмерные координаты. Вершины куба соединяются линиями, образуя его ребра. Каждой ребро присваивается уникальный номер.
Шаг 3: Построение граней куба
Соедините вершины куба линиями, образуя его грани. Каждой грани присваивается уникальный номер.
Шаг 4: Задание цветов граней
Задайте цвета граням куба. Это можно сделать с использованием таблицы цветов, в которой каждой грани соответствует определенный цвет. Таблица цветов представлена в виде HTML-тега <table>, где каждая ячейка таблицы является отдельной гранью куба.
Шаг 5: Отображение куба
Окончательным шагом является отображение куба, используя HTML-код. Для этого можно использовать теги <div> или <canvas>. Вставьте код, содержащий информацию о вершинах, ребрах, гранях и цветах куба в элемент HTML-страницы, и куб будет отображен.
Сферы применения формул сокращенного умножения (фсу) и примеры
Основное предназначение формул сокращенного умножения (фсу) объясняется их названием, то есть, оно состоит в кратком умножении выражений. Однако сфера применения ФСУ намного шире, и не ограничивается кратким умножением. Перечислим основные направления.
Несомненно, центральное приложение формулы сокращенного умножения нашли в выполнении тождественных преобразований выражений. Наиболее часто эти формулы используются в процессе упрощения выражений.
Пример.
Упростите выражение 9·y−(1+3·y)2.
Решение.
В данном выражении возведение в квадрат можно выполнить сокращенно, имеем 9·y−(1+3·y)2=9·y−(12+2·1·3·y+(3·y)2). Остается лишь раскрыть скобки и привести подобные члены: 9·y−(12+2·1·3·y+(3·y)2)=9·y−1−6·y−9·y2=3·y−1−9·y2.
Ответ:
9·y−(1+3·y)2=3·y−1−9·y2.
И если в 7 классе речь идет о преобразовании целых выражений с помощью формул сокращенного умножения, то в старших классах можно будет видеть применение ФСУ к преобразованию выражений всех других видов – дробных, иррациональных, логарифмических, тригонометрических и других. К примеру, тождества сокращенного умножения с переставленными частями позволяют представлять выражения в виде степеней или произведений, в частности, выполнять разложение многочленов на множители. Это очень полезно, к примеру, при сокращении алгебраических дробей.
Пример.
Сократите дробь .
Решение.
В числителе выражение представляет собой разность кубов двух выражений 2·x и z2, а в знаменателе – разность квадратов этих выражений. После применения соответствующих формул исходная дробь примет вид . Теперь можно сократить одинаковые множители в числителе и знаменателе: 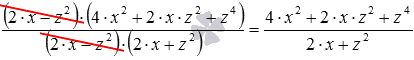 .
.
Оформим все решение кратко: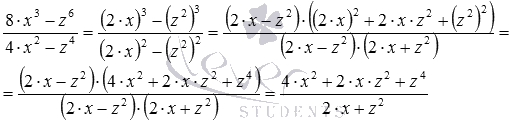
Ответ:
Формулы сокращенного умножения иногда позволяют рационально вычислять значения выражений. В качестве примера покажем, как можно возвести число 79 в квадрат с помощью формулы квадрата разности: 792=(80−1)2=802−2·80·1+12=6 400−160+1=6 241. Такой подход позволяет выполнять подобные вычисления даже устно.
В заключение скажем еще про одно важное преобразование – выделение квадрата двучлена, в основе которого лежит формула сокращенного умножения квадрат суммы. Например, выражение 4·x2+4·x−3 может быть преобразовано к виду (2·x)2+2·2·x·1+12−4, и первые три слагаемых заменяются с использованием формулы квадратом суммы. Так что выражение принимает вид (2·x+1)2−4
Подобные преобразования широко используются, например, при интегрировании.
Так что выражение принимает вид (2·x+1)2−4. Подобные преобразования широко используются, например, при интегрировании.
Список литературы.
- Алгебра: учеб. для 7 кл. общеобразоват. учреждений / ; под ред. С. А. Теляковского. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : ил. — ISBN 978-5-09-019315-3.
- Мордкович А. Г. Алгебра. 7 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. — 13-е изд., испр. — М.: Мнемозина, 2009. — 160 с.: ил. ISBN 978-5-346-01198-9.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Описание задачи
В данном руководстве будет рассмотрена задача о создании куба по математике. Задача заключается в том, чтобы построить трехмерную фигуру, имеющую форму правильного шестиугольника, с шестью одинаковыми квадратными гранями.
Для решения этой задачи необходимо понимать основные понятия геометрии, такие как длина стороны, угол, площадь и объем. Кроме того, потребуется использование формул для вычисления длины, площади и объема геометрических фигур.
Для начала необходимо определить длину стороны куба, используя заданный параметр или задачу. Затем нужно вычислить площадь одной грани куба, умножив длину стороны на саму себя. Для определения объема куба нужно умножить площадь грани на длину стороны.
Следующим шагом будет построение куба в пространстве, используя найденные значения для длины стороны, площади и объема. Для этого можно использовать различные методы и инструменты, такие как линейка, рулетка, геометрические фигуры и материалы для моделирования.
Важно следить за точностью при построении куба, чтобы все грани были перпендикулярны друг другу и все стороны были одинаковой длины. Также необходимо убедиться, что фигура получилась правильной и симметричной
После построения куба можно провести дополнительные расчеты и изучить его свойства, такие как диагонали, углы между гранями и длина прямой, соединяющей две противоположные вершины.
В результате выполнения данной задачи вы сможете создать куб, который является одной из основных геометрических фигур и имеет широкое применение в различных областях науки и техники.
Умножение чисел на 10, 100, 1000 …
Умножить числа на 10 значит простые единицы превратить в десятки, десятки в сотни и т. д., то есть повысить порядок всех цифр на единицу. Этого достигают, прибавляя справа один нуль. Умножить на 100 значит повысить все порядки множимого двумя единицами, то есть превратить единицы в сотни, десятки в тысячи и т. д.
Этого достигают, приписывая к числу два нуля.
Отсюда заключаем:
Для умножения целого числа на 10, 100, 1000 и вообще на 1 с нулями нужно приписать справа столько нулей, сколько их находится во множителе.
Умножение числа 6035 на 1000 выразится письменно:
Когда множитель есть число, оканчивающееся нулями, подписывают под множимым только значащие цифры, а нули множителя приписывают справа.
Как вычислить диагональ точного куба
Диагональ точного куба – это расстояние между двумя противоположными вершинами. Чтобы вычислить эту величину, необходимо знать длину ребра куба.
Формула для вычисления диагонали точного куба:
- Для простых случаев: диагональ = √3 × a, где a — длина ребра.
- Для случает, когда известна длина диагонали грани: диагональ = √2 × l, где l — длина диагонали грани.
- Для случает, когда известен объем куба: диагональ = ∛(√3 × V), где V — объем куба.
Например, если длина ребра куба равна 5 см, то диагональ будет равна √3 × 5 ≈ 8.66 см.
Эта формула может быть полезна при решении задач, связанных с геометрией и пространственной алгеброй.
Степени
Между различными произведениями заслуживают особого внимания такие, в которых производители равны. Так, например:
2 × 2 = 4, 3 × 3 = 9.
Квадраты. Произведение двух равных множителей называется квадратом числа.
В наших примерах 4 есть квадрат 2, 9 есть квадрат 3.
Кубы. Произведение трех равных множителей называется кубом числа.
Так, в примерах 2 × 2 × 2 = 8, 3 × 3 × 3 = 27, число 8 есть куб 2, 27 есть куб 3.
Вообще произведение нескольких равных множителей называется степенью числа. Степени получают свои названия от числа равных множителей.
Произведения двух равных множителей или квадраты называются вторыми степенями.
Произведения трех равных множителей или кубы называются третьими степенями, и т. д.
Выбор числа
Важно учитывать, что куб числа будет являться трехмерной фигурой, поэтому выбранное число должно быть положительным. Отрицательные числа также возможны, но результат будет иметь отрицательное значение и представлять собой куб, симметричный к положительному значению
Если вы новичок в математике, рекомендуется выбирать простые числа, такие как 2, 3, 4 и т.д. Начиная с них, вы сможете лучше понять основные принципы создания кубов чисел.
Однако, если вы уже знакомы с математикой и хотите попробовать более сложные числа, то почему бы и нет? В конце концов, создание кубов чисел — это отличный способ попрактиковаться в математике и логике.
Как выбрать материалы для куба?
При создании куба по математике, выбор правильных материалов играет важную роль
Ниже приведены несколько ключевых вещей, на которые стоит обратить внимание при выборе материалов для куба:
| Материал | Описание |
|---|---|
| Карточка или бумага | Один из самых простых и доступных вариантов материалов для создания куба. Карточка обеспечивает прочность и устойчивость конструкции, а бумага позволяет легко складывать и формировать куб. |
| Дерево или ДСП | Если вы хотите создать более прочный и долговечный куб, можно использовать дерево или древесно-стружечные плиты(DSP). Эти материалы не только обеспечат стабильность куба, но и позволят ему выдерживать большую нагрузку. |
| Пластиковые листы | Если вам нужен прозрачный куб, для отображения внутренних структур или иллюстраций, пластиковые листы могут быть отличным выбором. Они обладают легкостью и прочностью, а также предоставляют возможность применять различные графические элементы. |
| Металл или пластмасса | При создании куба, который будет использоваться для научных исследований или в инженерных целях, можно использовать металлические или пластиковые детали. Они обеспечат равномерность и прочность конструкции, необходимые для таких задач. |
В итоге, выбор материалов для куба зависит от ваших предпочтений, целей и доступности материалов. Будьте внимательны, чтобы выбранные материалы обеспечивали прочность, устойчивость и функциональность вашего куба. Всегда можно экспериментировать и найти оптимальное решение для ваших потребностей.
Свойства точного куба
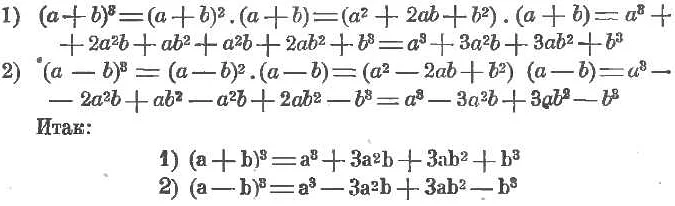
Точный куб является особым случаем куба. Он имеет несколько уникальных свойств, которые отличают его от других геометрических тел.
- Углы: Все углы точного куба равны 90 градусам.
- Ребра и грани: Все ребра и грани точного куба имеют одинаковую длину.
- Диагонали: Диагонали каждой грани точного куба пересекаются в центре куба.
- Объем и площадь: Объём точного куба можно найти, возводя длину ребра в куб. Общая площадь всех граней также может быть найдена, возводя длину ребра в квадрат и умножая на 6.
- Симметрия: Точный куб имеет 24 оси симметрии.
Точный куб встречается в ряде областей, включая математику, архитектуру и графический дизайн. Он может быть использован как основа для создания различных конструкций и моделей, а также как символ баланса и гармонии благодаря своей симметрии и правильной форме.
Как находить сторону точного куба по объёму
Для того чтобы найти сторону точного куба по заданному объёму, необходимо выполнить следующие шаги:
- Определить значение объёма куба.
- Найти кубический корень из значения объёма куба. Это и будет стороной точного куба.
Например, если известен объём точного куба и он равен 125 м3, то необходимо найти кубический корень из 125. Найденное значение будет равно 5, так как 5*5*5=125. Следовательно, сторона точного куба равна 5 м.
Также можно воспользоваться формулой для вычисления объёма куба, если известна его сторона:
V = a3
где V — объём куба, a — сторона точного куба.
Таким образом, если известна сторона точного куба, можно легко вычислить его объём, а если известен объём, то можно найти сторону точного куба.
Дидактическое пособие «Чудо-кубик» и способы его применения ⋆ Планета Детства
Цель: Развитие речи и мышления ребенка дошкольного возраста.
Задачи: Формирование у детей зрительного, тактильного, сенсорного восприятия предметов, развитие мелкой моторики пальцев рук, а так же развитие речи, пополнение активного словарного запаса детей, ориентировку на плоскости, мышление, память. Чудо-кубик раскрывает в себе такие темы как: фрукты и овощи, части лица, большой-маленький, геометрические формы, основные цвета, один-много, умение шнуровать обувь.
Алгоритм изготовления1. Для изготовления чудо-кубика размером 45 см использовался материал различной фактуры:• Габардин 6 цветов-по 0,5 м;• Флис 6 цветов- по 0,1м;• Хлопок- 0,1 м;• 7 цветов атласных лент- длинной 0,5 м, шириной 0,5 до 5 см;• Велюр 0,1 м;• Контактная лента 1 м;• Салфетки из микрофибры 4 цвета- по 0,5 м;• Одна потайная молния;• Для декора- пуговицы и шнуровка;• Для наполнения — поролон и утеплитель.
2. Изготовление шаблонов. Опираясь на размеры кубика были сделаны заготовки:• Фруктов• Овощей• Фигур• Лица• Обуви3. Пошив:• К каждой стороне кубика определенного цвета были закреплены английскими булавками заготовки, края которых были обработаны зигзагообразной строчкой, мелкими стежками• Вручную были пришиты пуговицы, вставлены шнурки и прорисованы некоторые детали заготовок• Затем были стачены стороны кубика в одну из которой была вставлена потайная застежка-молния (чтобы по мере загрязнения кубик можно было стирать)4. Для того, чтобы кубик держал форму, было решено в каждую грань вставить утеплитель, а затем наполнить поролоном.
Способы применения.
«Чудо-кубик» имеет развивающее, обучающее и воспитывающие значение. Его можно использовать практически в любых видах, игровой деятельности детей.Пособие может постоянно дополняется новыми элементами, есть возможность разработать огромное количество игр для детей. Каждая грань кубика посвящена отдельной теме.
Дидактическая игра «Собери лицо папы»
Цель: закрепление знаний о составных частях лица, их местонахождении.Ход игры: Ребята давайте с вами соберем лицо папы. Воспитатель просит ребенка найти на стороне кубика определенную часть лица (рот, нос, губы) и приклеить его уже на заготовленный шаблон лица. Игра повторяется с другими детьми.
Дидактическая игра «Найди что назову»
Цель: Развивать умение детей находить фрукт или овощ по названию, определенной фактуры. Обогащать словарь детей.Ход игры: Воспитатель называет фрукт(определенной фактуры: гладкий, ребристый, мягкий) или овощ, а дети должны найти и показать его на кубике
Дидактическая игра « Зашнуруй и завяжи»
Цель: развитие мелкой моторики рук, усидчивости и глазомера у детей. В процессе игры совершенствуется координация движений, гибкость кистей рук, пространственное ориентирование.Ход игры: Воспитатель просит ребенка зашнуровать и завязать бантик на обуви. Игра повторяется с другими детьми.
Дидактическая игра «Найди свой домик»
Цель: развитие внимания, восприятия, умение сравнивать.Ход игры: Воспитатель раскладывает перед ребенком геометрические фигуры разного размера и цвета, предлагает ребенку найти им определенный «домик». Игра повторяется с другими детьми.
Дидактическая игра « Покажи и назови»
Цель: Формировать у детей представление о цвете, научить различать и называть основные цвета.Ход игры: Воспитатель предлагает ребенку найти определенный цвет ленты и назвать его, если ребенок затрудняется ответить нужно помочь ребенку проговорить цвет вслух. Игра повторяется 2-3 раза.
Так же Чудо-Кубик можно использовать, в непосредственно образовательной деятельности, в качестве строительного материала, если изготовить несколько кубиков различных размеров.
Статья размещена в авторской редакции
Умножение однозначных чисел. Таблица Пифагора
Чтобы умножить два однозначных числа, нужно повторить одно число слагаемым столько раз, сколько в другом содержится единиц, и найти их сумму. Так как умножение целых чисел приводится к умножению однозначных чисел, то составляют таблицу произведений всех однозначных чисел попарно. Такая таблица всех произведений однозначных чисел попарно называется таблицей умножения.
Таблица Пифагора. Изобретение ее приписывают греческому философу Пифагору, по имени которого ее называют таблицей Пифагора. (Пифагор родился около 569 года до н. э.).
Чтобы составить эту таблицу, нужно написать первые 9 чисел в горизонтальный ряд:
1, 2, 3, 4, 5, 6, 7, 8, 9.
Затем под этой строкой надо подписать ряд чисел, выражающих произведение этих чисел на 2. Этот ряд чисел получится, когда в первой строке сложим каждое число само с собою. От второй строки чисел последовательно переходим к 3, 4 и т. д. Каждая последующая строка получается из предыдущей через прибавление к ней чисел первой строки.
Продолжая так поступать до 9 строки, мы получим таблицу Пифагора в следующем виде
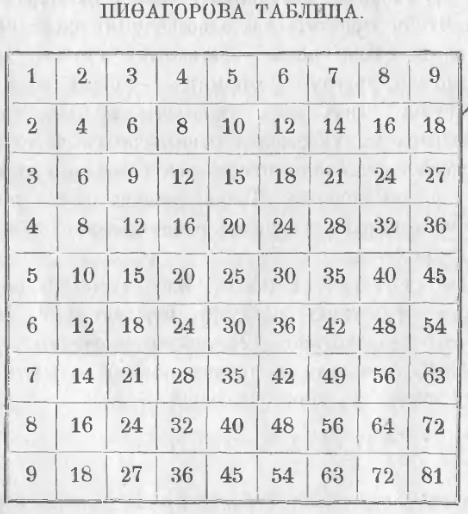
Чтобы по этой таблице найти произведение двух однозначных чисел, нужно отыскать одного производителя в первой горизонтальной строке, а другого в первом вертикальном столбце; тогда искомое произведение будет на пересечении соответствующих столбца и строки. Таким образом, произведение 6 × 7 = 42 находится на пересечении 6-й строки и 7-го столбца. Произведение нуля на число и числа на нуль всегда дает нуль.
Так как произведение числа на 1 дает само число и перемена порядка множителей не изменяет произведения, то все различные произведения двух однозначных чисел, на которые следует обратить внимание, заключаются в следующей таблице:

Произведения однозначных чисел, не содержащиеся в этой таблице, получаются по данным, если только изменить в них порядок множителе; таким образом, 9 × 4 = 4 × 9 = 36.
Если Вам нравится этот сайт…
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Для того что бы упростить алгебраические многочлены, существуют формулы сокращенного умножения
. Их не так уж и много и они легко запоминаются, а запомнить их нужно. Обозначения которые используются в формулах, могут принимать любой вид (число или многочлен).
Первая формула сокращенного умножения называется разность квадратов
. Она заключается в том что из квадрата одного числа отнимается квадрат второго числа равен величине разности данных чисел, а также их произведению.
а 2 — b 2 = (а — b)(a + b)
Разберем для наглядности:
22 2 — 4 2 = (22-4)(22+4)=18 * 26 = 468
9а 2 — 4b 2 c 2 = (3a — 2bc)(3a + 2bc)
Вторая формула о сумме квадратов
. Звучит она как, сумма двух величин в квадрате равняется квадрату первой величины к ней прибавляется двойное произведение первой величины умноженное на вторую, к ним прибавляется квадрат второй величины.
(а + b) 2 = a 2 +2ab + b 2
Благодаря данной формуле, становится намного проще вычислять квадрат от большого числа, без использования вычислительной техники.
Так к примеру:
квадрат от 112 будет равен
1) В начале разберем 112 на числа квадраты которых нам знакомы
112 = 100 + 12
2) Вписываем полученное в скобки возведенные в квадрат
112 2 = (100+12) 2
3) Применяя формулу, получаем:
112 2 = (100+12) 2 = 100 2 + 2 * 100 * 12 + 122 = 10000 + 2400+ 144 = 12544
Третья формула это квадрат разности
. Которая гласит о том, что две вычитаемые друг друга величины в квадрате равняются, тому что, от первой величины в квадрате отнимаем двойное произведение первой величины умноженное на вторую, прибавляя к ним квадрат второй величины.
(а +b) 2 = а 2 — 2аb + b 2
где (а — b) 2 равняется (b — а) 2 . В доказательство чему, (а-b) 2 = а 2 -2аb+b 2 = b 2 -2аb + а 2 = (b-а) 2
Четвертая формула сокращенного умножения называется куб суммы
. Которая звучит как: две слагаемые величины в кубе равны кубу 1 величины прибавляется тройное произведение 1 величины в квадрате умноженное на 2-ую величину, к ним прибавляется тройное произведение 1 величины умноженной на квадрат 2 величины, плюс вторая величина в кубе.
(а+b) 3 = а 3 + 3а 2 b + 3аb 2 + b 3
Пятая, как вы уже поняли называется куб разности
. Которая находит разности между величинами, как от первого обозначения в кубе отнимаем тройное произведение первого обозначения в квадрате умноженное на второе, к ним прибавляется тройное произведение первого обозначения умноженной на квадрат второго обозначения, минус второе обозначение в кубе.
(а-b) 3 = а 3 — 3а 2 b + 3аb 2 — b 3
Шестая называется — сумма кубов
. Сумма кубов равняется произведению двух слагаемых величин, умноженных на неполный квадрат разности, так как в середине нет удвоенного значения.
а 3 + b 3 = (а+b)(а 2 -аb+b 2)
По другому можно сказать сумму кубов можно назвать произведение в двух скобках.
Седьмая и заключительная, называется разность кубов
(ее легко перепутать с формулой куба разности, но это разные вещи). Разность кубов равняется произведению от разности двух величин, умноженных на неполный квадрат суммы, так как в середине нет удвоенного значения.
а 3 — b 3 = (а-b)(а 2 +аb+b 2)
И так формул сокращенного умножения всего 7, они похожи друг на друга и легко запоминаются, единственно важно не путаться в знаках. Они так же рассчитаны на то, что их можно использовать в обратном порядке и в учебниках собрано довольно много таких заданий
Будьте внимательны и все у вас получится.
Применяют для упрощения вычислений, а также разложение многочленов на множители, быстрого умножения многочленов. Большинство формул сокращенного умножения можно получить из бинома Ньютона — в этом Вы скоро убедитесь.
Формулы для квадратов
применяют в вычислениях чаще. Их начинают изучать в школьной программе начиная с 7 класса и до конца обучения формулы для квадратов и кубов школьники должны знать на зубок.
Формулы для кубов
не сильно сложные и их нужно знать при сведении многочленов к стандартному виду, для упрощения подъема суммы или разности переменной и числа к кубу.
Формулы обозначены красным получают из предыдущих группировкой подобных слагаемых.
Формулы для четвертого и пятого степени
в школьном курсе мало кому пригодятся, однако есть задачи при изучении высшей математики где нужно вычислять коэффициенты при степенях.
Формулы для степени
n
расписаны
через биномиальные коэффициенты с использованием факториалов следующие
Сложности при создании куба
Создание куба по математике может представить определенные сложности для начинающих. Во-первых, для построения куба необходимо иметь достаточное понимание геометрии и математических принципов. Это может потребовать определенного времени и усилий для освоения этих основ.
Во-вторых, при создании куба нужно иметь определенные инструменты, такие как линейка, угольник и карандаш. Без них будет сложно достичь точной и симметричной конструкции. Точные измерения и углы — ключевые факторы при построении куба.
Кроме того, при создании куба могут возникнуть трудности с монтажом его составных частей. Если не все грани и углы будут выровнены правильно, куб может получиться неровным и несимметричным.
Важно помнить, что создание куба — это процесс, который требует терпения и практики. Начав с простых моделей, постепенно можно освоить все тонкости и улучшить свои навыки
Не бойтесь делать ошибки и экспериментировать, ведь именно так можно достичь лучших результатов!
Предварительный просмотр:
Дидактическое пособие «Математический куб»
Пособие по формированию элементарных математических представлений для детей младшего дошкольного возраста «Математический куб» . Куб, потому что возможно реализовывать задачи многих разделов математики: «количество», ориентировка во времени», «форма» и «ориентировка в пространстве».
Куб представляет собой полый куб на колёсиках (для облегчения перемещения). Каждая сторона – это дидактическая игра по одному из разделов математики. Одна сторона – дверца. Материал для игр хранится внутри куба.


Игра №1. «Посчитай-ка – уравняй-ка» .
Задачи: упражнять в умении сравнивать две равные и неравные группы предметов способами приложения и наложения, пользоваться словами по много, поровну, столько-сколько, больше — меньше .


Задачи: развивать умение различать и называть геометрические фигуры (квадрат, треугольник). Развивать мелкую моторику, способности конструирования, умения действовать по образцу.


Задачи: упражнять в определении и назывании частей суток, соотнесении части суток и деятельности человека.


Задачи: упражнять в определении пространственных направлений (вверху, внизу, справа, слева).
Игра расположена на верхней горизонтальной стороне куба. Оформлена в виде карусели с посадочными местами для персонажей (зебры, колобка, собачки и ёжика). Ребёнку предлагается выполнить задание: покатать зверей на карусели, правильно их рассадив (например: зебру – слева, колобка наверху и т. д.) или разместить как хочет ребёнок, но потом рассказать кого и где он разместил
Что такое диагональ точного куба
Диагональ точного куба — это отрезок, который соединяет две противоположные вершины куба через его центр. Таким образом, диагональ точного куба проходит через три измерения куба и является его наибольшей диагональю.
Для вычисления длины диагонали точного куба можно использовать формулу:
d = a√3
где d — длина диагонали, a — длина ребра куба, а √3 — корень из трех.
Важно отметить, что диагональ точного куба, как и все его стороны, имеет равную длину. Это свойство делает точный куб особенно интересным объектом для изучения, а также связывает его с многими другими математическими концепциями