Геометрия

Трехмерные фигуры

Трехмерные фигуры – это объекты пространственной геометрии, которые имеют три измерения: длину, ширину и высоту. Они могут быть описаны различными параметрами, такими как объем, площадь поверхности и радиус-вектор. Такие фигуры являются важными элементами в инженерном, научном и графическом проектировании.

Среди трехмерных фигур можно выделить несколько классов. Наиболее распространенные из них – это параллелепипеды, пирамиды, цилиндры и сферы.

• Параллелепипеды представляют собой шестигранные блоки с прямоугольными гранями. Они имеют шесть граней и двенадцать ребер, объем параллелепипеда равен произведению длины, ширины и высоты.
• Пирамиды – это многоугольные фигуры, имеющие треугольную вершину и боковые грани в форме треугольников или многоугольников. Объем пирамиды вычисляется как произведение площади основания и высоты, деленное на три.
• Цилиндры – это тела вращения, полученные в результате вращения прямоугольников вокруг оси. У них две круглые грани и боковая поверхность. Объем цилиндра равен произведению площади основания на высоту.
• Сферы – это тела вращения, полученные в результате вращения полуокружности вокруг оси. Они имеют только одну поверхность и не имеют ребер и вершин. Объем сферы вычисляется по формуле, связывающей ее радиус с числом Пи.

Трехмерные фигуры имеют множество применений в различных областях, начиная от архитектурного дизайна и заканчивая медицинскими исследованиями

Их свойства и характеристики изучаются в рамках пространственной геометрии, которая является важной отраслью математики

Построение правильных многоугольников

При использовании транспортира или иного прибора, позволяющего откладывать заранее заданные углы, построение правильного многоуг-ка проблем не вызывает. Например, пусть надо построить пятиугольник со стороной, равной 5 см. Сначала по известной формуле вычисляем величину его угла:

Однако напомним, что в геометрии большой интерес вызывают задачи, связанные с построением с помощью всего двух инструментов – циркуля и линейки, то есть без использования транспортира. В таком случае построение многоугольников правильной формы становится значительно более сложной задачей. Если речь идет не о таких простых фигурах, как квадрат и равносторонний треугольник, то при построении обычно приходится использовать описанную окружность.

Сначала рассмотрим построение правильного шестиугольника по заранее заданной стороне. Ранее мы уже узнали, что его сторона имеет такую же длину, как и радиус описанной окружности:

a₆ = R

На основе этого факта предложен следующий метод построения шестиугольника. Сначала строится описанная окружность, причем в качестве ее радиуса берется заданная сторона а₆. Далее на окружности отмечается произвольная точка А, которая будет первой вершиной шестиугольника. Из нее проводится ещё одна окружность радиусом а₆. Точки, где она пересечет описанную окружность (В и F), будут двумя другими вершинами шестиугольника. Наконец, и из точек B и F проводим ещё две окружности, которые пересекутся с исходной окружностью в точках С и F. Наконец, из С (можно и из F)провести последнюю окружность и получить точку D. Осталось лишь соединить все точки на окружности (А, В, С, D, Еи F):

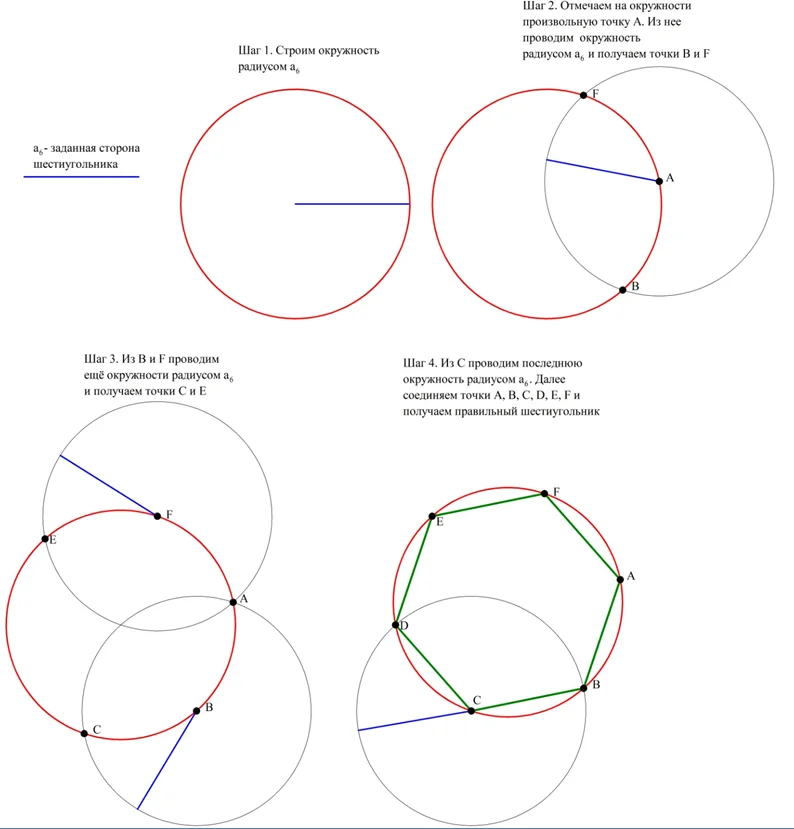
Данное построение довольно просто. Однако для пятиугольника построение несколько более сложное, а для семиугольника и девятиугольника вообще невозможно осуществить точное построение. Этот факт был доказан только в 1836 г. Пьером Ванцелем.

Если удалось возможно построить правильный n-угольник, вписанный в окружность, то несложно на его основе построить многоуг-к, у которого будет в два раза больше сторон (его можно назвать 2n-угольником) и который будет вписан в ту же окружность. Рассмотрим это построение на примере квадрата и восьмиугольника.

Изначально дан квадрат, вписанный в окружность. Надо построить восьмиугольник, вписанный в ту же окружность. Обозначим любые две вершины квадрата буквами А и В. Для начала нам надо разбить дугу ⋃АВ на две равные дуги. Для этого мы проводим из А и В окружности радиусом АВ. Они пересекутся в некоторых точках С и D. Соединяем их отрезком, который в свою очередь пересечется с исходной окружностью в точке Е.

Е – это середина дуги ⋃АВ. Точки А, В и Е как раз являются тремя первыми точками восьмиугольника. Для получения остальных точек необходимо из вершин квадрата строить окружности радиусом АЕ. Точки, где эти окружности пересекутся с исходной окружностью, и будут вершинами восьмиугольника. Также его вершинами являются вершины самого квадрата:

Аналогичным образом можно из шестиугольника получить 12-угольник, из восьмиугольника – 16-угольник, из 16-угольника – 32-угольник. То есть можно удвоить число сторон многоуг-ка.

Древние греки умели строить правильные многоуг-ки с 3, 4, 5, 6 и 15 сторонами, а также умели на их основе строить многоуг-ки с вдвое большим числом сторон. Лишь в 1796 г. Карл Гаусс смог построить 17-угольник. Также удалось найти способ построения 257-угольника и 65537-угольника, причем описание построения 65537-угольника занимает более 200 страниц.

В этом уроке мы узнали о правильных многоуг-ках и их свойствах

Особенно важно то, что для каждого такого многоуг-ка можно построить описанную и вписанную окружность, причем их центры совпадают. Это позволяет использовать правильные многоуг-ки для более глубокого исследования свойств окружности

Комбинаторные свойства[]

Символы Шлефли для правильных многогранников приведены в следующей таблице:

Многогранник	Вершины	Рёбра	Грани	Символ Шлефли
тетраэдр		4	6	4	{3, 3}
куб	Гексаэдр (куб)	8	12	6	{4, 3}
октаэдр		6	12	8	{3, 4}
додекаэдр		20	30	12	{5, 3}
икосаэдр	Икосаэдр	12	30	20	{3, 5}

Другой комбинаторной характеристикой многогранника, которую можно выразить через числа p и q, является общее количество вершин (В), рёбер (Р) и граней (Г). Поскольку любое ребро соединяет две вершины и лежит между двумя гранями, выполняются соотношения:
pΓ=2P=qB.{\displaystyle p\Gamma = 2\mbox{P} = q\mbox{B}.\,}

Из этих соотношений и формулы Эйлера можно получить следующие выражения для В, Р и Г:

B=4p4−(p−2)(q−2),P=2pq4−(p−2)(q−2),Γ=4q4−(p−2)(q−2).{\displaystyle \mbox{B} = \frac{4p}{4 — (p-2)(q-2)},\quad \mbox{P} = \frac{2pq}{4 — (p-2)(q-2)},\quad \Gamma = \frac{4q}{4 — (p-2)(q-2)}.}

Применение прямоугольника и четырехугольника с прямым углом в геометрии

В геометрии прямоугольник используется для измерения площади, периметра и диагонали фигур. Он также является базовой формой при построении многих других геометрических фигур.

Прямоугольник используется при решении задач на построение и нахождение геометрических параметров. Например, в архитектуре прямоугольник применяется для расчета площади помещений, строительства стен и фундаментов.

Четырехугольник с прямым углом является более узким понятием и имеет один прямой угол, а остальные углы могут быть произвольными. Он также играет важную роль в геометрии и находит свое применение в различных областях.

Прямоугольник и четырехугольник с прямым углом используются в геодезии, строительстве, архитектуре и проектировании, графике и дизайне. Они служат основой для построения планов зданий, карт городов, мебели и других предметов, а также для создания графических изображений и моделей в компьютерной графике.

Прямоугольник и четырехугольник с прямым углом являются универсальными фигурами, которые позволяют точно измерять и описывать объекты в пространстве. Их правильное применение способствует точности и надежности в различных областях, где требуется работа с геометрическими формами и параметрами.

Отношения между углами в треугольниках: теорема и примеры применения

Также существует ряд других отношений между углами треугольника. Например, теорема об углах, лежащих на одной прямой. Согласно этой теореме, сумма двух смежных углов дополняется до 180 градусов. Это значит, что если два угла лежат на одной прямой, то их сумма равна 180 градусам.

Применение этих отношений может быть полезным при решении различных геометрических задач. Например, при нахождении неизвестных углов треугольника или при доказательстве геометрических утверждений. Кроме того, знание отношений между углами в треугольниках помогает в понимании свойств треугольников и их связей с другими геометрическими фигурами.

Ромб: уникальные свойства и равные стороны

Одной из главных характеристик ромба являются его равные стороны. Все четыре стороны ромба имеют одинаковую длину, что делает его симметричным и равнобедренным.

Кроме того, ромб имеет две параллельные стороны и две параллельные диагонали, которые пересекаются под прямым углом. Это делает его особенно удобным и полезным в различных областях, включая геометрию, строительство и дизайн.

Ромб также является специальным случаем параллелограмма, где все четыре угла ромба равны между собой и равны 90 градусам.

Использование ромба в дизайне и архитектуре может придать ощущение гармонии, уравновешенности и уникальности. Его симметричная форма и равные стороны делают его привлекательным и эстетически приятным для глаза.

В заключение, ромб — это четырехугольник, который имеет особые свойства, такие как равные стороны, параллельные стороны и диагонали, а также прямые углы. Его уникальные форма и симметрия делают его интересным объектом изучения и использования в различных областях.

Ссылки[]

• Смирнов Е. Ю. Группы Кокстера и правильные многогранники // Летняя школа «Современная математика». — Дубна: 2008.
• Ошибка скрипта: Модуля «MathWorld» не существует.
• Фанаты математики/геометрия. (англ.)
• Бумажные модели правильных многогранников. (англ.)
• Наука/геометрия/платоновы и архимедовы тела. (англ.)
• Платоновы, Архимедовы тела, призмы, тела Кеплера-Пуансо и усечённые тела Кеплера-Пуансо. (англ.)
• Веннинджер Магнус. Модели многогранников. — Москва: Мир, 1974. — 236 с. (см. ISBN )

Гончар В. В. Модели многогранников. — Москва: Аким, 1997. — 64 с. — ISBN 5-85399-032-2. (см. ISBN )

Гончар В. В., Гончар Д. Р. Модели многогранников. — Ростов-на-Дону: Феникс, 2010. — 143 с. — ISBN 978-5-222-17061-8. (см. ISBN )

Многогранники. Волшебные грани — наборы для сборки моделей многогранников. — Москва: Многогранники, 2012. — С. 20. (см. ISBN )

 (рус.)

Это заготовка статьи по геометрии.

Википедия Правильный многогранник адрес Викисловарь — адрес Викицитатник — адрес Викиучебник — адрес Викитека — адрес Викиновости — адрес Викиверситет — адрес Викигид — адрес

Выделить Правильный многогранник и найти в: Вокруг света многогранник адрес Академик многогранник/ru/ru/ адрес Астронет адрес Элементы многогранник+&search адрес Научная Россия многогранник&mode=2&sort=2 адрес Кругосвет многогранник&results_per_page=10 адрес Научная Сеть Традиция — адрес Циклопедия — адрес Викизнание — многогранник адрес

Bing Yahoo Яндекс Mail.ru Рамблер Нигма.РФ Спутник Google Scholar Апорт Архив Интернета Научно-популярные фильмы на Яндексе Документальные фильмы

Список ru-вики Вики-сайты на русском языке Список крупных русскоязычных википроектов Каталог wiki-сайтов Русскоязычные wiki-проекты Викизнание:Каталог wiki-сайтов Научно-популярные сайты в Интернете Лучшие научные сайты на нашем портале Лучшие научно-популярные сайты Каталог научно-познавательных сайтов НАУКА В РУНЕТЕ: каталог научных и научно-популярных сайтов

• Страница — краткая статья
• Страница 1 — энциклопедическая статья
• Разное — на страницах: 2 , 3 , 4 , 5
• Прошу вносить вашу информацию в «Правильный многогранник 1», чтобы сохранить ее

Практическое применение различных четырехугольников:

Различные четырехугольники имеют разные свойства и характеристики, что позволяет использовать их в различных практических ситуациях. Рассмотрим некоторые из наиболее распространенных применений различных четырехугольников:

1. Прямоугольник:

   • Прямоугольники особенно полезны при построении зданий и сооружений. Благодаря своим прямым углам они обеспечивают устойчивость и прочность конструкции.
   • Прямоугольники также широко используются в проектировании и расположении мебели, например, столов, кроватей, шкафов.

2. Трапеция:

   • Трапеции используются в архитектуре для создания сложных форм, например, в крышах зданий.
   • В геометрических построениях трапеции могут использоваться для построения подобных фигур или разделения площади на различные сегменты.

3. Ромб:

   • Ромбы часто используются в ювелирной промышленности для создания драгоценных камней или ожерелий.
   • Ромбическая форма может быть использована для расположения участков, парков или садов.

4. Параллелограмм:

   • Параллелограммы используются в строительстве для создания устойчивых и прочных фундаментов.
   • В графике параллелограммы могут использоваться для создания эффекта глубины или перспективы.

5. Нерегулярные четырехугольники:

   • Нерегулярные четырехугольники широко используются в архитектуре и дизайне для создания уникальных форм и структур.
   • В проектировании садов и ландшафтов нерегулярные четырехугольники могут использоваться для создания интересных геометрических композиций.

В заключение, различные четырехугольники имеют свои особенности и применение в различных областях. Знание и понимание этих свойств помогает использовать четырехугольники в практических задачах и создавать устойчивые и эстетически привлекательные конструкции.

Классификация двумерных полиэдров

Наша задача состоит в том, чтобы связать символы Шлефли {n,m} с количеством вершин, ребер и граней. Для примера рассмотрим тетраэдр и попытаемся выяснить зависимость.

1. У тетраэдра 4 грани, в каждой из которых три угла. Т.о., если умножить 4 грани на 3 угла получим 12 чего-то там, что в два раза больше, чем количество его ребер (каждое из них посчитано дважды).

2. В каждой вершине сходятся m=3 граней. Если умножить 4 вершины на 3 грани получим 12 чего-то там, что в два раза больше количества ребер (их так же считали дважды

В качестве упражнения можно посчитать для куба. В каждой из 6 граней 4 угла, отсюда (6*4)/2 = 12 ребер. В каждой из 8 вершин сходятся 3 грани, что даёт (8*3)/2 = 12 ребер.

Получили три уравнения с тремя неизвестными, которые будем сейчас решать, чтобы получить в чистом виде зависимость от составляющих символа Шлефли:

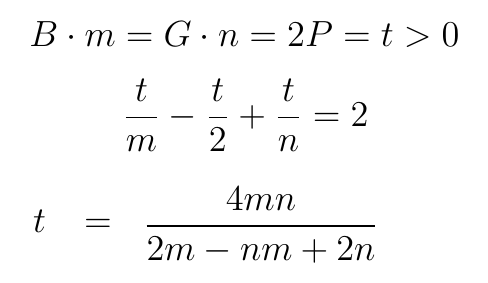Такую систему уравнений удобно решить, воспользовавшись параметризацией через некое t. Во второй строчке подставили данные в уравнение Эйлера и затем привели дроби к одному знаменателю

Из очевидных соображений, что t > 0 , мы должны потребовать положительности знаменателя. Остается в целых числах решить соответствующее неравенство:

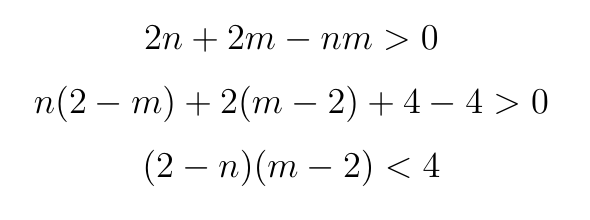
Не только лишь все натуральные числа при умножении дают результат, меньший 4, поэтому у нас не так много работы:

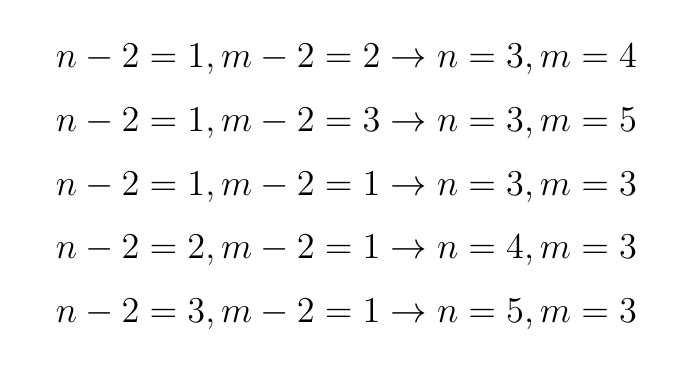
А теперь вспомните рисунок с символами Шлефли для платоновых тел! Как видите, мы получили одно и то же с помощью решения обычной системы уравнений! Алгебраизация — один из самых мощных способов исследования окружающего нас мира.

Может ли треугольник иметь плоскую вершину?

A трапеция представляет собой четырехстороннюю плоскую фигуру с одной парой противоположных параллельных сторон. Он выглядит как треугольник, верхняя часть которого срезана параллельно нижней.

Какой формы треугольник? В геометрии треугольник замкнутая двухмерная форма с тремя прямыми сторонами. Треугольник — это тоже многоугольник.

Как выглядит треугольник?

Является ли треугольник выпуклым? Многоугольник выпуклая, если все внутренние углы меньше 180 градусов. … Все треугольники выпуклые Невыпуклый треугольник нарисовать невозможно.

У треугольников четыре стороны?

Треугольник имеет 3 вершины. Мы должны сделать его многоугольником.Итак, мы должны соединить все 3 вершины вместе так, чтобы он мог образовать замкнутую ФИГУРУ.ЭТО возможно, если провести 3 линии. Таким образом, Треугольник не имеет 4 сторон.

Какой формы треугольник? В геометрии треугольник замкнутая двухмерная форма с тремя прямыми сторонами. Треугольник — это тоже многоугольник.

Алмаз — это форма?

Алмазы имеют уникальную форму, поскольку обладают множеством различных геометрических атрибутов. Бриллиант четырехугольник, двумерная плоская фигура с четырьмя замкнутыми прямыми сторонами. Но алмаз также относится к категории ромбов, потому что у него четыре равные стороны, а его противоположные углы равны.

Каковы углы алмаза? Каков наилучший угол короны для бриллианта? По мнению экспертов, лучший угол короны между 32-35 градусами. Когда угол короны бриллианта меньше 32 градусов, это называется разбросной огранкой, придающей бриллианту вид тумана.

Геометрические объемные тела

Поскольку эти тела имеют конечную размерность в трех пространственных направлениях, то для их описания в геометрии используют систему из трех координатных осей. Эти оси обладают следующими свойствами:

1. Они ортогональны друг другу, то есть перпендикулярны.
2. Эти оси нормализированы, то есть базисные вектора каждой оси имеют одинаковую длину.
3. Любая из осей координат — это результат векторного произведения двух других.

Говоря о геометрических объемных фигурах и их названиях, следует отметить, что все они принадлежат к одному из 2-х больших классов:

1. Класс полиэдров. Эти фигуры, исходя из названия класса, имеют прямые ребра и плоские грани. Грань — это плоскость, которая ограничивает фигуру. Место соединения двух граней называется ребром, а точка соединения трех граней — это вершина. К полиэдрам относятся геометрическая фигура куб, тетраэдры, призмы, пирамиды. Для этих фигур справедлива теорема Эйлера, которая устанавливает связь между числом сторон (С), ребер (Р) и вершин (В) для каждого полиэдра. Математически эта теорема записывается так: С + В = Р + 2.
2. Класс круглых тел или тел вращения. Эти фигуры имеют хотя бы одну поверхность, образующую их, изогнутой формы. Например, шар, конус, цилиндр, тор.

Что касается свойств объемных фигур, то следует выделить два самых важных из них:

1. Наличие определенного объема, который фигура занимает в пространстве.
2. Наличие у каждой объемной фигуры площади поверхности.

Оба свойства для каждой фигуры описываются конкретными математическими формулами.

Рассмотрим ниже самые простые геометрические объемные фигуры и их названия: куб, пирамиду, призму, тетраэдр и шар.

Разновидности четырехугольников

1. Прямоугольник — четырехугольник, у которого все углы прямые (равны 90 градусам). Прямоугольники имеют две пары параллельных сторон, а их диагонали равны.

2. Квадрат — четырехугольник, у которого все стороны равны и все углы прямые. Квадрат является подтипом прямоугольника и имеет все его свойства, но в дополнение к этому все стороны квадрата равны.

3. Ромб — четырехугольник, у которого все стороны равны. Ромб также обладает особенностью, что все его углы равны, но они не обязательно прямые. Диагонали ромба перпендикулярны между собой и делятся пополам.

4. Параллелограмм — четырехугольник, у которого противоположные стороны параллельны. Параллелограммы также имеют противоположные равные стороны и противоположные равные углы.

5. Трапеция — четырехугольник, у которого две стороны параллельны, но остальные две не параллельны. Трапеции обладают также специальным свойством, что основания трапеции равны.

Название	Описание	Свойства
Прямоугольник	Все углы прямые (равны 90 градусам)	Параллельные стороны, равные диагонали
Квадрат	Все стороны равны и все углы прямые	Параллельные стороны, равные диагонали
Ромб	Все стороны равны, углы могут быть непрямыми	Диагонали перпендикулярны и делятся пополам
Параллелограмм	Противоположные стороны параллельны	Противоположные равные стороны и равные углы
Трапеция	Две стороны параллельны	Равные основания

Это лишь несколько примеров разновидностей четырехугольников. Существует еще множество других четырехугольников с разными свойствами и характеристиками.

Слайды и текст этой презентации

Слайд 1Правильные фигуры
в геометрииУчитель математики Беленкова Ольга Александровна

равны и все углы равны.  Центром правильного многоугольника называется точка,

равноудаленная от всех его вершин и всех его сторон. Центральным углом правильного многоугольника называется угол, под которым видна сторона из его центра.

около окружности. Центр правильного многоугольника совпадает с центрами вписанной и

описанной окружностей.  Периметры правильных n-угольников относятся как радиусы описанных окружностей.

– но этот весьма скромный по численности отряд сумел пробраться

в самые глубины различных наук».

Слайд 6Многогранник- это такое тело, поверхность которого состоит из конечного  числа

плоских многоугольников.  Многогранник называется выпуклым, если он расположен по одну

сторону плоскости каждого плоского многоугольника на его поверхности. Общая часть такой плоскости и поверхности выпуклого многогранника называется гранью. Грани выпуклого многогранника являются плоскими выпуклыми многоугольниками. Стороны граней называются рёбрами многогранника, а вершины – вершинами многогранника.

Слайд 7Существует 5 видов правильных многогранников:
1)тетраэдр
2) гексаэдр
3) додекаэдр
4)октаэдр
5)икосаэдр 

противоположной грани, называется его медианой, опущенной из данной вершины.Отрезок, соединяющий середины скрещивающихся рёбер тетраэдра, называется его бимедианой, соединяющей данные рёбра.Отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани, называется его высотой, опущенной из данной вершины.Теорема. Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, считая от вершины. Эта точка делит бимедианы пополам.

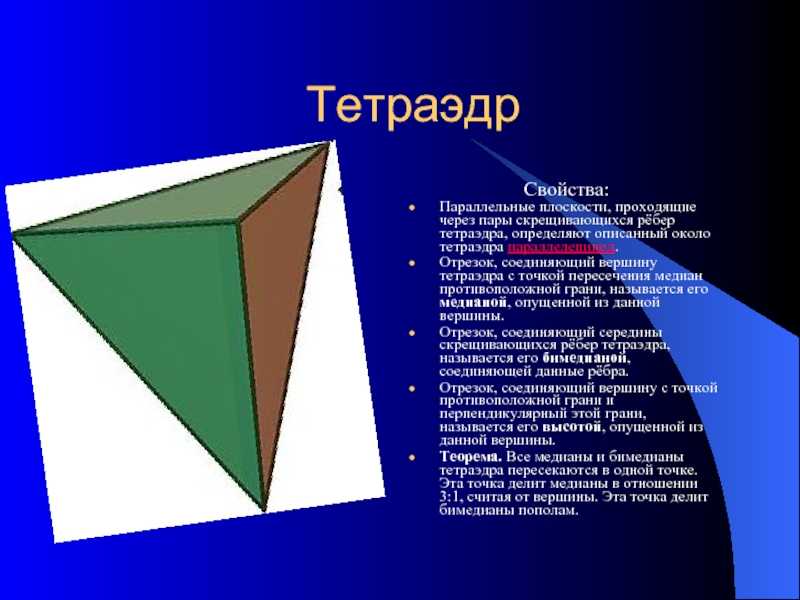
проходят через центр куба перпендикулярно четырём его главным диагоналям. В

куб можно вписать тетраэдрВ куб можно вписать тетраэдр двумя способами. В обоих случаях четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба и все шесть рёбер тетраэдра будут принадлежать граням куба. В первом случае все вершины тетраэдра принадлежат граням трехгранного угла, вершина которого совпадает с одной из вершин куба. Во втором случае попарно скрещивающиеся ребра тетраэдра принадлежат попарно противолежащим граням куба. Такой тетраэдр является правильным. В куб можно вписать октаэдр, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба. Куб можно вписать в октаэдр, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра. В куб можно вписать икосаэдр, при этом шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра — внутри куба. Все двенадцать вершин икосаэдра будут лежать на шести гранях куба.

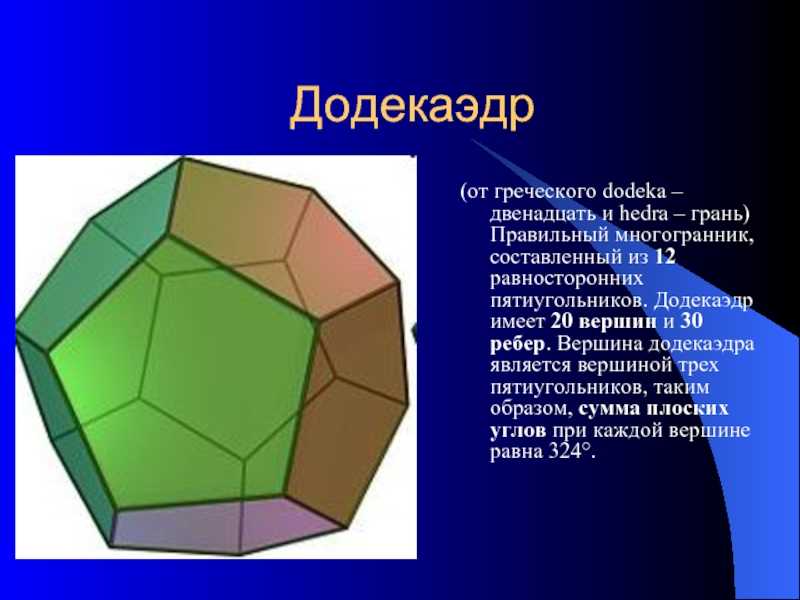
Слайд 10Додекаэдр(от греческого dodeka – двенадцать и hedra – грань) Правильный

многогранник, составленный из 12 равносторонних пятиугольников. Додекаэдр имеет 20 вершин

и 30 ребер. Вершина додекаэдра является вершиной трех пятиугольников, таким образом, сумма плоских углов при каждой вершине равна 324°.

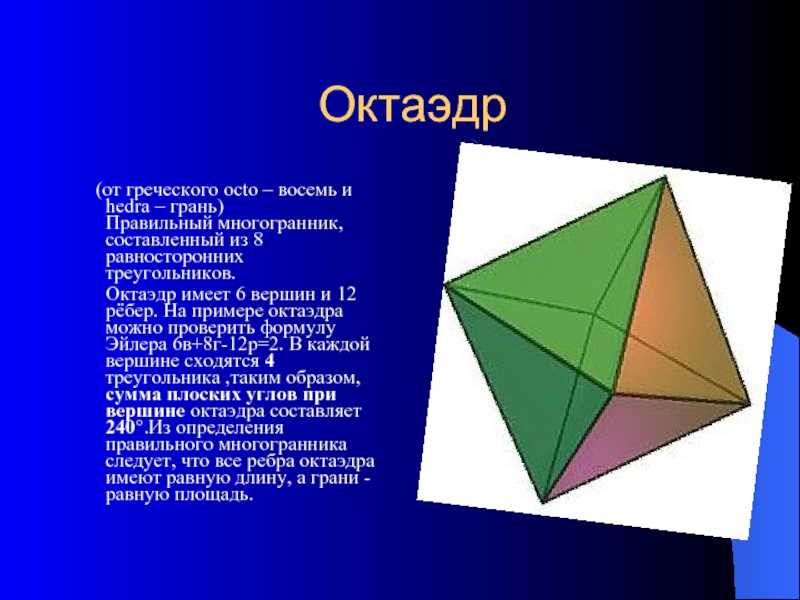
Слайд 11Октаэдр (от греческого octo – восемь и hedra –

грань)
Правильный многогранник, составленный из 8 равносторонних треугольников. Октаэдр

имеет 6 вершин и 12 рёбер. На примере октаэдра можно проверить формулу Эйлера 6в+8г-12р=2. В каждой вершине сходятся 4 треугольника ,таким образом, сумма плоских углов при вершине октаэдра составляет 240°.Из определения правильного многогранника следует, что все ребра октаэдра имеют равную длину, а грани — равную площадь.

рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные

24 ребра внутри куба, все двенадцать вершин икосаэдра будут лежать на шести гранях куба В икосаэдр может быть вписан тетраэдр, притом, четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра. Икосаэдр можно вписать в додекаэдр, при этом вершины икосаэдра будут совмещены с центрами граней додекаэдра. В икосаэдр можно вписать додекаэдр с совмещением вершин додекаэдра и центров граней икосаэдра. Усечённый икосаэдр может быть получен срезанием 12 вершин с образованием граней в виде правильных пятиугольников. При этом число вершин нового многогранника увеличивается в 5 раз (12×5=60), 20 треугольных граней превращаются в правильные шестиугольники (всего граней становится 20+12=32), а число рёбер возрастает до 30+12×5=90.

Равность правильных фигур

Частным и самым простым для сравнения является случай, когда многоугольник по условию правильный. Так называется фигура с одинаковыми сторонами и углами. Например, равносторонний треугольник и квадрат

Важно не забывать проверить равны ли углы, так как не каждая фигура правильная. Тот же ромб по определению имеет 4 совпадающие по длине стороны, но разные углы

При сравнении правильных многоугольников достаточно указать, что, хотя бы одна сторона фигуры равна стороне у другой. Это будет достаточное условие для доказательства «равности».

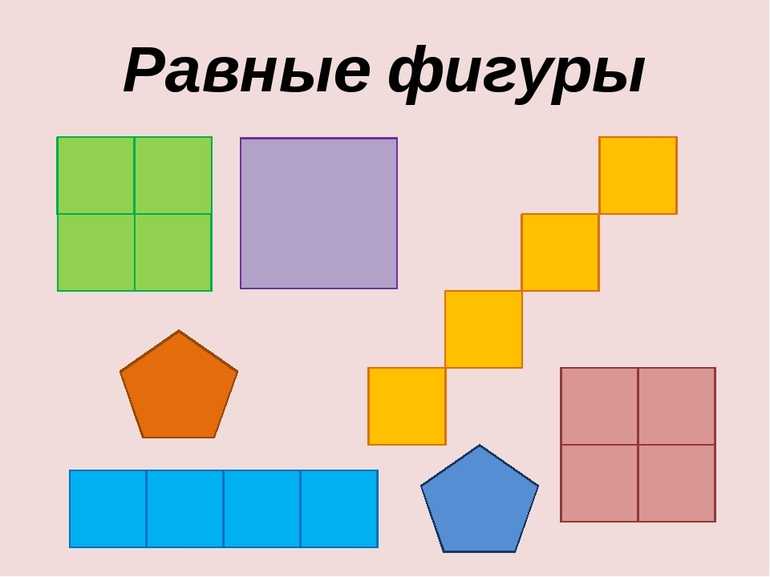
Самым простым и наглядным способом сверки двух фигур будет не геометрический с помощью правил, а путём наложения рисунков друг на друга. Разумеется, что он не претендует на точность, но изобразить параллелограмм и наложить его на другой нагляднее, чем сравнивать, например, углы. Понятно, что так можно только ознакомиться с концепцией «равности» и показать, какие фигуры называются равными, для упрощения в дальнейшем решения задач, но доказывать что-либо нельзя, ввиду неточности метода.

Если при сравнении двух тел оказывается, что их площади равны, такие тела (многоугольники) являются равновеликими. Как и в случае с прошлым, это определение звучит несложно. Проблемы могут начаться непосредственно при вычислении площадей. Самый простой многоугольник — треугольник. Для вычисления его площади существует множество способов.

Четырехугольник

Четырехугольник имеет столько же вариантов, сколько и треугольник. Однако существует только два основных типа — параллелограмм и трапеция.

Параллелограмм — это выпуклый четырехугольник, стороны которого попарно прямые и параллельные

Обратите внимание, что в определении треугольника никогда не используется параметр «выпуклый», о котором мы говорили в начале. Дело в том, что треугольники всегда выпуклые, а четырехугольники могут быть невыпуклыми. Параллелограмм, в зависимости от равенства элементов: углов а стороны делятся на следующие фигуры:

Параллелограмм, в зависимости от равенства элементов: углов а стороны делятся на следующие фигуры:

• Квадрат.
• Прямоугольник.
• Ромб.
• Произвольный параллелограмм.

Все эти известные нам фигуры являются разновидностями параллелограмма.

Рисунок 3. Типы параллелограммов.

Трапеция — это четырехугольник, две стороны которого параллельны, а две — нет. Однако существует множество четырехугольников, которые не принадлежат ни к одной группе. Такие фигуры называются произвольными четырехугольниками.

Геометрические фигуры

Базовыми фигурами в геометрии на плоскости являются треугольник, четырёхугольник, многоугольник, окружность. В пространстве — это призма, пирамида, сфера, конус.

«Треугольник» — простейшая фигура в геометрии, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих вершины треугольника. Отрезки при этом будут называться сторонами треугольника. У треугольника три угла и три стороны. Поэтому можно выделить прямоугольные треугольники (один из углов — прямой), остроугольные треугольники (все углы — острые), тупоугольные треугольники (если один угол тупой). Замечательным свойством треугольника будет формула о сумме его углов, которая равна 180°. Иными словами, если α, β, γ — углы треугольника, то верно равенство α + β + γ =180°.

Треугольник ABC

Если классифицировать треугольники с позиции сторон, то треугольники делятся на равносторонние (все стороны равны), равнобедренные (две стороны из трех равны, но не равны третьей) и произвольные.
В треугольник против наибольшего угла лежит наибольшая сторона и наоборот.
Огромное значение треугольники играют в геометрии благодаря тому, что почти любая фигура разбивается на треугольники каким-либо методом. Таким образом, чтобы уметь анализировать более сложные фигуры, нужно знать свойства треугольника.

Базовое значение в геометрии играет теорема Пифагора, которая гласит, что в любом прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов. a2+b2=c2{\displaystyle a^{2}+b^{2}=c^{2}} Для решения большинства задач в геометрии так или иначе используются теорема Пифагора.

«Четырёхугольник» — фигура, состоящая из четырёх вершин и четырёх отрезков, последовательно соединяющих его вершины, являющихся его сторонами, при этом никакие три вершины не лежат на одной прямой. Последнее требование позволяет исключить вырожденные четырёхугольники, которые представляют собой треугольники или прямые. Важными представителями четырёхугольников являются параллелограмм и трапеция, поскольку почти все остальные четырёхугольники можно анализировать на основе их свойств.

• Параллелограмм — четырёхугольник, у которого противоположные стороны попарно равны и параллельны.
• Трапеция — четырёхугольник, у которого две противоположные стороны параллельны и две другие не параллельны.

Наиболее популярными четырёхугольниками на практике являются квадраты, прямоугольники и ромбы, которые уже определяются на основе параллелограммов.

• Ромб — четырёхугольник, у которого все стороны равны.
• Прямоугольник — четырёхугольник, у которого все углы прямые.
• Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны.

Сфера с радиусом r и диаметром d

Любой многоугольник уже разбивается на вышеописанные фигуры, поэтому его свойства можно изучать на основе рассмотренных фигур. Особняком стоит окружность или круг. Введение понятие «окружности» или «равноудалённости» значительно расширяет функционал и угол зрения геометрической науки. В свою очередь широкое применение круга на практике заставляет геометров пристально изучать свойства окружности, чтобы найденные таким образом закономерности инженеры могли применить в промышленности и других практических областях.

Окружность — это множество точек одной плоскости, равноудаленных от одной точки (центра окружности). При этом расстояние от любой точки окружности до её центра называется радиусом окружности или круга. Термин круг используется, если требуется включить все точки внутри окружности в одну фигуру. Отсюда следует, что окружность в отличие от круга не имеет площади. Но окружность является границей круга.

Если в определении окружности убрать требование на нахождение точек в одной плоскости, то получится сфера или шар.

• Сфера — это множество точек пространства, равноудаленных от одной точки (центра сферы). Сфера является границей шара.
• Призма — многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. Эти параллелограммы называются боковыми гранями призмы, а оставшиеся два многоугольника называются её верхними и нижними основаниями. Наиболее популярной призмой является куб.
• Пирамида — многогранник, основанием которого является многоугольник, а остальные грани представляют собой треугольники, имеющие общую вершину.
• Конус — геометрическая фигура в пространстве, образованная множеством лучей (образующих конуса), соединяющих все точки некоторой плоской кривой (направляющей конуса) с данной точкой пространства (вершиной конуса).