Двоеточие (пунктуация)

Помощь двоеточия равно при отступах Python

При использовании двоеточия равно внутри структур управления, таких как циклы или условные операторы (if-else), оно указывает на начало блока кода, который будет выполнен внутри этой структуры. Блок кода должен иметь один и тот же отступ относительно двоеточия равно, чтобы быть корректным.

Например, рассмотрим следующий код:

В этом примере, двоеточие равно после выражения указывает на начало блока кода, который будет выполнен, если это условие истинно. В данном случае, если значение переменной больше 5, на экран будет выведено сообщение .

Кроме того, двоеточие равно также используется при определении функций или методов. Оно указывает на начало блока кода, который будет выполнен при вызове функции или метода.

Например, рассмотрим следующий код:

В этом примере, двоеточие равно после заголовка функции указывает на начало блока кода, в котором выполняются вычисления и определяется переменная . После выполнения блока кода, результат вычислений возвращается с помощью оператора .

Итак, двоеточие равно играет важную роль при отступах в языке Python, указывая на начало блоков кода внутри структур управления или при определении функций и методов.

Примеры применения в предложениях:

Пример 1:

Двоеточие используется для разделения главного предложения от пояснительной части:

Пример 2:

Двоеточие используется для обозначения перечисления или последовательности:

Пример 3:

Двоеточие используется перед цитатой или прямой речью:

Пример 4:

Двоеточие используется для обозначения продолжения речи или мысли:

Пример 5:

Двоеточие используется для обозначения обращения или адреса:

Пример 6:

Двоеточие используется в формальных документах для обозначения разделов или пунктов:

1:	Тема первого раздела
	Содержание первого раздела…
	…
2:	Тема второго раздела
	Содержание второго раздела…
	…

Математическое равенство и его обозначение

Математическое равенство — это утверждение о том, что два математических выражения или две величины имеют одинаковое значение. В математике равенство обозначается специальным символом, который называется знаком равенства: «=». Знак равенства ставится между выражениями или величинами, которые сравниваются.

Примеры математических равенств:

• 2 + 2 = 4
• 5 * 3 = 15
• x + 7 = 10

Здесь каждое выражение слева от знака равенства сравнивается с выражением, которое стоит справа от знака равенства. Если два выражения или величины равны, то мы можем сказать, что они эквивалентны друг другу.

Математическое равенство часто используется для решения уравнений, алгебраических задач и формулировки математических законов. Оно позволяет сравнивать различные выражения и величины, и находить различные решения и значение неизвестных величин.

Важно: Равенство — это симметричное отношение. Это означает, что порядок выражений или величин, стоящих слева и справа от знака равенства, не имеет значения

Например, «3 + 4 = 7» эквивалентно «7 = 3 + 4».

Учетные записи двоеточия в старых текстах

История происхождения двоеточия в русском языке интересна историкам и лингвистам. В старых текстах можно найти учетные записи, относящиеся к использованию двоеточия. Эти записи помогают нам понять, какова история этого пунктуационного знака в русском языке.

Двоеточие имело различные функции в старых текстах. В документах судебного характера двоеточие использовалось для обозначения вопросов и ответов. Например:

• Вопрос: Вы признаете свою вину?
• Ответ: Нет.

Двоеточие также использовалось в церковных текстах. Оно указывало на места, где нужно делать паузу при чтении или пении. Например:

1. Господи: помилуй нас,
2. Приими: молитву нашу,
3. Услыши: нас, грешных.

В литературных текстах двоеточие использовалось для выделения прямой речи:

Интересно, что в старых текстах двоеточие также использовалось для обозначения места рубрикации. Например, в книгах указывалось:

Глава:	1
Параграф:	2
Статья:	3

Таким образом, учетные записи двоеточия в старых текстах являются важным источником информации о его использовании в прошлом. Они позволяют нам понять, какова история происхождения этого пунктуационного знака в русском языке и какие функции он выполнял в различных сферах коммуникации.

Происхождение двоеточия

История происхождения двоеточия в русском языке начинается еще в древнегреческом и латинском алфавитах. Символ «:» был часто использован для обозначения отделительных и разделяющих знаков. В ходе развития и эволюции языка символ приобрел свое значение исключительно в русском алфавите.

В русском языке двоеточие имеет несколько функций:

• Обозначение прямой речи. Двоеточие ставится после реплики говорящего перед прямой речью.
• Выделение деталей и пояснений. Двоеточие используется для указания подробностей, примеров или списков.
• Обозначение присоединительного или пояснительного смысла. Двоеточие указывает, что следующая часть предложения объясняет или уточняет предыдущую.
• В математике и программировании. Двоеточие используется для обозначения диапазона или разделителя.

Использование двоеточия в русском языке требует знания и понимания правил пунктуации. Оно помогает структурировать текст, обозначать пробелы и связи между словами и предложениями.

Таким образом, происхождение двоеточия в русском языке связано с эволюцией символов и их функциональным использованием в различных контекстах. Знание правил пунктуации позволяет использовать двоеточие в тексте правильно и эффективно.

Известные использования двоеточия

Изощренное использование двоеточия в русском языке существует уже много веков. Ниже приведены некоторые известные случаи использования этого знака препинания:

Обозначение прямой речи. В русском языке двоеточие часто используется для обозначения прямой речи: «Она сказала: «Я приду завтра».

Разделение перечисления. Двоеточие часто используется для разделения элементов перечисления: «На столе лежали: книга, ручка, блокнот».

Выделение пояснительной информации. Двоеточие может использоваться для выделения пояснительной информации: «У него было одно желание: победить».

Заключение информации внутри предложения

Иногда двоеточие используется для заключения информации внутри предложения: «Намечается важное событие: свадьба моего друга».

Двоеточие в списке и перечислении

Двоеточие является одним из знаков пунктуации, который может использоваться в списках и перечислениях для разделения элементов или для указания дополнительной информации.

В списке элементов: двоеточие может использоваться для разделения пунктов списка и их описаний. Например:

Яблоки Груши Апельсины

Красные и сладкие Зеленые и сочные Апельсины с кислыми ломтиками

В данном примере двоеточие используется для соотнесения элементов списка с их соответствующими описаниями.

В перечислениях: двоеточие может использоваться для указания дополнительных деталей или подробностей. Например:

1. Заголовок новости

Текст новости: подробное описание происходящего.

Название продукта

Описание продукта: основные характеристики и особенности.

Список задач

Детали задачи: информация о дедлайне, исполнителе и приоритете.

В данном примере двоеточие используется для добавления дополнительных информаций к каждому элементу перечисления.

Использование двоеточия в списках и перечислениях помогает облегчить чтение и понимание информации, а также позволяет более ясно структурировать и описать различные элементы и их свойства.

История

Английский слово «двоеточие» происходит от латинского двоеточия (мн. кола), само из древнегреческого κῶλον (kôlon), что означает «конечность. «,» член «или» часть «. В греческой риторике и просодии этот термин относился не к пунктуации, а к самому выражению или отрывку. «Двоеточие» было частью законченной мысли или отрывка. Исходя из этого использования, в палеографии двоеточие — это раздел или группа предложений, записанных в виде строки в рукописи. В системе пунктуации, разработанной Аристофаном Византийским в 3-м веке до нашей эры, конец такого предложения, как считалось, вызывал вздох средней длины и был отмечен миддот ⟨· ⟩. (Это использовалось только время от времени, но в конечном итоге возродилось как ano teleia, современнегреческий точка с запятой.) символ двойной точки ⟨⁚⟩ между тем, позже он стал использоваться как точка или для обозначения смены говорящего. Вариант был введен в английская орфография около 1600 года, обозначая паузу между запятой и точкой. Еще в 18 веке уместность двоеточия все еще зависела от продолжительности паузы при чтении текста вслух, но молчаливое чтение в конечном итоге заменило это другими соображениями.

В Британии В английском языке когда-то после двоеточия следовало дефис или тире для обозначения спокойной паузы в типографской конструкции, известной как «dog’s bollocks «, хотя такое использование сейчас не рекомендуется.

Тире: как использовать знак для выделения фраз

Тире – это знак препинания, который используется для выделения фраз, добавления вводных слов и дополнения информации в предложениях. Оно может быть использовано в разных случаях и имеет несколько разных форматов.

Существует три основных варианта использования тире:

1. Выделение фразы или вводных слов от остальной части предложения.
2. Выделение дополнительной информации, добавленной после основной части предложения.
3. Использование тире вместо всех знаков препинания в сложносочинённых предложениях.

Первый вариант – выделение фразы или вводных слов – особенно полезен, когда требуется привлечь внимание читателя к конкретному моменту или исключительному случаю. Тире помогает выделить фразу, сделать её более заметной в предложении

Например:

Внимание! Мероприятие переносится на следующую неделю. Второй вариант – выделение дополнительной информации – используется, когда нужно добавить дополнительные сведения к основной части предложения

Тире помогает отделить эту информацию от остальной части предложения, позволяя читателю сосредоточиться на ней. Например:

Второй вариант – выделение дополнительной информации – используется, когда нужно добавить дополнительные сведения к основной части предложения. Тире помогает отделить эту информацию от остальной части предложения, позволяя читателю сосредоточиться на ней. Например:

Дети, которые обожают спорт, любят проводить время на улице – вот их самое любимое место.

Третий вариант – использование тире вместо всех знаков препинания в сложносочинённых предложениях – служит для упрощения текста и облегчения его понимания. Знаки препинания могут быть заменены одним тире, что позволяет сделать текст более легкочитаемым. Например:

Лена купила яблоки, мандарины, груши – все свежие и ароматные.

Однако, необходимо помнить о правилах использования тире и не злоупотреблять им. Оно не должно использоваться вместо других знаков препинания, таких как запятые, точки с запятой и двоеточия.

Важно: Использование тире должно быть ограничено и внимательно продумано. Перед использованием тире, рекомендуется ознакомиться с грамматическими правилами и примерами его правильного использования

Альтернативы использования двоеточия равно Python

Помимо двоеточия равно, которое в Python используется для присваивания значения переменной, существуют и другие операторы, которые могут выполнять аналогичные действия. Рассмотрим некоторые из них:

Оператор присваивания

Один из альтернативных операторов для присваивания значения переменной в Python — это оператор присваивания «=» (равно). Например, можно записать следующий код:

Методы класса

В Python можно определить методы класса, которые выполняют функцию по умолчанию при создании объекта этого класса. Например, в следующем коде задается класс «Person», у которого есть метод «__init__» для установки значения атрибута «name»:

Другие операторы присваивания

Python также поддерживает различные операторы присваивания, такие как «+=», «-=», «*=», «/=» и другие. Это сокращенная форма записи для выполнения операции и присваивания одновременно. Например:

эквивалентно

эквивалентно

Помимо этих альтернатив, в Python существует и другие способы присваивания значений переменным. Выбор определенного оператора зависит от конкретной задачи и удобства его использования.

Двоеточие равно () в Python играет важную роль в нескольких контекстах. В основном, оно используется для создания блока кода, таких как условные конструкции и циклы. Также, двоеточие равно определяет начало блока кода, который следует после него, используя отступы.

Роль двоеточия равно в Python можно охарактеризовать следующим образом:

Контекст использования	Роль двоеточия равно
Условные конструкции (if, elif, else)	Обозначает начало блока кода, который должен выполниться в случае истинности условия
Циклы (for, while)	Определяет начало блока кода, который будет выполняться в течение каждой итерации цикла
Определение функций и классов	Маркер начала блока кода функции или класса
Индексация и срезы (slice)	Обозначает, что после двоеточия равно будет указан индекс или срез в структуре данных

Использование двоеточия равно является одним из ключевых синтаксических элементов Python и требует строгого соблюдения правил отступов и форматирования кода

Важно помнить, что в Python отступы имеют семантическое значение и определяют вложенность блоков кода

• Двоеточие равно отмечает начало блока кода и требуется во многих конструкциях языка
• Отступы после двоеточия равно имеют семантическое значение и определяют вложенность блоков кода
• Корректное использование двоеточия равно и отступов в Python влияет на понятность и исполняемость кода

В общем, двоеточие равно играет важную роль в Python и позволяет структурировать код, делая его более понятным и читабельным.

Когда используется тире?

Не следует путать тире и дефис. Это два разных символа, которые используются в абсолютно разных случаях. Дефис ставится внутри одного слова, например, «во-первых», «как-нибудь». Тире ставится между словами в предложении и служит для целей, которые мы рассмотрим ниже.

Тире в бессоюзных сложных предложениях

Когда употребляется тире	Как проверить	Пример
Части сложного предложения имеют противопоставление друг другу	Можно подставить союзы «а», «но».	На улице жарко дома прохладно. Или: На улице жарко дома прохладно.
Главное предложение имеет значение времени или условия	Можно подставить в начало предложения союзы «если», «когда».	Ласточки летают высоко будет жарко. Или: ласточки летают высоко, будет жарко.
Придаточная часть следует из первой части	Между частями можно подставить союзы «так что», «вследствие чего», «поэтому».	Он весь месяц работал усердно ему начислили премию. Или: Он весь месяц работал усердно ему начислили премию.
Вторая часть предложения сравнивает первую с чем-либо	Вместо тире можно подставить союзы «будто», «словно».	Смеётся колокольчики звенят. Или: Смеётся колокольчики звенят.
Придаточное предложение имеет значение присоединения	Можно употребить слова «такой», «таков», «так», «это».	Каждое утро мама пьёт крепкий кофе её ежедневный ритуал. Или: Каждое утро мама пьёт крепкий кофе её ежедневный ритуал.
Если в бсп происходит быстрая смена событий	Можно поставить союз «и», а также слова «и внезапно», «и неожиданно».	Раздался выстрел из винтовки самолёт начал падать. Или: Раздался выстрел самолёт начал падать.

Тире и однородные члены предложения

В случаях, когда однородные члены предложения находятся в середине предложения, после них всегда ставится тире, вне зависимости от того, какое слово идёт дальше.

Подробнее об этом читайте в отдельной статье.

Тире при обособлении членов простого предложения с поясняющим значением

В простом предложении с поясняющим значением ставится запятая, если есть один из союзов:

• «а именно»;
• «то есть»;
• «или» (в значении то есть);
• «как то».

Если же такие союзы в подобном предложении отсутствуют, то вместо запятой ставят тире.

Другие случаи употребления тире

Если подлежащее выражено существительным, а сказуемое инфинитивом.

Перед словами: «это», «значит», «то есть» и так далее – в том случае, если сказуемое выражено существительным.

В некоторых случаях тире используется при оформлении прямой речи, например, перед словами автора.

Советы по использованию двоеточия

1. Разделяйте приведения определений от их значений.

Использование двоеточия для разделения определения от его значения является основой в математике. Например, «x: число, которое удовлетворяет уравнению x + 5 = 10» является примером определения.

2. Используйте двоеточие перед приведением фактов или утверждений.

Вы можете использовать двоеточие, чтобы разделить утверждение от следующей за ним информации. Например, «число Pi: это константа, которая представляет отношение длины окружности к ее диаметру» — где цитата описывает факт, который следует за утверждением.

3. Используйте двоеточие для разделения эпитетов или свойств от предмета.

Например, «округлый мяч: диаметр 22 сантиметра» указывает на свойства мяча, а не на его функцию или сущность.

4. Не используйте двоеточие вместо знака деления.

В математике есть знак деления, обозначаемый чертой, а для разделения чисел или числовых выражений с помощью двоеточия необходимо добавить дополнительный контекст.

5. Используйте двоеточие для разделения строк таблицы.

В HTML-коде вы можете использовать двоеточие для разделения строки таблицы, чтобы сделать таблицу более читабельной.

6. Избегайте излишнего использования двоеточия.

Используйте двоеточие только тогда, когда оно необходимо для формулировки определения, утверждения, свойства или при разделении строк таблицы.

Логика и алгебра

Логика и алгебра — это две тесно связанные области математики, которые находят свое применение как в теоретических исследованиях, так и в практических применениях. Они помогают нам рассуждать о формальных системах и процессах, обнаруживать закономерности и строить логические выводы.

Логика, в свою очередь, изучает правила рассуждений и вывода, а также формальные языки, которые нам позволяют выразить определенные понятия

Важно помнить, что логика не занимается изучением содержания этих понятий, а только их формой

Алгебра же, изучает алгебраические структуры, такие как группы, кольца и поля, а также операции и отношения между ними. Она помогает нам решать задачи в различных областях, таких как физика, химия, экономика и т.д.

Обе области математики тесно связаны друг с другом и находят свое применение вместе. Например, алгебраические структуры могут быть описаны через формальные языки и правила логики. Часто для решения задач требуется использовать комплексный подход, который сочетает в себе знания из обеих областей.

Двоеточие в цитатах и ссылках

Когда дело доходит до написания документов, статей и других типов академического или профессионального письма, важно понимать, как правильно использовать пунктуацию. Двоеточие — это мощный знак препинания, который может добавить ясности и выразительности вашему письму, особенно при использовании в цитатах и ссылках

Вот несколько важных моментов, которые нужно знать об использовании двоеточий в этом контексте:

• Используйте двоеточие для начала цитаты. Если вы цитируете чужие слова в своем письме, вы можете использовать двоеточие, чтобы создать цитату и придать ей контекст. Например: По словам Альберта Эйнштейна: «Воображение важнее знаний».
• Используйте двоеточие между заголовком и подзаголовком книги или статьи: При цитировании книги или статьи, обычно используется двоеточие для разделения заголовка и подзаголовка. Например: The Power of Now: A Guide to Spiritual Enlightenment
• Используйте двоеточие для разделения места и издателя в цитировании книги: При цитировании книги, это стандартная практика — указывать город и издателя книги после названия. Используйте двоеточие, чтобы разделить две части информации. Например: (Нью-Йорк: Penguin Random House)

Вот пример того, как эти правила могут сочетаться в цитировании книги:

Формат	Пример
Фамилия автора, Имя. Название книги: Подзаголовок. Издатель, год публикации.	Роулинг, Дж. К. Гарри Поттер и Философский камень: иллюстрированное издание. Arthur A. Levine Books, 2015.

Следуя этим рекомендациям по использованию двоеточий в цитатах и ссылках, вы можете гарантировать, что ваше письмо будет четким, профессиональным и должным образом отформатированы.

Сложные суждения[править]

Для построения сложных суждений в логиках с векторной семантикой рассматриваются следующие типы логических связок: 1-я и 2-я форма конъюнкции, 1-я и 2-я форма дизъюнкции и две формы отрицания.

Определение 1. Первой формой конъюнкции двух суждений a{\displaystyle a} и b{\displaystyle b} называется суждение c=a&b{\displaystyle c=a\&b}, значения аспектов истинности которого определяются по правилу:

ci=ai∙bi{\displaystyle c^{i}=a^{i}\bullet b^{i}}, если аспект позитивный;

ci=ai⊕bi{\displaystyle c^{i}=a^{i}\oplus b^{i}}, если аспект негативный.

Определение 2. Второй формой конъюнкции двух суждений a{\displaystyle a} и b{\displaystyle b} называется суждение c=a&2b{\displaystyle c=a\&_{2}b}, значения аспектов истинности которого определяются по правилу:

ci=ai∙bi{\displaystyle c^{i}=a^{i}\bullet b^{i}}.

Определение 3. Первой формой дизъюнкции двух суждений a{\displaystyle a} и b{\displaystyle b} называется суждение c=a∨b{\displaystyle c=a\lor b}, значения аспектов истинности которого определяются по правилу:

ci=ai⊕bi{\displaystyle c^{i}=a^{i}\oplus b^{i}}, если аспект позитивный;

ci=ai∙bi{\displaystyle c^{i}=a^{i}\bullet b^{i}}, если аспект негативный.

Определение 4. Второй формой дизъюнкции двух суждений a{\displaystyle a} и b{\displaystyle b} называется суждение c=a∨2b{\displaystyle c=a\lor _{2}b}, значения аспектов истинности которого определяются по правилу:

ci=ai⊕bi{\displaystyle c^{i}=a^{i}\oplus b^{i}}.

Здесь x∙y{\displaystyle x\bullet y}- t-норма, x⊕y{\displaystyle x\oplus y} — t-конорма (s-норма) в инфиксной записи. Примерами являются пары функций:

x∙y=min(x,y){\displaystyle x\bullet y=min(x,y)};

x⊕y=max(x,y){\displaystyle x\oplus y=max(x,y)};

x∙y=max(,x+y−1){\displaystyle x\bullet y=max(0,x+y-1)};

x⊕y=min(1,x+y){\displaystyle x\oplus y=min(1,x+y)};

x∙y=xy{\displaystyle x\bullet y=xy};

x⊕y=x+y−xy{\displaystyle x\oplus y=x+y-xy}.

Первые формы конъюнкции и дизъюнкции — это обобщения классических конъюнкции и дизъюнкции на векторный случай. Вторые возможны только в векторном случае.

Определение 5. Первой формой отрицания (отрицанием в форме перестановки) называется суждение ¬a{\displaystyle \neg a}, истинность которого получается из ‖a‖{\displaystyle \|a\|} путём перестановки местами значений позитивных и негативных компонентов (позитивные компоненты объявляются негативными, а негативные позитивными). Например, для VTF{\displaystyle V^{\mathrm {TF} }}-логик это выглядит как: ‖¬a‖=⟨a−;a+⟩{\displaystyle \|\neg a\|=\langle a^{-};a^{+}\rangle }.

Эта форма отрицания привязана к содержательному смыслу аспектов истинности и потому применима не для всех в.и.

Определение 6. Второй формой отрицания является отрицание в форме дополнения:
‖∼a‖=⟨1−a1;1−a2;…;1−an⟩{\displaystyle \|\!\sim \!a\|=\langle 1-a^{1};1-a^{2};…;1-a^{n}\rangle }.

Для этой формы отрицания выполняются законы де Моргана в виде:

‖∼(a&b)‖=‖∼a∨∼b‖{\displaystyle \|\!\sim \!\!(a\&b)\|=\|\!\sim \!\!a\lor \!\sim \!\!b\|};

‖∼(a∨b)‖=‖∼a&∼b{\displaystyle \|\!\sim \!\!(a\lor b)\|=\|\!\sim \!\!a\&\!\sim \!\!b}\|;

‖∼(a&2b)‖=‖∼a∨2∼b‖{\displaystyle \|\!\sim \!\!(a\&_{2}b)\|=\|\!\sim \!\!a\lor _{2}\!\sim \!\!b\|};

‖∼(a∨2b)‖=‖∼a&2∼b‖{\displaystyle \|\!\sim \!\!(a\lor _{2}b)\|=\|\!\sim \!\!a\&_{2}\!\sim \!\!b\|}.

Данная форма отрицания может использоваться для любых в.и.

Геометрические фигуры и формулы

Геометрические фигуры – это самые базовые объекты геометрии, которые могут быть описаны определенными формулами. Каждая фигура имеет свои характеристики и свойства, которые могут быть использованы для решения различных задач.

Треугольник – это геометрическая фигура, которая описывается формулой P=a+b+c, где P – периметр треугольника, a, b, c – длины сторон треугольника. Треугольник используется для измерения расстояния между двумя точками на карте, а также для нахождения площади земельного участка.

Прямоугольник – это геометрическая фигура, которая описывается формулой S=ab, где S – площадь прямоугольника, а и b – длины сторон прямоугольника. Прямоугольник широко используется в геометрии, строительстве, дизайне и архитектуре.

1. Круг, треугольник и прямоугольник – это основные геометрические фигуры;
2. Каждая фигура имеет свои уникальные свойства и формулы;
3. Фигуры могут быть использованы для решения различных задач в различных областях;
4. Математические формулы – это основа, на которой базируется геометрия и другие дисциплины.

Двоеточие как пунктуационный знак

Двоеточие — один из основных пунктуационных знаков, который широко используется в русском языке для обозначения различных отношений между частями предложения.

Основные случаи использования двоеточия:

Перечисление элементов или разъяснение чего-либо:

Пример
Объяснение
На столе лежали разные фрукты: яблоки, груши, бананы.
Двоеточие отделяет перечисление фруктов от главной части предложения.
С любым решением важно соблюдать несколько правил: учитывать все аспекты проблемы, обдумывать возможные последствия.
Двоеточие отделяет перечисление правил от основной части предложения.

Обращение к адресату:

Пример	Объяснение
Дорогой друг: я хотел бы поговорить с тобой.	Двоеточие отделяет обращение к адресату от основной части предложения.
Дамы и господа: объявляется перерыв на кофе.	Двоеточие отделяет обращение к адресатам от основной части предложения.

Цитирование речи или мысли:

Пример	Объяснение
Он произнес: «Я буду стараться делать все возможное».	Двоеточие отделяет цитату от говорящего.
Она подумала: «Мне нужно принять решение».	Двоеточие отделяет цитату от мысли говорящего.

Кроме указанных выше случаев, двоеточие используется в других ситуациях, например, при переходе к прямой речи, при обозначении диалогов и т.д

Важно помнить, что правильное использование двоеточия помогает ясно выражать свои мысли и структурировать текст

Правила записи формул

При записи формул придерживаются следующих правил.

1. Внешние скобки в формуле можно опускать. Например, вместо %%(A \lor B)%% пишем %%A \lor B%%.

2. Как и в арифметике, в алгебре высказываний у каждой операции есть свой приоритет. Приоритеты логических знаков, расположенные в порядке убывания, следующие:

   $$
   \overline{ }, \land, \lor, \rightarrow, \leftrightarrow.
   $$

   Приоритеты логических операций можно изменить, используя скобки.

Каждый предшествующий знак является «сильнее» последующего. Поэтому вместо записи %%(A \land B) \lor C%% можно писать %%A \land B \lor C%%, вместо записи %%A \leftrightarrow (B \lor C)%% — %%A \leftrightarrow B \lor C%%.

3. Если в формуле %%X = A \land B \land C \land \ldots \land Z%% опущены скобки, то подрузамевается левосторонняя расстановка скобок и считается, что %%X = \bigg(\Big((A \land B) \land C\Big) \land \ldots\bigg)\land Z%%. Аналогично для подобных формул, имеющих знак %%\lor%%, %%\rightarrow%% или %%\leftrightarrow%%.

Примеры

Пользуясь правилами %%1-3%% восстановить скобки в формуле

$$
X = A \lor B \land C \leftrightarrow A \rightarrow B \rightarrow C
$$

По правилам %%1-3%% имеем %%X = \Bigg(\Big(A \lor (B \land C)\Big) \leftrightarrow \Big((A \rightarrow B) \rightarrow C\Big)\Bigg)%%.

Пользуясь правилами %%1-3%% опустить лишние скобки в формуле
$$
X = \Bigg((A \leftrightarrow B) \lor \Big((A \land B) \land C\Big) \rightarrow \Big((B \lor C) \land A\Big)\Bigg)
$$

Решение, над знаком равно будут указаны номера правил которые применяются.

$$
\begin{array}{ll}
X &= \Bigg((A \leftrightarrow B) \lor \Big((A \land B) \land C\Big) \rightarrow \Big((B \lor C) \land A\Big)\Bigg) \overset{1}{=}\\
&\overset{1}{=} (A \leftrightarrow B) \lor \Big((A \land B) \land C\Big) \rightarrow \Big((B \lor C) \land A\Big) \overset{3}{=}\\
&\overset{3}{=} (A \leftrightarrow B) \lor (A \land B \land C) \rightarrow \Big((B \lor C) \land A\Big) \overset{2}{=}\\
&\overset{2}{=} (A \leftrightarrow B) \lor A \land B \land C \rightarrow \Big((B \lor C) \land A\Big) \overset{2}{=}\\
&\overset{2}{=} (A \leftrightarrow B) \lor A \land B \land C \rightarrow (B \lor C) \land A.
\end{array}
$$

Восклицательный знак — выражение сильных эмоций

Восклицательный знак (!) является одним из наиболее распространенных знаков препинания и используется для выражения сильных эмоций, удивления, радости, гнева, страха и других сильных чувств. Он помогает придать тексту эмоциональную окраску и выделить важные моменты.

Восклицательный знак может использоваться в различных видах текстов. В художественной литературе он часто используется для передачи эмоций персонажей и создания напряженности. Например:

• «Какая прекрасная новость!» — воскликнула она и обняла друга.
• «Она сказала «Да!»» — радостно крикнул Джон.

В деловой и официальной корреспонденции восклицательный знак может использоваться для подчеркивания важности или срочности информации. Например:

• Уведомление: Встреча переносится на завтра!
• Всем сотрудникам компании: Успех нашего проекта превзошел все ожидания!

В письмах и текстовых сообщениях восклицательный знак может использоваться для выражения эмоций. Например:

• Привет! Я так рада увидеть тебя!
• Спасибо огромное за подарок!

Восклицательный знак также может использоваться в названиях и заголовках, чтобы привлечь внимание читателя. Например:

• Уникальное предложение: получите скидку 50%!
• Как стать успешным предпринимателем!

Важно помнить, что восклицательный знак следует использовать с умеренностью. Большое количество восклицательных знаков может вызвать впечатление крика или недостатка эмоционального контроля

Поэтому рекомендуется использовать его сознательно и в нужных местах, чтобы не утратить эффективность его использования.

Что такое двоеточие?

В пунктуации русского языка ряд небуквенных орфографических символов используется для разделения слов, словосочетаний и простых предложений в составе сложного. Эти элементы в письменной речи употребляются как разделительные знаки препинания:

• запятая
• точка с запятой
• тире
• двоеточие

Рассмотрим разделительный знак препинания двоеточие, для чего он используется в предложении.

Определение из Википедии

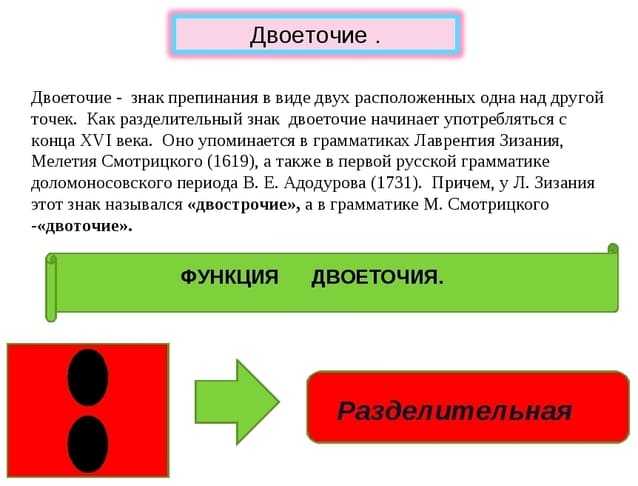
Двоето́чие (:) — знак препинания в виде двух расположенных одна над другой точек, употребляемый для указания на то, что часть текста после него связана причинными, пояснительными и т. п. смысловыми отношениями с частью текста перед ним.

В русском языке этот пунктуационный знак препинания востребован как в простом, так и в сложном предложении.

Двоеточие ставится в следующих случаях:

• после обобщающего слова в простом предложении с последующими однородными членами;
• в бессоюзном сложном предложении;
• в предложении с прямой речью.

Перед этим пунктуационным знаком тон голоса понижается и делается значительная интонационная пауза.

Вопросительный знак — обозначение интереса и ожидания ответа

Вопросительный знак — это знак препинания, который ставится в конце предложения, чтобы обозначить вопросительный характер высказывания. Он является одним из наиболее узнаваемых знаков препинания и часто используется в повседневной речи.

Вопросительный знак используется для выражения интереса, неопределенности или ожидания ответа на заданный вопрос. Он указывает на необходимость получения информации от адресата. Без вопросительного знака предложение становится утвердительным и теряет свой вопросительный смысл.

Вопросительный знак обычно ставится в конце предложения после вопросительного слова или перед глаголом-сказуемым в вопросительном предложении. Он помогает читателю или слушателю понять, что предложение является вопросом и требует ответа.

Примеры использования вопросительного знака в речи:

1. Какой день недели сегодня?
2. Что ты будешь делать в выходной?
3. Где находится ближайшая аптека?

Вопросительное слово	Пример
Кто	Кто пришел на вечеринку вчера?
Что	Что ты собираешься приготовить на ужин?
Куда	Куда ты собираешься в отпуск?

Вопросительный знак является важным средством общения, позволяющим уточнить информацию и поддерживать диалог. Его использование помогает создать коммуникацию между говорящим и слушающим. Ставить вопросительный знак в конце вопроса — это правило русского языка, которое стоит соблюдать, чтобы передать свои мысли и намерения ясно и четко.