Вариант 3
Когда я задумываюсь о математике, мое воображение наполняется яркими красками и магическими числами. Математика – это не просто набор формул и уравнений, она пронизывает каждый аспект моей жизни
В этом сочинении я хочу рассказать о том, как математика влияет на мою жизнь и почему я считаю ее невероятно важной
Математика – это язык, на котором говорит сама природа. Она помогает мне понимать и анализировать мир вокруг меня. Когда я изучаю геометрию, я узнаю о формах и пространстве, которые окружают меня повсюду – в строениях, в природе, в искусстве. Математика позволяет мне понять, почему солнечные лучи падают под определенным углом или как прекрасные фигуры возникают в геометрических узорах.
Математика также помогает мне развивать навыки решения проблем. Когда я сталкиваюсь с сложными задачами, математика учит меня анализировать информацию, находить паттерны и применять логику для нахождения верного решения. Эти навыки пригодятся мне не только в школе, но и во всей моей жизни. Я уверен(а), что математика учит меня быть настойчивым(ой) и не бояться вызовов, а также развивает мою способность мыслить критически и аргументировать свою позицию.
Однажды, когда мы с семьей путешествовали, мы решили сами составить маршрут посещения достопримечательностей. Мы использовали карты и навигационные инструменты, чтобы определить расстояния между городами и время, которое мы проведем в пути. Благодаря математике, мы смогли спланировать наше путешествие так, чтобы посетить все места, которые хотели увидеть, и не тратить время на лишние переезды.
Математика– это неотъемлемая часть моей жизни, которая пронизывает все ее сферы. Она помогает мне понимать мир, анализировать информацию и принимать обоснованные решения. Благодаря математике я развиваю свой ум, логическое мышление и способность решать проблемы. Я верю, что знания математики открывают передо мной множество возможностей и делают меня уверенным(ой) в своих силах. Поэтому я с радостью учусь математике и стремлюсь применять ее принципы и методы не только в учебе, но и в повседневной жизни.
Мне нравится1.1 k.Не нравится551
Действие №4: Учтите возможные последствия
При проведении операций прибавления и отнимания необходимо всегда учитывать возможные последствия этих действий. Даже если кажется, что изменение числа незначительное, оно может иметь серьезные последствия в определенных контекстах.
Перед началом любой операции прибавления или отнимания рекомендуется провести предварительный анализ и оценку возможных последствий. Особенно это касается финансовых или материальных операций, когда даже незначительное изменение может повлечь за собой серьезные финансовые потери или проблемы.
Также важно учитывать контекст и цель проводимых операций. Например, если речь идет о математической задаче или задаче программирования, необходимо учитывать условия задачи, возможные ограничения и требования
Неправильное прибавление или отнимание может привести к неверному решению задачи.
Кроме того, при работе с числами необходимо учитывать точность представления чисел. В некоторых случаях округление результатов прибавления или отнимания может привести к потере точности и некорректному результату.
В общем, перед проведением операций прибавления или отнимания необходимо тщательно взвесить все возможные последствия и учесть особенности контекста операции. Это поможет избежать ошибок и принять правильное решение.
Слайд 8 Высказывания известных людей о математике Как и другие науки, математика
возникла из практических нужд людей: из измерения площадей земельных участков и вместимости сосудов, из счисления времени и их механики.
Ф. Энгельс Великая книга природы написана математическими символами. Г. Галилей Часто говорят, что цифры управляют миром; по крайней мере нет сомнения в том, что цифры показывают, как он управляется. И. ГетеВ природе существует внутренне присущая ей скрытая гармония, отражающаяся в наших умах в виде простых математических законов. Именно этим объясняется, почему природные явления удаётся предсказывать с помощью комбинации наблюдений и математического анализа. Г. Вейль Задача заключается не в том, чтобы учить математике, а в том, чтобы при посредстве математики дисциплинировать ум.
В. ШрадерУмственный труд на уроках математики — пробный камень мышления. В. Сухомлинский

Математическое образование и карьерные возможности
Математическое образование играет важную роль в формировании карьерных возможностей. В современном мире, где технологии играют все более значимую роль, математика становится неотъемлемой частью многих профессий.
Одной из наиболее очевидных областей, в которых математическое образование полезно, является IT-сфера. Программисты, разработчики программного обеспечения и инженеры требуют глубоких знаний в области алгоритмов, структур данных и математической логики для решения сложных задач. Без математического образования эти профессии были бы недоступны.
Математика также широко применяется в финансовой сфере. Финансовые аналитики, трейдеры и актуарии используют математические модели для анализа рисков, прогнозирования рынков и принятия решений. Здесь математическое образование помогает принимать обоснованные и эффективные решения на основе численных данных.
Сферой, где математика играет ключевую роль, является научное исследование. Математические модели используются в различных областях науки, включая физику, биологию, экономику и социологию. Ученые используют математические методы для объяснения сложных явлений, построения моделей и предсказания результатов экспериментов.
Кроме того, математические навыки полезны при работе в сфере аналитики данных. Аналитики данных используют статистические методы и математическое моделирование для анализа больших объемов информации и выявления важных трендов и закономерностей.
Математическое образование также может быть полезно в управлении проектами, исследовании операций, логистике и других областях. Важным моментом является то, что математическое образование развивает логическое мышление, творческий подход к решению проблем и абстрактное мышление, что также может быть полезно в любой профессии.
Таким образом, математическое образование открывает множество карьерных возможностей. Оно не только помогает развить аналитические навыки, но и предоставляет инструменты для решения сложных задач и принятия обоснованных решений. Независимо от выбранной профессии, математические знания будут цениться и полезны в современном мире.
Примеры расчетов
При выполнении математических операций без скобок, сначала выполняются действия по приоритету: сначала умножение и деление, затем сложение и вычитание. Рассмотрим несколько примеров расчетов:
- Пример 1: 8 + 6 × 2
- Умножение имеет более высокий приоритет, чем сложение, поэтому сначала выполняем умножение: 8 + 12 = 20
- Пример 2: 14 ÷ 2 + 3
- Операция деления имеет более высокий приоритет, чем сложение, поэтому сначала выполняем деление: 7 + 3 = 10
- Пример 3: 12 — 3 × 4
- Умножение имеет более высокий приоритет, чем вычитание, поэтому сначала выполняем умножение: 12 — 12 = 0
ВыражениеПриоритет операцииРезультат
| 3 + 4 × 2 | Умножение | 11 |
| 8 — 12 ÷ 6 | Деление | 6 |
| 9 ÷ 3 × 2 | Деление | 6 |
Вопрос-ответ:
Какой приоритет операций в математике?
Приоритет операций в математике определяется следующим порядком: первыми выполняются операции в скобках, затем возведение в степень, умножение и деление (выполняются в порядке, в котором они встречаются слева направо), и в конце сложение и вычитание (выполняются в порядке, в котором они встречаются слева направо). Если в выражении несколько типов операций с одинаковым приоритетом, то они выполняются слева направо.
Можно ли изменить порядок выполнения операций?
Да, порядок выполнения операций может быть изменен при помощи использования скобок. Например, если нужно выполнить сложение перед умножением, то в скобки помещаются слагаемые, которые нужно сложить, а затем скобки умножают на другой множитель.
Как правильно выполнить операции с дробями?
Для выполнения операций с дробями нужно сначала привести их к общему знаменателю, затем производить операции с числителями. Результат дроби сокращается до необходимой формы.
Что такое алгебраические выражения?
Алгебраическое выражение представляет собой комбинацию чисел, переменных и арифметических операций, которые могут быть выражены в виде многочленов. В алгебраических выражениях используются такие операции, как сложение, вычитание, умножение, деление и возведение в степень.
Что такое многочлены?
Многочлен — это алгебраическое выражение, содержащее переменные и коэффициенты, умноженные на одну или несколько степеней переменных. Например, х² + 2х — 1 это многочлен второй степени.
Нужно ли обязательно использовать скобки?
Использование скобок определяется необходимостью явного выражения приоритета операции. Если операция выполняется до других операций, она не требует использования скобок. Однако в некоторых случаях скобки используются для упрощения записи выражения.
Практические применения
Действие, которое выполняется первым без скобок, является базовым принципом математики и используется в различных областях.
В экономике, например, порядок действий без скобок поможет исследователям решить сложные задачи, связанные с финансовыми моделями и прогнозами. Использование правильного порядка действий позволяет проводить математические расчеты для определения процентных ставок, финансовых инвестиций и прогнозирования экономического развития компаний.
В физике порядок действий без скобок имеет большое значение при решении задач, связанных с движением тел и законами сохранения энергии. Чтобы правильно рассчитать общую энергию тела, необходимо использовать правильный порядок действий.
Равным образом, порядок действий без скобок используется в программировании и статистике. Например, при использовании программного обеспечения для обработки данных необходимо использовать правильный порядок математических операций для получения точных результатов.
В целом, понимание порядка действий без скобок является необходимым навыком в жизни. Независимо от того, каким образом применяется математика, правильный порядок действий без скобок помогает получить точные результаты и избежать ошибок.
Где нужна математика в жизни
Можно выделить сферы, в которых может понадобиться «царица наук»:
- в быту;
- в учебе;
- для карьеры;
- для хобби и саморазвития.
Давайте разберем каждую сферу подробнее.
Быт
Применение математики в жизни напрямую связано с бытовыми моментами:
- «подбить» ежедневные и ежемесячные траты;
- высчитать, сколько плитки и обоев понадобится для ремонта;
- подсчитать калорийность рациона;
- рассчитать физическую активность;
- проанализировать, куда и сколько вложить средств.
Получается, что мы решаем разные бытовые задачки и применяем математические знания, сами того не замечая. Однако, как быть, если вы категорически не хотите и не можете решать сами бытовые мелочи? К счастью, в наше время компьютеров и смартфонов все эти задачи может решить техника:
- подсчитать количество калорий, ингредиентов, рассчитать физическую активность помогут специальные приложения на телефоне;
- подсчитать количество строительных материалов может работник в магазине в специальной компьютерной программе, вам достаточно лишь сказать размеры помещения;
- рассчитать стратегию вклада денежных средств поможет умная банковская система в личном кабинете вашего банка.
Учеба
Если говорить о значении математики в жизни и в быту, то центральное место занимает, конечно, учеба. Знакомство с математикой начинается еще в детском саду с освоения арифметики, потом начинаются контрольные работы в школе и зачеты и курсовые в вузе. В наших учебных заведениях математику изучают даже на самых гуманитарных направлениях.
Полностью избежать математики в учебе не получится. А вот облегчить себе учебу, а соответственно и жизнь можно:
- если вы учитесь по гуманитарному профилю, то можно попробовать вместо очередной контрольной работы подготовить доклад по истории математики;
- если вы получаете второе образование, то можно попытаться упросить преподавателя зачесть ваши предыдущие математические работы;
- можно попытаться поучаствовать в активностях, связанных с математикой. Например, поучаствовать в математической ярмарке, подготовить творческий номер для недели математики. Участие в таких мероприятиях поможет получить бонусы и дополнительные баллы по этому предмету;
- учащиеся, которые недолюбливают математику, могут объединиться в группы, где можно вместе решать задачи и помогать друг другу;
- можно найти репетитора, который сможет не просто объяснить сложные моменты, но и даже увлечь самой дисциплиной.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы.

Карьера
Математика нужна не только в тех профессиях, которые непосредственно с ней связаны. Формулы в Excel, тесты на определение уровня IQ, решение логических задач на собеседовании — математика нужна даже там, где казалось ее быть не может.
Чтобы быть хоть немного подготовленным к подобным испытаниям, важно периодически освежать в памяти основные моменты: повторять таблицу умножения, решать логические тесты и задачи и т.д
Хобби и саморазвитие
Математика в повседневной жизни человека может быть в качестве хобби да и просто для саморазвития.
Если вы хотите развить математические способности и регулярно делать зарядку для ума, можете присмотреться к:
- ментальной арифметике. Она улучшает память и увеличивает быстроту реакции.
- тематической литературе. Есть много интересных книг по математике, написанных простым языком. Например, «Математика для гуманитариев» Савватеева, «Великая теорема Ферма» Сингха, «Предисловие к математике» Успенского;
- ребусам, логическим задачам и головоломкам.
Математика развивает аналитическое мышление
Математика – это не только наука о числах, но и мощный инструмент для развития аналитического мышления. Решение математических задач требует логического и аналитического мышления, способности анализировать и рассуждать.
Изучение математики помогает развить навыки абстрактного мышления. Решая математические задачи, мы учимся видеть общие закономерности и правила, работать с абстрактными понятиями и символами. Это способствует развитию мыслительных процессов, которые могут быть применены не только в математике, но и в других областях знаний.
Еще одним аспектом развития аналитического мышления через изучение математики является способность формулировать и решать сложные проблемы. В процессе решения математических задач мы учимся разбивать сложные проблемы на более простые подзадачи, искать паттерны и анализировать. Эти навыки могут быть применены в реальной жизни для решения различных задач и проблем.
Изучение математики также способствует развитию критического мышления. Математика требует точности и логичности, и ошибки могут привести к неправильным ответам. При решении задач необходимо внимательно анализировать условия и использовать логические законы для достижения правильного результата. Это помогает развить навыки критического мышления и оценки информации.
Таким образом, изучение математики не только позволяет узнать о числах и формулах, но и развивает аналитическое мышление. Она помогает улучшить навыки абстрактного мышления, формулирования и решения проблем, а также критического мышления. Поэтому математика имеет огромное значение в развитии интеллекта и способностей мыслить логически.
Основные арифметические действия
Сначала решаем выражение в первых скобках. Помним, что сначала идет умножение, затем вычитание. Задача 1.
Особенности сложения и вычитания Сложение и вычитание: какая операция приоритетнее? В математике существует определенный порядок выполнения операций, который помогает решить сложные выражения. В рамках этого порядка определен приоритет различных операций, включая сложение и вычитание.
Но какая из этих операций приоритетнее? По правилам математики приоритет операций определяется так: сначала выполняется сложение и вычитание, а затем умножение и деление. Это означает, что при решении выражения нужно сначала выполнить все сложения и вычитания, а затем уже перемножить или разделить полученные результаты. Приоритет операций можно изменить с помощью скобок. Когда выражение в скобках, его нужно выполнить первым, игнорируя общий порядок операций.
А скобки имеют приоритет выше, чем умножение и деление. Все, что записано в скобках, вычисляется в первую очередь. Если скобки вложенные, то сначала вычисляется выражение во внутренних скобках. И это непреложное правило. Как только выражение в скобках вычислено, скобки пропадают, а на их месте возникает число.
Варианты раскрытия скобок с неизвестными здесь не рассматриваются. Так делают до тех пор, пока все они не исчезнут из выражения. Это как коробочки с конфетами в большом мешке. Пять конфет из коробочки сразу заслали отличнице Люде, которая приболела и в празднике не участвует. Потом добавить в мешок еще 2 пучка конфет, чтобы можно было поделить на троих детей без драки.
Признаки деления на 3 в данной статье не рассматриваются. Если вычислить первые скобки в выражении и переписать все заново, пример станет короче. Метод не быстрый, с большим расходом бумаги, зато удивительно эффективный. Заодно тренирует внимательность при переписывании. Пример приводится к виду, когда остается только один вопрос, сначала умножение или сложение без скобок.
То есть к такому виду, когда скобок уже и нет. Но ответ на этот вопрос уже есть, и нет смысла обсуждать, что идет сначала — умножение или сложение. Потому что именной ей придется объяснять второкласснику, что бывают отрицательные числа. Или рушить авторитет «МарьиВановны», которая сказала, что: «Нужно слева направо и по порядку». Он не совсем по рассматриваемой теме, что сначала — умножение или сложение.
Порядок выполнения арифметических действий в выражениях со скобками
Выражения часто содержат . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками, формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.
Пример.
Выполните указанные действия 5+(7−2·3)·(6−4):2.
Решение.
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3. В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1. Переходим ко второму выражению в скобках 6−4. Здесь лишь одно действие – вычитание, выполняем его 6−4=2.
Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2. В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6. На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2.
Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6.
Ответ:
5+(7−2·3)·(6−4):2=6.
Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Пример.
Выполните действия в выражении 4+(3+1+4·(2+3)).
Решение.
Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3). Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5. Подставив найденное значение, получаем 3+1+4·5. В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24. Исходное значение, после подстановки этого значения, принимает вид 4+24, и остается лишь закончить выполнение действий: 4+24=28.
Ответ:
4+(3+1+4·(2+3))=28.
Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.
Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1. Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1, то после этого исходное выражение примет вид (4+(4+1)−1)−1. Опять выполняем действие во внутренних скобках, так как 4+1=5, то приходим к следующему выражению (4+5−1)−1. Опять выполняем действия в скобках: 4+5−1=8, при этом приходим к разности 8−1, которая равна 7.
Примеры сложения и вычитания целых чисел
Первое чему следует научиться это складывать и вычитать целые числа с помощью координатной прямой. Совсем необязательно рисовать координатную прямую. Достаточно воображать её в своих мыслях и видеть, где располагаются отрицательные числа и где положительные.
Рассмотрим следующее простейшее выражение
1 + 3
Значение данного выражения равно 4
1 + 3 = 4
Этот пример можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1, нужно сдвинуться вправо на три шага. В результате мы окажемся в точке, где располагается число 4. На рисунке можно увидеть, как это происходит:
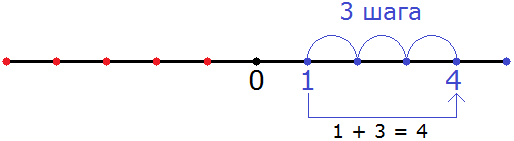
Знак плюса в выражении 1 + 3 указывает нам, что нужно двигаться вправо в сторону увеличения чисел.
Пример 2. Найдём значение выражения 1 − 3
Значение данного выражения равно −2
1 − 3 = −2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −2. На рисунке можно увидеть, как это происходит:
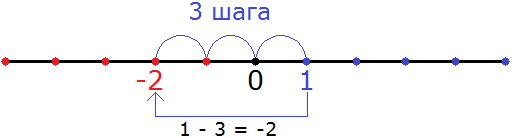
Знак минуса в выражении 1 − 3 указывает нам, что нужно двигаться влево в сторону уменьшения чисел.
Вообще, если осуществляется сложение, то нужно двигаться вправо в сторону увеличения. Если же осуществляется вычитание, то нужно двигаться влево в сторону уменьшения.
Пример 3. Найти значение выражения −2 + 4
Значение данного выражения равно 2
−2 + 4 = 2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на четыре шага. В результате мы окажемся в точке, где располагается положительное число 2
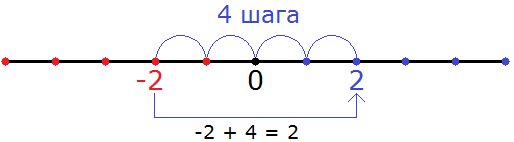
Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на четыре шага, и оказались в точке, где располагается положительное число 2.
Пример 4. Найти значение выражения −1 − 3
Значение данного выражения равно −4
−1 − 3 = −4
Этот пример опять же можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −4
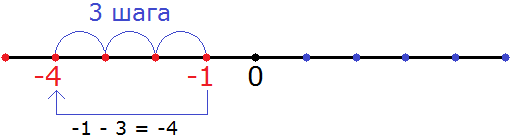
Видно, что мы сдвинулись из точки где располагается отрицательное число −1 в левую сторону на три шага, и оказались в точке, где располагается отрицательное число −4.
Пример 5. Найти значение выражения −2 + 2
Значение данного выражения равно 0
−2 + 2 = 0
Этот пример можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на два шага. В результате мы окажемся в точке, где располагается число 0
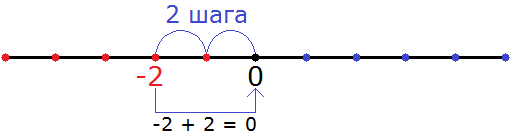
Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на два шага и оказались в точке, где располагается число 0.
Слайд 12Применение математики в пекарне
Ученица 5 класса Шиндина А. беседовала с пекарем ТОО «Каменка-1: — Пекарь выпекает различные виды хлебобулочных изделий.
С того времени, как человек научился выпекать хлеб, технология его производства значительно изменилась, однако профессия пекаря по-прежнему осталась уважаемой и востребованной. Математика необходима пекарю, так как ему нужно рассчитать, сколько необходимо взять муки, чтобы получилась нужная масса теста для определенного количества хлеба, булочек, батонов. Задача.Для выпечки 1 булки хлеба требуется 0,547 кг муки. Сколько муки необходимо взять для выпечки 80 булок хлеба?Решение. 0,547•80=43,76 кг муки

Работа и карьера
В финансовой сфере, математика помогает в анализе данных и прогнозировании финансовых результатов. Финансовые аналитики используют математические модели и статистику для прогнозирования изменений в экономике, а также для оценки рисков и принятия финансовых решений.
В инженерии, математика необходима для проектирования и создания различных инженерных систем и технологий. Знание математических законов и формул позволяет инженерам создавать эффективные решения для сложных технических задач.
В информационных технологиях, математика играет важную роль в разработке алгоритмов и программировании. Математические методы используются для решения проблем оптимизации, обработки данных и разработки искусственного интеллекта.
В маркетинге, математические модели используются для анализа поведения потребителей, определения целевой аудитории, расчета эффективности рекламных кампаний и принятия решений о размещении продукта на рынке.
В медицине, математические модели используются для предсказания распространения инфекционных заболеваний, разработки новых лекарств и методов лечения, а также для анализа медицинских данных и определения признаков болезней.
| Сфера работы | Примеры применения математики |
|---|---|
| Финансы | Анализ финансовых данных, прогнозирование роста и падения акций, оценка рисков и принятие финансовых решений |
| Инженерия | Проектирование и разработка инженерных систем, создание математических моделей и расчеты для оптимизации технических процессов |
| Информационные технологии | Разработка алгоритмов и программирование, использование математических методов для решения сложных задач и создания искусственного интеллекта. |
| Маркетинг | Анализ данных о поведении потребителей, определение целевой аудитории, расчет эффективности рекламных кампаний и оптимального размещения продукта |
| Медицина | Разработка математических моделей для предсказания распространения инфекций, разработка новых методов лечения и анализ медицинских данных |
Таким образом, математика имеет широкое применение в различных сферах работы, от финансов до медицины, и является необходимым инструментом для успешной карьеры. Понимание математических концепций и умение применять их на практике помогают в решении сложных задач и принятии важных решений.
Практическое применение вычислений в жизни

Вычисления в математике — это неотъемлемая часть нашей повседневной жизни. Мы используем математические вычисления во многих областях, например, в финансах, экономике, строительстве, науке и многих других. Каждый день мы сталкиваемся с вычислениями, которые необходимы для выполнения наших задач и достижения наших целей.
В финансовой сфере вычисления играют ключевую роль. Нам нужно вычислять наш бюджет, доходы, расходы, налоги и так далее. Чтобы справиться с ними, мы используем математические формулы и рассчитываем их с помощью калькулятора или компьютера. Это помогает нам контролировать наши финансы и планировать нашу жизнь.
В строительстве вычисления используются для расчета необходимого количества материалов, запасных частей и ремонтных работ. Это помогает сократить расходы на строительство и выполнить проект в соответствии с бюджетом и сроками.
В науке вычисления играют ключевую роль при проведении исследований. Математические модели и формулы используются для анализа данных, прогнозирования и обработки информации.
В заключение, можно сказать, что математические вычисления не только помогают нам решать наши повседневные задачи, но и служат ключевым инструментом в нашей жизни. Они помогают нам принимать правильные решения, управлять нашим бюджетом и достигать наших целей. Без математических вычислений наш мир стал бы неуправляемым и хаосом.
Вопрос-ответ:
Какие арифметические операции могут выполниться в вычислениях 2 класса?
В вычислениях 2 класса выполняются операции сложения и вычитания чисел до 100 без остатка, а также умножения на однозначное число.
Какие математические навыки и умения развиваются при выполнении вычислений во 2 классе?
Вычисление в 2 классе развивает навыки и умения в счете, арифметических операциях, понимании численных действий, отработке навыков представления и записи чисел.
Какие типы задач на вычисление бывают в математике 2 класса?
В 2 классе на вычисление могут быть предложены задачи на счет, арифметические действия, задачи на соответствие, выбор правильного ответа, сравнение и расстановка чисел в порядке возрастания/убывания.
Какие ошибки чаще всего допускают ученики при решении задач на вычисление во 2 классе?
Ученики могут допускать ошибки при переносе чисел при вычитании, при сложении чисел с использованием перехода через разряд, при умножении на ноль, а также при неправильном определении порядка выполнения арифметических действий.
Как сделать вычисление проще для учеников 2 класса?
Чтобы сделать вычисления проще для учеников 2 класса, нужно использовать наглядные материалы (абак, кубики), позволять детям использовать пальцы для счета, разбивать сложные задачи на несколько простых, останавливаться на каждом действии и проверять свои действия.
Как можно увлечь учеников математикой на уроке вычисления в 2 классе?
Чтобы увлечь учеников математикой на уроке вычисления в 2 классе, можно использовать методики игр и конкурсов, предлагать ребятам решать задачи в игровой форме, использовать реальные примеры и ситуации из жизни, знакомить детей с интересными головоломками и загадками.
Для успешного решения задач на вычисление в математике 2 класса нужно знать таблицу умножения, уметь складывать и вычитать однозначные числа, понимать взаимосвязь между арифметическими действиями, уметь применять наглядные материалы, владеть навыками отработки наиболее распространенных ошибок.


















