Алгоритмический язык - определение термина

Сложность алгоритма

Понятие «сложность» — одно из ключевых в изучении алгоритмов. Оно означает не то, насколько трудно понять тот или иной метод, а ресурсы, затраченные на вычисление. Если сложность высокая, алгоритм будет выполняться медленнее и, возможно, тратить больше аппаратных ресурсов; такого желательно избегать.

Сложность обычно описывают большой буквой O. После нее в скобках указывается значение, от которого зависит время выполнения. Это обозначение из математики, которое описывает поведение разных функций.

Какой бывает сложность. Полностью разбирать математическую O-нотацию, как ее называют, мы не будем — просто перечислим основные обозначения сложности в теории алгоритмов.

O(1) означает, что алгоритм выполняется за фиксированное константное время. Это самые эффективные алгоритмы.
O(n) — это сложность линейных алгоритмов. n здесь и дальше обозначает размер входных данных: чем больше n, тем дольше выполняется алгоритм.
O(n²) тоже означает, что чем больше n, тем выше сложность. Но зависимость тут не линейная, а квадратичная, то есть скорость возрастает намного быстрее. Это неэффективные алгоритмы, например с вложенными циклами.
O(log n) — более эффективный алгоритм. Скорость его выполнения рассчитывается логарифмически, то есть зависит от логарифма n.
O(√n) — алгоритм, скорость которого зависит от квадратного корня из n. Он менее эффективен, чем логарифмический, но эффективнее линейного.

Существуют также O(n³), O(nn) и другие малоэффективные алгоритмы с высокими степенями. Их сложность растет очень быстро, и их лучше не использовать.

Графическое описание сложности. Лучше разобраться в сложности в O-нотации поможет график. Он показывает, как изменяется время выполнения алгоритма в зависимости от размера входных данных. Чем более пологую линию дает график, тем эффективнее алгоритм.

O-нотацию используют, чтобы оценить, эффективно ли использовать ту или иную последовательность действий. Если данные большие или их много, стараются искать более эффективные алгоритмы, чтобы ускорить работу программы.

Определения алгоритма

Единого «истинного» определения понятия «алгоритм» нет.

«Алгоритм — это конечный набор правил, который определяет последовательность операций для решения конкретного множества задач и обладает пятью важными чертами: конечность, определённость, ввод, вывод, эффективность». (Дональд Эрвин Кнут)

«Алгоритм — это всякая система вычислений, выполняемых по строго определённым правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи». (Колмогоров, Андрей Николаевич)

«Алгоритм — это точное предписание, определяющее вычислительный процесс, идущий от варьируемых исходных данных к искомому результату». (Марков, Андрей Андреевич (младший))

«Алгоритм — точное предписание о выполнении в определенном порядке некоторой системы операций, ведущих к решению всех задач данного типа». (Философский словарь / Под ред. М. М. Розенталя)

«Алгоритм — строго детерминированная последовательность действий, описывающая процесс преобразования объекта из начального состояния в конечное, записанная с помощью понятных исполнителю команд». (Николай Дмитриевич Угринович, учебник «Информатика и информ. технологии»)

«Алгоритм — это последовательность действий, направленных на получение определённого результата за конечное число шагов».

«Алгоритм — однозначно, доступно и кратко (условные понятия — названия этапа) описанная последовательность процедур для воспроизводства процесса с обусловленным задачей алгоритма результатом при заданных начальных условиях. Универсальность (или специализация) алгоритма определяется применимостью и надёжностью данного алгоритма для решения нестандартных задач».

«Алгоритм — это понятные и точные предписания исполнителю совершить конечное число шагов, направленных на решение поставленной задачи».

«Алгоритм — это некоторый конечный набор рассчитанных на определённого исполнителя операций в результате выполнения которых через определённое число шагов может быть достигнута поставленная цель или решена задача определённого типа».

«Алгоритм — это последовательность действий, либо приводящая к решению задачи, либо поясняющая почему это решение получить нельзя».

«Алгоритм — это точная, однозначная, конечная последовательность действий, которую должен выполнить пользователь для достижения конкретной цели либо для решения конкретной задачи или группы задач».

«Алгоритм — это точное предписание, которое задает вычислительный (алгоритмический) процесс, начинающийся с произвольного исходного данного и напрвленный на получение полностью определяемым этим исходным данным результата».

Часто в качестве исполнителя выступает компьютер, но понятие алгоритма необязательно относится к компьютерным программам, так, например, чётко описанный рецепт приготовления блюда также является алгоритмом, в таком случае исполнителем является человек.

Применение алгоритмического языка в бизнесе

Алгоритмический язык – это язык программирования, который используется для создания алгоритмов и реализации программных решений. В бизнесе алгоритмический язык имеет широкое применение и может быть полезным инструментом для оптимизации процессов и повышения эффективности работы компании.

Автоматизация бизнес-процессов

Алгоритмический язык позволяет разработать программное обеспечение для автоматизации бизнес-процессов компании. С помощью алгоритмического языка можно создать программу, которая выполняет задачи по сбору и обработке данных, генерации отчетов, управлению запасами и многим другим. Автоматизация бизнес-процессов с помощью алгоритмического языка позволяет сократить время, затраченное на выполнение рутинных задач, и снизить вероятность ошибок.

Анализ данных

Анализ данных является важной задачей для многих компаний. Алгоритмический язык позволяет разработать программные решения для обработки и анализа больших объемов данных

Например, можно создать алгоритм, который проведет анализ данных о продажах и поможет определить рентабельность различных продуктов или каналов продаж.

Прогнозирование и оптимизация

Алгоритмический язык позволяет создавать программы для прогнозирования и оптимизации бизнес-процессов. Например, можно разработать алгоритм, который предсказывает спрос на товары и помогает оптимизировать их складские запасы. Такие программы могут значительно снизить издержки компании и улучшить ее конкурентоспособность.

Создание приложений и интерфейсов

Алгоритмический язык также позволяет создавать приложения и интерфейсы, которые могут быть использованы внутри компании или для взаимодействия с клиентами. С помощью алгоритмического языка можно разработать приложение для управления заказами, систему автоматического уведомления клиентов о статусе доставки или интерфейс для анализа и отслеживания данных.

Примеры инструментов для работы с алгоритмическим языком в бизнесе
Инструмент
Описание

Python
Универсальный язык программирования, который широко используется в бизнесе для разработки программных решений и анализа данных.

R
Язык программирования и среда разработки, направленные на анализ данных и статистическое моделирование.

SQL
Язык структурированных запросов, используемый для работы с базами данных и извлечения информации.

Использование алгоритмического языка в бизнесе позволяет компаниям создавать программные решения, которые помогают автоматизировать процессы, анализировать данные, прогнозировать результаты и оптимизировать бизнес-процессы. Такие решения позволяют компаниям быть более эффективными и конкурентоспособными.

Примечания[править]

Определение взято из книги Борисенко В. В., Основы программирования, Интернет ун-т информ. технологий. — М.: Интернет ун-т информ. технологий, 2005.
Следует отметить, что в различных системах символьных вычислений число π{\displaystyle \pi } представляется как число с бесконечной точностью как алгоритм, который по мере надобности вычисляет нужное число первых цифр десятичного представления числа π{\displaystyle \pi }. Такой алгоритм можно построить и на основе приведённой формулы, но этот алгоритм нельзя идентифицировать с самой формулой.
Для человека числа также не являются элементарными — обычно он думает о них как о наборе цифр в десятичной записи и для их сложения и умножения использует алгоритмы сложения и умножения чисел «столбиком», в которых эти операции сводятся к последовательности элементарных действий с цифрами.
Несмотря на то, что натуральное число не является элементарным объектом, мы в некоторых алгоритмах позволим себе работать с натуральными числами как с элементарными объектами. При этом мы будем подразумевать, что алгоритм работает лишь для небольших натуральных чисел или что за арифметическими операциями стоят соответствующие алгоритмы сложения, вычитания и умножения столбиком или алгоритм деления уголком сколь угодно больших чисел.
Эта неприятная альтернатива оказывается является неотъемлемой частью вычислений. Оказывается в принципе нельзя из множества всех программ каким-либо алгоритмическим образом выделить никогда не зависающие программы. Об этом вы можете подробно узнать на курсе по вычислимые функции (см. теоремы Тарского и Геделя).

Использование алгоритмов в IT

Мы приведем несколько примеров использования разных алгоритмов в отраслях программирования. На самом деле их намного больше — мы взяли только часть, чтобы помочь вам понять практическую значимость алгоритмов.

Разработка ПО и сайтов. Алгоритмы используются для парсинга, то есть «разбора» структур с данными, таких как JSON. Парсинг — одна из базовых задач, например в вебе. Также алгоритмы нужны при отрисовке динамических структур, выводе оповещений, настройке поведения приложения и многом другом.

Работа с данными. Очень активно алгоритмы применяются при работе с базами данных, файлами, где хранится информация, структурами вроде массивов или списков. Данных может быть очень много, и выбор правильного алгоритма позволяет ускорить работу с ними. Алгоритмы решают задачи сортировки, изменения и удаления нужных элементов, добавления новых данных. С их помощью наполняют и проходят по таким структурам, как деревья и графы.

Отдельное значение алгоритмы имеют в Big Data и анализе данных: там они позволяют обработать огромное количество информации, в том числе сырой, и не потратить на это слишком много ресурсов.

Поисковые задачи. Алгоритмы поиска — отдельная сложная отрасль. Их выделяют в отдельную группу, в которой сейчас десятки разных алгоритмов. Поиск важен в науке о данных, в методах искусственного интеллекта, в аналитике и многом другом. Самый очевидный пример — поисковые системы вроде Google или Яндекса. Кстати, подробности об используемых алгоритмах поисковики обычно держат в секрете.

Машинное обучение. В машинном обучении и искусственном интеллекте подход к алгоритмам немного другой. Если обычная программа действует по заданному порядку действий, то «умная машина» — нейросеть или обученная модель — формирует алгоритм для себя сама в ходе обучения. Разработчик же описывает модель и обучает ее: задает ей начальные данные и показывает примеры того, как должен выглядеть конечный результат. В ходе обучения модель сама продумывает для себя алгоритм достижения этого результата.

Такие ИИ-алгоритмы могут быть еще мощнее обычных и используются для решения задач, которые разработчик не в силах разбить на простые действия сознательно. Например, для распознавания предметов нужно задействовать огромное количество процессов в нервной системе: человек просто физически не способен описать их все, чтобы повторить программно.

В ходе создания и обучения модели разработчик тоже может задействовать алгоритмы. Например, алгоритм распространения ошибки позволяет обучать нейросети.

Другие термины на «А»

АдминАссемблерАВЛ-деревоАутсорсингАлгоритм ДейкстрыАсинхронное программирование
Все термины

2.2 Практические приемы алгоритмизации

Рассмотрим практические примеры, на примере следующей программы: пользовательское приложение «RSS Viewer», с помощью которого пользователь сможет загружать актуальные новости из различных новостных RSS источников.

Перечислим возможные состояния программы:

Исходное состояние.
Основное состояние.
Открыть файл.
Сохранить Файл.
Печать.
Просмотреть справку.
О программе.
Состояние завершения.

На рисунке 1 показана диаграмма переходов состояния программы.

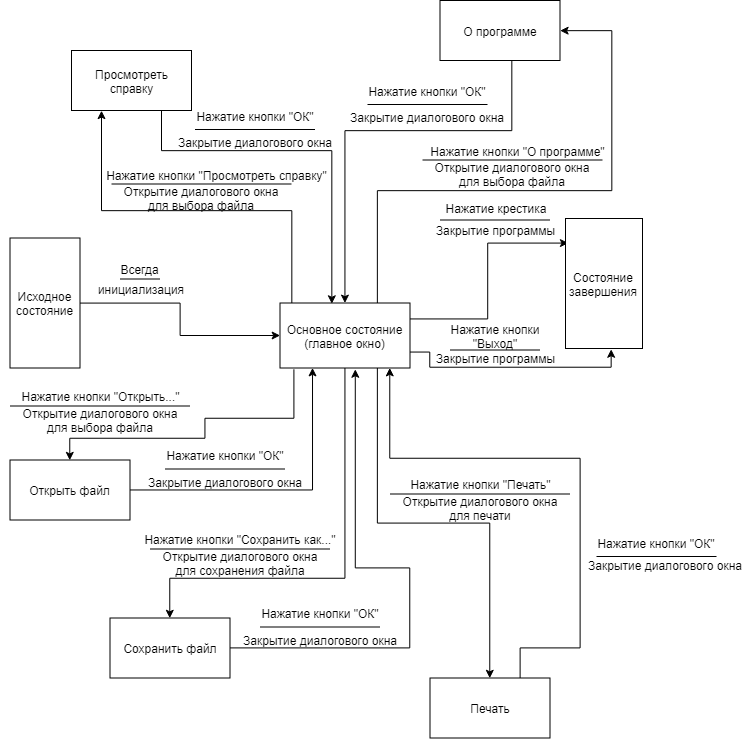
Рисунок 1 – Диаграмма переходов состояния

Представленная диаграмма описывает переходы программы из одного состояния в другое, учитывая условия перехода и действия, выполняющиеся при переходе.

Выделим основные варианты использования данной программы. Открывая приложение, пользователь сможет открыть новости из файла, получить новости с сайта, сохранить их, напечатать их, посмотреть справку, где будет показано, как пользоваться данной программой и посмотреть сведения о программе. Выше перечисленный функционал представим в виде диаграммы, показанной на рисунке 2.

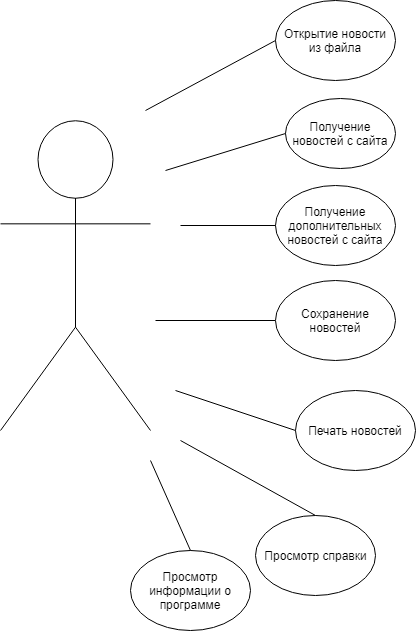
Рисунок 2 – Диаграмма вариантов использования

Разделим программу на предметные области (классы). В данных классах при необходимости выделим атрибуты. В качестве атрибутов представим некоторые, существенные с точки зрения решаемой задачи характеристики объектов.

У нас, например, атрибут – это количество новостей. Продемонстрируем связи(ассоциации) между классами с помощью стрелок, с указанием роли, которую соответствующие объекты играют по отношению друг к другу.

На рисунке 3 представлена концептуальная модель данной системы.

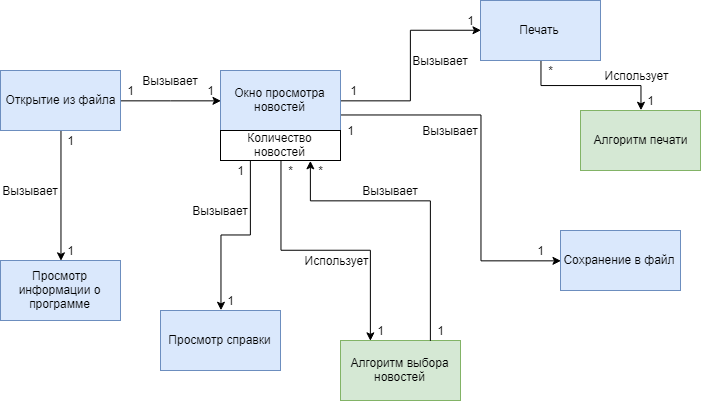
Рисунок 3 – Концептуальная модель предметной области

Наиболее сложной частью программы является запрос новостей с сайта и вывод их на экран.

При запросе новостей, происходит запрос к интернет ресурсу, получение html кода RSS страницы и его разбиение в строковый массив на отдельные новостные блоки. Затем каждый блок разбивается на заголовок, дату публикации, текст и ссылку. Далее все это выводится на экран через перенос строки.

Всё выше описанное можно представить в виде общего алгоритма программы, которое можно изобразить в виде блок-схемы (рисунок 4)

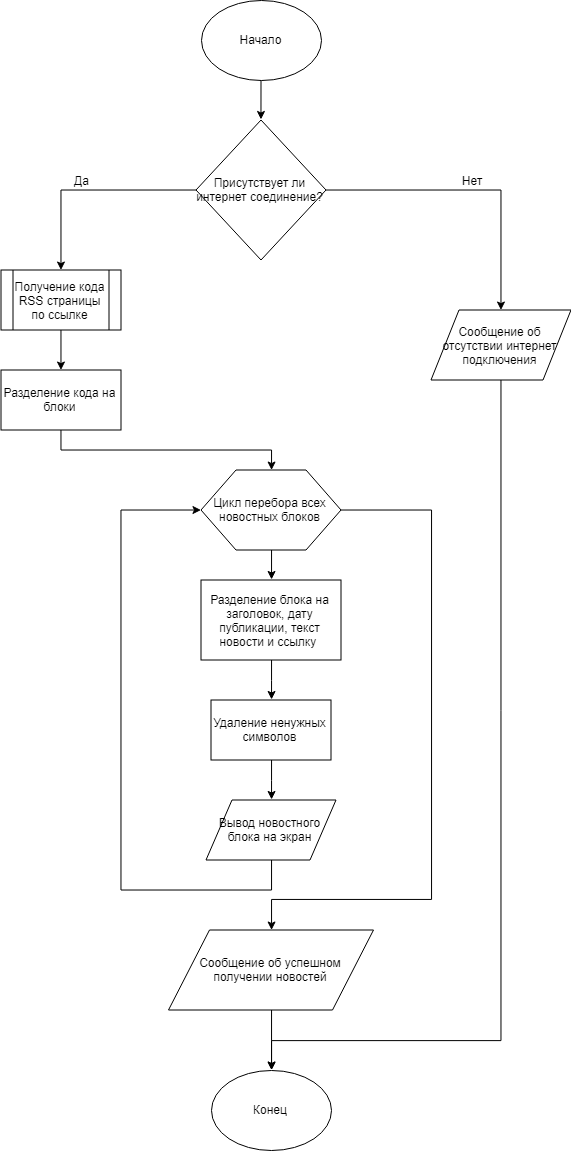
Рисунок 4 – Блок схема алгоритма

Рассмотрим примеры создания простейших алгоритмов на примере некоторых программ на Python.

1. Программа на Python для поиска факториала числа.

Факториал числа является произведением всех целых чисел от 1 до этого числа. Например, факториал 6 (обозначается как 6!) Равен 1 * 2 * 3 * 4 * 5 * 6 = 720. Факториал не определен для отрицательных чисел, а факторный нуль — один, 0! = 1. Подробный код программы показан в листинг кода 1.

Листинг кода 1.

# Программа для поиска факториала числа

# Ввод числа

num = int(input(«Введите число: «))

factorial = 1

# проверка числа

if num < 0:

print(«Факториала не существует для отрицательных чисел»)

elif num == 0:

print(«Факториал нуля равен 1»)

else:

for i in range(1,num + 1):

factorial = factorial*i

print(«Факториал»,num,» = «,factorial)

Алгоритм программы заключается в том, что здесь число, в котором находится факториал, хранится в num и мы проверяем, является ли число отрицательным, нулевым или положительным с использованием if…elif…else оператора. Если число положительное, мы используем for цикл и range() функцию для вычисления факториала.

2. Программа Python для поиска второго по величине числа в списке.

Программа берет список и печатает второе по величине число в списке.

Подробный код программы показан листингом кода 2.

Листинг кода 2.

a=[]

n=int(input(«Введите количество чисел:»))

for i in range(1,n+1):

b=int(input(«Введите элемент:»))

a.append(b)

a.sort()

print(«Второй по величине элемент:»,a)

Выполняемые шаги:

1. Берется количество элементов и сохраняется в переменной.

2. Далее перебираются элементы списка один за другим.

3. Сортируется список в порядке возрастания.

4. Выводится второй последний элемент списка.

5. Выход.

Пользователь должен ввести количество элементов и сохранить их в переменной. Далее пользователь должен затем вводить элементы списка один за другим, используя цикл for и сохраняя его в списке, затем список должен быть отсортирован. В конце печатается последний элемент списка, который также является самым большим элементом списка.

Применение алгоритмического языка в науке

Алгоритмический язык — это язык программирования, который используется для создания алгоритмов — последовательности инструкций, которые решают определенную задачу. Такой язык является важным инструментом в научных исследованиях, поскольку позволяет исследователям разрабатывать и тестировать сложные алгоритмы на компьютере.

Применение алгоритмического языка в науке имеет множество областей применения:

Математика и статистика: алгоритмический язык позволяет математикам и статистикам разрабатывать и тестировать математические модели, вычислять сложные функции, решать уравнения, проводить статистический анализ и многое другое.
Физика: алгоритмический язык позволяет ученым моделировать физические явления, проводить численные эксперименты, решать дифференциальные уравнения, анализировать и визуализировать данные.
Биология: с помощью алгоритмического языка биологи могут анализировать генетические данные, моделировать биологические процессы, исследовать эволюцию и проводить другие исследования в области биологии.
Информатика: алгоритмический язык является основой программирования и разработки компьютерных программ. Он используется для создания и тестирования алгоритмов, разработки программного обеспечения и создания компьютерных моделей.
Инженерия: алгоритмический язык позволяет инженерам моделировать и тестировать различные системы, проводить численные расчеты, оптимизировать процессы и дизайн.

Применение алгоритмического языка в научных исследованиях позволяет исследователям автоматизировать рутинные задачи, проводить сложные вычисления, получать численные результаты и анализировать данные. Это позволяет сократить время и усилия, затрачиваемые на выполнение научных исследований, и повысить точность и надежность получаемых результатов.

Язык программирования — средство записи алгоритмов для компьютеров

Достаточно универсальным исполнителем является компьютер. С его помощью можно выполнять разнообразные по видам алгоритмы: делать математические вычисления, обрабатывать текстовые данные, изменять графику и др. В каком-то смысле компьютер может делать многое, что и человек, а некоторые вещи намного быстрее. Однако человек и компьютер «разговаривают» на совершенно разных языках: один – на естественном (русском, английском и др.), а другой – на формальном (машинном) языке.

Разработав алгоритм, человек должен как-то «объяснить» его компьютеру. Для этих целей служат языки программирования, а результатом записи алгоритма на них является программа.

В настоящее время язык программирования – это скорее некий посредник между человеком и вычислительной машиной. Программа, написанная на языке программирования, в последствии переводится на машинный язык транслятором.

Операторы

5.2. Основные понятия алгоритмического языка

Каждое понятие алгоритмического языка подразумевает некоторую синтаксическую единицу (конструкцию) и определяемые ею свойства программных объектов или процесса обработки данных. Понятие языка определяется во взаимодействии синтаксических и семантических правил. Синтаксические правила показывают, как образуется данное понятие из других понятий и букв алфавита, а семантические правила определяют свойства данного понятия Основными понятиями в алгоритмических языках обычно являются: Имена (идентификаторы) – используются для обозначения объектов программы (переменных, массивов, функций и др.). Операции . Типы операций : Арифметические операции + , — , * , / и др. Логические операции и , или , не .

41 Операции отношения , = , = , .

43 Программирование – это теоретическая и практическая деятельность решения задачи средствами конкретного языка программирования и оформления полученных результатов в виде программы. В общем случае программа может иметь модульную структуру, т.е. состоять из нескольких программных единиц, связанных между собой командами передачи управления. Такой принцип построения программ называется модульным. Программная единица, с первой команды которой начинается выполнение программы, называется головной программой. Остальные программные единицы, входящие в единую программу, называются подпрограммами. Функция – это программная единица, которая может быть употреблена в выражении. Функция прямо возвращает величину, которая используется при вычислении этого выражения и, кроме того, может возвращать величины через параметры. Процесс разработки многомодульных программ эффективнее, особенно если разрабатывается программа большого размера, когда над реализацией проекта может работать несколько программистов, каждый из которых имеет возможность модифицировать фрагменты программы, не мешая работе остальных. Подпрограммы и функции позволяют создавать большие структурированные программы, которые можно делить на части. Это даёт преимущества в следующих ситуациях: если программа большая, разделение её на части облегчает создание, тестирование и её сборку; если программа большая и повторная компиляция всего исходного текста занимает много времени, разделение её на части экономит время компиляции; если процедуру надо использовать в разных случаях разным образом, можно записать её в отдельный файл и скомпилировать отдельно.

Лекция 5. Свойства алгоритмов.

Алгоритм должен быть составлен таким образом, чтобы исполнитель, в расчете на которого он создан, мог однозначно и точно следовать командам алгоритма и эффективно получать определенный результат. Это накладывает на записи алгоритмов ряд обязательных требований, суть которых вытекает, вообще говоря, из приведенного выше неформального толкования понятия алгоритма. Сформулируем эти требования в виде перечня свойств, которым должны удовлетворять алгоритмы, адресуемые заданному исполнителю.

Одно из первых требований, которое предъявляется к алгоритму, состоит в том, что описываемый процесс должен быть разбит на последовательность отдельных шагов. Возникающая в результате такого разбиения запись представляет собой упорядоченную совокупность четко разделенных друг от друга предписаний (директив, команд, операторов), образующих прерывную (или, как говорят, дискретную) структуру алгоритма. Только выполнив требования одного предписания, можно приступить к выполнению следующего. Дискретная структура алгоритмической записи может. Например, подчеркиваться сквозной нумерацией отдельных команд алгоритма, хотя это требование не является обязательным. Рассмотренное свойство алгоритмов называют дискретностью.
Используемые на практике алгоритмы составляются с ориентацией на определенного исполнителя. Чтобы составить для него алгоритм, нужно знать, какие команды этот исполнитель может понять и исполнить, а какие — не может. Мы знаем, что у каждого исполнителя имеется своя система команд. Очевидно, составляя запись алгоритма для определенного исполнителя, можно использовать лишь те команды, которые имеются в его СКИ. Это свойство алгоритмов будем называть понятностью.
Будучи понятным, алгоритм не должен содержать предписаний, смысл которых может восприниматься неоднозначно, т.е. одна и та же команда, будучи понятна разным исполнителям, после исполнения каждым из них должна давать одинаковый результат. Запись алгоритма должна быть настолько четкой, полной и продуманной в деталях, чтобы у исполнителя не могло возникнуть потребности в принятии решений, не предусмотренных составителем алгоритма. Говоря иначе, алгоритм не должен оставлять места для произвола исполнителя. Кроме того, в алгоритмах недопустимы также ситуации, когда после выполнения очередной команды алгоритма исполнителю неясно, какая из команд алгоритма должна выполняться на следующем шаге. Отмеченное свойства алгоритмов называют определенностью или детерминированностью.
Обязательное требование к алгоритмам — результативность. Смысл этого требования состоит в том, что при точном исполнении всех предписаний алгоритма процесс должен прекратиться за конечное число шагов и при этом должен получиться определенный результат. Вывод о том, что решения не существует — тоже результат.
Наиболее распространены алгоритмы, обеспечивающие решение не одной конкретной задачи, а некоторого класса задач данного типа. Это свойство алгоритма называют массовостью. В простейшем случае массовость обеспечивает возможность использования различных исходных данных.

СПИСОК ЛИТЕРАТУРЫ

Алиев, Ю.А. Практикум по алгоритмизации и программированию на языке Паскаль/ Ю.А. Алиев. – В. – Питер: 2007. – 527с
Буч Гради Объектно-ориентированное проектирование с примерами применения. — Конкорд, 2014. — 519 с.
Васильев А. Java. Объектно-ориентированное программирование. — Питер, 2013. — 397 с.
Дронов В. HTML 5, CSS 3 и Web 2.0. Разработка современных Web-сайтов. — БХВ-Петербург, 2013. — 408 с.
Дэвид Харрис, Сара Л. Харрис Цифровая схемотехника и архитектура компьютера. — ДМК Пресс, 2018. — 794 с.
Левчук Е. А. Технологии организации, хранения и обработки данных. — Вышэйшая школа, 2016. — 241 с.
Лутц М. Изучаем Python. 4-е издание. — Символ-Плюс, 2017. — 1272 с.
Мартин Роберт Идеальный программист. Как стать профессионалом разработки ПО. — Питер, 2011. — 240 с.
Орлов С. А. Теория и практика языков программирования. — Питер, 2017. — 688 с.
Щеглов К.А., Щеглов А.Ю. Защита информации: основы теории. Учебник для бакалавриата и магистратуры. — Юрайт, 2017. — 310 с.
Paul Barry Head First Python: A Brain-Friendly Guide. — O’Reilly Media, 2016. — 624 p.
Luciano Ramalho Fluent Python: Clear, Concise, and Effective Programming. — O’Reilly Media, 2015. — 792 p.
Программирование Понятие «программирование». Режим доступа:
https://sites.google.com/site/wwwprogrammirovaniecom/home/ponatie Дата обращения (21.01.2020)
Сайт с образовательными программами История программирования и алгоритмических языков перспективы развития средств автоматизации. Режим доступа: http://emirb.org/zadacha-avtomatizacii-sostoit-v-osushestvlenii-avtomaticheskog.html?page=9 Дата обращения (21.01.2020)
Life-Prog Основные понятия. Программный продукт Режим доступа: https://life-prog.ru/2_13687_osnovnie-ponyatiya-programmniy-produkt.html Дата обращения (21.01.2020)
Алгоритмизация и программирование Алгоритмические конструкции. Режим доступа: https://xn—-7sbbfb7a7aej.xn--p1ai/informatika_kabinet/programm/programm_03.html Дата обращения (21.01.2020)
Itandlife Роль алгоритмов в информационных технологиях. Режим доступа: http://itandlife.ru/science/computer-science/rol-algoritmov-v-informacionnyx-texnologiyax/ Дата обращения (21.01.2020)

Теория происхождения права (Признаки и особенности права)
Контроль за оперативно-розыскной деятельностью (Понятие оперативно-розыскной деятельности. Правовые основы и значение контроля за оперативно-розыскной деятельностью)
Теория и практика разделения властей (Парламентаризм и разделение властей)
Основные структуры алгоритмов: сравнительный анализ и примеры их использования (Блок-схема алгоритма)
Действие права (Социальный (неюридический) аспект действия права)
Понятие и признаки государства (Подходы к пониманию государства)
РОЛЬ КРЕДИТА В СОВРЕМЕННОЙ ЭКОНОМИКЕ (Сущность, понятие и формы кредита)
Профессионально-личностные деформации субъекта труда (Теоретические аспекты профессиональных деформаций)
Понятие и виды наследования
История и развитие методологии объектно-ориентированного программирования. Сферы применения (Теоретические основы объектно-ориентированного программирования)
Учет амортизации основных средств (Понятие износа и амортизации и их виды)
Политические партии в политической системе общества»

Как алгоритмические методы помогают в решении задач