Геометрическая фигура угол: определение угла, измерение углов, обозначения и примеры

Альфа как мера угла

Альфа как мера угла позволяет определить величину и положение угла относительно других углов. Мера угла обычно выражается в градусах, минутах и секундах.

Например, если мы имеем треугольник ABC и хотим измерить угол BAC, мы можем записать меру угла BAC как α.

Угол	Мера угла (α)
Угол BAC	α

Используя меру угла α, мы можем сравнить разные углы и определить, является ли один угол больше или меньше другого. Например, если у нас есть два угла α и β, мы можем сказать, что α больше β, если мера угла α больше меры угла β.

Альфа как мера угла имеет множество применений в геометрии, физике и других областях науки. Она позволяет нам анализировать и измерять углы и использовать их в различных вычислениях и моделях.

Определение угла альфа

Угол альфа обычно обозначается символом α. Он является одним из основных элементов геометрии и играет важную роль в решении различных математических задач.

Примеры использования угла альфа:

• В треугольниках угол альфа может быть одним из углов, например, углом противоположным стороне AB.
• Угол альфа может использоваться для определения направления, например, угол между направлением движения и вектором.
• В тригонометрии, угол альфа используется для определения значений тригонометрических функций.

Свойства угла альфа

Угол альфа имеет несколько свойств, которые используются в математике для решения различных задач. Вот некоторые из них:

1. Угол альфа является геометрической фигурой, образованной двумя лучами, исходящими из одной точки, называемой вершиной. Альфа обычно обозначается греческой буквой α.

2. Угол альфа может быть острый, прямой, тупой или полный. Острый угол имеет меньше 90 градусов, прямой — ровно 90 градусов, тупой — больше 90 градусов, а полный — ровно 180 градусов.

3. Углы альфа, имеющие общую вершину и общую сторону, называются смежными углами. Смежные углы могут быть смежными нулевого порядка, линейными или вертикальными. Смежные углы нулевого порядка имеют одну общую вершину и их стороны лежат на одной прямой. Линейные смежные углы имеют общую вершину и они располагаются на одной прямой. Вертикальные смежные углы имеют общую вершину, но они расположены на разных прямых.

4. Угол альфа может иметь дополнительный угол, который в сумме с ним образует прямой угол, равный 90 градусов. Дополнительные углы, обозначенные буквой бета, могут быть найдены как разность между прямым углом и углом альфа.

5. Углы альфа могут быть равны или совпадать между собой. Если два угла имеют одинаковую меру, они считаются равными. Если два угла имеют одинаковое положение в пространстве, они считаются совпадающими.

Знание и понимание свойств угла альфа помогает в решении геометрических и алгебраических задач, а также в проведении доказательств и построений.

Свойства альфа в геометрии

Альфа — это угол, который обычно обозначается греческой буквой α и широко используется в геометрии. Углы могут быть мерой поворота или сопоставляться с отрезками на окружности. Некоторые из свойств альфа в геометрии включают:

• Мера угла: Альфа может быть использована для измерения угла между двумя линиями, отрезками или плоскостями.
• Отрезки на окружности: В геометрии альфа может быть использована для определения соотношений между отрезками на окружности. Например, если альфа является мерой угла между двумя радиусами окружности, то отношение длины этих отрезков будет пропорционально мере угла.
• Группировка углов: Альфа может быть использована для группировки углов на плоскостях или в трехмерном пространстве. Например, альфа может быть использована для определения пары углов, образованных пересечением двух прямых. Связанные с этим свойства альфа могут использоваться для решения различных геометрических задач.

В итоге, альфа является общим понятием в геометрии, которое используется для определения углов и их свойств на плоскости и окружности.

Альфа и другие углы

Углы играют важную роль в геометрии и в различных научных областях. Один из углов, который часто встречается в геометрии, называется «альфа».

Альфа — это угол, который обозначается символом альфа (α). Другие популярные углы в геометрии включают угол бета (β), угол гамма (γ) и так далее.

Эти углы могут быть различной величины и могут иметь различные свойства. Например, угол альфа может быть остроугольным (меньше 90 градусов), прямым (равным 90 градусам) или тупым (больше 90 градусов).

Углы могут быть измерены в градусах, минутах и секундах. Одна полная оборотная мера равна 360 градусам. Таким образом, угол альфа может быть измерен в градусах от 0 до 360.

Углы также могут быть классифицированы как ортогональные (пересекающиеся под прямым углом), параллельные (не пересекающиеся) или пересекающиеся.

Углы играют важную роль в различных областях, включая геометрию, физику, инженерию и дизайн. Например, в архитектуре углы используются для создания прямых линий и геометрических форм, в физике — для измерения направления движения тела и в инженерии — для определения направления силы и планирования строительства.

Альфа и длины сторон

В геометрии понятие «альфа» относится к углу в треугольнике, который обозначается как α. Он может иметь различные значения в зависимости от длин сторон треугольника.

Альфа является одним из углов треугольника и может быть остроугольным, прямым или тупоугольным. Остроугольный угол α находится между двумя сторонами, которые образуют острый угол в треугольнике. Прямой угол α равен 90 градусам и находится между перпендикулярной стороной и любой другой стороной треугольника. Тупоугольный угол α находится между двумя сторонами, которые образуют тупой угол в треугольнике.

Длины сторон треугольника также имеют важное значение при определении значения альфа. Закон косинусов используется для нахождения угла α, когда известны длины всех трех сторон треугольника

Формула выглядит следующим образом:

cos α = (b² + c² — a²) / (2bc)

Где a, b и c — длины сторон треугольника. Зная длины сторон и применяя эту формулу, можно определить значение альфа.

В случае, если известны значения угла α и одной из сторон треугольника, можно использовать тригонометрические функции, такие как синус или косинус, для нахождения длины других сторон треугольника.

Таблица ниже содержит примеры нахождения альфа и длин сторон треугольника:

Сторона a	Сторона b	Сторона c	Угол α
3	4	5	90°
5	5	7	49.47°
8	10	12	30°

В каждом из этих примеров альфа и длины сторон треугольника определяются с использованием соответствующих формул и свойств геометрии.

В заключение, альфа в геометрии связана с углами и длинами сторон треугольника. Зная длины сторон треугольника, альфу можно определить, а также наоборот — зная значение альфы и одну из сторон треугольника, можно найти длины остальных сторон.

Ссылки

Wikimedia Foundation . 2010 .

Смотреть что такое «Альфа (буква)» в других словарях:

Альфа, буква — Альфа (Alpha) первая буква греческого алфавита, обозначающая краткий и долгий звук а; ее название взято из финикийского языка, где называется aleph; ее форма происходит от первоначально иероглифического египетского образа бычачьей головы; в… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Альфа (буква греч. алфавита) — Альфа (A), первая буква греческого алфавита. Перен. А. и омега ‒ главное, основное, всё полностью; от А. до омеги ‒ от начала до конца … Большая советская энциклопедия

Альфа буква греческого алфавита — (Alpha) первая буква греческого алфавита, обозначающая краткий и долгий звук а; ее название взято из финикийского языка, где называется aleph; ее форма происходит от первоначально иероглифического египетского образа бычачьей головы; в церковно… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

АЛЬФА — (греч.). 1) первая буква греческой азбуки; в переносном смысле: начало. Альфа и Омега (первая и последняя буквы греческой азбуки): начало и конец. 2) символ вечности у древних христиан. 3) лицо Спасителя в Апокалипсисе. Словарь иностранных слов,… … Словарь иностранных слов русского языка

Буква А — Буква кириллицы А Кириллица А Б В Г Ґ Д … Википедия

буква — Знак (азбучный), письмена (множ. ч.), иероглиф (гиероглиф), каракуля, руны. Нагородил какие то каракули, и читай. .. Ср. знак. Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. буква … Словарь синонимов

альфа-ритм — ритм энцефалограммы в состоянии относительного покоя. Имеет частоту 8 13 Гц и среднюю амплитуду 30 70 мкВ с периодическим усилением и ослаблением (альфа веретена). Возбуждается таламокортикальными и интракортикальными процессами. Анализ… … Большая психологическая энциклопедия

альфа-тренинг — психотерапевтический прием, основанный на связи обратной биологической. Заключается в обучении по схеме обусловливания инструментального регулированию таких психофизиологических процессов, что прежде считались недоступными сознательному контролю … Большая психологическая энциклопедия

Альфа-Переживание — (от греч. alpha первая буква греческого алфавита) при произвольном усилении альфа ритма мозга в условиях обеспечения биологической обратной связи испытуемые чаще всего ощущают приятное, расслабленное, медитативное состояние. В дальнейшем… … Психологический словарь

«Я есмь Альфа и Омега, начало и конец … Который есть и был и грядет…» (Откр. 1:8)

Символика окружает людей со всех сторон. Изучая знаки, человек расширяет свое сознание и может по-новому смотреть на мир.

Геометрические фигуры и знаки

Вот некоторые основные геометрические фигуры и их знаки:

• Прямая (→) — это бесконечное множество точек, расположенных на одной линии.
• Отрезок (—) — это часть прямой, ограниченная двумя точками.
• Угол (∠) — это область плоскости, образованная двумя лучами, исходящими из одной точки.
• Треугольник (△) — это фигура, имеющая три стороны и три угла.
• Прямоугольник () — это четырехугольник, у которого все углы прямые.
• Квадрат (□) — это четырехугольник, у которого все стороны равны и все углы прямые.
• Круг (○) — это множество точек, расположенных на одинаковом расстоянии от центра.

Эти знаки и символы помогают удобно и компактно записывать и изображать геометрические фигуры и их характеристики. Знание этих обозначений позволяет более точно и ясно описывать и анализировать геометрические объекты.

Треугольник

Основные характеристики треугольника:

• Стороны: каждая сторона — это отрезок, соединяющий две вершины треугольника.
• Углы: каждый угол — это область между двумя сторонами, их началами и общим концом.
• Медианы: медианы треугольника — это отрезки, соединяющие вершины треугольника с серединами противоположных сторон.
• Высоты: высоты треугольника — это отрезки, проведенные из вершин треугольника к противоположным сторонам и перпендикулярные им.
• Биссектрисы: биссектрисы треугольника — это отрезки, соединяющие вершину треугольника с серединой противоположного угла и делящие этот угол пополам.
• Окружность вписанная в треугольник: это окружность, которая касается всех сторон треугольника.
• Окружность описанная вокруг треугольника: это окружность, которая проходит через все вершины треугольника.
• Тригонометрические функции: синус, косинус и тангенс углов треугольника помогают решать задачи в геометрии и тригонометрии.

Треугольники могут быть разными по размерам и формам. Основные типы треугольников:

1. Равносторонний треугольник: все три стороны равны, все три угла равны 60 градусов.
2. Равнобедренный треугольник: две стороны равны, два угла равны.
3. Прямоугольный треугольник: один из углов равен 90 градусов.
4. Остроугольный треугольник: все углы острые, меньше 90 градусов.
5. Тупоугольный треугольник: один из углов больше 90 градусов.

Треугольники важны в геометрии и имеют много применений в реальном мире. Они помогают определить расстояния, углы, площади и объемы различных объектов.

Квадрат

Знаки, используемые при обозначении квадрата:

• S — площадь квадрата. Площадь квадрата можно найти, умножив длину одной стороны на саму себя. Обозначается символом S.

• P — периметр квадрата. Периметр квадрата можно найти, умножив длину одной стороны на 4. Обозначается символом P.

• d — диагональ квадрата. Диагональ квадрата — это отрезок, соединяющий две противоположные вершины квадрата. Обозначается символом d.

Примеры:

Если сторона квадрата равна 5 см, то его площадь будет 25 см² (5 × 5 = 25) и периметр будет 20 см (5 + 5 + 5 + 5 = 20). Диагональ квадрата можно найти с помощью теоремы Пифагора: d = √2 × a, где a — длина стороны квадрата.

Круг

Круг обозначается латинской буквой «О».

Основные характеристики круга:

• Радиус — расстояние от центра круга до его любой точки;
• Диаметр — отрезок, соединяющий две точки на окружности, проходящие через центр круга;
• Окружность — граница круга, представляющая собой замкнутую кривую, состоящую из всех точек на плоскости, находящихся на одном и том же расстоянии от центра круга;
• Площадь — количество плоскости, заключенной внутри круга;
• Дуга — часть окружности, состоящая из двух точек и дуги, соединяющих их;
• Центр — фиксированная точка, от которой все точки на окружности находятся на одинаковом расстоянии.

Двугранный угол и перпендикулярность плоскостей

Построить линейный угол двугранного угла с ребром ВD и линейный угол двугранного угла с ребром АD. Вычислительная задача. Найти величину двугранного угла с ребром АD и площадь параллелограмма. Домашнее задание.

Если две плоскости пересекаются, то они образуют сразу 4 двугранных угла.

Если среди них есть острый угол, то его величина считается углом между плоскостями. Перпендикулярны друг другу пол и стены в доме, смежные грани кубика, стенки коробки. Существует особый признак перпендикулярности плоскостей. Тогда m и n должны пересекаться в какой-нибудь точке К. Из доказанного признака вытекает следующее утверждение: Прямоугольный параллелепипед Ранее мы уже узнали про параллелепипед.

Это фигура с 6 гранями, каждая из которых представляет собой параллелограмм. Особый интерес представляет его частный случай — прямоугольный параллелепипед. Такую форму имеют многие шкафы, другие предметы мебели, коробки для обуви, небоскребы. Изображают прямоугольный параллелепипед так: Для обозначения вершин параллелепипеда применяют латинские буквы. Очень часто для вершин одной грани используют 4 буквы без индекса на рисунке выше это А, В, С, D , а другие 4 вершины обозначают такими же буквами, но с нижним индексом 1: А1, B1, C1 и D1.

При этом одноименные вершины например, А и А1 находятся на одном ребре, которое располагается на рисунке вертикально. Докажем некоторые свойства прямоугольного параллелепипеда. Значит, оно перпендикулярно этим граням точнее говоря, оно перпендикулярно плоскостям, проходящим через эти грани. Получается, что ребро AD перпендикулярно 2 прямым в грани CDD1C1 которые при этом пересекаются , и потому оно перпендикулярно и всей грани. То же самое можно продемонстрировать для любого ребра прямоугольного параллелепипеда и любой грани, которую она пересекает.

Эти грани пересекаются по ребру А1D1. Хотя у прямоугольного параллелепипеда есть 12 граней, многие из них имеют одинаковую длину. Поэтому для описания размеров этой фигуры достаточно указать только три параметра. Обычно их называют длиной, шириной и высотой: Эти параметры также называют измерениями прямоугольного параллелепипеда. Зная их, можно вычислить длину диагонали прямоугольного параллелепипеда.

Можно дать и такое определение куба: Трехгранный угол Выберем в пространстве произвольную точку K. Далее из нее проведем три луча КА, КВ и КС так, чтобы они не находились в одной плоскости: В результате мы получили фигуру, которую именуют трехгранным углом. Эти углы так и называются — плоские углы трехгранного угла. Сам же трехгранный угол обозначают четырьмя буквами: КАВС. Таким образом, название «трехгранный» угол показывает, что в точке К сходятся три грани.

Чаще всего в стереометрии такой угол возникает при рассмотрении вершин тетраэдра, в котором есть сразу четыре трехгранных угла: Доказательство.

Исторические сведения о двугранном угле являются важным аспектом его понимания и применения. Знание о его происхождении и особенностях позволяет лучше понять его значение и применение в различных науках и практических областях. Особенности двугранного угла Другая особенность двугранного угла заключается в том, что сумма мер двух его смежных углов всегда равна 180 градусов.

Это связано с тем, что двугранный угол образуется пересечением двух прямых, которые образуют линию. Из этого следует, что углы, образованные линией и одной из сторон угла, являются смежными и их сумма равна 180 градусов. Кроме того, двугранный угол может быть конкавным или выпуклым. Конкавный двугранный угол имеет стороны, направленные внутрь угла, в то время как выпуклый двугранный угол имеет стороны, направленные наружу угла.

Такие геометрические формы могут быть использованы в различных областях, таких как архитектура, конструирование и геодезия. Виды двугранных углов и их назначение Существуют два основных вида двугранных углов: Вид угла.

Геометрический способ удобен в задачах, где условие задано в наглядной форме чертежа или описания пространственной конфигурации. Сравнение способов Аналитический способ быстрее применять, если известны координаты всех точек. Но при этом возрастает вероятность вычислительных ошибок. Геометрический способ нагляднее и менее подвержен ошибкам.

Но его сложнее формализовать для автоматизированных расчетов. Рекомендации по выбору способа Для простых конфигураций лучше применять геометрический способ. А при сложных многогранниках и комбинациях плоскостей — использовать аналитический. При решении задач на вычисление удобно сочетать оба способа — сначала найти координаты ключевых точек геометрически, затем подставить их в аналитические формулы. Добавить комментарий.

Решение задач

Использование альфа в геометрии

В геометрии, альфа обычно используется для обозначения угла. Угол альфа (α) — это угол между двумя лучами или отрезками. Альфа может быть измерен в градусах или радианах, и он играет важную роль во многих геометрических расчетах и конструкциях.

Вот несколько примеров использования альфа в геометрии:

• Измерение углов: Альфа используется для обозначения угла в градусах или радианах. Например, угол между двумя сторонами треугольника может быть обозначен как α.
• Расчеты в треугольниках: Альфа может быть использован для решения различных задач в треугольниках. Например, с помощью альфа можно найти значения углов, сторон или площади треугольника.
• Геометрические конструкции: Альфа используется для построения различных фигур. Например, с помощью альфа можно построить равнобедренный треугольник или круг.

Также альфа может быть использована в комбинации с другими символами или переменными, чтобы обозначить различные геометрические величины или свойства.

В заключение, альфа играет важную роль в геометрии и используется для обозначения углов, решения задач, построений и других геометрических операций.

Угол альфа в треугольнике

Угол альфа в геометрии — это один из углов, образованных сторонами треугольника. В треугольнике угол альфа может быть расположен на любой из его трех вершин.

Чтобы найти значение угла альфа, необходимо знать значения других углов треугольника или длины его сторон. Существуют различные способы для вычисления угла альфа, включая использование тригонометрических функций, теоремы синусов и теоремы косинусов.

Угол альфа может быть прямым (равным 90 градусов), остроугольным (меньше 90 градусов) или тупоугольным (больше 90 градусов). Знание значения угла альфа позволяет определить тип треугольника — прямоугольный, остроугольный или тупоугольный.

Примеры задач, связанных с углом альфа в треугольнике:

1. Найти значение угла альфа, если известны два других угла треугольника.
2. Определить, является ли треугольник прямоугольным при известных значениях угла альфа и других углов или длин сторон.
3. Рассчитать значения сторон треугольника, если известны значения угла альфа и других углов или длин сторон.

Знание угла альфа в треугольнике играет важную роль в геометрии и позволяет анализировать и решать различные задачи, связанные с треугольниками.

Альфа в круге

В геометрии альфа (α) в круге обычно обозначает центральный угол, который измеряется в радианах. Он измеряет угол между двумя радиусами, идущими от центра круга к двум точкам на его окружности. Альфа может быть любым углом от 0 до 360 градусов (или от 0 до 2π радиан).

Альфа имеет особое значение в геометрии круга, потому что он позволяет вычислить длины дуги и площадь сектора. Длина дуги (L) может быть вычислена с помощью формулы:

L = α * r

где r — радиус круга.

Площадь сектора (A) может быть вычислена с помощью формулы:

A = (α/360) * π * r^2

где π ≈ 3,14.

Альфа также используется для нахождения других характеристик круга, таких как длина окружности и площадь круга. Длина окружности (C) вычисляется по формуле:

C = 2 * α * r

Площадь круга (S) вычисляется поформуле:

S = π * r^2

Таким образом, знание значения альфа позволяет определить различные параметры и характеристики круга.

Ваш комментарий к вопросу:

Отображаемое имя (по желанию):

Напишите мне, если после меня будет добавлен комментарий:Напишите мне, если после меня добавят комментарий

Конфиденциальность: Ваш электронный адрес будет использоваться только для отправки уведомлений.

Анти-спам проверка:

Чтобы избежать проверки в будущем, пожалуйста войдите или зарегистрируйтесь

Второй способ

Чтобы набрать символ альфы (строчный), нужно поступить иначе.

Нажмите Win+R для запуска окна «Выполнить».

Добавьте команду charmap.exe, затем нажмите ОК или клавишу Enter.

Запущена таблица символов.

Найдите строчный символ альфы (в примере используется шрифт Arial), выберите его, после чего поочередно нажмите на клавиши «Выбрать» и «Копировать».

Значок был скопирован, можете вставить его.

А вот что у вас должно получиться:

Ссылки

• Α на сайте Scriptsource.org (англ.)
• α на сайте Scriptsource.org (англ.)

Эта страница в последний раз была отредактирована 1 апреля 2021 в 17:10.

Как только страница обновилась в Википедии она обновляется в Вики 2.
Обычно почти сразу, изредка в течении часа.

Углы между плоскостями

Мы точно знаем, что угол между стеной и полом равен 90°. Также, как и угол между стеной и потолком, или полом и любым предметом мебели. 

Но чему равен угол между двумя открытыми страницами тетради? Или угол между стеной и полуоткрытой дверью? Угол между перилами и плоскостью пола? Все эти углы достаточно легко найти. И ответы на все эти вопросы нам дает именно стереометрия. 

Начнем разбирать в углах между плоскостями с того, что введем понятие двугранного угла. 

Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу. 

Если мы откроем книгу не полностью и посмотрим на пространство между двумя страницами, это пространство и будет двугранным углом.

На рисунке: АВ — общая прямая для плоскостей, ее называют ребром двугранного угла;a, b  — плоскости, которые образуют двугранный угол, они называются гранями двугранного угла.  

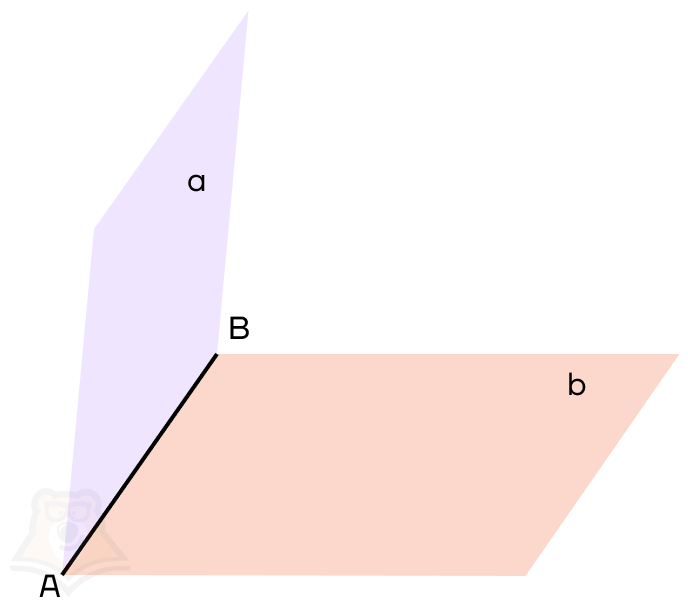
Как мы сталкиваемся с двугранными углами, когда читаем книгу?Если раскрыть книгу не полностью, то ее страницы будут образовывать двугранный угол, то есть часть пространства, заключенную между двумя страницами.

Заметим, что при пересечении двух плоскостей обычно образуется четыре двугранных угла. Нас интересует меньший из них.

Настало время ввести понятие угла между двумя плоскостями. Но для этого нам нужно провести перпендикуляры к ребру двугранного угла в каждой плоскости

Важно, чтобы перпендикуляры пересекались в одной точке

Проведенные перпендикуляры образовали четыре угла. Меньший из них и будет называться углом между плоскостями.

Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях. 

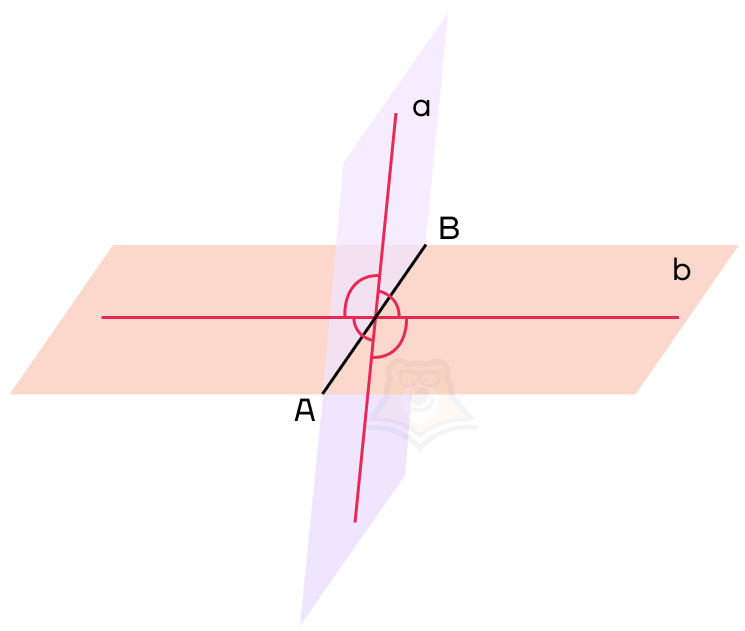
Обозначим нужный нам угол на рисунке как угол COD. Он и будет являться углом между данными плоскостями. 

Угол COD также будет называться линейным углом двугранного угла. 

Линейный угол двугранного угла показывает градусную меру двугранного угла. Поскольку двугранный угол — это часть пространства, то в этом пространстве можно провести множество линейных углов, которые будут равны между собой. 

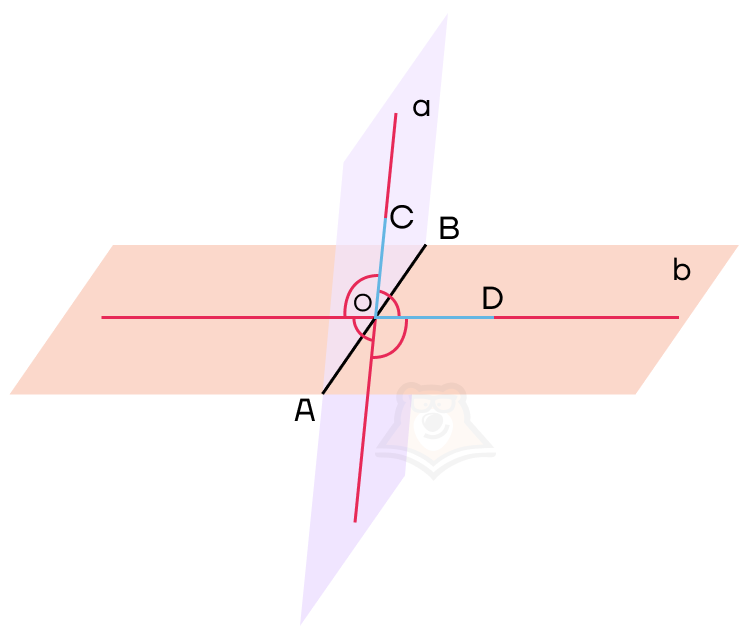
Как и обычные углы, углы между плоскостями бывают трех видов:

• Острые, то есть меньше 90
• Прямые, равные 90
• Тупые, которые больше 90и меньше 180

Как уже было сказано выше, за угол между плоскостями всегда принимается острый угол, образованный этими плоскостями.

А что будет, если между плоскостями получится прямой угол?

Такие плоскости называются перпендикулярными. 

Где в комнате можно найти перпендикулярные плоскости?Достаточно посмотреть на стены и пол, или стены и потолок. А еще на углы потолка — в них будет три перпендикулярные плоскости.

У перпендикулярных плоскостей есть одна очень интересная особенность: все углы, образованные ими, равны между собой и равняются 90° градусам. 

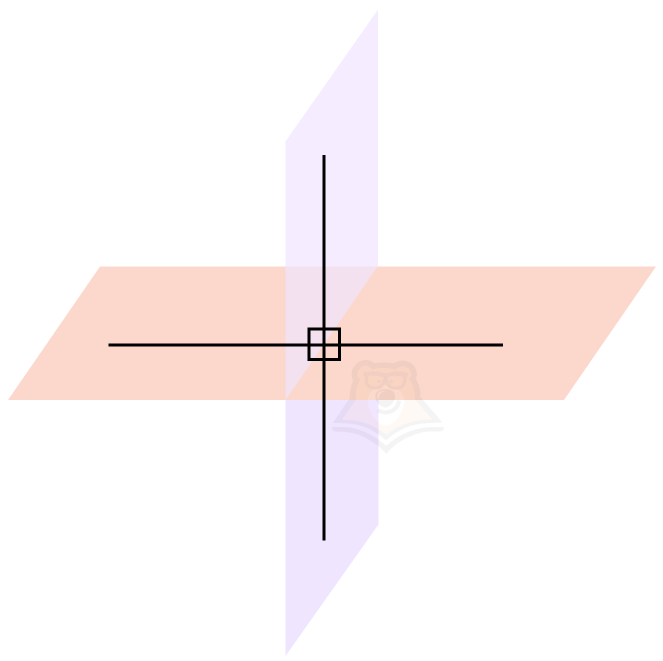
Чтобы найти угол между плоскостями, необходимо следовать следующему алгоритму. 

Алгоритм нахождения угла между плоскостями1 шаг. Найти линию пересечения плоскостей.2 шаг. Достроить к этой линии перпендикуляр в каждой плоскости. 3 шаг. Найти острый угол между построенными перпендикулярами.

Угол альфа и угол бета. Расшифровка

Положение суставов и головки бедренной кости оценивается не только визуально. Для определения их состояния используется специальное измерение углов по таблице Графа. Есть угол Альфа и угол Бета.

• Альфа обозначает развитие костной части ветлужной ямки.
• Бета описывает хрящевое пространство внутри ветлужной впадины.

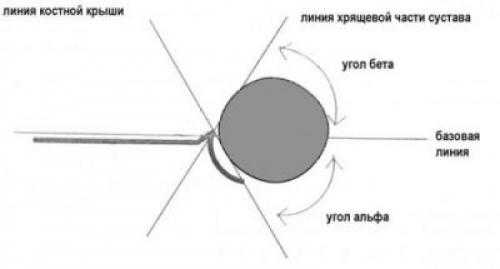
Для здоровых детей считается нормальным, если угол Альфа составляет более 60 градусов, а угол Бета — менее 55 градусов.

Небольшое превышение нормы в 55 градусов допустимо, такой сустав считается нормальным, зрелым. Но если угол Бета составит 77 градусов, врач поставит в заключении подозрение на вывих или подвывих. Также на патологию указывает угол Альфа, который находится в диапазоне от 43 градусов.

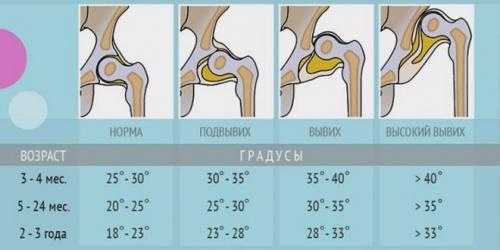
Норма углов в таблице выглядит следующим образом.

Угол «Альфа»	Угол «Бета»	Костный выступ	Заключение
Более 60 градусов	В пределах 55 градусов	Сглаженный	Зрелый здоровый сустав
50-59 градусов	Менее 55 градусов, плотно облегает головку бедра	Скругленный	Физиологически незрелый сустав
50-59 градусов	Менее 55 градусов	Круглый, почти плоский	Задержка оссификации
43-49 градусов	Менее 77 градусов	Уплощенный	Неблагоприятный прогноз
43-49 градусов	Более 77 градусов	Уплощенный или плоский	Начальная децентрация
Менее 43 градусов	Не охватывает головку	Плоский	Децентрация, полная незрелость сустава

В ходе роста ребенка показатели могут меняться, именно это будет учитывать доктор во время проведения УЗИ. Если ребенку уже исполнилось четыре месяца, наиболее правильным и точным методом обследования станет рентгеновский снимок.

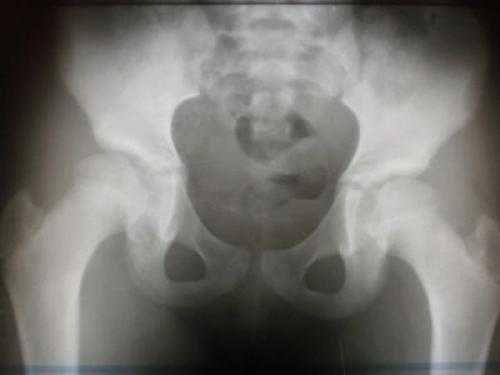
В случае обнаружения проблем врачи стараются обследовать одновременно и костное строение малого таза. Довольно часто патология тазобедренного сустава отражается именно на нем.

В заключении доктор может быть немногословен и предпочтет ограничиться буквенно-числовым обозначением типа сустава, обнаруженного у ребенка. Запомните, что здоровый сустав всегда обозначается как 1А или 1В.

Если в заключении указано, что обнаружен сустав 2А или 2В, это означает, что у ребенка есть признаки физиологической незрелости, которая пройдет самостоятельно с огромной вероятностью, но все-таки потребует наблюдения у детского ортопеда.

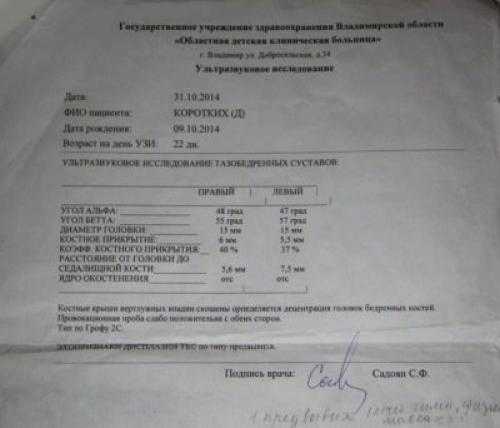
Сустав 2С — сустав с признаками предвывиха. Обязательно требуется наблюдение у врача и выполнение всех его рекомендаций. 3А и 3В — суставы с подвывихом. Самая тяжелая патология — сустав 4 типа. Именно так обозначается тазобедренный сустав с признаками вывиха (дисплазии).

Знаки геометрии и их значения

Один из наиболее распространенных знаков в геометрии — это знак прямой (|), который используется для обозначения отрезка. Например, AB означает отрезок, соединяющий точки A и B.

Знаки равенства ( = ) и неравенства ( ≠ ) используются для обозначения равенства или неравенства двух объектов, таких как отрезки, углы или фигуры. Например, AB = CD означает, что отрезок AB равен отрезку CD.

Знаки угола ( ∠ ) используются для обозначения углов. Например, ∠ABC означает угол, образованный линиями AB и BC.

Знаки параллельности ( || ) и перпендикулярности ( ⊥ ) используются для обозначения особых отношений между линиями. Например, AB || CD означает, что линии AB и CD параллельны, а AB ⊥ CD означает, что линия AB перпендикулярна линии CD.

Знаки конгруэнтности ( ≅ ) и подобия ( ~ ) используются для обозначения подобия и равенства фигур. Например, ΔABC ≅ ΔDEF означает, что треугольник ABC равен по сторонам и углам треугольнику DEF, а ΔABC ~ ΔDEF означает, что треугольник ABC подобен треугольнику DEF.

Знак пересечения ( ∩ ) и объединения ( ∪ ) используются для обозначения операций над множествами. Например, A ∩ B обозначает пересечение множеств A и B, а A ∪ B обозначает их объединение.

Знаки больше ( > ), меньше ( В означает, что число А больше числа В, а ∠ABC

Знаки взаимности ( ⇔ ) и следствия ( ⇒ ) используются для обозначения логических отношений между утверждениями. Например, утверждение «Если А, то В» можно обозначить как А ⇒ В, а утверждение «А равносильно В» — как А ⇔ В.

Знакы ∞ и O ∞ используются для обозначения бесконечности. ∞ обозначает положительную бесконечность, а O ∞ — отрицательную.

Знаки геометрии имеют свои уникальные значения и требуют внимания и точности в использовании, чтобы избежать недоразумений и ошибок при работе с геометрическими объектами.

Омега в трехмерной геометрии

Омега — это одно из основных понятий в трехмерной геометрии. Оно используется для описания видов пространственных фигур и свойств, связанных с их геометрической формой.

Омега представляет собой объем фигуры в трехмерном пространстве. Он вычисляется путем умножения трех основных размеров фигуры: длины, ширины и высоты. Формула для вычисления объема фигуры обычно записывается в виде:

V = L * W * H

где V — объем фигуры, L — длина, W — ширина и H — высота.

Омега имеет ряд свойств, которые могут быть полезны при изучении пространственных фигур и их характеристик:

• Объем фигуры всегда положителен. Он не может быть отрицательным.
• Объем фигуры может быть равен нулю только в случае, когда хотя бы одна из его размерностей равна нулю.
• Объем фигуры линейно зависит от его размеров. Если увеличить одну из размерностей в 2 раза, то объем увеличится в 2 раза.

Омега широко используется в различных областях, связанных с трехмерной геометрией. Например, в архитектуре он используется для расчета объема помещений и строительных конструкций. В медицине он может быть использован для расчета объема органов или опухолей. В инженерии его можно применить для расчета объема материала, необходимого для конкретной конструкции.

Итак, омега — это важное понятие в трехмерной геометрии, позволяющее описать объем пространственной фигуры и использовать его для различных расчетов и анализа формы объектов