Формулы в excel для начинающих с примерами: как пользоваться, создавать и изменять

Построение логарифмической функции в Excel: шаг за шагом

Шаг 1: Откройте Excel и создайте новый документ.

Первым шагом является открытие Excel и создание нового документа, в котором мы будем строить нашу логарифмическую функцию.

Шаг 2: Введите значения входных данных.

Для построения логарифмической функции нам нужны значения входных данных. Например, давайте предположим, что у нас есть набор значений X и Y, и мы хотим построить логарифмическую функцию Y = log(X).

Шаг 3: Создайте новый столбец для логарифмических значений.

Теперь нам нужно создать новый столбец, где будут располагаться логарифмические значения наших входных данных. Выберите ячейку в столбце, где хотите разместить первое логарифмическое значение, и введите формулу «=LOG(X1)», где X1 — адрес ячейки с соответствующим значением X. Затем скопируйте эту формулу и примените ее ко всем остальным значениям X.

Шаг 4: Постройте график логарифмической функции.

Теперь, когда у нас есть логарифмические значения наших входных данных, мы можем построить график логарифмической функции. Выберите столбец с логарифмическими значениями и соответствующий столбец с Y-значениями, затем откройте вкладку «Вставка» и выберите тип графика (например, диаграмму рассеяния или линейный график). Excel автоматически создаст график с логарифмической функцией на основе ваших данных.

Шаг 5: Настройте график.

Чтобы сделать график более наглядным и информативным, можно настроить его параметры. Например, можно изменить масштаб осей, добавить заголовок или легенду, а также внести другие изменения в соответствии с вашими потребностями и предпочтениями.

Шаг 6: Улучшайте и используйте свою логарифмическую функцию.

Теперь, когда ваша логарифмическая функция построена, вы можете использовать ее для обработки данных и анализа результатов. Например, вы можете использовать логарифмическую функцию для прогнозирования значений на основе имеющихся данных или для определения тренда в наборе данных.

Вот и все! Теперь вы знаете, как построить логарифмическую функцию в Excel шаг за шагом. Вы можете использовать эту функцию для решения различных задач и анализа данных. Будьте креативны и экспериментируйте с различными типами функций и настройками графика, чтобы получить наилучшие результаты!

Как пользоваться логарифмической функцией в Excel

Независимо от версии программного обеспечения, установленного на компьютере, расчёт логарифмов подразделяется на несколько этапов:

Запустить Excel и создать небольшую таблицу из двух столбцов.
В первом столбце прописать семь любых чисел. Их количество выбирается на усмотрение пользователя. Во второй колонке будут выводиться значения логарифмов числовых значений.

Создание таблицы чисел для вычисления логарифмов в Excel

Кликнуть ЛКМ по числу в первом столбце, чтобы выделить его.
В левой части строки формул найти значок математической функции и нажать по нему. Это действие означает «Вставить функцию».

Открытие окна «Вставка функций». Нужно нажать на значок слева от строки формул

После выполнения предыдущей манипуляции отобразится окошко «Вставка функции». Здесь нужно развернуть колонку «Категория», нажав по стрелочке справа, из списка выбрать вариант «Математические» и щёлкнуть по «ОК».
В открывшемся списке операторов кликнуть по строке «LOG», а затем нажать на «ОК» для подтверждения действия. Теперь должно отобразиться меню настроек логарифмической формулы.

Выбор функции LOG для первого значения в таблице

Указать данные для расчёта. В поле «Число» нужно записать числовое значение, из которого будет рассчитываться логарифм, кликнув мышкой по соответствующей ячейке в созданной таблице, а в строчке «Основание» в данном случае потребуется прописать число 3.

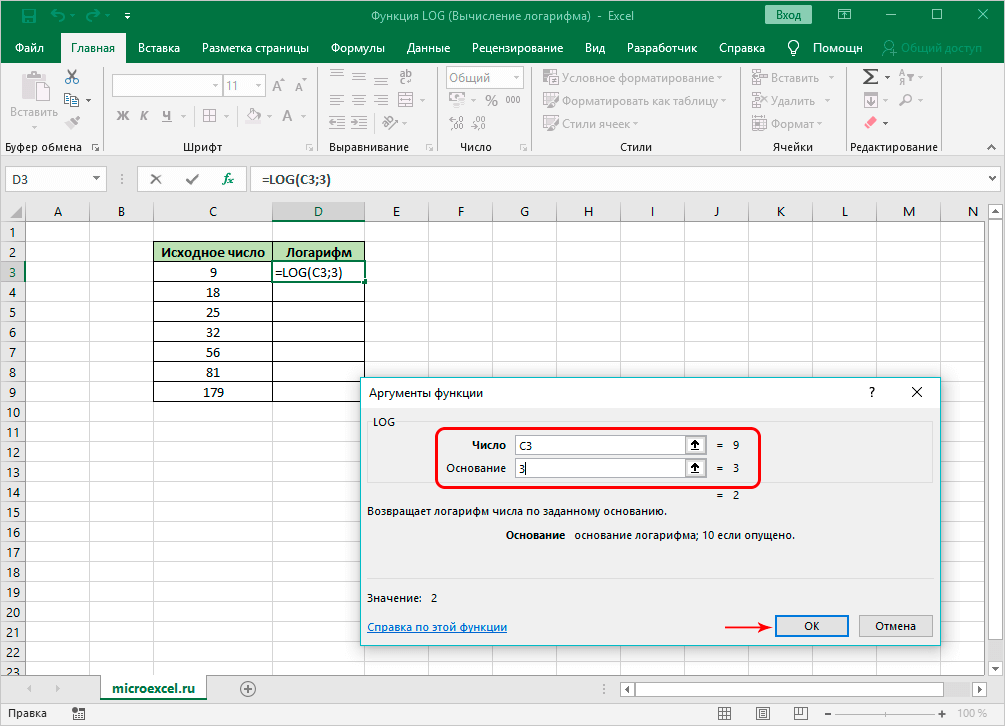
Заполнение аргументов функции. Надо указать число и основание для логарифмирования

Нажать на «Enter» либо на «ОК» внизу окна и проверить результат. Если действия выполнены правильно, то в выбранной ранее ячейке таблицы отобразится результат вычисления логарифма. Если нажать на это число, то в строке сверху появится расчётная формула.

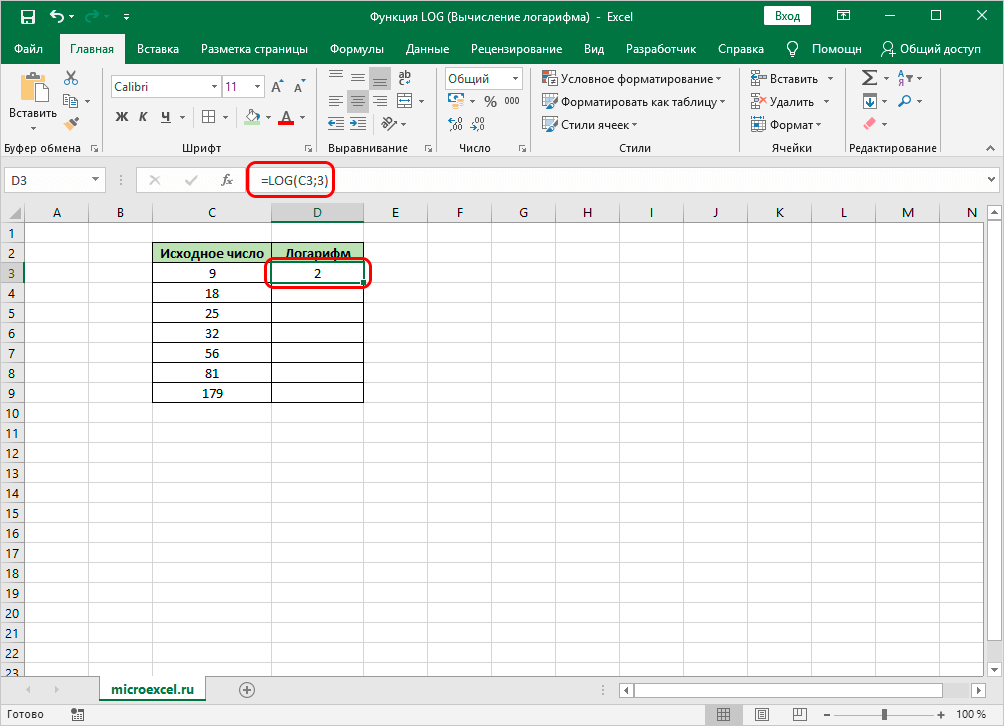
Проверка результата. Необходимо навести курсор мыши на строку формул сверху окна

Проделать ту же операцию с оставшимися числами в таблице, чтобы посчитать их логарифм.

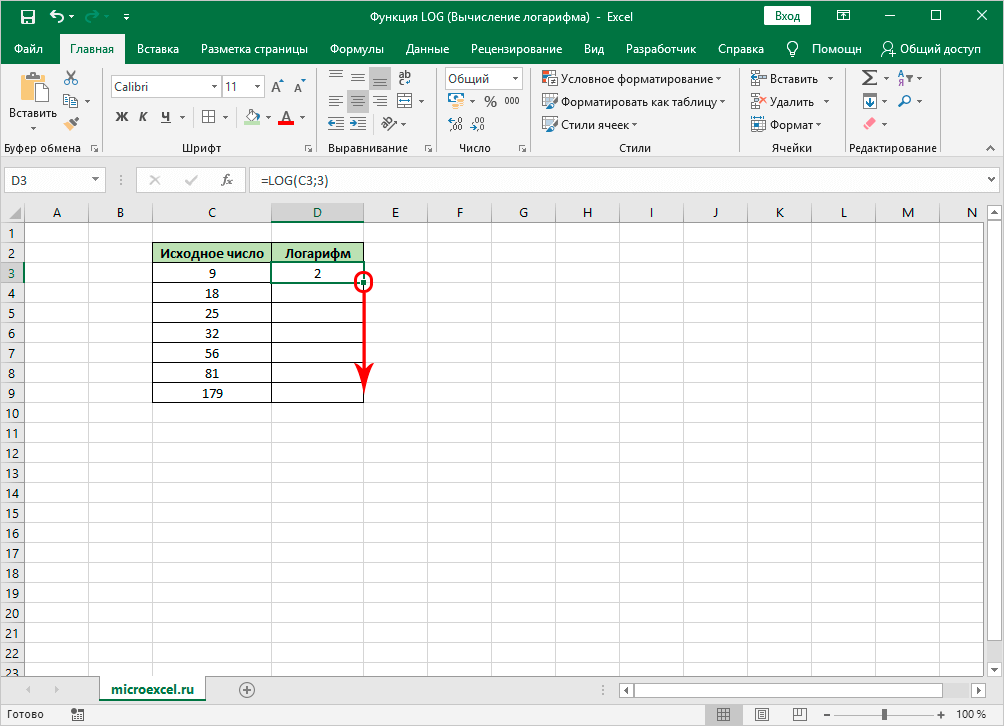
Растягивание формулы для автоматического заполнения оставшихся строк

Применение оператора LOG10

А сейчас предлагаем познакомимся с оператором LOG10. Теперь наша задача – это получении десятичных логарифмов исходных чисел.

Проделываем те же действия, что и при первом способе, т.е. выбираем верхнюю ячейку столбца, куда будем выводить результаты и жмем кнопку “Вставить функцию”.
В перечне математических операторов кликаем по строке “LOG10”, после чего подтверждаем выбор нажатием OK.
Затем выполняем настройку функции. В данном случае она имеет всего лишь один аргумент – “Число”. Указываем адрес нужной ячейки с числом, логарифм из которого нужно рассчитать, и жмем кликаем по кнопке OK, чтобы получить результат.
В итоге, в выбранной ячейке с формулой будет выведен результат вычислений десятичного логарифма от заданного числового значения. Методом, который был описан в первом способе, растягиваем формулу на все оставшиеся строки результирующего столбца.

Функция LN в Excel

Это встроенная функция в MS Excel. LN excel относится к категории «Математические функции» в MS Excel. Excel LN используется для вычисления натурального логарифма числа.

Что такое функция натурального логарифма?

Натуральный логарифм числа — это его логарифм по основанию математической константы e , где e — иррациональное и трансцендентное число, примерно равное 2,718281828459. Функция натурального логарифма x обычно записывается как ln x , loge x или иногда, если основание e неявно, просто log x .

Итак, Ln (Number) = LOG (Number, e)

Где e ~ = 2,7128

Ниже представлен график функции LN.

В приведенном выше графике функций LN ось X указывает номер, для которого необходимо вычислить журнал, а ось Y указывает значения журнала. Например, log (1) равен 0, как показано на графике функций LN.

Формула LN в Excel

Формула функции LN Excel выглядит следующим образом:

LN Formula имеет три аргумента, два из которых являются необязательными. Где,

число = Это обязательный параметр. Он указывает число, для которого должна быть вычислена функция натурального логарифма. Число должно быть положительным действительным числом.
Если параметр является отрицательным числом, возвращается ошибка с # ЧИСЛО! с указанием ошибки с номером.
Если параметр равен нулю, возвращается ошибка с # ЧИСЛО! с указанием ошибки с номером.
Если параметр является нечисловым значением, он возвращает ошибку с #VALUE! указывает на ошибку сгенерированного значения.

Как использовать функцию LN в Excel?

Указанная функция является функцией рабочего листа (WS). Как функцию WS, функцию Excel LN можно ввести как часть формулы в ячейку рабочего листа. Обратитесь к примерам, приведенным ниже, чтобы лучше понять.

Пример # 1 — Дробное число

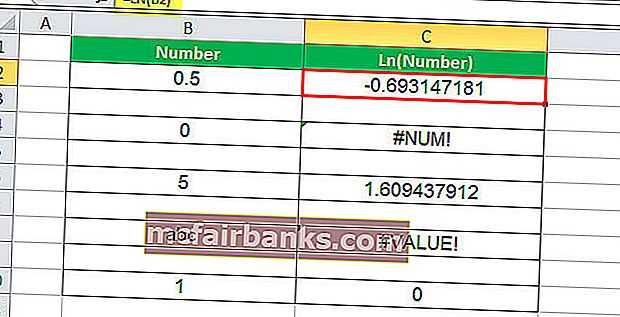
В этом примере с ячейкой C2 связана формула LN. Итак, C2 — это ячейка результата. Первый аргумент LN — это B2, число, для которого необходимо вычислить журнал. Число 0,5, а логарифм 0,5 — -0,693147. Итак, значение результирующей ячейки равно -0,693147.

Пример # 2 — Нулевое число

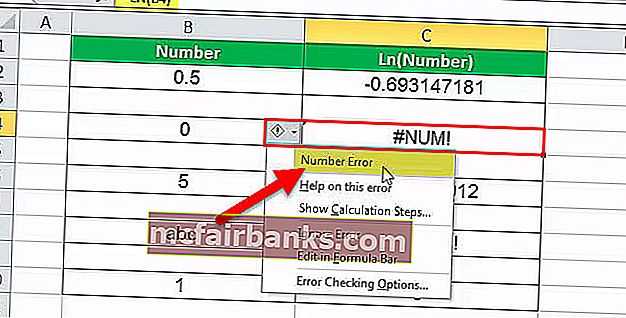
В этом примере с ячейкой C4 связана формула LN. Итак, C4 — это ячейка результата. Первый аргумент LN — это B4, число, для которого необходимо вычислить журнал. Число равно 0, а логарифм 0 не может быть вычислен. Функция LN в Excel не принимает числовое значение как ноль, поэтому в ответ выдается ошибка. Ошибка # ЧИСЛО! что означает, что номер ошибочный.

Пример # 3 — Целое число

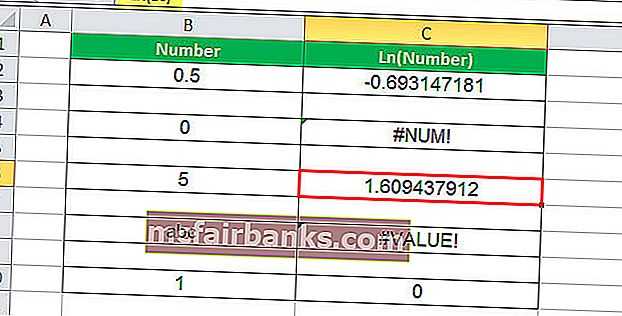
В этом примере с ячейкой C6 связана формула LN. Итак, C6 — это ячейка результата. Первый аргумент LN — это B6, число, для которого необходимо вычислить журнал. Число 5, а логарифм 5 — 1,609437912. Итак, значение в результирующей ячейке — 1,609437912.

Пример # 4 — Нечисловое значение

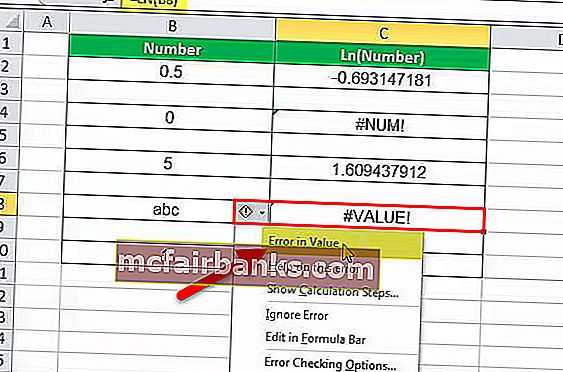
В этом примере с ячейкой C8 связана формула LN. Итак, C8 — это ячейка результата. Первый аргумент LN в Excel — это B8, число, для которого необходимо вычислить журнал. Число — «abc», и журнал нечисловых значений не может быть вычислен. Функция LN в Excel возвращает ошибку, если журнал не может быть рассчитан для такого значения. Ошибка #VALUE! что означает, что значение ошибочно.

Пример # 5 — Отрицательное число

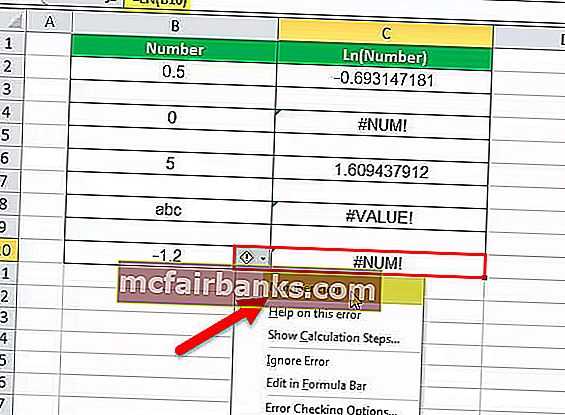
В этом примере с ячейкой C10 связана формула LN. Итак, C10 — это ячейка результата. Первым аргументом LN в Excel является B10, число, для которого необходимо вычислить журнал. Число равно -1,2, и логарифм отрицательного числа не может быть вычислен. Поскольку значение отрицательное, функция LN в Excel возвращает ошибку, указывающую, что значение является ошибочным. Итак, значение в результирующей ячейке — # ЧИСЛО! что означает, что номер ошибочный.

То, что нужно запомнить

Функция LN в Excel принимает в качестве параметра только положительное действительное число. Делитель не может быть нулевым.
Если параметр является отрицательным числом, возвращается ошибка с # ЧИСЛО! с указанием ошибки с номером.
Если параметр равен нулю, возвращается ошибка с # ЧИСЛО! с указанием ошибки с номером.
Если параметр является нечисловым значением, он возвращает ошибку с #VALUE! указывает на ошибку сгенерированного значения.

Excel VBA для аналогичной цели

VBA имеет отдельную встроенную функцию для вычисления функции натурального логарифма, которая называется LOG. Его можно использовать следующим образом.

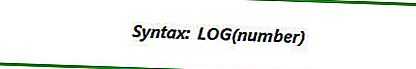
Пример :

Давайте посмотрим на пример, приведенный ниже, для лучшего понимания.

Здесь 5 — это число, для которого должна быть вычислена функция натурального логарифма. Лог (5) по основанию e равен 1.609437912. Итак, переменная logVal содержит значение 1.609437912.

Калькулятор депозита со сложными процентами в Excel

Пример 2. Клиент банка внес вклад в размере 50 000 с процентной ставкой 14,5% (сложные проценты). Определите, сколько времени потребуется, чтобы удвоить вложенную сумму?

Интересный факт! Для быстрого решения этой проблемы можно использовать эмпирический метод приблизительной оценки сроков (в годах) удвоения инвестиций, вложенных под сложные проценты. Так называемое правило 72 (или 70, или правило 69). Для этого используйте простую формулу — число 72 делится на процентную ставку: 72/14,5 = 4,9655 года. Главный недостаток правила «волшебного» числа 72 — в погрешности. Чем выше процентная ставка, тем выше ошибка в правиле 72. Например, при процентной ставке 100% годовых ошибка в годах достигает 0,72 (а в процентах это целых 28%!).

Чтобы точно рассчитать удвоение сроков инвестирования, мы будем использовать функцию LOG. За одно и проверьте погрешность правила 72 при процентной ставке 14,5% годовых.

Просмотреть исходную таблицу:

S — ожидаемая сумма по истечении срока действия;
A — размер депозита;
n — процентная ставка;
t — срок хранения депозитных средств в банке.

Для этого примера эту формулу можно записать в виде 100 000 = 50 000*(100% + 14,5%) t или 2 = (100% + 14,5%) t . Затем, чтобы найти t, вы можете переписать уравнение как t = log_(114,5%) 2 или t = log_1,1452.

Чтобы найти значение t, мы напишем следующую формулу сложных процентов по депозиту в Excel:

B4/B2 — отношение ожидаемой и начальной сумм, являющееся показателем логарифма;
1 + B3 — увеличение в процентах (по основанию логарифма).

В результате вычислений получаем:

Депозит удвоится чуть более чем через 5 лет. Чтобы точно определить годы и месяцы, мы используем формулу:

Функция TRUNC отбрасывает в дробном числе все, что стоит после запятой, как и вся функция INT. Разница между функциями TRUNC и INT только в вычислениях с отрицательными дробными числами. Кроме того, TRUNC имеет второй аргумент, в котором вы можете указать количество оставшихся десятичных разрядов. Поэт в этом случае может использовать любую из этих двух функций по выбору пользователя.

Получилось 5 лет и 1 месяц и 12 дней. Теперь сравним точные результаты с правилом 72 и определим величину ошибки. Для этого примера формула выглядит следующим образом:

Мы должны умножить значение ячейки B3 на 100, так как ее текущее значение равно 0,145, которое отображается в процентном формате. В результате:

Затем скопируйте формулу из ячейки B6 в ячейку B8, а в ячейке B9:

Рассчитать время возникновения ошибки:

Затем в ячейке B10 снова скопируйте формулу из ячейки B6. В итоге получаем разницу:

Наконец, вычисляем разницу в процентах, чтобы проверить, как изменяется размер отклонения и насколько существенно рост процентной ставки влияет на уровень расхождения правила 72 и факта:

Теперь для наглядности пропорциональная зависимость увеличения ошибки и роста процентной ставки поднимет процентную ставку до 100% годовых:

На первый взгляд, погрешность незначительна по сравнению с 14,5% годовых — всего около 2 месяцев и 100% годовых — в течение 3 месяцев. Но доля ошибки в сроке окупаемости более ¼, а точнее 28%.

Сделаем простой график для визуального анализа того, как соотносится зависимость изменения процентной ставки и процента ошибки правила 72 от факта:

Чем выше процентная ставка, тем хуже работает правило 72. В итоге можно сделать следующий вывод: до 32,2% годовых можно смело использовать правило 72. Тогда погрешность меньше 10 процентов. Будет хорошо, если вам потребуются не точные, а сложные расчеты по сроку окупаемости вложений в 2 раза.

Альтернативный метод расчета логарифмов в Excel

В Microsoft Office Excel есть более простой способ вычисления логарифмов тех или иных чисел. Он помогает сэкономить время, необходимое на выполнение математической операции. Данный метод вычисления подразделяется на следующие шаги:

В свободной ячейке программы написать число 100. Можно указать любое другое значение, это не принципиально.
Выделить курсором мыши другую свободную ячейку.
Переместиться в строку формул в верхней части главного меню программы.
Прописать формулу «=LOG(число;)» и нажать «Enter». В данном примере после открытия скобки надо выделить мышкой ячейку, в которой прописано число 100, затем поставить точку с запятой и указать основание, к примеру 10. Далее следует закрыть скобку и кликнуть по «Enter», чтобы завершить формулу. Значение посчитается автоматически.

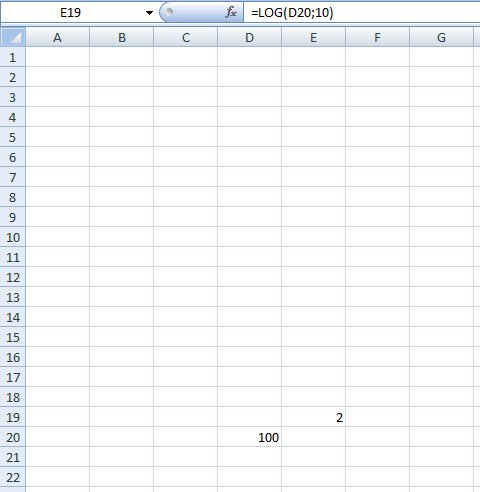Альтернативный метод расчёта логарифмов в Excel

Примеры использования функций LN, LOG и LOG10 в Excel

Пример 1. Археологи нашли останки древнего животного. Для определения их возраста было решено использовать метод радиоуглеродного анализа. В результате измерений выяснилось, что содержание радиоактивного изотопа С14 составляет 17% от количества, обычно встречающегося в живых организмах. Рассчитайте возраст останков, если период полураспада изотопа углерода-14 составляет 5760 лет.

Просмотр исходной таблицы:

Для решения используем следующую формулу:

Эта формула была получена на основе формулы x=t*(lgB-lgq)/lgp, где:

q — количество изотопа углерода в первый момент (при гибели животного), выраженное в единицах (или 100%);
B – количество изотопа на момент анализа останков;
t – период полураспада изотопа;
р — числовая величина, показывающая, во сколько раз количество вещества (изотопа углерода) изменяется за период времени t.

В результате расчетов получаем:

Найденным останкам почти 15 тысяч лет.

Использование оператора LOG10 в Excel

На основании рассмотренного выше примера можно изучить работу функции LOG10. Для упрощения задачи оставим таблицу с теми же числами, предварительно удалив рассчитанные ранее логарифмы во втором столбце. Принцип работы оператора LOG10 можно охарактеризовать следующим образом:

Выделить первую ячейку во втором столбце таблицы и нажать на кнопку «Вставить функцию» слева строки для ввода формул.
По рассмотренной выше схеме указать категорию «Математические», выбрать функцию «LOG10» и щелкнуть по «Enter или нажать на «ОК» внизу окошка «Вставка функции».
В открывшемся меню «Аргументы функции» нужно прописать только числовое значение, по которому будет производиться логарифмирование. В данном поле необходимо указать ссылку на ячейку с числом в исходной таблице.

Нажать на «ОК» или на «Enter» и проверить результат. Во втором столбце должен посчитаться логарифм указанного числового значения.
Аналогичным образом растянуть посчитанное значение на оставшиеся в таблице строки.

Встроенные функции программы

В Excel есть функции на все случаи жизни. Их использование необходимо для решения различных задач на работе, учебе.

Некоторыми из них можно воспользоваться всего один раз, а другие могут и не понадобиться. Но есть ряд функций, которые используются регулярно.

Если выбрать в главном меню раздел «формулы», то здесь сосредоточены все известные функции, в том числе финансовые, инженерные, аналитические.

Для того чтобы выбрать, следует выбрать пункт «вставить функцию».

Выбор функции из предлагаемого списка

Эту же операцию можно произвести с помощью комбинации на клавиатуре — Shift+F3 (раньше мы писали о горячих клавишах Excel).

Если поставить курсор мышки на любую ячейку и нажать на пункт «выбрать функцию», то появляется мастер функций.

С его помощью можно найти необходимую формулу максимально быстро. Для этого можно ввести ее название, воспользоваться категорией.

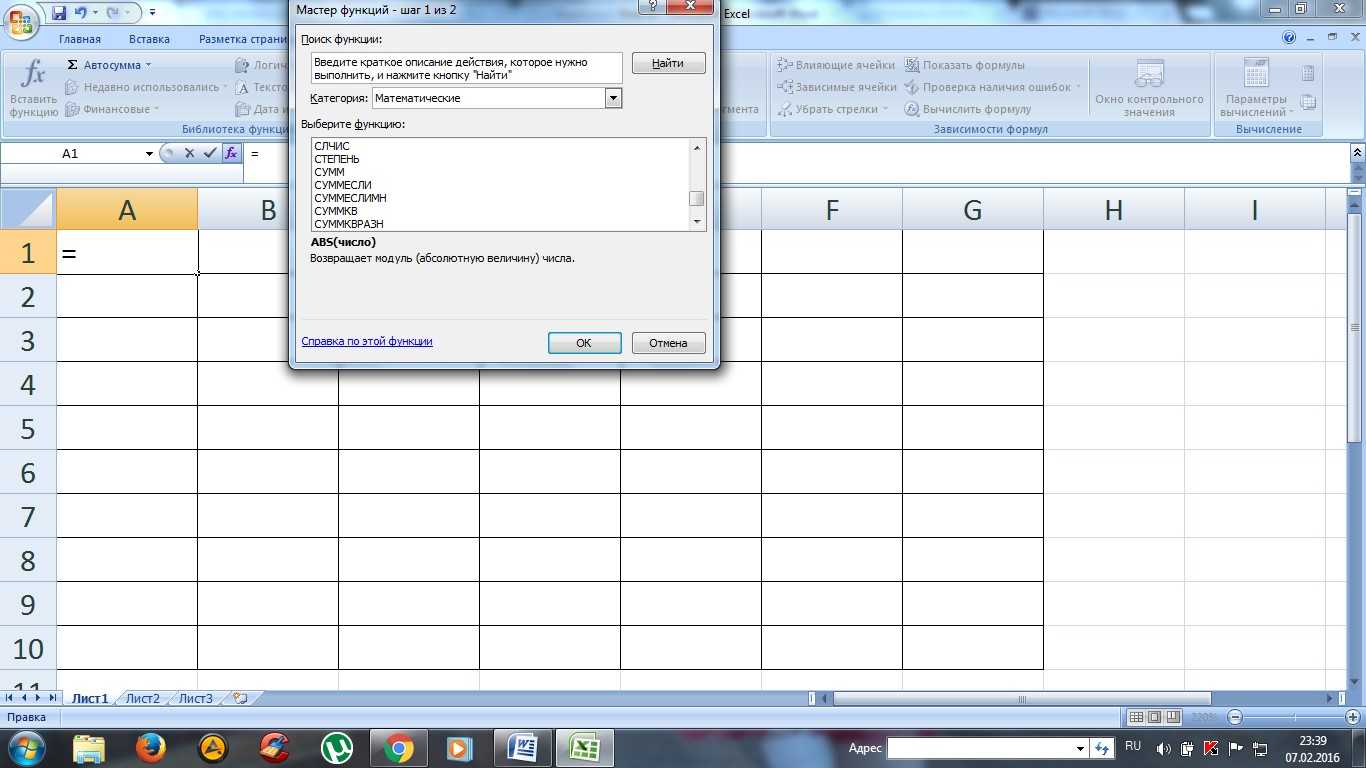
Мастер функций

Программа Excel очень удобна и проста в использовании. Все функции разделены по категориям. Если категория необходимой функции известна, то ее отбор осуществляется по ней.

В случае если функция неизвестна пользователю, то он может установить категорию «полный алфавитный перечень».

Например, дана задача, найти функцию СУММЕСЛИМН. Для этого нужно зайти в категорию математических функций и там найти нужную.

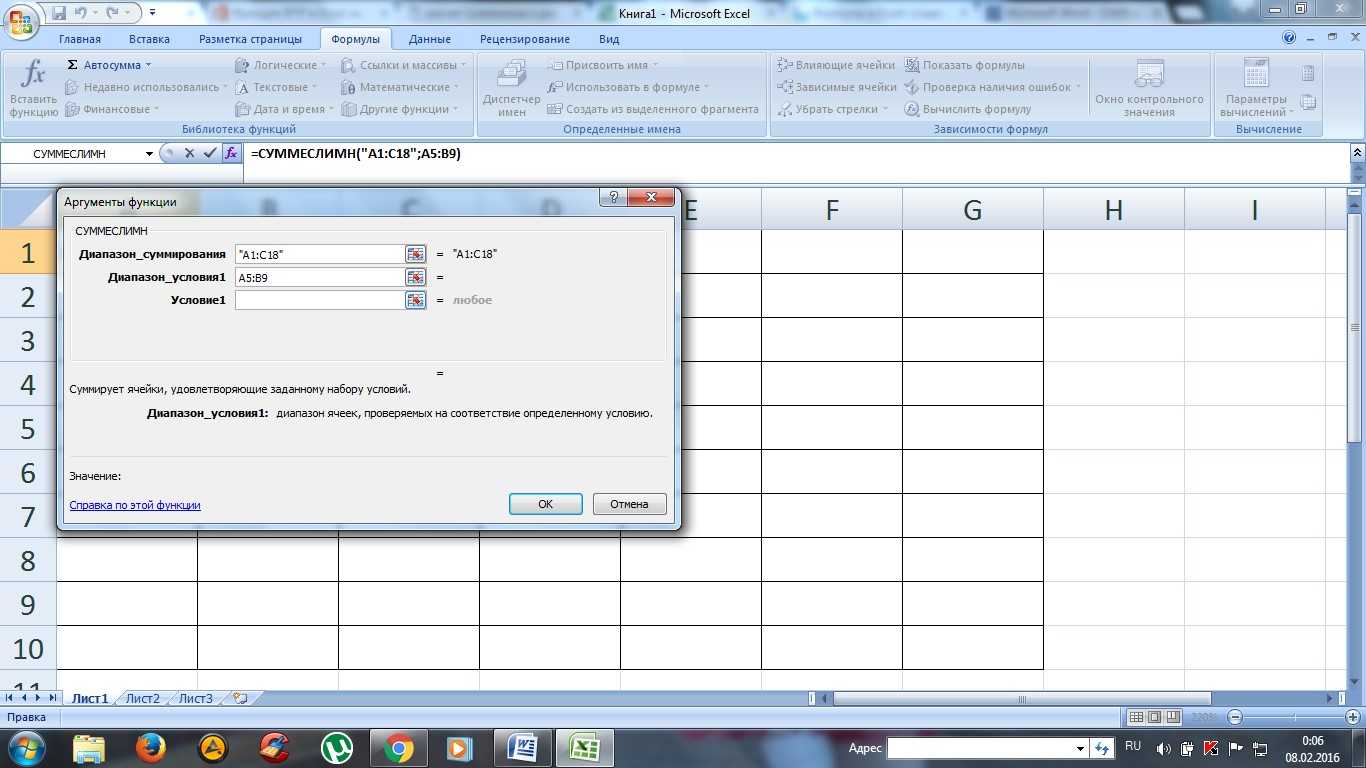
Выбор функции и заполнение полей

Далее нужно заполнить поля чисел и выбрать условие. Таким же способом можно найти самые различные функции, в том числе «СУММЕСЛИ», «СЧЕТЕСЛИ».

Вам это может быть интересно:

Использование оператора LOG

Оператор LOG относится к категории математических функций. Его задача состоит в том, чтобы вычислить логарифм данного числа по данному основанию. Синтаксис оператора set чрезвычайно прост:

=LOG(число;базовое число)

Как видите, у функции всего два аргумента.

Аргумент число — это число, от которого должен быть вычислен логарифм. Он может принимать форму числового значения и быть ссылкой на ячейку, содержащую его.

Базовый аргумент — это основа, по которой должен быть вычислен логарифм. Он также может иметь как числовую форму, так и выступать в качестве ссылки на ячейку. Этот аргумент является необязательным. Если опущено, основание считается нулевым.

Кроме того, в Excel есть еще одна функция, позволяющая вычислять логарифмы — LOG10. Основное отличие от предыдущей в том, что она может вычислять логарифмы исключительно по основанию 10, то есть только десятичные логарифмы. Синтаксис еще проще, чем у ранее введенного оператора:

=LOG10(число)

Как видите, единственным аргументом этой функции является «Число», то есть числовое значение или ссылка на ячейку, в которую оно помещено. В отличие от оператора LOG, у этой функции вообще не берется базовый аргумент, поскольку он предполагает, что база значений, которые он обрабатывает, равна 10.

Способ 1: применение функции LOG

Теперь давайте рассмотрим использование оператора LOG на конкретном примере. У нас есть столбец числовых значений. Нам нужно вычислить логарифм по основанию 5 из них.

Выбираем первую пустую ячейку на листе в той колонке, куда планируем вывести итоговый результат. Затем щелкните значок «Вставить функцию», расположенный рядом с панелью формул.
Откроется окно мастера функций. Перейдите в категорию «Математика». Выбираем в списке операторов название «LOG», после чего нажимаем на кнопку «ОК».
Откроется окно Аргументы функции LOG. Как видите, у него есть два поля, соответствующие аргументам этого оператора.В поле «Число» в нашем случае следует ввести адрес первой ячейки в столбце, где находятся исходные данные. Это можно сделать, введя его вручную в поле. Но есть и более практичный способ. Ставим курсор в указанное поле, а затем кликаем левой кнопкой мыши по ячейке таблицы, содержащей нужное нам числовое значение. Координаты этой ячейки сразу появятся в поле «Число».
В поле «Основа» просто введите значение «5», так как оно будет одинаковым для всей обрабатываемой числовой серии.

После выполнения этих манипуляций нажмите на кнопку «ОК».
Результат обработки функцией ЛОГ сразу отображается в ячейке, указанной нами на первом шаге данной инструкции.
Но мы заполнили только первую ячейку в столбце. Чтобы заполнить остальные, скопируйте формулу. Устанавливаем курсор в правый нижний угол ячейки, которая его содержит. Появится маркер заполнения, представленный в виде креста. Нажмите левую кнопку мыши и перетащите крестик в конец столбца.
Вышеописанная процедура привела к тому, что все ячейки в столбце «Логарифм» были заполнены результатом вычисления. Дело в том, что ссылка, указанная в поле «Номер», является относительной. По мере перемещения по клеткам он тоже меняется.

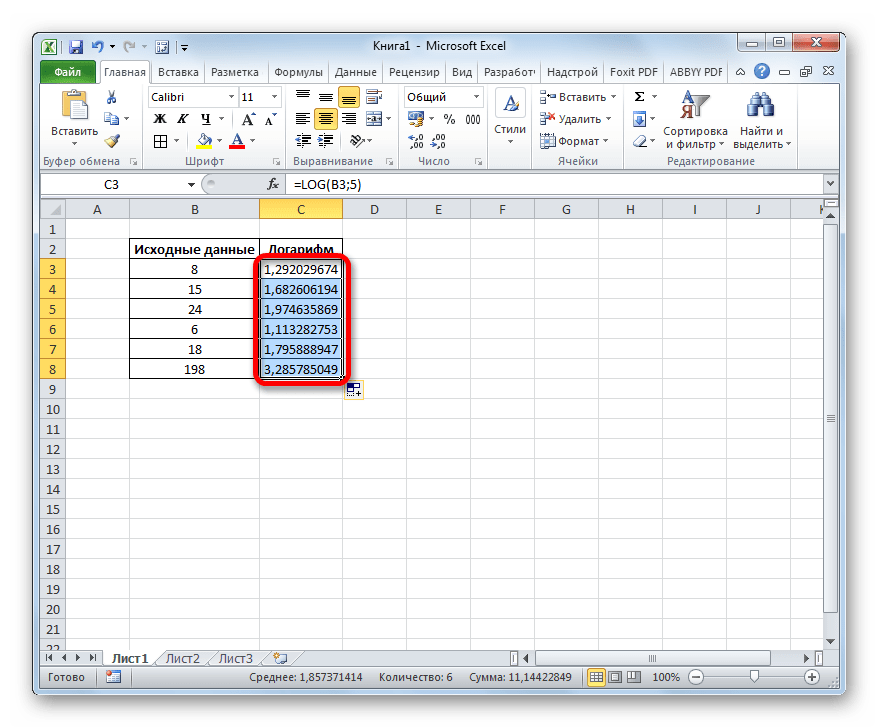
Способ 2: применение функции LOG10

Теперь давайте рассмотрим пример с оператором LOG10. Для примера возьмем таблицу с теми же исходными данными. Но теперь, конечно, задача состоит в том, чтобы вычислить логарифм чисел в столбце «Исходные данные» по основанию 10 (десятичный логарифм).

Выбираем первую пустую ячейку в столбце «Логарифм» и нажимаем на значок «Вставить функцию».
В открывшемся мастере функций снова переключаемся на категорию «Математическая», но на этот раз останавливаемся на названии «LOG10». Нажмите на кнопку «ОК» внизу окна».
Активируется окно аргументов функции LOG10. Как видите, в нем всего одно поле — «Число». Вводим в нее адрес первой ячейки в графе «Исходные данные», так же, как мы использовали в предыдущем примере. Затем нажмите кнопку ОК в нижней части окна.
Результат обработки данных, а именно десятичный логарифм заданного числа, отображается в заранее заданной ячейке.
Для выполнения расчетов для всех остальных чисел, представленных в таблице, копируем формулу с помощью маркера заполнения, так же, как и в прошлый раз. Как видите, результаты вычисления логарифмов чисел отображаются в ячейках, а это значит, что задание выполнено.

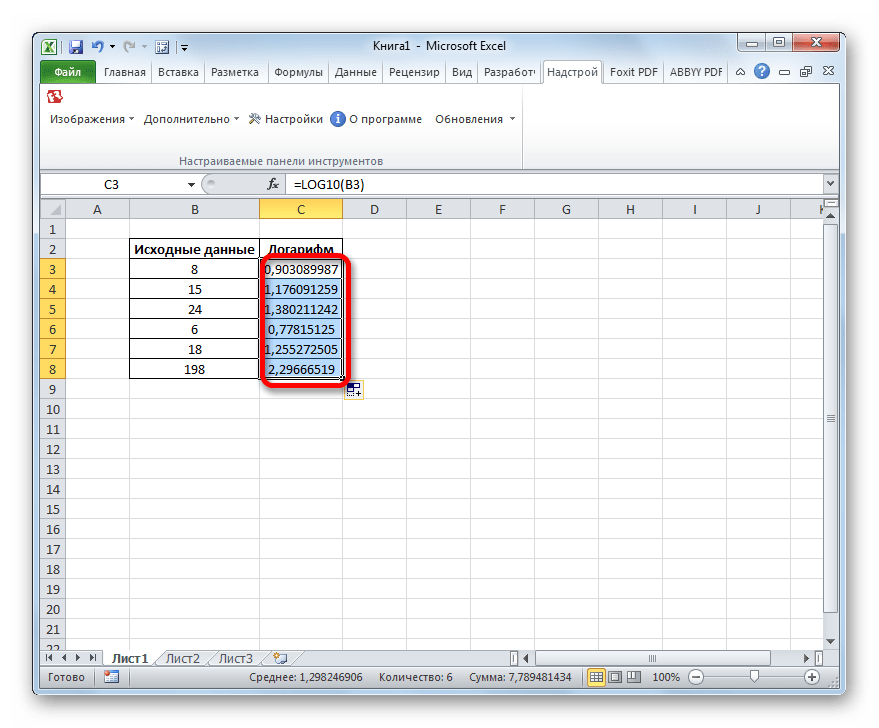
Используя функцию ЛОГ, Excel может легко и быстро вычислить логарифм указанного числа по заданному основанию. Этот же оператор может вычислять и десятичный логарифм, но для этих целей рациональнее использовать функцию LOG10.

Депозитный калькулятор со сложным процентом в Excel

Пример 2. Клиент банка внес депозит на сумму 50000 рублей с процентной ставкой 14,5% (сложные проценты). Определить, сколько времени потребуется на удвоение вложенной суммы?

Интересный факт! Для быстрого решения данной задачи можно воспользоваться эмпирическим способом приблизительной оценки сроков (в годах) на удвоение инвестиций, вложенных под сложный процент. Так называемое правило 72 (или 70 или правило 69). Для этого нужно воспользоваться простой формулой – число 72 разделить на процентную ставку: 72/14,5 = 4,9655 лет. Главный недостаток правила «магического» числа 72 заключается в погрешности. Чем выше процентная ставка, тем выше погрешность в правиле 72. Например, при процентной ставки 100% годовых погрешность в годах достигает до 0,72 (а в процентах это аж 28%!).

Для точного расчета сроков удвоения инвестиций будем использовать функцию LOG. За одно и проверим величину погрешности правила 72 при процентной ставке 14,5% годовых.

Вид исходной таблицы:

Для расчета будущей стоимости инвестиции при известной процентной ставке можно использовать следующую формулу: S=A(100%+n%)t, где:

S – ожидаемая сумма по истечению срока;
A – размер депозита;
n – процентная ставка;
t – срок хранения депозитных средств в банке.

Для данного примера эту формулу можно записать как 100000=50000*(100%+14,5%)t или 2=(100%+14,5%)t. Тогда для нахождения t можно переписать уравнение как t=log_(114,5%)2 или t=log_1,1452.

Для нахождения значения t запишем следующую формулу сложного процента по депозиту в Excel:

=LOG(B4/B2;1+B3)

Описание аргументов:

B4/B2 – соотношение ожидаемой и начальной сумм, которое является показателем логарифма;
1+B3 – прирост процентов (основание логарифма).

В результате расчетов получим:

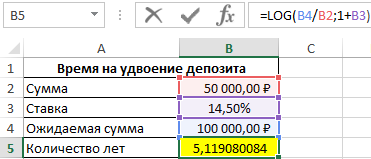
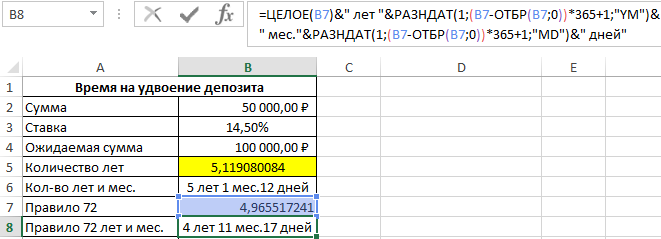
Депозит удвоится спустя немного более чем 5 лет. Для точного определения лет и месяцев воспользуемся формулой:

Функция ОТБР отбрасывает в дробном числе все что после запятой подобно функции ЦЕЛОЕ. Разница между функциями ОТБР и ЦЕЛОЕ заключается лишь в расчетах с отрицательными дробными числами. Кроме того, ОТБР имеет второй аргумент где можно указать количество оставляемых знаков после запятой. Поэтом в данном случаи можно воспользоваться любой из этих двух функций на выбор пользователя.

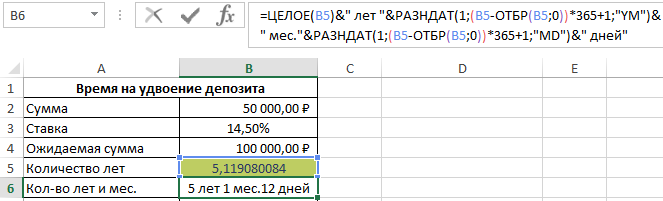
Получилось 5 лет и 1 месяц и 12 дней. Теперь сравним точные результаты с правилом 72 и определим величину погрешности. Для данного примера формула, следующая:

=72/(B3*100)

Мы должны умножить значение ячейки B3 на 100 так как ее текущее значение 0,145, которое отображается в процентном формате. В результате:

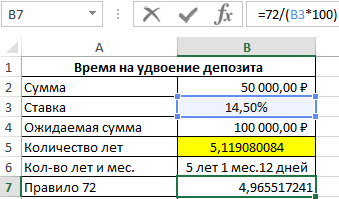
После скопируем формулу из ячейки B6 в ячейку B8, а в ячейке B9:

Посчитаем сроки погрешности:

=B5-B7

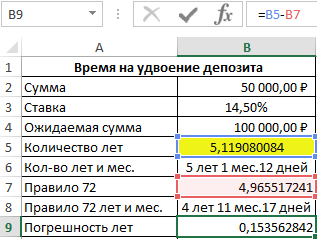
Затем в ячейку B10 снова скопируем формулу из ячейки B6. В результате получим разницу:

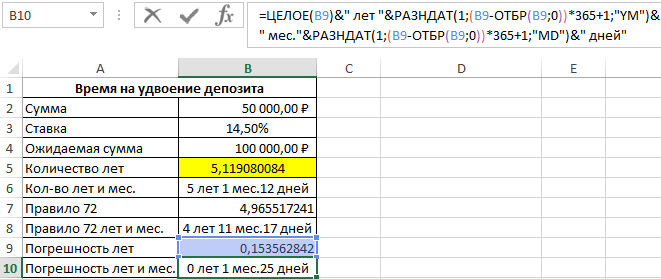
И наконец посчитаем разницу в процентах, чтобы проверить как изменяется размер отклонения и насколько существенно влияет рост процентной ставки на уровень расхождения правила 72 и факта:

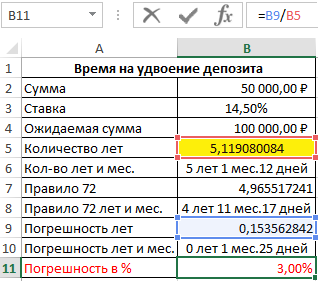
Теперь для наглядности пропорциональной зависимости роста погрешности и роста уровня процентной ставки повысим процентную ставку до 100% годовых:

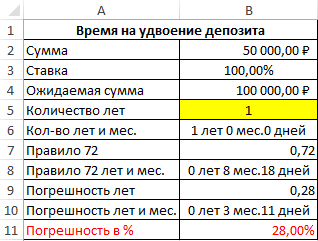
На первый взгляд разница погрешности не существенная по сравнению с 14,5% годовых — всего около 2-ух месяцев и 100% годовых — в пределах 3-х месяцев. Но доля погрешности в сроках окупаемости более чем ¼, а точнее 28%.

Составим простой график для визуального анализа как коррелируется зависимость изменения процентной ставки и процента погрешности правила 72 от факта:

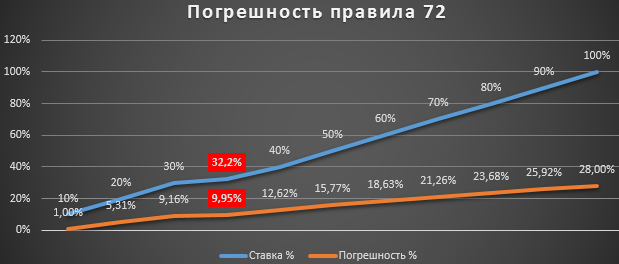
Чем выше процентная ставка, тем хуже работает правило 72. В итоге можно сделать следующий вывод: до 32,2% процентов годовых можно смело пользоваться правилом 72. Тогда погрешность составляет менее 10-ти процентов. Вполне сойдет если не требуются точные, но сложные расчеты по срокам окупаемости инвестиций в 2 раза.