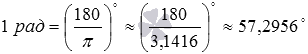Конвертация градусов в радианы в excel

Excel — конвертировать градусы в радианы и радианы в градусы

В сегодняшней статье мы поговорим о преобразовании углов в радианы, а затем радианы в градусы. Выполним эту задачу на основе выборочных данных с рис. 1.

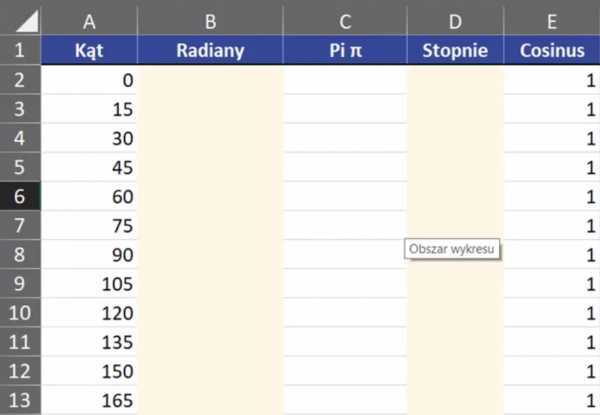
Вы должны знайте, что у нас есть 360 градусов, а это целый круг. Есть еще один способ написать это круги как радианы. Достаточно вспомнить формулу периметра, равную 2*π*r, где r — радиус окружности.Если в градусах весь круг дает 360 на , весь круг в радианах равен 2*pi. В Excel мы можем использовать функция RADIANS , аргументом которой является угол , который является значением угла, напишите формула должна выглядеть так:

= РАДИАНЫ (A2)

По подтвердив формулу и скопировав ее в строчки ниже, мы получим значение каждого углы в радианах (рис. 2).

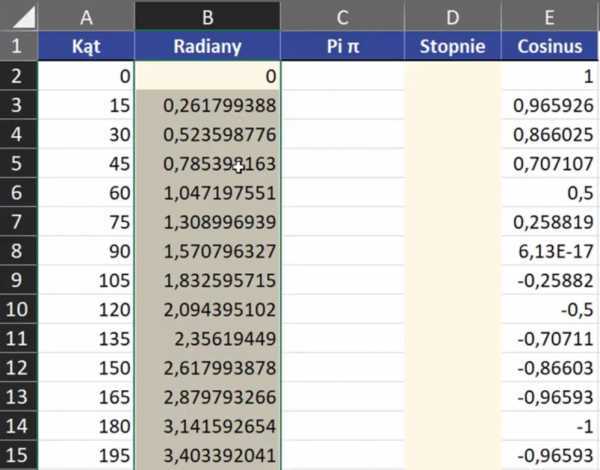
As эти значения в столбце Радианы у нас есть значение π.Чтобы точнее увидеть, какая часть значение π представляет заданный угол, нам нужно разделить значение угла в радианах по значению π. Чтобы получить значение π, мы можем использовать функцию в Excel ИП . Формула должна быть записана следующим образом:

= Б2/ПИ()

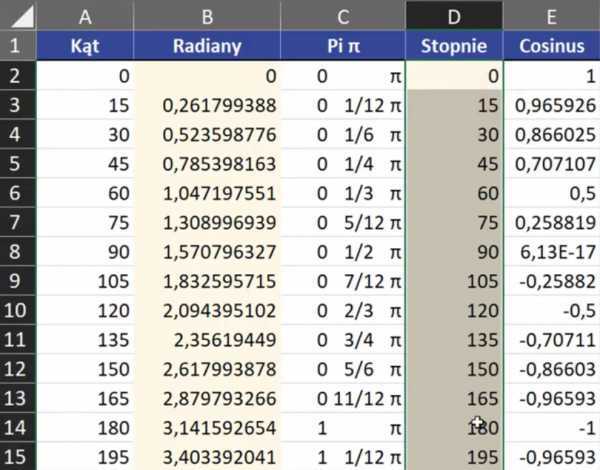
выше утверждаем формулу и копируем в ячейки ниже. Мы получим данные показан на рис.№ 3.

Сейчас сделаем обратное преобразование, т.е. переведем радианы в градусы.Мы будем использовать для этой функции ГРАДУСОВ , аргумент , угол , выраженный в радианы. Формула должна быть записана следующим образом:

= ГРАДУСЫ (B2)

выше утверждаем формулу и копируем в ячейки ниже. Получаем углы, выраженные в шаги, показанные на рис.4.

Значимое заключается в том, что тригонометрические функции, такие как косинус, используют радианы в Excel.Функция COSINUS должна выглядеть так:

= КОСИНУС (B2)

Приведенная выше формула мы утверждаем и копируем вниз. Получаем значения функции косинуса для отдельные уголки показаны на рис.№ 5,

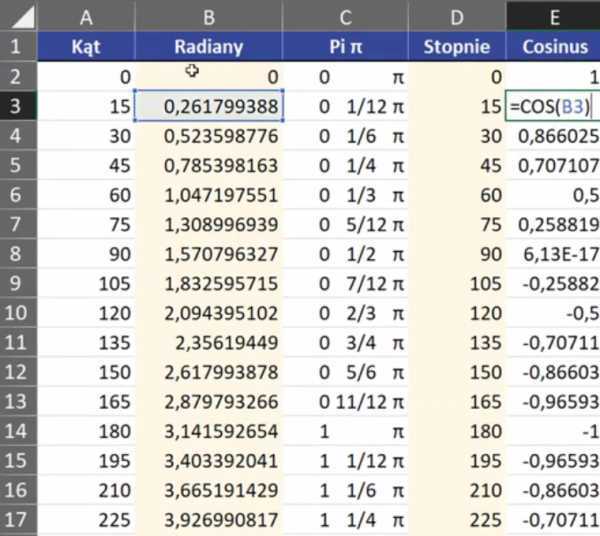
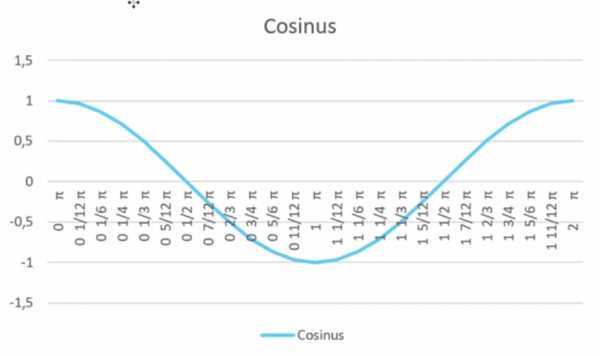
синусоида (рис. 6).

Мастер-книга Excel + промо к 35-летию

Хочу сообщить вам, что мне наконец удалось собрать средства и выполнить все формальности, чтобы стало вторым изданием моей книги Excel Master (я стал издателем) Второе издание дополнено главой (№22) Представляем блестящее дополнение (Power Query) к Excel, используемое для загрузки, объединения и предварительной обработки данных из нескольких источников.

The Excel Master Book — это история Роберта , которому нужно , чтобы хорошо знать Excel для новой работы . Книга написана в форме бесед Роберта с тренером, благодаря чему ее легче читать, чем стандартные технические книги, написанные языком «лекций».

Беседы разделены на 22 тематических главы , которые шаг за шагом знакомят вас с секретами Excel . Роберт начинает изучать интересные аспекты сортировки и фильтрации данных в Excel, проходит условное форматирование, сводные таблицы, функции поиска и многие другие темы и, наконец, изучает вводную информацию о VBA и Power Query. И все это на основе практических примеров и с большим количеством фотографий .

Чтобы вы могли следить за успехами Роберта, в книгу включены файлы Excel, над которыми работает Роберт.

В настоящее время в рамках акции ко дню рождения вы можете получить Excel Master по сниженной цене, если введете код 35 ДЕНЬ РОЖДЕНИЯ https://exceliadam.pl/produkt/ksiazka-mistrz-excela

На вышеуказанной странице вы найдете более подробное описание книги, мнения людей, купивших первое издание, и превью первой главы книги, чтобы убедиться, что форма бесед при изучении Excel для вас. Если вам понравилась книга , расскажите о ней своим друзьям.

В качестве акции к моему 35-летию вы также можете получить каждый из моих видеокурсов на Udemy всего за 35 долларов. Ссылки на курсы представлены ниже. В каждом курсе есть видео, доступные для просмотра, чтобы вы могли понять, подходит ли вам этот курс.

Power Query https://www.udemy.com/course/mistrz-power-query/?couponCode=35 ДЕНЬ РОЖДЕНИЯ

Excel Master https: // www.udemy.com/mistrz-excela/?couponCode=35URODZINY

Информационные панели https://www.udemy.com/course/excel-dashboardy/?couponCode=35 ДЕНЬ РОЖДЕНИЯ

Мастер Формулы https://www.udemy.com/course/excel-mistrz-formul/?couponCode=35 ДЕНЬ РОЖДЕНИЯ

VBA https://www.udemy.com/course/excel-vba-makra/?couponCode=35 ДЕНЬ РОЖДЕНИЯ

Microsoft Power BI https://www.udemy.com/course/power-bi-microsoft/?couponCode=35 ДЕНЬ РОЖДЕНИЯ

Формулы перевода градусов в радианы и радианов в градусы

Из равенства вида , которое мы получили в предыдущем пункте, легко выводятся формулы перевода радианов в градусы и градусов в радианы
.

Разделив обе части равенства на пи, получаем формулу, выражающую один радиан в градусах: . Эта формула означает, что градусная мера угла в один радиан равна 180/π
. Если же поменять местами левую и правую части равенства , после чего разделить обе части на 180
, то получим формулу вида . Она выражает один градус в радианах.

Чтобы удовлетворить свое любопытство, вычислим приближенную величину угла в один радиан в градусах и величину угла в один градус в радианах. Для этого возьмем значение числа пи с точностью до десятитысячных, подставим его в формулы и , и проведем вычисления. Имеем 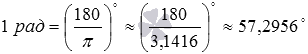и . Итак, один радиан приближенно равен 57
градусам, а один градус – 0,0175
радиана.

Наконец, от полученных соотношений и перейдем к формулам перевода радианов в градусы и наоборот, а также рассмотрим примеры применения этих формул.

Формула перевода радианов в градусы
имеет вид: . Таким образом, если известна величина угла в радианах, то умножив ее на 180
и разделив на пи, получим величину этого угла в градусах.

Пример.

Дан угол в 3,2
радиана. Какова мера этого угла в градусах?

Решение.

Воспользуемся формулой перехода от радианов к градусам, имеем

Ответ:

.

Формула перевода градусов в радианы
имеет вид . То есть, если известна величина угла в градусах, то умножив ее на пи и разделив на 180
, получим величину этого угла в радианах. Рассмотрим решение примера.

Необходимость в измерении углов появилась у людей с тех пор, как цивилизация достигла минимального технического уровня. Всем известна феноменальная точность соблюдения наклона и ориентации по странам света, обеспеченная строителями египетских пирамид. Современную градусную меру углов, как сейчас считается, изобрели древние аккадцы.

Использование формулы в Excel для перевода радиан в градусы

• Откройте программу Excel.
• Выберите ячейку, в которой будет находиться результат перевода радиан в градусы.
• Введите формулу в выбранную ячейку: =ГРАДУСЫ(радианы). Замените радианы на значение, которое нужно перевести в градусы.
• Нажмите клавишу Enter, чтобы вычислить результат.
• Excel автоматически выполнит операцию и покажет результат перевода радиан в градусы в выбранной ячейке.
• Для перевода нескольких значений одновременно, повторите шаги 2-5 для каждого значения.

Используя эту простую формулу, вы можете быстро и легко перевести радианы в градусы в программе Excel. Это особенно полезно, если у вас есть большой набор данных, который требуется перевести в другие единицы измерения.

Функция ГРАДУСЫ для выполнения геометрических расчетов в Excel

Функция ГРАДУСЫ в Excel используется для преобразования радианной меры угла в соответствующей величину, выраженную в градусах, и возвращает полученное значение.

Примеры использования функции ГРАДУСЫ в Excel

Пример 1. Для определения количества оборотов вала электродвигателя используется датчик, который определяет и возвращает значение угла в радианах. Спустя минуту работы двигателя было получено значение 2350π. Определить количество оборотов за 1 минуту.

Исходные данные:

Для расчета используем формулу:

=ГРАДУСЫ(2350*ПИ())/360

Описание составляющих:

• 2350*ПИ() – функция, преобразует радианную меру угла 2350*ПИ() и возвращающая значение, выраженное в градусах.
• 360 – полное количество градусов в окружности.

В результате получим:

То есть, двигатель сделал 1175 оборотов за 1 минуту.

Расчет траектории движения с помощью функции ГРАДУСЫ в Excel

Пример 2. Автомобиль движется по круговой трассе. Определить, на какой угол он отклонится относительно начальной точки пути через 17 минут, если за 10 минут он проехал расстояние, равное радиусу окружности трассы.

Исходные данные:

Для определения угловой скорости разделим количество радиан на время пути. Известно, что за 10 минут был пройден путь, равный радиусу окружности. Из этого следует, что автомобиль отклонился на 1 радиан от начальной точки пути. Искомая угловая скорость:

• 1 – количество радиан;
• 10 – время пути в минутах.

Результат:

То есть, 1 рад/мин. Для нахождения искомого угла используем формулу:

Описание:

• B3 – скорость в рад/мин;
• 17 – время пути в минутах.

Результат вычислений:

То есть, автомобиль отклонится примерно на 97°.

Как перевести радианы в градусы в Excel

Пример 3. Определить угол (в градусах), который проходит минутная стрелка механических часов, если часовая успела отклониться от момента отсчета на 0,05236 радиана?

Исходные данные:

Описание величин:

• B3 – количество делений для минутной стрелки.
• B3/B2 – количество делений, которые проходит часовая стрелка за полный оборот минутной. То есть, выражение B3/(B3/B2) определяет, во сколько раз скорость минутной стрелки превышает скорость часовой стрелки.
• B4 – отклонение часовой стрелки в радианах.

Полученный результат:

Минутная стрелка отклонится на 36°.

Особенности использования функции ГРАДУСЫ в Excel

Функция ГРАДУСЫ имеет следующую синтаксическую запись:

=ГРАДУСЫ(угол)

Единственным аргументом данной функции является угол (обязательный для заполнения). Он характеризует величину угла, выраженную в радианах.

Примечания 1:

1. Excel выполняет автоматическое преобразование данных к требуемому типу в тех случаях, где это возможно. Например, запись типа =ГРАДУСЫ(ИСТИНА) соответствует записи =ГРАДУСЫ(1) и вернет значение 57,29577951, то есть количество градусов в 1 радиане.
2. Рассматриваемая функция может принимать в качестве аргумента числа из диапазона отрицательных значений. Например, если в аргументе функции указано значение (-1,5), тогда результат равен -85,94366927.
3. Функция вернет код ошибки #ЗНАЧ!, если в качестве аргумента была передана текстовая строка, которая не может быть преобразована в числовой тип данных.

Примечания 2:

1. В геометрии углом считается фигура, образованная двумя лучами, которые проведены из одной точки (точки их пересечения), при этом данные лучи называются сторонами угла, а точка – его вершиной.
2. Градусы и радианы являются двумя количественными характеристиками размера угла.
3. 1 градус соответствует 1/180 развернутого угла, то есть угла, стороны которого лежат на одной прямой.
4. Если точка пересечения сторон угла (вершина) является центром окружности, а его стороны – радиусы данной окружности, то радиан – центральный угол, радиусы и длина образованной данным углом дуги являются равными величинами (AO=BO=AmB):
5. Между градусной и радианной мерами угла установлена следующая взаимосвязь: град=2π*рад/360°, где рад – количество радиан, а град – рассчитываемое количество градусов.

Вычисление значения арктангенса

Арктангенс является тригонометрическим выражением. Он исчисляется в виде угла в радианах, тангенс которого равен числу аргумента арктангенса.

Для вычисления данного значения в Экселе используется оператор ATAN, который входит в группу математических функций. Единственным его аргументом является число или ссылка на ячейку, в которой содержится числовое выражение. Синтаксис принимает следующую форму:

Способ 1: ручной ввод функции

Для опытного пользователя, ввиду простоты синтаксиса данной функции, легче и быстрее всего произвести её ручной ввод.

1. Выделяем ячейку, в которой должен находиться результат расчета, и записываем формулу типа:

   Вместо аргумента «Число», естественно, подставляем конкретное числовое значение. Так арктангенс четырех будет вычисляться по следующей формуле:

   Если числовое значение находится в какой-то определенной ячейке, то аргументом функции может служить её адрес.

2. Для вывода результатов расчета на экран нажимаем на кнопку Enter.

Способ 2: вычисление при помощи Мастера функций

Но для тех пользователей, которые ещё не полностью овладели приемами ручного ввода формул или просто привыкли с ними работать исключительно через графический интерфейс, больше подойдет выполнение расчета с помощью Мастера функций.

1. Выделяем ячейку для вывода результата обработки данных. Жмем на кнопку «Вставить функцию», размещенную слева от строки формул.
2. Происходит открытие Мастера функций. В категории «Математические» или «Полный алфавитный перечень» следует найти наименование «ATAN». Для запуска окна аргументов выделяем его и жмем на кнопку «OK».

3. После выполнения указанных действий откроется окно аргументов оператора. В нем имеется только одно поле – «Число». В него нужно ввести то число, арктангенс которого следует рассчитать. После этого жмем на кнопку «OK».

   

   

   

   

   

   

   

   

   

   

   Также в качестве аргумента можно использовать ссылку на ячейку, в которой находится это число. В этом случае проще не вводить координаты вручную, а установить курсор в область поля и просто выделить на листе тот элемент, в котором расположено нужное значение. После этих действий адрес этой ячейки отобразится в окне аргументов. Затем, как и в предыдущем варианте, жмем на кнопку «OK».

4. После выполнения действий по вышеуказанному алгоритму в предварительно обозначенной ячейке отобразится значение арктангенса в радианах того числа, которое было задано в функции.

Урок: Мастер функций в Excel

Как видим, нахождение из числа арктангенса в Экселе не является проблемой. Это можно сделать с помощью специального оператора ATAN с довольно простым синтаксисом. Использовать данную формулу можно как путем ручного ввода, так и через интерфейс Мастера функций.

Мы рады, что смогли помочь Вам в решении проблемы.

Помогла ли вам эта статья?

Да Нет

Разберем как перевести градусы в радианы (и наоборот) с помощью стандартных функций Excel, а также узнаем как это можно сделать без применения функций.

В повседневной жизни мы привыкли оперировать градусами, как основной единицей измерения углов. Однако не всегда градусы удобно использовать в расчетах, к примеру, в математическом анализе при работе с тригонометрическими функциями аргумент по умолчанию считается выраженным в радианах.

Вдобавок в тригонометрических функциях в Excel, таких как SIN (синус), COS (косинус), TAN (тангенс), в качестве аргумента указывается угол в радианной мере, поэтому для корректной работы с данными формулами необходимо предварительно перевести его в радианы. И наоборот, в обратных тригонометрических функциях в Excel, таких как ASIN (арксинус), ACOS (арккосинус), ATAN (арктангенс), уже возвращаемое значение выражается в радианной мере, поэтому при необходимости результат нужно будет переводить уже в градусы.

Перед тем как перевести угол из градусной меры в радианную вспомним, что радиан — это угол, соответствующий дуге, длина которой равна ее радиусу. Из определения следует, что один полный оборот в 360° составляет 2π радиан, откуда можно получить формулу перевода угла из одной системы измерения в другую:

В Excel есть две стандартные функции, которые позволяют перевести градусы в радианы и наоборот. Давайте подробно остановимся на особенностях применения каждой из них.

Как сделать тангенс в excel?

Формулы тригонометрии – редкая и сложная задача для работы в Майкрософт Эксель. Тем не менее, здесь есть ряд встроенных функций, помогающих в геометрических расчетах. В этом посте мы рассмотрим основные из них, которые, в компании с учебниками и справочниками, могут решить многие математические задачи. Они участвуют в расчете площади, объема, угла наклона и т.д. Если Вы школьник, студент, или работаете, например, в сфере строительства, эта статья будет Вам очень полезна.

Для корректного расчета геометрических величин, Вам понадобятся познания в элементарных расчетах и некоторые из функций Excel. Так, функция КОРЕНЬ извлечет квадратный корень из заданного числа. Например, запишем: =КОРЕНЬ(121), и получим результат «11». Хотя правильным решением будет «11» и «-11», программа возвращает только положительный результат в таких случаях.

Еще одна функция – ПИ(), не нуждается в аргументах и является зарезервированной константой. Ее результатом будет известное число 3,1415, описывающее соотношение длины окружности к ее диаметру. Эту функцию-константу можно активно применять в расчетах.

Тригонометрические функции Excel, до которых мы еще доберемся, используют запись угла в радианах. Эта общепринятая практика часто бывает ненаглядной, ведь нам привычнее выражать угол в градусах. Чтобы устранить эту проблему, есть две функции преобразования величин:

• ГРУДУСЫ(Угол в радианах) – преобразует радиальные величины в градусы
• РАДИАНЫ(Угол вградусах) – наоборот, преобразует градусы в радианы.

Пользуясь этими функциями, Вы обеспечиваете совместимость и наглядность вычислений.

Конечно, Вы знаете эти функции:

• COS(Угол в радианах) – косинус угла, соотношение между прилежащим катетом и гипотенузой прямоугольного треугольника
• SIN(Угол в радианах) – синус угла, отношение противолежащего катета к гипотенузе

Для удобства чтения формул, можно использовать вложенную функцию РАДИАНЫ и задать угол в градусах. Например, формула =COS(РАДИАНЫ(180)) вернет результат «-1».

Еще две функции Вам так же знакомы – это тангенс и котангенс:

• TAN(Угол в радианах) – отношение длины противолежащего катета к прилежащему
• COT(Угол в радианах) – обратная величина – соотношение прилежащего угла к противолежащему.

Здесь так же рекомендую использовать функции преобразования величин РАДИАНЫ и ГРАДУСЫ.

Среди прочих тригонометрических функций можно выделить секанс и косеканс:

• SEC(Угол в радианах) – отношение гипотенузы к прилежащему катету
• CSC(Угол в радианах) – отношение гипотенузы к противолежащему катету

Легко заметить, что секанс – обратно-пропорциональная величина к косинусу, косеканс – к синусу.

Такие функции выполняют обратный расчет по отношению к перечисленным выше:

• Арккосинус – это угол, который образуют прилежащий катет и гипотенуза с определенным косинусом. Чтобы посчитать эту величину, используйте функцию ACOS(Значение косинуса).
• Арксинус – угол между противолежащим катетом и гипотенузой с определенным синусом, вычисляется так: ASIN(Значение синуса).
• Арктангенс – угол между противолежащим и прилежащим катетами для заданного тангенса: ATAN(Значение тангенса).
• Арккотангенс – угол, для которого справедливо заданное значение котангенса: ACOT(Значение котангенса).

Все перечисленные функции вернут угол в радианах. Естественно, для перевода его в градусы, используем функцию ГРАДУСЫ.

Знание и умелое применение перечисленных функций, конечно, не сделает Вас богом в тригонометрии, но все же позволит выполнить сложные расчеты, «стоимость» которых часто довольно высока. Научитесь комбинировать их с другими функциями, построением графиков, чтобы получить максимальный эффект от полученных знаний.

Это все о тригонометрических функциях, спасибо, что читаете мой блог и развиваетесь в своих знаниях. Следующую статью я напишу об округлении чисел и очень Вам рекомендую ее не пропустить!

Поделиться, добавить в закладки или статью

Арктангенс входит в ряд обратных тригонометрических выражений. Он противоположен тангенсу. Как и все подобные величины, он вычисляется в радианах. В Экселе есть специальная функция, которая позволяет производить расчет арктангенса по заданному числу. Давайте разберемся, как пользоваться данным оператором.

Что означают градус и радиан

Так вот, мерой расхождения двух лучей, проведённых из одной точки друг от друга, будет градусное расстояние
. Что такое градус? В переводе «градус» означает «шаг». Всего таких «шагов» может быть 360°. Это число было придумано ещё в глубокой древности математиками и астрономами, пользовавшимися шестидесятиричной системой счисления. Они брали круг, из центра которого проводили два радиуса. Мерой расхождения этих радиусов друг от друга был градус. Когда расстояние между радиусами в градусах отсчитывали против часовой стрелки, такой угол считался положительным, а когда против часовой — отрицательным.

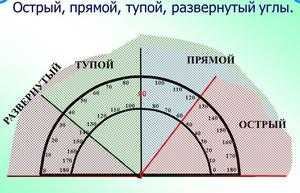Вращая один радиус относительно другого против часовой стрелки, мы будем получать разные углы. Когда эти отрезки совпадают, то между ними будет 0°, когда же отрезки отсекают сектор круга, равный одной четверти полного круга, то угол между ними составит 90°. Вращая дальше таким образом, мы получим следующие углы: 180° — радиусы лежат на диаметре круга и делят его пополам, 270° — радиусы отсекают три четверти круга, 360° — радиусы совпадают. Таким образом, полный круг составляет 360°. Для измерения углов существует транспортир
.

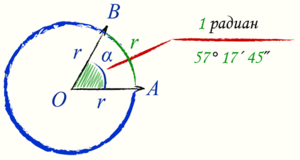Кроме градусной меры для измерения углов применяют меру радианную
. Радиан — это мера центрального угла. «Радиан» означает «связанный с радиусом». Если из центра окружности радиусом R провести два луча, то они на ней отсекут дугу, длина которой l. Так вот, угол α между указанными лучами называется центральным
. Чтобы его измерить, нужно длину дуги окружности разделить на её радиус: α=l/R. Получится значение, выраженное в радианах (рад). Поскольку любому углу на плоскости можно сопоставить такой же центральный угол, то встаёт вопрос, как от обычной градусной меры перейти к радианной.

Функции Excel для перевода из РАДИАНЫ в ГРАДУСЫ и обратно

Функция РАДИАНЫ (на английском RADIANS) – это одна из математических и тригонометрических функций, которая часто применяется для инженерных расчетов. Данная функция в Excel легко преобразует градусы в радианы – угол, соответствующий дуге, а длина этой дуги равна ее радиусу.

Как работает функция индекс в Excel?

ПРИМЕР 1. Для инженерных расчетов связанных с движением по окружности зачастую необходимо вычислять угловые скорости и переводить градусы в радианы и радианы в градусы. В Excel для этого предусмотрены специальные функции. Для упрощения математических расчетов может потребоваться выразить в одной и второй величине.

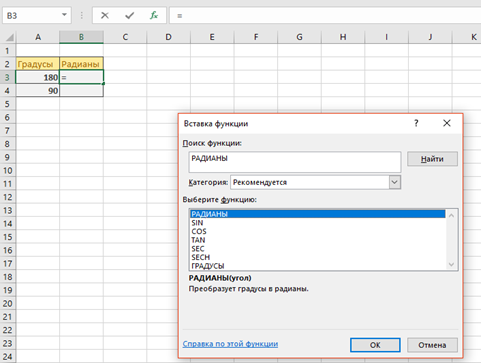
Нам необходимо найти сколько будет в Радианах 180°. Нажимаем кнопку fx возле строки формул для вызова окна выбора функций «Вставка функции» (SHIFT+F3) и в окне поиска вводим функцию «РАДИАНЫ». Выбираем высветившуюся нужную функцию, как показано на ниже рисунке.

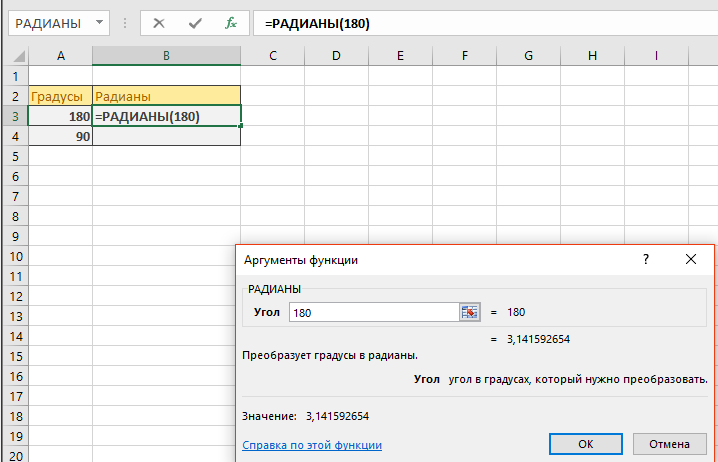
Появляется окно, в которое нужно ввести аргументы функции. Вводим значение 180, так как нам нужно найти сколько будет радиан в 180 градусах. Жмем ОК.

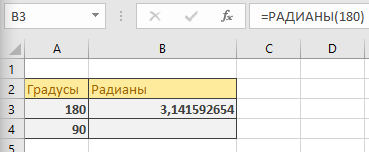
В 180 градусах будет 3,1415 радиан.

Найдем радианы для угла в 90°. Откроем окно функций и введем функцию, что необходимо вычислить. Находим ее в окне мастера функций и выбираем аргумент 90.

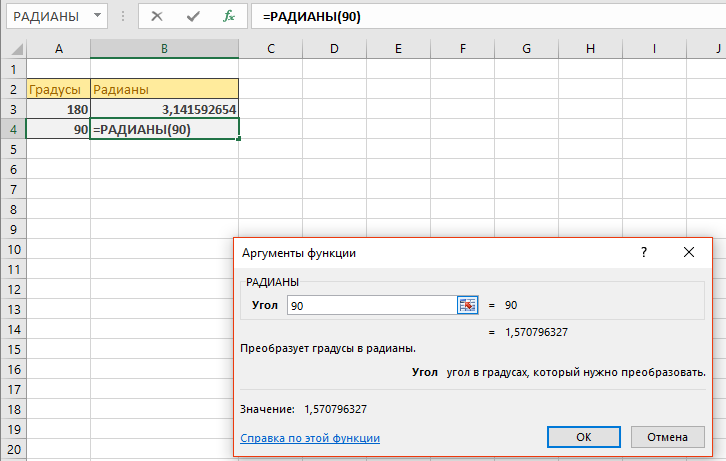
ОК. В 90 градусах будет 1,5707 радиан.

В следующих примерах рассмотрим, как конвертировать эти единицы измерения углов в обоих направлениях.

Как перевести Радианы в Градусы средствами Excel

ПРИМЕР 2. Иногда нужно единицу измерения углов rad перевести в значение gradus° . Для этого предусмотрена функция ГРАДУСЫ. Она позволяет перевести значения выраженные в радианах в градусы в десятичном исчислении.

Нам нужно найти сколько будет в градусах 4,1 радианы. Нажимаем кнопку fx для вызова окна выбора функции и в окне поиска вводим соответствующее название функции.

Появляется окно в которое нужно ввести аргументы функции. Вводим значение 4,1, так как нам следует найти сколько будет gradus° в 4,1 rad . Нажимаем ОК.

Для исходного значения 4,1 получаем ровно 235 градусов.

Таким образом выполняется перевод из радиан в градусы в Excel.

Сколько радиан в нескольких значениях градуса?

ПРИМЕР 3. Иногда нужно определить сколько радиан в сразу нескольких значениях градуса и вводить тогда каждый раз аргумент очень долго. В таком случае можно воспользоваться немного иным способом конвертирования величин для измерения углов.

Требуется найти сколько будет в Радианах 45, 67, 23, 12, 57 градусов. Нажимаем кнопку fx (SHIFT+F3) для вызова окна выбора функции и в окне поиска вводим необходимо функцию как показано ниже на рисунке. Указываем на высветившуюся функцию.

Выбираем диапазон градусов (А3 по А7) и нажимаем на кнопку ОК.

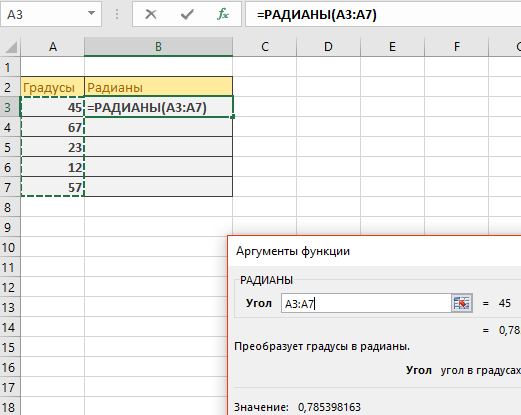
Протягиваем строку вниз для того, чтобы мы могли узнать сколько радиан во всех приведенных градусах, не вызывая функцию по несколько раз.

Получаем сразу значения всех радиан:

Для 45 градусов – это 0,7853, для 67 градусов – это 1,1693, для 23 градусов – это 0,4014, для 12 градусов – это 0,2094, для 57 градусов – это 0,9948 в радианах.

• Excel Formula Examples
• Создать таблицу
• Форматирование
• Функции Excel
• Формулы и диапазоны
• Фильтр и сортировка
• Диаграммы и графики
• Сводные таблицы
• Печать документов
• Базы данных и XML
• Возможности Excel
• Настройки параметры
• Уроки Excel
• Макросы VBA
• Скачать примеры