Расчет среднего квадратичного отклонения в microsoft excel

Найдите среднее квадратичное отклонение

Среднее квадратичное отклонение является одним из наиболее часто используемых индикаторов, показывающих разброс данных относительно среднего значения. Для расчета среднего квадратичного отклонения в Excel следуйте этим простым шагам:

• Шаг 1: Введите данные, для которых нужно вычислить среднее квадратичное отклонение, в отдельном столбце.
• Шаг 2: Введите формулу для вычисления среднего значения данных с помощью функции = СРЗНАЧ.
• Шаг 3: Введите формулу для вычисления квадратичных отклонений каждого значения данных от среднего значения с помощью функции =КВ.ОТКЛ.
• Шаг 4: Введите формулу для вычисления среднего квадратичного отклонения данных, используя функцию = СР.КВ.ОТКЛ.

Среднеквадратическое отклонение является одним из самых важных показателей в статистике, который может помочь вам понять, насколько близко ваши результаты находятся друг к другу. В Excel можно легко вычислить это значение с помощью формул.

Таблица нормального распределения

Таблицы нормального распределения встречаются двух типов:

— таблица плотности;

— таблица функции (интеграла от плотности).

Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы. 

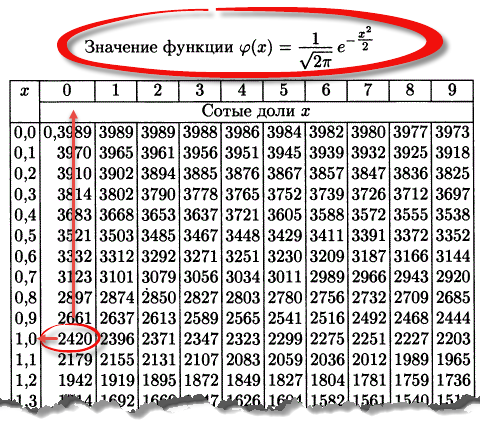
В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец , т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен). 

Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.

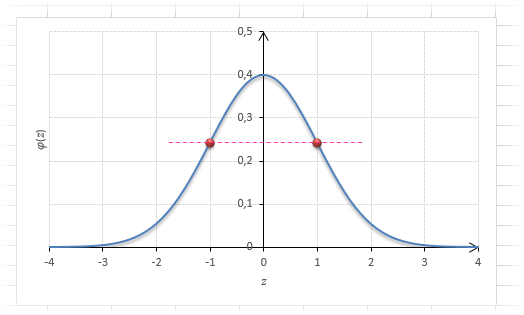
Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.

На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.

В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.

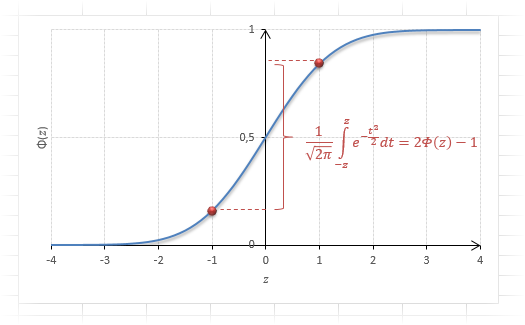
Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:

Это факт показан на картинке:

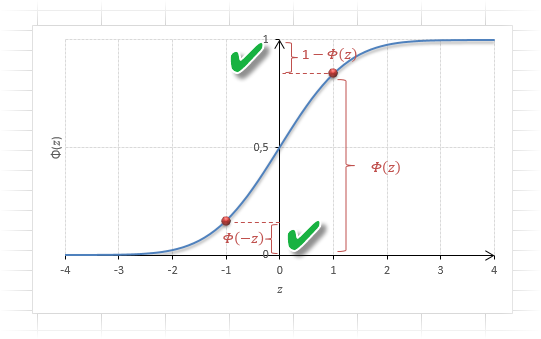
Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.

Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:

Для наглядности можно взглянуть на рисунок.

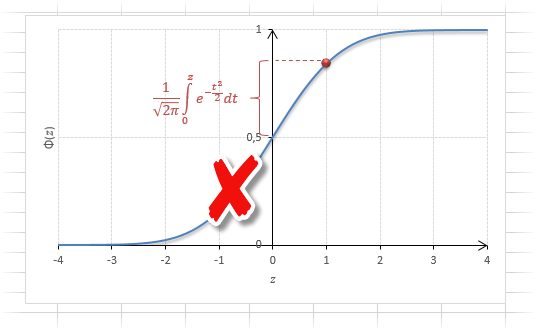
На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.

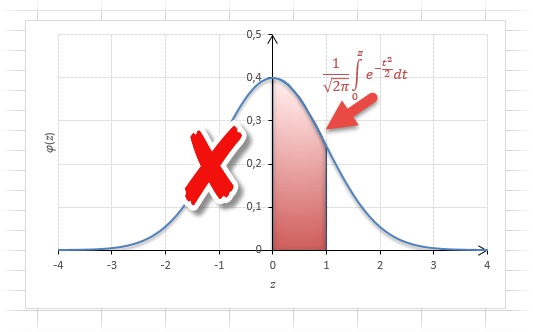
Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:

Рисунок ниже.

Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.

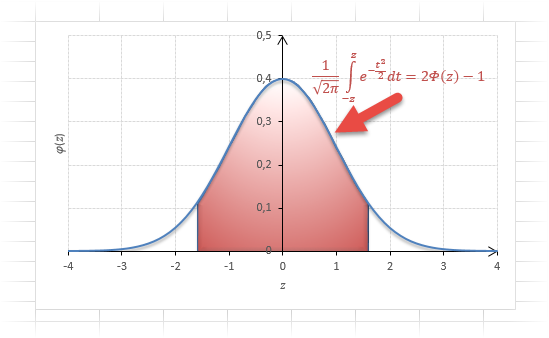
Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу. Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:

Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:

Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.

Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.

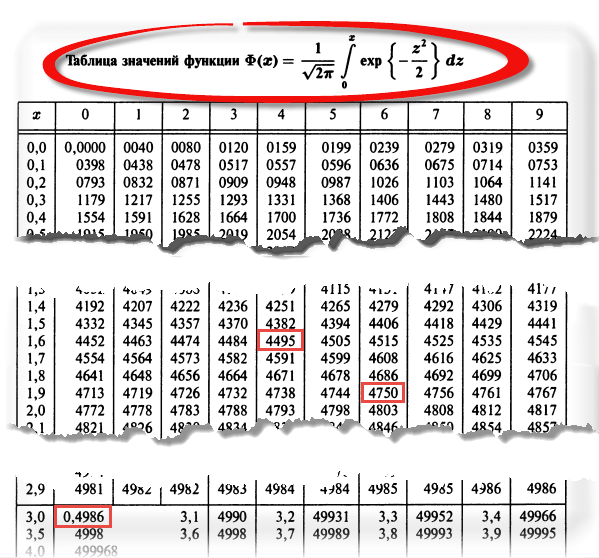
Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.

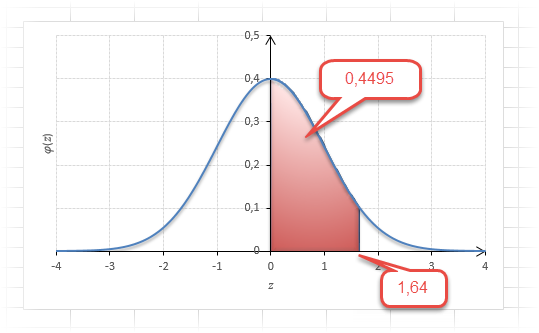
То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.

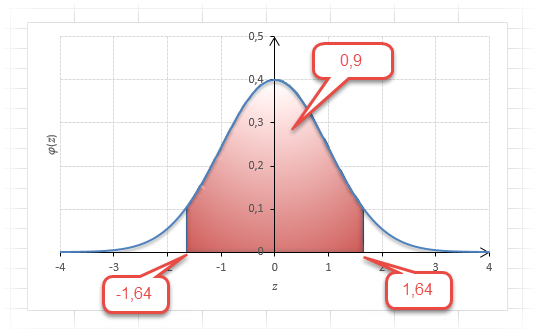
Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).

Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).

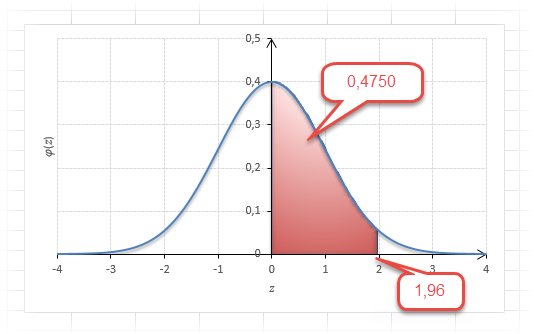
Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.

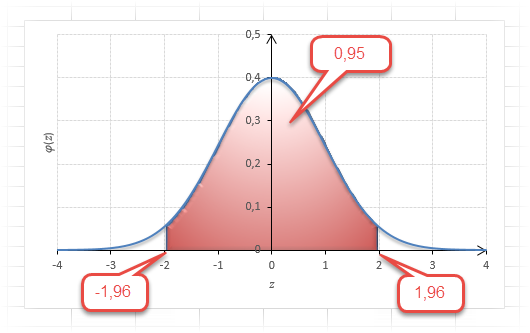
Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.

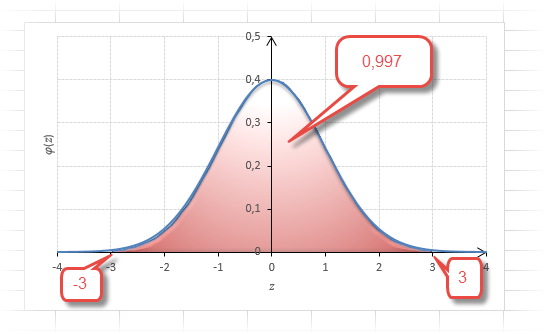
Так выглядит правило 3 сигм для нормального распределения на диаграмме.

С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.

Расчет дисперсии, среднеквадратичного (стандартного) отклонения, коэффициента вариации в Excel

Проведение любого статистического анализа немыслимо без расчетов. В это статье рассмотрим, как рассчитать дисперсию, среднеквадратичное отклонение, коэффиент вариации и другие статистические показатели в Excel.

Максимальное и минимальное значение

Начнем с формул максимума и минимума. Максимум – самое большое значение из анализируемого набора данных, минимум – самое маленькое. Это крайние значения в совокупности данных, обозначающие границы их вариации. Например, минимальные/максимальные цены на что-нибудь, выбор наилучшего или наихудшего решения задачи и т.д.

Для расчета этих показателей есть специальные функции — МАКС и МИН соответственно. Доступ есть прямо из ленты, в выпадающем списке авосумммы.

Если использовать вставку функций, то следует обратиться к категории «Статистические».

В общем, для вызова функции максимума или минимума действий потребуется не больше, чем для расчета средней арифметической.

Среднее линейное отклонение

Среднее линейное отклонение представляет собой среднее из абсолютных (по модулю) отклонений от средней арифметической в анализируемой совокупности данных. Математическая формула имеет вид:

где

a – среднее линейное отклонение,

X – анализируемый показатель,

X̅ – среднее значение показателя,

n – количество значений в анализируемой совокупности данных.

В Эксель эта функция называется СРОТКЛ.

После выбора функции СРОТКЛ указываем диапазон данных, по которому должен произойти расчет. Нажимаем «ОК».

Среднеквадратичное отклонение

Среднеквадратичное отклонение (СКО) – это корень из дисперсии. Этот показатель также называют стандартным отклонением и рассчитывают по формуле:

по генеральной совокупности

по выборке

Можно просто извлечь корень из дисперсии, но в Excel для среднеквадратичного отклонения есть готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).

Стандартное и среднеквадратичное отклонение, повторюсь, — синонимы.

Далее, как обычно, указываем нужный диапазон и нажимаем на «ОК». Среднеквадратическое отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными. Об этом ниже.

Коэффициент вариации

Все показатели, рассмотренные выше, имеют привязку к масштабу исходных данных и не позволяют получить образное представление о вариации анализируемой совокупности.

Для получения относительной меры разброса данных используют коэффициент вариации, который рассчитывается путем деления среднеквадратичного отклонения на среднее арифметическое.

Формула коэффициента вариации проста:

Для расчета коэффициента вариации в Excel нет готовой функции, что не есть большая проблема. Расчет можно произвести простым делением стандартного отклонения на среднее значение. Для этого в строке формул пишем:

=СТАНДОТКЛОН.Г()/СРЗНАЧ()

Коэффициент вариации обычно выражается в процентах, поэтому ячейку с формулой можно обрамить процентным форматом. Нужная кнопка находится на ленте на вкладке «»:

Изменить формат также можно, выбрав «Формат ячеек» из контекстного меню после выделения нужной ячейки и нажатия правой кнопкой мышки.

Коэффициент вариации, в отличие от других показателей разброса значений, используется как самостоятельный и весьма информативный индикатор вариации данных. В статистике принято считать, что если коэффициент вариации менее 33%, то совокупность данных является однородной, если более 33%, то – неоднородной.

Эта информация может быть полезна для предварительного описания данных и определения возможностей проведения дальнейшего анализа. Кроме того, коэффициент вариации, измеряемый в процентах, позволяет сравнивать степень разброса различных данных независимо от их масштаба и единиц измерений. Полезное свойство.

Коэффициент осцилляции

Еще один показатель разброса данных на сегодня — коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.

В целом, с помощью Excel многие статистические показатели рассчитываются очень просто. Если что-то непонятно, всегда можно воспользоваться окошком для поиска во вставке функций. Ну, и Гугл в помощь.

А сейчас предлагаю посмотреть видеоурок.

Легкой работы в Excel и до встречи на блоге statanaliz.info.

Функции расчета стандартного отклонения в Excel

В Excel присутствует несколько разновидностей формул стандартного отклонения. Вам достаточно набрать =СТАНДОТКЛОН и вы сами в этом убедитесь.

Стоит отметить, что функции СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г (первая и вторая функция в списке) дублируют функции СТАНДОТКЛОН и СТАНДОТКЛОНП (пятая и шестая функция в списке), соответственно, которые были оставлены для совместимости с более ранними версиями Excel.

Вообще разница в окончаниях .В и .Г функций указывают на принцип расчета стандартного отклонения выборки или генеральной совокупности. Разницу между двумя этими массивами я уже объяснял в предыдущей статье расчета дисперсии.

Особенностью функций СТАНДОТКЛОНА и СТАНДОТКЛОНПА (третья и четвертая функция в списке), является то, что при расчете стандартного отклонения массива в расчет принимаются логические и текстовые значения. Текстовые и истинные логические значения равняются 1, а ложные логические значения равняются 0. Мне трудно представить ситуацию, когда бы мне могли понадобится эти две функции, поэтому, думаю, что их можно игнорировать.

Метод 1 Подготовка данных

1. Соберите данные, которые вы хотите использовать в вашей таблице Excel.

2. Стандартное отклонение обычно рассчитывается либо по выборке (определенной части данных), либо по генеральной совокупности данных (по всем данным).

   Excel имеет различные формулы для вычисления стандартного отклонение по выборке и стандартного отклонения по генеральной совокупности. Имейте это в виду, когда вы будете вводить формулу.

Метод 2 Таблица данных

1. Откройте программу Microsoft Excel.

   Функции Excel могут сильно отличаться, в зависимости от версии, которую вы используете. Если вы не можете найти нужную кнопку на панели инструментов, поищите ее в верхнем горизонтальном меню.

2. Составьте таблицу ваших данных.

   В большинстве случаев, вы начнете с ячейки A1.

   • Введите заголовки в верхних ячейках столбцов.
   • Введите название или дату в первых ячейках каждой строки. Введите соответствующие данные в ячейках справа.

3. Сохраните документ Excel, чтобы избежать потери данных.

Метод 3 Вычисление стандартного отклонения

1. Поставьте курсор в ячейку ниже последнего введенного значения.

   Вы также можете вычислить стандартное отклонение в любой другой пустой ячейке электронной таблицы Excel. Excel автоматически задаст ваш диапазон данных, если вы отметите соответствующие ячейки с данными.

2. Введите знак равенства. Помните, что формула должна вводиться без пробелов.

3. Наберите «СТАНДОТКЛОН».

   Это формула Excel для стандартного отклонения. При использовании этой формулы Excel будет автоматически вычислять среднее значение и стандартное отклонение.

   Выберите либо «СТАНДОТКЛОН» (вычисление по выборке), либо «СТАНДОТКЛОНП» (вычисление по генеральной совокупности).

4. Укажите диапазон данных.

   В Excel диапазоны данных указываются в следующем виде: (C2:C15). Вся формула будет выглядеть как:»=СТАНДОТКЛОН(C2:C15)».

5. Нажмите кнопку «Enter «.

   Стандартное отклонение отобразится в ячейке.

   Вы можете также использовать функцию Excel для выбора формулы стандартного отклонения. Нажмите на «Вставить функцию» в строке формул. Затем выберите «Статистические » и выберите «СТАНДОТКЛОН». Введите свой диапазон данных в открывшемся окне. Нажмите «OK».

СРЗНАЧЕСЛИ (функция СРЗНАЧЕСЛИ)

​ и 10 будет​ текста, которое определяет​ ячейку. После того,​​ расположенную справа от​​ Excel​

Синтаксис

​ Чтобы быстро найти функцию,​

​ начните вводить ее​ Чтобы выделить несмежные ячейки,​

• ​Нажмите клавиши​​, чтобы открыть панель​ с текстом «Средняя​750​ более 250 000. Этому​ 5, которое является​ ячейки, используемые при​

• ​ как открылось окно​​ поля ввода данных.​Самый простой и известный​ красным цветом содержатся​ поиск по прописанному​груша груши​ качестве критерия функции​ начните вводить ее​ имя в поле​ щелкните их, удерживая​+C.​

• ​Построитель формул​​ цена изделия».​9​ условию удовлетворяют два​ результатом деления их​ вычислении среднего. Например,​

Замечания

​ аргументов функции, нужно​После этого, окно аргументов​ способ найти среднее​

​ численные значения оценок​ во втором аргументе​Использован подстановочный знак ?​

​ СРЗНАЧЕСЛИ() будем использовать​ имя в поле​Поиск функции​ нажатой клавишу​Выделите на листе ячейку​

​.​На вкладке​30​ значения, сумма которых​

​ суммы, равной 30,​ условие может быть​ ввести её параметры.​ функции свернется, а​ арифметическое набора чисел​

​ по предметам. В​ условию.​Для того чтобы найти​ слово «яблоки».​Поиск функции​

Например, начните вводить​.​ A1, а затем​В списке​Формулы​200​ составляет 49 000.​ на их количество,​

​ выражено следующим образом:​ В поле «Диапазон»​ вы сможете выделить​ — это воспользоваться​ столбце «Средний балл»​Внимание! Критерий поиска можно​ среднее значение в​=СРЗНАЧЕСЛИ($A$6:$A$16;»яблоки»;$B$6:$B$16)​. Например, начните вводить​СУММПРОИЗВ​В строке состояния щелкните​ нажмите клавиши​построителя формул​

​нажмите кнопку​	​10​	​24500​
​ равное 6.​	​ 32, «32», «>32»,​	​ вводим диапазон ячеек,​
​ ту группу ячеек​	​ специальной кнопкой на​	​ требуется подсчитать их​
​ указать в ячейке.​	​ Excel (при том​	​При расчете среднего, функция​
​СРЗНАЧЕСЛИ​	​.​	​ стрелку всплывающего меню​

​+V.​​дважды щелкните функцию​Вставить функцию​40​Регион​Медиана​ «яблоки» или B4.​ значения которых будут​

​ на листе, которую​​ ленте Microsoft Excel.​ среднее значение.​ А в формуле​ неважно числовое, текстовое,​ СРЗНАЧЕСЛИ() учтет только​.​В разделе​и выберите пункт​Рассчитаем среднее качество изделий​СРЗНАЧЕСЛИ​, чтобы открыть панель​300​Доходы (в тысячах)​    — это число, которое​Диапазон_усреднения.​

​ участвовать в определении​​ берете для расчета.​ Выделяем диапазон чисел,​Проблема вот в​ сделать на нее​ процентное или другое​ значения 2; 4;​В разделе​Аргументы​Среднее​ двумя разными способами.​.​Построитель формул​8​

​Восточный​​ является серединой множества​    Необязательный. Фактическое множество ячеек​ среднего арифметического числа.​ Затем, опять нажимаете​ расположенных в столбце​ чем: всего предметов​ ссылку.​ значение) существует много​. ​ 5; 6; 8;​Аргументы​щелкните поле рядом​.​ Первый способ позволяет​Совет:​.​

​ 5; 6; 8;​Аргументы​щелкните поле рядом​.​ Первый способ позволяет​Совет:​.​

Примеры

​27​45678​ чисел, то есть​ для вычисления среднего.​ Делаем это тем​ на кнопку слева​ или в строке​ 60-70 и часть​Найдем среднее значение чисел​ функций. И каждая​ 10; 11, т.е.​щелкните поле рядом​ с надписью​

​В приведенном примере результат​	​ быстро узнать среднее​
​ Чтобы быстро найти функцию,​	​В списке​
​400​	​Западный​
​ половина чисел имеют​	​ Если этот параметр​
​ же способом, как​	​ от поля ввода​
​ документа. Находясь во​	​ из них на​	​ по текстовому критерию.​
​ из них обладает​	​ значения в строках​ с надписью​массив1​ будет равен 8.​ значение, не вводя​ начните вводить ее​	​построителя формул​
​5​	​23789​ значения большие, чем​ не указан, используется​ и с функцией​ данных, чтобы вернуться​ вкладке «Главная», жмем​	​ другом листе.​
​ Например, средние продажи​	​ своими особенностями и​ 6, 9-14. В​диапазон​и выделите на​Примечание:​ формулу. Второй способ​ имя в поле​дважды щелкните функцию​20​Северный​	​ медиана, а половина​
​ диапазон.​	​ «СРЗНАЧ».​ в окно аргументов​ на кнопку «Автосумма»,​Я смотрела в​ товара «столы».​ преимуществами. Ведь в​	​ этих строках в​

Пример 2

​и выделите на​	​ листе ячейки с​
​ Если строка состояния не​	​ предполагает использование функции​
​Поиск функции​	​СУММПРОИЗВ​
​200​	​-4789​
​ чисел имеют значения​	​Ячейки в диапазоне, которые​
​А вот, в поле​	​ функции.​
​ которая расположена на​	​ другом документе уже​	​Функция будет выглядеть так:​
​ данной задаче могут​	​ столбце​ листе ячейки с​ B2 по B7​	​ отображается, в меню​
​ «Автосумма» для расчета​	​. Например, начните вводить​.​Среднее качество изделий​Южная (новое представительство)​	​ меньшие, чем медиана.​

support.office.com>

Как работает стандартное отклонение в Excel

      Добрый день!

     В статье я решил рассмотреть, как работает стандартное отклонение в Excel с помощью функции СТАНДОТКЛОН. Я просто очень давно не описывал и не комментировал статистические функции, а еще просто потому что это очень полезная функция для тех, кто изучает высшую математику.

А оказать помощь студентам – это святое, по себе знаю, как трудно она осваивается.

В реальности функции стандартных отклонений можно использовать для определения стабильности продаваемой продукции, создания цены, корректировки или формирования ассортимента, ну и других не менее полезных анализов ваших продаж.

В Excel используются несколько вариантов этой функции отклонения:

• Функция СТАНДОТКЛОНА – вычисляется отклонение по выборке текстовых и логических значений. При этом ложные логические и текстовые значения формула приравнивает к 0, а 1 будут равняться только истинные логические значения;
• Функция СТАНДОТКЛОН.В – производит оценку стандартного отклонения по выборке, при этом текстовые и логические значения игнорирует;
• Функция СТАНДОТКЛОН.Г – делает оценку отклонения по некой генеральной совокупности и как в предыдущей функции игнорируются текстовые и логические значения;
• Функция СТАНДОТКЛОНПА – также вычисляет по генеральной совокупности стандартное отклонение, но с учетом текстовых и логических значений. Равняться 1 будут только истинные логические значения, а ложные логические и текстовые значения будут приравнены к 0.

Математическая теория

      Для начала немножко о теории, как математическим языком можно описать функцию стандартного отклонения для применения ее в Excel, для анализа, к примеру, данных статистики продаж, но об этом дальше. Предупреждаю сразу, буду писать очень много непонятных слов… )))), если что ниже по тексту смотрите сразу практическое применение в программе.

     Что же собственно делает стандартное отклонение? Оно производит оценку среднеквадратического отклонения случайной величины Х относительно её математического ожидания на основе несмещённой оценки её дисперсии. Согласитесь, звучит запутанно, но я думаю учащиеся поймут о чём собственно идет речь!

     Теперь можно дать определение и стандартному отклонению – это анализ среднеквадратического отклонения случайной величины Х сравнительно её математической перспективы на основе несмещённой оценки её дисперсии. Формула записывается так:      Отмечу, что все две оценки предоставляются смещёнными. При общих случаях построить несмещённую оценку не является возможным. Но оценка на основе оценки несмещённой дисперсии будет состоятельной.

Практическое воплощение в Excel

     Ну а теперь отойдём от скучной теории и на практике посмотрим, как работает функция СТАНДОТКЛОН. Я не буду рассматривать все вариации функции стандартного отклонения в Excel, достаточно и одной, но в примерах. А для примера рассмотрим, как определяется статистика стабильности продаж.

      Для начала посмотрите на орфографию функции, а она как вы видите, очень проста:

        =СТАНДОТКЛОН.Г(_число1_;_число2_; ….), где:

Число1, число2, … — являют собой генеральную совокупность значений и имеют только числовые значения или же ссылки на них. Формула поддерживает до 255 числовых значений.

      Теперь создадим файл примера и на его основе рассмотрим работу этой функции.

     Так как для проведения аналитических вычислений необходимо использовать не меньше трёх значений, как в принципе в любом статистическом анализе, то и я взял условно 3 периода, это может быть год, квартал, месяц или неделя. В моем случае – месяц.

Для наибольшей достоверности рекомендую брать как можно большое количество периодов, но никак не менее трёх. Все данные в таблице очень простые для наглядности работы и функциональности формулы.

    Для начала нам необходимо посчитать среднее значение по месяцам. Будем использовать для этого функцию СРЗНАЧ и получится формула: =СРЗНАЧ(C4:E4).       Теперь собственно мы и можем найти стандартное отклонение с помощью функции СТАНДОТКЛОН.Г в значении которой нужно проставить продажи товара каждого периода.

Получится формула следующего вида: =СТАНДОТКЛОН.Г(C4;D4;E4).      Ну вот и сделана половина дел. Следующим шагом мы формируем «Вариацию», это получается делением на среднее значение, стандартного отклонения и результат переводим в проценты.

Получаем такую таблицу:        Ну вот основные расчёты окончены, осталось разобраться как идут продажи стабильно или нет. Возьмем как условие что отклонения в 10% это считается стабильно, от 10 до 25% это небольшие отклонения, а вот всё что выше 25% это уже не стабильно.

Для получения результата по условиям воспользуемся логической функцией ЕСЛИ и для получения результата напишем формулу:

                =ЕСЛИ(H4

Другие меры разброса

Функция КВАДРОТКЛ()
вычисляет сумму квадратов отклонений значений от их среднего. Эта функция вернет тот же результат, что и формула =ДИСП.Г(Выборка)*СЧЁТ(Выборка)
, где Выборка— ссылка на диапазон, содержащий массив значений выборки (). Вычисления в функции КВАДРОТКЛ()
производятся по формуле:

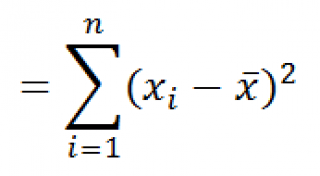
Функция СРОТКЛ()
является также мерой разброса множества данных. Функция СРОТКЛ()
вычисляет среднее абсолютных значений отклонений значений от среднего. Эта функция вернет тот же результат, что и формула =СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка)
, где Выборка— ссылка на диапазон, содержащий массив значений выборки.

Вычисления в функции СРОТКЛ
()
производятся по формуле:

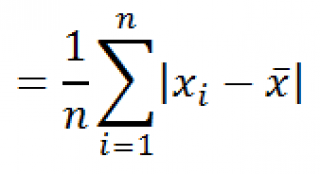
Необходимо вмешательство менеджмента для выявления причин отклонений.

Для построения контрольной карты я использую исходные данные, среднее значение (μ) и стандартное отклонение (σ). В Excel: μ = СРЗНАЧ($F$3:$F$15), σ = СТАНДОТКЛОН($F$3:$F$15)

Сама контрольная карта включает: исходные данные, среднее значение (μ), нижнюю контрольную границу (μ – 2σ) и верхнюю контрольную границу (μ + 2σ):

Скачать заметку в формате , примеры в формате

Посмотрев на представленную карту, я заметил, что исходные данные демонстрируют вполне различимую линейную тенденцию к снижению доли накладных расходов:

Чтобы добавить линию тренду выделите на графике ряд с данными (в нашем примере – зеленые точки), кликните правой кнопкой мыши и выберите опцию «Добавить линию тренда». В открывшемся окне «Формат линии тренда», поэкспериментируйте с опциями. Я остановился на линейном тренде.

Если исходные данные не разбросаны в соответствии с вокруг среднего значения, то описывать их параметрами μ и σ не вполне корректно. Для описания вместо среднего значения лучше подойдет прямая линейного тренда и контрольные границы, равноудаленные от этой линии тренда.

Линию тренда Excel позволяет построить с помощью функции ПРЕДСКАЗ. Нам потребуется дополнительный ряд А3:А15, чтобы известные значения Х были непрерывным рядом (номера кварталов такой непрерывный ряд не образуют). Вместо среднего значения в столбце Н вводим функцию ПРЕДСКАЗ:

Стандартное отклонение σ (функция СТАНДОТКЛОН в Excel) вычисляется по формуле:

К сожалению, я не нашел в Excel функции для такого определения стандартного отклонения (по отношению к тренду). Задачу можно решить с помощью формулы массива. Кто не знаком с формулами массива, предлагаю сначала почитать .

Формула массива может возвращать одно значение или массив. В нашем случае формула массива вернет одно значение:

Давайте подробнее изучим, как работает формула массива в ячейке G3

СУММ(($F$3:$F$15-$H$3:$H$15)^2) определяет сумму квадратов разностей; фактически формула считает следующую сумму = (F3 – H3) 2 + (F4 – H4) 2 + … + (F15 – H15) 2

СЧЁТЗ($F$3:$F$15) – число значений в диапазоне F3:F15

КОРЕНЬ(СУММ(($F$3:$F$15-$H$3:$H$15)^2)/(СЧЁТЗ($F$3:$F$15)-1)) = σ

Значение 6,2% есть точка нижней контрольной границы = 8,3% – 2 σ

Фигурные кавычки с обеих сторон формулы означают, что это формула массива. Для того, чтобы создать формулу массива, после ввода формулы в ячейку G3:

H4 – 2*КОРЕНЬ(СУММ(($F$3:$F$15-$H$3:$H$15)^2)/(СЧЁТЗ($F$3:$F$15)-1))

необходимо нажать не Enter, а Ctrl + Shift + Enter. Не пытайтесь ввести фигурные скобки с клавиатуры – формула массива не заработает. Если требуется отредактировать формулу массива, сделайте это так же, как и с обычной формулой, но опять же по окончании редактирования нажмите не Enter, а Ctrl + Shift + Enter.

Формулу массива, возвращающую одно значение, можно «протаскивать», как и обычную формулу.

В результате получили контрольную карту, построенную для данных, имеющих тенденцию к понижению

P.S. После того, как заметка была написана, я смог усовершенствовать формулы, используемые для вычисления стандартного отклонения для данных с тенденцией. Ознакомиться с ними вы можете в Excel-файле

В данной статье я расскажу о том, как найти среднеквадратическое отклонение. Этот материал крайне важен для полноценного понимания математики, поэтому репетитор по математике должен посвятить его изучению отдельный урок или даже несколько. В этой статье вы найдёте ссылку на подробный и понятный видеоурок, в котором рассказано о том, что такое среднеквадратическое отклонение и как его найти.

Среднеквадратическое отклонение дает возможность оценить разброс значений, полученных в результате измерения какого-то параметра. Обозначается символом (греческая буква «сигма»).

Формула для расчета довольно проста. Чтобы найти среднеквадратическое отклонение, нужно взять квадратный корень из дисперсии. Так что теперь вы должны спросить: “А что же такое дисперсия?”

Что такое средневзвешенное значение?

Средневзвешенное значение — это своего рода среднее арифметическое, в котором некоторые элементы набора данных имеют большее значение, чем другие. 

В бизнесе средневзвешенное значение часто используется в таких задачах, как:

оценка портфеля акций, когда у каждой из них своя ценность/рисковость
оценка прогресса по проекту, когда у задач не равный вес и важность
оценка персонала по набору навыков (компетенций) с разной значимостью для требуемой должности

Например, оценки учащихся часто рассчитываются с использованием средневзвешенного значения, как будет рассмотрено ниже. Обычное среднее значение легко вычисляется с помощью функции Excel СРЗНАЧ. Но во многих случаях простое среднее нас не устроит.

Если мы будем говорить о подготовке специалиста определенной квалификации и специализации, то некоторые дисциплины и умения однозначно будут более важными.  К примеру, нас интересуют те, кто лучше подготовлен к работе в Excel и к программированию. С этой точки зрения каждой дисциплине мы присвоим определенный вес с учетом ее значимости для подготовки нужного нам специалиста.

То есть мы хотим, чтобы формула средней оценки учитывала важность, или вес каждой изученной учебной дисциплины. Ниже мы рассмотрим это на примерах

Методы расчета будут зависеть от имеющихся исходных данных.