Термодинамика идеального газа

Связь с другими законами состояния идеального газа

С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса и один трех макропараметров (давление, температура или объем) — остаются неизменными.

Количественные зависимости между двумя параметрами газа при фиксированном третьем параметре называют газовыми законами, которые связывают эти параметры.

Изопроцессы — это термодинамические процессы, во время протекания которых количество вещества и один из макропараметров состояния: давление, объем, температура или энтропия — остается неизменным.

В зависимости от того, какой параметр остается неизменным различают разные процессы, которые выражаются законами, являющимися следствием уравнения состояния газа:

• изотермический процесс (T=const);
• изохорный процесс (V=const);
• изобарный процесс (p=const).

Изотермический процесс (T=const)

Процесс изменения состояния термодинамической системы при постоянной температуре называют изотермическим.

Для поддержания температуры газа постоянной необходимо, чтобы он мог обмениваться теплотой с большой системой — термостатом. Им может служить атмосферный воздух, если температура его заметно не меняется на протяжении всего процесса.

Согласно уравнению Клапейрона-Менделеева, в любом состоянии с неизменной температурой произведение давления газа на объем одно и то же, то есть постоянно:

Этот закон был открыт экспериментально английским ученым Бойлем и несколько позднее французским ученым Мариоттом. Именно поэтому он называется закон Бойля-Мариотта.

Закон Бойля-Мариотта справедлив для любых газов, а также для смеси газов (например, для воздуха).

Зависимость давления газа от объема при постоянной температуре изображается графической кривой — изотермой. Изотерма для различных температур представлена в координатах pV на рис.1. и представляет собой гиперболу.

Рис.1. Изотерма в pV — координатах.

Изохорный процесс (V=const)

Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным.

Из уравнения состояния следует, что отношение давлений газа данной массы при постоянно объеме равно отношению его абсолютных температур:

p 1 p 2 = T 1 T 2

Газовый закон был установлен экспериментально в 1787 г. французским физиком Ж. Шарлем и носит название закона Шарля: давление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре.

Так, если в качестве одного из состояний газа выбрать состояние газа при нормальных условиях, тогда

p = p 0 T T 0 = p 0 γ T

Коэффициент γ называют температурным коэффициентом давления газа. Он одинаков для всех газов.

Зависимость давления газа от температуры при постоянном объеме изображается графически прямой, которая называется изохорой (Рис.2).

Рис.2 Изображение изохоры в pT-координатах.

Изобарный процесс (p=const)

Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным.

Из уравнения Клапейрона-Менделеева вытекает, что отношение объемов газа данной массы при постоянном давлении равно отношению его абсолютных температур.

V 1 V 2 = T 1 T 2

Если в качестве второго состояния газа выбрать состояние при нормальных условиях (нормальном атмосферном давлении, температуре таяния льда) следует:

V = V 0 T T 0 = V 0 α T

Этот газовый закон был установлен экспериментально в 1802 г французским ученым Гей-Люссаком.

Закон Гей-Люссака: объем данной массы газа при постоянном давлении прямо пропорционален абсолютной температуре.

Коэффициент α называют температурным коэффициентом объемного расширения газов.

Зависимость объема газа от температуры при постоянном давлении изображается графической прямой, которая называется изобарой (Рис.3).

Рис. 3. Изобара в VT-координатах.

Уравнение состояния идеального газа

теория по физике молекулярная физика, МКТ, газовые законы

Уравнение состояния идеального газа было открыто экспериментально. Оно носит название уравнения Клапейрона — Менделеева. Это уравнение устанавливает математическую зависимость между параметрами идеального газа, находящегося в одном состоянии. Математически его можно записать следующими способами:

Уравнение состояния идеального газа

Внимание! При решении задач важно все единицы измерения переводить в СИ. Пример №1. Кислород находится в сосуде вместимостью 0,4 м 3 под давлением 8,3∙10 5 Па и при температуре 320 К

Чему равна масса кислорода? Молярная масса кислорода равна 0,032 кг/моль

Кислород находится в сосуде вместимостью 0,4 м 3 под давлением 8,3∙10 5 Па и при температуре 320 К. Чему равна масса кислорода? Молярная масса кислорода равна 0,032 кг/моль

Пример №1. Кислород находится в сосуде вместимостью 0,4 м 3 под давлением 8,3∙10 5 Па и при температуре 320 К. Чему равна масса кислорода? Молярная масса кислорода равна 0,032 кг/моль.

Из основного уравнения состояния идеального газа выразим массу:

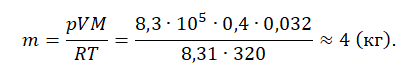
Уравнение состояния идеального газа следует использовать, если газ переходит из одного состояния в другое и при этом изменяется его масса (количество вещества, число молекул) или молярная масса. В этом случае необходимо составить уравнение Клапейрона — Менделеева отдельно для каждого состояния. Решая систему уравнений, легко найти недостающий параметр.

Подсказки к задачам

Важна только та масса, что осталась в сосуде. Поэтому:

Пример №2. В баллоне содержится газ под давлением 2,8 МПа при температуре 280 К. Удалив половину молекул, баллон перенесли в помещение с другой температурой. Определите конечную температуру газа, если давление уменьшилось до 1,5 МПа.

Так как половина молекул была выпущена, m₂ = 0,5m₁. Объем остается постоянным, как и молярная масса. Учитывая это, запишем уравнение состояния идеального газа для начального и конечного случая:

Преобразим уравнения и получим:

Приравняем правые части и выразим искомую величину:

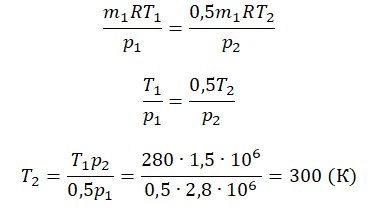
На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.

Алгоритм решения

График построен в координатах (V;E_k). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:

Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.

Запишем уравнение Менделеева — Клапейрона:

Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:

ν R = p 1 V 1 T 1 . . = p 2 V 2 T 2 . .

Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.

Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.

pазбирался: Алиса Никитина | обсудить разбор | оценить

На высоте 200 км давление воздуха составляет примерно 10 –9 от нормального атмосферного давления, а температура воздуха Т – примерно 1200 К. Оцените плотность воздуха на этой высоте.

Физика 7 класс. Давление газа и жидкости. Закон Паскаля.

Физика 7 класс. Конспект. Давление газаДавление газа. Передача давления жидкостями и газами. Закон Паскаля. Расчет давления жидкости.

Задачи на тему Давление

Газы, в отличие от твердых тел и жидкостей, заполняют весь сосуд, в котором находятся.

Газ, находясь в каком-либо сосуде, оказывает давление на стенки, дно и крышку тела, в котором находится. Молекулы газа беспорядочно движутся, сталкиваясь друг с другом и со стенками сосуда, внутри которого находятся. Давление газа на стенки сосуда (и на помещенное в газ тело) вызывается ударами молекул газа.

При уменьшении объема газа его давление увеличивается, а при увеличении объема давление уменьшается при условии, что масса и температура газа остаются неизменными.

Давление газа в закрытом сосуде тем больше, чем выше температура газа, при условии, что масса газа и объем не изменяются.

Из опытов получен общий вывод, что давление газа тем больше, чем чаще и сильнее молекулы ударяют о стенки сосуда.

Закон Паскаля:

Давление, производимое на жидкость или газ, передается в любую точку без изменений во всех направлениях.

Опыт иллюстрирует закон Паскаля

Свойство газов передавать давление используют в технике при устройстве различных пневматических машин и инструментов.

На жидкости, как и на все тела на Земле, действует сила тяжести. Поэтому каждый слой жидкости, налитой в сосуд, своим весом создает давление на другие слои, которое по закону Паскаля передается по всем направлениям. Следовательно, внутри жидкости существует давление.

Опыты подтверждают, что внутри жидкости существует давление и на одном и том же уровне оно одинаково по всем направлениям. С глубиной давление увеличивается.

Давление жидкости на дно и стенки сосуда зависит только от плотности и высоты столба жидкости.

Расчет давления жидкости на дно и стенки сосуда:

где p – давление (Па), ρ – плотность жидкости (кг/м3), h– высота столб жидкости (м), g– ускорение свободного падения (Н/кг).

Сосуды, соединенные между собой (например, чайник, лейка и т.п.), называют сообщающимися.

В сообщающихся сосудах любой формы и сечения поверхности однородной жидкости устанавливаются на одном уровне (при условии, что давление воздуха над жидкостью одинаково).

При равенстве давлений высота столба жидкости с большей плотностью будет меньше высоты столба с меньшей плотностью.

Конспект составлен на основании теоретического материала учебника «Физика 7 класс» А.В. Перышкин

Задачи

Атмосферное давление

Скачать конспект:

teoriya_7_davleniegaza

Для выпуска расплавленного металла из литейного ковша делают на дне ковша отверстие, закрываемое спе…

Почему футбольные и баскетбольные мячи помещают в прочные кожаные чехлы?

Поршневой насос может произвести давление 5·10 5 Па. На какую высоту можно поднять воду этим насосом…

При сжатии поршнем кислорода в закрытом сосуде изменяется ли: а) Масса кислорода; б) объем кислорода…

Использование универсального уравнения для решения задачи

В реальности проводятся различные физико-химические процессы. Рассмотрим каким образом уравнение состояния идеального газа и законы, связанные с ним находят применение для решения физических и химических задач.

Определить давление кислорода в баллоне объемом 1 м 3 при температуре t = 27 C o . Масса кислорода 1 кг.

Так как в уравнении даны объем и температура — два из трех макроскопических параметров, а третий (давление) нужно определить, то мы можем использовать уравнение Клапейрона-Менделеева:

p V = n R T = m M R T

Не забываем перевести температуру в Кельвины:

T = t + 273 = 27 + 273 = 300 K

Молярная масса кислорода известна из таблицы Менделеева:

M ( O 2 ) = 2 * 16 = 32 г / м о л ь = 32 * 10 — 3 к г / м о л ь

Выразим из уравнения состояния давления и поставим все имеющиеся данные:

p = n R T V = m R T M V = 1 * 8 . 31 * 300 32 * 10 — 3 * 1 = 77 . 906 П а = 78 к П а

Ответ: p = 78 кПа.

Каким может быть наименьший объем баллона, содержащего кислород массой 6,4 кг, если его стенки при t = 20 C o выдерживают p = 1568 Н / с м 2 ?

Используем уравнение Менделеева-Клапейрона, из которого выражаем объем кислорода, который нужно найти:

p = n R T V = m R T M V

Молярная масса кислорода предполагается равной:

M ( O 2 ) = 2 * 16 = 32 г / м 3

Не забываем перевести температуру в Кельвины:

T = t + 273 = 20 + 273 = 293 K

Переводим давление: p = 15680000 Па

Выражаем из уравнения Клапейрона-Менделеева объем и подставляем значения, данные в условиях задачи:

V = n R T p = m R T M p = 6 . 4 * 8 . 31 * 293 15680000 * 32 * 10 — 3 = 3 . 1 * 10 — 2 м 3 = 31 л .

Используя уравнение состояния идеального газа, доказать, что плотность любого газа равна половине плотности водорода ( ρ Н 2 ) , взятого при тех же условиях, умноженной на относительную молекулярную массу этого газа M_r, то есть ρ = ρ Н 2 * M r 2 .

Согласно уравнению Менделеева-Клапейрона:

p = n R T V = m R T M V

Плотность — это величина, характеризующая массу некоторого объема и находится по формуле:

ρ = m V и л и V = m ρ

Тогда p m ρ = n R T = m R T M

Откуда выражаем плотность газа:

Для водорода эта формула запишется следующим образом:

ρ H 2 = p M H 2 R T

По условию задачи водород и любой другой газ находятся при одинаковых условиях, откуда следует, что:

ρ H 2 M H 2 = p R T

Поставим последнее выражение в выражение для плотности любого газа:

ρ = M * ρ H 2 M H 2

Молярная масса водорода, исходя из таблицы Менделеева равна 2 г/моль и тогда. Молекулярная масса численно равная молярной и представляет собой массу молекулы в атомных единицах, поэтому в дальнейшем мы совершили переход к молекулярной массе.

ρ = M r * ρ H 2 2

Вывод: плотность любого газа равна половине плотности водорода ( ρ Н 2 ) , взятого при тех же условиях, умноженной на относительную молекулярную массу этого газа M_r, то есть ρ = ρ Н 2 * M r 2 .

Рассмотрим несколько задач на законы, связанные с уравнение Клапейрона-Менделеева, то есть на изотермические, изохорные, изобарные процессы.

При уменьшении давления газа в 2,5 раза его объем увеличился на 12 л. Какой объем занимал газ в начальном состоянии, если температура на протяжении всего процесса оставалась постоянной?

По условию задачи температура в ходе всего процесса оставалась постоянной, откуда следует, что у нас изотермический процесс, и мы можем воспользоваться для решения законом Бойля-Мариотта.

p 1 V 1 = p 2 V 2 , г д е p 1 – давление газа в начальном состоянии (до расширения), V 1 — объем газа в начальном состоянии, p 2 = p 1 2 . 5 — давление газа в конечном состоянии (после расширения), V 2 = V 1 + ∆ V — объем газа в конечном состоянии.

Откуда можем найти начальный объем:

p 1 V 1 = p 1 2 . 5 ( V 1 + ∆ V ) = p 1 2 . 5 V 1 + p 1 2 . 5 ∆ V

V 1 ( p 1 — p 1 2 . 5 ) = p 1 2 . 5 ∆ V

p 1 2 . 5 V 1 ( 2 . 5 — 1 ) = p 1 2 . 5 ∆ V

V 1 = ∆ V 1 , 5 = 8 л

Ответ: первоначальный объем газа был равен 8 л.

Газ находится в баллоне при температуре 400 К. До какой температуры нужно нагреть газ, чтобы его давление увеличилось в 1,5 раза?

Так как нагревание газа по условиям данной задачи происходит при постоянном объеме, значит перед нами изохорный процесс.

При изохорном процессе:

p 1 T 1 = p 2 T 2

T 2 = p 2 T 1 p 1

p 2 p 1 = 1 . 5 T 2 = 1 . 5 * T 1 = 1 . 5 * 400 = 600 K

При 27°C объем газа равен 600 мл. Какой объем займет газ при 57°C, если давление будет оставаться постоянным?

Так как давление по условию остается постоянным, то можем использовать закон Гей-Люссака.

V 1 V 2 = T 1 T 2

V_2 – искомый объем

Для правильного расчета необходимо перевести температуры из Цельсий в Кельвины:

T 1 = 273 + 27 = 300 K

T 2 = 273 + 57 = 330 K

T 2 V 1 T 1 = V 2

V 2 = ( 600 * 330 ) / 300 = 660 м л

Газ в трубе плавильной печи охлаждается от температуры t 1 = 1150 ° С д о t 2 = 200 ° С . Во сколько раз увеличивается плотность газа при этом? Давление газа не меняется.

Так как по условию задания давления газа не изменяется, значит перед нами изобарный процесс. Для решения воспользуемся законом Гей-Люссака:

V 1 V 2 = T 1 T 2

Перейдем к абсолютной температуре:

T 1 = 1150 + 273 = 1423 K

T 2 = 200 + 273 = 473 K

Масса газа: m = ρ 1 V 1 = ρ 2 V 2

Использование этих формул приводит к следующему:

Что такое уравнение Клапейрона-Менделеева

Идеальный газ — это газ, в котором пренебрегают взаимодействием молекул газа между собой.

Идеальными считают разреженные газы. Особенно близкими к идеальным считают гелий и водород.

Идеальный газ — это упрощенная математическая модель, которая широко применяется для описания свойств и поведения реальных газов при атмосферном давлении и комнатной температуре.

Давление, объем и температура — это основные параметры состояния системы, и они связаны друг с другом. Соотношение, при котором определяется данная связь, называется уравнением состояния данного газа.

Существует эквивалентная макроскопическая формулировка идеального газа — это такой газ, который одновременно будет подчиняться закону Бойля-Мариотта и Гей-Люссака, то есть:

p V = c o n s t * T

В представленном выше уравнении состоянии газа под const подразумевается количество молей.

Свойства классического и квазиклассического идеального газа описываются уравнением состояния идеального газа, которое называется уравнением Менделеева-Клапейрона, ниже представлена формула Менделеева-Клапейрона.

p V = m M R T = n R T , где m — масса газа, M — молярная масса газа, R = 8 , 314 Д ж / ( м о л ь * К ) — универсальная газовая постоянная, T — температура (К), n — количество молей газа.

Таким образом давление и объем прямо пропорциональны количеству молей и температуре.

Также уравнение Клапейрона-Менделеева можно записать в ином виде:

p V = N k T , где N — это количество молекул газа массой m , k = 1 , 38 * 10 — 23 Д ж / К — постоянная Больцмана, которая определяет «долю» газовой постоянной, приходящуюся на одну молекулу и определяется по формуле:

N = m N A M , где

N A = 6 . 02 * 10 23 м о л ь — 1 ; — это постоянная Авогадро.

Слайд 21Опр. Соприкосновение тел, при котором возможна лишь передача тепла от одного

тела к другому, будем наз. тепловым контактом этих тел. Мы говорим, две системы имеют равные температуры, если при тепловом контакте их состояния не меняются.Впервые понятие температуры возникло из субъективных ощущений в области восприятия «степени нагретости» тела. Объективная возможность введения понятия температуры связана с важным постулатом термоди­намики: «Если две термодинамические системы находятся в тепловом равновесии с третьей, то они должны быть в равновесии и между собой». Указанное равновесие не зависит от объема, давления, плотности и других (помимо температуры) величин, определяющих состояние систем.

Слайд 34Термометрические шкалыУвеличение объема термического тела при нагревании и дает косвенную информацию

об изменении температуры. Если зависимость объема от температуры линейна, то достаточно выбрать две реперные точки, приписать этим точкам определенные значения температуры t l и t 2 и разделить полученный интервал на некоторое число промежутков (делений температурной шкалы). Наличие такой шкалы и позволяет измерять значение температуры в интервале между реперными точками. Очевидно, что подобные единицы измерения температур и температурные шкалы являются эмпирическими и условными. Наиболее известны три эмпирические шкалы температур: Цельсия, Реомюра и Фаренгейта, отличающиеся значениями температур реперных точек. В качестве реперных точек Цельсий выбрал температуру таяния льда (t1 = 0°С) и ки­пения воды (t2 = 100°С) при нормальном давлении и разделил промежуток t2-tl на 100 интервалов — градусов. (Приведен современный вариант шкалы Цельсия).

Методы измерения плотности газа

1. Метод гравиметрии: Этот метод основан на измерении массы газа, заполненного в конкретный объем. Газовый образец помещается в прибор с известным объемом, после чего определяется его масса с помощью весов. Затем, используя формулу плотности, рассчитывается значение плотности газа.
2. Метод давления: В этом методе используется закон Бойля-Мариотта, который устанавливает прямую зависимость между давлением и плотностью газа. Измеряется давление газа в известном объеме, а затем с помощью уравнения состояния газа рассчитывается его плотность.
3. Метод ультразвука: Этот метод основан на использовании ультразвуковых волн для измерения плотности газа. Ультразвуковая волна проходит через газовый образец и затем измеряется время, за которое волна проходит через определенное расстояние. С помощью физических законов и формул рассчитывается значение плотности газа.
4. Метод диффузии: В этом методе используется явление диффузии газов. Газовые смеси разных плотностей разностепенно проходят через тонкую перегородку, и время прохождения газов по перегородке измеряется. Из полученных данных рассчитывается плотность газа.

Выбор метода измерения плотности газа зависит от его свойств, доступного оборудования и точности, которую требуется достичь. Каждый из этих методов имеет свои преимущества и ограничения, и их выбор должен быть обоснован исходя из конкретных условий опыта или промышленного процесса.

Калорические параметры состояния идеального газа

Рисунок 3. Уравнение адиабаты для идеального газа. Автор24 — интернет-биржа студенческих работ

К калорическим основным параметрам состояния исследуемого физического элемента относятся следующие термодинамические величины:

1. Энтропия. Согласно этому показателю теплота элементарной частицы не является функцией состояния, так как количество теплового процесса зависит от взаимодействия движущихся в системе элементов.
2. Энтальпия. Данный критерий представляет собой сумму внутренней энергии материального тела и произведения давления на его объем. Удельная энтальпия может определять отношение вещества к собственной массе, следовательно, можно определить количество теплоты, участвующее в процессе
3. Внутренняя энергия. Эта величина демонстрирует калорический параметр общего состояния, поэтому ее изменение не зависит от термодинамического процесса, а определяется исключительно начальными и конечными состояниями концепции.

При детальном исследовании указанных процессов возможно определить уравнение системы в координатах и связь между основными параметрами состояния идеального газа, измерение внутреннего энергетического потенциала, а также реальную величину внешней работы и количество поглощенной теплоты.

Идеальный газ

В газах расстояния между молекулами обычно значительно больше их размеров. Силы взаимодействия между молекулами на таких больших расстояниях малы, и каждая молекула движется вдоль прямой линии до очередного столкновения с другой молекулой или со стенкой сосуда. Среднее расстояние между молекулами воздуха при нормальных условиях порядка 10-8 м, то есть в сотни раз превышает размер молекул. Слабое взаимодействие между молекулами объясняет способность газов расширяться и заполнять весь объем сосуда. В пределе, когда взаимодействие стремится к нулю, мы приходим к представлению об идеальном газе.

Идеальный газ — это газ, молекулы которого не взаимодействуют друг с другом, за исключением процессов упругого столкновения и считаются материальными точками.

В молекулярно-кинетической теории количество вещества принято считать пропорциональным числу частиц. Единица количества вещества называется молем (моль). Моль — это количество вещества, содержащее столько же частиц (молекул), сколько содержится атомов в 0,012 кг углерода 12C. Молекула углерода состоит из одного атома. Таким образом, в одном моле любого вещества содержится одно и то же число частиц (молекул). Это число называется постоянной Авогадро: NА = 6,022·1023 моль-1.

Постоянная Авогадро — одна из важнейших постоянных в молекулярно-кинетической теории. Количество вещества определяется как отношение числа N частиц (молекул) вещества к постоянной Авогадро NА, или как отношение массы к молярной массе:

Массу одного моля вещества принято называть молярной массой M. Молярная масса равна произведению массы m0 одной молекулы данного вещества на постоянную Авогадро (то есть на количество частиц в одном моле). Молярная масса выражается в килограммах на моль (кг/моль). Для веществ, молекулы которых состоят из одного атома, часто используется термин атомная масса. В таблице Менделеева молярная масса указана в граммах на моль. Таким образом имеем еще одну формулу:

где: M – молярная масса, NA – число Авогадро, m0 – масса одной частицы вещества, N – число частиц вещества содержащихся в массе вещества m. Кроме этого понадобится понятие концентрации (количество частиц в единице объема):

Напомним также, что плотность, объем и масса тела связаны следующей формулой:

Если в задаче идет речь о смеси веществ, то говорят о средней молярной массе и средней плотности вещества. Как и при вычислении средней скорости неравномерного движения, эти величины определяются полными массами смеси:

Не забывайте, что полное количество вещества всегда равно сумме количеств веществ, входящих в смесь, а с объемом надо быть аккуратными. Объем смеси газов не равен сумме объемов газов, входящих в смесь. Так, в 1 кубометре воздуха содержится 1 кубометр кислорода, 1 кубометр азота, 1 кубометр углекислого газа и т.д. Для твердых тел и жидкостей (если иное не указано в условии) можно считать, что объем смеси равен сумме объемов ее частей.

Газовые законы

Решение задач на расчет параметров газа значительно упрощается, если Вы знаете, какой закон и какую формулу применить. Итак, рассмотрим основные газовые законы.

1. Закон Авогадро. В одном моле любого вещества содержится одинаковое количество структурных элементов, равное числу Авогадро.
2. Закон Дальтона. Давление смеси газов равно сумме парциальных давлений газов, входящих в эту смесь:

Парциальным давлением газа называют то давление, которое он бы производил, если бы все остальные газ внезапно исчезли из смеси. Например, давление воздуха равно сумме парциальных давлений азота, кислорода, углекислого газа и прочих примесей. При этом каждый из газов в смеси занимает весь предоставленный ему объем, то есть объем каждого из газов равен объему смеси.

3. Закон Бойля-Мариотта. Если масса и температура газа остаются постоянными, то произведение давления газа на его объем не изменяется, следовательно:

Процесс, происходящий при постоянной температуре, называют изотермическим

Обратите внимание, что такая простая форма закона Бойля-Мариотта выполняется только при условии, что масса газа остается неизменной

4. Закон Гей-Люссака. Сам закон Гей-Люссака не представляет особой ценности при подготовке к экзаменам, поэтому приведем лишь следствие из него. Если масса и давление газа остаются постоянными, то отношение объема газа к его абсолютной температуре не изменяется, следовательно:

Процесс, происходящий при постоянном давлении, называют изобарическим или изобарным

Обратите внимание, что такая простая форма закона Гей-Люссака выполняется только при условии, что масса газа остается неизменной. Не забывайте про перевод температуры из градусов Цельсия в кельвины

5. Закон Шарля. Как и закон Гей-Люссака, закон Шарля в точной формулировке для нас не важен, поэтому приведем лишь следствие из него. Если масса и объем газа остаются постоянными, то отношение давления газа к его абсолютной температуре не изменяется, следовательно:

Процесс, происходящий при постоянном объеме, называют изохорическим или изохорным

Обратите внимание, что такая простая форма закона Шарля выполняется только при условии, что масса газа остается неизменной. Не забывайте про перевод температуры из градусов Цельсия в кельвины

6. Универсальный газовый закон (Клапейрона). При постоянной массе газа отношение произведения его давления и объема к температуре не изменяется, следовательно:

Обратите внимание, что масса должна оставаться неизменной, и не забывайте про кельвины

Примеры решения задач

Задание	Вычислите плотность по хлору смеси 55 л азота и 180 л кислорода.
Решение	Найдем объемные доли веществ в смеси:

φ (N₂) = 55 / (55 + 180) = 55 / 235 = 0,23.

φ (O₂) = 180 / (180 + 55) = 180 / 235 = 0,77.

Объемные доли газов будут совпадать с молярными, т.е. с долями количеств веществ, это следствие из закона Авогадро. Найдем условную молекулярную массу смеси:

M_r conditional (mixture) = 0,23 × 28 + 0,77 × 32 = 6,44 + 24,64 = 31,08.

Найдем относительную плотность смеси по водороду:

Относительную молекулярную массу воздуха принимают равной 29 (с учетом содержания в воздухе азота, кислорода и других газов). Следует отметить, что понятие «относительная молекулярная масса воздуха» употребляется условно, так как воздух – это смесь газов.

M_r(NOCl) = A_r(N) + Ar(O) + Ar(Cl) = 14 + 16 + 35,5 = 65,5.

Основное уравнение мкт идеального газа:

Основное уравнение
МКТ позволяет вычислить давление газа,
если известны масса молекулы, среднее
значение квадрата скорости и концентрация
молекул.

Давление идеального
газа
заключается
в том, что молекулы при столкновениях
со стенками сосуда взаимодействуют с
ними по законам механики как упругие
тела. При столкновении молекулы со
стенкой сосуда проекция скорости v x
вектора
скорости на ось OX,
перпендикулярную стенке, изменяет свой
знак на противоположный, но остается
постоянной по модулю. Поэтому в результате
столкновений молекулы со стенкой
проекция ее импульса на ось OX
изменяется от mv 1x =-mv x
до mv 2x =mv x .
Изменение импульса молекулы при
столкновении со стенкой вызывает сила
F 1 ,
действующая на нее со стороны стенки.
Изменение импульса молекулы равно
импульсу этой силы:

Во
время столкновения, согласно третьему
закону Ньютона, молекула действует на
стенку с силой F 2 ,
равной по модулю силе F 1
и направленной противоположно.

Молекул
много, и каждая передает стенке при
столкновении такой же импульс. За секунду
они передают импульс
,
гдеz
– число столкновений всех молекул со
стенкой, которое пропорционально
концентрации молекул в газе, скорости
молекул и площади поверхности стенки:
.
К стенке движется только половина
молекул, остальные движутся в обратную
сторону:.
Тогда полный импульс, переданный стенке
за 1 секунду:.
Согласно второму закону Ньютона изменение
импульса тела за единицу времени равно
действующей на него силе:

Учитывая,
что не все молекулы имеют одинаковую
скорость, сила, действующая на стенку
будет пропорциональна среднему квадрату
скорости. Так как молекулы движутся во
всех направлениях, средние значения
квадратов проекций скорости равны.
Следовательно, средний квадрат проекции
скорости:
;.
Тогда давление газа на стенку сосуда
равно:

— основное уравнение
МКТ.

Обозначив
среднее значение кинетической энергии
поступательного движения молекул
идеального газа:

,
получим

Какое значение имеет универсальная газовая постоянная

Универсальная газовая постоянная (R) — это величина, которая является константой, численно равная работе расширения одного моля идеального газа в изобарном процессе при увеличении температуры на 1 K.

Значение данной константы находится как произведение постоянной Больцмана ( k = 1 , 38 * 10 — 23 Д ж / К ) на число Авогадро ( N A = 6 . 02 * 10 23 м о л ь — 1 \) . Таким образом универсальная газовая постоянная принимает следующее значение: R = 8 , 314 Д ж / ( м о л ь * К ) .

Постоянную Больцмана используют в формулах, описывающих изучаемое явление или поведение рассматриваемого объекта с микроскопической точки зрения, тогда как универсальная газовая постоянная более удобна при расчетах, касающихся макроскопических систем, когда число частиц задано в молях.

Давление газа

Как уже неоднократно отмечалось, давление газа возникает в результате ударов молекул о стенки сосуда. Если мы считаем, что молекулы взаимодействуют со стенкой по законам абсолютно упругого удара, то частица передает стенке импульс, равный изменению импульса самой молекулы. Направим ось Х перпендикулярно стенке (рис.1), в этом случае изменение импульса стенки при ударе одной молекулой:

Получи помощь с рефератом от ИИ-шки

ИИ ответит за 2 минуты

где $m_0$- масса молекулы.

Рис. 1

Поток импульса, который передается стенке за счет ударов молекулами, которые движутся со скоростями близкими к v, направлен к стенке, равен $nf(v)m_0{v_x\ }^2dv$, отсюда:

где

В результате непосредственного интегрирования получаем:

Так как мы уже отмечали, что рассматриваем единичную площадку стены в течение времени. равном 1с, то можно записать, что давление будет равно:

Давление газа изотропно, это величина скалярная.

При постоянном объеме давление газа массы m подчиняется закону Шарля:

где $p_0$- давление газа при температуре $T_0=273\ К$.

Давление смеси идеальных газов равно сумме их парциальных давлений:

\

Уравнение (7) имеет название — это закон Дальтона.

Парциальным давлением называют давление компоненты смеси газа, каким оно бы было, если бы других газов в смеси не было.

Ряд важных уравнений молекулярной физики, в которые входит давление:

1. Уравнение состояния идеального газа(1):

   $p=nkT$(8).

2. Уравнение состояния идеального газа(2) в виде уравнения Менделеева — Клайперона:

   $pV=\nu RT$(9).

3. Основное уравнение МКТ:

   \

4. Работа газа:

   \

Пример 1

Задание: В процессе сжатия 1-2 с линейной зависимостью р(V). Давление идеального газа возросло в 3 раза. Затем газ сжали в изобарном процессе 2-3 до первоначального объема. Найти отношение работ, совершенных газом в процессах расширения и сжатия. Температуры в состояниях 1 и 2 считать одинаковыми.

Рис. 2

Решение:

Работу газа (или над газом) можно рассчитать по формуле:

\

Если мы рассматриваем процесс (как в условиях нашей задачи) в осях p(V), то исходя из геометрического смысла интеграла работа A будет равна площади криволинейной трапеции (в общем случае), а в нашем площади прямоугольника, когда газ расширяется и площади трапеции, когда газ сжимают. Найдем эти площади.

Площадь прямоугольника:

\

Площадь трапеции:

\

Из условий задачи имеем:

\

Найдем отношение $\frac{A_{2\to 3}}{A_{1\to 2}}$:

\

Ответ: Работа, которую совершает газ в процессе 2-3 в 1,5 больше, чем работа по сжатию газа при заданных условиях.

Пример 2

Задание: Определите, как изменяется давление постоянной массы идеального газа, если в процессе объем увеличивают, температура уменьшается?

Решение:

За основу решения возьмем уравнение Менделеева — Клайперона:

\

Выразим из него давление:

\

Ответ: В данном процессе давление уменьшается.

Пример 3

Задание: В процессе, график которого приведен на рисунке (рис.3) давление $p\sim T^n.\ $Найти значение n, если масса газа постоянна.

Рис. 3

Решение:

Из рисунка имеем зависимость p(V):

\

Из уравнения Менделеева — Клайперона:

\

Используем (3.1) заменив объем, получим:

\

Ответ: Получили $p\sim T^{\frac{1}{2}}$, следовательно, $n=\frac{1}{2}.$