1.1. Прямоугольный импульс и его спектр.
Тем или иным способом сформировать прямоугольный видеоимпульс и, используя встроенную функцию БПФ (FFT), построить его амплитудный спектр.
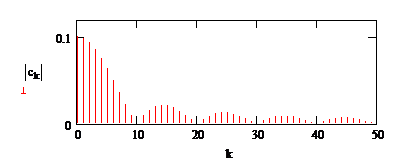 Рис.1. Амплитудный спектр прямоугольного импульса.
Рис.1. Амплитудный спектр прямоугольного импульса.
Длительность сигнала выбрать из соображений наглядности представления спектра.
1.1.1. Определить уровни 2-ого, 3-его, 4-ого лепестков спектра по отношению к главному (отношение уровня лепестков спектра к постоянной составляющей).
1.1.2. Определить изменение амплитудного спектра при изменении длительности импульса.
1.1.3. Определить влияние смещения начала импульса на его спектр.
1.1.4. Определить спектр сигнала типа «меандр» (длительность импульса = T/2).
Здесь и далее в качестве отчета по выполняемым заданиям представить файлы MathCAD, содержащие необходимые пояснения по результатам выполняемых заданий.
Рекомендуется каждое задание оформлять отдельным файлом.
Для иллюстрации различных операций, требующих сравнения результатов (например, как по данному заданию для определения влияния на вид спектра длительности импульса) следует в файле одновременно представить несколько вариантов.
1.Суммирование функций и построение графика суммы.
Рассмотрим
разложение в усеченный ряд Фурье
периодической последовательности
импульсов со скважностью s
и числом слагаемых N:
Для построения графика суммы воспользуемся
компьютерной программой MathCAD:
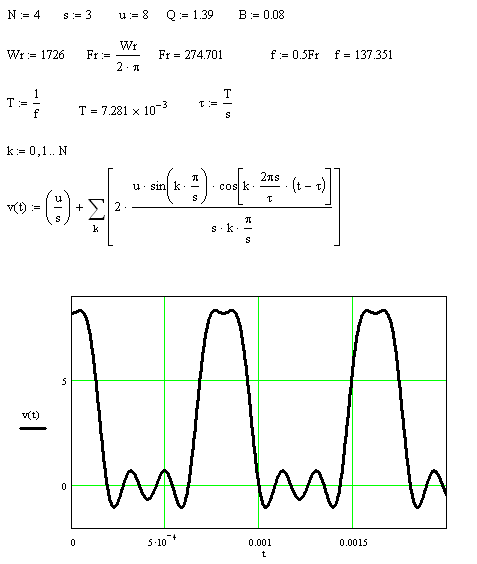

2.Амплитудный
спектр воздействия.
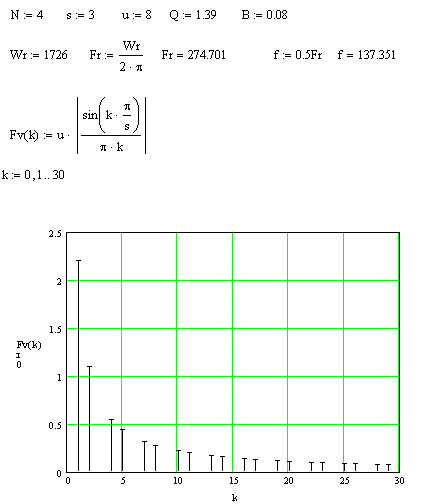
3.Фазный спектр
воздействия.
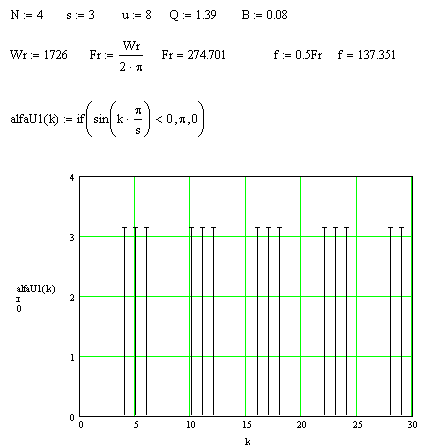
. Рассчитаем
амплитудный и фазный спектры реакции:
В пункте 1.3 были
получены амплитудный и фазовый спектры
сигнала воздействия. Определим, какова
будет реакция исследуемого ARC
– фильтра, если на его вход воздействовать
периодическим сигналом (см. п.п. 1.3).
1. Амплитудный
спектр реакции:

 Рис.
Рис.
6 График амплитудного спектра реакции.
Из графика видно,
что при k=2
наблюдается максимальная пропускная
способность фильтра. Это обусловлено
тем, что к
где
частота
основной гармоники.
2.
Фазный спектр реакции:
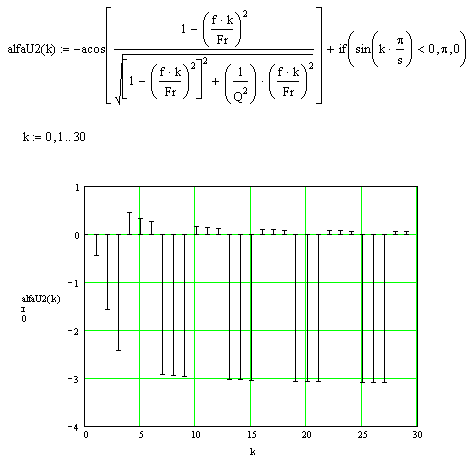
Рис. 8 Фазный спектр
реакции.
1.5. Построим
график функции времени реакции цепи на
заданное воздействие:
По
амплитудному и фазному спектрам (см.
п.п. 1.3) можно построить соответствующую
им функцию времени по формулам (14).
Для построения графика функции времени
воспользуемся компьютерной программой
MathCAD:


 Рис.9.
Рис.9.
График функции времени.
На Рис. 9 представлены
графики сигналов воздействия ()
и реакции ()
ARC
– фильтра.
1.6. Рассчитаем и
построим графики амплитудного и фазного
спектров воздействия и реакции, а также
временные функции воздействия и реакции
с периодом в два раза больше.
В п.п. 1.3. – 1.4 мы
исследовали реакцию фильтра при
воздействие на него периодическим
сигналом, частотой
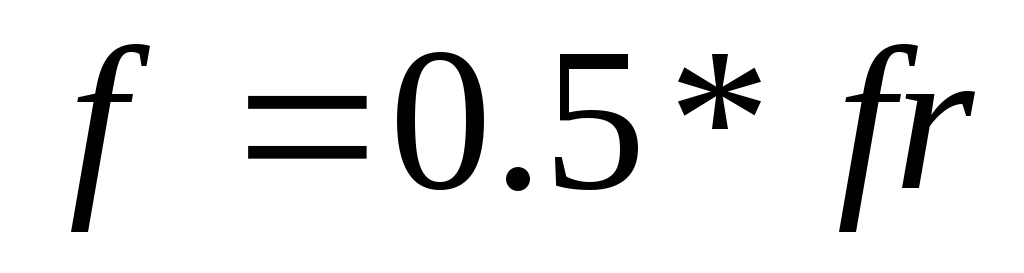 ,
,
где —
—
резонансная частота данногоARC
— фильтра. По условию данного пункта
примем частоту сигнала воздействия
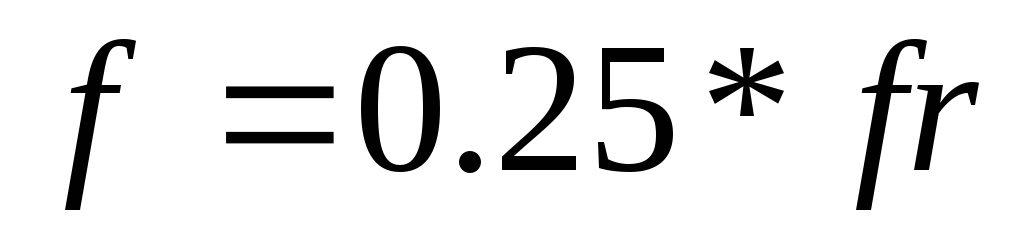 .
.
График
суммы:
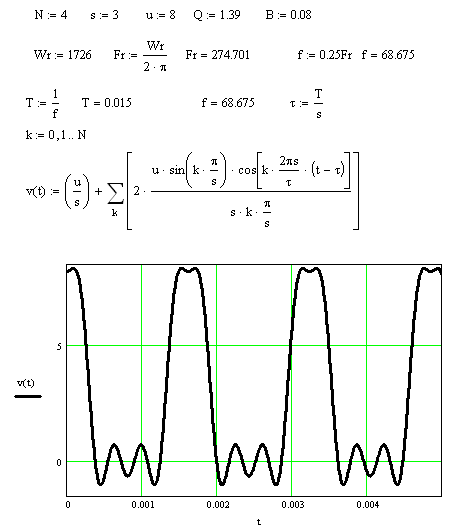
Рис. 10. График
суммы.
Амплитудный
спектр воздействия.

Рис. 4 Амплитудный
спектр воздействия.
Амплитудный спектр
реакции имеет следующий вид:
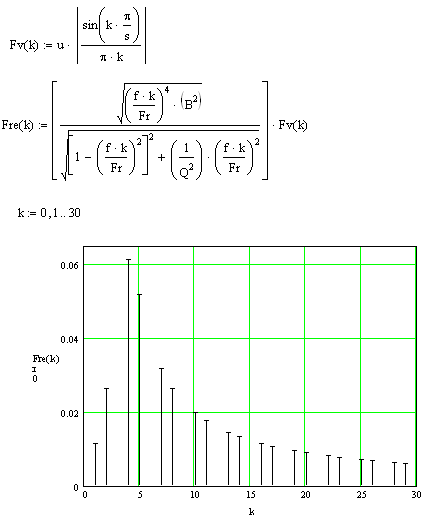
Рис. 11Амплитудный
спектр реакции.
Фазный спектр
воздействия.
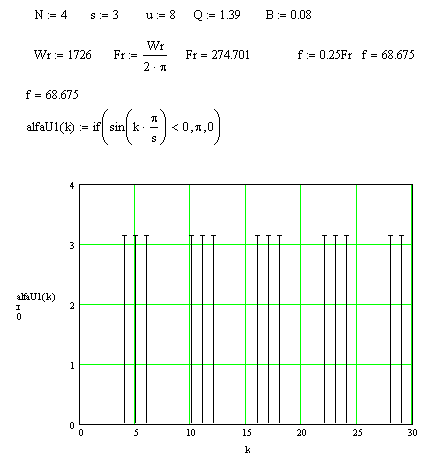
Рис. 5 Фазный спектр
воздействия.
Фазный спектр
реакции имеет следующий вид:
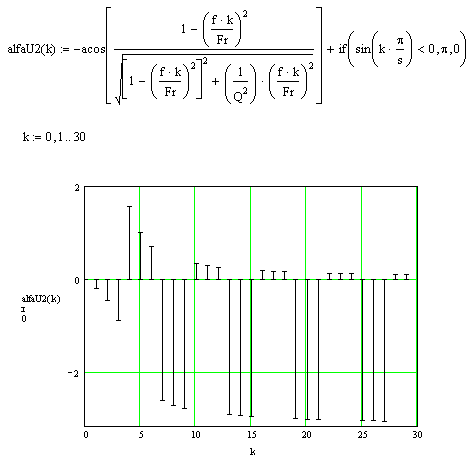
Рис. 12 Фазный спектр
реакции
Временные функции:
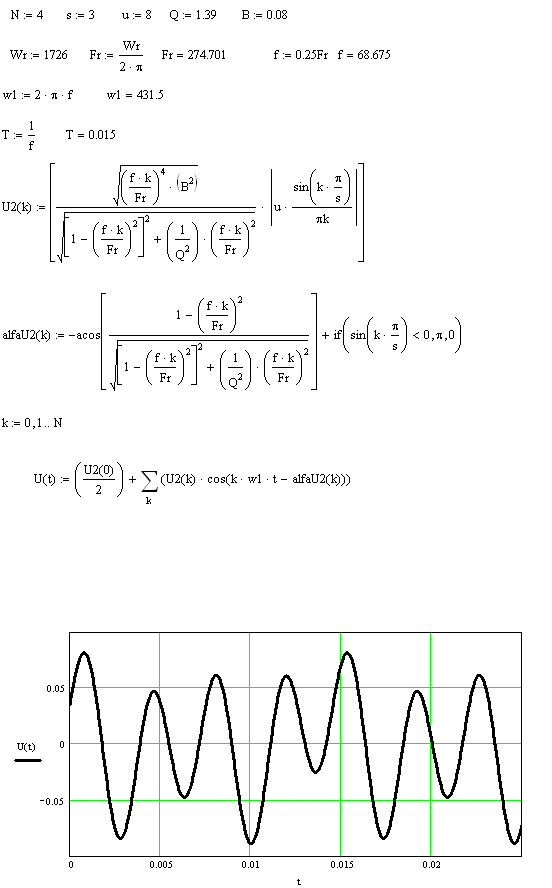
Рис.13 График
функции времени.
3.3.1. Гармоническая модуляция с малым индексом
А.
Вызовите сигнал (Рис. 15))из файлаFMB
0″5.
dat
. Зарисуйте его спектр. Сравните спектр
с теоретическим (см. рис.10,а)
Обратите
внимание на его отличие от спектра АМ
Б.
По спектру определите несущую
частотуf
o
,
частоту модуляцииF
,
начальные фазы
о
и
. Измерьте
амплитуды составляющих спектра, по ним
найдите индекс
Рис. 15. модуляции
.
Определите ширину спектра.
3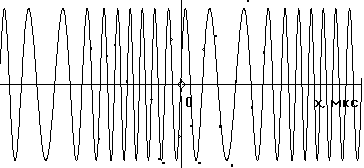 .3.2.
.3.2.
Гармоническая ЧМ с индексом
>1
А.
Вызовите файлFMB
«5.
dat
,
где записан сигнал с индексом=5
(Рис. 16). Зарисуйте сигнал и его спектр.
Б.
Определите частоту модуляцииF
,
число боковых составляющих спектра и
его ширину. Найдите девиацию частоты
f
,
пользуясь
Рис. 16.
формулой
f
F
. Сравните девиацию
с измеренной шириной спектра.
В.
Измерьте относительные амплитуды
С(f)/C max первых трех-четырех составляющих спектра
и сравните их с теоретическими значениями,
определяемыми функциями Бесселя.
Обратите внимание на фазы спектральных
составляющих. Несущая частота радиоимпульса (частота заполнения):
Несущая частота радиоимпульса (частота заполнения):
, ,
Определим ширину спектра Δf:
f max
– определена по графику амплитудного спектра одиночного прямоугольного видеоимпульса (рис.5), по 10% уровню от |S(f)| max , т.е. по уровню 0.1|S(f)| max .
К узкополосным сигналам (радиосигналам) относятся сигналы, спектры которых сосредоточены в относительно узкой по сравнению со средней частотой полосе. Узкополосный сигнал описывается выражением:
ω 0 – частота несущего колебания
V(t), Φ(t) – амплитуда и фаза сигнала
В частном случае, когда , а V(t)=s(t) – непериодический видеосигнал, (5) описывает радиоимпульс:
Таким образом, аналитическое выражение
для полученного радиоимпульса:
где S(t) –
заданный сигнал (см.. п.1)
Временная диаграмма одиночного радиоимпульса представлена на рис.8.
Спектральная плотность радиоимпульса определяется спектральной плотностью его огибающей:
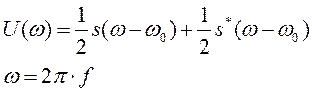
Спектр радиоимпульса U(ω) получается путём переноса спектра его огибающей S(ω) из окрестности нулевой частоты в окрестность несущей частоты ±ω 0 (с коэффициентом 1/2):
S(2π(f–f 0)) и S(2π(f+f 0))
– спектральные плотности видеоимпульса, составляющих заданный сигнал, определённые в п.1.
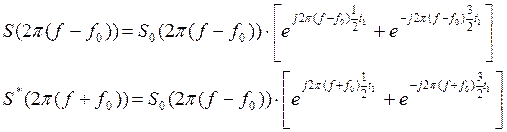
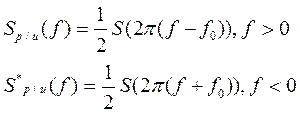
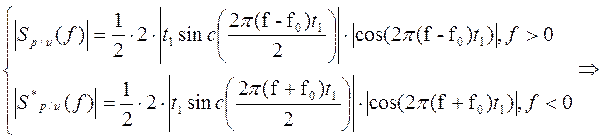
Амплитудный спектр радиоимпульса:
График при f0 относительно оси ординат.
График амплитудного спектра одиночного радиоимпульса представлен на рис. 9.
4. Спектральный анализ периодической последовательности радиоимпульсов.
Спектральный анализ сигнала в виде периодической последовательности радиоимпульсов основан на его представлении в виде ряда Фурье:
коэффициенты которого связаны с коэффициентами ряда Фурье периодического видеосигнала (3) соотношением:
V n – амплитудный спектр периодической последовательности радиоимпульсов.
Аналитическое выражение для последовательности радиоимпульсов:
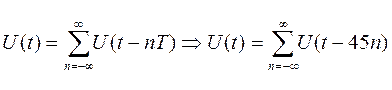
U(t) – одиночный радиоимпульс
Временная диаграмма периодической последовательности радиоимпульсов представлена на рис.10.
,
Определим амплитудный спектр периодической последовательности радиоимпульсов по:
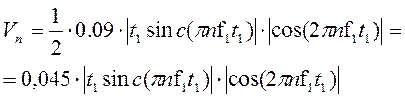 График амплитудного спектра периодической последовательности радиоимпульсов V n представлен на рис.11
График амплитудного спектра периодической последовательности радиоимпульсов V n представлен на рис.11
5. Корреляционный анализ непериодического сигнала
Автокорреляционная функция определяется следующим интегралом:
, (7)
и характеризует взаимосвязь между значениями сигнала в различные моменты времени.
Для действительного сигнала корреляционная функция является действительной чётной функцией
Максимального значения, равного энергии сигнала корреляционная функция достигает при τ=0:
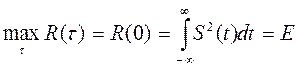
Непосредственное интегрирование в формуле (7) даёт выражение для правой ветви автокорреляционной функции (рис.)
Замена в полученном выражении τ =| τ | позволяет перейти к аналитическому описанию автокорреляционной функции, как для положительных значений τ>0, так и для отрицательных τ
По свойствам автокорреляционной функции
S(t±t 0), t 0 >0 => R(τ)=R(τ)
Корреляционная функция пачки импульсов
, где S(t) – 1-й импульс в пачке,
при условии, что интервал следования в пачке t 1 больше или равен τ 0 – длительность 1-го импульса в пачке S 0 (t), взаимосвязана с корреляционной функцией R 0 (τ) соотношением
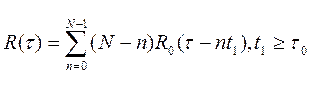 , (8)
, (8)
Воспользуемся выражением (8):
N=2 – количество импульсов
График АКФ представлен на рис.12
6.Спектральный анализ линейной цепи
рис.13. Заданная схема цепи рис.14. Эквивалентная схема замещения
КЧХ определяется по следующей формуле:
Согласно эквивалентной схеме замещения:
;
По формуле делителя напряжения :
– постоянная RC цепи .
Определим АЧХ:
Ряд Фурье.
Зададим
на отрезке времени рассмотренный
в гл. I ортонормированцый базис,
образованный гармоническими функциями
с кратными частотами;

Любая
функция из
этого базиса удовлетворяет условию
периодичности (2.1). Поэтому, — выполнив
ортогональное разложение сигнала в
этом базисе, т. е. вычислив коэффициенты
получим спектральное
разложение
справедливое на
всей бесконечности оси времени.
Ряд
вида (2.4) называется рядом Фурье даннрго
сигнала. Введем основную
частоту последовательности,
образующей периодический сигнал.
Вычисляя коэффициенты разложения по
формуле (2.3), запишем ряд Фурье для
периодического сигнала
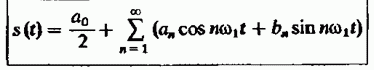
с коэффициентами
(2.6)
Итак,
в общем случае периодический сигнал
содержит не зависящую от времени
постоянную составляющую и бесконечный
набор гармонических колебаний, так
называемых гармоник с частотами кратными
основной частоте последовательности.
Каждую
гармонику можно описать ее амплитудой и
начальной фазой Для
этого коэффициенты ряда Фурье следует
записать в виде
Подставив эти
выражения в (2.5), получим другую, —
эквивалентную форму ряда Фурье:

которая иногда
оказывается удобнее.
2.2. Спектральные характеристики непериодических сигналов
Задача 2.2.1. Построить спектры амплитуд и фаз сигнала U(t) на выходе генератора линейно изменяющегося напряжения (ГЛИН) при исходных данных: скорость изменения Vm:=4 volt∙Sec -1 и длительность τ:=2 Sec.
Аналитическое выражение сигнала
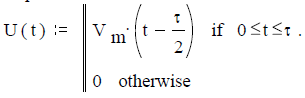
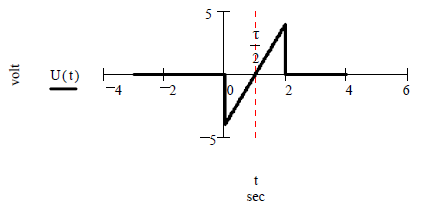
Рисунок 15 – Сигнал U(t)

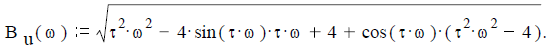

Задача 2.2.2. Найти спектр косинусоидальной функции y(t), заданной на интервале -τ/2 ≤t≤ τ/2 показанной на рисунке 16, при исходных данных: амплитуда Um:= 0.5, длительность τ:= 0.2, при N:= 8 частота f:= N/τ или ω:= 2 ∙ π ∙ f, возможная периодичность повторения T:= 2 ∙ τ.
Аналитическое выражение функции
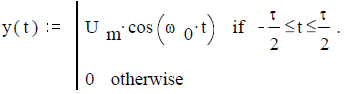
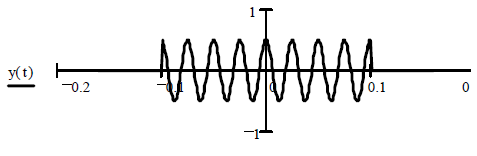
Рисунок 16 – Сигнал y(t)
Ответ.Спектр функции y(t)
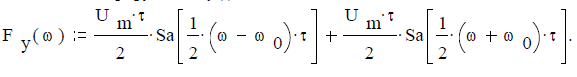
Задача 2.2.3. Найти амплитудный спектр одиночного видеоимпульса S(t) синусоидальной формы при исходных данных: амплитуда Um:= 2 volt; длительность τ:= 10 -1 sec; при N:= 2 частота f:= 1/ (N∙τ) (угловая частота ω:= 2 ∙ π ∙ f) и период T:= N∙τ.
Аналитическое выражение сигнала:
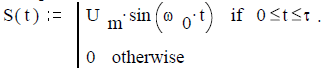
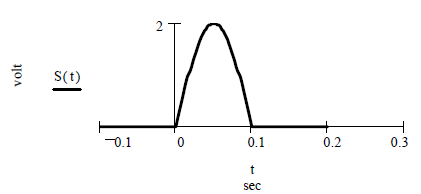
Рисунок 17 – Видеоимпульс S(t)
Ответ. Амплитудный спектр
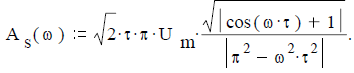
График амплитудного спектра видеоимпульса S(t) синусоидальной формы приведен на рисунке 18 при изменении угловой частоты ω в долях несущей частоты ω:= 2π/Т в случае периодического продолжения импульсного сигнала с периодом T, а именно при

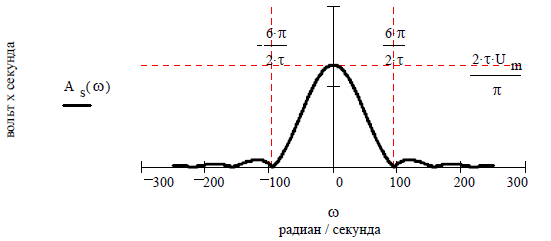
Рисунок 18 – График амплитудного спектра видеоимпульса S(t)
Задача 2.2.4. Решить задачу 2.2.3 с использованием теоремы о временном сдвиге.
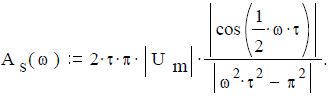
Задача 2.2.5. Найти спектры амплитуд и фаз экспоненциального видеоимпульса E(t), t≥0 sec с амплитудой Um:= 1volt и коэффициентом затухания α:=0.1 sec -1 .
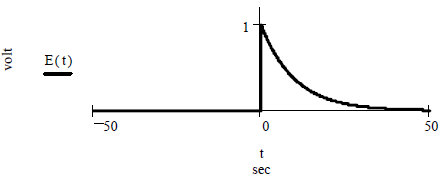
Рисунок 19 – Видеоимпульс E(t)
Математическая модель сигнала
Задача 2.2.6. Найти амплитудный спектр экспоненциального радиоимпульса E1(t), t≥0 sec (рисунок 20) с параметрами: амплитуда Um:= 5volt; коэффициент затухания α:= 400 sec -1 ; частота f:= 1000 Hz (ω:= 2πf).
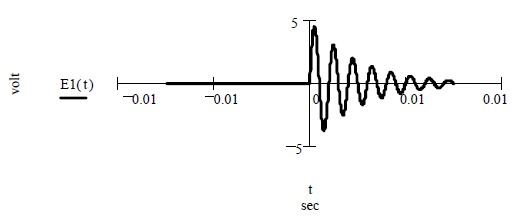
Рисунок 20 – Экспоненциальный радиоимпульс E1(t)
Математическая модель сигнала
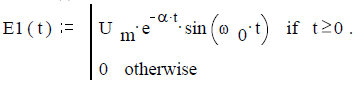
Ответ.Амплитудный спектр экспоненциального радиоимпульса

График амплитудного спектра приведен на рисунке 21 при
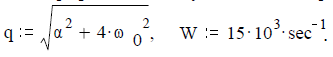
и изменении угловой частоты
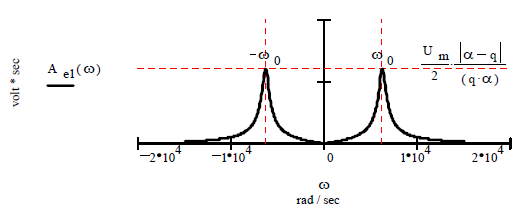
Рисунок 21 – График амплитудного спектра
Задача 2.2.7. Найти в рамках Mathcad спектры некоторых специальных функций:
дельта-функция δ (t) или функция Дирака
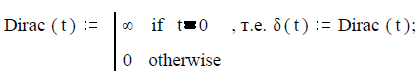
единичный скачок d(t) или функция Хевисайда
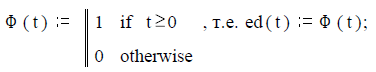
комплексная синусоида (пусть ω:= 5)
постоянная функция p(t) := A
ПРИМЕЧАНИЕ. Все эти функции абсолютно не интегрируемы, но путем предельного перехода для них можно найти интегральное преобразование Фурье.

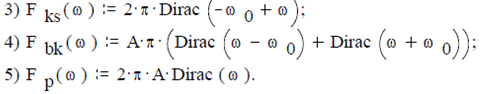
ПРИМЕЧАНИЕ. Если интеграл непосредственно не берется, то следует использовать в Mathcad команды прямого преобразования Фурье «Fourier Transform» и обратного преобразования Фурье «Inverse Fourier Transform» меню Symbolic и Transforms.
Задача 2.2.8. Амплитудный спектр сигнала S(t) имеет параметры:
а) плотность амплитуд H:= 0.5 volt∙sec;
б) частоты среза спектра ωc1:= 4 sec -1 и ωc2:= 3 ωc1.
Амплитудный спектр описывается выражением

Спектр фаз равен нулю. Требуется найти вид сигнала S(t). График частотной характеристики (амплитудного спектра) приведен на рисунке 22 при W:=18 sec -1 и ω:= -W, -W + W/200 .. W.
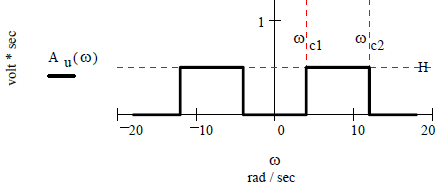
Рисунок 22 – График частотной характеристики
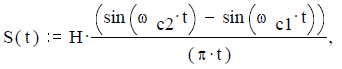
причем при t:=0 имеем
График сигнала при T:= 5sec и t:= 1.0 ∙ T, — 1.0 ∙ T + T/400 .. 1.0 ∙ T приведен на рисунке 23.
Автоматизация инженерной деятельности
Тема 1. Формирование элементарных сигналов и вычисление их спектров. 2
1.1. Прямоугольный импульс и его спектр. 2
1.2. Прямоугольный радиоимпульс и его спектр. 2
1.3. Прямоугольный видеоимпульс с экспоненциальными фронтами и его спектр. 3
1.4. Сравнение спектров прямоугольного и колоколообразного (гауссового) импульсов. 3
1.5. Особенности применения БПФ (FFT) для гармонических сигналов. 4
1.6. Спектр амплитудно-модулированных сигналов. 4
1.7. Спектр частотно-модулированного сигнала. 5
По текстовым файлам «Формирование сигналов в среде MathCAD» и «Спектральный анализ сигналов» ознакомиться со способами формирования сигналов и особенностях вычисления их спектров встроенными функциями.
Ознакомиться также с файлом MathCAD «Формирование элементарных сигналов».
*3.2.8. Формирование и исследование ам-сигналов
Программа SASWinпозволяет
формировать сигналы с различными и
достаточно сложными видами модуляции.
Вам предлагается, используя приобретенный
опыт работы с программой, сформировать
АМ-сигнал, параметры и форму огибающей
которого установите самостоятельно.
А.
В опцииPlot, пользуясь
мышкой или курсором, создайте желаемый
вид сигнала модуляции. Рекомендуется
не увлекаться слишком сложной его
формой. Зарисуйте спектр вашего сигнала.
Б.
Занесите сигнал в память, нажав
кнопку вертикального меню R
AM>
и присвоив сигналу какое-нибудь имя
или номер.
В.
Войдите в опциюInstalи
укажите тип сигнал .
В
открывшемся меню видов модуляции
выберите Обычный вариант Амплитудной
модуляции и нажмите кнопку .
Г.
На
запрос «Закон изменения амплитуды»
укажите .
Д.
Появится вертикальное меню
сигналов, находящихся в памятиRAM.
Выберите ваш сигнал и нажмите кнопку
.
Например: Несущая частота, кГц =
100,
Фаза несущей
= 0,
Границы частотного окна fminиfmaxдля вывода спектра
Нажать кнопку
Сформированный сигнал отображается
в левом окне, а его спектр – в правом.
Ж.
Зарисуйте сформированный сигнал
и его спектр. Сравните их с формой и
спектром сигнала модуляции.
З.
Сигнал можно записать в памятьRAMили в файл и далее
использовать его по надобности.
И.
При желании повторите исследования
с другими сигналами модуляции.
1.6. Спектр амплитудно-модулированных сигналов.
Смоделировать амплитудную модуляцию несущей частоты одной гармоникой низкой частоты.
Аналитическое выражение АМ-сигнала:
Модулирующее колебание (с амплитудой = 1):
Um – амплитуда несущей частоты колебания (без модуляция) – принять = 1;
m – коэффициент модуляции;
F – частота модуляции.
Построить спектр АМ-сигнала с помощью FFT.
Напомним, что для получения «правильного» результата расчета спектра по FFT как f0, так и F должны быть кратны 1/T (целое число периодов на интервале моделирования), т. е. присвоить частотам значения:
где n и N – число периодов колебаний частоты f0 и F на интервале T.
Рис.6. АМ сигнал и его спектр.
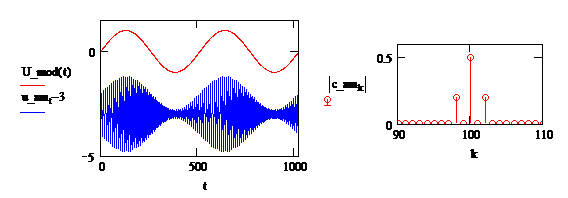 |
Определить соотношение между гармоникой несущей и гармониками боковых частот при различных коэффициентах амплитудной модуляции m = 1; 0.7; 0.5.
Выяснить форму АМ-сигнала при перемодуляции (m > 1).
Спектральная диаграмма периодического сигнала.
Так принято называть
графическое изображение коэффициентов
ряда Фурье для конкретного сигнала.
Различают амплитудные и фазовые
спектральные диаграммы (рис. 2.1).
Здесь по горизонтальной
оси в некотором масштабе отложены
частоты гармоник, а по вертикальной оси
представлены их амплитуды и начальные
фазы.

Рис. 2.1. Спектральные
диаграммы некоторого периодического
сигнала: а — амплитудная; б — фазовая
Особо интересуются
амплитудной диаграммой, которая позволяет
судить о процентном содержании тех или
иных гармоник в спектре периодического
сигнала.
Изучим несколько
конкретных примеров.
Пример
2.1. Ряд Фурье периодической последовательности
прямоугольных видеоимпульсов с
известными параметрами ,
четной относительно точки t = 0.
В
радиотехнике отношение называют
скважностью последовательности. По
формулам (2.6) находим

Окончательную
формулу ряда Фурье удобно записать в
виде

На рис. 2.2 представлены
амплитудные диаграммы рассматриваемой
последовательности в двух крайних
случаях.
Важно
отметить, что последовательность
коротких импульсов, следующих друг за
другом достаточно редко ,
обладает богатым спектральным составом
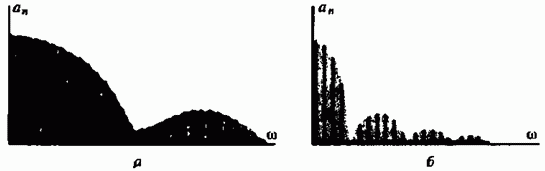
Рис. 2.2
Амплитудный
спектр периодической последовательности
ррямоугольных видеоимпульсов: а — при
большой скважности; б — при малой
скважности
Пример
2.2. Ряд Фурье периодической последовательности
импульсов, образованной гармоническим
сигналом вида ограниченным
на уровне (предполагается,
что ).
Введем
специальный параметр — угол отсечки ,
определяемый из соотношения откуда
В
соотаетствии с этим величина равна
длительности одного импульса, выраженной
в угловой мере:
Аналитическая
запись импульса, порождающего
рассматриваемую последовательность,
имеет вид
Постоянная
составляющая последовательности
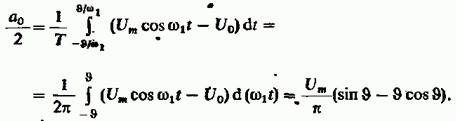
Амплитудный
коэффициент первой гармоники
Аналогично
вычисляют амплитуды —
гармонических составляющих при
Полученные
результаты обычно записывают так:
где так
называемые функции Берга:

Графики некоторых
функций Берга приведены на рис. 2.3.
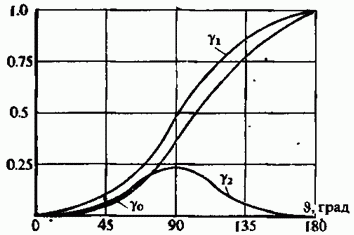
Рис. 2.3. Графики
нескольких первых функций Берга
Спектральная плотность сигналов.
Прямое и обратное преобразования Фурье.
2.1 Спектральные характеристики периодических сигналов
Задача 2.1.1. Разложить функцию x(t):= t,в тригонометрический ряд Фурье на интервале (0,1).
Ряд Фурье (1.1) при числе гармоник k:= 0,1,2 имеет вид
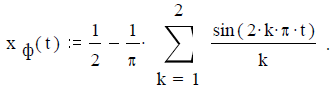
Задача 2.1.2. Разложить функцию x(t):= t из примера 1.1 в экспоненциальный ряд Фурье на интервале (0,1).
Экспоненциальный ряд Фурье (1.4) при числе гармоник m:= 5 имеет вид
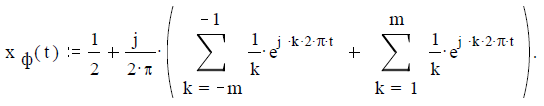
Задача 2.1.3. Построить амплитудный спектр периодической последовательности идеальных прямоугольных импульсовZ(t), график которой приведен на рисунке 10, на базе тригонометрического ряда Фурье.
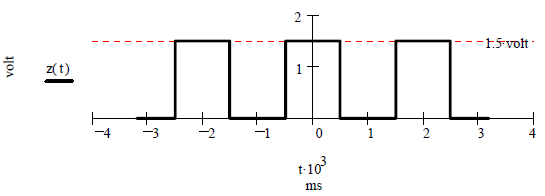
Рисунок 10 – График идеальных прямоугольных импульсов
Ответ. При единице времени одна миллисекунда ms:= 10 -3 sec, номерах гармоник k:= 0 .. 5, амплитуде Um:= 1.5volt, периоде T:= 2 ms, частоте 1-й гармоникиf1:= 1/Tи k-й гармоники fk:= k∙f1амплитудный спектр
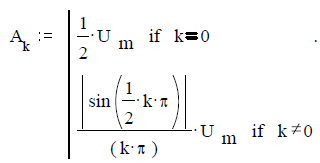
График амплитудного спектра в виде столбчатой диаграммы приведен на рисунке 11.
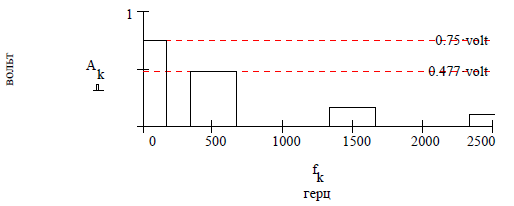
Рисунок 11 – График амплитудного спектра
Задача 2.1.4. Найти амплитудный и фазовый спектры сигналаU(t) на выходе однополупериодного выпрямителя на основе комплексного ряда Фурье. График сигнала показан на рисунке 12.
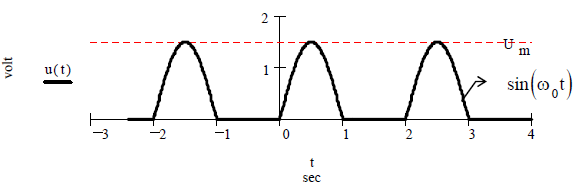
Рисунок 12 – График сигнала U(t)
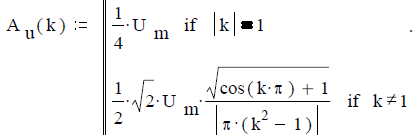
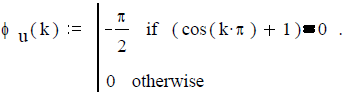
Задача 2.1.5. Найти амплитудный и фазовый спектры сигналаS(t) на выходе двух полупериодного выпрямителя на основе комплексного ряда Фурье. График сигнала показан на рисунке 13.
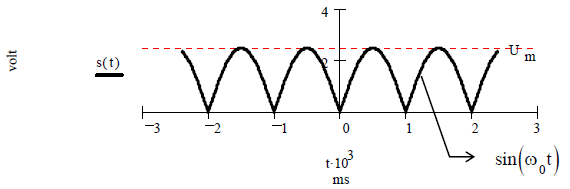
Рисунок 13 – График сигнала S(t)
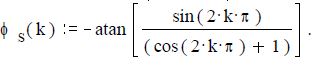
Задача 2.1.6. Найти амплитудный и фазовый спектры периодической последовательности идеальных прямоугольных импульсов P(t), график которой приведен на рисунке 14, на базе комплексного ряда Фурье.
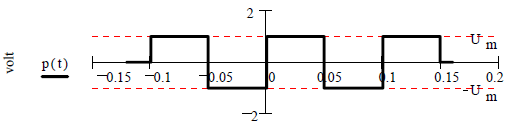
Рисунок 14 – График импульсов P(t)


Гармонические и негармонические сигналы.
И для начала давайте чуть подробнее разберемся, как же классифицируются сигналы. В первую очередь нас интересуют гармонические сигналы, форма которых повторяется через определенный интервал времени , называемый периодом. Периодические
сигналы в свою очередь делятся на два больших класса – гармонические и негармонические. Гармонический сигнал – это сигнал, который можно описать следующей функцией:
Здесь – амплитуда сигнала, – циклическая частота, а – начальная фаза. Вы спросите – а как же синус? Разве синусоидальный сигнал не является гармоническим? Конечно, является, дело в том, что , то есть сигналы отличаются начальной фазой, соответственно, синусоидальный сигнал не противоречит определению, которое мы дали для гармонических колебаний
Вторым подклассом периодических сигналов являются негармонические колебания
. Вот пример негармонического сигнала:
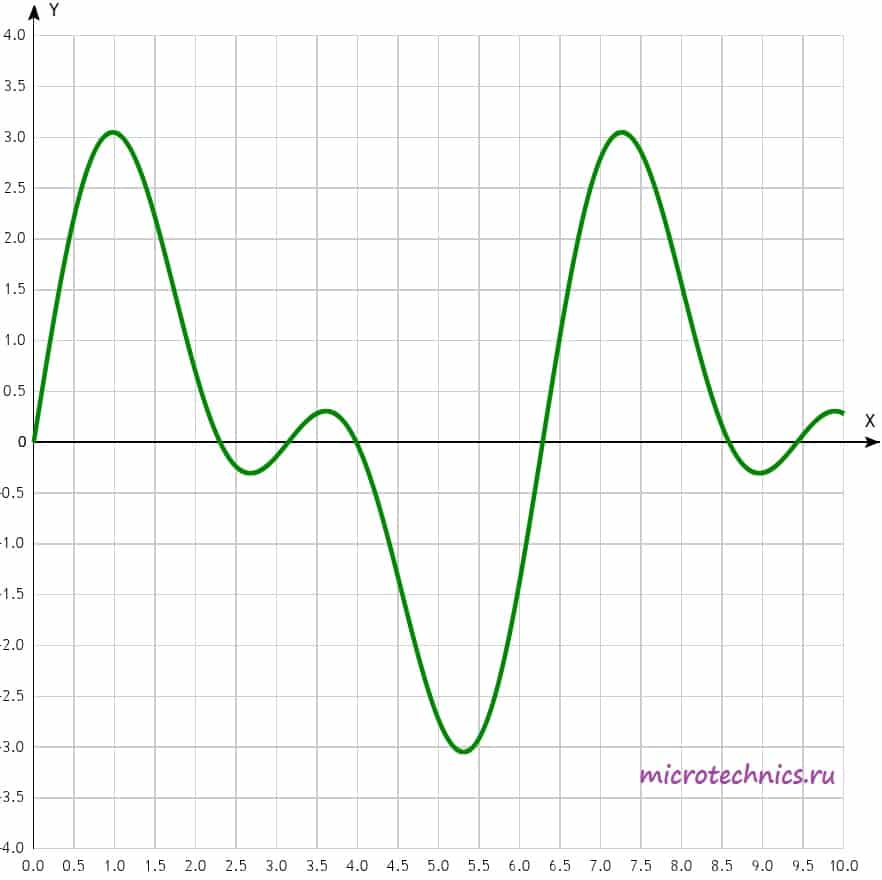
Как видите, несмотря на “нестандартную” форму, сигнал остается периодическим, то есть его форма повторяется через интервал времени, равный периоду.
Для работы с такими сигналами и их исследования существует определенная методика, которая заключается в разложении сигнала в ряд Фурье
. Суть методики состоит в том, что негармонический периодический сигнал (при выполнении определенных условий) можно представить в виде суммы гармонических колебаний с определенными амплитудами, частотами и начальными фазами. Важным нюансом является то, что все гармонические колебания, которые участвуют в суммировании, должны иметь частоты, кратные частоте исходного негармонического сигнала. Возможно это пока не совсем понятно, так что давайте рассмотрим практический пример и разберемся чуть подробнее Для примера используем сигнал, который изображен на рисунке чуть выше. Его можно представить следующим образом:
Давайте изобразим все эти сигналы на одном графике:
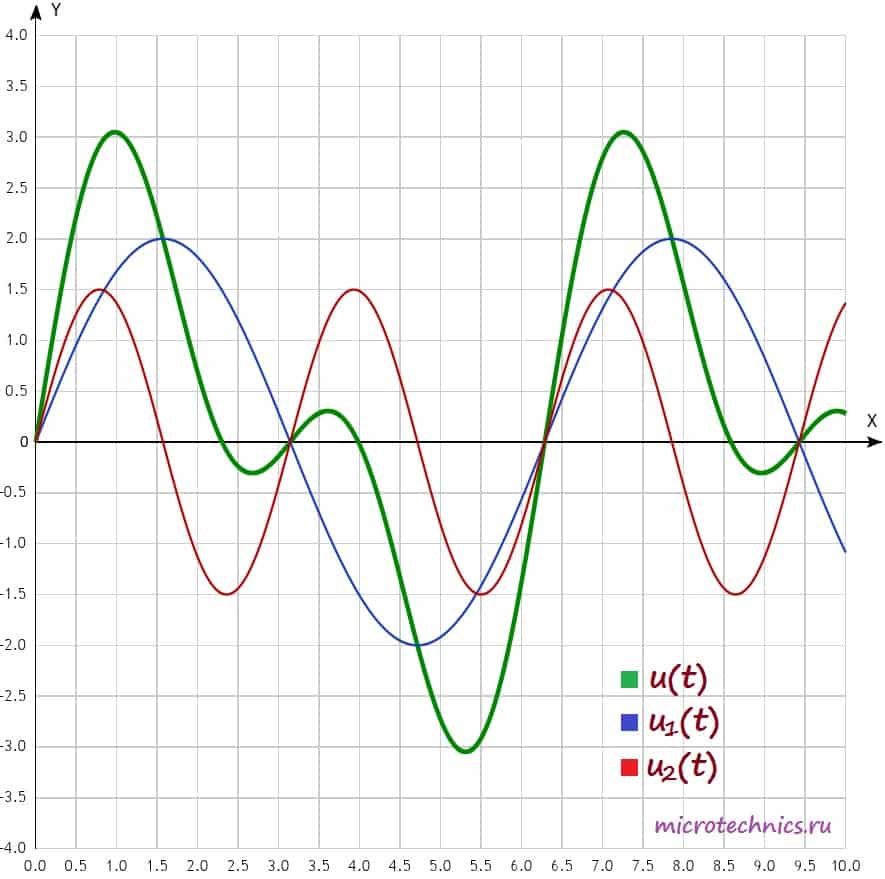
Функции , называют гармониками
сигнала, а ту из них, период которой равен периоду негармонического сигнала, называют первой или основной гармоникой
. В данном случае первой гармоникой является функция (ее частота равна частоте исследуемого негармонического сигнала, соответственно, равны и их периоды). А функция представляет из себя ни что иное как вторую гармонику сигнала (ее частота в два раза больше). В общем случае, негармонический сигнал раскладывается на бесконечное число гармоник:
В этой формуле – амплитуда, а – начальная фаза k-ой гармоники. Как мы уже упомянули чуть ранее, частоты всех гармоник кратны частоте первой гармоники, собственно, это мы и видим в этой формуле – это нулевая гармоника, ее частота равна 0, она равна среднему значению функции за период. Почему среднему? Смотрите – среднее значения функции синуса за период равно 0, а значит при усреднении в этой формуле все слагаемые, кроме будут равны 0.
Совокупность всех гармонических составляющих негармонического сигнала называют спектром
этого сигнала. Различают фазовый и амплитудный спектр сигнала:
- фазовый спектр сигнала – совокупность начальных фаз всех гармоник
- амплитудный спектр сигнала – амплитуды всех гармоник, из которых складывается негармонический сигнал
Давайте рассмотрим амплитудный спектр поподробнее. Для визуального изображения спектра используют диаграммы, представляющие из себя набор вертикальных линий определенной длины (длина зависит от амплитуды сигналов). На горизонтальной оси диаграммы откладываются частоты гармоник:
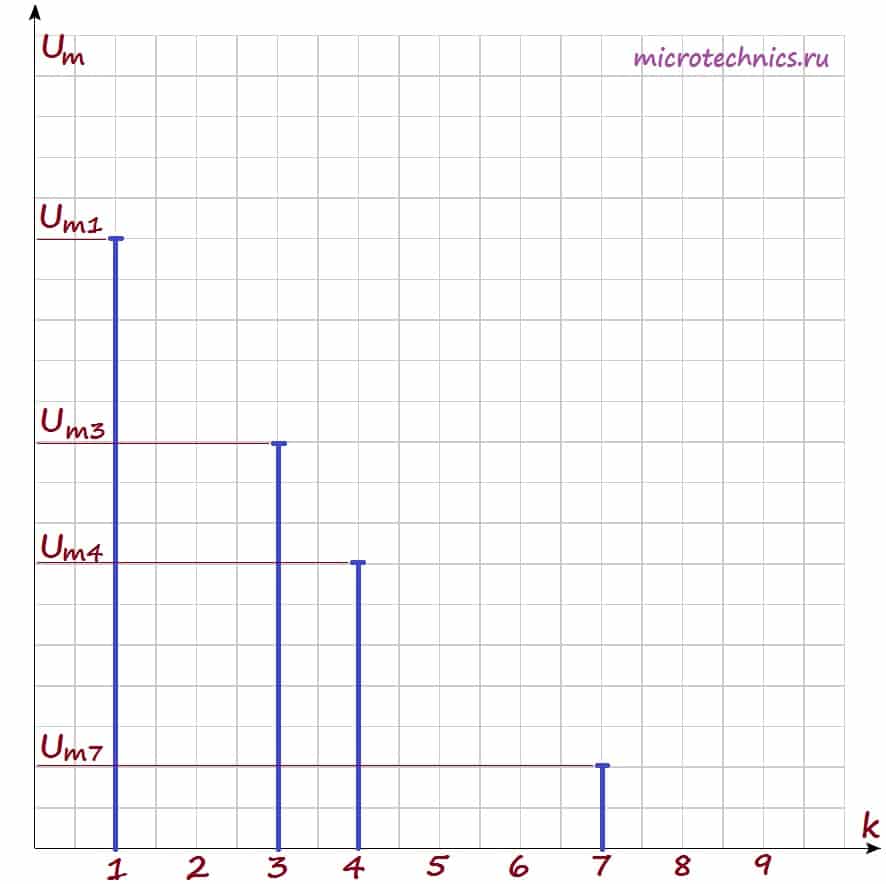
По горизонтальной оси могут откладываться как частоты в Гц, так и просто номера гармоник, как в данном случае. А по вертикальной оси – амплитуды гармоник, тут все понятно:). Давайте построим амплитудный спектр сигнала для негармонического колебания, которое мы рассматривали в качестве примера в самом начале статьи. Напоминаю, что его разложение в ряд Фурье выглядит следующим образом:
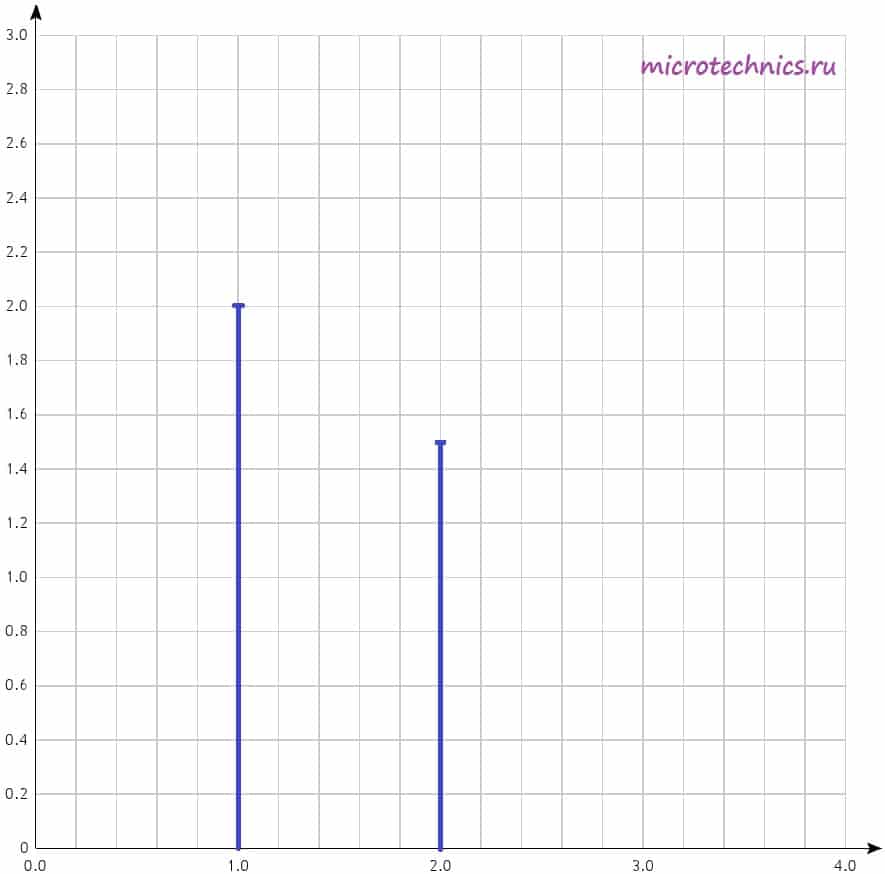
У нас есть две гармоники, амплитуды которых равны, соответственно, 2 и 1.5. Поэтому на диаграмме две линии, длины которых соответствуют амплитудам гармонических колебаний.
Фазовый спектр сигнала строится аналогично, за той лишь разницей, что используются начальные фазы гармоник, а не амплитуды.
Итак, с построением и анализом амплитудного спектра сигнала мы разобрались, давайте перейдем к следующей теме сегодняшней статьи – к понятию амплитудно-частотной характеристики.
1.7. Спектр частотно-модулированного сигнала.
Частотная модуляция аналитически описывается выражением:
Um – амплитуда сигнала (при ЧМ амплитуда постоянна);
m – индекс частотной модуляции.
При ЧМ модуляции одной частотой Ω (F):
индекс модуляции равен m= ΔfF (или ΔωΩ); здесь амплитуда модулирующего сигнала принята равной 1.
Δf (Δω) – девиация частоты – максимальное отклонение несущей частоты под воздействием модулирующего сигнала от средней – f0.
Опуская здесь математическое обоснование, отметим, что ЧМ сигнал теоретически может быть представлен бесконечным рядом гармоник, вычисляемых через функции Бесселя:

где Jk(m) – значение функции Бесселя первого рода порядка k (k – номер гармоники ряда Фурье) при значении аргумента m (значении индекса модуляции).
Используя файл «Частотная модуляция», определить изменение спектра ЧМ сигнала в зависимости от частоты модуляции F (от N – числа периодов модулирующего сигнала на интервале T) и от девиации частоты Δf (в % от несущей частоты).
N менять в пределах 1…5, девиацию в % — в пределах 5…15%
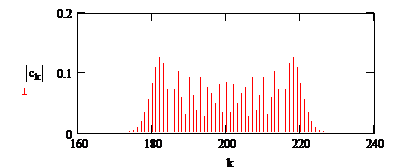 |
Рис.7. Спектр ЧМ сигнала.
Спектр ЧМ сигнала бесконечен (см. выше), но на практике полагают, что полоса частот, занимаемая ЧМ сигналом, примерно равна:
(В пределах такой полосы сосредоточена основная мощность ЧМ сигнала).
Используя указанный выше файл, определить связь между девиацией частоты и шириной спектра ЧМ сигнала (т. е. убедиться в справедливости практических предположений о ширине спектра).
В вышеуказанном файле расчет гармоник спектра ЧМ сигнала выполнен методом быстрого преобразования Фурье (FFT).
Не безынтересно сравнить результаты расчета спектра ЧМ сигнала по FFT c теоретическими значениями.
В MathCAD имеются встроенные функции Бесселя Jn(j,x):
— где j — порядок функции, x – аргумент функции.
Применимо к ЧМ сигналу x – это значение индекса модуляции m;
j — номер гармоники боковой полосы спектра;
Для сравнения результатов расчета спектра по FFT с теоретическими значениями вывести значения нескольких гармоник, рассчитанных разными способами и сравнить их:
Построить несколько функций Бесселя:
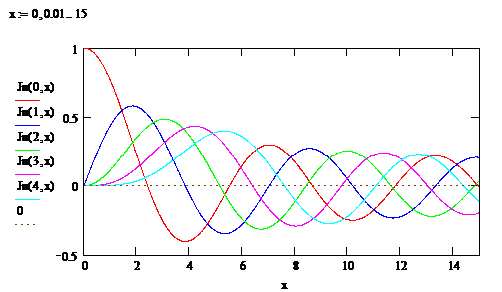 |
Рис.8. Функции Бесселя первого рода порядка 0…4.
Найти одно из значений индекса модуляции m (порядка 6-и), при котором гармоника несущей частоты будет равна нулю, т. е. будет подавлена (Jn(0,x)=0).
Естественно, для определения x (m), при котором Jn(0,x)=0, т. е. для определения численных значений функции и аргумента по построенным графикам можно воспользоваться режимом измерений MathCAD Trace. Однако при этом не всегда обеспечивается требуемая точность получения результатов, т. к. указатель для измерения устанавливается только на расчетные точки.
В таких случаях (а также и при других расчетах) удобно использовать встроенную функцию root для вычисления корня уравнения.
Вычисление корня уравнения f(x) в MathCAD реализовано в двух вариантах:
f(x) – уравнение, x – переменная уравнения, относительно которой вычисляется корень.
Вычисление корня уравнения выполняется численным методом Ньютона (методом касательной), поэтому перед заданием функции root(f(x),x) следует задать начальное значение (первое приближение к корню) x0.
Здесь вместо задания начального (первого) приближения к корню уравнения задается диапазон, в пределах которого и следует искать корень. (MathCAD первое приближение вычисляет как середину заданного в root диапазона).
Применимо к рассматриваемой задаче определения индекса частотной модуляции для подавления несущей частоты m_0 можно воспользоваться вычислением:
m_0:=root(Jn(0,x),x, x_min, x_max)
По найденному значению индекса модуляции задать выражение для вычисления девиации частоты Df (уже не через %) и выполнить моделирование ЧМ сигнала, вычислить и построить его спектр (гармоника на несущей частоте должна быть = 0).

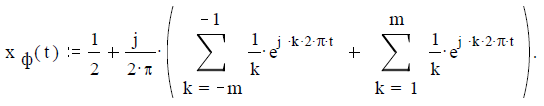















![12.5. примеры построения согласованных фильтров [1977 гоноровский и.с. - радиотехнические цепи и сигналы]](http://dvorik56.ru/wp-content/uploads/6/1/2/6127649a4434d06f81dee59703521cd9.jpeg)













