Таблица степеней

Таблица степеней по алгебре: числа в квадрате

Расписать абсолютно каждое число и найти его значение во всех степенях — невозможно. В сложных примерах рекомендуется использовать онлайн калькуляторы. Мы же рассматриваем наиболее примитивные и распространенные случаи. В основном, в средней школе (вплоть до 11 класса) рассматриваются примеры с перемножением незначительное количество раз. Часто используется квадрат (a2). Некоторые числа мы уже возводили в него (от 1 до 25). Значения больших чисел же можно искать тут:

_{*Для лучшего понимания примеры подсвечены голубым.}

С левой стороны указаны десятки, а сверху — единицы. Т.е., для возведения в квадрат числа 24 ищем пересечение его десятка и единицы (2 — десяток, 4 — единица). Получаем показатель 576. Таким образом данная таблица степеней натуральных чисел может использоваться для возведения в квадрат цифр до 99.

Пример 3. Возводим большие значения в квадрат.

Задача. Найти 632.

Решение. В числе «63» 6 десятков и 3 единицы. Десятки у нас находятся с левой стороны, а единицы — в верхней строчке. Ищем нужные значения в таблице степеней по алгебре и находим число, находящееся на их пересечении.

Ответ. 3969.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Объём куба: как его вычислить

Формула	Описание
V = a³	Объём куба равен длине ребра в третьей степени

Где «V» – объём куба, а «a» – длина ребра.

Например, если длина ребра куба равна 5 сантиметрам, то его объём можно вычислить по формуле: V = 5³ = 5 * 5 * 5 = 125 сантиметров кубических.

Зная формулу вычисления объёма куба, можно легко определить объём кубического объекта в повседневной жизни. Например, при рассмотрении объёма коробки, можно измерить длину одной стороны и применить формулу a³. Это позволит определить, сколько предметов можно поместить в коробку или какой объём он займет.

Формула вычисления объёма куба

Чтобы вычислить объём куба, необходимо знать длину его стороны. Формула для вычисления объёма куба проста:

V = a3

где V – объём куба, а a – длина стороны.

Таким образом, чтобы найти объём куба, нужно возвести длину его стороны в куб. Полученное число будет являться объёмом куба. Например, если длина стороны куба равна 3 см, то объём куба будет равен 33 = 27 см3.

Объём куба измеряется в кубических единицах длины, таких как кубический сантиметр (см3), кубический метр (м3) и т.д. Это показывает, сколько пространства занимает куб.

Формула вычисления объёма куба является базовой для изучения объёма других геометрических объектов, таких как параллелепипеды, призмы и т.д. Знание этой формулы позволяет решать задачи связанные с определением объёма различных фигур в геометрии и применять её в повседневной жизни, например, при расчёте объёма коробки или емкости сосуда.

Наблюдаемый объём куба в повседневной жизни

В повседневной жизни мы часто сталкиваемся с кубами и используем их без особого задумываясь. Так, многие предметы, с которыми мы взаимодействуем ежедневно, имеют кубическую форму.

Например, мы можем наблюдать куб в виде игрального кубика. Он имеет шесть граней, каждая из которых имеет форму квадрата. Когда мы бросаем такой кубик, на его верхней грани может выпасть любое число от 1 до 6. Игра с использованием кубика позволяет нам принимать решения случайным образом, что делает ее интересной и увлекательной.

Кроме того, кубическую форму можно увидеть в различных предметах быта. Многие книги, коробки, телевизоры, мониторы имеют форму куба или приближенную к нему. Это объясняется тем, что куб имеет простую и устойчивую форму, которая позволяет удобно размещать и хранить предметы.

Также кубическая форма используется в архитектуре. Многие здания и сооружения имеют кубическую форму или элементы, напоминающие куб. Например, многие дома имеют форму прямоугольного параллелепипеда, который является производным от куба.

Кубическая форма может быть встречена и в природе. Некоторые кристаллы и минералы образуют кубические структуры. Такие структуры обладают определенной геометрической регулярностью и симметрией.

В целом, куб имеет множество практических применений в повседневной жизни. Его форма и свойства делают его удобным и функциональным для использования в различных сферах, начиная от игр и развлечений до архитектуры и науки.

Таблица кубов чисел от 1 до 100

13 = 1 23 = 8 33 = 27 43 = 64 53 = 125 63 = 216 73 = 343 83 = 512 93 = 729 103 = 1000	113 = 1331 123 = 1728 133 = 2197 143 = 2744 153 = 3375 163 = 4096 173 = 4913 183 = 5832 193 = 6859 203 = 8000	213 = 9261 223 = 10648 233 = 12167 243 = 13824 253 = 15625 263 = 17576 273 = 19683 283 = 21952 293 = 24389 303 = 27000	313 = 29791 323 = 32768 333 = 35937 343 = 39304 353 = 42875 363 = 46656 373 = 50653 383 = 54872 393 = 59319 403 = 64000	413 = 68921 423 = 74088 433 = 79507 443 = 85184 453 = 91125 463 = 97336 473 = 103823 483 = 110592 493 = 117649 503 = 125 000
513 = 132651 523 = 140608 533 = 148877 543 = 157464 553 = 166375 563 = 175616 573 = 185193 583 = 195112 593 = 205379 603 = 216000	613 = 226981 623 = 238328 633 = 250047 643 = 262144 653 = 274625 663 = 287496 673 = 300763 683 = 314432 693 = 328509 703 = 343000	713 = 357911 723 = 373248 733 = 389017 743 = 405224 753 = 421875 763 = 438976 773 = 456533 783 = 474552 793 = 493039 803 = 512000	813 = 531441 823 = 551368 833 = 571787 843 = 592704 853 = 614125 863 = 636056 873 = 658503 883 = 681472 893 = 704969 903 = 729000	913 = 753571 923 = 778688 933 = 804357 943 = 830584 953 = 857375 963 = 884736 973 = 912673 983 = 941192 993 = 970299 1003 = 1000000

Кубы чисел от 10 до 99

РАЗ	ЕДИНИЦЫ
	1	2	3	4	5	6	7	8	9
1	1000	1331	1728	2197	2774	3375	4096	4913	5832	8659
2	8000	9261	10648	12167	13824	15625	17576	19683	21952	24389
3	27000	29791	32768	35937	39304	42875	46656	50653	54872	59319
4	64000	68921	74088	79507	85184	91125	97336	103823	110592	117649
5	125 000	132651	140608	148877	157464	166375	175616	185193	195112	205379
6	216000	226981	238328	250047	262144	274625	287496	300763	314432	328509
7	343 000	357911	373248	389017	405224	421875	438976	456533	474552	493039
8	512 000	531441	551368	571787	592704	614125	636056	658503	681472	704969
9	729 000	753571	778688	804357	830584	857375	884736	912673	941192	970299

Как пользоваться таблицей:

Уровень в первом столбце, один в верхнем ряду. Кость определенного числа ставится на пересечение нужных десятков и единиц.

Допустим, что нам нужно найти куб числа 64. В столбце десятков ищем число 6, в ряду единиц — число 4. Их пересечение соответствует числу 262144 — ответ, который мы хотели найти.

Возведение в степень: определение

Возведение числа в натуральную степень — это умножение его на само себя определенное количество раз. Это такая же операция в алгебре, как сложение, вычитание, умножение или деление.

Если определенное число нужно умножить на себя несколько раз, это значит, что его необходимо возвести в соответствующую степень. Например, если четыре нужно умножить само на себя три раза, это равно тому, что четыре следует возвести в третью степень. Закодировать это выражение можно следующей арифметической записью:

43, где 4 — это основание, а 3 — показатель. Также 43 = 4·4·4 = 64

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Основные правила выполнения данных вычислений:

• итог возведения отрицательного основания в четную степень — положительный;
• итог возведения отрицательного основания в нечетную — отрицательный;
• итог возведения положительного основания в любую — положительный;
• любое основание с показателем один равно себе;
• ноль при любом возведении в результате дает ноль;
• единица с любым показателем равна единице;
• любое основание с показателем ноль равно единице.

Таблица представляет собой ряд чисел, возведенных в определенные степени.

Что такое степень числа в математике — основные понятия

Степень в алгебре и информатике — это выражение, которое записано в виде:

\({{a}^{b}}\),

где a обозначает основание степени, а b играет роль ее показателя, который может быть квадратом, в том числе.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Записанную информацию следует читать, как: «а в степени b».

Таким образом, показатель степени b обозначает количество раз, в течение которых число а умножают само на себя.

Пример 1

Требуется возвести число 2 в третью степень. Тогда запишем 2 в степени 3:

\(2^{3} = 2\cdot 2 \cdot 2\)

В данном случае 2 является основанием степени, число 3 обозначает показатель степени.

Перечислим несколько принципов, которые следует учитывать при решении задач со степенями:

1. Если отрицательное число возвести в четную степень, то получится положительное число.
2. Если отрицательное число возвести в нечетную степень, то получится число со знаком минус.
3. При возведении положительного число в какую-либо степень результатом является положительное число.
4. Ноль при возведении в какую-либо степень дает ноль.
5. При возведении какого-либо числа в нулевую степень получается единица.

Степень с целым показателем является такой степенью, показатель которой записан в виде натурального числа, то есть целого или положительного числа.

Степень с рациональным показателем представляет собой степень с показателем, имеющим знак минус или записанным в виде дробного числа.

Степень с иррациональным показателем — это такая степень, которая имеет на месте показателя бесконечную десятичную дробь или корень.

Таблица кубов

1	8	27	64	125	216	343	512	729
1	1000	1331	1728	2197	2744	3375	4096	4913	5832	6859
2	8000	9261	10648	12167	13824	15625	17576	19683	21952	24389
3	27000	29791	32768	35937	39304	42875	46656	50653	54872	59319
4	64000	68921	74088	79507	85184	91125	97336	103823	110592	117649
5	125 000	132651	140608	148877	157464	166375	175616	185193	195112	205379
6	216000	226981	238328	250047	262144	274625	287496	300763	314432	328509
7	343 000	357911	373248	389017	405224	421875	438976	456533	474552	493039
8	512 000	531441	551368	571787	592704	614125	636056	658503	681472	704969
9	729 000	753571	778688	804357	830584	857375	884736	912673	941192	970299

Третья степень — куб

После предыдущих размышлений, этот факт уже совсем очевиден. Если хотим найти третью степень числа, то строим куб, со стороной равной этому числу.

Рассмотрим на примере числа 6. Так как мы перешли в пространство, то заменяем круги на соответствующие им пространственные фигуры — шары. Получаем такой куб:

Если мы посчитаем, сколько шаров нам для этого понадобилось, то как раз и получим куб числа 6 . В этом случае мы уже считаем не площадь, а объем. Итого:

Факты, изложенные в этой статье, конечно, просты. Но, как мне кажется, довольно занимательны. Некоторым это покажется совсем очевидным. Однако, далеко не все об этом знали. Поэтому, надеюсь что мои читатели сочтут эту статью познавательной.

Виды таблиц

Таблица степеней натуральных чисел

Натуральными являются те числа, которые получаются при счете предметов. Наименьшее — один, наибольшего не существует.

Чтобы вычислить результат возведения, нужно основание умножить само на себя столько раз, сколько указано в показателе. То есть основание а с показателем n значит, что а нужно умножить на себя n раз.

аn = а·а·…·а

Таблица для чисел от одного до десяти:

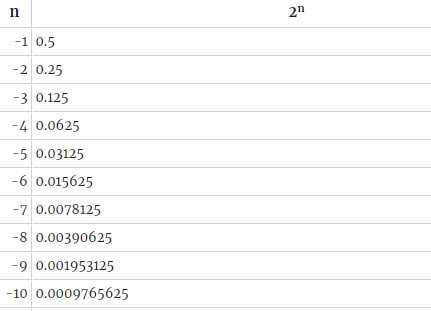
Таблица отрицательных степеней

Деление является обратной операцией умножению. Отрицательный показатель указывает на то, сколько раз необходимо разделить число. Легче всего представить в виде десятичной дроби:

\(а^{-n} = \frac{1}{а*а*\dots*а}\)

Для вычисления \(а^{-n}\) нужно:

1. Возвести а в степень n.
2. Затем разделить единицу на полученный результат, то есть \(\frac{1}{a^n}\).

Пример таблицы для двойки:

3х в кубе — 2у в кубе — 6х в квадрате умножить у в квадрате + ху при х = две третьих и у = одна вторая?

3х в кубе — 2у в кубе — 6х в квадрате умножить у в квадрате + ху при х = две третьих и у = одна вторая.

Вопрос Одна третья в кубе это?, расположенный на этой странице сайта, относится к категории Алгебра и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

100 — (43 + 28) = 29% — прошел в третий день 14, 5 : 29 = 0, 5 км — составляет 1% 43 * 0, 5 = 21, 5 км. — прошел в 1 день 28 * 0, 5 = 14 км. — прошел во 2 день 21, 5 + 14 + 14, 5 = 50 км. — дли на маршрута.

5 / 6х + 1 2 / 3 = 2х — 3 1 2 / 3 + 3 = 2х — 5 / 6х 4 2 / 3 = 1 1 / 6х Х = 4 2 / 3 : 1 1 / 6 Х = 4. Ответ : 4.

Вам нужно так? Пишите, если есть вопросы.

X ^ 4 = y + 2 x = (y + 2) ^ 1 / 4  x ^ 4 = y + 2.

Решение в приложении ниже.

Внешнее действие — извлечение корня квадратного, следовательно, внешняя элементарная функция — степенная с показателем степени 0, 5 либо корень квадратный : или Внутреннее действие — десятичный логарифм, следовательно, внутренняя элементарная функц..

Б) 2 и 4 сокращаем. В знаменателе остается 2. Ответ а ^ 2 / 2b в)n сокращаем, 10 делим на 5. Остается 2 / m г) с сокращаем, а / а ^ 2 = 1 / a. Остается b / a.

Возведение в степень, основные свойства

Возведение в степень представляет собой арифметическое действие в виде итога множественного умножения числа самого на себя.

Обозначают степень, основание которой равно а, и натуральный показатель составляет b, таким образом:

\(a^{b}=\underbrace {a\cdot a\cdot \ldots \cdot a} _{b}\),

где b — число множителей, то есть умножаемых чисел.

Пример 2

Запишем несколько степеней для примера:

\(3^{2}=3\cdot 3=9\)

\(2^{4}=2\cdot 2\cdot 2\cdot 2=16\)

Существуют ключевые свойства, которые распространяют свое действие на операции возведения в степень чисел из множества натуральных, целых, рациональных и вещественных. При этом если требуется возвести в степень комплексное число, то показатель должен быть натуральным. Перечислим эти свойства:

1. \(a^{1}=a\)
2. \(\left(ab\right)^{n}=a^{n}b^{n}\)
3. \(\left({a \over b}\right)^{n}={{a^{n}} \over {b^{n}}}\)
4. \(a^{n}a^{m}=a^{n+m}\)
5. \(\left.{a^{n} \over {a^{m}}}\right.=a^{n-m}\)
6. \(\left(a^{n}\right)^{m}=a^{nm}.\)

Следует отметить, что выражение \(a^{n^{m}}\) лишено свойства ассоциативности (сочетательности). Таким образом, в общем случае:

\( (a^{n})^{m}\neq a^{\left({n^{m}}\right)}\)

Пример 3

\((2^{2})^{3}=4^{3}=64\)

\(2^{\left({2^{3}}\right)}=2^{8}=256\)

В процессе решения математических задач данные записи можно считать равнозначными:

\(a^{n^{m}}\)

\(a^{\left({n^{m}}\right)}\)

Руководствуясь записанным свойством, допустимо упростить запись:

\((a^{n})^{m}\)

\(a^{nm}.\)

Операция возведения в степень не характеризуется свойством коммутативности (переместительности):

\(a^{b}\neq b^{a}\)

Пример 4

\(2^{5}=32\)

\(5^{2}=25.\)

Традиционная таблица степеней натуральных чисел: от 1 до 10

Проще всего находить значение многократного перемножения небольших натуральных чисел. Для поиска решения можно использовать следующую подсказку:

По методу вычисления эта таблица натуральных степеней схожа с таблицей умножения. Чтобы найти результат произведения числа нужное количество раз, достаточно найти соответствующую формулу в столбике.

Пример 1. Используем простую таблицу степеней по алгебре.

Задача. Найти 79.

Решение. Находим 79. Расположено значение во втором столбике нижней строки.

Ответ. 40353607.

Пример 2. Используем простую таблицу по алгебре.

Задача. Найти 17.

Решение. В данном случае найти значение выражения можем без использования вспомогательных инструментов. Достаточно вспомнить одно из свойств степеней: единица всегда остается единицей.

Ответ. 1.

Как найти корень кубический в калькуляторе

Корень кубический — это число, которое умноженное на себя два раза дает исходное число. Корень кубический можно найти в калькуляторе, используя функцию встроенную в большинство научных калькуляторов.

Для поиска корня кубического в калькуляторе необходимо ввести исходное число, затем нажать кнопку «3 √x». Результат будет выведен на экран. Если результатом окажется дробное число, то следует округлить его до нужного числа знаков после запятой.

При работе с калькулятором следует учитывать, что значение корня кубического может быть как положительным, так и отрицательным. Калькулятор может выдавать только положительный результат, поэтому в таких случаях следует использовать формулу для нахождения корня кубического вручную.

Для поиска корня кубического вручную необходимо использовать формулу:

Где х — исходное число, y — корень кубический. Чтобы избежать ошибок в вычислениях, следует использовать калькулятор для выполнения промежуточных операций.

Вопрос-ответ

Вопрос: Как найти корень кубический из отрицательного числа?

Ответ: Для нахождения корня кубического из отрицательного числа необходимо возвести его в куб и затем извлечь из него корень. Полученный результат нужно домножить на (-1), чтобы получить корень из исходного отрицательного числа. Например, корень кубический из -27 равен -3, так как (-3) * (-3) * (-3) = -27.

Вопрос: Можно ли найти корень кубический из комплексного числа?

Ответ: Да, корень кубический из комплексного числа можно найти. Для этого необходимо использовать формулу Муавра и найти все три корня, как для обычных действительных чисел. Однако результат будет также комплексным числом, а не только действительным.

Вопрос: Можно ли найти корень кубический из нецелого числа?

Ответ: Да, из нецелого числа также можно найти корень кубический. Для этого достаточно возвести его в степень 1/3. Если число нецелое, то ответ также будет нецелым, но это не мешает найти корень.

Вопрос: Можно ли найти корень кубический без использования калькулятора?

Ответ: Да, корень кубический можно найти без использования калькулятора, если известны таблицы степеней чисел или если известны формулы для нахождения корней кубических. Однако в большинстве случаев использование калькулятора упрощает задачу и экономит время.

Вопрос: Как найти корень кубический по методу Герона?

Ответ: Метод Герона, также известный как метод брахистохроны, является одним из методов нахождения корней уравнения. Для нахождения корня кубического методом Герона нужно выбрать начальное приближение, затем подставить его в формулу и повторять вычисления с новыми значениями, пока ответ не станет достаточно близким к искомому. Этот метод может потребоваться, когда другие способы нахождения корня кубического не применимы.

Главная — Полезно — Простые шаги для поиска корня кубического: полезные советы и методы

Комментарии

Дмитрий

5.0 out of 5.0 stars5.0

Nikita88
5.0 out of 5.0 stars5.0

Честно говоря, я всегда считал, что поиск корня кубического сложный процесс, но благодаря этой статье все оказалось намного проще. Все шаги описаны детально и понятно, а примеры помогли на практике закрепить материал. Рекомендую всем, кто сталкивается с этой задачей!

Александр
5.0 out of 5.0 stars5.0

Я инженер-механик и нередко сталкиваюсь с задачами, связанными с вычислением корней, в том числе и кубического. До этой статьи я часто использовал специальные программы или калькуляторы. Однако, после прочтения, я убедился, что все это можно сделать вручную и достаточно просто.

В целом, статья очень полезна и информативна. Я уверен, что она будет полезна не только инженерам, но и студентам и школьникам, изучающим математику на более продвинутом уровне.

Иван Петров
5.0 out of 5.0 stars5.0

Поначалу казалось, что материал немного сложный для меня, но благодаря ясному изложению и примерам, я смог разобраться. Очень пригодится в учебе, я буду рекомендовать эту статью своим друзьям.

Сергей Иванов
5.0 out of 5.0 stars5.0

Статья помогла мне быстро разобраться в поиске корня кубического. Спасибо автору!

Maximus24
5.0 out of 5.0 stars5.0

Статья очень полезная, я нашел то, что искал, спасибо!

Применение корня третьей степени в реальной жизни

Корень третьей степени – это математическая операция, которая позволяет извлекать кубический корень числа. В реальной жизни корень третьей степени широко применяется в различных областях, включая науку, инженерию, экономику и финансы. Вот несколько примеров применения корня третьей степени:

1. Физика и наука

   В физике корень третьей степени используется для решения задач, связанных с объемом, плотностью и массой тел. Например, в задачах о нахождении объема куба со сферическим вырезом требуется извлечь кубический корень из объема вырезанной фигуры, чтобы найти длину ребра куба.

2. Инженерия и архитектура

   В инженерных и архитектурных расчетах часто требуется извлечь кубический корень из объема или площади. Например, при проектировании водопроводной трубы необходимо определить диаметр трубы, зная общий объем воды, скорость потока и давление.

3. Экономика и финансы

   Корень третьей степени может быть использован для вычисления среднего показателя или индекса. Например, при анализе доходности инвестиций или финансовых показателей компании может потребоваться извлечь кубический корень из общей прибыли или общего объема продаж для определения среднего значения.

4. Медицина и биология

   В медицине и биологии корень третьей степени может использоваться для анализа роста организмов или для расчетов объемов жидкости, необходимой для введения в организм. Например, при определении дозы лекарства для пациента требуется извлечь кубический корень из общего объема лекарственного препарата, чтобы определить количество, которое необходимо ввести.

Это лишь некоторые из примеров применения корня третьей степени. В реальной жизни корень третьей степени находит множество применений в различных областях, и его использование справедливо и интересно для людей, связанных с наукой, техникой, финансами и другими областями знания.

Практическое применение куба числа

Куб числа является полезным понятием в математике и имеет множество практических применений. Например, куб числа может быть использован для определения объема трехмерной фигуры.

Также, куб числа является важным понятием в физике. Например, скорость куба числа будет равна ускорению в квадрате, умноженному на время.

Куб числа также может быть использован для вычисления площади поверхности трехмерной фигуры. Например, если мы имеем куб со стороной длиной 2, то его площадь поверхности будет равна 24.

• Применение куба числа в программировании:
  • Куб числа может использоваться в математических алгоритмах, таких как алгоритмы шифрования.
  • Куб числа может использоваться для вычисления сложных математических функций, таких как квадратный корень.

Таким образом, куб числа является важным математическим понятием, имеющим широкий спектр практических применений в различных областях жизни и производства.

Вопрос-ответ:

Как вычислить куб числа?

Чтобы вычислить куб числа, нужно число умножить само на себя три раза. То есть, если нужно найти куб числа 4, нужно умножить 4 на 4 на 4, получив результат 64.

Зачем нужен куб числа?

Куб числа может использоваться в различных математических формулах, а также в физике и других науках. Например, скорость света в вакууме равна кубу числа 10, или 1000.

Какие есть способы вычисления куба числа?

Существует несколько способов вычисления куба числа, например, умножение числа самого на себя три раза, использование формулы куба суммы двух чисел или куба разности двух чисел, или использование тождества (a+b)³=a³+3a²b+3ab²+b³, где a и b — любые числа.

Какие числа можно возводить в куб?

В куб можно возводить все действительные и комплексные числа, в том числе и отрицательные. Например, куб числа -2 равен -8, а куб комплексного числа 2+3i равен -46+9i.

Как связаны куб числа и квадрат числа?

Куб числа может быть выражен через квадрат числа, так как куб числа равен квадрату числа, умноженному на само число. Например, куб числа 5 равен 25 умножить на 5, то есть 125.

Как использовать куб числа в алгебре?

Куб числа может использоваться в алгебре для решения различных задач, например, вычисления корней кубического уравнения или поиска объема куба со стороной заданной длины. Кроме того, куб числа может использоваться в формулах сумм и разностей кубов чисел.

Примеры решения задач

Задача 1

Дано выражение, значение которого требуется определить:

\({{3}^{7}}+{{5}^{6}}-{{9}^{4}}\)

Решение

С помощью таблицы вычислим значения всех компонентов выражения:

\({{3}^{7}}=2187\)

\({{5}^{6}}=15625\)

\({{9}^{4}}=6561\)

Путем подстановки преобразуем начальное выражение:

\({{3}^{7}}+{{5}^{6}}-{{9}^{4}}=2187+15625-6561=11251\)

Ответ: \({{3}^{7}}+{{5}^{6}}-{{9}^{4}}=11251.\)

Задача 2

Необходимо определить степень, в которую следует возвести число 8 для получения в результате числа 32768.

Решение

По таблице степеней определим:

\({{8}^{5}}=32768\)

Таким образом, нужная степень равна 5.

Ответ: 5.

Задача 3

Дано выражение, значение которого требуется вычислить:

\(\frac{(4^3)^{-4}}{4^{-11}}\)

Решение

Зная, что возведение степени в степень заключается в необходимости умножения показателей этих степеней, преобразуем числитель:

\( (4^3)^{-4} = 4^{-12}\)

В результате:

\(\frac{(4^3)^{-4}}{4^{-11}}=\frac{4^{-12}}{4^{-11}}=4^{-12-(-11)}=4^{-1}=\frac{1}{4}=0,25\)

Ответ: 0,25.

Задача 4

Требуется вычислить значение выражения:

\(6^{-8} \cdot (6^2)^3\)

Решение

В процессе возведения степени в степень необходимо найти произведение показателей этих степеней. Заметим так же, что при умножении степеней, которые имеют идентичные основания, показатели суммируют. Выполним соответствующие преобразования:

\(6^{-8} \cdot (6^2)^3 = 6^{-8} \cdot 6^6 = 6^{-8+6}=6^{-2} = \frac{1}{36}\)

Ответ: \(\frac{1}{36}.\)

Задача 5

Дано выражение, значение которого необходимо вычислить:

\(5^{12} \cdot (5^5)^{-3}\)

Решение

Воспользуемся свойствами степени и выполним соответствующие преобразования:

\(5^{12} \cdot (5^5)^{-3} = 5^{15} \cdot 5^{-15} = 5^{12-15}=5^{-3} = \frac{1}{5^3} = \frac{1}{125}\)

Ответ: \( \frac{1}{125}.\)

Задача 6

Необходимо рассчитать значение следующего выражения:

\(\frac{2^{2} \cdot 8^{-2}}{2^{-5}}\)

Решение

Каждую из степеней требуется привести к основанию в виде числа 2:

\(8^{-2} = {(2^3)}^{-2} = 2^{-6}\)

В результате:

\(\frac{2^{2} \cdot 8^{-2}}{2^{-5}} = \frac{2^{2} \cdot 2^{-6}}{2^{-5}} = 2^{2-6-(-5)} = 2^{1} = 2\)

Ответ: 2.

Задача 7

Нужно найти значение следующего выражения:

\(\frac{5^{6} }{25^{3}\cdot 5^{-2}}\)

Решение

Следует привести каждую из представленных степеней к основанию 5:

\(25^{3} = {(5^2)}^{3} = 5^{6}\)

Таким образом:

\(\frac{5^{6} }{25^{3}\cdot 5^{-2}} = \frac{5^{6} }{5^{6}\cdot 5^{-2}} = 5^{6-6-(-2)}=5^2=25\)

Ответ: 25.

Задача 8

Дано выражение, значение которого нужно вычислить:

\(\frac{l^{6} \cdot {(l^{2})}^{-2}}{l^{-3}}\)

Решение

Заметим, что в процессе возведения степени в степень требуется найти произведение показателей этих степеней:

\({(l^{2})}^{-2} = l^{-4}\)

В результате:

\(\frac{l^{6} \cdot {(l^{2})}^{-2}}{l^{-3}} = \frac{l^{6} \cdot l^{-4}}{l^{-3}} = l^{6-4-(-3)}=l^{5}\)

Ответ: \( l^{5}.\)

Задача 9

Необходимо определить значение такого выражения:

\(\frac{p^{4} \cdot {(p^{2})}^{-3}}{p^{-5} \cdot p^{3}}\)

Решение

Возвести степень в степень можно путем умножения их показателей:

\({(p^{2})}^{-3} = p^{-6}\)

В результате:

\(\frac{p^{4} \cdot {(p^{2})}^{-3}}{p^{-5} \cdot p^{3}} = \frac{p^{4} \cdot p^{-6}}{p^{-5} \cdot p^{3}} = p^{4-6-(-5)-3}=p^{0}=1\)

Ответ: 1.

Задача 10

Дано несколько чисел, среди которых требуется выбрать самое большое:

\(2,5 \cdot 10^{-5}\)

\(1,05 \cdot 10^{-3}\)

\(0,1 \cdot 10^{-3}\)

Решение

Преобразуем перечисленные выражения так, чтобы привести их к виду:

\(a \cdot 10^{-6}\)

В результате:

\(2,5 \cdot 10^{-5} = 2, 5 \cdot 10 \cdot 10^{-6} = 25 \cdot 10^{-6},\)

\(0,1 \cdot 10^{-3}= 0,1 \cdot 10^3 \cdot 10^{-6} = 100 \cdot 10^{-6},\)

\(1,05 \cdot 10^{-3} = 1,05 \cdot 10^3 \cdot 10^{-6} =1050 \cdot 10^{-6}.\)

При сравнении чисел со знаком плюс справедливо, что:

\(a < b\)

\(ac < bc\)

В таком случае целесообразно сравнить множители перед \(\cdot 10^{-6}\). Тогда наибольшим является число \(1,05 \cdot 10^{-3}\).

Ответ: \(1,05 \cdot 10^{-3}.\)

Определение и особенности

Основной особенностью куба является то, что все его грани являются квадратами. Все грани смежные и с равными сторонами, а также перпендикулярны друг другу. Благодаря этим свойствам куб обладает симметрией и регулярностью, что делает его удобным объектом для изучения и применения в геометрии и математике.

Куб также обладает другими интересными особенностями. Например, все его диагонали имеют одинаковую длину и проходят через центры граней. Это делает его еще более регулярным и помогает в решении различных задач и расчетов.

Куб используется не только в геометрии и математике, но и на практике. Его правильная форма и симметрия делают его удобным для хранения и транспортировки различных предметов. Кубы используются в строительстве для создания устойчивых и прочных конструкций, а также в играх и пазлах для развития логического мышления.

Важно отметить, что объем куба может быть вычислен с помощью специальной формулы. Это позволяет точно рассчитать объем различных объектов, которые имеют форму куба, и использовать эту информацию для различных целей и задач

Особенности	Значение
Количество граней	6
Количество ребер	12
Количество вершин	8
Формула объема	V = a³, где a — длина ребра

Как выглядит куб?

Куб имеет симметрию относительно центра, что значит, что он выглядит одинаково независимо от того, с какой стороны его рассматривать. Каждая грань куба является прямоугольником, а все грани куба имеют одинаковую форму и размер.

Одна из особенностей куба – это его ребра. Ребра куба являются прямыми отрезками, соединяющими вершины куба. Все ребра куба равны между собой по длине и пересекаются под прямыми углами.

Вершины куба представляют собой точки, где пересекаются ребра. В кубе есть восемь вершин, исключающих друг друга парно. Каждая вершина куба является общей для трех ребер и трех граней.

Таким образом, куб — это простая, но важная геометрическая фигура, которая обладает рядом уникальных свойств и характеристик.

Сколько граней, вершин и ребер в кубе?

Грани куба, как и вершины, являются трехмерными объектами. Грань — это плоская поверхность, образованная смежными ребрами. В кубе каждая вершина соединена с тремя ребрами, и смежные ребра встречаются в каждой вершине под прямым углом.

Количество граней, вершин и ребер в кубе можно посчитать с помощью формулы Эйлера: F — E + V = 2, где F — количество граней, E — количество ребер, V — количество вершин. В случае куба, подставив значения F = 6, E =12 и V = 8 в формулу, мы получим 6 — 12 + 8 = 2, что соответствует ожидаемому результату.

Куб является одним из наиболее известных тел в геометрии и математике. Его регулярная форма и относительная простота делают его полезным объектом для изучения и использования в различных задачах. В геометрии куб используется для демонстрации принципов объема, площади и длины. В математике куб также является основой для изучения пространства и формулы объема.

Зачем используется куб в геометрии и математике?

В геометрии куб является одним из основных многогранных тел. Он характеризуется тем, что у него все грани одинаковой формы и размера, и все углы прямые. Это делает его идеальным объектом для изучения и анализа различных геометрических проблем и задач.

Куб также широко используется в математике. Он является примером правильного многогранника, и его особые свойства позволяют решать различные задачи и проблемы в математических исследованиях.

Один из ключевых аспектов использования куба в геометрии и математике — это его связь с объемом и площадью. Объем куба можно легко вычислить по его стороне или диагонали с использованием специальной формулы. Это позволяет решать задачи, связанные с расчетом объема объектов, например, при проектировании зданий или изучении физических свойств материалов.

Куб также используется в различных играх и головоломках, которые помогают развивать пространственное мышление, логическое мышление и навыки решения проблем.

В целом, куб играет важную роль в геометрии и математике, предоставляя нам мощный инструмент для анализа и решения различных задач. Его геометрические и математические характеристики позволяют использовать его в широком диапазоне областей, от науки до повседневной жизни.

Видео:УКРАИНСКАЯ ШКОЛА МАТЕМАТИКИ ПРОТИВ РОZZИЙСКОЙ ! СКОЛЬКО БУДЕТ ТРИ В КУБЕ ?Скачать

Почему вторая степень это квадрат, а третья — куб

Здравствуйте, дорогие читатели! Некоторые степени имеют свои специфичные названия, которые мы воспринимаем как должное. Из моего опыта я заметила, что далеко не все (почти никто) не задумывается, откуда взялись эти названия и чем они объясняются.

Стыдно сказать, но почему-то, когда я училась в школе, этот вопрос мне тоже не приходил на ум. И только поступив в университет, я задалась этим вопросом и сразу же нашла на него ответ.

Вы находитесь на канале Trifler, где я разбираю интересные математические задачи, а также рассуждаю на некоторые околоматематические темы. Если Вы искренне увлечены математикой, но еще не подписаны на этот канал, то самое время это исправить! Подписаться