Проекции на чертеже

Шаги создания изометрической проекции куба

Шаг 1: Постройте куб, используя линейки и карандаши. На листе бумаги нарисуйте квадрат в произвольном месте. Затем отметьте внизу и сверху этого квадрата равные отрезки, на которых нарисуйте еще два квадрата одинакового размера. Соедините соответствующие углы полученных квадратов линейкой, чтобы получить куб.

Шаг 2: Определите направление света, чтобы понять, откуда будет исходить свет в вашей изометрической проекции. Выберите место, откуда будет падать свет, и отметьте его на верхней части одной из сторон куба.

Шаг 3: Начертите параллельные линии, отходящие от каждой точки света до соответствующей стороны куба. Эти линии должны быть параллельными и равными между собой.

Шаг 4: Добавьте тени, чтобы создать эффект объема. Определите места теней на каждой стороне куба, и проведите линии, соединяющие эти точки с противоположной стороной куба. Тени на изометрической проекции будут представлять собой параллельные линии, а их длина будет равна длине соответствующей стороны куба.

Шаг 5: Добавьте детали, чтобы сделать изометрическую проекцию куба более реалистичной. Нарисуйте мелкие линии на каждой стороне куба, чтобы обозначить грани и стыки. Это поможет придать вашей проекции больше объема и глубины.

Следуя этим шагам, вы можете создать изометрическую проекцию куба, сохраняющую пропорции и объемность объекта.

Шаг 1: Подготовка основы

Перед тем, как начать строить куб в изометрии, необходимо подготовить основу для работы:

Выберите лист бумаги или подложку для рисования. Рекомендуется использовать лист клетчатой бумаги или специальный блок для изометрического рисования.
Убедитесь, что у вас есть линейка и карандаш. Линейка поможет вам провести ровные линии, а карандаш позволит вносить поправки и корректировать рисунок.
Продумайте масштаб рисунка. Решите, насколько большим или маленьким будет ваш куб

Важно соблюдать пропорции, чтобы куб выглядел реалистично.

Рекомендуется использовать материалы достаточно прозрачные, чтобы было удобно видеть клетки на бумаге и следить за правильностью проведения линий.

После подготовки основы, можно приступать к следующему шагу — построению куба в изометрической проекции.

Черчение

§ 8. Аксонометрические проекции предметов, имеющих круглые поверхности

8.1. Фронтальные диметрические проекции окружностей. Если на аксонометрическом изображении хотят некоторые элементы. например окружности (рис. 64), сохранить неискаженными, то применяют фронтальную диметрическую проекцию. Построение фронтальной диметрической проекции детали с цилиндрическим отверстием, два вида которой даны на рисунке 64, а, выполняют так:

1. Пользуясь осями х, у, z, строят тонкими линиями очертания внешней формы детали (рис. 64, б).
2. Находят центр отверстия на передней грани. Через него параллельно оси у проводят ось отверстия и откладывают на ней половину толщины детали. Получают центр отверстия, расположенный на задней грани.
3. Из полученных точек как из центров проводят окружности, диаметр которых равен диаметру отверстия (рис. 64, в).
4. Удаляют лишние линии и обводят видимый контур детали (рис. 64, г).

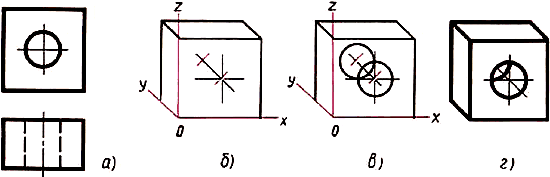
Рис. 64. Построение фронтальной диметрической проекции

Постройте в рабочей тетради фронтальную диметрическую проекцию детали, изображенной на рисунке 64, а. Ось у направьте в другую сторону. Величину изображения увеличьте примерно в два раза.

Рис. 65. Изображение в изометрической проекции окружностей вписанных в куб

Вначале строят ромб со стороной, равной диаметру изображаемой окружности (рис. 66, а). Для этого через точку О проводят изометрические оси х и у. На них от точки О откладывают отрезки, равные радиусу изображаемой окружности. Через точки а, b, с и d проводят прямые, параллельные осям; получают ромб.

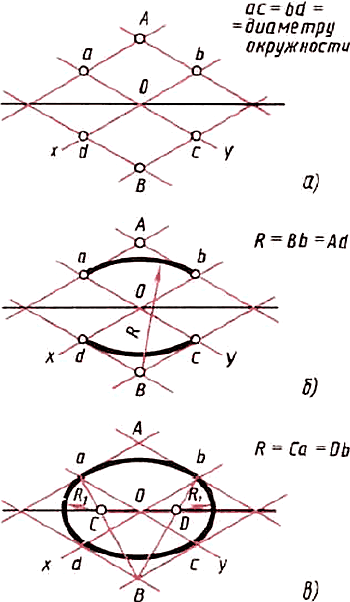
Рис. 66. Построение овала

Большая ось овала располагается на большой диагонали ромба.

После этого вписывают в ромб овал. Для этого из вершин тупых углов (точек А и В) описывают дуги. Их радиус R равен расстоянию от вершины тупого угла (точек А и В) до точек с, d или a, b соответственно (рис. 66, б).

Через точки В и а, В и b проводят прямые. В пересечении прямых Ва и ВЬ с большей диагональю ромба находят точки С и D (рис. 66, а). Эти точки будут центрами малых дуг. Их радиус R1 равен Са (или Db). Дугами этого радиуса плавно соединяют большие дуги овала.

Мы рассмотрели построение овала, лежащего в плоскости, перпендикулярной оси z (овал 1 на рисунке 65). Овалы, находящиеся в плоскостях, перпендикулярных оси у (овал 2) и оси х (овал 3), строят также. Только для овала 2 построение ведут на осях х и z (рис. 67, а), а для овала 3— на осях у и z (рис. 67, б). Рассмотрим, как применяются изученные построения на практике.

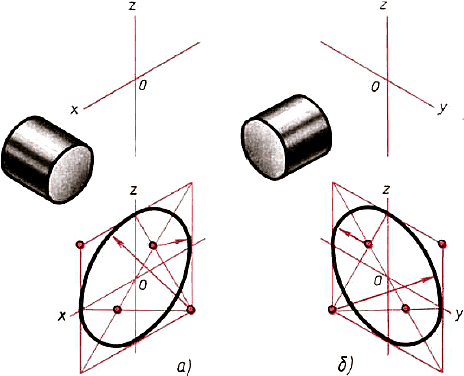
Рис. 67. Построение овалов: а лежащего в плоскости, перпендикулярной оси у; б — лежащего в плоскости, перпендикулярной оси x

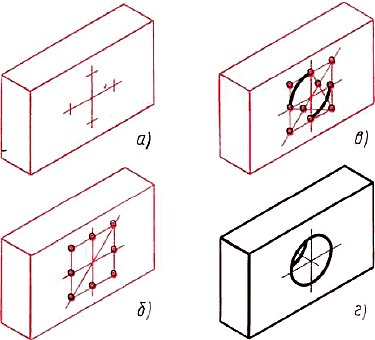
Рис. 68. Построение изометрической проекции детали с цилиндрическим отверстием

8.3. Способ построения аксонометрических проекций предметов, имеющих круглые поверхности. На рисунке 68, а дана изометрическая проекция планки. Надо изобразить цилиндрическое отверстие, просверленное перпендикулярно передней грани. Построение выполняют так:

1. Находят центр отверстия па передней грани. Определяют направление изометрических осей лля построения ромба (см. рис. 65). Из найденного центра проводят оси (рис. 68, а) и откладывают на них отрезки, равные радиусу окружности.
2. Строят ромб. Проводят его большую диагональ (рис. 68, б).
3. Описывают большие дуги. Находят центры для малых дуг (рис. 68. в).
4. Проводят из найденных центров малые дуги.

Такой же овал строят на задней грани, но обводят лишь видимую его часть (рис. 68, г).

1. На рисунке 69, а проведены оси для построения трех ромбов. Укажите, на какой грани куба — верхней, боковой правой, боковой левой (см. рис. 65) —будет расположен каждый ромб. Какой оси будет перпендикулярна плоскость каждого из этих ромбов? А какой оси перпендикулярна плоскость каждого из овалов (рис. 69, б)?

   Рис. 69. Задание для упражнений

2. Стороны ромбов на рисунке 65 равны 30 мм. Чему равны диаметры окружностей, проекции которых представлены овалами, вписанными в эти ромбы?
3. Постройте овалы, соответствующие проекциям окружностей, вписанных в грани куба, данного в изометрической проекции (по примеру на рисунке 65). Сторона куба равна 80 мм.

Шаг 3: Подготовка вертикальных сторон

После того, как мы построили горизонтальные стороны куба, необходимо приступить к созданию вертикальных сторон.

1. Нарисуйте вертикальные линии на каждом углу горизонтальной основы куба. Они будут образовывать боковые грани куба.
2. Соедините вертикальные линии между собой, чтобы получить границы вертикальных граней.
3. Укажите отдельные грани, используя штриховку или цветовую заливку. Это поможет наглядно выделить каждую грань.

Итак, на данном этапе мы подготовили вертикальные стороны куба. Теперь можно переходить к следующему шагу — отображению объема и деталей куба, чтобы создать иллюзию трехмерности.

Слайд 59Список использованной литературыБалягин, С.К. Черчение: справочное пособие. – М.: Астрель, 2005.

— 421с.Борисов Д.М. Черчение. Учебное пособие для студентов педагогических институтов. — М.: Просвещение, 2011, с изменениями. – 351 с. Ботвинников А.Д., Виноградов В.Н., Вышнепольский И.С. Методическое пособие по черчению для учителей. — М.: Астрель, 2012. – 159 с. Ботвинников А.Д., Виноградов В.Н., Вышнепольский И.С. Черчение: Учебник для 7-8 классов общеобразовательных учреждений. — М.: Астрель, 2014. – 221 с. Василенко Е.А. Методика обучения черчению. Учебное пособие для студентов и учащихся. – М.: Просвещение, 2000.-186с. Василенко Е.А., Жукова Е.Т. Карточки – задания по черчению. — М.: Просвещение, 2010. – 413 с. Воротников И.А. Занимательное черчение. Книга для учащихся средней школы. – М.: Просвещение, 2010. — 192 с. Гервер В.А. Творческие задачи по черчению. — М.: Просвещение, 2009.- 128 с. Дембинский С.И., Кузьменко В.И. Методика преподавания черчения в средней школе. — М.: Просвещение, 1977. — 335 с. Занимательное черчение на уроках и внеклассных занятиях/авт.-сост. С.В. Титов. — Волгоград: Учитель, 2011.-210с. Коваленко Л.Н. Макарова М.Н. Логические задачи на уроках черчения // Школа и производство. — 1990. — №2 — С.78-80. Макарова М.Н. Таблицы по черчению, 7 класс: Пособие для учителей. – М.: Академический проект, 2012.-496 с.Николаев Н. С. Проведение олимпиад по черчению: пособие для учителей. — М.: Просвещение, 2008.-109с. Подшибякин В.В. Черчение практикум. – Саратов: Лицей, 2006 .– 144 с Рабочие тетради по черчению. Под ред. Т.В. Кучуковой, Н.Г. Преображенской. – М.: Вентана – Граф, 2014. – 76 с. Рассохин В.В., Розов С.В., Целинский Н.А. Занимательные задачи по проекционному черчению. — М.: Машиностроение, 1969. — 176 с. Ройтман И.А. Методика преподавания черчения. – М.: ВЛАДОС, 2002. – 237 с. Якиманская И.С. Развитие пространственного мышления школьников. — М.: Педагогика, 1980. — 240 с.

Слайд 41Получение и построение аксонометрических проекцийАксонометрической проекцией называют изображение, полученное при параллельном

проецировании предмета вместе с осями прямоугольных координат на какую-либо плоскость.

Перспективный рисунок

С одной точкой схода

С двумя точками схода

Аксонометрическая проекция

Диметрическаяпроекция

Изометрическаяпроекция

Положение аксонометрических осей и размеры, откладываемые на них.

Косоугольная фронтальная диметрическая проекция

Прямоугольная изометрическая проекция

В аксонометрических проекциях из каждой вершины многогранного объекта всегда выходят три луча (видимых или невидимых).

Любой предмет имеет вершины и стороны, поэтому построение аксонометрических проекций — это построение вершин предмета с последующим их соединением.

Слайд 15Упражнение 6Написать в таблицу, какие предметы изображены на рисунке. Придумать, изобразить

и дописать в таблицу другие знакомые предметы.

Упражнение 7

Вставить пропущенные слова в текст определений.Существует __________ и __________ проецирование.Если __________ лучи выходят из одной точки, проецирование называется __________.Если __________ лучи направлены параллельно, проецирование называется __________ .Если __________ лучи направлены параллельно друг другу и под углом __________ к плоскости проекций, то проецирование называется __________ .Натуральное изображение предмета на плоскости проекций получается только при ___________ __________ проецировании.

Шаг 2: Построение плоскостей куба

После того как мы построили ось видимости и определили ее угол наклона, мы можем приступить к построению плоскостей куба.

Куб состоит из шести одинаковых квадратных плоскостей, но мы будем строить их по очереди. Начнем с верхней горизонтальной плоскости.

1. Возьмите точку, которая будет являться центром верхней плоскости куба и обозначьте ее.

2. Из центра плоскости проведите горизонтальную прямую влево и вправо на одинаковое расстояние. Эти прямые будут представлять верхние стороны куба.

   

   

   

   

   

   

   

   

   

   

3. Соедините концы верхних сторон прямыми линиями, образуя квадрат.

4. Затем отметьте точку внизу куба, которая будет являться верхним углом передней грани куба.

5. Проведите прямую линию от центра верхней плоскости к этой точке. Эта линия будет представлять переднюю сторону куба.

6. Соедините концы передней стороны с помощью вертикальных прямых линий, образуя прямоугольник с верхней гранью куба.

7. Повторите аналогичные шаги для остальных граней куба, соединяя их с уже построенными гранями.

После завершения всех шагов по построению плоскостей куба, вы получите изображение куба в изометрии.

Изометрическое строительство куба

Изометрическая проекция является одним из способов визуализации трехмерных объектов на двухмерной плоскости. С помощью изометрии можно построить куб, который будет иметь правильные пропорции во всех трех измерениях.

Для построения куба в изометрии можно использовать следующие шаги:

1. Нарисуйте горизонтальную ось, которая будет служить дном куба. Пусть эта ось будет находиться на некотором расстоянии от верха листа бумаги.
2. Отметьте точку на этой оси, которая будет являться центром куба.
3. Проведите две диагональные линии из центра куба вверх и вниз. Эти линии будут образовывать переднюю и заднюю грани куба.
4. Проведите две диагональные линии из центра куба влево и вправо. Эти линии будут образовывать боковые грани куба.
5. На боковых гранях куба отметьте точки, которые будут являться вершинами куба.
6. Соедините вершины куба прямыми линиями, чтобы получить его окончательный вид.

После выполнения всех этих шагов вы получите изображение куба в изометрии. Теперь можно приступать к его детализации и раскрашиванию.

Строительство куба в изометрии требует некоторой навыков и понимания принципов плоскостей и линий. Поэтому, если вы впервые сталкиваетесь с изометрией, некоторая практика и опыт помогут вам в достижении лучших результатов.

Шаг 4: Сборка куба

После того, как вы нарисовали все необходимые грани куба по шаблону и вырезали их, настало время начать сборку.

Не забудьте пронумеровать каждую грань куба! Это поможет вам правильно собрать куб. Нумерация обычно производится в правом верхнем углу каждой грани.

Для сборки куба вам потребуется:

1. Набор граней куба, вырезанных по шаблону.
2. Клей или двухсторонний скотч.

Для начала возьмите грань куба с номером 1 и нанесите клей (или приклейте двухсторонний скотч) на ее торцы. Затем приклейте эту грань к первой грани основания куба. Убедитесь, что она правильно выровнена и закреплена.

Затем проделайте те же действия с гранью номер 2, приклеивая ее к грани номер 1 и к соответствующей грани основания.

Продолжайте этот процесс до тех пор, пока все грани куба не будут приклеены и правильно расположены.

После сборки куба остается только дождаться, пока клей или скотч полностью высохнут. После этого ваш куб будет готов к использованию!

Если вам трудно контролировать выравнивание граней, вы можете воспользоваться специальными кубическими шаблонами-сборщиками, которые помогут вам собрать куб правильно и без проблем.

Подсказка: Если вы хотите придать вашему кубу объемность и реалистичность, можно добавить тени на его грани. Это поможет создать эффект трехмерности и сделает вашу изометрическую конструкцию более живой.

Необходимые материалы и инструменты

Для построения куба в изометрии вам потребуются следующие материалы и инструменты:

• Бумага формата А4 или листы графического блока;
• Карандаш или ручка;
• Линейка;
• Эксцентрик или круглый компас;
• Циркуль;
• Ластик;
• Цветные карандаши или маркеры (по желанию).

Бумага формата А4 или листы графического блока лучше подходят для черчения в изометрии, так как они имеют стандартные размеры и более удобны в работе.

Карандаш или ручка — основные инструменты для черчения. Вы можете выбрать любой из этих инструментов в зависимости от вашего предпочтения.

Линейка поможет вам сохранить прямые линии и равные отрезки при построении куба.

Эксцентрик или круглый компас позволят вам легко проводить дуги и окружности.

Циркуль пригодится для построения окружностей и узнавания радиуса или длины отрезков.

Ластик необходим для исправления ошибок и удаления лишних линий.

Цветные карандаши или маркеры часто используются для визуализации и раскрашивания ваших изометрических рисунков.

Аксонометрические проекции на чертеже

Работа по выполнению аксонометрических проекций начинается с построения осей. Оси необходимо построить в трех направлениях: горизонтальная ось Х, вертикальная ось Y и ось, идущая под углом – Z.В изометрической проекции вертикальная и горизонтальная ось располагаются под углом в тридцать градусов к горизонтальной линии.

В аксонометрической проекции масштабы по всем осям равны.

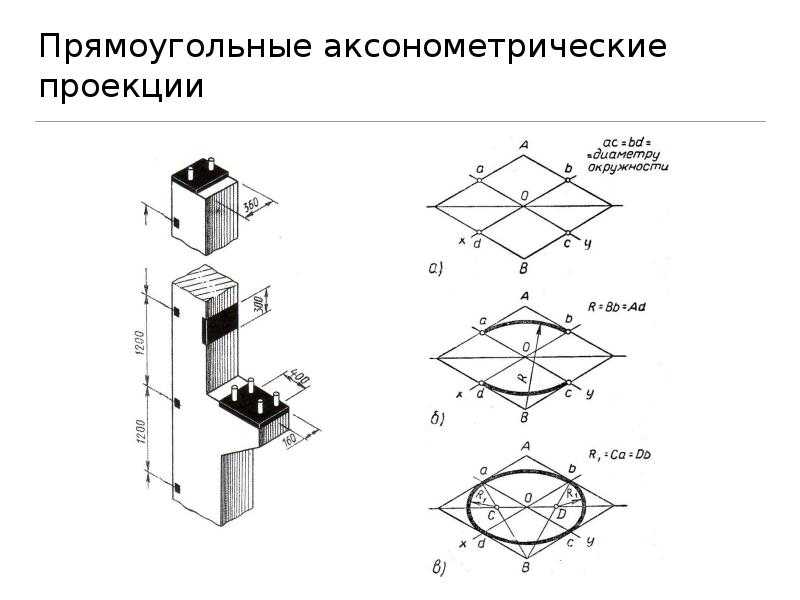Рисунок 2. Аксонометрическая проекция

Аксонометрическая проекция по чертежу в Компас

При выполнении аксонометрической проекции в программе Компас работа сводятся к построению проекций точек и их соединению в определённой последовательности.

Рассмотрим порядок действий на примере прямоугольника. Вначале в меню «Создать» выбираем «Деталь», в «Дерево модели» раскрываем меню «Начало координат» и выбираем плоскость ХY, затем переходим в двухмерное построение, нажимаем инструмент «Прямоугольник» вводим соответствующие размеры. Закрыв двухмерный эскиз переходим, в трехмерный режим создания детали. С помощью инструмента «Выдавливание» создаем объект.

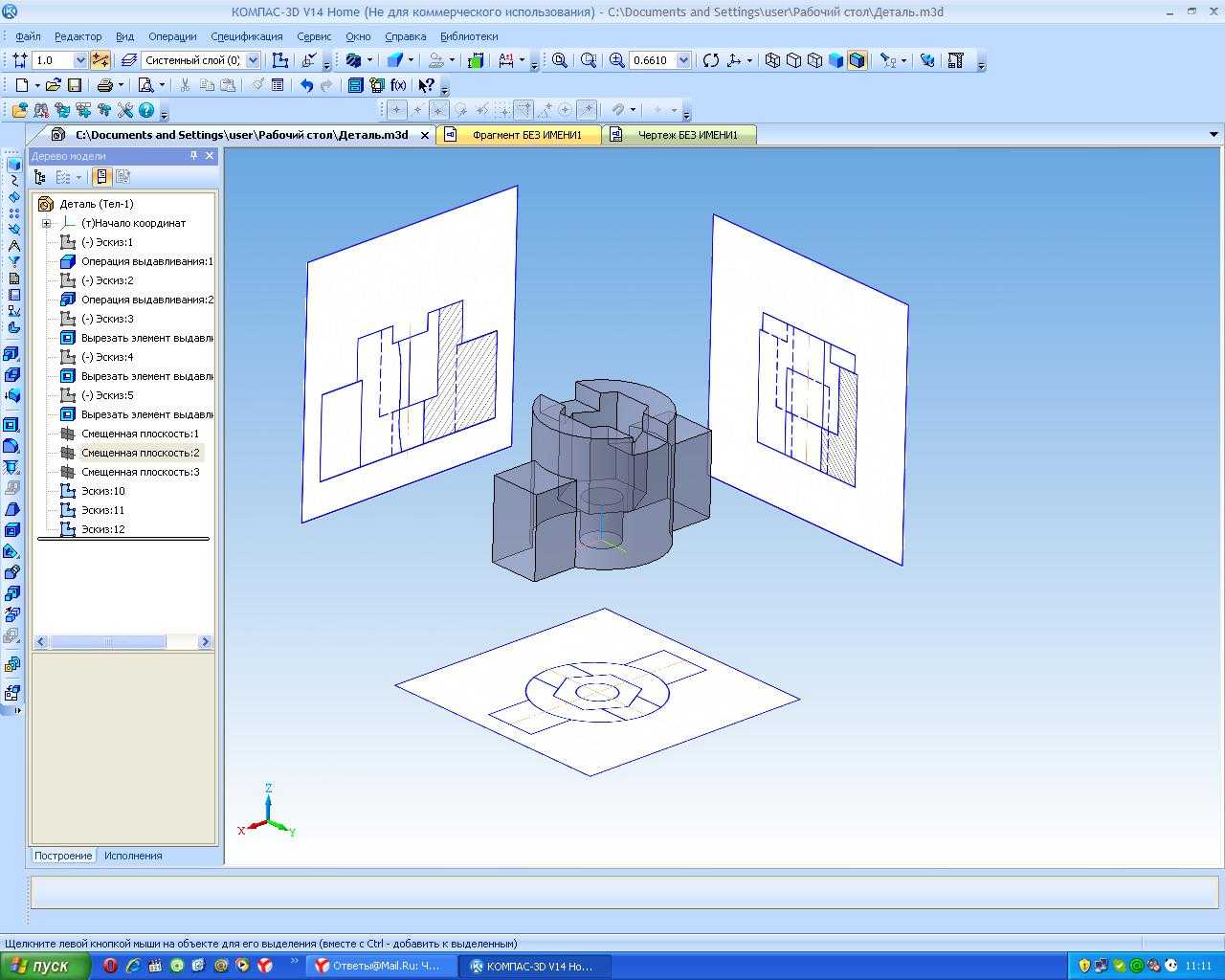Рисунок 3. Аксонометрическая проекция в Компас

Расположение основных элементов куба

Грани: Куб имеет шесть граней, каждая из которых является квадратом. Грани куба располагаются таким образом, что каждая грань смежна с тремя другими гранями.

Вершины: Куб имеет восемь вершин, в которых пересекаются три грани. Вершины куба располагаются по углам, образуя правильный кубический кристаллический решетку.

Ребра: Куб имеет двенадцать ребер, каждое из которых является отрезком прямой линии, соединяющим две соседние вершины. Ребра куба располагаются таким образом, что каждое ребро смежно с четырьмя другими ребрами.

Диагонали: Куб имеет четыре диагонали, которые соединяют две противоположные вершины. Диагонали куба располагаются внутри тела куба и проходят через его центр.

Знание расположения основных элементов куба является базовым для создания изометрической проекции данной фигуры.

Чертежи в системе прямоугольных проекций

Согласно названию используют ортогональное проецирование на одну, две или три плоскости. Если плоскость расположена перед наблюдающим, то она называется фронтальной, проекция на нее строится первой. Предмет располагается так, чтобы его поверхности были параллельными плоскости проекции. Выполнив построение в двух плоскостях проекции, можно получить основные данные о высоте, ширине и длине детали и мысленно представить себе ее в объеме. Но этой информации недостаточно для выявление характерных особенностей, к примеру формы выемки в детали, поэтому требуется третья проекция.

Слайд 24Упражнение 15Вставить пропущенные слова в текст определений.1. Чертеж представленный ______

видами, называется _________ чертежом.2. Главный вид детали изображается на ______ плоскости проекций.3. ______ плоскость проекций располагается под углом ____ к фронтальной.4. _____ и _____ плоскости проекций пересекаются по оси _____.5. Горизонтальная плоскость проекций обозначается буквой ______.6. На горизонтальной плоскости проекций изображают вид ______.7. Оба вида на чертеже соединяются _____ _______ связи.8. Линии ______ связи являются проекциями ________________.9. На главном виде наносят размеры ______ и ______ детали.10. На виде сверху наносят размеры ______ и ______ детали.11. На чертеже плоские фигуры треугольник и круг определяют ____________ .12.Геометрические тела на чертеже определяются плоскими фигурами: круг и прямоугольник — _______, два круга — ______, два прямоугольника — ________, два квадрата — _______.