воскресенье, 4 августа 2019 г.
Дописывал постскриптум к статье о и увидел в Википедии этот замечательный текст:
Читаем: «… богатая теоретическая основа математики Вавилона не имела целостного характера и сводилась к набору разрозненных приемов, лишенных общей системы и доказательной базы.»
Вау! Какие мы умные и как хорошо можем видеть недостатки других. А слабо нам посмотреть на современную математику в таком же разрезе? Слегка перефразируя приведенный текст, лично у меня получилось следующее:
Богатая теоретическая основа современной математики не имеет целостного характера и сводится к набору разрозненных разделов, лишенных общей системы и доказательной базы.
За подтверждением своих слов я далеко ходить не буду — имеет язык и условные обозначения, отличные от языка и условных обозначений многих других разделов математики. Одни и те же названия в разных разделах математики могут иметь разный смысл. Наиболее очевидным ляпам современной математики я хочу посвятить целый цикл публикаций. До скорой встречи.
Определение тригонометрических функций через окружность[]
Пусть на плоскости задана прямоугольная система координат с началом в точке O{\displaystyle O} и с осями OX{\displaystyle {OX}} и OY{\displaystyle {OY}} . Возьмём в этой системе координат окружность с центром в точке O{\displaystyle O} и радиусом, равным единице. Пусть отрезок OA{\displaystyle {OA}} поворачивается на произвольный угол ϑ{\displaystyle \vartheta} вокруг центра O.{\displaystyle O.}
Синусом угла ϑ{\displaystyle \vartheta} называется отношение ординаты точки A{\displaystyle A} к длине отрезка OA.{\displaystyle {OA}.} Обозначают sinϑ=ACOA.{\displaystyle \sin\vartheta=\frac{AC}{OA}.} Так как длина отрезка OA{\displaystyle {OA}} равна 1{\displaystyle 1}, то sinϑ=AC.{\displaystyle \sin\vartheta={AC}.}
Косинусом угла ϑ{\displaystyle \vartheta} называется отношение абсциссы точки A{\displaystyle A} к длине отрезка OA.{\displaystyle {OA}.} Обозначают cosϑ=OCOA.{\displaystyle \cos\vartheta=\frac{OC}{OA}.} Так как длина отрезка OA{\displaystyle {OA}} равна 1, то cosϑ=OC.{\displaystyle \cos\vartheta={OC}.}
Тангенсом угла ϑ{\displaystyle \vartheta} называется отношение ординаты точки A{\displaystyle A} к абсциссе точки A{\displaystyle A}. Обозначают tgϑ=ACOC{\displaystyle \operatorname{tg}\,\vartheta=\frac{AC}{OC}} (в англоязычной литературе tanϑ).{\displaystyle \tan\vartheta ).} Так как AC=sinϑ{\displaystyle {AC}=\sin \vartheta} и OC=cosϑ,{\displaystyle {OC}=\cos\vartheta,} то tgϑ=sinϑcosϑ.{\displaystyle \operatorname{tg}\,\vartheta=\frac{\sin\vartheta}{\cos\vartheta}.}
Котангенсом угла ϑ{\displaystyle \vartheta} называется отношение абсциссы точки A{\displaystyle A} к ординате точки A{\displaystyle A}. Обозначают ctgϑ=OCAC{\displaystyle \operatorname{ctg}\,\vartheta=\frac{OC}{AC}} (в англоязычной литературе cotϑ).{\displaystyle \cot\vartheta ).} Так как AC=sinϑ{\displaystyle {AC}=\sin \vartheta} и OC=cosϑ,{\displaystyle {OC}=\cos\vartheta,} то ctgϑ=cosϑsinϑ.{\displaystyle \operatorname{ctg}\,\vartheta=\frac{\cos\vartheta}{\sin\vartheta}.} Котангенс равен обратному значению тангенса: ctgϑ=1tgϑ.{\displaystyle \operatorname{ctg}\,\vartheta=\frac{1}{\operatorname{tg}\,\vartheta}.}
Секансом угла ϑ{\displaystyle \vartheta} называется отношение длины отрезка OA{\displaystyle {OA}} к абсциссе точки A{\displaystyle A}. Обозначают secϑ=OAOC.{\displaystyle \sec\vartheta=\frac{OA}{OC}.} Так как длина отрезка OA{\displaystyle {OA}} равна 1, то secϑ=1OC.{\displaystyle \sec\vartheta=\frac{1}{OC}.} Секанс равен обратному значению косинуса: secϑ=1cosϑ.{\displaystyle \sec\vartheta=\frac{1}{\cos\vartheta}.}
Косекансом угла ϑ{\displaystyle \vartheta} называется отношение длины отрезка OA{\displaystyle {OA}} к ординате точки A{\displaystyle A}. Обозначают cosecϑ=OAAC{\displaystyle \operatorname{cosec}\,\vartheta=\frac{OA}{AC}} (в англоязычной литературе cscϑ).{\displaystyle \csc \vartheta ).} Так как длина отрезка OA{\displaystyle {OA}} равна 1{\displaystyle 1}, то cosecϑ=1AC.{\displaystyle \operatorname{cosec}\,\vartheta=\frac{1}{AC}.} Косеканс равен обратному значению синуса: cosecϑ=1sinϑ.{\displaystyle \operatorname{cosec}\,\vartheta=\frac{1}{\sin\vartheta}.}
Из определения следует: если косинус угла равен нулю, то тангенс и секанс этого угла не существуют. Аналогично для котангенса и косеканса: если синус угла равен нулю, то котангенс и косеканс этого угла не существуют.
Определение знака
Достоверность результата зависит от правильного решения. Неверный знак функции способен кардинально его изменить. Для безошибочного определения значений потребуются еще кое-какие знания. К ним относятся следующие: понятие о системе координат и теорема Пифагора, а также умение чертить окружность с определенным радиусом.
Системы координат, которые применяются при решении задач бывают полярными и декартовыми. Последние используются чаще, чем первые. Полярные применяются для решения задач из области высшей математики, а также в других сложных дисциплинах с физико-математическим уклоном.
Дополнительные сведения
Для определения знака применяется обыкновенная система координат с двумя осями. Одна из них (ОХ) является осью абсцисс, а другая (ОУ) — ординат. Ее центром, который совпадает с центром тригонометрической окружности, является точка «О». Очень часто для работы необходимо знание теоремы Пифагора. Ее формулировка имеет следующий вид: в любом прямоугольном треугольнике выполняется равенство квадрата гипотенузы и суммы квадратов катетов. Вторая формулировка записывается в виде формулы: с^2 = a^2 + b^2 (c, a и b — гипотенуза и два катета соответственно).
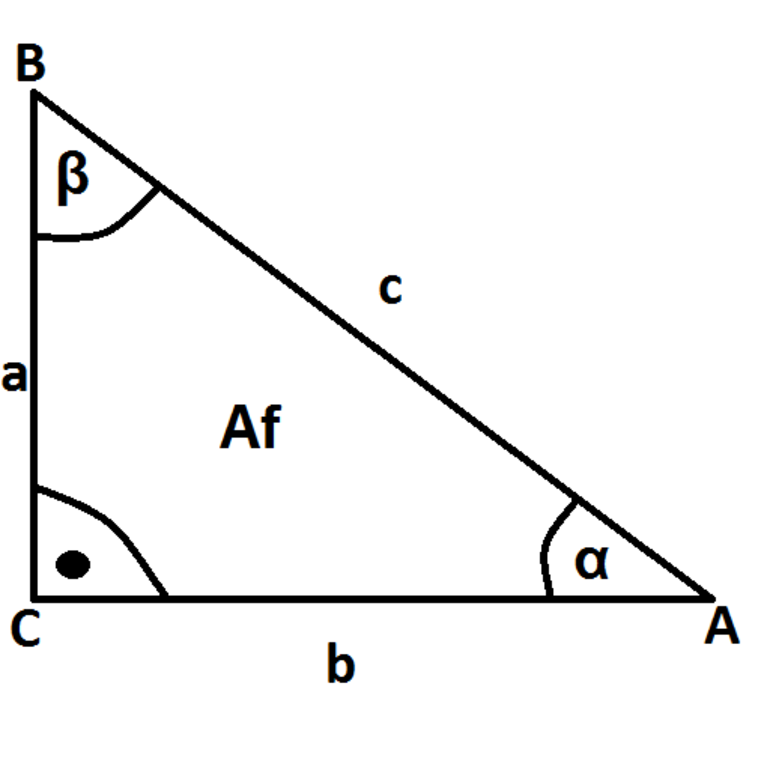
Необходимо обратить внимание на следующий факт: сумма всех углов треугольника составляет 180 градусов, то есть является развернутым углом. Математически утверждение можно записать следующим образом через углы а, b и c: а + b + c = 180
Кроме того, существуют и другие соотношения между острыми углами прямоугольного треугольника: cos (a) = sin (b), cos (b) = sin (a), tg (a) = ctg (b), и tg (b) = ctg (a).
Чтобы найти знаки тангенса и котангенса по четвертям, используются такие соотношения: tg (a) = sin (a) / cos (a) и ctg (a) = cos (a) / sin (a).
Построение окружности
Сделать «инструмент», который значительно ускорит процесс решения задач довольно просто. Для этого нужно построить декартовую систему координат и единичную окружность с центром в точке О (точка пересечения осей абсцисс и ординат). Горизонтальная ось обозначается «х», а вертикальная — «у».
Рекомендуется чертить произвольную окружность. Чертеж должен быть простым и понятным. Это называется масштабирование, при котором изображение не соответствует действительному размеру объекта. Его примером является обыкновенная географическая карта. Кроме того, при проектировании очень мелких деталей применяются чертежи, которые в несколько десятков или сотен раз превышают натуральные размеры. Обозначение точки на плоскости выполняется следующим образом:
- Координаты заключаются в круглые скобки и разделяются «;».
- На первом месте стоит значение, соответствующее оси абсцисс, а на втором — ординат: (x;y).
Окружность пересекает оси в четырех точках: (1;0), (0;1), (-1;0) и (0;-1). Четвертями называются области, которые делят систему координат на четыре равные части. Отсчет выполняется от первой четверти (x>0 и y>0) против часовой стрелки:
- Значения по x и y больше 0 соответствуют первой четверти (I).
- II: x<0 и y>0.
- III: x<0 и y<0.
- IV: x>0 и y<0.
Ось ординат соответствует всем значениям sin углов альфа и бета, а абсцисс — всем cos. Следовательно, по тригонометрической окружности можно определить знаки косинуса и синуса по четвертям. Рекомендуется отметить для удобства значения углов в радианах рядом с точками пересечения следующим образом:
- 0 и 2ПИ (0 и 360 градусов) — (1;0).
- ПИ/2 (90) — (0;1).
- 3ПИ/2 (270) — (1;0).
Использование готового инструмента
Однако необязательно самостоятельно чертить единичную окружность для определения знаков. Можно воспользоваться уже готовыми вариантами (например, рис. 1).
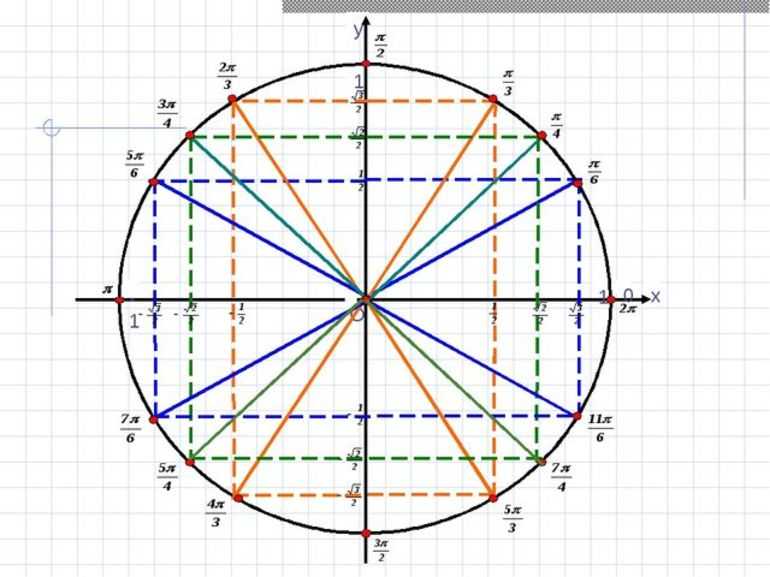
Рисунок 1. Пример тригонометрического круга.
Косинус положителен в четвертях I и IV. Существуют области, где синус положителен: I и II. Функции tg и ctg положительны только в I и III четвертях. Однако перед тем, как приступить к решению задач, нужно понять термин «четность и нечетность функции». В тригонометрии они обладают такими свойствами:
- cos(-a) = cos(a).
- sin(-a) = -sin(a).
- tg(-a) = -tg(a).
- ctg(-a) = -ctg(a).
С помощью единичной окружности можно не только находить знаки функций, но и их значения. Например, для определения знака и значения cos(270) следует воспользоваться таким алгоритмом:
- Определить четверть, в которой находится угол: 240 = 4ПИ/3 соответствует III четверти.
- В III четверти величина функции принимает только отрицательные значения. Значит, перед ней следует поставить знак «минус».
- Вычислить: cos(4ПИ/3) = — 1/2.
Когда угол представлен отрицательным значением, то следует правильно раскрыть скобки. Например, sin(-4ПИ/3) = — (-1/2) = 1/2.
Тригонометрические формулы сложения углов
cos (α — β) = cos α · cos β + sin α · sin β
sin (α + β) = sin α · cos β + sin β · cos α
sin (α — β) = sin α · cos β — sin β · cos α
cos (α + β) = cos α · cos β — sin α · sin β
Тангенс и котангенс суммы углов
альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций:
Тангенс суммы углов
равен дроби, числитель которой — сумма тангенса первого и тангенса второго угла, а знаменатель — единица минус произведение тангенса первого угла на тангенс второго угла.
Тангенс разности углов
равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель — единице плюс произведение тангенсов этих углов.
Котангенс суммы углов
равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла.
Котангенс разности углов
равен дроби, числитель которой — произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов.
Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов.
Доказательство
Теперь перейдем непосредственно к выводу формул понижения степени тригонометрических функций.
Чтобы доказать их для квадрата, нам понадобятся фождества двойного угла `cos \ 2\alpha=1-2 \ sin^2 \alpha` и `cos \ 2\alpha=2 \ cos^2 \alpha-1`.
Формулу понижения степени синуса в квадрате получим, разрешив первое равенство относительно ` sin^2 \alpha`: `sin^2 \alpha=\frac{1-cos \ 2\alpha}2`.
Аналогично и с косинусом в квадрате, получим тождество, разрешив второе равенство относительно ` cos^2 \alpha`: `cos^2 \alpha=\frac{1+cos \ 2\alpha}2`.
Формула понижения степени тангенса и котангенса автоматически выводится из определений этих функций. Поскольку `tg \alpha=\frac {sin \alpha}{cos \alpha}`, то `tg^2 \alpha=\frac {sin^2 \alpha}{cos^2 \alpha}=` `\frac {\frac{1-cos \ 2\alpha}2}{\frac{1+cos \ 2\alpha}2}=\frac{1-cos \ 2\alpha}{1+cos \ 2\alpha}`. Аналогично получим `ctg^2 \alpha=\frac {cos^2 \alpha}{sin^2 \alpha}=` `\frac {\frac{1+cos \ 2\alpha}2}{\frac{1-cos \ 2\alpha}2}=\frac{1+cos \ 2\alpha}{1-cos \ 2\alpha}`.
Для лучшего усвоения теоретического материала рекомендуем посмотреть видео, где подробно описывается процесс доказательстве первых двух формул:
Если формулы тройного угла `sin \ 3\alpha=3 \ sin \ \alpha-4sin^3 \alpha` и
`cos \ 3\alpha=4cos^3 \alpha-3 \ cos \ \alpha` разрешить относительно `sin \ 3\alpha` и `cos \ 3\alpha`, то получим формулы понижения степени для синуса и косинуса в кубе: `sin^3 \alpha=\frac{3sin \ \alpha-sin \ 3\alpha}4` и `cos^3 \alpha=\frac{3cos \ \alpha+cos \ 3\alpha}4`.
Доказать данной равности для синуса и косинуса можно, воспользовавшись два раза формулами понижения квадратов:
`sin^4 \alpha=(sin^2 \alpha)^2=(\frac{1-cos \ 2\alpha}2)^2=` `\frac{1-2cos \ 2\alpha+cos^2 2\alpha}4=\frac{1-2cos \ 2\alpha+\frac{1+cos \ 4\alpha}2}4=` `\frac{3-4cos \ 2\alpha+cos \ 4\alpha}8`;
`cos^4 \alpha=(cos^2 \alpha)^2=(\frac{1+cos \ 2\alpha}2)^2=` `\frac{1+2cos \ 2\alpha+cos^2 2\alpha}4=\frac{1+2cos \ 2\alpha+\frac{1+cos \ 4\alpha}2}4=` `\frac{3+4cos \ 2\alpha+cos \ 4\alpha}8`.
Общий вид формул понижения степени
Для четных показателей степени (n=1, 2, 3,…):
`sin^n \alpha=\frac {C_\frac n 2^n}{2^n}+\frac1{2^{n-1}} \cdot \sum_{k=0}^{\frac n 2 -1} (-1)^{\frac n 2 -k} \cdot C_k^n \cdot cos((n-2k) \alpha)` и `cos^n \alpha=\frac {C_\frac n 2^n}{2^n}+\frac1{2^{n-1}} \cdot \sum_{k=0}^{\frac n 2 -1} C_k^n \cdot cos((n-2k) \alpha)`.
Для нечетных показателей степени (n=3, 5, 7,…):
`sin^n \alpha=\frac1{2^{n-1}} \cdot \sum_{k=0}^{\frac {n-1}2} (-1)^{\frac {n-1} 2 -k} \cdot C_k^n \cdot sin((n-2k) \alpha)` и `cos^n \alpha=\frac1{2^{n-1}} \cdot \sum_{k=0}^{\frac {n-1}2} C_k^n \cdot cos((n-2k) \alpha)`.
Комплекс операций инженерного калькулятора
Встроенный математический калькулятор поможет вам провести самые простые расчеты: умножение и суммирование, вычитание, а также деление. Калькулятор степеней онлайн быстро и точно возведет любое число в выбранную вами степень.
Представленный инженерный калькулятор содержит в себе все возможные вариации онлайн программ для расчетов. Kalkpro.ru содержит тригонометрический калькулятор (углы и радианы, грады), логарифмов (Log), факториалов (n!), расчета корней, синусов и арктангенсов, косинусов, тангенсов онлайн – множество тригонометрический функций и не только.
Работать с вычислительной программой можно онлайн с любого устройства, в каждом случае размер интерфейса будет подстраиваться под ваше устройство, либо вы можете откорректировать его размер на свой вкус.
Ввод цифр производится в двух вариантах:
- с мобильных устройств – ввод с дисплеем телефона или планшета, клавишами интерфейса программы
- с персонального компьютера – с помощью электронного дисплея интерфейса, либо через клавиатуру компьютера любыми цифрами
Примеры преобразований выражений, содержащих обратные тригонометрические функции
Пример 1.
Упростить выражение cos (arcsin х), где .
Решение:
Положим arcsin х = у. Тогда sin у = х, . Нужно найти cos у.
Известно, что
значит,
Но , а на отрезке
косинус принимает лишь неотрицательные значения. Поэтому т.е.
Пример 2.
Вычислить .
Решение:
Положим . Тогда
Нужно вычислить
Имеем ; значит,
Так как, далее, 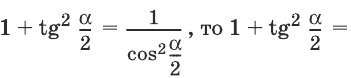
откуда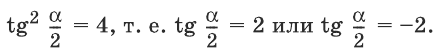
По условию, значит, а в интервале имеем
Итак, т. е.
Пример 3.
Доказать, что для любого х из справедливо тождество
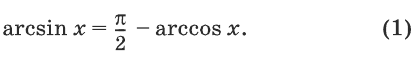
Решение:
Вычислим значения синуса левой и правой частей проверяемого равенства:
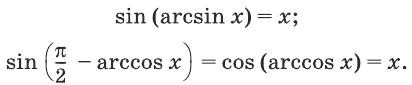
Синусы, как мы видим, равны, поэтому, чтобы убедиться в справедливости равенства (1), осталось показать, что
принадлежат одно-му и тому же промежутку монотонности функции у = sin х (без проверки этого условия можно получить неверный результат, ведь тригонометрические функции могут принимать одинаковые значения и для различных значении аргумента, например 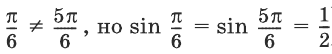 )
)
Имеем
Далее, а поэтому
Итак, arcsin х и
принадлежат одному промежутку монотонности
функции у = sin х. Теперь можно считать, что тождество (1) доказано. Аналогично можно доказать, что
Сумма и разность функций
В каком виде можно представить действия
Использование этих формул позволяет перейти от суммы или разности функций углов \(\alpha\) и \(\beta\) к произведению функций углов \(\frac{\alpha\;+\;\beta}2\;\) и \(\;\frac{\alpha\;-\;\beta}2\).
Примеры формул
\(\sin\left(\alpha\right)\;+\;\sin\left(\beta\right)\;=\;2\;\times\;\sin\left(\frac{\alpha\;+\;\beta}2\right)\;\times\;\cos\left(\frac{\alpha\;-\;\beta}2\right)\)
\(\sin\left(\alpha\right)\;-\;\sin\left(\beta\right)\;=\;2\;\times\;\sin\left(\frac{\alpha\;-\;\beta}2\right)\;\times\;\cos\left(\frac{\alpha\;+\;\beta}2\right)\)
\(\cos\left(\alpha\right)\;+\;\cos\left(\beta\right)\;=\;2\;\times\;\cos\left(\frac{\alpha\;+\;\beta}2\right)\;\times\;\cos\left(\frac{\alpha\;-\;\beta}2\right)\)
\(\cos\left(\alpha\right)\;-\;\cos\left(\beta\right)\;=\;-2\;\times\;\sin\left(\frac{\alpha\;+\;\beta}2\right)\;\times\;\sin\left(\frac{\alpha\;-\;\beta}2\right)\)
Формула Муавра
Пусть дано комплексное число в тригонометрической форме:
\
Возведём его в квадрат, умножив на само себя:
\
Затем возведём в куб, умножив на себя ещё раз:
\
Несложно догадаться, что будет дальше — при возведении в степень $n$. Это называется формула Муавра.
Простая формула, которая ускоряет вычисления раз в десять! И кстати: эта формула работает при любом $n\in \mathbb{R}$, а не только натуральном. Но об этом позже. Сейчас примеры:
Последним шагом мы воспользовались периодичностью синуса и косинуса, уменьшив аргумент сразу на 28π.
Следующую задачу в разных вариациях любят давать на контрольных работах и экзаменах:
Вот так всё просто! Следующие два раздела предназначены для углублённого изучения. Для тех, кто хочет действительно разобраться в комплексных числах.
Произведение тригонометрических функций
Если формулы суммы и разности функций позволяют перейти к их произведению, то формулы произведения тригонометрических функций осуществляют обратный переход — от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.
Формулы произведения тригонометрических функций
sinα·sinβ=12·(cos(α-β)-cos(α+β))cosα·cosβ=12·(cos(α-β)+cos(α+β))sinα·cosβ=12·(sin(α-β)+sin(α+β))
Произведение косинусов
Сложим базовые равенства I и II — косинус разности и косинус суммы:
cos(α−β) + cos(α+β) = = cos(α)×cos(β) + sin(α)×sin(β) + cos(α)×cos(β) − sin(α)×sin(β) = {одинаковые произведения синусов сокращаются} = cos(α)×cos(β) + cos(α)×cos(β) = 2×cos(α)×cos(β)
Получаем равенство:
cos(α−β) + cos(α+β) = 2×cos(α)×cos(β)
В этом равенстве можно и левую и правую части поделить на 2 и поменять местами и получится искомое выражение для произведения косинусов:
cos(α)×cos(β) = / 2,
т.е. произведение косинусов равно полусумме косинуса разности и косинуса суммы.
Произведение тангенса на тангенс
Выведем формулу произведения тангенса на тангенс (d).
|
. |
Другую формулу произведения тангенса на тангенс (формула (d’)) получим применяя формулы (a) и (c):
|
. |
Произведение синусов
Воспользуемся базовыми формулами I и II — косинус разности и косинус суммы. Из равенства I вычтем равенство II:
cos(α−β) — cos(α+β) = = cos(α)×cos(β) + sin(α)×sin(β) — cos(α)×cos(β) + sin(α)×sin(β) = {одинаковые произведения косинусов сокращаются} = sin(α)×sin(β) + sin(α)×sin(β) = 2×sin(α)×sin(β)
Получаем равенство:
cos(α−β) — cos(α+β) = 2×sin(α)×sin(β)
В этом равенстве можно левую и правую части поделить на 2 и поменять местами и получится искомое выражение для произведения синусов:
sin(α)×sin(β) = / 2,
т.е. произведение синусов равно полуразности косинуса разности и косинуса суммы.
Произведение синуса на косинус
Сложим базовые равенства III и IV — синус суммы и синус разности:
sin(α−β) + sin(α+β) = = sin(α)×cos(β) − cos(α)×sin(β) + sin(α)×cos(β) + cos(α)×sin(β) = {одинаковые cos(α)×sin(β) сокращаются} = sin(α)×cos(β) + sin(α)×cos(β) = = 2×sin(α)×cos(β)
Получаем равенство:
sin(α−β) + sin(α+β) = 2×sin(α)×cos(β)
В этом равенстве можно левую и правую части поделить на 2 и поменять местами и получится искомое выражение для произведения синуса на косинус:
sin(α)×cos(β) = / 2,
т.е. произведение синуса на косинус равно полусумме синуса разности и синуса суммы.
Произведение котангенса на котангенс
Выведем формулу произведения котангенса на котангенс (e).
| . |
Другую формулу произведения котангенса на котангенс (формула (e’)) получим применяя формулы (a) и (c):
| . |
Примеры применения формул произведения тригонометрических функций
Пример 1. Вычислить точное значение следующего выражения:.
Решение. Так как невозможно найти точное решение ни для , ни для
попробуем использовать формулу (d’):
Ответ:.
Пример 2. Вычислить точное значение следующего выражения:.
Решение. Так как несуществует точного решения ни для , ни для ,то попробуем использовать формулу (a):
Ответ:.
Пример 1.
Вычислить sin 75°.
Решение:
Имеем sin 75° = sin (30° + 45°). Воспользовавшись формулой (3) при
получим
sin (30° + 45°) = sin 30° cos 45° + cos 30° sin 45°.
Известно, что 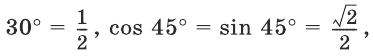
(см. п. 99). Значит, 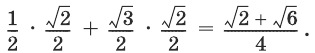
Итак, 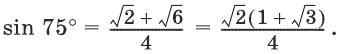
Упростить выражение
Решение:
Воспользуемся для
и
формулами (3) и (1) и учтем, что
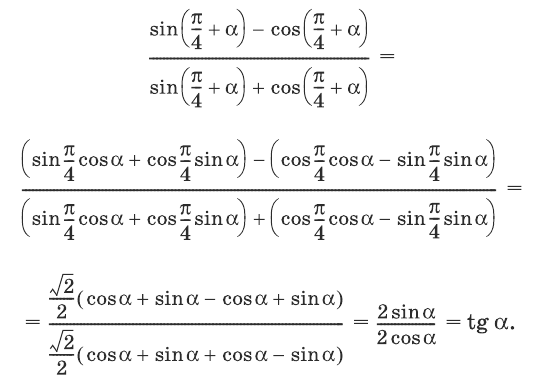
Пример 3.
Вычислить cos 15°.
Решение:
Имеем 15° = 45° — 30°. Воспользовавшись формулой (2) при
получим
cos 15° = cos (45° — 30°) = cos 45° cos 30° + sin 45° sin 30° =
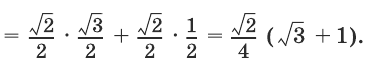
Соотношения между тригонометрическими функциями одного и того же аргумента
Если в формуле (2) из п. 125 положить , то получим
![]()
откуда, в свою очередь, находим, что
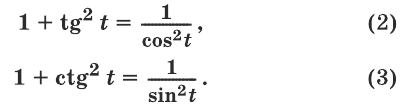
Тождество (2) справедливо при
а тождество (3) — при
Равенства (1), (2), (3) связывают между собой различные тригонометрические функции одного и того же аргумента. Известны еще два равенства, связывающие между собой различные тригонометрические функции одного и того же аргумента:
Перемножая эти равенства, получаем равенство
![]()
справедливое при
Пример 1.
Известно, что , причем
Найти cos t, tg t, ctg t.
Решение:
Из формулы (1) получаем Подставив вместо sin t его значение, получим
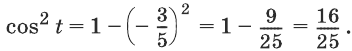
Итак, <br>; значит, либо
По условию, , т. е. аргумент t принадлежит III четверти. Но в III четверти косинус отрицателен; значит, из двух указанных выше возможностей выбираем одну:
Зная sin t и cos t, находим tg t и ctg t:
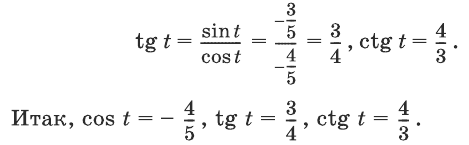
Пример 2.
Известно, что , причем . Найти sin t, cos t, tg t.
Peшeние:
Из формулы (3) находим
Подставив вместо ctg t его значение, получим
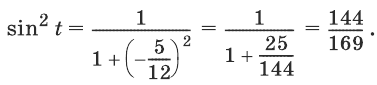
Итак, . Значит, либо , либо
По условию,
Значит, t принадлежит II четверти, а во II четверти синус положителен. Поэтому из двух указанных возможностей выбираем одну: Для отыскания значения cos t воспользуемся определением котангенса: . Из этого равенства находим
![]()
Осталось вычислить значение tg t. Из равенства
находим, что . Итак,
![]()
Формулы отрицательных углов
Что такое отрицательный угол и как с ним работать? На самом деле, все просто: чтобы получить отрицательный угол, достаточно поставить перед аргументом минус. Например, sin(-x).
Применять такой угол при решении выражений с тригонометрическими функциями очень неудобно, поэтому от минуса обычно избавляются. Однако делать это нужно по правилам: нельзя просто его не написать.
Чтобы правильно избавиться от минуса, нужно понимать, что отрицательные углы напрямую связаны с графиками тригонометрических функций, а именно с четностью функций. Подробнее про четность функции можно прочесть в статье «Определение и график функции».
Четность функции можно сравнить со снежинкой. Если мы посмотрим на нее под микроскопом и мысленно проведем ось посередине, то окажется, что левая и правая части одинаковые. Единственное их отличие – они отзеркалены.
Также и четные функции: справа и слева они имеют одинаковые отзеркаленные части.

Четная функция – функция, для которой выполняется равенство \(f(x)=f(-x)\).
Повторим, такие функции симметричны относительно оси ординат. Можно представить, что вместо оси у у нас стоит зеркало, в которой график функции отражается.
Если мы вспомним графики тригонометрических функций и проверим их симметричность, то заметим, что четным является только косинус. Этим он выделяется среди других функций.

Синус, тангенс и котангенс – нечетные функции. Для них будет справедливо уравнение \(f(-x)=-f(x)\). Их графики не симметричны относительно оси у.
Таким образом, опираясь на четность функции, мы можем вывести четыре формулы:
\(cos(-x)=cos x\)\(sin(-x)=-sin x\)\(tg(-x)=-tg x\)\(ctg(-x)=-ctg x\)
Пользуясь этими формулами, можно легко избавляться от минуса в аргументах функции.
Итак, мы попробовали изменить аргумент с помощью минуса. А если попробовать поставить перед аргументом коэффициент, например, 2?
Формулы понижения степени
Для чего применяются
С их помощью можно приводить тригонометрические уравнения к уравнениям более низких степеней, вплоть до первой степени
Важно помнить, что при понижении степени аргумент увеличивается
Общий вид
Для четных n:
\(\sin^n\left(\alpha\right)\;=\;\frac{C_n^\frac n2}{2^n}\;+\;\frac1{2^{n-1}}\;\times\;\sum_{k=0}^{{\textstyle\frac n2}-1}{(-1)}^{{\textstyle\frac n2}-k}\;\times\;C_n^k\;\times\;\cos\left((n-2\times k)\times\alpha\right)\)
\(\cos^n\left(\alpha\right)\;=\;\frac{C_n^\frac n2}{2^n}\;+\;\frac1{2^{n-1}}\;\times\;\sum_{k=0}^{{\textstyle\frac n2}-1}C_n^k\;\times\;\cos\left((n-2\times k)\times\alpha\right)\)
Для нечетных n:
\(\sin^n\left(\alpha\right)\;=\;\frac1{2^{n-1}}\;\times\;\overset{\textstyle\frac{n-1}2}{\underset{k=0}{\sum{(-1)}^{\frac{n-1}2-k}\;\times\;}}C_n^k\;\times\;\sin\left((n-2\times k)\times\alpha\right)\)
\(\cos^n\left(\alpha\right)\;=\;\frac1{2^{n-1}}\;\times\;\overset{\textstyle\frac{n-1}2}{\underset{k=0}{\sum\;}}C_n^k\;\times\;\cos\left((n-2\times k)\times\alpha\right)\)
\(C_p^q\;=\;\frac{p!}{q!(p-q)!}\)
Это означает число сочетаний из p элементов по q.

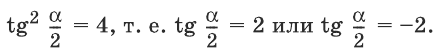
















![Тригонометрические выражения и тригонометрические формулы [wiki.eduvdom.com]](http://dvorik56.ru/wp-content/uploads/2/c/3/2c31f79bd764421a2b4669bc466b9793.jpeg)








