Колебательный контур

Что означает добротность динамика и как она определяется

Добротность динамика – это характеристика, которая определяет способность динамической системы к поддержанию колебаний при отсутствии внешних воздействий или при наличии малых внешних воздействий.

Определение добротности динамика основывается на времени затухания колебаний, когда система со временем переходит из начального положения равновесия в равновесное состояние. Чем медленнее затухают колебания, тем выше добротность динамика.

Добротность динамика может быть измерена и численно определена. Она рассчитывается по формуле:

Q = 2π * (энергия системы) / (потери энергии за один период колебаний)

Значение добротности динамика может быть меньше единицы, равно единице или больше единицы. Если добротность динамика больше единицы, то система является колебательной и колебания будут происходить в течение длительного времени. Если добротность динамика меньше единицы, то система является апериодической и колебания затухают быстро.

Высокая добротность динамика может быть полезна в различных областях, например, в радиоэлектронике и связи, в медицине, в физике и в других науках. Например, высокая добротность динамика в резонаторе позволяет создать лазер с высокой мощностью и малым расходом энергии.

Резонанс напряжений

Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:

и конденсатор в 1000 пФ

Из них собираю последовательный колебательный контур. Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.

Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор — это не есть хорошо, но что не сделаешь ради науки!

Ну что же, приступим ;-). Давайте сначала посчитаем резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.

Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:

Размах амплитуды 4 Вольта

Хотя на генераторе частоты размах более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.

Теперь небольшой прикол

Вот этот сигнал мы подаем на наш последовательный колебательный контур:

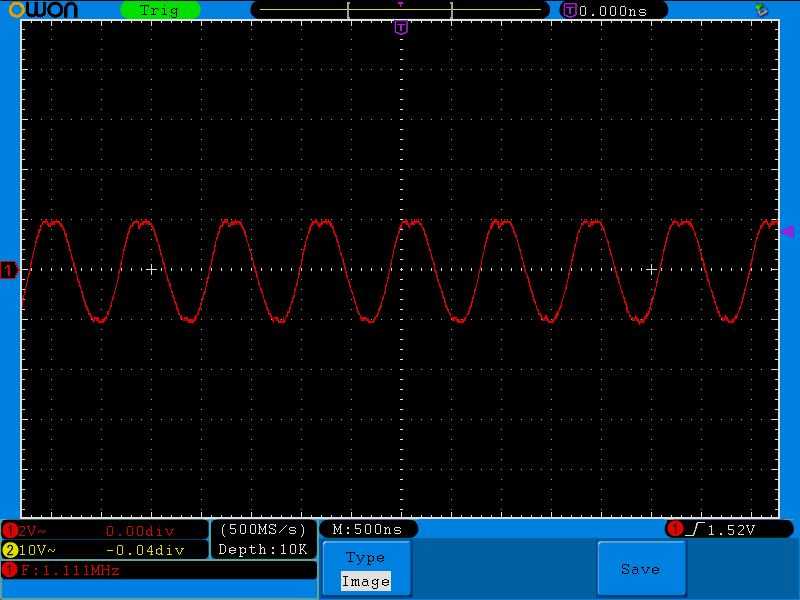
Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.

Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:

Смотрим напряжение на конденсаторе:

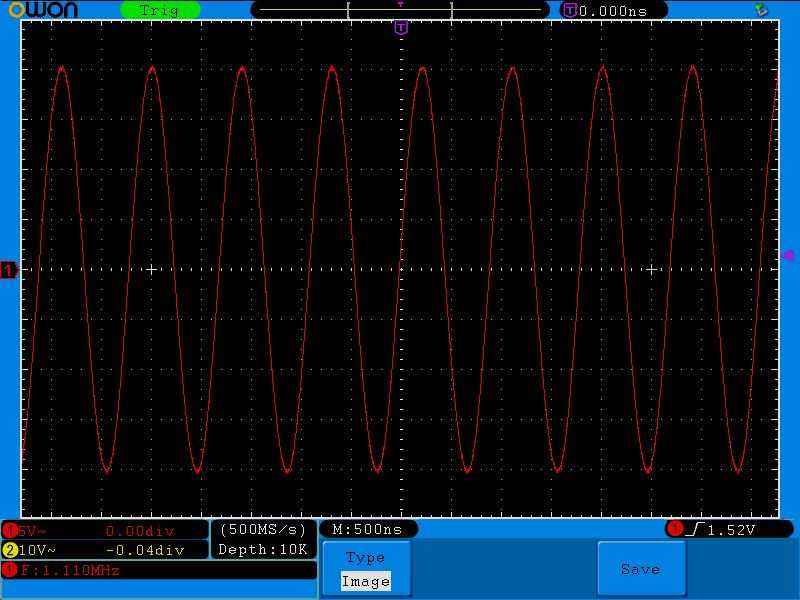
Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!

Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:

Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию с конденсатора или с катушки!

Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как среднеквадратичное напряжение будет где-то Вольт 14, и цепляю поочередно к ним лампочку:

Как видите — полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока — увы! Поэтому, последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!

Объяснение резонанса напряжения

При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.

При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение U_L = IX_L, а на конденсаторе U_C = IX_C. А так как при резонансе у нас X_L= X_C, то получаем что U_L= U_C , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.

Влияние добротности на электрические цепи

Сопротивление в электрических цепях вызывает потери энергии в виде тепла, что приводит к ослаблению колебаний. Чем меньше потери энергии, тем больше добротность контура.

Добротность контура напрямую связана с его волновыми свойствами. При высокой добротности контура, в нем возникают высокочастотные, гармонические колебания. Такие колебания приводят к повышению резонанса в цепи, что может быть полезно при создании усилителей сигнала или резонансных фильтров.

Для высокой добротности контура, значения сопротивления и индуктивности должны быть оптимально подобраны. При этом достигается наилучшее соотношение между потерями в цепи и энергией колебаний.

Фаза колебаний также зависит от добротности контура. При высокой добротности, фаза колебаний поддерживается близкой к нулю, что означает, что напряжение и ток колеблются практически в одной фазе. Это позволяет лучше использовать энергию колебаний и повышает эффективность работы цепи.

Таким образом, добротность колебательного контура очень важна для электрических цепей. Она определяет энергетические потери, резонансные свойства и фазовую характеристику колебаний. Правильное подбор значения добротности позволяет достичь наилучших результатов в работе электрической цепи.

Улучшение качества сигнала

Добротность колебательного контура описывает степень подавления потерь, происходящих в контуре. Чем выше добротность, тем меньше потерь и тем качественнее будет сигнал.

Потери в колебательном контуре могут возникать из-за сопротивления проводников, распределенных емкостей и индуктивностей, а также из-за излучения электромагнитных волн. Чем ниже уровень потерь, тем эффективнее будет передача энергии и четче будут проявляться колебания.

Когда добротность колебательного контура достигает своего максимума, возникает явление резонанса. Это состояние, когда энергия в контуре переходит из одной формы в другую с наибольшей эффективностью. При резонансе фаза сигнала также имеет свое значение и находится в оптимальном положении для передачи информации.

Таким образом, улучшение добротности колебательного контура позволяет повысить качество сигнала в электрических цепях, снизить уровень потерь и достичь оптимальных условий для передачи энергии и информации.

Потери энергии в контуре

В колебательном контуре существуют потери энергии, которые могут возникать из-за сопротивления проводников, диэлектрических потерь или излучения электромагнитных волн. Эти потери приводят к уменьшению амплитуды колебаний и преобразованию энергии в другие формы.

Одной из основных причин потерь энергии является сопротивление контура. Это сопротивление обусловлено как внутренним сопротивлением элементов контура (например, проводов и резисторов), так и внешним сопротивлением, через которое контур подключен к источнику энергии. Сопротивление создает потери энергии в виде тепла.

Кроме того, в колебательных контурах могут возникать диэлектрические потери. Они связаны с неполной изоляцией между элементами контура, что приводит к разрядам через изоляцию и потерям энергии. Диэлектрические потери становятся особенно заметными при работе контура на больших частотах, где возникают высокие напряжения и электрические поля.

Еще одной причиной потерь энергии в колебательном контуре является излучение электромагнитных волн. Возникающие колебания создают электромагнитное поле, которое излучается и переносит энергию на некоторое расстояние от контура. Это приводит к уменьшению общей энергии контура.

Суммарные потери энергии в контуре можно измерить с помощью добротности (Q-фактора) контура. Добротность определяет соотношение между максимальной запасенной энергией и потерями энергии за один период колебаний. Чем выше значение добротности, тем меньше потери энергии и тем более эффективно работает контур. Добротность контура связана с его сопротивлением, индуктивностью и емкостью через формулу:

D	=	ωL	R

где ω — частота колебаний контура, L — индуктивность, R — сопротивление.

Настройка контура на резонанс может уменьшить потери энергии и повысить его добротность. Резонанс достигается, когда индуктивность контура и его емкость таковы, что их реактивные сопротивления в точности компенсируют друг друга, и реальное сопротивление становится минимальным. В этой точке потери энергии становятся минимальными, и контур работает с наибольшей эффективностью.

В целом, потери энергии в колебательном контуре должны быть минимизированы для обеспечения стабильности и эффективности работы электрических цепей.

Принцип работы

Принцип работы контура состоит в поочередном обмене электрической энергией между элементами емкости и индуктивности. Происходит превращение емкостной в индуктивную и обратно. Процессы следует рассмотреть подробнее. Для этого нужно зарядить конденсатор до величины напряжения Uc. Энергия будет определяться по формуле Wс = (C * U2) / 2. Если к конденсатору подсоединить катушку индуктивности, то это вызовет в ней ЭДС самоиндукции.

При этом энергия электромагнитного поля станет рассчитываться по такому соотношению: Wl = (L * I2) / 2. Из-за нее будет постепенно уменьшаться ток в электрической цепи контура. Векторы токов конденсатора и катушки направлены в разные стороны. Следовательно, они компенсируют друг друга по I закону Кирхгофа и не выходят за пределы системы.

При постоянной работе генератора (источника питания) результирующий ток в системе начнет возрастать. Энергия Wc будет полностью переходить в катушку, пока не разрядится полностью конденсатор (Wc = 0). Далее в ней появляется электромагнитное поле за счет ЭДС самоиндукции, и обкладки конденсатора будут снова заряжаться до тех пор, пока Wl не будет равна 0. Такая особенность обмена энергиями порождает колебания. Их длительность зависит от коэффициента затухания контура.

Архив записей

Архив записейВыберите месяц Ноябрь 2022 (1) Сентябрь 2022 (1) Январь 2022 (2) Сентябрь 2021 (1) Июль 2021 (1) Июнь 2021 (2) Май 2021 (1) Апрель 2021 (1) Март 2021 (1) Сентябрь 2020 (1) Август 2020 (2) Июль 2020 (2) Июнь 2020 (2) Декабрь 2019 (3) Ноябрь 2019 (4) Октябрь 2019 (3) Сентябрь 2019 (2) Май 2019 (1) Октябрь 2018 (1) Июнь 2018 (1) Апрель 2018 (1) Январь 2018 (1) Ноябрь 2017 (1) Октябрь 2017 (1) Сентябрь 2017 (2) Август 2017 (4) Июль 2017 (5) Июнь 2017 (4) Май 2017 (5) Апрель 2017 (2) Март 2017 (1) Февраль 2017 (1) Январь 2017 (3) Декабрь 2016 (1) Ноябрь 2016 (2) Октябрь 2016 (3) Сентябрь 2016 (4) Август 2016 (6) Июль 2016 (9) Июнь 2016 (4) Май 2016 (5) Апрель 2016 (6) Март 2016 (5) Февраль 2016 (8) Январь 2016 (8) Декабрь 2015 (9) Ноябрь 2015 (4) Июль 2015 (1) Март 2015 (1) Февраль 2015 (1) Январь 2015 (1) Июль 2014 (1) Июль 2013 (1) Март 2013 (2) Декабрь 2012 (1) Ноябрь 2012 (1) Сентябрь 2012 (3) Август 2012 (4) Июль 2012 (4) Июнь 2012 (4) Май 2012 (4) Апрель 2012 (5) Март 2012 (7) Февраль 2012 (8) Январь 2012 (7) Декабрь 2011 (5) Ноябрь 2011 (1)

Размерность добротности

Добротность (Q-фактор) — это величина, характеризующая способность колебательной системы сохранять энергию за время одного колебания.

Размерность добротности зависит от типа системы и дает информацию о том, насколько быстро колебательная система затухает или наоборот, сохраняет свою энергию. Так как добротность является безразмерной величиной, ее размерность обычно не указывается.

Для определения добротности используются различные методы, такие как измерение ширины резонансной кривой или времени затухания колебаний.

Добротность может принимать значения от 0 до бесконечности, причем высокие значения добротности свидетельствуют о высокой эффективности системы в сохранении энергии.

Знание добротности позволяет оценить эффективность различных колебательных систем и использовать их в различных областях науки и техники, таких как электроника, оптика, механика и другие.

Связь с другими физическими величинами

Добротность является одной из основных характеристик колебательной системы. Она описывает способность системы сохранять энергию, которую она получает от внешних источников. Добротность тесно связана с другими физическими величинами, которые определяют поведение колебательных систем.

Добротность можно выразить через такие величины, как частота колебаний системы, сопротивление среды, индуктивность или емкость элементов системы и т.д

Важно отметить, что добротность не имеет физической размерности, она является безразмерной величиной

Существует несколько формул, которые позволяют выразить добротность через другие физические параметры системы. Например, для колебательной системы, состоящей из индуктивности и сопротивления, добротность можно выразить следующим образом:

Для параллельного контура: Q = ωL/R, где Q — добротность, ω — частота колебаний, L — индуктивность, R — сопротивление.
Для последовательного контура: Q = R/ωL, где Q — добротность, ω — частота колебаний, L — индуктивность, R — сопротивление.

Кроме того, добротность может быть связана с другими величинами, такими как ширина резонансной кривой, время затухания колебаний, качество системы и т.д. Все эти показатели отражают способность системы сохранять энергию и выполнять свои функции с минимальными потерями.

Поэтому изучение добротности и ее связь с другими физическими величинами позволяет более полно понять и описать поведение колебательной системы и оптимизировать ее работу в различных условиях.

Единицы измерения добротности

Добротность — это важная характеристика, которая используется для измерения степени затухания колебаний.

Обычно добротность обозначается символом Q и может быть представлена в различных единицах измерения. Наиболее часто используемыми единицами измерения добротности являются:

Безразмерная величина;
Размерность, обратная времени (секунды);
Отношение энергии к затратам энергии в единицу времени (джоули/секунда).

Безразмерная величина добротности не имеет единиц измерения и обозначает просто отношение затухания колебаний к их амплитуде. Чем выше безразмерная величина, тем меньше затухание колебаний и тем больше добротность.

Размерность добротности обратная времени и обычно измеряется в секундах. Чем больше значение добротности в секундах, тем меньше затухание колебаний.

Отношение энергии к затратам энергии в единицу времени также может быть использовано для измерения добротности. Обычно измеряется в джоулях/секунда. Чем больше значение добротности в джоулях/секунда, тем меньше затухание колебаний.

Добротность является важным показателем во многих областях науки и техники, таких как электроника, оптика, механика и телекоммуникации. Понимание единиц измерения добротности позволяет более точно оценивать и анализировать характеристики колебательных систем.

Резонансные колебательные системы

Работа посвящена экспериментальному изучению практического применения колебательных контуров как резонансных систем. С общим теоретическим описанием процессов в контуре необходимо познакомиться в параграфе 4 общего введения к сборнику. Ниже приведены лишь минимальные теоретические сведения, необходимые для практической работы.

Колебательный контур является типичным представителем резонансных колебательных систем, играющих важную роль в большинстве разделов физики. Резонансные системы имеют три важных свойства:

свойство избирательно реагировать на внешние источники сигналов, выделяя только те из них, частоты которых совпадают с собственной частотой колебательной системы;
свойство запасать энергию колебаний, возбужденных внешним источником, поддерживая колебания в течение определенного времени после выключения внешнего источника;
свойство сохранять энергию в своей системе в виде циклического перехода одного ее вида в другой, например, потенциальная $\leftrightarrow $ кинетическая, магнитная $\leftrightarrow $ электрическая и т.д.

Колебательные системы бывают с сосредоточенными и распределенными параметрами. Пример механической резонансной системы с распределенными параметрами — струна или упругий стержень, электрической — СВЧ резонаторы. Примерами колебательных систем с сосредоточенными параметрами являются различного рода маятники и колебательные контуры.

Любая резонансная система характеризуется двумя основными параметрами: частотой собственных колебаний $\omega _0$ и добротностью $Q,$ определяющей отношение мощности энергии собственных колебаний к мощности потерь за период.

Понятие добротности

Резонансный контур – это электрическая схема, состоящая из индуктивной катушки, конденсатора и сопротивления, которая обладает свойством резонанса при определенном значении частоты.

Добротность резонансного контура является мерой его энергетических потерь. Она характеризует способность контура сохранять энергию, поданную на него. Чем выше добротность, тем меньше происходит потерь энергии и тем более эффективно контур работает.

Добротность резонансного контура определяетсся формулой:

Q = 1 / R_{точечное} * √(L / C)

Где Q — добротность контура, R_{точечное} — сопротивление контура на частоте резонанса, L — индуктивность катушки, С — емкость конденсатора.

Чем больше значение Q, тем меньше энергии теряется, и тем выше добротность.

Высокая добротность резонансного контура позволяет обеспечить более точное воспроизведение сигнала на частоте резонанса. Такие контуры используются в различных устройствах, включая радиоприемники, колебательные контуры и фильтры.

Определение добротности

Добротность — это важный параметр резонансного контура в области электротехники. Она определяет эффективность контура и характеризует его способность поддерживать колебания на определенной частоте.

Добротность обозначается символом Q. Чем выше значение добротности, тем более эффективно контур поддерживает колебания. Низкое значение добротности указывает на большую потерю энергии и менее эффективную работу контура.

Определение добротности может быть различным в зависимости от вида резонансного контура и его параметров. В общем случае, добротность можно выразить как отношение энергии, запасенной в контуре к энергии, потерянной за период одного полного колебания.

Формула для расчета добротности может иметь различные варианты в зависимости от параметров контура, например, активное сопротивление, индуктивность и емкость контура. Для рассмотрения конкретных формул необходимо обращаться к соответствующей технической литературе или обращаться к специалистам в области электротехники.

Значение добротности в электротехнике

Добротность является важным показателем резонансного контура в электротехнике. Резонансный контур состоит из индуктивной катушки (катушки индуктивности) и конденсатора, соединенных последовательно или параллельно.

Добротность (Q-фактор) контура определяет его способность к накоплению энергии и поддержанию колебаний на определенной частоте. Чем выше значение добротности, тем больше энергии может накопиться в контуре и тем более узкополосные колебания можно получить на резонансной частоте.

Добротность контура может быть вычислена по формуле:

Q = 2πf₀L / R

где:

Q — добротность контура;
f₀ — резонансная частота контура;
L — индуктивность катушки;
R — сопротивление контура.

Чем меньше сопротивление контура, тем выше значение его добротности. Отборочное сопротивление, или потери, играет важную роль в контуре — чем они меньше, тем выше добротность. В идеальном случае, при отсутствии потерь, добротность будет бесконечной и колебания будут поддерживаться без затухания на резонансной частоте.

Высокая добротность резонансного контура обладает множеством применений в электротехнике. Она используется в качестве фильтра, для выделения определенной частоты из спектра, а также для усиления сигналов на резонансной частоте.

Влияние добротности на резонансный контур

Добротность резонансного контура является одним из основных параметров, определяющих его характеристики в области электротехники. Добротность определяет эффективность системы при переходе от энергии приведения электрического тока к энергии приведения максимального заряда на конденсаторе контура.

Чем выше добротность резонансного контура, тем меньше потери энергии в контуре, а значит, выше эффективность его работы. Добротность контура определяется соотношением между активным и реактивным сопротивлением.

Резонансный контур с высокой добротностью способен сохранить большую часть энергии в виде колебательных процессов и дольше поддерживать колебания при заданной частоте. Такие контуры находят применение в системах, где требуется точная настройка на заданную частоту, например, в радиоэлектронике или радиосвязи.

Однако при работе с такими контурами необходимо учитывать, что высокая добротность может привести к возникновению резкого резонансного пика, который может быть опасен для некоторых устройств и компонентов. Поэтому, при проектировании резонансных контуров, необходимо учитывать как требуемую добротность контура, так и его безопасность и стабильность работы.

Примеры влияния добротности на резонансный контур:

Добротность контура
Влияние

Высокая
— Большая эффективность работы контура

— Большое удержание энергии

— Точная настройка на заданную частоту

Низкая
— Меньшая эффективность работы контура

— Большие потери энергии

— Необходимость дополнительной подстройки при изменении условий работы

Таким образом, добротность играет важную роль в определении характеристик резонансного контура в электротехнике. Она влияет на эффективность работы контура, его способность удерживать энергию и точную настройку на заданную частоту. При проектировании резонансных контуров необходимо учитывать как требуемую добротность, так и безопасность и стабильность работы системы.

Качество резонансного контура

Качество резонансного контура – это параметр, характеризующий его способность сохранять энергию в колебательном процессе. В области электротехники резонансный контур играет важную роль, поскольку является основой для создания различных устройств, таких как фильтры низких и высоких частот, генераторы, усилители и т.д.

Добротность (Q-фактор) резонансного контура определяет, насколько экономично контур обменяет энергию с внешними источниками. Она выражается отношением реактивной энергии, хранящейся в контуре, к активной энергии, расходуемой на преодоление сопротивлений.

Чем выше значение добротности, тем меньше энергии теряется при колебаниях в резонансном контуре. Высокая добротность позволяет контуру быть более селективным по отношению к определенным частотам, а также обеспечивает более устойчивые и качественные колебания.

Добротность резонансного контура может быть вычислена по формуле:

Q =	ω₀L
	R

где Q — добротность, ω₀ — собственная частота контура, L — индуктивность, R — сопротивление.

Резонансный контур с высокой добротностью является эффективным инструментом в электротехнике для работы с сигналами определенных частот, а также для фильтрации и усиления электрических сигналов.

Влияние добротности на амплитуду и фазу сигнала

Добротность резонансного контура является одним из важных параметров, характеризующих его эффективность. Она определяет, как быстро колебания в контуре затухают после включения или выключения источника сигнала.

Влияние добротности на амплитуду и фазу сигнала проявляется при работе контура в резонансе, то есть когда частота сигнала совпадает с собственной частотой колебаний контура. При резонансе амплитуда сигнала в контуре достигает максимального значения.

Чем выше добротность резонансного контура, тем меньше затухание сигнала и тем больше его амплитуда при работе в резонансе. Это связано с тем, что при высокой добротности потери энергии в контуре минимальны, и энергия сохраняется в колебаниях системы.

Фазовый сдвиг сигнала в контуре также зависит от его добротности. При работе в резонансе фазовый сдвиг составляет 0 градусов или 180 градусов, в зависимости от типа контура. При низкой добротности фазовый сдвиг может отличаться от этих значений, что влияет на форму и качество сигнала.

Итак, добротность резонансного контура в электротехнике имеет прямое влияние на амплитуду и фазу сигнала. Чем выше добротность, тем больше амплитуда и меньше фазовый сдвиг в контуре при работе в резонансе.

3.2. Электромагнитные затухающие колебания

Электромагнитные затухающие колебания возникают в электромагнитной колебательной систему, называемой LCR – контур (Рисунок 3.3).

Рисунок 3.3.

Дифференциальное уравнение получим с помощью второго закона Кирхгофа для замкнутого LCR – контура: сумма падений напряжения на активном сопротивлении (R) и конденсаторе (С) равна ЭДС индукции, развиваемой в цепи контура:

Падение напряжения:

— на активном сопротивлении: , где I – сила тока в контуре;

— на конденсаторе (С): , где q – величина заряда на одной из обкладок конденсатора.

ЭДС, развиваемая в контуре – это ЭДС индукции, возникающая в катушке индуктивности при изменении тока в ней, а следовательно, и магнитного потока сквозь ее сечение: (закон Фарадея).

Подставим значения U_R, U_C, в уравнение, отражающее закон Кирхгофа, получим:

Сила тока определяется как производная от заряда , тогда , и дифференциальное уравнение примет вид:

Обозначим , , получим в этих обозначениях дифференциальное уравнение затухающих колебаний в виде:

Решение дифференциального уравнения или уравнение колебаний для заряда на обкладках конденсатора имеет вид:

или

Амплитуда затухающих колебаний заряда имеет вид:

, где .

Частота затухающих колебаний в LCR – контуре:

Период затухающих электромагнитных колебаний:

Возьмем уравнение для заряда в виде , тогда уравнение для напряжения на обкладках конденсатора можно записать так .

Величина называется амплитудой напряжения на конденсаторе.

Ток в контуре меняется со временем. Уравнение для силы тока в контуре можно получить, используя соотношение и векторную диаграмму.

Окончательное уравнение для силы тока таково:

где — начальная фаза.

Она не равна α, так как сила тока изменяется не по синусу, что дала бы производная от заряда, а по косинусу.

Энергия колебаний в контуре складывается из энергии электрического поля

и энергии магнитного поля

Полная энергия в любой момент времени:

где W – полная энергия контура в момент времени t=0.

Определение

Физика дает следующее определение добротности. Добротностью называют параметр колебательной системы, который определяет ширину резонанса и характеризует, насколько запасы энергии в системе больше возникающих ее потерь во время изменения фазы на один радиан. Дело в том, что данный показатель определяет разницу вынужденных колебаний при резонансе с определенной амплитудой колебаний на каком-то удалении от места резонанса. При этом амплитуда вынужденных колебаний не имеет никакой зависимости от их частоты. Параметр находит применение не только при расчетах электрических цепей. Его применяют так же в механике, акустике и химии.

Добротность колебательной системы в англоязычных ресурсах называют Quality factor и обозначают буквой «Q». Данная величина является основной характеристикой всех колебательных систем, но сделать измерения данной величины невозможно, ведь ее можно только вычислить, используя различные формулы. Степень идеальности имеет прямое влияние на коэффициент потерь энергии за время одного колебательного периода. Чем меньше величина, тем выше потери самой энергии. Данное значение обратно пропорционально скорости затухания собственных колебаний системы.

Получается, что колебательный контур является разницей между входящим реактивным сопротивлением и выходящим активным. Если в колебательном контуре имеется емкость C, индуктивность L и нагрузка R, то для расчета Q используется формула:

В данной формуле за резонансную частоту электроцепи ω0 отвечает показатель 1/R.

Параметр добротности измеряется при настройке генератора электросигналов на частоту резонансных колебаний. Сама частота резонанса равна максимальному выходному напряжению такой цепи.